암만-베네커 타일링

암만의 비주기적인 A5 타일 세트에 의한 타일의 일부로, 무한하고 전역적인 구조를 강제하는 유한하고 로컬 매칭 규칙으로 장식되어 암만-빈커 타일의 일부입니다.

기하학에서 Ammann-Beenker 타일링은 비주기적 타일링으로 1970년대 Robert Ammann에 의해 수행된 것과 같은 프로토타일의 비주기적 세트 또는 F. P. M. Beenker에 의해 독립적으로 수행된 절단 및 프로젝트 방법에 의해 생성될 수 있습니다. 그것들은 암만에 의해 발견되었고 틸링과 패턴에 기술된 다섯 세트의 타일링 중 하나입니다.^[1]

암만-베네커 타일은 더 유명한 펜로즈 타일과 유사한 많은 특성을 가지고 있습니다.

비주기적이므로 번역 대칭성이 부족합니다.
그들의 비주기성은 계층 구조에 의해 암시됩니다: 타일링은 더 크고 더 큰 패치를 성장시키기 위한 대체 규칙에서 발생하는 대체 타일링입니다. 이 대체 구조는 다음을 의미하기도 합니다.
타일의 유한 영역(패치)은 해당 타일에서 무한히 많이 나타나며, 실제로는 다른 타일에서도 나타납니다. 따라서 유한한 조각만 본다면 무한한 타일링은 모두 서로 비슷하게 보입니다.
그들은 준결정적입니다: 물리적 구조로 구현된 암만-빈커 타일링은 브래그 회절을 생성할 것입니다. 회절도는 기본 8배 대칭과 장거리 순서를 모두 보여줍니다. 이 순서는 틸팅이 번역 대칭이 아니라 때때로 "디플레이션" 또는 "인플레이션"이라고 불리는 과정을 통해 조직화된다는 사실을 반영합니다.
이 모든 무한한 전역 구조는 한 쌍의 타일에 대한 로컬 매칭 규칙을 통해 강제됩니다. 지금까지 발견된 타일 중 가장 간단한 비주기적인 세트인 Ammann's A5 세트입니다.

타일링을 설명하기 위한 다양한 방법이 제안되었습니다: 일치 규칙, 대체, 절단 및 프로젝트 계획 및 피복.^[3]^[4] 1987년 왕, 첸, 쿠오는 팔각대칭성을 가진 준결정체의 발견을 발표했습니다.^[5]

타일 설명

일치하는 규칙으로 장식된 A5 타일의 암만 A와 B 쌍; 이러한 타일에 의한 타일은 반드시 비주기적이므로 타일은 비주기적입니다.

Amman A5 대체 규칙, A5 타일은 비주기적 계층 타일만 형성할 수 있으므로 비주기적 타일임을 증명하는 데 사용됩니다.

그의 쌍 A5에 있는 암만의 A와 B 타일은 45-135도 마름모와 45-45-90도 삼각형으로, 각 영역에서 특정 배열만을 허용하는 일치 규칙으로 장식되어 무한한 수의 개별 암만-빈커 타일 각각의 비주기적, 계층적, 준주기적 구조를 강제합니다.

암만이 발견하고 그 tiles바움(Grünbum)과 셰퍼드(Shephard)에서 암만 4(Ammann 4)라고 이름 붙인 대체 타일 세트는 볼록하지 않은 직각의 두 조각으로 구성되어 있습니다. 하나는 작은 정사각형 위에 겹쳐진 두 개의 정사각형으로 구성되어 있고, 다른 하나는 작은 정사각형 위에 붙어 있는 큰 정사각형으로 구성되어 있습니다. 아래 다이어그램은 조각과 타일의 일부를 보여줍니다.

대체 타일 집합의 대체 규칙입니다.

두 타일 세트 사이의 관계.

일반적인 타일 집합의 가장자리 화살표 외에도 두 타일 집합의 일치 규칙은 큰 화살표 조각을 정점에 그려서 전체 화살표로 조각을 맞추도록 함으로써 표현할 수 있습니다.

Katz는^[6] 정점 제약 조건을 삭제하고 모서리 화살표가 일치하는 요구 사항만 부과함으로써 허용되는 추가 타일링을 연구했습니다. 이 요구 사항은 대체 규칙에 의해 자체적으로 유지되므로, 모든 새 타일은 대체 규칙의 연속적인 적용으로 얻은 "확대된" 복사본의 무한한 시퀀스를 가집니다. 시퀀스의 각 타일은 연속적으로 더 큰 규모의 진정한 Ammann-Beenker 타일과 구별할 수 없습니다. 이러한 타일 중 일부는 주기적이기 때문에 타일의 유한한 부분을 보면 비주기성을 강제하는 타일의 장식을 결정할 수 없습니다. 비주기성을 강제하는 정점 화살표의 방향은 전체 무한 타일로부터만 추론할 수 있습니다.

타일링은 또한 극한적인 특성을 가지고 있습니다. 마름모가 번갈아 나타나는 타일링(즉, 두 마름모가 정사각형 한 줄로 인접하거나 분리될 때마다 서로 다른 방향으로 나타나는) 사이에서 Ammann-Beenker 타일링에서 정사각형의 비율은 최소인 것으로 나타났습니다.^[7]

펠 및 실버 비율 기능

암만-벤커 틸팅은 은 비율( $1+{\sqrt {2}}$ + $1+{\sqrt {2}}$ ${\$ 및 Pell 숫자와 밀접한 관련이 있습니다.

대체 $R\to RrR;r\to R$ R → $R\to RrR;r\to R$ r $;$ r → R {\displaystyle R\to RrR; r\to R} 이 비율을 스케일링 팩터로 도입합니다: 그 매트릭스는 Pell 대체 매트릭스이고, 그리고 치환에 의해 생성된 일련의 단어들은 $r$ ${\display$ r $}$ 와 $r$ R ${\display R}$ 의 $R$ 수가 연속되는 Pell 수와 같다는 특성을 갖습니다.
대체 행렬의 고유값은 $1$ + 2 ${\$ 1 $+{\sqrt {2}}$ 및 $1+{\sqrt {2}}$ $1-{\sqrt {2}}$ - $1-{\sqrt {2}}$ ${\$ 입니다 $1-{\sqrt {2}}$
대체 타일 집합에서 긴 $1+{\sqrt {2}}$ 는 $1+{\sqrt {2}}$ $모서리$ 보다 1 $1+{\sqrt {2}}$ + 2 ${\$ 1 $+{\sqrt {2}}$ 배 $1+{\sqrt {2}}$ 긴 변을 갖습니다.
대퇴골의 짧고 긴 대각선에 의해 형성된 콘웨이 웜의 한 세트는 위의 문자열을 형성하며, r을 짧은 대각선, R을 긴 대각선으로 합니다. 따라서 암만 막대는 Pell 순서 격자도 형성합니다.^[8]

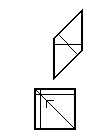암만 바는 일반 타일 세트입니다. 굵은 외부 선의 길이가 $2{\sqrt {2}}$ ${\$ 인 경우 $2{\sqrt {2}}$ 막대는 가장자리를 $1+{\sqrt {2}}$ $1+{\sqrt {2}}$ + 2 ${\$ 및 ${\sqrt {2}}-1$ - ${\sqrt {2}}-1$ ${\sqrt {2}-1$ 의 세그먼트로 분할합니다 ${\sqrt {2}}-1$ 이 타일을 암만 A5 타일이라고 합니다.

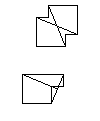암만 바는 대체 타일 세트를 위한 것입니다. 비대칭 타일의 막대는 부분적으로 외부로 확장됩니다. 이 타일을 암만 A4 타일이라고 합니다.

절단 및 프로젝트 시공

테세랙틱 벌집은 테세랙틱의 8배 회전 대칭에 해당하는 8배 회전 대칭을 가지고 있습니다. 이 대칭을 나타내는 회전 행렬은 다음과 같습니다.

A={\begin{bmatrix}0&0&0&-1\\1&0&0&0\\0&-1&0&0\\0&0&-1&0\end{bmatrix}}.

이 행렬을 다음에 의해 주어진 새로운 좌표로 변환하기

B={\begin{bmatrix}-1/2&0&-1/2&{\sqrt {2}}/2\\1/2&{\sqrt {2}}/2&-1/2&0\\-1/2&0&-1/2&-{\sqrt {2}}/2\\-1/2&{\sqrt {2}}/2&1/2&0\end{bmatrix}}

다음을 생성합니다.

BAB^{-1}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\-{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\0&0&-{\sqrt {2}}/2&{\sqrt {2}}/2\\0&0&-{\sqrt {2}}/2&-{\sqrt {2}}/2\end{bmatrix}}.

그러면 이 세 번째 행렬은 45°(처음 두 차원에서) 회전과 135°(마지막 두 차원에서) 회전 모두에 해당합니다. 그런 다음 새로운 좌표 중 처음 두 개 또는 마지막 두 개를 따라 하이퍼큐브의 슬래브를 투영하여 암만-벤커 타일링을 얻을 수 있습니다.

또는 45도 각도로 겹쳐진 동일한 규모의 정사각형 격자 쌍의 교점을 중심으로 마름모와 정사각형을 그려서 Ammann-Beenker 타일링을 얻을 수 있습니다. 이 두 가지 기술은 빈커가 그의 논문에서 개발한 것입니다.

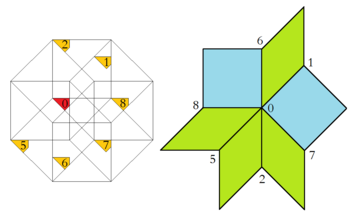
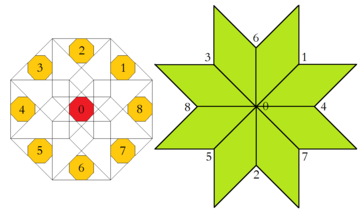
테세랙틱 벌집에 내장된 관련 고차원적인 것은 여기 Baake와 Joseph 논문의 적용에 자세히 나와 있는 Klotz 구조입니다.^[9] 따라서 팔각형 허용 도메인은 부분으로 더 분리될 수 있으며, 각 부분은 정확히 하나의 정점 구성을 생성합니다. 또한 이 두 영역 중 하나의 상대적인 면적은 무한 타일 내에서 해당 정점 구성의 빈도와 동일합니다.

허용 도메인 영역 및 해당 정점 구성

참고문헌 및 참고문헌

^ ^a ^b ^c Grünbaum, B.; Shephard, G. C. (1986). Tilings and Patterns. New York: Freeman. ISBN 0-7167-1193-1.
^ Beenker FPM, 두 개의 단순한 구성 블록에 의한 평면의 비주기적 틸팅에 대한 대수 이론: 정사각형과 마름모, TH Report 82-WSK-04 (1982), Technische Hogeschool, Eindhoven
^ F. Gähler, 제6차 준결정 국제 회의 의사록, S 편집. 타케우치와 T. Fujiwara, World Scientific, Singapore, 1998, p. 95.
^ Ben-Abraham, S. I.; Gähler, F. (1999). "Covering cluster description of octagonal MnSiAl quasicrystals" (PDF). Physical Review B. 60 (2): 860–864. doi:10.1103/PhysRevB.60.860. Archived from the original (PDF) on June 17, 2007.
^ Wang, N.; Chen, H.; Kuo, K. H. (1987). "Two-dimensional quasicrystal with eightfold rotational symmetry" (PDF). Physical Review Letters. 59 (9): 1010–1013. Bibcode:1987PhRvL..59.1010W. doi:10.1103/PhysRevLett.59.1010. PMID 10035936.
^ Katz, A (1995). "Matching rules and quasiperiodicity: the octagonal tilings". In Axel, F.; Gratias, D. (eds.). Beyond quasicrystals. Springer. pp. 141–189. doi:10.1007/978-3-662-03130-8_6. ISBN 978-3-540-59251-8.
^ Bédaride, N.; Fernique, T. (2013). "The Ammann-Beenker Tilings Revisited". In Schmid, S.; Withers, R.; Lifshitz, R. (eds.). Aperiodic Crystals. Springer. pp. 59–65. arXiv:1208.3545v1. doi:10.1007/978-94-007-6431-6_8. ISBN 978-94-007-6430-9. S2CID 8483564.
^ Socolar, J E S (1989). "Simple octagonal and dodecagonal quasicrystals". Physical Review B. 39 (15): 10519–10551. Bibcode:1989PhRvB..3910519S. doi:10.1103/PhysRevB.39.10519. PMID 9947860. MR0998533.
^ Baake, M; Joseph, D (1990). "Ideal and Defective Vertex Configurations in the Planar Octagonal Quasilattice". Physical Review B. 42 (13): 8091–8102. Bibcode:1990PhRvB..42.8091B. doi:10.1103/physrevb.42.8091. PMID 9994979.

외부 링크

[ReferenceA-1] Grünbaum, B.; Shephard, G. C. (1986). Tilings and Patterns. New York: Freeman. ISBN 0-7167-1193-1.

[2] Beenker FPM, 두 개의 단순한 구성 블록에 의한 평면의 비주기적 틸팅에 대한 대수 이론: 정사각형과 마름모, TH Report 82-WSK-04 (1982), Technische Hogeschool, Eindhoven

[3] F. Gähler, 제6차 준결정 국제 회의 의사록, S 편집. 타케우치와 T. Fujiwara, World Scientific, Singapore, 1998, p. 95.

[4] Ben-Abraham, S. I.; Gähler, F. (1999). "Covering cluster description of octagonal MnSiAl quasicrystals" (PDF). Physical Review B. 60 (2): 860–864. doi:10.1103/PhysRevB.60.860. Archived from the original (PDF) on June 17, 2007.

[5] Wang, N.; Chen, H.; Kuo, K. H. (1987). "Two-dimensional quasicrystal with eightfold rotational symmetry" (PDF). Physical Review Letters. 59 (9): 1010–1013. Bibcode:1987PhRvL..59.1010W. doi:10.1103/PhysRevLett.59.1010. PMID 10035936.

[6] Katz, A (1995). "Matching rules and quasiperiodicity: the octagonal tilings". In Axel, F.; Gratias, D. (eds.). Beyond quasicrystals. Springer. pp. 141–189. doi:10.1007/978-3-662-03130-8_6. ISBN 978-3-540-59251-8.

[7] Bédaride, N.; Fernique, T. (2013). "The Ammann-Beenker Tilings Revisited". In Schmid, S.; Withers, R.; Lifshitz, R. (eds.). Aperiodic Crystals. Springer. pp. 59–65. arXiv:1208.3545v1. doi:10.1007/978-94-007-6431-6_8. ISBN 978-94-007-6430-9. S2CID 8483564.

[8] Socolar, J E S (1989). "Simple octagonal and dodecagonal quasicrystals". Physical Review B. 39 (15): 10519–10551. Bibcode:1989PhRvB..3910519S. doi:10.1103/PhysRevB.39.10519. PMID 9947860. MR0998533.

[9] Baake, M; Joseph, D (1990). "Ideal and Defective Vertex Configurations in the Planar Octagonal Quasilattice". Physical Review B. 42 (13): 8091–8102. Bibcode:1990PhRvB..42.8091B. doi:10.1103/physrevb.42.8091. PMID 9994979.

[1]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search