폴리토페 화합물

Polytope compound

다면 화합물은 공통의 중심을 공유하는 여러 다면체로 구성된 형상이다.그것들은 육각형과 같은 다각형 화합물의 3차원 아날로그들이다.

화합물의 바깥쪽 정점들은 그것의 볼록한 선체라고 불리는 볼록한 다면체를 형성하기 위해 연결될 수 있다.화합물은 그것의 볼록한 선체를 방조하는 것이다.

또 다른 볼록한 다면체는 화합물의 모든 구성원에 공통되는 작은 중심 공간에 의해 형성된다.이 다면체는 일련의 용접의 핵심으로 사용될 수 있다.

정규 화합물

일반 다면 화합물은 일반 다면체와 마찬가지로 정점-변환, 가장자리-변환성, 얼굴-변환성이 있는 화합물로 정의할 수 있다.다면체의 경우와는 달리, 이것은 깃발에서 전이적으로 작용하는 대칭군과는 동등하지 않다; 두 개의 사면체의 화합물은 그 성질을 가진 유일한 정규 화합물이다.다면체의 5가지 일반 화합물이 있다.

정규 화합물
(콕시터 기호)		 사진 구면 볼록 선체 공통핵 대칭군 부분군
제한적인
일대일로
구성의		 이중정기화합물
사면체 2개
{4,3}[2{3,3}]{3,4}		 Compound of two tetrahedra.png Spherical compound of two tetrahedra.png 큐브

[1]

팔면체 *432
[4,3]
Oh 		*332
[3,3]
Td 		사면체 2개
5 4면체
{5,3}[5{3,3}]{3,5}		 Compound of five tetrahedra.png Spherical compound of five tetrahedra.png 도데카헤드론

[1]

이코사헤드론

[1]

532
[5,3]+
I 		332
[3,3]+
T 		치랄 쌍둥이
(에반토모르프)
십사면체
2{5,3}[10{3,3}]2{3,5}		 Compound of ten tetrahedra.png Spherical compound of ten tetrahedra.png 도데카헤드론

[1]

이코사헤드론 *532
[5,3]
Ih 		332
[3,3]
T 		십사면체
5 큐브
2{5,3}[5{4,3}]		 Compound of five cubes.png Spherical compound of five cubes.png 도데카헤드론

[1]

롬빅 삼권면체

[1]

*532
[5,3]
Ih 		3*2
[3,3]
Th 		오옥타헤드라
오옥타헤드라
[5{3,4}]2{3,5}		 Compound of five octahedra.png Spherical compound of five octahedra.png 이코시다데카헤드론

[1]

이코사헤드론

[1]

*532
[5,3]
Ih 		3*2
[3,3]
Th 		5 큐브

가장 잘 알려진 것은 케플러에 의해 붙여진 이름인 스텔라 옥탄굴라 불리는 두 개의 4면체의 규칙적인 화합물이다.두 개의 4면체의 정점은 정육면체를 정의하고, 두 개의 교차점은 정육면체를 정의하는데, 이 정육면체는 화합물과 동일한 얼굴 평면을 공유한다.따라서 두 개의 사면체의 화합물은 팔면체의 단층이며, 사실 그 단 하나의 유한한 단층이다.

5개의 4면체의 정규 화합물은 두 개의 반동형 형태로 나타나는데, 이 두 화합물은 모두 10개의 4면체의 정규 화합물을 이룬다.[1]10개의 4면체의 정규 화합물도 5개의 스텔라 옥탄굴레로 건설할 수 있다.[1]

각각의 일반적인 사면 화합물은 치랄 쌍둥이와 자가 이중 또는 이중이다; 5입방과 5옥타헤드라의 정규 화합물은 서로 이중이다.

따라서 일반 다면 화합물은 이중 정규 화합물로도 간주할 수 있다.

일반 화합물에 대한 콕세터의 표기법은 슐레플리 기호를 통합하여 위의 표에 제시되어 있다.대괄호 안의 재료인 [d{p,q}]는 화합물의 성분: d 별개의 {p,q}을(를) 나타낸다.대괄호 앞의 재료는 화합물의 꼭지점 배열을 나타낸다. c{m,n}[d{p,q}]는 {m,n} c의 정점을 공유하는 d {p,q}의 화합물이다.대괄호 뒤에 있는 재료는 화합물의 전면 배열을 나타낸다. [d{p,q}]e{s,t}는 {s,t}의 얼굴을 e회수로 나눈 d {p,q}의 합성물이다.이러한 것들은 결합될 수 있다: 따라서 c{m,n}[d{p,q}]e{s,t}는 {m,n} c의 정점과 {s,t}의 얼굴이 e회 계수된 정점을 공유하는 d {p,q}의 합성어다.이 표기법은 여러 치수의 화합물에 일반화할 수 있다.[2]

이중 화합물

잘린 사면체(빛) 및 삼면체(어두운)
스너브 큐브(빛) 및 오각형 이코사이드론(어두움)
이코시도데카헤드론(빛) 및 롬빅 삼콘타헤드론(어두움)
아르키메데스와 카탈루냐 고체의 이중 화합물

이중 화합물은 다면체와 그 이중으로 구성되며, 하나의 다면체의 가장자리가 이중 다면체의 이중 가장자리와 교차하도록 공통 중간자위에 대해 왕복으로 배열된다.일반 다면체에는 5개의 이중 화합물이 있다.

핵심은 두 고체의 정류다.선체는 이 정류의 이중이며, 그 회전면에는 대각선으로 두 고체의 교차 가장자리가 있다(그리고 그들의 네 가지 정점이 있다).볼록 고형물의 경우 이것이 볼록 선체다.

이중 화합물 사진 선체 코어 대칭군
사면체 2개
(두 개의 사면체, 스테로이드 옥타헤드론 조합) 		Dual compound 4 max.png 큐브 팔면체 *432
[4,3]
Oh
큐브와 팔면체
(입방체와 팔면체의 조합) 		Dual compound 8 max.png 롬빅 도데카헤드론 큐폭타헤드론 *432
[4,3]
Oh
도데카헤드론과 이코사헤드론
(도면체 및 이코사면체 조합) 		Dual compound 20 max.png 롬빅 삼권면체 이코시다데카헤드론 *532
[5,3]
Ih
작은 도마뱀붙이와 큰 도마뱀붙이
(sD와 gD의 조합) 		Skeleton pair Gr12 and dual, size m (crop), thick.png 중합성삼정면체
(콘벡스: 이코사헤드론) 		도데카데카헤드론
(콘벡스: 도데카헤드론) 		*532
[5,3]
Ih
대이코사면체 및 대염기 도데면체
(gI와 gsD의 조합) 		Skeleton pair Gr20 and dual, size s, thick.png 대범삼문자
(콘벡스: 도데카헤드론) 		대이코시다데카헤드론
(콘벡스: 이코사헤드론) 		*532
[5,3]
Ih

사면체는 자가이중이므로 이중으로 된 사면체의 이중 화합물은 정규 사면 팔면체다.

팔면체 및 이코사면체 이중 화합물은 각각 큐옥타면체와 이코시도데카면체의 첫 번째 단면이다.

균일 화합물

주요 기사:균일다면 화합물

1976년 존 스킬링은 회전 대칭이 있는 균일한 폴리헤드라로부터 만들어진 75개의 화합물(무한 프리즘성 화합물 집합으로 6개를 포함, #20-#25)을 열거한 균일한 폴리헤드라의 균일한 화합물을 발표했다. (모든 정점은 정점 변환이고 모든 정점은 다른 모든 정점과 전이된다.)이 목록은 위의 5가지 일반 화합물을 포함한다.[1]

75개의 균일한 화합물은 아래 표에 열거되어 있다.대부분은 각 다면체 원소에 의해 특이하게 색칠되어 나타난다.얼굴 그룹의 일부 치랄 쌍은 각 다면체 내의 얼굴 대칭에 의해 색칠된다.

  • 1-19: 잡종 (4,5,6,9,17은 5개의 정규 화합물)
UC01-6 tetrahedra.png UC02-12 tetrahedra.png UC03-6 tetrahedra.png UC04-2 tetrahedra.png UC05-5 tetrahedra.png UC06-10 tetrahedra.png
UC07-6 cubes.png UC08-3 cubes.png UC09-5 cubes.png UC10-4 octahedra.png UC11-8 octahedra.png UC12-4 octahedra.png
UC13-20 octahedra.png UC14-20 octahedra.png UC15-10 octahedra.png UC16-10 octahedra.png UC17-5 octahedra.png UC18-5 tetrahemihexahedron.png
UC19-20 tetrahemihexahedron.png
UC20-2k n-m-gonal prisms.png UC21-k n-m-gonal prisms.png UC22-2k n-m-gonal antiprisms.png UC23-k n-m-gonal antiprisms.png UC24-2k n-m-gonal antiprisms.png UC25-k n-m-gonal antiprisms.png
UC26-12 pentagonal antiprisms.png UC27-6 pentagonal antiprisms.png UC28-12 pentagrammic crossed antiprisms.png UC29-6 pentagrammic crossed antiprisms.png UC30-4 triangular prisms.png UC31-8 triangular prisms.png
UC32-10 triangular prisms.png UC33-20 triangular prisms.png UC34-6 pentagonal prisms.png UC35-12 pentagonal prisms.png UC36-6 pentagrammic prisms.png UC37-12 pentagrammic prisms.png
UC38-4 hexagonal prisms.png UC39-10 hexagonal prisms.png UC40-6 decagonal prisms.png UC41-6 decagrammic prisms.png UC42-3 square antiprisms.png UC43-6 square antiprisms.png
UC44-6 pentagrammic antiprisms.png UC45-12 pentagrammic antiprisms.png
  • 46-67: 팔면 대칭 또는 이면 대칭에 포함된 사면 대칭,
UC46-2 icosahedra.png UC47-5 icosahedra.png UC48-2 great dodecahedra.png UC49-5 great dodecahedra.png UC50-2 small stellated dodecahedra.png UC51-5 small stellated dodecahedra.png
UC52-2 great icosahedra.png UC53-5 great icosahedra.png UC54-2 truncated tetrahedra.png UC55-5 truncated tetrahedra.png UC56-10 truncated tetrahedra.png UC57-5 truncated cubes.png
UC58-5 quasitruncated hexahedra.png UC59-5 cuboctahedra.png UC60-5 cubohemioctahedra.png UC61-5 octahemioctahedra.png UC62-5 rhombicuboctahedra.png UC63-5 small rhombihexahedra.png
UC64-5 small cubicuboctahedra.png UC65-5 great cubicuboctahedra.png UC66-5 great rhombihexahedra.png UC67-5 great rhombicuboctahedra.png
UC68-2 snub cubes.png UC69-2 snub dodecahedra.png UC70-2 great snub icosidodecahedra.png UC71-2 great inverted snub icosidodecahedra.png UC72-2 great retrosnub icosidodecahedra.png UC73-2 snub dodecadodecahedra.png
UC74-2 inverted snub dodecadodecahedra.png UC75-2 snub icosidodecadodecahedra.png

기타 화합물

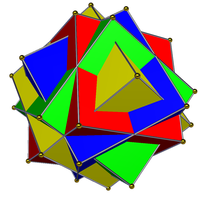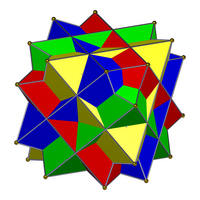Compound of 4 cubes.png Compound of 4 octahedra.png
네 개의 정사각형(왼쪽)의 화합물은 일반 화합물도 아니고, 이중 화합물도 아니며, 균일한 화합물도 아니다.그것의 이중, 4옥타헤드라의 화합물(오른쪽)은 균일한 화합물이다.

화합물이지만 제자리에 단단히 고정된 두 개의 다면체는 작은 복합 이코시다면체(이코사면체와 큰 도데면체)와 큰 복합 이코사면체(작은 스티로이드 도데면체와 큰 이코사면체)이다.균일한 다면체의 정의가 일반화되면 균일하다.

스킬링 목록에서 에반토모르프 쌍에 대한 섹션은 펜타그램 면이 일치하므로 두 개의 위대한 스눕 도데시코디도데카헤드라의 혼합물을 포함하지 않는다.일치된 면을 제거하면 20옥타헤드라의 화합물이 된다.

4차원 화합물

직교 투영
Regular compound 75 tesseracts.png Regular compound 75 16-cells.png
75 {4,3,3} 75 {3,3,4}

4차원에서는 일반 폴리토페스의 일반 화합물이 많이 있다.콕시터는 이것들 중 몇 가지를 그의 책 "일반적인 폴리토페스"에 열거했다.[3]맥뮬런은 자신의 논문 4폴리토페스의 새로운 일반 화합물 6개를 추가했다.[4]

자체 이중화:

화합물 구성 요소 대칭
5시 120분 5세포 [5,3,3], 14400개[3] 주문
5시(var) 120분 5세포 1200을[4] 주문하다
5층 720번지 5세포 [5,3,3], 14400개[3] 주문
24로5길 24셀 [5,3,3], 14400개[3] 주문

이중 쌍:

화합물 1 화합물 2 대칭
16강로3길[5] 큐브 3개 [3,4,3], 1152번[3] 주문
16로15번길 15 큐테렌트 [5,3,3], 14400개[3] 주문
16로75번길 75 큐세렌트 [5,3,3], 14400개[3] 주문
16로75번길(var) 75 큐세렌트(var) 600개를[4] 주문하다
30016로16번길 3백 테세렌트 [5,3,3],+ 7200개[3] 주문
16로600번길 육백 테세렌트 [5,3,3], 14400개[3] 주문
24로25번길 24로25번길 [5,3,3], 14400개[3] 주문

볼록한 4폴리탑이 있는 균일한 화합물 및 듀얼:

화합물 1
정점 변환 		화합물 2
세포전환 		대칭
16-182로[6] 2 2 큐세렌트 [4,3,3] 주문 384[3]
24로100번길 24로100번길 [5,3,3],+ 7200개[3] 주문
24로200번길 24로200번길 [5,3,3], 14400개[3] 주문
600로560번길 120평로520번길 [5,3,3],+ 7200개[3] 주문
600로10길 120로10길 [5,3,3], 14400개[3] 주문
24로25번길(var) 24로25번길(var) 600개를[4] 주문하다

위 표의 위첨자(var)는 라벨로 표시된 화합물이 동일한 수의 성분을 가진 다른 화합물과 구별됨을 나타낸다.

일반 항성 4폴리탑이 있는 화합물

자체 이중 항성 화합물:

화합물 대칭
5 {5,5/2,5} [5,3,3],+ 7200개[3] 주문
10 {5,5/2,5} [5,3,3], 14400개[3] 주문
5 {5/2,5,5/2} [5,3,3],+ 7200개[3] 주문
10 {5/2,5,5/2} [5,3,3], 14400개[3] 주문

복합 별의 이중 쌍:

화합물 1 화합물 2 대칭
5 {3,5,5/2} 5 {5/2,5,3} [5,3,3],+ 7200개 주문
10 {3,5,5/2} 10 {5/2,5,3} [5,3,3], 14400개 주문
5 {5,5/2,3} 5 {3,5/2,5} [5,3,3],+ 7200개 주문
10 {5,5/2,3} 10 {3,5/2,5} [5,3,3], 14400개 주문
5 {5/2,3,5} 5 {5,3,5/2} [5,3,3],+ 7200개 주문
10 {5/2,3,5} 10 {5,3,5/2} [5,3,3], 14400개 주문

균일한 복합 별 및 듀얼:

화합물 1
정점 변환 		화합물 2
세포전환 		대칭
5 {3,3,5/2} 5 {5/2,3,3} [5,3,3],+ 7200개 주문
10 {3,3,5/2} 10 {5/2,3,3} [5,3,3], 14400개 주문

듀얼이 있는 화합물

이중 위치:

화합물 구성 요소 대칭
2 5셀 5세포 [[3,3,3]], 주문 240
2 24셀 24셀 [3,4,3], 2304 주문
큐빅 1개, 16셀 1개 테세락트, 16셀
120 셀 1개, 600 셀 1개 120 셀, 600 셀
훌륭한 120 셀 2 대단한 120셀
그랜드스텔 120 셀 2대 장대형 120셀
이코사이드 120 셀 1개, 소형 스텔링 120 셀 1개 이코사이드 120셀, 작은 스티어 120셀
그랜드 120 셀 1개, 대단한 스텔링 120 셀 1개 웅장한 120셀, 대단한 기장을 한 120셀
웅장한 120셀, 거대한 동면체 120셀 1개. 웅장하고 웅장한 120셀, 거대한 이두상 120셀
120셀에 600셀에 1개의 그랜드 스텔링된 1개의 그랜드 셀 대천연감 120셀, 대천연백셀

집단 이론

집단 이론에 따르면, G가 다면화합물의 대칭군이고, 그 집단이 다면화합물에 대해 전이적으로 작용하는 경우(즉, 균일한 화합물에서와 같이 각 다면화합물은 다른 어떤 것으로도 보내질 수 있다), H가 단일 선택된 다면체의 스태빌라이저라면, 다면화합물은 궤도 공간 G/H – 코제트 GH 코제트 GH 코레로 식별할 수 있다.다면체 g가 선택된 다면체를 보내는 연못

틸팅 화합물

유클리드 평면의 정규 복합 테셀레이션의 2-모수 계열이 18개 있다.쌍곡면에서는 5개의 1-모수 패밀리와 17개의 고립된 사례가 알려져 있지만, 이 목록의 완전성은 열거되지 않았다.

유클리드 및 쌍곡성 화합물 패밀리 2 {p,p} (4 ≤ p ≤ ∞, p 정수)는 구형 스텔라 옥탄굴라, 2 {3,3}과 유사하다.

유클리드 및 쌍곡성 정규화합물의 몇 가지 예
셀프듀얼 듀얼스 셀프듀얼
2 {4,4} 2 {6,3} 2 {3,6} 2 {∞,∞}
Kah 4 4.png Compound 2 hexagonal tilings.png Compound 2 triangular tilings.png Infinite-order apeirogonal tiling and dual.png
3 {6,3} 3 {3,6} 3 {∞,∞}
Compound 3 hexagonal tilings.png Compound 3 triangular tilings.png Iii symmetry 000.png

5개 이상의 차원으로 구성된 일반 유클리드 화합물 꿀콤의 알려진 집단은 다른 하이퍼큐빅 벌컴과 정점과 얼굴을 공유하는 하이퍼큐빅 벌컴의 무한한 화합물이다.이 화합물에는 고농축 꿀콤이 얼마든지 있을 수 있다.

이중 정규 타일링 화합물도 있다.간단한 예로 육각형 타일링의 E2 화합물과 삼각형 타일링이 있는데, 이 타일링의 가장자리를 델토이탈 삼각형 타일링과 나눈다.두 개의 고농축 허니컴의 유클리드 화합물은 둘 다 규칙적이고 이중 규칙적이다.

각주

  1. ^ a b c d e f g h i j "Compound Polyhedra". www.georgehart.com. Retrieved 2020-09-03.
  2. ^ Coxeter, Harold Scott MacDonald (1973) [1948]. Regular Polytopes (Third ed.). Dover Publications. p. 48. ISBN 0-486-61480-8. OCLC 798003.
  3. ^ a b c d e f g h i j k l m n o p q r s 일반 다상체, 표 7, 페이지 305
  4. ^ a b c d McMullen, Peter (2018), 4-Polytopes의 새로운 일반 화합물, 직관 기하학의 새로운 경향, 27: 307–320
  5. ^ Klitzing, Richard. "Uniform compound stellated icositetrachoron".
  6. ^ Klitzing, Richard. "Uniform compound demidistesseract".

외부 링크

참조

  • Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554.
  • Cromwell, Peter R. (1997), Polyhedra, Cambridge.
  • Wenninger, Magnus (1983), Dual Models, Cambridge, England: Cambridge University Press, pp. 51–53.
  • Harman, Michael G. (1974), Polyhedral Compounds, unpublished manuscript.
  • Hess, Edmund (1876), "Zugleich Gleicheckigen und Gleichflächigen Polyeder", Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg, 11: 5–97.
  • Pacioli, Luca (1509), De Divina Proportione.
  • 일반 폴리토페스(3판, 1973), 도버판, ISBN 0-486-61480-8
  • Anthony Pugh (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7. p. 87 5개의 정규 화합물
  • McMullen, Peter (2018), "New Regular Compounds of 4-Polytopes", New Trends in Intuitive Geometry, 27: 307–320, doi:10.1007/978-3-662-57413-3_12.