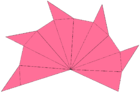
대이코사면체
Great icosahedron기하학에서 대 아이코사헤드론은 4개의 케플러-푸인소트 폴리헤드라(비콘벡스 정규 폴리헤드라) 중 하나로 슐래플리 기호가 {3,5⁄2}, 콕시터-딘킨 도표가 있으며 20개의 교차 삼각형 면으로 구성되어 있으며, 각 정점에서 5개의 삼각형이 5개씩 오각형으로 만나 있다.
거대한 이코사헤드론은 그림이 정규면을 되찾을 때까지 코어 nD 폴리토프(대 이코사헤드론의 등방 삼각형, 펜타그램의 선분할)의 (n-1)-D 심플렉스 면의 확장을 통해 그것의 2차원 아날로그인 펜타그램과 유사하게 구성될 수 있다. 그랜드 600 셀은 같은 과정을 사용하는 4차원 아날로그로 볼 수 있다.
이미지들
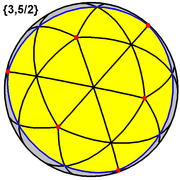 이 다면체는 7의 밀도를 가진 구면 타일링을 나타낸다. (하나의 구면 삼각형 면은 위에 표시되며, 파란색 윤곽은 파란색으로, 노란색은 노란색으로 채워짐) |
얼간이로서
대 이코사면체는 다른 색깔의 얼굴들과 오직 사면 대칭만을 가진 균일한 스너브를 만들 수 있다. 이 구조는 잘린 팔면체의 부분적인 면으로서 이면체의 스너브 사면체 대칭과 유사하게 [1]역면체 사면체 또는 역면체 사면체라고 불릴 수 있다. 또한, 또는 , 로서 두 가지 색의 삼각형과 화리토헤드 대칭으로 구성될 수 있으며, 역행형 옥타헤드론이라고 불린다.
관련 다면체
정점 배열을 일반 볼록한 이코사면체와 동일하다. 그것은 또한 작은 나선형 도데카헤드론과 같은 가장자리 배열도 공유한다.
큰 고드름에 반복적으로 적용되는 잘림 수술은 일련의 균일한 다면체를 생성한다. 가장자리를 포인트까지 잘라내면 큰 이코사헤드론은 바로잡을 수 있는 큰 이코사헤드론으로서 생성된다. 이 과정은 양방향으로 완료되어 원래의 얼굴을 포인트로 축소하고, 큰 구멍이 뚫린 도데면체를 생산한다.
잘린 큰치마돌은 퇴행성 다면체로, 잘린 정점으로부터 20개의 삼각형 면과 12개의 (숨긴) 오각형 면({10/2})을 원래의 오각형 면의 잘라낸 것으로서 두 개의 큰 도데카헤드라를 형성하고 이두면체의 가장자리를 공유한다.
| 이름 | 대단하다 찌든 도데면체 | 잘린 대절개 도데카헤드론 | 대단하다 이코시다데카헤드론 | 잘림 대단해, 이코사헤드론 | 대단하다 이코사헤드론 |
|---|---|---|---|---|---|
| 콕시터딘킨 도표를 만들다 | |||||
| 사진 |  |  |  |  |  |
참조
- ^ Klitzing, Richard. "uniform polyhedra Great icosahedron".
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3. MR 0676126. (제1회 Edn University of Toronto (1938년)
- H.S.M. Coxeter, 일반 폴리토페스, (3판, 1973년), 도버판, ISBN 0-486-61480-8, 3.6 6.2 플라토닉 고형물 스텔링, 페이지 96–104
외부 링크
| 이코사면체의 눈에 띄는 흔적 | |||||||||
| 정규 | 균일 듀얼 | 정규 화합물 | 항성 | 다른이들 | |||||
| (콘벡스) 이코사면체 | 작은삼각형 이코사면체 | 중삼면체 | 대삼면체 | 5옥타헤드라 화합물 | 5개의 사면체 화합물 | 사면체 10개 화합물 | 대이코사면체 | 발굴된 도데면체 | 파이널 스텔레이션 |
|---|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  | |
 |  |  |  |  |  |  |  |  | |
| 이코사헤드론에서의 스텔레이션 과정은 많은 관련 다면체와 이코사면 대칭을 가진 화합물을 생성한다. | |||||||||