항정신병 프리즘 화합물

n p/q-gonal 항정신병 복합체
n=2 5/3-곤 5/2-곤
유형	균일 화합물
색인	q 홀수: UC23 q 짝수: UC25
폴리헤드라	n p/q-gonal 반격
슐레플리 기호 (n=2)	ß{2,2p/q} ßr{2,p/q}
콕시터 도표 (n=2)
얼굴	2n {p/q}(p/q=2 제외), 2np 삼각형
가장자리	4np
정점	2np
대칭군	nq 홀수: np-폴드 항균(Dnpd) nq 짝수: np-폴드 프리즘(Dnph)
하나의 구성 요소로 제한되는 부분군	q 홀수: p-폴드 항균(Dpd) q 짝수: p-폴드 프리즘(Dph)

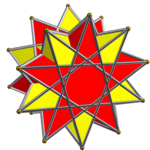
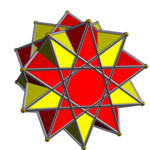
기하학에서 항정신병 프리즘 화합물은 균일한 다면 화합물의 범주다.이 균일한 다면 화합물의 무한 계열의 각 구성원은 회전 대칭의 공통 축을 공유하는 항정신병들의 대칭 배열이다.

무한가족

이 무한가족은 다음과 같이 열거할 수 있다.

• 각 양의 정수 n³1과 각 합리적인 수 p/q>3/2에 대해(p와 qcoprime로 표현) 대칭 그룹을 갖는 np/q-gonal 항정신병 화합물이 발생한다.
  • d_npd nq가 홀수인 경우
  • d_nph nq가 짝수인 경우

p/q=2에서 구성요소는 사면체(또는 이차 항정신병)이다.이 경우 n=2일 경우 화합물은 대칭(O_h)이 높은 스텔라 옥탄굴라다.

두 개의 반항의 화합물

두 개의 n-antiprism의 화합물은 2n-prism과 정점을 공유하며, 두 개의 정점 집합으로 존재한다.

n-곤 기반과 이등변 삼각망이 있는 항정신병 정점에 대한 데카르트 좌표는 다음과 같다.

• ${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n},(-1)^{k}h\right)}}$
• ${\displaystyle \left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n},(-1)^{k+1}h\right)}}$

0에서 2n-1까지의 범위로 삼각형이 정삼각형이면

${\displaystyle 2h^{2}=\cos {\frac {\pi }{n}-\cos {\frac {2\pi }{n}}.}$

2개 항정신병 화합물

디지널란티프리스 2개 (tetrahedra)	삼각형 2개 (옥타헤드라)	정사각형 2개	육각방체 2개	2 펜타그램 십자수

두 개의 사다리꼴(이중)의 화합물

항정신병 프리즘 화합물의 이중은 사다리꼴의 화합물이다.

큐브 2개 (트리거 사다리꼴 헤드라)

세 개의 반격의 화합물

3개의 디지온 항정신병 화합물의 경우 60도 회전하고, 3개의 삼각 항정신병은 40도 회전한다.

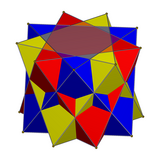사면체 3개	삼팔면체

참조

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.