데카곤
Decagon| 정십각형 | |
|---|---|
 정십각형 | |
| 유형 | 정다각형 |
| 모서리 및 꼭짓점 | 10 |
| 슐레플리 기호 | {10}, t{5} |
| 콕서터-딩킨 도표 | |
| 대칭군 | 이면체 (D10), 주문 2x10 |
| 내각(도) | 144° |
| 특성. | 볼록, 순환, 등변, 등변, 등변 |
| 이중다각형 | 자신 |
십각형(十角形, )은 기하학에서 십각형(十角形) 또는 십각형(十角形)인 δέκα 데카와 γωνία 고니아에서 따온 것입니다.단순한 십각형의 내각의 합은 1440°입니다.
정십각형
일반적인 십각형은 모든 변의 길이가 같고 각 내각은 항상 144°[1]입니다.슐레플리 기호는 {10}이며 두 가지 유형의 가장자리를 번갈아 사용하는 준정형 십각형인 잘린 오각형 t{5}로도 구성할 수 있습니다.
변길이
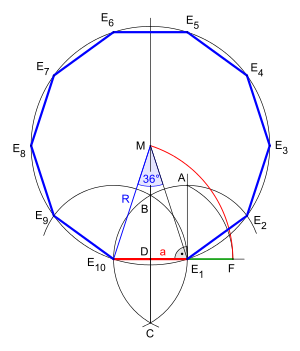
그림은 측면 가 이고 외접원의 반지름이 인 일반 십각형을 보여줍니다.
- 삼각형 에는 가 R 인 두 개의 똑같이 긴 다리와 가 인 밑면이 있습니다.
- 이 인 주위의 원이 a} 점그림에서 지정되지 않음)에서
- 이제 삼각형 P 는 꼭짓점 E 이 이고 밑각이 m인 이등변 삼각형입니다. ∠ 1 P = m ∠ = ∘{\ = 입니다
- 따라서 ∠ = ∘ - ⋅ ∘ = ∘ } =}= 36∠ 1 P= ∘ - ∘ }P=^{\이므로 1 도 꼭짓점 가 인 이등변 삼각형입니다.다리 길이가 이므로 의 는 R -a 입니다
- 이등변삼각형 E 과 은(는) 꼭지점에서 36°의 각도가 같으므로 유사합니다. a = - }}={\
- 분모 > 과의 곱셈은 2차 방정식으로 이어집니다: = - }=
- 의 길이 a에 대한 이 방정식에는 a= ( - +5 ){\ = {\이(가) 있습니다.
그래서 규칙적인 십각형은 자와 나침반으로 만들 수 있습니다.
- 추가결론
2 - = (+ 1) ={\}}={\ 1 즉 [ D 은 R - / ) 2 h {\}} {\이며 삼각형의 넓이는 다음과 같습니다. = a + } = {\ = {\
지역
변의 길이 a인 정십각형의 넓이는 다음과 같습니다.[3]
아포테머(내접 그림 참조)의 관점에서 면적은 다음과 같습니다.
원반지름 R로 환산하면 넓이는 다음과 같습니다.
대안적인 은A = . da{\ A =2이며, d는 평행변 사이의 거리 또는 데카곤이 한 면에 베이스로 서 있을 때의 높이 또는 데카곤의 내접원의 직경입니다.단순 삼각법으로
대수적으로 다음과 같이 쓸 수 있습니다.
사이드스
일반적인 십각형은 10개의 면을 가지고 있고 등변형입니다.35개의 대각선을 가지고 있습니다.
시공
페르마 소수점의 2배의 힘인 10 = 2 × 5와 같이, 정십각형은 나침반과 직선을 이용하거나 정십각형의 가장자리 이등분으로 구성할 수 있습니다.
대안적인(비슷한) 방법은 다음과 같습니다.
- 오각형을 만드는 방법 중 하나로 원 안에 오각형을 만듭니다.
- 오각형의 각 꼭짓점에서 원의 중심을 지나 같은 원의 반대쪽으로 선을 연장합니다.각 선이 원을 자르는 곳은 십각형의 꼭짓점입니다.다시 말해, 한 점의 반사 아래에 있는 정오각형의 상은 동심 합동 오각형이고, 두 오각형은 모두 동심 정오각형의 꼭짓점을 가지고 있습니다.
- 오각형의 다섯 모서리는 십각형의 교대 모서리를 구성합니다.이 점들을 인접한 새 점에 결합하여 데카곤을 형성합니다.
비볼록 정십각형
황금 삼각형의 두 등변의 길이 비율은 황금 비율이며, φ 또는그 곱셈 역으로 표시됩니다.
데카곤의 황금 비율
지정된 원형뿐만[5] 아니라 지정된 측면 길이를 갖는 건축물 모두에서 선분을 외부 분할로 나누는 황금 비율이 결정적인 건축 요소입니다.
- 주어진 외둘레를 가진 구조에서 반지름 GE를3 가진 G 주위의 원호는 황금 비율에 해당하는 세그먼트 AH를 생성합니다.
대칭성

정십각형은 Dih10 대칭이고 순서는 20입니다.부분군 이면체 대칭은 세 가지입니다.Dih5, Dih2, Dih1 및 4개의 순환군5 대칭: Z10, Z, Z2 및 Z1.
이 8개의 대칭은 십각형에서 10개의 서로 다른 대칭으로 볼 수 있는데, 반사선이 꼭짓점이나 모서리를 통과할 수 있기 때문에 더 큰 숫자입니다.존 콘웨이는 이것들을 편지와 그룹 순서로 분류합니다.[7]정칙형의 완전한 대칭은 r20이고 어떤 대칭도 a1로 표시되지 않습니다.다면체 대칭은 꼭짓점(대각선의 경우 d) 또는 모서리(직각선의 경우 p)를 통과하는지, 반사선이 양쪽 모서리와 꼭짓점을 통과할 때 i에 따라 나뉩니다.가운데 열의 순환 대칭은 중심 회전 순서에 대해 g로 표시됩니다.
각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용합니다.g10 부분군만 자유도가 없지만 방향이 지정된 가장자리로 볼 수 있습니다.
가장 높은 대칭 불규칙 데카곤은 긴 가장자리와 짧은 가장자리를 번갈아 사용할 수 있는 5개의 거울로 구성된 등각 데카곤인 d10과 등각 데카곤인 p10입니다.이 두 형태는 서로의 쌍대칭이며 정십각형의 대칭 순서의 절반을 갖습니다.
해부학
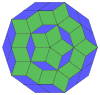
| 10큐브 프로젝션 | 마름모꼴 40개 | |||
|---|---|---|---|---|
 |  |  |  |  |
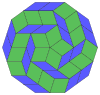 | 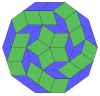 |  |  |  |
콕서터는 모든 조노곤(대변이 평행하고 길이가 같은 2m-곤)을 m(m-1)/2 평행도그램으로 분해할 수 있다고 말합니다.[8]특히 변이 균등하게 많은 일반 다각형의 경우에 해당되며, 이 경우 평행도형은 모두 마름모꼴입니다.정십각형의 경우 m=5이며, 아래의 예를 들어 10개의 홈으로 나눌 수 있습니다.이 분해는 5-큐브의 페트리 다각형 투영 평면에서 80개의 면 중 10개로 볼 수 있습니다.해부는 마름모꼴 삼각뿔의 30개 면 중 10개를 기준으로 합니다.목록 OEIS: A006245는 첫 번째 대칭 형태에 대해 2개의 방향이 있고 나머지 6개에 대해 10개의 방향이 있는 62개의 해로 정의합니다.
 5큐브 | 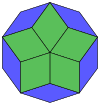 |  | 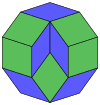 |
 |  |  |  |
꼬챙이 십각형
| {5}#{ } | {5/2}#{ } | {5/3}#{ } |
|---|---|---|
 |  |  |
| 일반적인 스큐 데카곤은 오각형 반프리즘, 오각형 반프리즘, 오각형 교차 안티프리즘의 지그재그 가장자리로 보여집니다. | ||
스큐 데카곤(skew decagon)은 꼭짓점과 모서리가 10개이지만 같은 평면에 존재하지 않는 스큐 다각형입니다.이러한 십각형의 내부는 일반적으로 정의되지 않습니다.스큐 지그재그 데카곤은 두 평행 평면 사이에서 번갈아 가며 꼭짓점을 갖습니다.
일반적인 스큐 십각형은 모서리 길이가 동일한 꼭짓점 전이형입니다.3차원에서 그것은 지그재그 스큐 데카곤이 될 것이고 동일한 D5d, [2+,10] 대칭을 갖는 오각형 반프리즘, 오각형 반프리즘, 오각형 교차 반프리즘의 꼭짓점과 측면 가장자리에서 볼 수 있습니다.
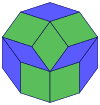
이들은 정이십면체 대칭을 갖는 볼록 다면체 4개에서도 볼 수 있습니다.이 돌출부의 둘레에 있는 다각형은 일반적인 스큐 데카곤입니다.
 십이면체 |  정이십면체 |  정이십면체 | 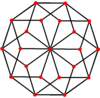 마름모삼면체 |
페트리폴리곤
일반적인 스큐 데카곤은 다양한 콕서터 평면의 직교 투영에서 나타나는 많은 고차원 다포체에 대한 페트리 다각형입니다.[9]페트리 다각형의 변의 수는 각 대칭 패밀리에 대한 콕서터 수 h와 같습니다.
| A9 | 라6 | 나5 | ||
|---|---|---|---|---|
 9- simplex | 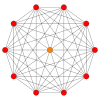 411 |  131 |  5오트홀플렉스 |  5큐브 |
참고 항목
참고문헌
- ^ a b Sidebotham, Thomas H. (2003), The A to Z of Mathematics: A Basic Guide, John Wiley & Sons, p. 146, ISBN 9780471461630.
- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 9, ISBN 9780521098595.
- ^ The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59The elements of plane and spherical trigonometry, Society for Promoting Christian Knowledge, 1850, p. 59이 자료는 a를 모서리 길이로 사용하고 공접합의 인수를 라디안이 아닌 도 단위의 각도로 제공합니다.
- ^ Ludlow, Henry H. (1904), Geometric Construction of the Regular Decagon and Pentagon Inscribed in a Circle, The Open Court Publishing Co..
- ^ a b Green, Henry (1861), Euclid's Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II, London: Simpkin, Marshall,& CO., p. 1162016년 2월 10일 Green, Henry (1861), Euclid's Plane Geometry, Books III–VI, Practically Applied, or Gradations in Euclid, Part II, London: Simpkin, Marshall,& CO., p. 116회수.
- ^ a b Köller, Jürgen (2005), Regelmäßiges Zehneck, → 3. Section "Formeln, Ist die Seite a gegeben ..." (in German)2016년 2월 10일 Köller, Jürgen (2005), Regelmäßiges Zehneck, → 3. Section "Formeln, Ist die Seite a gegeben ..." (in German)회수.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) 사물의 대칭, ISBN 978-1-56881-220-5 (20장, 일반화된 Schaefli 기호, 다각형의 대칭 유형 pp. 275-278)
- ^ Coxeter, 수학 레크리에이션과 에세이, 13판, p.141
- ^ Coxeter, 일반 폴리토프, 12.4 Petrie Polygon, pp. 223-226
외부 링크
- Weisstein, Eric W. "Decagon". MathWorld.
- 대화형 애니메이션을 사용한 데카곤의 정의 및 속성

 반지름이
반지름이 


![{\displaystyle ]M\,E_{10}[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bcf4736cf5ac35905ffbc33204c4731761aeea8)
![{\displaystyle [P\,E_{10}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23903f75c2d0e1f1043f909cf590df64f41c5a65)















