정규지도(그래프 이론)

육각형 호소헤드론( hex hexagonalagonal)은 정점 2개, 가장자리 6개, 면 6개, 국기 24개가 있는 구상의 일반 지도다.

16면, 32 꼭지점, 48 가장자리가 있는 토러스 상의 일반 지도 {6,3}_4,0

수학에서 정규 지도는 닫힌 표면을 대칭적으로 다듬은 것이다.더 정확히 말하면, 일반 지도는 2차원 다지관(구, 토러스 또는 실제 투영면 등)을 위상학적 원반으로 분해하여 모든 국기(사건 정점-끝면 3중)가 분해의 대칭에 의해 다른 국기로 변형될 수 있도록 하는 것이다.일반 지도는 어떤 의미에서 플라토닉 고형물의 위상학적 일반화다.지도 이론과 그 분류는 리만 표면, 쌍곡 기하학, 갈루아 이론과 관련이 있다.일반 지도는 지지 표면의 속과 방향성, 기초 그래프, 또는 자동모형 그룹 중 하나에 따라 분류된다.

개요

일반 지도는 전형적으로 세 가지 방법으로 정의되고 연구된다: 토폴로지, 집단지리학, 그래프지리학.

위상학적 접근법

지형학적으로 지도는 폐쇄형 콤팩트 2-매니폴드의 2-셀 분해다.

지도 M의 속 g는 오일러의 관계 $\chi (M)=|V|-|E|+|F|$ ( M $\chi (M)=|V|-|E|+|F|$ ) $\chi (M)=|V|-|E|+|F|$ = $\chi (M)=|V|-|E|+|F|$ - $\chi (M)=|V|-|E|+|F|$ + F $displaystyle \chi (M)$ = V - E + F $}$ 에 의해 주어지는데, 지도 $\chi (M)=|V|-|E|+|F|$ 방향이 맞지 않으면 $2-2g$ $2-2g$ - $2-g$ $2-2g$ ${\displaystyle 2-2g},$ 방향성이 맞지 않으면 $2-g$ $2-g$ - ${\displaystystyle 2-g}$ 과 같다.토러스(torus)를 제외한 모든 오리엔테이블 속(non-zero)에 대해 유한(비-zero)의 정규 지도가 존재한다는 것은 결정적인 사실이다.

집단이론적 접근법

그룹 이론적으로 정규 지도 M의 순열 표현은 고정 지점의 자유 비자발성 3개₀, r₁, r₂, r 만족(r₀₂)=² I에 의해 생성된 플래그 $\오메가$ 중 $\Omega$ $\Oomega }$ 에 있는 전이 순열 그룹 C이다.이 정의에서 면은 F = <r₀, r₁>의 궤도, 가장자리는 E = <r₀, r>의 궤도, 꼭지점은 V = <r₁, r₂₂>의 궤도다.보다 추상적으로 말하면, 어떤 정규지도의 오토모피즘 집단은 <2,m,n>-삼각형의 비감소 동형상이다.

그래프이론적 접근법

그래프 이론적으로, 지도는 파란색, 노란색, 빨간색 가장자리가 있는 $\Gamma$ 입방 그래프 $\Gamma$ 이다. $\Gamma$ $\Gamma$ 이 $\감마$ (가) 연결되고, 모든 꼭지점이 각 색의 한쪽 가장자리와 충돌하며, 노란색이 아닌 가장자리의 주기는 길이가 4이다. $\Gamma$ $\Gamma$ 은(는) 맵의 플래그 그래프 또는 그래프 인코딩 맵(GEM)이며 $\Gamma$ , 플래그 $\Omega$ $\Oomega}$ 의 꼭지점에 정의되어 있으며 $\Omega$ 맵의 골격 G = (V,E)가 아니라는 점에 유의하십시오.일반적으로 Ω $\Oomega$ $\Omega$ = 4E .

지도 M은 자동(M)이 깃발에 정기적으로 작용하는 경우 일반이다.정규지도의 Aut(M)은 M의 꼭지점, 가장자리, 면면에서 transitive. 지도 M은 if aut(M)이 정규이고 자동형 $\phi$ ${\displaystyle \phi$ }을 $\phi$ 포함하고 있어 정점 v와 면 f를 모두 고정하지만 가장자리의 순서를 역전시킨다고 한다.규칙적이지만 반사되지 않는 지도는 치랄이라고 한다.

예

정기적인 지도인 헤미큐브.

대두면체(大頭面體)는 제4종의 방향성 표면에 오각형의 얼굴이 있는 일반 지도다.
헤미큐브는 투사 평면에 있는 유형 {4,3}의 정규 지도다.
헤미도면체(hemi-dodeheadron)는 투영 평면에 피터슨 그래프를 오각형으로 내장하여 제작한 정규 지도다.
p-hosohedron은 유형 {2,p}의 정규 맵이다.
다이크 지도는 속-3 표면에 있는 12옥타곤의 정규 지도다.그것의 기초 그래프인 Dyck 그래프는 또한 토러스 안에 16헥사곤의 정규 지도를 형성할 수 있다.

다음은 양의 오일러 특성인 χ의 표면에 있는 정규 지도 전체 목록이다: 구체와 투영면이다.^[1]

χ	g	슐레플리	Vert.	가장자리	얼굴	그룹	주문	그래프	메모들
2	0	{p,2}	p	p	2	C₂ × Dih_p	4p	C_p	다이헤드론
2	0	{2,p}	2	p	p	C₂ × Dih_p	4p	p-폴드₂ K	호소헤드론
2	0	{3,3}	4	6	4	S₄	24	K₄	사면체
2	0	{4,3}	8	12	6	C₂ × S₄	48	K₄ × K₂	큐브
2	0	{3,4}	6	12	8	C₂ × S₄	48	K_2,2,2	팔면체
2	0	{5,3}	20	30	12	C₂ × A₅	120		도데카헤드론
2	0	{3,5}	12	30	20	C₂ × A₅	120	K₆ × K₂	이코사헤드론
1	n1	{2p,2}/2	p	p	1	디흐_2p	4p	C_p	헤미다이드론^[2]
1	n1	{2,2p}/2	2	p	p	디흐_2p	4p	p-폴드₂ K	헤미호소헤드론^[2]
1	n1	{4,3}/2	4	6	3	S₄	24	K₄	헤미큐브
1	n1	{3,4}/2	3	6	4	S₄	24	2배₃ K	헤미오크타헤드론
1	n1	{5,3}/2	10	15	6	A을₅	60	피터슨 그래프	헤미도데카헤드론
1	n1	{3,5}/2	6	15	10	A을₅	60	K₆	헤미이코사면체

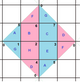
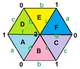
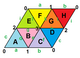
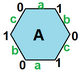
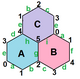
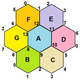
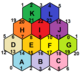
아래 이미지는 슐레플리 기호가 표시된 트리플 토러스 20개의 일반 지도 중 3개를 보여준다.

{6,4}
{4,8}
{8,4}

토로이드 다면체

네트로 시각화된 예
{4,4}_1,0 (v:1, e:2, f:1)	{4,4}_1,1 (v:2, e:4, f:2)	{4,4}_2,0 (v:4, e:8, f:4)	{4,4}_2,1 (v:5, e:10, f:5)	{4,4}_2,2 (v:8, e:16, f:8)
{3,6}_1,0 (v:1, e:3, f:2)	{3,6}_1,1 (v:3, e:9, f:6)	{3,6}_2,0 (v:4, e:12, f:8)	{3,6}_2,1 (v:7, e:21, f:14)	{3,6}_2,2 (v:12, e:36, f:24)
{6,3}_1,0 (v:2, e:3, f:1)	{6,3}_1,1 (v:6, e:9, f:3)	{6,3}_2,0 (v:8, e:12, f:4)	{6,3}_2,1 (v:14, e:21, f:7)	{6,3}_2,2 (v:24, e:36, f:12)

일반 지도는 유클리드 틸팅의 유한 부분으로서 토오헤드 다면체로 존재하며, 평평한 토루스로서 두오실린더 표면에 싸여 있다.이들은 사각형 타일링과 관련된 사람에 대해 {4,_b,c4}, {4},^[3] {3,_b,c6}, 6각형 타일링과 관련된 삼각 타일링 {6,_b,c3}, {6}, b와 c는 정수다.^[4]반사대칭이 있는 특수사례(b,0)와 (b,b)가 2개 있는 반면, 일반사례는 키랄쌍(b,c)과 (c,b)로 존재한다.

{4,4}_m,0 형식의 정기 지도는 4차원 m×m 듀오프리즘의 정사각형 면으로 보이는 유한정규 다면체 {4,4 m}로 나타낼 수 있다.

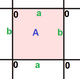
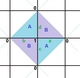
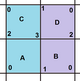
여기 체스보드에서 실린더 섹션으로 토러스까지 매핑된 {4,4}_8,0의 예가 있다.실린더에서 토러스까지의 투영은 기하학을 3차원으로 왜곡하지만 4차원에서는 왜곡 없이 할 수 있다.

예를 들어 지도 {6,4}₃을(를) {6,4}(_4,0으)로 볼 수 있다.반대쪽 가장자리를 따라 4개의 16진법을 순서대로 통과시킨다.

오일러 특성이^[5] 0인 일반 지도

g	슐레플리	Vert.	가장자리	얼굴	그룹	주문	메모들
1	{4,4}_b,0 n=b²	n	2n	n	[4,4]_(b,0)	8n	납작한 토로이드 다면체 {4,4 b}과(와) 동일
1	{4,4}_b,b n=2b²	n	2n	n	[4,4]_(b,b)	8n	납작한 토로이드 다면체 수리된 {4,4 b}과(와) 동일
1	{4,4}_b,c n=b²+c²	n	2n	n	[4,4]⁺ _{_(b,c)}	4n	편평한 치랄 토로이드 다면체
1	{3,6}_b,0 t=b²	t	3t	2t	[3,6]_(b,0)	12t	납작한 토로이드 다면체
1	{3,6}_b,b t=2b²	t	3t	2t	[3,6]_(b,b)	12t	납작한 토로이드 다면체
1	{3,6}_b,c t=b²+bc+c²	t	3t	2t	[3,6]⁺ _{_(b,c)}	6t	편평한 치랄 토로이드 다면체
1	{6,3}_b,0 t=b²	2t	3t	t	[3,6]_(b,0)	12t	납작한 토로이드 다면체
1	{6,3}_b,b t=2b²	2t	3t	t	[3,6]_(b,b)	12t	납작한 토로이드 다면체
1	{6,3}_b,c t=b²+bc+c²	2t	3t	t	[3,6]⁺ _{_(b,c)}	6t	편평한 치랄 토로이드 다면체

일반적으로 정규적인 toroidal polyedra {p,q}_b,c은(는) 위의 유핵종만 4차원에서는 toroidal polyedra로 존재할 수 있지만 p 또는 q가 짝이라면 정의할 수 있다.{2p,q}에서 경로(b,c)는 직선 면으로 스텝링하는 것으로 정의할 수 있으며, 이중 {p,2q} 형태는 경로(b,c)를 직선 면의 스테핑 정점-에지-베르텍스로 본다.

참고 항목

참조

^ 콕시터(1980)
^ ^a ^b Séquin, Carlo. "Symmetrical immersions of low-genus non-orientable regular maps" (PDF). Berkeley University.
^ Coxeter 1980, 8.3 토러스 상의 유형 {4,4}.
^ Coxeter 1980, 8.4 Torus에 {3,6} 또는 {6,3} 유형의 맵.
^ Coxeter 및 Moser, 이산 그룹에 대한 생성자 및 관계, 1957년, 8장, 정규 지도, 8.3 유형별 지도, 8.4 유형별 지도, 유형별 지도 {3,6} 또는 유형별 지도 {6,3}

Coxeter, H. S. M.; Moser, W. O. J. (1980), Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 14 (4th ed.), Springer Verlag, ISBN 978-0-387-09212-6.
van Wijk, Jarke J. (2009), "Symmetric tiling of closed surfaces: visualization of regular maps" (PDF), Proc. SIGGRAPH (ACM Transactions on Graphics), 28 (3): 12, doi:10.1145/1531326.1531355, archived from the original (PDF) on 2011-06-09.
Conder, Marston; Dobcsányi, Peter (2001), "Determination of all regular maps of small genus", Journal of Combinatorial Theory, Series B, 81 (2): 224–242, doi:10.1006/jctb.2000.2008.
Nedela, Roman (2007), Maps, Hypermaps, and Related Topics (PDF).
Vince, Andrew (2004), "Maps", Handbook of Graph Theory.
Brehm, Ulrich; Schulte, Egon (2004), "Polyhedral Maps", Handbook of Discrete and Computational Geometry.

[1] 콕시터(1980)

[csequin-2] Séquin, Carlo. "Symmetrical immersions of low-genus non-orientable regular maps" (PDF). Berkeley University.

[3] Coxeter 1980, 8.3 토러스 상의 유형 {4,4}.

[4] Coxeter 1980, 8.4 Torus에 {3,6} 또는 {6,3} 유형의 맵.

[5] Coxeter 및 Moser, 이산 그룹에 대한 생성자 및 관계, 1957년, 8장, 정규 지도, 8.3 유형별 지도, 8.4 유형별 지도, 유형별 지도 {3,6} 또는 유형별 지도 {6,3}

[1]

[2]

[3]

[4]

[5]

Search