균일 벌집
Uniform honeycomb기하학에서 획일적인 벌집이나 획일적인 다듬기 또는 무한의 획일적인 폴리토프는 획일적인 폴리토프 면으로 만들어진 정점 변환 벌집이다. 모든 정점은 동일하며 각 정점에 동일한 얼굴 조합과 배열이 있다. 그것의 치수는 n차원 벌집합을 위한 n-허니콤으로 명확히 할 수 있다.
n차원 균일 벌집형 은 n-sprees의 표면, n-차원 유클리드 공간, n-차원 쌍곡선 공간에 구성할 수 있다. 2차원 균일 벌집은 흔히 균일 타일링 또는 균일 테셀레이션이라고 불린다.
거의 모든 균일한 테셀레이션은 와이토프 건설에 의해 생성될 수 있으며, Coxeter-Dynkin 도표로 표현된다. 균일 다면체, 균일 4폴리토프, 균일 5폴리토프, 균일 6폴리토프, 균일 타일링, 볼록 균일 벌집 기사에 사용되는 볼록 균일 다면체의 용어는 노먼 존슨이 만들었다.
와이토피안 테셀레이션은 꼭지점 수치로 정의할 수 있다. 2차원 기울기의 경우 모든 꼭지점 주위의 면 순서를 나열한 꼭지점 구성에 의해 기울기를 지정할 수 있다. 예를 들어 4.4.4.4는 각 꼭지점에 4개의 정사각형이 있는 정사각형 타일링인 정규 테셀레이션을 나타낸다. 일반적으로 n차원 균일 다듬기 정점 그림은 정수로 라벨이 표시된 가장자리를 가진 (n-1)-폴리토프로 정의되며, 정점에서 방사되는 각 가장자리의 다각형 면의 면 수를 나타낸다.
균일한 꿀벌의 예
| 2차원 테셀레이션 | ||||
|---|---|---|---|---|
| 구면 | 유클리드 주 | 쌍곡선 | ||
| 콕시터 다이어그램 | ||||
| 사진 |  잘린 이코시다데카헤드론 |  잘린 3hexangel 타일링 | 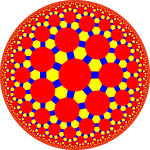 잘린 3헥타르 정사각형 타일 (푸앵카레 디스크 모델) | 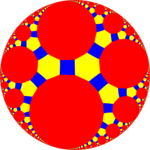 잘린 3각 타일링 |
| 정점수 |  |  |  | |
| 3차원 벌집 | ||||
| 3시 30분 | 3-유클리드 주 | 3각형의 | ||
| 그리고 파라콤팩트 균일한 벌집모양. | ||||
| 콕시터 다이어그램 | ||||
| 사진 |  (철사 투영) 16 셀 |  입방 벌집 |  order-4 deadecheadral honeycomb. (벨트라미-클레인 모델) |  order-4 육각형 타일링 벌집 (푸앵카레 디스크 모델) |
| 정점수 |  (옥타헤드론) |  (옥타헤드론) |  (옥타헤드론) |  (옥타헤드론) |
참고 항목
참조
- 조지 올셰프스키, 균일 파노플로이드 테트라콤브스, 원고(2006) (11개의 볼록 균일 기울기, 28개의 볼록 균일 벌집, 143개의 볼록 균일 테트라콤 목록)
- 브란코 그룬바움, 3공간의 균일한 기울기. Gembinatorics 4(1994), 49–56.
- 노먼 존슨 제복 폴리토페스, 원고(1991)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman and Company. ISBN 0-7167-1193-1.
- H. S. M. Coxeter, 일반 폴리토페스, 제3판 도버 뉴욕, 1973년
- Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
- N.W. 존슨: 균일다각체와 허니컴의 이론, 박사학위. 1966년 토론토 대학교의 논문
- A. 안드레이니, 술레 레티디 리골라리 e 세미레골라리 e 설레 코리스폰덴티 레티 상관관계(폴리헤드라의 정규망과 반정형 그물 및 그에 상응하는 상관 그물 위에), 멤. 소시에타 이탈리아아 델라 시엔제, 세르.3, 14 (1905) 75–129.
외부 링크
- Weisstein, Eric W. "Uniform tessellation". MathWorld.
- 테셀레이션스 오브 더 플레인
- Klitzing, Richard. "2D Euclidean tesselations".




