정두면체
Regular dodecahedron| 정두면체 | |
|---|---|
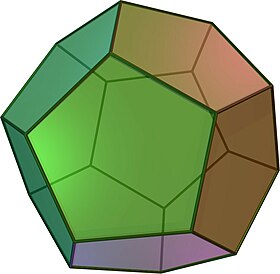 (모델을 회전하려면 여기를 클릭하십시오.) | |
| 유형 | 플라토닉 고체 |
| 쇼트코드 | 5d |
| 요소들 | F = 12, E = 30 V = 20(수평 = 2) |
| 옆얼굴 | 12{5} |
| 콘웨이 표기법 | D |
| 슐레플리 기호 | {5,3} |
| 면 구성 | V3.3.3.3.3 |
| 와이토프 기호 | 3 2 5 |
| 콕시터 다이어그램 | |
| 대칭 | Ih, H3, [5,3], (*532) |
| 회전군 | I, [5,3]+, (532) |
| 참조 | U23, C26, W5 |
| 특성. | 규칙적이고 볼록한 |
| 디헤드각 | 116.56505° = 아크코사스1⁄√5) |
 5.5.5 (Vertex 그림) |  정삼면체 (이중 다면체) |
 그물 | |
정점 도두면체 또는 오각형 도두면체는 정점인 도두면체로서, 정점마다 3번의 만남을 갖는 12개의 정점으로 구성되어 있다. 그것은 다섯 개의 플라토닉 고체 중 하나이다. 면 12개, 정점 20개, 가장자리 30개, 대각선 160개(얼굴 대각선 60개, 공간 대각선 100개)를 가지고 있다.[1] 슐레플리 기호 {5,3}로 표현된다.
치수
일반 도데면체의 가장자리 길이가 " " 경우, 원형으로 된 구(모든 정점에 일반 도데면체에 닿는 구)의 반지름은
그리고 새겨진 구체의 반지름(일반 도데카헤드론 각 면에 접선)은
각 가장자리의 가운데에 닿는 미드라디우스(midradius)가 있는 동안.
이 수량은 또한 다음과 같이 표현될 수 있다.
여기서 ϕ은 황금비율이다.
엣지 길이 1의 정규 도데면체를 볼 때, r은u 가장자리 길이 cube의 입방체 주위에 있는 원추형의 구 반지름이며, r은i 가장자리 길이 ϕ의 정규 오각형의 아포테헴이다.
표면 면적 및 부피
가장자리 길이 a의 일반 도데카헤드론의 표면적 A와 볼륨 V는 다음과 같다.
또한 일반 도면체의 표면적과 부피는 황금비율과 관련이 있다. 가장자리 길이가 한 단위인 도데카헤드론에는 다음 특성이 있다.[2]
2차원 대칭 투영
일반 도두면체에는 정점과 오각형 면 중앙에 A와2 H2 Coxeter 평면에 해당하는 두 개의 특별한 직교 돌출부가 있다.
| 중심: | 꼭지점 | 가장자리 | 면 |
|---|---|---|---|
| 이미지 | 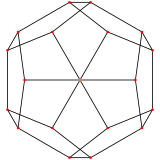 |  |  |
| 투영적 대칭 | [[3]] = [6] | [2] | [[5]] = [10] |
원근법 투영에서, 오각형 얼굴 위에서 볼 때, 일반 도데카헤드론은 선형날짜 슐레겔 도표 또는 구형 다면체로서의 입체 투영으로 볼 수 있다. 이 투영법은 도데카헤드라 120개로 구성된 4차원 폴리토프인 4차원 120셀을 3차원까지 투영하는 데도 사용된다.
| 투영 | 정사영 | 투시 투영 | |
|---|---|---|---|
| 슐레겔 도표 | 입체 투영법 | ||
| 정두면체 | 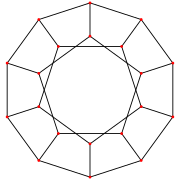 | 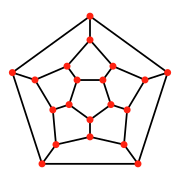 |  |
| 도데카플렉스 (120셀) |  |  |  |
구면 타일링
일반적인 도데카헤드론은 구면 타일링으로도 표현될 수 있다.
 |  |
| 직교 투영법 | 입체 투영법 |
|---|
데카르트 좌표, 평행 좌표.
다음의 데카르트 좌표는 원점을 중심으로 적절한 스케일 및 방향의 일반 도데카헤드론의 20 정점을 정의한다.[3]
- (±1, ±1, ±1)
- (0, ±ϕ, ±1/ϕ)
- (±1/ϕ, 0, ±ϕ)
- (±ϕ, ±1/ϕ, 0)
여기서 ϕ = 1 + √5/2는 황금비(또한 τ) ≈ 1.1618이다. 가장자리 길이는 2/10 = √5 - 1이다. 배반자는 √3이다.
면-정의 방정식
정점 좌표의 대칭과 유사하게, 일반 도데면체의 12면 방정식은 계수에 대칭을 나타낸다.
- x ± ϕy = ± ϕ2
- y ± ϕz = ± ϕ2
- z ± ϕx = ± ϕ2
특성.
- 일반 도두면체의 치골각은 2 아크탄(ϕ) 또는 약 116.565°(여기서 다시 = = 1 + 55/2, 황금비)이다. OEIS: A137218 이음각의 탄젠트는 정확히 -2이다.
- 원래 일반 도데면체의 가장자리 길이가 1이면 이중 이코사면체의 가장자리 길이가 ϕ이다.
- 5개의 플라토닉 고형물이 같은 부피로 만들어지면 일반 도데카헤드론은 가장 짧은 가장자리를 가진다.
- 그것은 43,380개의 그물을 가지고 있다.
- 일반 도면체 얼굴의 지도 채색 번호는 4이다.
- 가장자리로 연결되지 않은 동일한 면의 정점 사이의 거리는 가장자리 길이의 times 곱하기이다.
- 두 가장자리가 공통 정점을 공유하는 경우, 가장자리의 중간점은 신체 중심과 함께 36-72-72 삼각형을 형성한다.
구성으로
이 구성 매트릭스는 도데카헤드론을 나타낸다. 행과 열은 정점, 가장자리 및 면에 해당한다. 대각선 숫자는 각 원소가 전체 도면체에서 얼마나 많이 발생하는지 말해준다. 비대각 숫자는 열의 요소 중 몇 개가 행의 요소 안에서 또는 열 요소에서 발생하는지 알려준다.[4][5]
여기에 k-face 요소와 k-figures로 확장된 구성이 있다. 대각선 요소 카운트는 전체 Coxeter 그룹 H3, 순서 120의 비율로, 미러 제거와 함께 부분군의 순서로 나눈 값이다.
| H3 | k-face | fk | f0 | f1 | f2 | K-figure | 메모들 | |
|---|---|---|---|---|---|---|---|---|
| A을2 | ( ) | f0 | 20 | 3 | 3 | {3} | H3/A2 = 120/6 = 20 | |
| A1A1 | { } | f1 | 2 | 30 | 2 | { } | H3/A1A1 = 120/4 = 30 | |
| H2 | {5} | f2 | 5 | 5 | 12 | ( ) | H3/H2 = 120/10 = 12 |
기하학적 관계
일반 도데카헤드론은 오각형 사다리꼴의 두 축 정점을 잘라 만들 수 있는 절단 사다리꼴의 무한 세트 중 세 번째다.
일반 도데카헤드론의 장식은 케플러-푸인소트 다면체 4개 중 3개를 차지한다.
교정된 일반 도데카헤드론은 이코시다데카헤드론을 형성한다.
일반 도두면체에는 A × Z의2 추상적인 그룹 구조와5 함께 콕시터 그룹[5,3], 순서 120의 이두면체 대칭 Ih, 콕시터 그룹 [5,3], order 120이 있다.
정삼면체와의 관계
일반 도두면체를 구에 새겼을 때 같은 구에 새긴 고두면체(60.55%)보다 구의 부피(66.49%)를 더 많이 차지한다.
가장자리 길이가 1인 일반 도두면체는 가장자리가 같은 이두면체의 부피(7.663...)의 3배 반 이상을 가지고 있다. 2.181...)과 비교하여 이 비율은 약 3.4646117975 또는 정확한 용어로 3/5(3˚ + 1) 또는 (1.8˚ + 0.6)이다.
일반 도두면체에는 12개의 얼굴과 20개의 정점이 있는 반면, 일반 이두면체에는 20개의 정점과 12개의 정점이 있다. 둘 다 30개의 가장자리를 가지고 있다.
중첩된 큐브에 대한 관계
정육면체는 5개의 다른 위치에서 등거리 정점 중 8개에 부착된 일반 도데카헤드론 안에 삽입될 수 있다.[6] 사실, 5개의 정육면체들이 일반 도데체 안에서 겹치고 서로 맞물려 5개의 정육면체들이 합쳐질 수 있다.
그러한 일반 도데면체 내부에 내장된 정육면체 가장자리와 일반 도데면체 가장자리의 비율은 1 : ϕ 또는 ( ( - 1) : 1이다.
그러한 일반 도면체 내부에 내장되어 있는 입방체의 부피에 대한 일반 도면체 부피의 비율은 1 : 2/2 + ϕ 또는 1 + ϕ/2 : 1 또는 (5 + √5) : 4이다.
예를 들어 볼륨 64(및 에지 길이 4)의 내장형 큐브는 볼륨 64 + 32˚(및 에지 길이 4㎛ - 4)의 일반 도데면체 내에 중첩된다.
따라서 포괄하는 일반 도데체론과 밀폐된 입방체 사이의 부피 차이는 항상 입방체 시간의 절반인 ϕ이다.
이러한 비율에서 가장자리 길이가 a인 일반 도데면체의 부피에 대한 간단한 공식으로 황금 평균을 구한다.
- V = (aϕ)3 · 1/4(5 + √5)
- V = 1/4(14˚ + 8)a3
황금 직사각형과의 관계
비율의 황금 직사각형(ϕ+1) : 1과 ϕ : 1 또한 일반 도두면체 내에 완벽하게 들어맞는다.[7] 이 황금 사각형에 비례하여 폐쇄된 입방체의 가장자리는 ϕ이며, 이때 사각형의 긴 길이는 ϕ + 1(또는 ϕ2)이고 짧은 길이는 1(일반 도데카헤드론과 공유하는 가장자리)이다.
또한, 일반 도데카헤드론 각 면의 중앙은 세 개의 교차하는 금색 직사각형을 형성한다.[8]
6관 3면체와의 관계
6-큐브에서 롬빅삼정면체의 선체를 형성하는 동일한 기본 벡터를 사용해 6차원 6데미큐브에서 3D로 투영할 수 있다. 여기에 표시된 바와 같이, 6D 표준 길이 22의 외부 선체 가장자리로 연결되지 않은 내부 12 정점들은 정기적인 동면체를 형성한다.
사용된 3D 투영 기준 벡터 [u,v,w]는 다음과 같다.
- u = (1, ϕ, 0, −1, ϕ, 0)
- v = (sv, 0, 1, ϕ, 0, -1)
- w = (0, 1, ϕ, 0, −1, ϕ)
역사와 사용
규칙적인 도두면체 물체는 몇 가지 실용적인 용도를 발견했고, 시각 예술과 철학에서도 역할을 했다.
Iamblichus는 피타고라스 사람인 히파수스가 바다에서 죽은 것은 그가 "12개의 펜타곤이 있는 구"를 처음 누설했다고 자랑했기 때문이라고 말한다.[9] 플라톤의 대화인 테아에토스에서 플라톤은 고전적인 원소들이 5개의 균일한 규칙적인 고체로 만들어졌다고 가설을 세웠다; 이것들은 후에 플라토닉 고체로 알려지게 되었다. 다섯 번째 플라토닉 고체, 도데카헤드론 중에서 플라톤은 "...신께서 온 천국에 별자리를 배열하는 데 [그것]을 사용하셨다"고 분명히 말했다. 티마이오스(Timaeus,c. 기원전 360년)는 플라톤의 대화 의인으로서 다른 4개의 플라톤 고형물을 4개의 고전 원소와 연관시키고 있으며, 비록 일반적으로 보통의 도데카헤드론과 관련이 있지만 결코 직접적으로 언급되지 않는 5번째 고체 패턴이 있다고 덧붙인다: "이 신은 우주의 묘사에서 사용되었다."[10] 아리스토텔레스는 또한 하늘이 아이트르( 라틴어로 에테르, 미국 영어로는 에테르)라고 부르는 다섯 번째 원소로 이루어져 있다고 가정했다.
테에토스는 다섯 가지 모두에 대해 수학적 설명을 했으며, 다른 볼록한 정규 다면체가 존재하지 않는다는 최초의 알려진 증거에 책임이 있었을지도 모른다. 유클리드는 그 성질에 바쳐진 마지막 책(Book XIII)인 원소에 플라토닉 고형물을 완전히 수학적으로 묘사했다. 13-17권에서는 13-17권에서는 사면체, 팔면체, 입방체, 고면체 및 도면체의 구성을 그 순서로 기술하고 있다. 각 고체 유클리드에게 있어 가장자리 길이에 대한 구형의 지름의 비율을 찾는다. 발의안 제18호에서 그는 더 이상 볼록한 규칙적인 다면체는 없다고 주장한다.
일반적인 도데카헤드라는 주사위나 아마도 점액으로 사용되었을 것이다. 헬레니즘 시대에는 작고 속이 빈 청동 로마 도데카헤드라가 만들어졌고 유럽의 여러 로마 유적에서 발견되었다. 그들의 목적은 확실하지 않다.
20세기 미술에서 도데카헤드라는 그의 석판화 파충류(1943년)와 중력(1952년)과 같은 M. C. 에셔의 작품에 등장한다. 살바도르 달리의 그림 최후의 만찬의 성찬(1955년)에서 그 방은 속이 빈 일반 도데카헤드론이다. 제라드 카리스는 그의 모든 예술 작품 전모를 일반 도데카헤드론과 펜타곤에 바탕을 두었는데, 이것은 펜타곤주의라는 신조어인 새로운 예술 운동으로 제시되고 있다.
현대 롤플레잉 게임에서 일반 도데카헤드론은 흔히 다면 주사위 중 하나인 12면 주사위로 사용된다.
카메라 제조사인 임메시브미디어는 초당 1억 화소 이상, 초당 30프레임으로 모든 방향에서 고해상도 영상을 동시에 캡처하는 세계 최초의 360° 풀모션 카메라인 도데카 2360 카메라를 만들었다.[promotional language] 그것은 보통의 도데카헤드론에 기초하고 있다.[citation needed]
메가믹스 트위스티 퍼즐은 크고 작은 순서의 유사점과 함께 일반적인 도데카헤드론 모양을 하고 있다.
어린이 소설 '팬텀 톨게이트'에서 일반 도데카헤드론은 수학의 땅에 등장인물로 등장한다. 그의 얼굴들은 각각 다른 표정을 짓고 있다. 예를 들어, 그는 자신의 기분에 맞추기 위해 앞쪽으로 회전한다.
자연에서
단세포 연안 식물성 플랑크토닉 알가인 coccolithophore Braudosphaera bigelowi(그림 참조) 화석은 탄산칼슘 껍데기를 가지고 있으며, 직경 약 10마이크로미터의 정규적인 도두면 구조를 가지고 있다.[11]
일부 퀘이시크리스탈은 도면체 형태를 가지고 있다(그림 참조). 가넷, 다이아몬드 등 일부 일반 결정체도 '도데카헤드론'의 습성을 나타낸다고 하지만, 이 말은 사실 롬브릭 도데카헤드론 모양을 가리킨다.[12]
우주의 모양
우주의 전지구적 기하학을 위한 다양한 모델들이 제안되었다. 원시 기하학 외에도, 이러한 제안들은 푸앵카레 도데카헤드랄 공간도 포함하고 있는데, 이 공간은 정반대의 얼굴이 (작은 비틀림으로) 대응하는 일반 도데카헤드론으로 구성되는 양의 곡선 공간이다. 이는 장피에르 루미넷과 동료들이 2003년 제안했으며 2008년 모델 하늘에서 최적의 방향을 제시한 것으로 추정됐다.[13][14][15]
베르트랑 러셀의 1954년 단편 "수학자의 악몽: 스퀘어펀트 교수의 비전"이라는 숫자 5는 다음과 같이 말했다: "나는 손에 쥐는 손가락의 숫자다. 나는 펜타곤과 펜타그램을 만든다. 하지만 나에게 있어 도데카헤드라는 존재할 수 없었다; 그리고 모두가 알다시피, 우주는 도데카헤드론이다. 그래서, 그러나 나에겐 우주가 있을 수 없었다."
큐브와 빌루나비로툰다로 채워진 공간
일반 도데카헤드라는 정육면체와 빌루나비로툰다(존슨솔리드91)로 공간을 1 대 1 대 3의 비율로 채운다.[16][17] 도데카헤드라만 해도 가장자리부터 가장자리까지의 피리토헤드라 격자를 만든다. 빌루나비 로툰다스가 심방 틈새를 메운다. 각 입방체는 세 방향으로 6개의 빌루나비 로툰다를 만난다.
 블록 모형 |  |  도데카헤드라 격자 |  정육면체 주위에 6개의 빌루나비 로툰다. |
관련 다면체 및 틸팅
일반 도두면체는 꼭지점 그림 n에3 의한 일련의 기울기와 위상학적으로 관련이 있다.
| *n32 일반 틸팅의 대칭 돌연변이: {n,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 구면 | 유클리드 주 | 콤팩트 하이퍼브. | 파라코. | 비대칭 쌍곡선 | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
일반 도두면체는 잘림 순서에 의해 그 이중인 이두면체로 변형될 수 있다.
| 균일한 이두면체 다면체 계열 | |||||||
|---|---|---|---|---|---|---|---|
| 대칭: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| 이중에서 균일한 폴리헤드라까지 | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
| 균일한 팔면체 다면체 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [4,3], (*432) | [4,3]+ (432) | [1+,4,3] = [3,3] (*332) | [3+,4] (3*2) | |||||||
| {4,3} | t{4,3} | r{4,3} r{31,1} | t{3,4} t{31,1} | {3,4} {31,1} | rr{4,3} s2{3,4} | tr{4,3} | sr{4,3} | h{4,3} {3,3} | h2{4,3} t{3,3} | s{3,4} s{31,1} |
= | = | = | ||||||||
| 이중에서 균일한 폴리헤드라까지 | ||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V34.4 | V33 | V3.62 | V35 |
일반 도데카헤드론은 그 외의 다른 통일되지 않은 다면체 및 틸팅의 시퀀스의 구성원으로, 얼굴 구성이 있는 펜타곤(V3.3.3.3.n)으로 구성된다(n > 6의 경우, 시퀀스는 쌍곡면의 틸팅으로 구성된다). 이 얼굴 변환 수치는 회전 대칭을 가지고 있다.
| n32 스너브 틸팅의 대칭 변이: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 대칭 n32년 | 구면 | 유클리드 주 | 콤팩트 쌍곡선 | 파라콤. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| 스너브 수치 |  |  |  |  |  |  |  |  |
| 구성 | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| 자이로 수치 |  |  |  |  |  |  |  |  |
| 구성 | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.1987 |
정점 배열
일반 도데면체는 4개의 비콘벡스 균일한 다면체 및 3개의 균일한 다면체 화합물과 정점 배열을 공유한다.
5개의 정육면체는 그 가장자리로 일반 도데면체 얼굴의 대각선으로 되어 있으며, 이 정육면체들은 5개의 정육면체로 이루어진 일반적인 다면체 화합물을 이룬다. 2개의 4면체 정점에 들어갈 수 있기 때문에 5와 10개의 4면체도 일반 도면체에도 들어갈 수 있다.
 그레이트 스틸 도데카헤드론 |  소형 이코시다데카헤드론 |  직교 도데코데카헤드론 |  대직류 이코시다데카헤드론 |
 정육면체 5개 혼합물 |  5개의 사면체 화합물 |  사면체 10개 화합물 |
스텔링스
일반 도데카헤드론의 3개 스텔레이션은 모두 정규(비콘벡스) 다면체: (케플러-푸인소트 다면체)
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 스텔레이션 |  정두면체 |  소절개도면체 |  대두면체 |  그레이트 스틸 도데카헤드론 |
| 면도 |  |  |  |  |
도데카헤드 그래프
| 일반 도데면체 그래프 | |
|---|---|
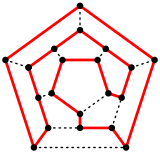 도데카헤드론에서의 해밀턴의 사이클이다. | |
| 정점 | 20 |
| 가장자리 | 30 |
| 반지름 | 5 |
| 지름 | 5 |
| 둘레 | 5 |
| 자동형성 | 120(A52 × Z)[18] |
| 색수 | 3 |
| 특성. | 해밀턴, 정규, 대칭, 거리 정규, 거리 변환, 3VERx 연결, 평면 그래프 |
| 그래프 및 모수 표 | |
도데카헤드론(정점과 가장자리)의 골격은 그래프를 형성한다. 그것은 5개의 플라토닉 그래프 중 하나인데, 각각 플라토닉 고체의 골격이다.
이 그래프는 일반화된 피터슨 그래프 G(10,2)로도 구성할 수 있다. 폴리곤의 높은 대칭도는 거리-변환성, 거리-정규성, 대칭성인 이 그래프의 속성에 복제된다. 오토모피즘 그룹은 120개의 질서를 가지고 있다. 꼭지점은 가장자리처럼 3가지 색상으로 색칠할 수 있으며 지름은 5이다.[19]
도두면 그래프는 해밀턴어 - 모든 정점을 포함하는 주기가 있다. 실제로, 이 이름은 이코시안 게임인 윌리엄 로완 해밀턴에 의해 1857년에 발명된 수학 게임에서 유래되었다. 이 게임의 목적은 도데카헤드론의 가장자리를 따라 해밀턴의 사이클을 찾는 것이었다.
 |
참고 항목
- 120세포, 일반 폴리초론 (표면이 120개의 도데카메랄 세포로 구성된 4D 폴리토프)
- Braurudosphaera bigelowi - 도데카헤드론 모양의 coccolithophore(단세포 식물성 플랑크톤 조류)
- 도데카헤드란(분자)
- 펜타키스 도데카헤드론
- 스너브 도데카헤드론
- 잘린 도두면체
참조
- ^ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865.
- ^ Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. pp. 70–1. ISBN 0-7679-0816-3.
- ^ Weisstein, Eric W. "Icosahedral group". MathWorld.
- ^ Coxeter, 일반 폴리탑, 1.8초 구성
- ^ Coxeter, 복합 일반 폴리토페스, 페이지 117
- ^ http://mathworld.wolfram.com/images/eps-gif/DodecahedronCube_700.gif
- ^ http://davidf.faricy.net/polyhedra/images/dodecarect.gif
- ^ http://www.toshen.com/images/dodecahedronwithgoldrectang.gif
- ^ 플로리안 카조리, A 수학사 (1893)
- ^ 플라톤, 티마이오스, 조웨트 번역[라인 1317–8]; 디라멘테이션으로 번역된 그리스어는 디아조센헤인(diazogenhein)으로, 생명에 가까운 모습으로 그린다.
- ^ 하기노·케이·오누마·R·가와치·M·호리구치·T.(2013년) "브라루도인산소 비글로위(Prymnesiophyaea bigelowi)에서 내생성 질소 고정 시아노박테리움 UCYN-A 발견" PLoS 1, 8(12): e81749. doi:10.1371/journal.pone.0081749.
- ^ 2009년 4월 12일 웨이백머신에 보관된 도데카헤드 크리스탈 습관
- ^ Dumé, Belle (Oct 8, 2003). "Is The Universe A Dodecahedron?". PhysicsWorld. Archived from the original on 2012-04-25.
- ^ Luminet, Jean-Pierre; Jeff Weeks; Alain Riazuelo; Roland Lehoucq; Jean-Phillipe Uzan (2003-10-09). "Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background". Nature. 425 (6958): 593–5. arXiv:astro-ph/0310253. Bibcode:2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579. S2CID 4380713.
- ^ Roukema, Boudewijn; Zbigniew Buliński; Agnieszka Szaniewska; Nicolas E. Gaudin (2008). "A test of the Poincaré dodecahedral space topology hypothesis with the WMAP CMB data". Astronomy and Astrophysics. 482 (3): 747. arXiv:0801.0006. Bibcode:2008A&A...482..747L. doi:10.1051/0004-6361:20078777. S2CID 1616362.
- ^ "Dodecahedron and Bilunabirotunda – Wolfram Demonstrations Project".
- ^ http://www.lcv.ne.jp/~hase/m09_08b.properties
- ^ Frucht, Roberto (1936–1937), "Die gruppe des Petersen'schen Graphen und der Kantensysteme der regulären Polyeder", Comment. Math. Helv., 9: 217–223, doi:10.1007/bf01258190, S2CID 121791222
- ^ Weisstein, Eric W. "Dodecahedral Graph". MathWorld.
외부 링크
| 위키미디어 커먼즈에는 도데카헤드론과 관련된 미디어가 있다. |
- Weisstein, Eric W. "Regular Dodecahedron". MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra o3o5x – doe".
- 대화형 3D 보기를 사용하여 도데면체의 편집 가능한 인쇄 가능 네트
- 균일 폴리헤드라
- Orgami Polyedra – 모듈식 Orgami로 만든 모델
- 도데카헤드론 – 브라우저에서 작동하는 3-d 모델
- 가상현실 폴리헤드라 폴리헤드라 백과사전
- K.J.M. MacLan, 5개의 플라토닉 고형분 및 기타 반정규 다면체의 기하학적 해석
- 도데카헤드론 3D 시각화
- 스텔라: 다면 탐색기: 이 페이지에서 일부 이미지를 생성하는 데 사용되는 소프트웨어.
- 스티로폼 큐브에서 도데카헤드론 만드는 법
- 그리스, 인도, 중국 원소 - 7 원소 이론
| 가족 | A을n | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정규 다각형 | 삼각형 | 사각형 | p-곤 | 육각형 | 펜타곤 | |||||||
| 균일다면체 | 사면체 | 옥타헤드론 • 큐브 | 데미큐브 | 도데카헤드론 • 이코사헤드론 | ||||||||
| 균일 폴리초론 | 펜타코론 | 16-셀 • 테세락트 | 데미테세락트 | 24셀 | 120 셀 • 600 셀 | |||||||
| 제복5폴리토프 | 5와섹스 | 5정형 • 5정형 | 5데미큐브 | |||||||||
| 제복6폴리토프 | 6-630x | 6-정통 • 6-118 | 6데미큐브 | 122 • 221 | ||||||||
| 제복7폴리토프 | 7시 15분 | 7정맥 • 7정맥 | 7데미큐브 | 132 • 231 • 321 | ||||||||
| 제복8폴리토프 | 8시 15분 | 8정형 • 8정형 | 8데미큐브 | 142 • 241 • 421 | ||||||||
| 제복9폴리토프 | 9시 15분 | 9-정통 • 9-11 | 9데미큐브 | |||||||||
| 균일 10폴리토프 | 10센트짜리 | 10정형 • 10정형 | 10데미큐브 | |||||||||
| 균일 n폴리토프 | n-제곱스 | n-직관 • n-직관 | n-데미큐브 | 1k2 • 2k1 • k21 | n-자갈 폴리토프 | |||||||
| 주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록 | ||||||||||||






















