스큐 폴리곤

사방형 분산형(빨간색)의 측면 가장자리는 일반적인 지그재그 스큐 사각형을 나타낸다.

기하학에서 스큐 폴리곤은 정점이 모두 일직선이 아닌 폴리곤이다. 꼬치 다각형은 정점이 4개 이상 있어야 한다. 이러한 다각형의 내부 표면(또는 면적)은 고유하게 정의되지 않는다.

스큐 무한 다각형(Afeirogons)은 모두 콜린어(colinar)가 아닌 정점을 가지고 있다.

지그재그 스큐 폴리곤 또는 반선호도 폴리곤은^[1] 두 평면에서 교차하는 정점을 가지므로 반드시 짝수여야 한다.

3차원의 일반 스큐 폴리곤(그리고 2차원의 일반 스큐 아페이로곤)은 항상 지그재그다.

3차원의 항정신적 꼬치 다각형

균일한 n-곤 항정신병에는 측면 가장자리를 따라 정의된 2n-side 정규 스큐 폴리곤이 있다.

일반 스큐 폴리곤은 가장자리 길이가 같은 등각형이다. 3차원에서 일반 스큐 폴리곤은 지그재그 스큐(또는 항정신병적) 폴리곤으로, 정점이 두 평면에서 교차한다. n-안티프리즘의 측면 가장자리는 정규 스큐 2n-곤을 정의할 수 있다.

일반 스큐 n-곤에는 일반 폴리곤 {p}과(와) 직교선 세그먼트 { ^[2]}의 혼합으로 Schléfli 기호 {p}#{}를 부여할 수 있다. 순차 정점 사이의 대칭 연산은 활공 반사다.

일률적인 정사각형과 오각형 반격대에 예가 나와 있다. 항성 항정신병도 상·하 폴리곤의 연결 순서가 다른 일반 스큐 폴리곤을 생성한다. 채워진 상단과 하단의 폴리곤은 구조적인 선명성을 위해 그려지며, 스큐 폴리곤의 일부가 아니다.

일반 지그재그 꼬치 다각형
스큐 사각형	스큐 육각형	꼬치 팔각형	꼬치 데카곤			스큐 도데카곤
{2}#{ }	{3}#{ }	{4}#{ }	{5}#{ }	{5/2}#{ }	{5/3}#{ }	{6}#{ }

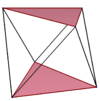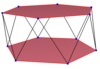s{2,4}	s{2,6}	s{2,8}	s{2,10}	sr{2,5/2}	s{2,10/3}	s{2,12}

일반 복합 스큐 2n곤은 회전으로 두 번째 스큐 폴리곤을 추가하여 유사하게 구성할 수 있다. 이것들은 반격의 프리즘 화합물과 같은 정점을 공유한다.

지그재그 꼬치 다각형의 일반 화합물
스큐 사각형		스큐 육각형	스큐 디카곤
두 {2}#{ }	세 {2}#{ }	두 {3}#{ }	두 {5/3}#{ }

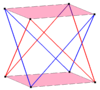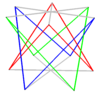Petrie polygon은 일반 다면체와 다면체 내에 정의된 일반 꼬치 다각형이다. 예를 들어, 5개의 플라토닉 고형물은 각각의 투영 봉투 주위에 빨간색 가장자리가 있는 직교 돌출부에서 볼 수 있듯이 4면, 6면 및 10면 정규 스큐 다각형을 가지고 있다. 사면체와 팔면체는 각각의 지그재그 꼬치 다각형의 정점을 모두 포함하고 있으며, 각각 지그재그 항정신병, 삼각 항정신병이라고 볼 수 있다.

일반 스큐 다면체의 꼭지점 도형으로서의 정규 스큐 폴리곤

정사각형 다면체는 정각 다각형 면과 정점 모양의 정사각형을 가지고 있다.

3개의 무한정 일반 스큐 폴리에드라는 3개의 공간을 채운다. 다른 것들은 4개의 공간에 존재하며, 일부는 균일한 4-폴리토프 안에 있다.

무한정 정규 3개의 스큐 다면체의 스큐 정점 그림

{4,6 4}	{6,4 4}	{6,6 3}
일반 꼬치 육각형 {3}#{ }	정사각형 {2}#{ }	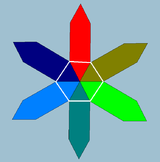일반 꼬치 육각형 {3}#{ }

3차원의 등각 스큐 다각형

등각 스큐 폴리곤은 하나의 꼭지점 유형을 갖는 스큐 폴리곤으로, 두 가지 유형의 가장자리로 연결된다. 가장자리 길이가 같은 등각 스큐 폴리곤도 쿼시레곤으로 간주할 수 있다. 한쪽 가장자리가 반대쪽 면으로 교차하고 다른 가장자리가 같은 면에 머무르게 하는 것을 제외하고는 두 면에 존재하는 지그재그 꼬치 다각형과 비슷하다.

등각 스큐 폴리곤은 균일한 면의 n-곤 프리즘에 정의될 수 있으며, 한쪽 다각형의 가장자리를 교대로 따르고, 다각형 사이를 이동할 수 있다. 예를 들어, 큐브의 꼭지점. 꼭지점들은 위쪽과 아래쪽 정사각형들 사이에 빨간 가장자리가 있고, 양쪽을 따라 파란 가장자리가 번갈아 나타난다.

팔각형			도데카곤			이코시카이트라곤
정육면체, 정사각형	큐브	크로스 큐브	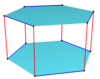육각 프리즘	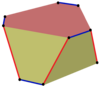육각 프리즘	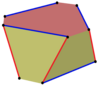육각 프리즘	트위스트 프리즘

4차원의 일반 스큐 다각형

4차원의 일반 스큐 폴리곤은 클리포드 토러스 위에 정점을 가질 수 있으며 클리포드 변위에 의해 관련된다. 지그재그 스큐 폴리곤과 달리 이중 회전 시 스큐 폴리곤은 변의 홀수를 포함할 수 있다.

일반 4폴리탑의 페트리 폴리곤은 일반 지그재그 스큐 폴리곤을 정의한다. 각 공차군 대칭에 대한 Coxeter 숫자는 Petrie 폴리곤이 얼마나 많은 면을 가지고 있는지를 나타낸다. 이것은 5셀은 5면, 16셀은 8면, 24셀은 12면, 120셀과 600셀은 30면이다.

Coxeter 평면에 직교 투영될 때, 이러한 일반 스큐 폴리곤은 평면에서 일반 폴리곤 봉투로 나타난다.

A₄, [3,3,3]	B₄, [4,3,3]		F₄, [3,4,3]	H₄, [5,3,3]
펜타곤	팔각형		도데카곤	트라이아콘타곤
5세포 {3,3,3}	큐테릭트 {4,3,3}	16 셀 {3,3,4}	24셀 {3,4,3}	120 셀 {5,3,3}	600셀 {3,3,5}

n-n 듀오프라임과 듀얼 듀오프라임에도 2n-곤의 페트리 폴리곤이 있다. (테서락트는 4-4 듀오프라미드, 16셀은 4-4 듀오프라미드)

육각형		데카곤		도데카곤
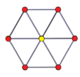3-3 듀오프리즘	3-3 듀오피라미드	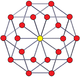5-5 듀오프리즘	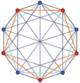5-5 듀오피라미드	6-6 듀오프리즘	6-6 듀오피라미드

참고 항목

참조

^ 일반 복합 폴리토페스, 페이지
^ 추상 일반 폴리토페스, 페이지 217

McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, ISBN 0-521-81496-0 25 페이지
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. "Skew Polygons (Saddle Polygons)" §2.2
Coxeter, H.S.M.; 일반 복합 폴리토페스 (1974년). 제1장 일반 다각형, 1.5. n차원의 일반 다각형, 1.7. 지그재그 및 항정신병 다각형, 1.8. 헬리컬 다각형. 4.3. 기와 직교체, 11.3. 페트리 폴리곤
콕시터, H. S. M. 페트리 폴리곤스. 일반 폴리토페스, 3부. 뉴욕: 도버, 1973년. (sec 2.6 Petrie Polygons 페이지 24–25 및 12장, 페이지 213–235, 일반화된 Petrie Polygon)
Coxeter, H. S. M. & Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9. (1차 에드, 1957년) 5.2 페트리 폴리곤 {p,q}.
존 밀너: 매듭의 전체 곡률에 대해서, 앤. 수학 52 (1950) 248–257.
J.M. 설리번: 유한 총 곡률, ArXiv:math.0606007v2

외부 링크

[rcp-1] 일반 복합 폴리토페스, 페이지

[2] 추상 일반 폴리토페스, 페이지 217

[1]

[2]

Search