잘린 삼옥각 타일링
Truncated trioctagonal tiling| 잘린 삼옥각 타일링 | |
|---|---|
 쌍곡면의 푸앵카레 디스크 모델 | |
| 유형 | 쌍곡선 균일 타일링 |
| 꼭지점 구성 | 4.6.16 |
| 슐레플리 기호 | tr{8,3} 또는 { |
| 와이토프 기호 | 2 8 3 |
| 콕시터 다이어그램 | |
| 대칭군 | [8,3], (*832) |
| 이중 | 3-8키스롬빌 주문 |
| 특성. | 정점 변환 |
기하학에서 잘린 삼각형 타일링은 쌍곡면의 반정형 타일링이다. 각 꼭지점에는 정사각형 1개, 육각형 1개, 육각형 16면체 1개가 있다. 그것은 tr{8,3}의 Schléfli 기호를 가지고 있다.
대칭
이 타일링의 이중인 3-8 kisrhombille 순서는 [8,3] (*832) 대칭의 기본 영역을 나타낸다. 거울 제거와 교대로 [8,3]부터 구성된 3개의 작은 지수 부분군이 있다. 이러한 이미지에서 기본 도메인은 흑백으로 번갈아 가며 색상의 경계에는 거울이 존재한다.
[8,3*]로 구성된 큰 지수 6 부분군은 [(4,4,4)], (*444)가 된다. 중간 지수 3 부분군은 [8,3⅄]로 구성되며, 2/3의 청색 미러가 제거된다.
| 색인 | 1 | 2 | 3 | 6 | |
|---|---|---|---|---|---|
| 도표 | 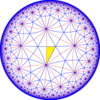 | 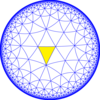 |  | 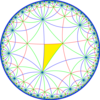 |  |
| 콕시터 (svifold) | [8,3] = (*832) | [1+,8,3] = (*433) | [8,3+] = (3*4) | [8,3⅄] = (*842) | [8,3*] = (*444) |
| 직접 부분군 | |||||
| 색인 | 2 | 4 | 6 | 12 | |
| 도표 |  |  |  |  | |
| 콕시터 (svifold) | [8,3]+ = (832) | [8,3+]+ = (433) | [8,3⅄]+ = (842) | [8,3*]+ = (444) | |
3-8키스롬빌 주문
| 잘린 삼옥각 타일링 | |
|---|---|
 | |
| 유형 | 이중 반정형 쌍곡선 타일링 |
| 얼굴 | 직삼각형 |
| 가장자리 | 무한 |
| 정점 | 무한 |
| 콕시터 다이어그램 | |
| 대칭군 | [8,3], (*832) |
| 회전군 | [8,3]+, (832) |
| 이중 다면체 | 잘린 삼옥각 타일링 |
| 면 구성 | V4.6.16 |
| 특성. | 면직의 |
3-8 kisrhombille 오더는 쌍곡면의 반정형 이중 타일링이다. 각 꼭지점에서 4개, 6개, 16개의 삼각형이 만나는 합치 우측 삼각형으로 구성된다.
이미지는 쌍곡면의 푸앵카레 디스크 모델 투영을 보여준다.
각 직각 삼각형 면에는 정점의 세 가지 유형이 있기 때문에 V4.6.16이라는 레이블이 붙는다. 하나는 4개의 삼각형을 가지고 있고, 하나는 6개의 삼각형을 가지고 있고, 다른 하나는 16개의 삼각형을 가지고 있기 때문이다. 잘린 삼옥각형 타일링의 이중 다듬기인데, 각 꼭지점에 정사각형 1개와 팔각형 1개, 육각형 1개가 있다.
이름 지정
대체 명칭은 콘웨이가 3-8 kisrhombille로 보고 3-8 rhombic tiling으로 보고 kis 연산자로 나누어 각 rhombus에 중앙점을 추가하고 4개의 삼각형으로 나눈다.
관련 다면체 및 틸팅
이 타일링은 [8,3] 쌍곡 대칭과 3개의 대칭[1+,8,3], [8,3+] 및 [8,3]+으로 구성된 10개의 균일한 기울기 중 하나이다.
| 균일한 팔각/삼각형 틸팅 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 대칭: [8,3], (*832) | [8,3]+ (832) | [1+,8,3] (*443) | [8,3+] (3*4) | ||||||||||
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} | tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
| 균일 듀얼 | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
이 타일링은 꼭지점 수치 (4.6.2p)와 Coxeter-Dynkin 도표를 가진 일련의 균일한 패턴의 구성원으로 간주될 수 있다. p < 6의 경우, 시퀀스의 구성원은 구면 기울기로서 아래에 표시된 전위절제 다면체(조노헤드론)이다. p > 6의 경우 잘린 3헥타르 타일링부터 시작하여 쌍곡면의 기울기이다.
| *n32 전분해 틸팅의 대칭 변이: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] | 구면 | 유클리드 | 콤팩트 하이퍼브. | 파라코. | 비대칭 쌍곡선 | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i,3] | [9i,3] | [6i,3] | [3i,3] | |
| 수치 |  |  |  |  |  |  |  |  |  |  |  | |
| 구성. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| 듀얼스 |  |  |  |  |  |  |  |  |  |  |  |  |
| 구성. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.1987 | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
참고 항목
| 위키미디어 커먼즈에는 Uniform tiling 4-6-16과 관련된 미디어가 있다. |
| 위키미디어 커먼즈에는 Uniform dual tiling V 4-6-16과 관련된 미디어가 있다. |
참조
- 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭, ISBN978-1-56881-220-5 (19장, 쌍곡선 아르키메데스 테셀레이션)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
외부 링크
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- 쌍곡선 및 구형 타일링 갤러리
- KaleidoTile 3: 구형, 평면 및 쌍곡선 기울기를 만드는 교육용 소프트웨어
- 쌍곡 평면 테셀레이션, 돈 해치





