심플렉스

기하학에서, 심플렉스(복수: 심플렉스 또는 단순)는 삼각형 또는 사면체의 개념을 임의의 차원으로 일반화한 것입니다.심플렉스는 주어진 치수에서 선 세그먼트로 만들어진 가장 단순한 폴리토프를 나타내기 때문에 이렇게 명명되었습니다.

예를들면,

• 0~160x는 포인트입니다.
• 1-610x는 선분입니다.
• 2제곱x는 삼각형입니다.
• 3제곱x는 사면체입니다.
• 4비트x는 5셀입니다.

구체적으로, k-심플렉스는 k + 1 정점의 볼록 선체인 k 차원 폴리토프이다.좀 더 형식적으로 k + 1 $포인트{\displaystyle {}_{}}$ ${\displaystyle {u\mathrm{}}_{}}$0${\displaystyle }$,${\displaystyle }$… , ${\displaystyle u_{}}$ k${\displaystyle {}_{}{\mathbb{}}^{}}$ ${\displaystyle {}^{}}$k , \ $displaystyle u$_ {$0$${\displaystyle {}_{}}$, \ $dots$$, u$_ { $k$} \ $in$\$mathbb${ $R$$}^$ {$k$$$}가 친화적으로 독립되어 있다고 가정합니다.$즉{\displaystyle {}_{}}$, ${\displaystyle u_{}{}_{}{}_{}{}_{}}$-$$ 0 , ${\displaystyle ...}$ ,${\displaystyle }$u { $displaystyle u u$u$$}$입니다.$그러면 이들에 의해 결정되는 심플렉스는 포인트 집합이다.

$({displaystyle C=\left\{\theta _{0}u_{k}+\theta +\theta _{k}~{\Bigg }~\sum _{i=0}^{k}\theta _{i}=1gmbox{ 및 }}})는 다음과 같습니다.$

가중 꼭지점의 관점에서 이러한 표현을 중심 좌표계라고 한다.

일반^[1] 심플렉스는 일반 폴리토프이기도 한 심플렉스입니다.새로운 정점을 모든 원래 정점에 공통 가장자리 길이로 연결함으로써 정규 k-심플렉스를 정규(k - 1)-심플렉스로 구성할 수 있다.

표준 심플렉스 또는 확률 심플렉스는 정점이 k 표준 단위 벡터인 k - 1차원 심플렉스이다.

${\displaystyle \left\in \mathbb {R}^{k:x_{0}+\display +x_{k-1}=1,x_{i}\geq 0 」텍스트{}i=0,\displaystyle,k-1\right\}.}$

topology와 combinatorics에서는 심플한 콤플렉스를 형성하기 위해 심플한 것을 「접합」하는 것이 일반적입니다.연관된 조합 구조는 추상 단순 복합체라고 불리며, 여기서 "simplex"라는 단어는 단순히 유한한 정점 집합을 의미합니다.

역사

심플렉스의 개념은 윌리엄 킹던 클리포드에 의해 알려졌는데, 그는 1886년에 이 모양들에 대해 썼지만 "주요 경계"라고 불렀다.앙리 푸앵카레는 1900년에 대수적 위상에 대해 쓴 글에서 그것들을 "일반화된 사면체"라고 불렀다.1902년 피에터 헨드릭 슈테는 이 개념을 처음에는 라틴어 최상급 단순어("simplest")로 기술한 후, 같은 라틴어 형용사를 심플렉스("simply")^[3]로 기술했다.

정규 심플렉스 패밀리는 도널드 콕서터에 의해 α로 표시된_n 세 개의 정규 폴리토프 패밀리의 첫 번째 패밀리와 β로 표시된_n 교차 폴리토프 패밀리와 β로_n 표시된 하이퍼큐브이다.네 번째 패밀리, 무한히 많은 하이퍼큐브에 의한 n차원 공간의 테셀레이션, 그는 ^[4]δ라고_n 이름 붙였다.

요소들

n-단순을 정의하는 n + 1 점의 비어 있지 않은 부분 집합의 볼록한 선체를 심플렉스의 면이라고 합니다.얼굴 자체는 단순하다.특히 크기 m + 1(n + 1 정의점)의 부분 집합의 볼록한 선체는 n-단순의 m-면이라고 불리는 m-단순이다.0-면(즉, 크기 1의 집합으로 정의되는 점 자체)은 정점(단일: 정점), 1-면은 가장자리, (n - 1)-면은 면, 유일한 n-면은 전체 n-단순함이다.일반적으로 m-faces의 수는 ${\displaystyle 이항계수\genfrac{}{}{0ex}{}{(\mathrm{n}}{}}$ + ${\displaystyle \genfrac{}{}{0ex}{}{\mathrm{m}}{}}$ +${\displaystyle \genfrac{}{}{0ex}{}{}{}}$1)$${displaystyle ${tbinom {n+1}{m+1$^[5]와 같습니다.$따라서$ n-simplex의 m-faces의 수는 파스칼 삼각형의 행(n + 1)의 열(m + 1)에 있습니다.B가 A의 면이라면 A는 B의 면이다.단순 복합체의 단순화 유형을 설명할 때 면과 면은 서로 다른 의미를 가질 수 있습니다. 자세한 내용은 단순 복합체를 참조하십시오.

n-simplex의 1면수(edge)는 n번째 삼각형수이고, n-simplex의 2면수(edge)는 n번째 사면체수이며, n-simplex의 3면수(edge)는 n번째 5셀수이다.

n-Simplex 요소^[6]

Δn	이름.	슐레플리 콕서터	0- 얼굴 (표준)	1- 얼굴 (표준)	2- 얼굴 (얼굴)	3- 얼굴 (표준)	4- 얼굴	5- 얼굴	6- 얼굴	7- 얼굴	8- 얼굴	9- 얼굴	10- 얼굴	합 = 2n+1 - 1
Δ0	0 ~ 160x (포인트)	( )	1											1
Δ1	1160x (선분)	{ } = ( ) ∨ ( ) = 2 ⋅ ( )	2	1										3
Δ2	2배속 (표준)	{3} = 3 ⋅ ( )	3	3	1									7
Δ3	31200x (4면체)	{3,3} = 4 ⋅ ( )	4	6	4	1								15
Δ4	41200x (5셀)	{33} = 5파운드 ( )	5	10	10	5	1							31
Δ5	51200x	{34} = 6파운드 ( )	6	15	20	15	6	1						63
Δ6	61200x	{35} = 7 † ( )	7	21	35	35	21	7	1					127
Δ7	71200x	{36} = 8파운드 ( )	8	28	56	70	56	28	8	1				255
Δ8	8180x	{37} = 9 ⋅ ) ( )	9	36	84	126	126	84	36	9	1			511
Δ9	9169x	{38} = 10 † ( )	10	45	120	210	252	210	120	45	10	1		1023
Δ10	10-1996x	{39} = 11 ⋅ ) ( )	11	55	165	330	462	462	330	165	55	11	1	2047

일반인의 용어로, n-심플렉스는 n개의 차원이 필요한 단순한 모양(다각형)입니다.선분 AB를 1차원 공간의 "모양"으로 간주합니다(1차원 공간은 세그먼트가 있는 선입니다).새로운 점 C는 선에서 벗어난 곳에 배치할 수 있습니다.새로운 형태인 삼각형 ABC는 2차원을 필요로 한다; 원래의 1차원 공간에 들어갈 수 없다.삼각형은 2차원을 필요로 하는 단순한 모양인 2-심플렉스입니다.2차원 공간(삼각형이 있는 평면)의 도형인 삼각형 ABC를 생각해 보십시오.비행기에서 떨어진 어딘가에 새로운 점 D를 배치할 수 있습니다.새로운 형태인 사면체 ABCD는 3차원이 필요합니다. 원래 2차원 공간에 들어갈 수 없습니다.4면체는 3차원을 필요로 하는 단순한 형태인 3심플렉스이다.3차원 공간(사면체가 있는 3차원 공간)의 형상인 사면체 ABCD를 생각해 보십시오.새 점 E를 3공간 바깥 어딘가에 배치할 수 있습니다.5셀이라고 불리는 새로운 형태의 ABCDE는 4차원을 필요로 하고 4차원으로 불린다; 그것은 원래의 3차원 공간에 들어갈 수 없다.(또한 쉽게 시각화할 수 없습니다.)이 아이디어는 일반화할 수 있습니다.즉, 현재 점유하고 있는 공간 외부에 새로운 점을 하나 추가함으로써 새로운 형상을 유지하기 위해 다음으로 높은 차원으로 이동해야 합니다.이 아이디어는 역방향으로도 사용할 수 있습니다.처음 시작한 선분은 1차원 공간을 필요로 하는 심플한 형태입니다.선분은 1심플렉스입니다.선분 자체는 0차원 공간의 단일 점(이 초기 점은 0-simplex)에서 시작하여 두 번째 점을 추가함으로써 형성되었으며, 1차원 공간으로 증가해야 했습니다.

보다 형식적으로는 (n+1)-심플렉스를 n-심플렉스와 점의 결합(θ 연산자)으로 구성할 수 있으며 ()-심플렉스는 m-심플렉스와 n-심플렉스의 결합으로 구성할 수 있다.두 단순화는 서로 완전히 정규 분포를 따르도록 배치되어 있으며, 두 단순화와 직교하는 방향으로 변환됩니다.1-sqx는 2개의 포인트의 결합입니다. ( ) = 2 ( （ ） 。일반적인 2-심플렉스(scalene triangle)는 3개의 점( ( )의 결합입니다.이등변삼각형은 1심플렉스와 점 { } ( ( )의 결합입니다.정삼각형은 3µ ( ) 또는 {3}입니다.일반적인 3-심플렉스는 ( ) ( ( ) ( ( ) ( ( ) ( ( )의 4개의 점의 결합입니다.거울 대칭을 가진 3-심플렉스는 에지의 결합으로, 삼각 대칭을 가진 3-심플렉스는 정삼각형과 1: 3( )의 결합으로 표현할 수 있습니다.정4면체는 4µ( ) 또는 {3,3} 등입니다.

위 표의 면 수는 왼쪽 대각선 없이 파스칼의 삼각형과 동일합니다.

면의 총수는 항상 2 빼기 1의 거듭제곱입니다.이 그림(테서랙트의 투영)은 사면체의 15개 면의 중심체를 보여준다.

규칙에 ^[7]따라 빈 집합은 (-1)-simplex로 정의됩니다.위의 심플렉스의 정의는 n = -1인 경우에도 여전히 의미가 있습니다.이 규칙은 폴리토프의 연구보다 대수적 위상(단순 호몰로지 등)에 적용하는 데 더 일반적이다.

규칙 단순화의 대칭 그래프

이러한 Petrie 폴리곤(스큐 직교 투영)은 원에 있는 일반 심플렉스의 모든 정점과 모서리로 연결된 모든 정점 쌍을 표시합니다.

1	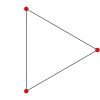2	3	4	5
6	7	8	9	10
11	12	13	14	15
16	17	18	19	20

표준 심플렉스

표준 n-simplex(또는 단위 n-simplex)는 다음과 같이 주어진 R의ⁿ⁺¹ 서브셋이다.

$\displaystyle \Delta ^{n}=\left\{(t_{0},\display,t_{n})\in \mathbb {R}^{n+1}~{\\\\Bigg }~\sum _{i=0}^{n}t_{i}=1개 텍스트{및 }}t_{i}\geq 0개 텍스트{}i=0,\ldots,n\right\}}$

심플렉스 Ω은ⁿ 위의 정의에서 제한_i t 00을 삭제하여 얻은 아핀 하이퍼플레인에 있습니다.

표준 n-simplex의 n + 1 정점은 e rⁿ⁺¹ R 지점이다_i.

e₀ = (1, 0, 0, 0, ..., 0),

e₁ = (0, 1, 0, ..., 0),

⋮

e_n = (0, 0, 0, ..., 1)

표준 n-simplex에서 임의의 n-simplex로의 표준 맵은 다음과 같이 주어진 정점(v₀, ..., v_n)을 가진다.

$\displaystyle (t_{0},\ldots,t_{n}\mapsto \sum _{i=0}^{n}t_{i}v_{i}}$

계수_i t를 n-단순에서 점의 중심 좌표라고 합니다.이러한 일반 심플렉스는 표준 맵이 아핀 변환임을 강조하기 위해 종종 아핀 n-심플렉스라고 불린다.표준 맵이 방향을 보존하거나 반전할 수 있음을 강조하기 위해 방향성 아핀 n-심플렉스라고도 합니다.

보다 일반적으로, 표준${\displaystyle }$(${\displaystyle n}$ ${\displaystyle -1}$)$${$displaystyle (n-1)}$ -simplex$$ (n개의 정점이 있는)에서 n개의 정점이 있는 임의의 폴리토프까지의 표준 맵이 있으며, 동일한 방정식(색인 수정)에 의해 주어진다.

$\displaystyle(t_{1},\ldots,t_{n})\mapsto \sum _{i=1}^{n}t_{i}v_{i}}$

이것들은 일반화된 중심 좌표라고 불리며$,$ 모든 폴리토프를 심플렉스의 이미지로 나타냅니다. ${\displaystyle {\delta }^{}}$ n${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$† ${\displaystyle P}$.$$\ $displaystyle$\$Delta$^ {$n-1}$ \ $twohead$ right $arrow$ P }

R에서ⁿ 표준${\displaystyle }$내부(${\displaystyle n}$ ${\displaystyle -1}$) ${displaystyle (n-1)}$ -simplex까지$$ 일반적으로 사용되는 함수는 softmax 함수 또는 정규화된 지수 함수이며, 이는 표준 로지스틱 함수를 일반화합니다.

예

• δ는 R의¹ 점 1이다⁰.
• δ는¹ R의 선분 결합(1, 0) 및 (0, 1²)입니다.
• δ는² R의 정점(1, 0, 0), (0, 1, 0) 및 (0, 0³, 1)을 갖는 정삼각형이다.
• δ는³ 정점(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0) 및 (0, 0, 0, 0, 1)이⁴ R에 있는 정4면체이다.
• δ는⁴ 정점(1, 0, 0, 0, 0, 0), (0, 0, 0, 0, 0, 0), (0, 0, 0, 1, 0), (0, 0, 0, 1, 0) 및 (0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1)을⁵ R로 하는 정규 5 셀입니다.

좌표 증가

대체 좌표계는 무기한 합계를 취함으로써 주어진다.

${\displaystyle\s{0}s_{0}&=0\s_{1}&=s_{0}+t_{0}}=t_{0}\s_{2}&=s_{1}+t_{1}}=t_{0}+t_{1}\\s_{3}&=s_{2}+t_{2}}=t_{0}+t_{1}+t_{2}\\&\;\vdots \\s_{n}&=s_{n-1}+t_{0}+t_{1}+\cdots + t_{n-1}\s_{n+1}&=s_{n}+{n}+cdots + cdots_{cdots$

이를 통해 순서별로 대체 표현을 할 수 있습니다.즉, 0과 1 사이의 n-tuples가 해제되지 않습니다.

$\displaystyle \Delta _{*}^{n}=\left\{(s_{1}\ldots,s_{n}\mid 0=s_{0}\leq s_{2}\leq \leq \leq s_{n}\left\{n}\in \mathbbbb {R}\mid 0=s_{n}}$

기하학적으로 이것은 R${\displaystyle {}^{}}$ + $({$ 스타일$$$\mathbb {R})$이$아닌$R $($ 치수, 코드 확장 0)의 n차원 서브셋이다.표준 심플렉스에서 하나의 좌표 소실(${\displaystyle t_{}}$ i $=$ ${\displaystyle 0}$ ${\displaystyle ,}$여기서 {$displaystyle t_{i$}=$0,})$에 해당하는 패싯은 연속 좌표가 동일한 ${\displaystyle s_{}}$ i$=$ ${\displaystyle s_{}}$ +${\displaystyle {}_{}{1}_{}}$, {$display s_${i} =$s_{i+$1}인$$ 반면, 내부는 엄격해지는 불평등(증가 시퀀스)에 해당합니다.

이들 프레젠테이션의 주요 차이점은 좌표를 허용하는 동작입니다.표준 심플렉스는 좌표를 허용함으로써 안정화되지만, "순서 있는 심플렉스"의 요소는 일반적으로 순서가 매겨지지 않으므로 불변하게 두지 않습니다.실제로, 순서 심플렉스는 n-입방체에서의 대칭 그룹의 작용을 위한 (닫힌) 기본 도메인이다. 즉, 대칭 그룹의 n! 요소 아래의 순서 심플렉스의 궤도가 n-입방체를 n$!\displaystyle$ n$!$으로 나눈다는 것을 의미하며, 이 단순체는 (경계를 제외한) 대부분 분리된 단순함을 나타낸다.$volume{\displaystyle \mathrm{}}$1/$n$!\$displaystyle$ 1/n$$$!}$ 또는 반복 적분에 의해 볼륨을 계산할 수 있습니다.${\displaystyle {}^{}}$ 대신, 연속되는 $적분$은${\displaystyle 1}$, ${\displaystyle {}^{}}$ ${\displaystyle {x\mathrm{}}^{}}$ ${\displaystyle {}^{}}$/${\displaystyle {}^{}x\mathrm{}}$ 3${\displaystyle }$/${\displaystyle }$3 ${\displaystyle !,{}^{}{x}^{}}$ n${\displaystyle }$/ n$!(\displaystyle$ 1$,x,x^{2}/2,x^3$}/$3,\dots,x^{n}/n!)$입니다.

이 프레젠테이션의 또 다른 특성은 덧셈이 아닌 순서를 사용한다는 것입니다.따라서 임의의 순서 집합에 대해 임의의 차원으로 정의할 수 있으며, 예를 들어 합계의 수렴 문제가 없는 무한 차원 심플렉스를 정의하는 데 사용할 수 있습니다.

표준 심플렉스에 투영

특히 확률론의 수치적 적용에서 표준 심플렉스에 대한 투영법이 흥미롭다.( ${\displaystyle p_{}{}_{}}$i ) ${\displaystyle i_{}}${ $displaystyle$($p$_ {$i$}$_${ i$$ }${\displaystyle }$( ( 、 심플렉스 상의 가장 ${\displaystyle {{}_{}}_{}}{\displaystyle {}_{}}$점 (${\displaystyle {{}_{}{t}_{}}_{}}$ $i$) i \$displaystyle \ left$ ( $t _$ { i } \ right )$_$$${ i$}$ 에는 좌표가 있습니다.

$\displaystyle t_{i}=\max\{p_{i}+\Delta \,0\}$

여기서$\delta {\displaystyle \mathrm{}}$ \ $displaystyle$\ $Delta }$는$\underset{}{}i$ i$$max { ${}_{}{i}_{}$ + $\mathrm{\delta }\}$ $=1$.$${ $textstyle \sum$_ { $i$} \ $max$\ { $p$_ i$$} + \ $Delta$\ , 0 \ } $=$$1$ 로 선택됩니다.$}$

$δ$\ $displaystyle$\$$^[8]Delta$$ $}$ 은 정렬$pi$에서 ${\displaystyle {쉽게}_{}}$ $계산$할 수 ${\displaystyle \mathrm{있습니다}}$.정렬 방법에는${\displaystyle O}$(${\displaystyle n}$ ${\displaystyle \log )}$ n$)$ {\$displaystyle$ O$(n\log$ n$)}$의 복잡도가 $필요$하며, 중앙값 검색 알고리즘을 ^[9]통해 O$)$ {\$displaystyle$ O$(n)}$의 복잡도로 $개선$할 수 있습니다.심플렉스에 투영하는 것은 § $(\$$})$ 볼에 투영하는 것과 계산적으로 유사합니다.

입방체 모서리

마지막으로 간단한 변형은 "summing to 1"을 "summing to most 1"로 대체하는 것입니다. 그러면 치수가 1씩 상승하므로 표기법을 단순화하기 위해 인덱스가 변경됩니다.

$\displaystyle \Delta _{c}^{n}=\left\{(t_{1}\ldots,t_{n}\in \mathbb {R}^{n}~{\Bigg}~\sum _{i=1}^{n}\leq 1개 텍스트 {및 }\leq}\t_{i}\gtht_{n}\gtht_{n}\gth} gth} gth} 。}$

이 값은 n-simplex를 n-입방체의 모서리로 나타내며, 표준 직교 심플렉스탠다드 직교 심플렉스입니다.이는 원점에 기반을 두고 n개의 패싯을 가진 폴리토프 상의 정점을 로컬로 모델링하는 심플렉스 방법에 사용되는 심플렉스입니다.

R의ⁿ 정규 n차원 심플렉스에 대한 데카르트 좌표

R에ⁿ 규칙 n-심플렉스를 쓰는 한 가지 방법은 처음 두 꼭지점이 될 두 점을 선택하고, 등변 삼각형을 만들 세 번째 점을 선택하고, 규칙 4면체를 만들 네 번째 점을 선택하는 것입니다.각 단계는 이전에 선택된 정점과 함께 새롭게 선택된 각 정점이 정규 심플렉스를 형성하도록 보장하는 만족스러운 방정식을 필요로 합니다.이 목적을 위해 기록하고 사용할 수 있는 방정식 세트가 몇 가지 있습니다.여기에는 정점 사이의 모든 거리의 동일성, 심플렉스의 중심까지의 모든 거리의 동일성, 이전에 선택된 두 정점에 의해 새로운 정점을 통해 기울어진 각도가${\displaystyle }\theta {\displaystyle }$ /$$$3$이라는 사실, 그리고 $시뮬레이션$의 중심을 통해 기울어진 각도가 포함됩니다$.$임의의 2개의 정점에 의한 플렉스는 ${\displaystyle \arccos }$ ${\displaystyle (}$( -${\displaystyle 1}$ /${\displaystyle n}$ $){$ $displaystyle \arccos(-$1/$n$ 입니다.

또한 R에 특정ⁿ 정규 n-simplex를 직접 기록할 수 있으며, 이 경우 원하는 대로 변환, 회전 및 스케일링이 가능합니다.이를 위한 한 가지 방법은 다음과 같습니다.R의 기저ⁿ 벡터를 e~e로_n 나타낸다₁.basis 벡터의 볼록한 껍질인 standard (n - 1)-simplex부터 시작한다.추가 정점을 더함으로써, 이것들은 정규 n-단순의 면이 된다.추가 정점은 표준 심플렉스의 중심과 수직인 선 위에 있어야 하며, 따라서 어떤 실수 α에 대해 (α/n, ..., α/n) 형태를 가집니다.두 개의 기저 벡터 사이의 제곱 거리는 2이므로, 추가 정점이 규칙 n-단순을 형성하기 위해서는, 그것들과 기저 벡터 사이의 제곱 거리 또한 2가 되어야 한다.이것은 α에 대한 2차 방정식을 산출한다.이 방정식을 풀면 추가 정점에 대해 두 가지 선택사항이 있음을 알 수 있습니다.

${\displaystyle {\frac {1}{n}}\left(1\pm {n+1}\오른쪽)\cdot(1,\cdot,1)}$

이들 중 하나는 표준 기저 벡터와 함께 규칙적인 n-단순을 산출한다.

위의 정규 n-simplex는 원점을 중심으로 하지 않습니다.정점의 평균을 빼서 원점으로 변환할 수 있습니다.재스케일링으로 단위측 길이를 지정할 수 있습니다.따라서 정점이 다음과 같은 심플렉스가 생성됩니다.

${\displaystyle {\fracrt {2}}\mathbf {e}_{i}-{\frac {1}{nfrcrt {n+1}{\bigg}}\cdot(1,\frac {1})$

$1{\displaystyle \mathrm{}i}$ i ${\displaystyle 、}$n \ $display$ 1 \ $leq$i \ $leq$ n$$、

${\displaystyle\pm {1}{\displayrt {2(n+1)}}\cdot(1,\cdot,1)}$

여기서 설명하는 두 가지 정점 세트가 있습니다.한 세트는 각 계산에서$$+(\$displaystyle +)$를 사용합니다$.{\displaystyle }$다른 세트는 각 계산에 -$\displaystyle$ -$}$을 사용합니다$$.

이 심플렉스는 $반지름n{\displaystyle \sqrt{}}$/${\displaystyle \sqrt{}}$( ${\displaystyle \sqrt{2}}$(${\displaystyle \sqrt{n}}$ +${\displaystyle \sqrt{1}}$)$${ $displaystyle${$sqrt {n$/ ( $2 ( n$ + 1$)$} $\}$ 의 하이퍼스피어에 새겨져 있습니다.

다른 재스케일링은 단위 초저공에 내접된 심플렉스를 생성합니다.이 작업이 완료되면 꼭지점은 다음과 같습니다.

${\displaystyle {1+n^{-1}}\cdot \mathbf {e}_{i}-n^{-3/2}({\displayrt {n+1}}\pm 1)\cdot(1,\cdisplay,1)}$

$여기$서 1${\displaystyle i}$ i $、$ \ $display$ 1 \ $leq$i \ $leq$ n$、$

$\displaystyle \pm n^{-1/2}\cdot(1,\cdot,1)}$

이 심플렉스의 측면 길이는 2$\sqrt{}$($\sqrt{\mathrm{n}}$ $\sqrt{+}$1) $\sqrt{/}$ {\$textstyle {2(n+1)/n$ 입니다.

규칙 n-단순을 구성하는 매우 대칭적인 방법은 직교 행렬에 의한 순환군_n+1 Z의 표현을 사용하는 것입니다.이것은 Q = I가ⁿ⁺¹ 항등행렬인 n × n 직교행렬 Q이지만, Q의 낮은 거듭제곱은 아니다. 이 행렬의 거듭제곱을 적절한 벡터 v에 적용하면 정규 n-제곱x의 정점이 생성된다.이를 수행하려면 먼저 직교 행렬 Q에 대해 Q가 블록 대각 행렬인 기준의 선택이 있는지 관찰하십시오.

${{displaystyle Q=\operatorname {diag}(Q_{1},Q_{2},\dots,Q_{k}),}$

여기서 각_i Q는 직교이며 2 × 2 또는 1 × 1 중 하나입니다.Q의 차수가 n + 1이 되려면 이 모든 행렬의 차수가 n + 1이어야 합니다.따라서_i 각 Q는 엔트리가 1인 1 × 1 행렬이거나, n이 홀수인 경우 -1이거나, 또는 형식의 2 × 2 행렬이다.

$({displaystyle {pmatrix}\cos {frac {2\pi \opha _{i}}{n+1}}&\sin {frac {2\pi \opha _{i}}{n+1}}\sin {frac {2\pi \opha _i {i}}}{n+1})\cos {pmatrix {pm1}\cos {f}$

여기서 각 θ는_i 0과 n 사이의 정수입니다.점의 궤도가 정칙 심플렉스가 되기 위한 충분한 조건은 행렬_i Q가 Z의_n+1 비삼차적 불가분실표현의 기초를 형성하고 회전하는 벡터가 어느 것에 의해서도 안정화되지 않는 것이다.

실제 용어로, n 이마저도 모든_i 행렬 Q가 2 × 2라는 것을 의미하며, 집합의 등식이 존재한다.

${\displaystyle \{1},n+1-\Omega _{1},\displays,\Omega _{n/2},n+1-\Omega _{n/2}\}=\{1,\displays,n\}$

또한_i 모든 Q에 대해 Q가 동작하는v_i 엔트리는 둘 다 0이 아닙니다.예를 들어, n = 4일 때, 하나의 가능한 행렬은 다음과 같습니다.

$(\displaystyle {pmatrix}\cos(2\pi /5)&-\sin(2\pi /5)&\cos(2\pi /5)&\cos(0\pi /5)&\sin(4\pi /5)&\sin(4\pi /5)&5/0\pi /0\pi (5)&0\cos(0\pi /5)&5)&pi /0\pi /0\pi (5)&0\pi /0\pi (\pi (\pi (0)&5)&pi (0)}$

이를 벡터(1, 0, 1, 0)에 적용하면 정점이 다음과 같은 심플렉스가 생성됩니다.

$\displaystyle {pmatrix} 1 \ \ \ \ \ \ \ \ \ \ \ cos ( 2 \ pi / 5 ) \ \ sin ( 4 \ pi / 5 ) \ \ sin ( 4 \ pi / 5 ) \ \ \ \ \ sin ( 4 \ pi / 5 ) \ \ \ \ \ \ pmatrix \ pi 4 \ 5 } cos 4 . 5 )5)\\sin(8\pi/5)\\cos(6\pi/5)\sin(6\pi/5)\end{pmatrix}}$

각각 5파운드의 거리를 가지고 있다.n이 홀수일 경우 이 조건은 대각선 블록 중 정확히 하나가 1 × 1, -1이고 v의 0이 아닌 엔트리에 작용함을 의미합니다. 반면 나머지 대각선 블록(예를₁ 들어 Q_{(n − 1) / 2}, ..., Q)은 2 × 2인 반면 집합은 동일합니다.

${\displaystyle \left\{1},-\Omega_{1},\obe,\obe_{n-1)/2}\right\}=\left\{1,\obe,(n-1)/2,(n+3)/2,\obe,\right\}$

각 대각 블록은 둘 다 0이 아닌 v 엔트리의 쌍에 작용합니다.따라서, 예를 들어, n = 3일 때, 행렬은 다음과 같을 수 있습니다.

$(\displaystyle {pmatrix} 0&-1&0&0&0&0\end {pmatrix})}$

벡터(1, 0, 1/µ2)의 경우 결과 심플렉스는 정점을 가진다.

${\displaystyle {pmatrix}1\\0/\surd 2\end{pmatrix}, {\surd {pmatrix}0\1\1/\surd 2\end {pmatrix}, {\surd 2\pmatrix}-1/{pmatrix}\1/\1/\surd 2\1\1/\surd {pmatrix}1\1/\1\1\surd {pmatrix}$

각각 2의 거리를 가지고 있습니다.

기하학적 특성

용량

꼭지점 (v₀, ..., v_n)이 있는 n차원 공간에서의 n-심플렉스의 부피는 다음과 같다.

${\displaystyle \mathrm {Volume} = flac {1}{n!}}\left \det {pmatrix}v_{1}-v_{0}&v_{2}-v_{0}&\cdots &\end {pmatrix}\right }$

여기서 n × n 행렬식의 각 열은 정점₀ v에서 다른 정점_k ^[10]v를 가리키는 벡터이다.이 공식은 v $({$이 원본일 때 $특히{\displaystyle {}_{}}$ 유용합니다.

표현

${\displaystyle \mathrm {Volume} = flac {1}{n!}}\det \left[{\begin{pmatrix}v_{1}^{T}-v_{0}^{T}\\v_{2}^{T}-v_{0}^{T}\\vdots\\v_{n}^{T}-v_{0}^{T}\end{pmatrix}{\begin{pmatrix}v_{1}-v_{0}&v_{2}-v_{0}&\cdots &\cdots &\{n}-v_{0}\end{pmatrix}\right]^1/2}$

는 그램 행렬식을 사용하며, 예를 들어 ${\displaystyle {\mathrm{}}^{}}$ 3$(\$의 삼각형과 같이 n개 이상의 차원을 가진 유클리드 공간에 있는 경우에도 작동합니다.

${\displaystyle {}^{}}$ n$$\$displaystyle \mathbb {R}^{n}$에서 n-simplex의 부피를 계산하는 보다 대칭적인 방법은 다음과 같습니다.

${\displaystyle \mathrm {Volume} = {1 \over n!}\left \det {pmatrix}v_{0}&v_{1}&\cdots &\1&\cdots &1\end{pmatrix}\right .}$

심플렉스의 부피를 계산하는 또 다른 일반적인 방법은 케이리-멘저 행렬식을 사용하는 것인데, 이것은 n-심플렉스의 정점이 ^[11]n차원 이상의 유클리드 공간에 있을 때에도 작용한다.

1/n!이 없으면 n-병렬로토프의 체적에 대한 공식입니다.이는 다음과 같이 이해할 수 있습니다.P가 ($v$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {e\mathrm{}}_{}}$1,${\displaystyle \dots ,}$ ${\displaystyle e_{}}$ n$)$ $(\$$displaystyle$ ($v_{0, e_{$1},\$ldots, e_{$n})의 기준$(\backslash {\displaystyle }$$displaystyle$$$\$mathbbb$${R}^{n$$})$으로 구성되었다고 가정합니다${\displaystyle .}$변환된 {\$style{\displaystyle }$ \sigma$}$은 ${\displaystyle 1,}$${\displaystyle {v\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$, ${\displaystyle \text{v}{}_{}{1\mathrm{}}_{}}$ , ${\displaystyle ...}$ , ${\displaystyle v_{}}$n { $display style$ v _ { $0$, \ v$_$ { $1$, \$ldots$,$v$$$_ { $n$} 、 n - path :

$\displaystyle v_{1}=v_{0}+e_{\display(1)\v_{1}+e_{\display(2)},\ldots,v_{n}=v_{n-1}+e_{\display(n)}}$

(따라서 n!$n-displaystyle v_{n}$은(는) 치환에 의존하지 않습니다).다음의 어설션이 유효합니다.

P가 단위 n-하이퍼큐브일 경우, 각 n-경로의 볼록한 껍질에 의해 형성된 n-심플렉스의 결합은 P이며, 이들 심플렉스는 일치하고 쌍으로 ^[12]겹치지 않는다.특히, 이러한 심플렉스의 부피는

${\displaystyle\frac\operatorname{Vol\(P)}{n!}}=black{1}{n!}}.}$

만약 P는 일반적인 parallelotope 있다는 점을 제외하고 더 이상 진실이 아니다 단위의 Rn{\displaystyle의 정준기를 보내는 선형 유질 동상 때문에 업체들은 n-parallelotope는 이미지 n-hypercube, 같은 주장, 치수>에서;2, simplexes에 쌍별 congruent이 필요합니다;지만 그들의 볼륨 같은 여전히 가집니다.\m$athbb {R}^{n}$ ~${\displaystyle {}_{}}$ 1,${\displaystyle \dots ,}$ e$$ {\$displaystyle e_{1},\ldots, e_{n$ 이는 n 경로에서 오는 심플렉스의 볼륨이 다음과 같은 것을 의미합니다.

${\displaystyle\frac\operatorname{Vol\(P)}{n!}}=paramfrac {det(e_{1},\ldots,e_{n}}{n!}}.}$

$반대$로, $n$의 n-displaystyle $(v$ 0${\displaystyle {}_{}}$ ${\displaystyle \text{v}{}_{}{1\mathrm{}}_{}}$, ${\displaystyle {v\mathrm{}}_{}}$2,${\displaystyle }$… ${\displaystyle {}_{}{n}_{}}$ $){displaystyle (v_{0},\ v_{1},\ v_{$$n$이 주어진 경우 $벡터{\displaystyle {}_{}}$ ${\displaystyle {e\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}{}_{}{1\mathrm{}}_{}}$ - ${\displaystyle {}_{}}$ ${\displaystyle {v\mathrm{}}_{}{}_{}{}_{}{}_{}}$라고 가정할 수 있습니다.${1}=v_{1}-v_{0},\ e_{$2}=$v_{$2}-$v_{1},\ldots e_{n$}=$v_{n}-v_{n-1}}$은(는) R ${\displaystyle {}^{}}${\$displaystyle \mathbf${R}$^{$n}} {$n$$\}$ 。v_styledisplay 0$${ e e v v_ $v_0}$ $v$ v v v v v_ v_0} { v v v_style로 구성된 병렬 도포트를 고려합니다.x.

마지막으로, 이 섹션의 첫머리에 있는 공식은 다음을 관찰함으로써 얻을 수 있다.

$\displaystyle \det(v_{1}-v_{0},v_{2}-v_{0},\ldots,v_{n}-v_{0}=\det(v_{1}-v_{1}-v_{1},\ldots,v_{n}-{n-1}).}$

이 공식으로부터, 표준 n-simplex(즉, 원점과 R의ⁿ⁺¹ 심플렉스 사이) 아래의 부피는 즉시 다음과 같다.

${\displaystyle {1\over (n+1)!}}$

단위 변의 길이가 있는 일반 n-simplex의 부피는 다음과 같습니다.

$displaystyle(디스플레이 스타일) {frac {n+1}({2^{n}}}}}}}}:$

으로서 xn+1에 의해, n-simplex에 따라 그 꼭지점 거리의 함수로 계산은 발신지에서 볼륨, x에 대하여 차별화,)=1/2{\displaystyle x=1/{\sqrt{2}}}(는n-simplex 면의 길이가 1은)에 정상화 길이 d에 의해 x/n+1{\displ 이전 공식을 곱하여 볼 수 있다.ays( ${\displaystyle d}$ x / (${\displaystyle }$n$$${\displaystyle }$+ ${\displaystyle 1}$) , ${\displaystyle ...}$$$, d x /${\displaystyle }$($$${\displaystyle \mathrm{n}}$ +${\displaystyle }$1 ) \ $displaystyle$ ($display$style /${\displaystyle }$( ${\displaystyle n}$+ ${\displaystyle 1}$ )$$（ $display$ style / ( n + $1$) 、 \$ldots ,$ / / ( n + 1$)$）$$$。{\displaystyle }$

정n-단순의 이면각

정 n차원 단순체의 두 (n - 1)차원 면은 그 자체가 규칙적인 (n - 1)차원 단순체이며, 같은 이면각⁻¹ cos(1/n)^[13][14]를 가진다.

이는 표준 심플렉스의 중심이$$($\frac{1}{}$n +$\frac{}{}\frac{1}{}$,$\dots ,$ $1\frac{\mathrm{}}{n}$ +$\frac{}{}\frac{1}{}$)(\$textstyle$$\left({\frac {1}{n+1}\dots,$ {\$frac {1}{n+$1}\right$)$이고 면의 중심은 ($0\mathrm{},$ $\frac{1}{}$,$)$의$$좌표순열임을 알 수 $있습니다.$$)\}.$ 다음으로 대칭적으로 ($\frac{1}{}$ n$\frac{}{}$+ $\frac{1}{}$, $...$ , $\frac{1}{}$n +$\frac{}{}\frac{1}{}$ )$${ $textstyle \left$( { \ $frac$ { { \ frac {$1}$ {$n$$+1}$, \$$$dots$$$, { \ $frac$ {$1$} )$\}$ ~ ($$0 , $1\frac{\mathrm{}}{}$ $\frac{n}{}$, $...$ , $1\frac{n}{}$ ) { $textstyle \$ ( $0$ , 0 , { 0 , { \ $frac$ { \ frac { \ 1 } ) } { $dots$} ) } { dots } } { dots } { dots } { dots } } } } } 따라서 면에 수직인 벡터는 (${\displaystyle }$-${\displaystyle n}$ ,${\displaystyle 1}$, ${\displaystyle ...}$,$$ ) {$displaystyle$( -$n$ ,$1$ , \$dots$ ,$$1$$)의${\displaystyle }$순열이며, 여기서부터 이면각이 계산됩니다.

'직교 코너'를 사용한 심플함

여기서 "직교 코너"는 인접한 모든 모서리가 쌍으로 직교하는 정점이 있음을 의미합니다.그 직후에 인접한 모든 면은 쌍으로 직교합니다.이러한 단순화는 직각삼각형의 일반화이며, 직각삼각형의 경우 n차원 버전의 피타고라스 정리가 존재한다.

직교 모서리에 인접한 면의 제곱(n - 1)차원 부피의 합계는 직교 모서리에 반대되는 면의 제곱(n - 1)차원 부피와 같습니다.

$\displaystyle \sum _{k=1}^{n} A_{k} ^{2} = A_{0} ^{2}$

${\displaystyle {여기}_{}}$서 A 1${\displaystyle {}_{}}$… ${\displaystyle {}_{}}$\ $displaystyle$ A$_$ { 1 } \$ldots$A $_${ n }는 서로 쌍으로 직교하지만 직교 모서리 반대쪽 ${\displaystyle {면}_{}}$인 A$$0 \ $displaystyle A _$ { 0 $\}$과는 $직교$하지 않는 면입니다.

2-단순의 경우 정리는 직각 삼각형의 경우 피타고라스 정리이고 3-단순의 경우 직교 모서리가 있는 사면체의 경우 드 구아의 정리이다.

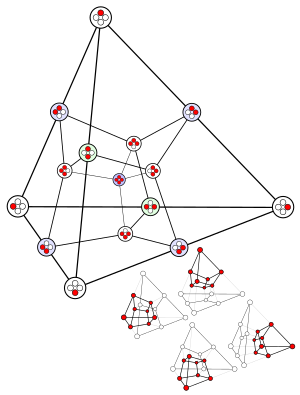
(n + 1)-하이퍼큐브와의 관계

n-심플렉스의 면 격자의 하세 다이어그램은 (n + 1)-하이퍼큐브의 모서리 그래프와 동일하며, 하이퍼큐브의 정점은 전체 심플렉스와 널 폴리토프를 포함한 각 n-심플렉스의 요소에 매핑됩니다(하이퍼큐브의 두 정점에 매핑됨).이 사실은 심플렉스의 면 격자를 효율적으로 열거하는 데 사용될 수 있다. 왜냐하면 더 일반적인 면 격자 열거 알고리즘은 계산적으로 더 비싸기 때문이다.

n-심플렉스는 (n + 1)-하이퍼큐브의 꼭지점 도형이기도 합니다.또한 (n + 1)-정직선의 면이기도 합니다.

토폴로지

위상적으로 n-simplex는 n-ball과 같다.모든 n-심플렉스는 모서리가 있는 n차원 다양체이다.

확률

확률론에서, (n + 1)-공간에서 표준 n-simplex의 점들은 n + 1개의 가능한 결과로 구성된 유한 집합에서 가능한 확률 분포의 공간을 형성한다.대응은 다음과 같습니다.합계가 (필요한) 1인 순서(n + 1)-튜플 확률로 설명된 각 분포에 대해, 우리는 중심 좌표가 정확히 그러한 확률인 단순체의 점을 연관시킨다.즉, 심플렉스의 k번째 정점은 (n + 1)-튜플의 k번째 확률을 중심 계수로 갖도록 할당됩니다.이 대응은 아핀 동형사상입니다.

컴파운드

모든 단순화는 자기 이중화이므로 일련의 화합물을 형성할 수 있다.

• 두 개의 삼각형이 육각형 {6/2}을(를) 형성합니다.
• 두 개의 사면체는 두 개의 사면체 또는 스텔라 옥탄굴라로 이루어진 화합물을 형성한다.
• 2개의 5셀이 4차원으로 2개의 5셀의 컴파운드를 형성합니다.

대수 위상

대수적 위상학에서 단순화는 단순 복합체라고 불리는 흥미로운 위상 공간의 클래스를 구성하기 위한 구성 요소로 사용됩니다.이러한 공간은 단순함을 조합 방식으로 접착하여 구축됩니다.단순 복합체는 단순 호몰로지라고 불리는 특정한 종류의 호몰로지를 정의하는데 사용된다.

R의 열린ⁿ 부분 집합에 포함된 k-심플렉스의 유한 집합을 아핀 k-사슬이라고 한다.체인 내의 심플렉스는 일의일 필요는 없습니다.다양성과 함께 발생할 수 있습니다.표준 집합 표기법을 사용하여 아핀 체인을 나타내는 대신, 집합 내의 각 부재를 분리하기 위해 더하기 기호를 사용하는 것이 표준 관행입니다.일부 심플렉스의 방향이 반대인 경우 이들 앞에 마이너스 기호가 붙습니다.집합에서 일부 심플렉스가 두 번 이상 발생할 경우 이러한 심플렉스 앞에 정수 카운트가 붙습니다.따라서 아핀 사슬은 정수 계수를 갖는 합계의 상징적 형태를 취합니다.

n-simplex의 각 패싯은 아핀(n - 1)-simplex이므로 n-simplex의 경계는 아핀(n - 1)-chain이다.따라서, 만약 우리가 하나의 긍정적인 방향의 아핀 심플렉스를 다음과 같이 나타낸다면,

$\displaystyle \displaystyle =[v_{0},v_{1},v_{2},\ldots,v_{n}}$

$({$가 정점을 나타내면 is의 경계$∂({displaystyle\displaystyle$\display\$display\$display$})$가 체인입니다.

${\displaystyle \dots =\sum _{j=0}^{n}(-1)^{j}[v_{0},\ldots,v_{j-1},v_{j+1},\ldots,v_{n}}.}$

이 식과 경계 연산자의 선형성으로부터 심플렉스의 경계는 0이 됩니다.

$\displaystyle \dots ^{2}\dots =\left(\sum _{j=0}^{n}(-1)^{j}[v_{0},\ldots,v_{j+1},\ldots,v_{n}\right)=0.}$

마찬가지로 체인 경계는 0입니다. likewise${\displaystyle {\mathrm{}}^{2\mathrm{}}}$ ${\displaystyle \mathrm{\rho }}$ ${\displaystyle =}$ 0 \$displaystyle$ \$displaystyle$^ {2} $\rho$=$$0 $。$

보다 일반적으로, 심플렉스(및 체인)는 매끄럽고 미분 가능한 맵${\displaystyle }f{\displaystyle }$ : R ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ \$style$ f$\display \mathbb {R}$^{$n}\to$ M$\}$에 의해 매니폴드에 삽입될 수 있다. 이 경우 집합을 나타내기 위한 합산 규칙과 경계 연산이 모두 삽입으로 통근한다.그것은,

${\displaystyle f\left(\sum \sum \sum \sumimits _{i}\sum \sum \sum \sumits _{i}f(\sum _ {i}f})$

${\displaystyle {여기}_{}}$서 i$\$는 방향과 다양성을 나타내는 정수입니다.경계 연산자 $"\displaystyle\partial$의 경우 다음 중 하나가 있습니다.

${\displaystyle\f(\rho)=f(\displaystyle\rho)}$

여기서 is는 체인입니다.결국 체인은 세트로 정의되고 조금 더 많은 것으로 정의되기 때문에 경계 연산은 매핑과 일치하며 세트 연산은 항상 맵 연산과 일치합니다(맵의 정의에 따라).

위상공간 X에 대한 $연속지도{\displaystyle }$f : ${\displaystyle \theta }$ ${\displaystyle \to }$X \ $displaystyle$ f$:\ displaystyle$ \ $to$X 를 흔히 단수 n-displax 라고 한다. (지도가 연속성 등의 바람직한 성질을 갖지 못할 경우 일반적으로 "displate"라고 하며, 이 경우 연속지도는 포함시킬 필요가 없음을 나타내는 것을 의미한다.)g)^[15]

대수기하학

고전 대수기하학이 부등식이 아닌 다항식 방정식에 대해 말할 수 있도록 하기 때문에, 대수 표준 n-단순은 일반적으로 아핀(n + 1) 차원 공간의 부분 집합으로 정의되며, 여기서 모든 좌표가 1까지 합산된다(따라서 부등식 부분을 제외).이 집합의 대수적 설명은 다음과 같다.

이는 스킴에 따른 설명${\displaystyle {}_{}{\delta n}_{}}$ (${\displaystyle R}$ ) $=$ ${\displaystyle \mathrm{Spec}}$ ${\displaystyle （R}$ [ ${\displaystyle {\delta }^{}}$ ${\displaystyle {}^{}}$n$]){ display$ \ $Delta _$ {n}(R)=\$operatorname {Spec}(R[\Delta$^{$n})}}}}$과 같습니다.

대수적 n-simplex의 정규 함수 링($임의$의 링$$R(\$displaystyle$R))$$

기존의 n-simplex와 동일한 정의를 사용하여 서로 다른 치수 n의 n-simple이 하나의 단순한 객체로 결합되며,${\displaystyle }링{\displaystyle }$ R [ ${\displaystyle {]}^{}}$ ${\displaystyle n^{}}$ $]$ \ $displaystyle$R [ \ $Delta$${\displaystyle {}^{}}$ { n$$}$$assemble$$ cos cos cos cos cos cos cos cos${\displaystyle }${ { cos cos cos cos cos { { { $by{\displaystyle }$ by by { by by by by by by by,,,, by R [ \ $display style ]$로 결합됩니다.얼굴 지도와 퇴행성 지도는 모두 다항식이기 때문이다.)

대수적 n-단순은 높은 K 이론과 높은 Chow 그룹의 정의에 사용된다.

적용들

이 섹션은 확장해야 합니다.추가함으로써 도움이 될 수 있습니다. (2009년 12월)

• 통계학에서 단순화는 구성 데이터의 표본 공간이며, 삼원 그래프에서와 같이 하위 모집단의 비율과 같이 1이 되는 양을 표시하는 데에도 사용됩니다.
• 산업 통계학에서, 단순화는 문제 공식과 알고리즘 해법에서 발생한다.빵의 디자인에서 생산자는 효모, 밀가루, 물, 설탕 등을 조합해야 한다.이러한 혼합물에서는 성분의 상대적 비율만 문제가 됩니다.최적의 빵 혼합물을 위해 밀가루가 두 배로 늘어나면 효모는 두 배로 증가해야 한다.이러한 혼합 문제는 종종 정규화된 제약조건으로 공식화되므로 음이 아닌 성분이 1이 되고, 이 경우 실현 가능한 영역이 심플렉스를 형성합니다.빵 혼합물의 품질은 반응 표면 방법론을 사용하여 추정할 수 있으며, 순차 2차 ^[16]프로그래밍과 같은 비선형 프로그래밍 방법을 사용하여 국소 최대값을 계산할 수 있다.
• 운영 연구에서 선형 프로그래밍 문제는 George Dantzig의 심플렉스 알고리즘으로 해결할 수 있습니다.
• 기하학적 설계와 컴퓨터 그래픽스에서, 많은 방법들이 먼저 도메인의 간단한 삼각측량을 수행한 후 보간 다항식을 각 ^[17]단순식에 맞춥니다.
• 화학에서, p-블록에 있는 대부분의 원소의 수소화물은 각 원자를 연결하기 위해 단순체와 유사할 수 있다.네온은 수소와 반응하지 않기 때문에 하나의 수소원자와의 불소결합과 선분을 형성하고, 두 개의 수소원자와의 산소결합과 삼각형을 닮은 구부러진 형태이며, 질소는 반응하여 4면체를 형성하고, 탄소는 5셀의 슐레겔도와 유사한 구조를 형성한다.이러한 추세는 수소 원자가 할로겐 원자로 대체되는 경우뿐만 아니라 각 원소의 무거운 유사체에도 계속됩니다.
• 회귀 미적분 및 인과 역학 삼각 측량과 같은 양자 중력에 대한 일부 접근법에서 단순화는 시공간 이산화의 구성 요소, 즉 단순 다양체를 구축하는 데 사용됩니다.

「 」를 참조해 주세요.

메모들

References

• Rudin, Walter (1976). Principles of Mathematical Analysis (3rd ed.). McGraw-Hill. ISBN 0-07-054235-X. (See chapter 10 for a simple review of topological properties.)
• Tanenbaum, Andrew S. (2003). "§2.5.3". Computer Networks (4th ed.). Prentice Hall. ISBN 0-13-066102-3.
• Devroye, Luc (1986). Non-Uniform Random Variate Generation. ISBN 0-387-96305-7. Archived from the original on 2009-05-05.
• Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). Dover. ISBN 0-486-61480-8.
  • pp. 120–121, §7.2. see illustration 7-2A
  • p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n dimensions (n ≥ 5)
• Weisstein, Eric W. "Simplex". MathWorld.
• Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization. Cambridge University Press. ISBN 978-1-107-39400-1. As PDF

v t Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds