등면체
Isohedral figure기하학에서 치수 3(다면체) 이상의 폴리토프는 모든 얼굴이 동일할 때 등면체 또는 얼굴 변환이다. 보다 구체적으로 말하면, 모든 얼굴은 단순히 일치할 뿐 아니라 전이적이어야 한다. 즉, 동일한 대칭 궤도 내에 있어야 한다. 즉, 어떤 면 A와 B에 대해서도 A를 B에 매핑하는 회전과 반사에 의해 전체 고체의 대칭성이 있어야 한다. 이러한 이유로 볼록한 등면체 다면체는 공정한 주사위를 만들어 줄 형상이다.[1]
등면체 다면체를 등면체라고 한다. 얼굴 구성으로 설명할 수 있다. 등면체이고 정점이 규칙적인 형태도 가장자리 전이성(이소독성)이며 퀘이레규어 이중이라고 한다:일부 이론가들은 이 수치들을 같은 대칭을 공유하기 때문에 진정한 콰이레규어라고 여기지만, 이것은 일반적으로 받아들여지지 않는다. 등면체에는 고른 수의 얼굴이 있다.[2]
등면체인 다면체에는 정점 변환(이항체)인 이중 다면체가 있다. 카탈로니아 고형물, 두피라미드, 사다리꼴은 모두 등면체다. 그것들은 각각 이등분 아르키메데스 고형물, 프리즘, 반격의 이중성이다. 플라토닉 고형물은 자가이중이거나 다른 플라토닉 고형물과 이중으로 되어 있는 정점, 가장자리, 얼굴-변환성(등소, 동위원소, 등면체)이다. 등면체, 등면체, 등면체인 다면체는 고결하다고 한다.
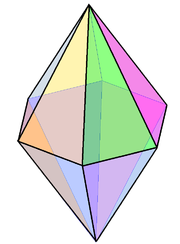
모든 이소조노헤드라가[3] 이등면인 것은 아니다.[4] 예: 롬빅 아이코사헤드론은 이소노헤드론이지만 이소헤드론은 아니다.[5]
예
| 볼록스 | 오목한 | ||
|---|---|---|---|
 육각형 bipyramid, V4.4.6은 등면 다면체의 비정규적인 예다. |  등면 카이로 오각형 타일링, V3.3.4.3.4 |  Rhombic dodecahedral honeycomb는 등면체(및 등면체) 공간을 채우는 벌집의 한 예다. |  위상학적 사각 타일링이 나선형 H 형상으로 변형되었다. |
대칭에 의한 이소헤드라의 등급
| 얼굴 | 면 구성의 | 클래스 | 이름 | 대칭 | 주문 | 볼록스 | 코플라나르 | 논콘벡스 |
|---|---|---|---|---|---|---|---|---|
| 4 | V33 | 플라토닉 | 사면체 사방형 분산형 마름모꼴의 | Td, [3,3], (*332) D2d, [2+,2], (2*) D2, [2,2]+, (222) | 24 4 4 4 |   | ||
| 6 | V34 | 플라토닉 | 정육면체 삼각 사다리꼴 비대칭 삼각 사다리꼴 | Oh, [4,3], (*432) D3d, [2+,6] (2*3) D3 [2,3]+, (223) | 48 12 12 6 |   | ||
| 8 | V43 | 플라토닉 | 팔면체 사각의 두피라미드 고무 바이프라미드 정방 치석 | Oh, [4,3], (*432) D4h,[2,4], (*224) D2h, [2,2], (*222) D2d, [2+,4](2*2) | 48 16 8 8 |      |  | |
| 12 | V35 | 플라토닉 | 정두면체 피리토헤드론 사타르의 | Ih, [5,3], (*532) Th, [3+,4], (3*2) T, [3,3]+, (*332) | 120 24 12 |   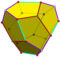 | 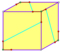 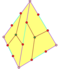 |   |
| 20 | V53 | 플라토닉 | 정삼면체 | Ih, [5,3], (*532) | 120 |  | ||
| 12 | V3.62 | 카탈루냐 주 | 삼면체 | Td, [3,3], (*332) | 24 |  |   |  |
| 12 | V(3.4)2 | 카탈루냐 주 | 진드기 도데면체 살충성 도두면체 | Oh, [4,3], (*432) Td, [3,3], (*332) | 48 24 |    |  |   |
| 24 | V3.82 | 카탈루냐 주 | 삼면체 | Oh, [4,3], (*432) | 48 |  |   | |
| 24 | V4.62 | 카탈루냐 주 | 테트라키스 육면체 | Oh, [4,3], (*432) | 48 |   |   |   |
| 24 | V3.43 | 카탈루냐 주 | 살상성 이코시테트라헤드론 | Oh, [4,3], (*432) | 48 |  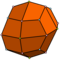 |    |  |
| 48 | V4.6.8 | 카탈루냐 주 | 이디야키스 도데카헤드론 | Oh, [4,3], (*432) | 48 |  |    |   |
| 24 | V34.4 | 카탈루냐 주 | 오각형 이코시테트라헤드론 | O, [4,3]+, (432) | 24 |  | ||
| 30 | V(3.5)2 | 카탈루냐 주 | 3면체 | Ih, [5,3], (*532) | 120 |  | ||
| 60 | V3.102 | 카탈루냐 주 | 삼면체 | Ih, [5,3], (*532) | 120 |  |     | |
| 60 | V5.62 | 카탈루냐 주 | 펜타키스 도데면체 | Ih, [5,3], (*532) | 120 |  |      | |
| 60 | V3.4.5.4 | 카탈루냐 주 | 망상 육면체 | Ih, [5,3], (*532) | 120 |  |  |  |
| 120 | V4.6.10 | 카탈루냐 주 | 이디야키스 삼권면체 | Ih, [5,3], (*532) | 120 |  |    |    |
| 60 | V34.5 | 카탈루냐 주 | 오각 육면체 | I, [5,3]+, (532) | 60 |  | ||
| 2n | V33.n | 극지 | 사다리꼴 비대칭 사다리꼴 | Dnd, [2+,2n], (2*n) Dn, [2,n]+, (22n) | 4n 2n |  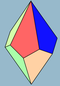    | ||
| 2n 4n | V42.n V42.2n V42.2n | 극지 | 정규 n-yramid. 동위원소 2n-162yramid 2n-나노헤드론 | Dnh, [2,n], (*22n) Dnh, [2,n], (*22n) Dnd, [2+,2n], (2*n) | 4n |    |     |
K면체
다면체(또는 일반적으로 다면체)는 대칭 기본 영역 내에 k면을 포함하는 경우 k-isoheadral이다.[6]
이와 유사하게 k-isohedral tiling은 k개의 개별 대칭 궤도를 가지고 있다(일부 m < k>에 대해 m 다른 모양의 면을 포함할 수 있다).[7]
단면체 다면체 또는 단면체 타일링(m = 1)은 하나 이상의 대칭 위치에서 발생하는 직접적이거나 반사적으로 일치하는 면을 가지고 있다. r-headral polyheadra 또는 tiling은 r 타입의 얼굴(각각 2 또는 3의 3면이라고도 함)[8]을 가지고 있다.
얼굴이 k 대칭 위치에 의해 색칠된 k-isohedral 다면체와 틸팅의 몇 가지 예가 여기에 있다.
| 3면체의 | 4면체의 | 등면체의 | 2면체의 |
|---|---|---|---|
| (2-헤드) 정면의 다면체 | 단면다면체 | ||
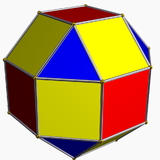 | 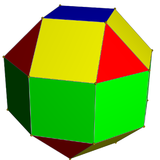 | 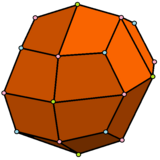 | 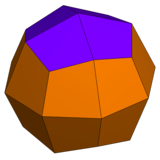 |
| Rhombicuboctahedron은 1개의 삼각형과 2개의 사각형을 가지고 있다. | 사이비 롬비큐옥타헤드론은 삼각형 1종과 정사각형 3종을 가지고 있다. | 델토피탈 이코시테트라헤드론은 1종류의 얼굴을 가지고 있다. | 사이비-델타성 이코시트라헤드론은 동일한 모양의 얼굴 2종을 가지고 있다. |
| 2면체의 | 4면체의 | 등면체 | 3면체의 |
|---|---|---|---|
| (2-헤드) 정면의 기울기 | 단면 기울기 | ||
 |  |  | |
| 피타고라스 타일링은 두 가지 크기의 정사각형을 가지고 있다. | 이 3개의 균일 타일링은 3개의 동일한 모양의 삼각형과 1개의 사각형을 가지고 있다. | 청어뼈 문양은 1종류의 직사각형 면을 가지고 있다. | 이 오각형 타일링은 동일한 모양의 불규칙한 오각형 면 3종을 가지고 있다. |
관련 용어
세포전환형 또는 이소치형 피규어는 세포가 서로 응고되고 전이되는 n-폴리토프(n > 3) 또는 벌집형이다. 3차원 허니컴에서, 균일한 허니컴에 대한 듀얼은 이소콜릭이다. 4차원에서는 20개의 세포까지 이소콜릭 폴리토페스가 열거되었다.[9]
면 변환 또는 동위원소 수치는 면(n-1)-페이스(faces) 결합형 및 전이성을 갖는 n차원 폴리토페스 또는 벌집형이다. 동위원소의 이중은 이등분 폴리토프다. 정의에 따르면, 이 동위원소 속성은 균일한 폴리토프의 이중에 공통적이다.
- 동위원소 2차원 수치는 동위원소(에지 변환)이다.
- 동위원소 3차원 그림은 등면체(얼굴-변환)이다.
- 동위원소 4차원 수치는 이소치(세포 변환 세포)이다.
참고 항목
메모들
- ^ McLean, K. Robin (1990), "Dungeons, dragons, and dice", The Mathematical Gazette, 74 (469): 243–256, doi:10.2307/3619822, JSTOR 3619822.
- ^ 그룬바움 (1960년)
- ^ Weisstein, Eric W. "Isozonohedron". mathworld.wolfram.com. Retrieved 2019-12-26.
- ^ Weisstein, Eric W. "Isohedron". mathworld.wolfram.com. Retrieved 2019-12-21.
- ^ Weisstein, Eric W. "Rhombic Icosahedron". mathworld.wolfram.com. Retrieved 2019-12-21.
- ^ Socolar, Joshua E. S. (2007). "Hexagonal Parquet Tilings: k-Isohedral Monotiles with Arbitrarily Large k" (corrected PDF). The Mathematical Intelligencer. 29: 33–38. arXiv:0708.2663. doi:10.1007/bf02986203. S2CID 119365079. Retrieved 2007-09-09.
- ^ 크레이그 S. 카플란 "컴퓨터 그래픽을 위한 초기 타일링 이론". 2009. 제5장 "부시드랄 틸링" 페이지 35.
- ^ 틸링 및 패턴, 페이지 20, 23
- ^ http://www.polytope.net/hedrondude/dice4.htm
참조
- 피터 R. Cromwell, Polyedra, Cambridge University Press 1997, ISBN 0-521-55432-2, 페이지 367 Transitivity
외부 링크
- Olshevsky, George. "Isotope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Weisstein, Eric W. "Isohedral tiling". MathWorld.
- Weisstein, Eric W. "Isohedron". MathWorld.
- 면의 수가 유한한 이소헤드라 25종류
- 주사위 실험실의 주사위 설계