보로노이 도표

20 포인트와 그 Voronoi 셀(아래 더 큰 버전)

수학에서, 보로노이 다이어그램은 주어진 객체 집합 각각에 가까운 영역으로 평면을 분할한 것입니다.가장 단순한 경우, 이러한 개체는 평면에서 완전히 많은 점(시드, 사이트 또는 생성기라고 함)에 불과합니다.각각의 씨앗에는 다른 어떤 것보다 그 씨앗에 더 가까운 평면의 모든 점으로 구성된 Voronoi 셀이라고 불리는 대응하는 영역이 있습니다.포인트 세트의 Voronoi 다이어그램은 Delaunay 삼각 측량과는 다릅니다.

보로노이 다이어그램은 게오르기 보로노이 테셀레이션, 보로노이 분해, 보로노이 파티션 또는 디리클레 테셀레이션(피터 구스타프 레준 디리클레의 이름을 따옴)이라고도 불린다.보로노이 세포는 티에센 ^[1]^[2]^[3]폴리곤으로도 알려져 있다.보로노이 다이어그램은 주로 과학기술 분야뿐만 아니라 시각 ^[4]^[5]예술 분야에서도 실용적이고 이론적인 응용 분야를 가지고 있다.

가장 간단한 경우

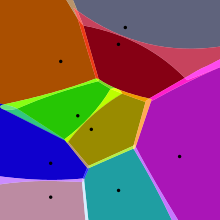
가장 간단한 경우, 첫 번째 그림에 나와 있는 것처럼, 우리는 유클리드 평면에서 유한한 점 집합₁ {p_n, ..., p}이 주어집니다.이 경우 각 사이트_k p는 단순한 점이며, 대응하는 Voronoi 셀_k R은 p까지의 거리가_k 다른 p와의_k 거리보다 작거나 같은 유클리드 평면의 모든 점으로 구성된다.이러한 각 셀은 반공간의 교차점에서 얻어지기 때문에 (볼록한) ^[6]다면체이다.Voronoi 다이어그램의 선분은 평면에서 가장 가까운 두 개의 부지와 동일한 거리에 있는 모든 지점입니다.Voronoi 정점(노드)은 3개(또는 그 이상)의 사이트에 해당하는 지점입니다.

형식적 정의

$X(\textstyle$ X $)$ 를 ${\textstyle X}$ ${\textstyle d}$ d(\ $textstyle$ d ${\textstyle d}$ 의 메트릭공간으로 합니다 $.$ $(\$ K $)$ 를 ${\textstyle K}$ 인덱스 세트, ( $P_{k}_$ K})를 ${\textstyle (P_{k})_{k\in K}}$ X(\ $textstyle$ X ${\textstyle X}$ ${\textstyle X}$ 의 빈 서브셋이 아닌 튜플(순서 있는 집합)로 합니다. ${\textstyle P_{k}}$ $(\$ })와 ${\textstyle P_{k}}$ 연관된 Voronoi 셀( $또는$ Voronoi $영역)$ R ${\textstyle R_{k}}$ k ${\textstyle R_{k}}$ $textstyle$ R_{k $})$ 는 ${\textstyle X}$ ${\textstyle X}$ X(\ $textstyle$ X)의 모든 점 집합으로, ${\textstyle P_{k}}$ k $(\$ })와의 ${\textstyle P_{k}}$ ${\textstyle P_{k}}$ 가 다른 ${\textstyle P_{j}}$ $(\$ 와의 거리보다 크지 않습니다. $tstyle$ j는 ${\textstyle j}$ k $(\textstyle$ k $)$ 와는 다른 인덱스입니다.즉 ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ d( ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ A ) $=$ ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ { ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ d ( ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ , $a$ a ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ A $}$ { $textstyle$ d ( $x$ , a ) $inf$ \ $inf$ \ $d$ ( $x$ , a )\ inf \ d ( x , a )\ $inf$ \ d ( x , a ) }인 ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ ${\textstyle x}$ ${\textstyle d(x,\,A)=\inf\{d(x,\,a)\mid a\in A\}}$ ${\textstyle x}$ 점 x, $mid$ a \ $textstyle과$ 점 ${\textstyle A}$ 의 거리를 나타냅니다.

\displaystyle R_{k}=\{x\in X\mid d(x,P_{k})\leq d(x,P_{j})\;{\text{for all}\;j\neq k\}

Voronoi 다이어그램은 단순히 ${\textstyle (R_{k})_{k\in K}}$ k ${\textstyle (R_{k})_{k\in K}}$ k ${\textstyle (R_{k})_{k\in K}}$ K(\ $textstyle (R_{k})_{k\in$ K ${\textstyle (R_{k})_{k\in K}}$ 의 튜플입니다.원칙적으로 일부 사이트는 교차할 수 있고 일치할 수도 있지만(아래에 상점을 나타내는 사이트에 대해서는 응용 프로그램이 설명되지만) 일반적으로는 분리된 것으로 간주됩니다.또한 정의에서 무한히 많은 사이트가 허용되지만(이 설정은 숫자와 결정학의 기하학에서 적용됨), 많은 경우 최종적으로 많은 사이트만 고려됩니다.

특히 공간이 유한 차원 유클리드 공간이고, 각 부위가 점이며, 점이 매우 많고, 모두 다른 경우, 보로노이 셀은 볼록 다면체이며, 그 정점, 변, 2차원 면 등을 이용하여 조합적으로 나타낼 수 있다.때로는 유도 조합 구조를 보로노이 다이어그램이라고 합니다.그러나 일반적으로 Voronoi 세포는 볼록하지 않을 수도 있고 심지어 연결되어 있을 수도 있다.

일반적인 유클리드 공간에서 우리는 일반적인 용어로 공식적인 정의를 다시 쓸 수 있다.각 Voronoi ${\textstyle R_{k}}$ R $(\$ })는 ${\textstyle R_{k}}$ 생성점 ${\textstyle P_{k}}$ k $(\$ 와 관련지어집니다. $(\textstyle$ X $)$ 를 ${\textstyle X}$ 유클리드 공간의 모든 점 집합으로 합니다. ${\textstyle R_{2}}$ 1 $(\$ 을 ${\textstyle P_{1}}$ R 2(\ ${\textstyle R_{1}}$ $R_{2$ 를 생성하는 ${\textstyle R_{1}}$ P 2 $(\$ $textstyle$ P_ ${$ $2})$ 및 ${\textstyle P_{2}}$ ${\textstyle R_{3}}$ 3 $(\textstyle R_{$ $3$ ${\textstyle R_{3}}$ 을 ${\textstyle P_{3}}$ 생성하는 ${\textstyle P_{3}}$ 으로 $합니다$ .그 후,^[7] Tran 등에 의해 표현되었듯이, "Voronoi 폴리곤의 모든 위치는 유클리드 평면의 Voronoi 다이어그램의 다른 생성점보다 해당 폴리곤의 생성점에 더 가깝다."

일러스트

간단한 예로, 도시에 있는 상점 그룹을 생각해 보십시오.특정 상점의 고객 수를 추정하려고 합니다.다른 모든 것(가격, 제품, 서비스 품질 등)이 동일하기 때문에 고객은 단순히 거리를 고려하여 원하는 가게를 선택한다고 가정하는 것이 타당하다. 즉, 가장 가까운 곳에 있는 가게로 가는 것이다.이 경우, 특정 $P_{k}$ $Pk$ 의 Voronoi $R_{k}$ $R_{k}$ $({$ $R_$ ${k})$ 를 $R_{k}$ $P_k$ 사용하여 이 숍에 방문하는 잠재 고객 수를 대략적으로 추정할 수 있습니다(이 값은 우리 도시의 한 지점에서 모델화).

대부분의 도시에서 점 사이의 거리는 익숙한 유클리드 거리를 사용하여 측정할 수 있다.

{\displaystyle _{2}=d\left[\left(a_{1},a_{2}\right),\left(b_{1}\right)\rt {{2}+\left(a_{2}-b_{1}\right}}}}{}}}{}}}}}}}\right}}}}}}}\rightsignrongrt.

또는 맨해튼 거리:

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

[ (

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

,

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

a

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

)

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

, (

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

1 ,

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

2

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

)

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

- b

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

+

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

-

d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|

2 \

displaystyle

d

\

left [ \ left (

a _

{

1

,

a

_ {

2 }

\ right ], \

left

(

b _

{

1

} -

b _

{

2

\

right

)

=

\

right left

a _ { 1

}

+ {

2

}

대응하는 Voronoi 다이어그램은 거리 메트릭에 따라 다르게 보입니다.

두 가지 측정 기준 아래 20개 점의 Voronoi 다이어그램

유클리드 거리

맨해튼 거리

특성.

Voronoi 다이어그램의 이중 그래프(점 사이트가 있는 유클리드 공간의 경우)는 동일한 점 집합에 대한 Delaunay 삼각 측량에 해당합니다.
가장 가까운 점 쌍은 Voronoi 다이어그램에서 인접한 두 셀에 해당합니다.
설정이 유클리드 평면이고 이산적인 점 집합이 주어졌다고 가정합니다.그러면 집합의 두 점이 볼록 선체에 인접하게 됩니다. Voronoi 셀이 무한히 긴 변을 공유하는 경우에만 그렇습니다.
공간이 규범화된 공간이고 각 사이트까지의 거리가 확보된 경우(예를 들어 사이트가 콤팩트 세트 또는 닫힌 볼인 경우), 각 Voronoi 셀은 ^[8]해당 사이트에서 나오는 선분의 결합으로 표현될 수 있다.여기에 나타나 있듯이 이 속성은 거리에 도달하지 못할 때 반드시 유지되는 것은 아닙니다.
비교적 일반적인 조건 하에서 (공간은 무한 차원 균일 볼록 공간일 수 있으며, 일반적인 형태의 부위가 무한히 많을 수 있음 등)Voronoi 세포는 일정한 안정성 특성을 가지고 있습니다.예를 들어, 일부 번역이나 왜곡에 의한 사이트 모양의 작은 변화도 Voronoi 세포 모양의 작은 변화를 일으킵니다.이것은 보로노이 ^[9]다이어그램의 기하학적 안정성입니다.여기서 나타내는 것처럼, 공간이 2차원(그러나 균일하지 않은 볼록함, 특히 비유클리드)이고 장소가 점이라고 해도, 이 속성은 일반적으로 유지되지 않는다.

역사와 연구

보로노이 다이어그램의 비공식 사용은 1644년 데카르트로 거슬러 올라갈 수 있다.Peter Gustav Lejeun Dirichlet은 1850년 2차 형식에 대한 그의 연구에서 2차원 및 3차원 보로노이 도표를 사용했다.영국의 의사 존 스노우는 1854년 보로노이와 같은 그림을 사용하여 브로드 스트리트 콜레라로 사망한 대부분의 사람들이 다른 어떤 양수기보다 감염된 브로드 스트리트 펌프에 가까이 사는 방법을 설명했다.

보로노이 다이어그램은 ^[10]1908년 일반적인 n차원 사례를 정의하고 연구한 게오르기 페오도시에비치 보로노이에서 이름을 따왔다.지구물리학 및 기상학에서 공간적으로 분포된 데이터(강우량 측정 등)를 분석하기 위해 사용되는 보로노이 다이어그램은 미국 기상학자 알프레드 H의 이름을 따서 티에센 폴리곤이라고 불린다. 티센.이 개념(또는 이 개념의 특정 중요한 경우)에 대한 기타 동등한 이름:Voronoi 다면체, Voronoi 다면체, 영향 영역, Voronoi 분해, Voronoi 테셀레이션, Dirichlet 테셀레이션.

예

이것은 3D 박스 내의 임의의 포인트 세트의 Voronoi 다이어그램의 슬라이스입니다.일반적으로 3D Voronoi 테셀레이션의 단면은 2D Voronoi 테셀레이션 자체가 아닙니다.(이 세포들은 모두 볼록 다면체이다.)

2차원 또는 3차원 점의 규칙적인 격자의 보로노이 테셀레이션은 많은 익숙한 테셀레이션을 일으킨다.

2D 격자는 점 대칭을 가진 동일한 육각형의 불규칙한 벌집 테셀레이션을 제공합니다.정규한 삼각 격자의 경우 정칙입니다.사각형 격자의 경우 육각형이 행과 열의 직사각형으로 감소합니다. 정사각형 격자는 정사각형의 규칙적인 테셀레이션을 제공합니다; 직사각형과 정사각형 c는 다른 격자에 의해서도 생성됩니다(예를 들어 벡터(1,0) 및 (1/2, 1/2)에 의해 정의된 격자는 제곱을 제공합니다).
단순한 입방체 격자는 입방체 벌집을 만들어 줍니다.
육각형 밀착 격자는 트라페조-롬빅 도데카헤드라로 공간의 테셀레이션을 제공한다.
면중심 입방체 격자는 마름모꼴 십이면체로 공간의 테셀레이션을 제공한다.
체심 입방체 격자는 잘린 팔면체를 가진 공간의 테셀레이션을 제공한다.
정삼각형 격자가 서로의 중심에 정렬된 평행 평면은 육각형 프리즘 벌집을 제공합니다.
특정 신체 중심 사각형 격자는 마름모-헥사각형 도데카헤드라로 공간의 테셀레이션을 제공한다.

이산 집합 X에 x가 있고 이산 집합 Y에 y가 있는 점 집합(x, y)의 경우 점이 반드시 중심에 있을 필요는 없는 직사각형 타일을 얻을 수 있습니다.

고차 Voronoi 다이어그램

통상적인 Voronoi 셀은 S의 단일점에 가장 가까운 점의 집합으로 정의되지만, n차 Voronoi 셀은 S의 특정 n개 점의 집합을 n개의 가장 가까운 이웃으로 갖는 점의 집합으로 정의된다.고차 Voronoi 다이어그램도 공간을 세분화합니다.

고차 Voronoi 다이어그램을 재귀적으로 생성할 수 있다.세트 S에서 n차^th Voronoi 다이어그램을 생성하려면 (n - ^th1)차 다이어그램에서 시작하여 X = {x₁, x₂, ..., x_n−1}에서 생성된 각 셀을 세트 S - X에서 생성된 Voronoi 다이어그램으로 바꿉니다.

최단점 보로노이 다이어그램

n개의 포인트 세트에 대해 (n - ^th1)차 Voronoi 다이어그램을 가장 먼 포인트 Voronoi 다이어그램이라고 합니다.

주어진 점 집합 S₁ = {p₂, p_n, ..., p}에 대해, 가장 먼 점 Voronoi 다이어그램은 P의 동일한 점이 가장 먼 점인 셀로 평면을 나눈다.P점은 P의 볼록한 선체의 정점일 경우에만 원점 보로노이 다이어그램에 셀을 가진다.P의 H){h1, h2,..., hk}이 볼록 선체, 비행기의가 세포, 한 H의 각 점에 대해에 만일 d(q, 안녕하세요)한 점 q은 세포에 부지를 안녕에 해당하는 있다고 하는 성질을 가진 다음farthest-point 보로노이 다이어그램 하위 구분,;각각의 pj에 d(q, pj)자 S가 d(p, q)은 유클리드 거리 betwe 안녕 ≠ pj과 ∈.앙 두 points p 및 ^[11]^[12]q.

가장 먼 점의 보로노이 다이어그램의 세포 경계는 잎으로 무한 광선을 갖는 위상수 구조를 가지고 있다.모든 유한 트리는 가장 먼 점의 보로노이 ^[13]다이어그램에서 이렇게 형성된 트리와 동형이다.

일반화와 변화

정의에 따라 보로노이 셀은 마할라노비스 거리나 맨해튼 거리 등 유클리드 이외의 메트릭에 대해 정의할 수 있다.그러나, 이 경우, 2차원의 경우에도 두 점에 대한 등거리 궤적이 공디멘션 1의 부분공간이 될 수 없기 때문에, 보로노이 세포의 경계는 유클리드 경우보다 더 복잡할 수 있다.

포인트 세트의 대략적인 Voronoi 다이어그램입니다.Voronoi 셀의 흐릿한 경계에 혼합된 색상이 있습니다.

가중치 Voronoi 다이어그램은 Voronoi 셀을 정의하기 위한 한 쌍의 점의 함수가 발생점에 할당된 곱셈 또는 가산 가중치에 의해 수정된 거리 함수이다.거리 측정인 거리를 사용하여 정의된 Voronoi 셀의 경우와는 달리, 이 경우 Voronoi 셀 중 일부는 비어 있을 수 있습니다.파워 다이어그램은 파워 거리를 사용하는 원의 집합에서 정의된 Voronoi 다이어그램의 한 종류입니다. 또한 각 원의 반지름에서 정의된 가중치가 원의 ^[14]중심에서 유클리드 거리 제곱에 더해지는 가중치 Voronoi 다이어그램으로도 생각할 수 있습니다.

d\ $displaystyle$ d} 차원 $n$ 공간에 $d$ $있는$ $n개$ 의 \ $displaystyle$ n개의 점의 Voronoi $다이어그램$ 에는 O $(n d$ d / $2 )$ ) $개$ 의 ${\textstyle O(n^{\lceil d/2\rceil })}$ 정점을 ${\textstyle O(n^{\lceil d/2\rceil })}$ 수 있으며, 이에 대한 명시적인 설명을 저장하기 위해 필요한 메모리 양에 동일한 경계가 필요합니다.따라서 보통 또는 고차원에서는 Voronoi 다이어그램을 사용할 수 없습니다.보다 공간 효율적인 대안은 대략적인 Voronoi ^[15]다이어그램을 사용하는 것입니다.

또한 보로노이 다이어그램은 중앙축(이미지 분할, 광학 문자 인식 및 기타 계산 애플리케이션에서 응용 프로그램을 발견), 직선 골격 및 구역 다이어그램과 같은 다른 기하학적 구조와도 관련이 있습니다.

적용들

기상/수문학

기상학 및 공학 수문학에서 지역(수면)의 관측소 강수량 데이터에 대한 가중치를 구하기 위해 사용된다.폴리곤을 생성하는 지점은 강수량 데이터를 기록하는 다양한 측점입니다.수직 이등분선은 임의의 두 측점을 연결하는 선에 그려집니다.그 결과 스테이션 주위에 폴리곤이 형성됩니다.스테이션 포인트에 접하는 영역 $(A_{i})$ $(A_{i})$ $){displaystyle (A_{i})$ 을 $(A_{i})$ 스테이션의 영향 영역이라고 합니다. ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$ 강수량은 P ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$ ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$ ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$ A ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$ A $（$ $displaystyle$ { $P$ } = {\ $frac$ { $sum$ A _ { $i$ } P $_$ { i } } { \ $sum$ A _ { i ${\bar {P}}={\frac {\sum A_{i}P_{i}}{\sum A_{i}}}$ } } } } the the the the the the the the the the the the the the the the the the the the the the the the the the the the

인문학

고전 고고학, 특히 미술사에서, 조각상 머리의 대칭을 분석하여 잘린 머리가 어떤 조각상에 속했을지 결정한다.Voronoi 셀을 사용한 예로는 고해상도 폴리곤 ^[16]^[17]메쉬를 사용한 Sabouroff 헤드의 식별이 있습니다.
변증법에서 Voronoi 세포는 조사점 간의 언어적 연속성을 추정하기 위해 사용된다.

자연과학

보로노이 테셀레이션은 씨앗에서 바깥쪽으로 방사상으로 성장함으로써 나타납니다.

생물학에서, 보로노이 다이어그램은 세포와 뼈 마이크로아키텍처를 ^[19]포함한^[18] 많은 다른 생물학적 구조를 모델링하는데 사용된다.실제로, Voronoi 테셀레이션은 생물학적 ^[20]조직의 구성을 움직이는 물리적 제약을 이해하기 위한 기하학적 도구로서 기능합니다.
수문학에서 보로노이 다이어그램은 일련의 점 측정을 바탕으로 지역의 강우량을 계산하기 위해 사용됩니다.이 사용법에서는 일반적으로 이러한 폴리곤을 티센 폴리곤이라고 부릅니다.
생태학에서, 보로노이 다이어그램은 숲과 숲의 캐노피의 성장 패턴을 연구하기 위해 사용되며, 산불의 예측 모델을 개발하는 데에도 도움이 될 수 있다.
컴퓨터 화학에서 리간드 결합 사이트는 기계 학습 애플리케이션을 위한 Voronoi 다이어그램으로 변환된다(예: ^[21]단백질의 결합 포켓을 분류하기 위해).다른 응용 분야에서는 분자 내 핵의 위치에 의해 정의된 보로노이 세포가 원자전하를 계산하는데 사용된다.이는 Voronoi 변형 밀도법을 사용하여 수행됩니다.
천체물리학에서 Voronoi 다이어그램은 각 이미지에 신호 플럭스를 추가하여 영상에서 적응적 평활 영역을 생성하는 데 사용됩니다.이러한 절차의 주요 목적은 모든 영상에서 신호 대 노이즈 비율을 비교적 일정하게 유지하는 것입니다.
계산유체역학에서 포인트 세트의 Voronoi 테셀레이션은 예를 들어 이동메쉬 우주론 코드 AREPO에서와 ^[22]같이 유한체적 방법에 사용되는 계산영역을 정의하기 위해 사용될 수 있다.
컴퓨터 물리학에서, Voronoi 다이어그램은 고에너지 밀도 ^[23]물리학에서 섀도우그래프와 양성자 방사선 촬영으로 물체의 프로파일을 계산하는데 사용된다.

헬스

의학 진단에서, Voronoi 다이어그램에 기초한 근육 조직 모델은 신경 근육 ^[20]질환을 검출하기 위해 사용될 수 있다.
역학에서, Voronoi 다이어그램을 사용하여 전염병의 감염원을 상관시킬 수 있다.보로노이 다이어그램의 초기 응용 프로그램 중 하나는 존 스노우가 1854년 영국 소호에서 발생한 브로드 스트리트 콜레라 발생을 연구하기 위해 구현했다.그는 센트럴 런던 지도에서 주민들이 특정 양수기를 사용하고 있는 주택 지역과 ^[24]발병으로 인해 가장 많은 사망자가 발생한 지역 사이의 상관관계를 보여주었다.

공학 기술

고분자 물리학에서, 보로노이 다이어그램은 고분자의 자유로운 부피를 나타내기 위해 사용될 수 있다.
재료 과학에서 금속 합금의 다결정 미세 구조는 일반적으로 Voronoi 테셀레이션을 사용하여 표현됩니다.섬 성장에서, 보로노이 다이어그램은 개별 ^[25]^[26]^[27]^[28]^[29]섬의 성장률을 추정하기 위해 사용된다.고체물리학에서 위그너-세이츠 셀은 고체의 보로노이 테셀레이션이고, 브릴루인 존은 공간 그룹의 대칭을 가진 결정의 역(파형) 공간의 보로노이 테셀레이션입니다.
항공에서 보로노이 다이어그램은 항공기가 비행 계획을 진행함에 따라 비행 중 회항(ETOPS 참조)을 위한 가장 가까운 비행장을 식별하기 위해 해양 플롯 차트에 중첩된다.
건축에서, 보로노이 패턴은 아트 센터 골드 ^[30]코스트 재개발의 입상작의 기초가 되었습니다.
도시 계획에서, Voronoi 다이어그램을 사용하여 화물 적재 구역 ^[31]시스템을 평가할 수 있습니다.
광산에서, Voronoi 폴리곤은 귀중한 물질, 광물 또는 다른 자원의 매장량을 추정하기 위해 사용됩니다.탐색 드릴홀은 Voronoi 폴리곤의 포인트 세트로 사용됩니다.
표면 도량형에서 Voronoi 테셀레이션은 표면 거칠기 ^[32]모델링에 사용할 수 있다.
로봇 공학에서, 다중 로봇 시스템의 제어 전략과 경로 계획 알고리즘^[33] 중 ^[34]^[35]일부는 환경의 Voronoi 분할에 기초한다.

기하학.

Voronoi 다이어그램 위에 포인트 위치 데이터 구조를 구축하여 주어진 쿼리 포인트에 가장 가까운 객체를 찾고자 하는 가장 가까운 네이버 쿼리에 응답할 수 있습니다.가장 가까운 네이버쿼리에는 다수의 응용 프로그램이 있습니다.예를 들어 데이터베이스에서 가장 가까운 병원이나 가장 유사한 개체를 찾을 수 있습니다.대규모 애플리케이션은 데이터 압축에 일반적으로 사용되는 벡터 양자화입니다.
기하학에서, Voronoi 다이어그램은 점 집합에서 가장 큰 빈 원을 찾는 데 사용할 수 있으며, 예를 들어 특정 도시에 있는 기존의 모든 슈퍼마켓에서 가능한 한 멀리 떨어진 새로운 슈퍼마켓을 건설하는 데 사용할 수 있다.
Voronoi 다이어그램과 가장 먼 점의 Voronoi 다이어그램을 함께 사용하여 ^[11]점 집합의 둥근 정도를 계산하는 효율적인 알고리즘을 제공합니다.또한 Voronoi 접근방식은 좌표 측정 기계에서 데이터 집합을 평가하는 동안 원형성/원형성 평가에도 사용된다.

정보학

네트워킹에서 Voronoi 다이어그램은 무선 네트워크 용량의 도출에 사용할 수 있다.
컴퓨터 그래픽스에서 Voronoi 다이어그램은 3D 파쇄/파쇄 지오메트리 패턴을 계산하기 위해 사용됩니다.또한 절차적으로 유기물이나 용암처럼 생긴 질감을 만드는 데도 사용됩니다.
Autonomous Robot Navigation에서는 명확한 경로를 찾기 위해 Voronoi 다이어그램을 사용합니다.점이 장애물인 경우 그래프의 가장자리는 장애물(및 이론적으로 모든 충돌)에서 가장 먼 경로가 됩니다.
기계학습에서 Voronoi 다이어그램은 1-NN ^[36]분류에 사용됩니다.
랜덤 센서 사이트와 불안정한 웨이크 플로우, 지구물리학 데이터 및 3D 난류 데이터를 포함한 글로벌 장면 재구축에서 Voronoi 테셀레이션은 딥 ^[37]러닝과 함께 사용됩니다.
사용자 인터페이스 개발에서 Voronoi 패턴을 사용하여 특정 ^[38]포인트의 최적의 호버 상태를 계산할 수 있습니다.

공민학과 계획

멜버른에서 공립학교 학생들은 항상 그들이 사는 곳에서 가장 가까운 초등학교나 고등학교에 다닐 수 있는 자격이 있습니다.그러므로 스쿨존 지도는 보로노이 ^[39]도표이다.

베이커리

우크라이나 페이스트리 요리사 Dinara Kasko는 Voronoi 다이어그램의 수학적 원리를 사용하여 3D 프린터로 만든 실리콘 틀을 만들어 오리지널 케이크를 만듭니다.

알고리즘

Voronoi 도표를 직접(도표 자체로서) 구성하거나 Delaunay 삼각측량에서 시작하여 이중을 얻는 방법으로 몇 가지 효율적인 알고리즘이 알려져 있다.다이렉트 알고리즘은 평면상의 포인트 세트로부터 Voronoi 다이어그램을 생성하기 위한 O(n log(n) 알고리즘인 Fortune 알고리즘을 포함한다.Bowyer-Watson 알고리즘은 임의의 수의 차원으로 Delaunay 삼각측량을 생성하기 위한 O(n log(n) ~ O(n²) 알고리즘으로, Voronoi 다이어그램의 간접 알고리즘에 사용할 수 있습니다.점프 플래딩 알고리즘은 일정한 시간에 대략적인 Voronoi 다이어그램을 생성할 수 있으며 상용 그래픽 ^[40]^[41]하드웨어에 적합합니다.

Lloyd의 알고리즘과 Linde-Buzo-Gray 알고리즘(일명 k-평균 클러스터링)을 통한 일반화에서는 서브루틴으로 Voronoi 다이어그램의 구성을 사용한다.이러한 방법은 시드 포인트 세트에 대해 Voronoi 다이어그램을 구성하는 단계와 시드 포인트를 셀 내에서 보다 중심적인 새로운 위치로 이동하는 단계를 번갈아 수행합니다.이 방법들은 임의의 차원의 공간에서 중심 보로노이 테셀레이션이라고 불리는 특수한 형태의 보로노이 다이어그램으로 반복적으로 수렴하기 위해 사용될 수 있으며, 여기서 사이트는 셀의 기하학적 중심이기도 한 점으로 이동되었다.

「」를 참조해 주세요.

메모들

^ Burrough, Peter A.; McDonnell, Rachael; McDonnell, Rachael A.; Lloyd, Christopher D. (2015). "8.11 Nearest neighbours: Thiessen (Dirichlet/Voroni) polygons". Principles of Geographical Information Systems. Oxford University Press. pp. 160–. ISBN 978-0-19-874284-5.
^ Longley, Paul A.; Goodchild, Michael F.; Maguire, David J.; Rhind, David W. (2005). "14.4.4.1 Thiessen polygons". Geographic Information Systems and Science. Wiley. pp. 333–. ISBN 978-0-470-87001-3.
^ Sen, Zekai (2016). "2.8.1 Delaney, Varoni, and Thiessen Polygons". Spatial Modeling Principles in Earth Sciences. Springer. pp. 57–. ISBN 978-3-319-41758-5.
^ Aurenhammer, Franz (1991). "Voronoi Diagrams – A Survey of a Fundamental Geometric Data Structure". ACM Computing Surveys. 23 (3): 345–405. doi:10.1145/116873.116880. S2CID 4613674.
^ Okabe, Atsuyuki; Boots, Barry; Sugihara, Kokichi; Chiu, Sung Nok (2000). Spatial Tessellations – Concepts and Applications of Voronoi Diagrams (2nd ed.). John Wiley. ISBN 978-0-471-98635-5.
^ Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization. Exercise 2.9: Cambridge University Press. p. 60.{{cite book}}: CS1 유지보수: 위치(링크)
^ Tran, Q. T.; Tainar, D.; Safar, M. (2009). Transactions on Large-Scale Data- and Knowledge-Centered Systems. p. 357. ISBN 9783642037214.
^ 2009년을 맞이합니다.
^ 2011년 리엠
^ 보로노 1908a와 보로노 1908b.
^ ^a ^b de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2008). Computational Geometry (Third ed.). Springer-Verlag. ISBN 978-3-540-77974-2. 7.4 최단점 보로노이 다이어그램.알고리즘에 대한 설명을 포함합니다.
^ 에는 가장 먼 점의 Voronoi 다이어그램을 계산하는 간단한 알고리즘이 포함되어 있습니다Skyum, Sven (18 February 1991). "A simple algorithm for computing the smallest enclosing circle". Information Processing Letters. 37 (3): 121–125. doi:10.1016/0020-0190(91)90030-L..
^ Biedl, Therese; Grimm, Carsten; Palios, Leonidas; Shewchuk, Jonathan; Verdonschot, Sander (2016). "Realizing farthest-point Voronoi diagrams". Proceedings of the 28th Canadian Conference on Computational Geometry (CCCG 2016).
^ 를 클릭합니다Edelsbrunner, Herbert (2012) [1987]. "13.6 Power Diagrams". Algorithms in Combinatorial Geometry. EATCS Monographs on Theoretical Computer Science. Vol. 10. Springer-Verlag. pp. 327–328. ISBN 9783642615689..
^ Sunil Arya, Sunil; Malamatos, Theocharis; Mount, David M. (2002). "Space-efficient approximate Voronoi diagrams". Proceedings of the thiry-fourth annual ACM symposium on Theory of computing. pp. 721–730. doi:10.1145/509907.510011. ISBN 1581134959. S2CID 1727373.
^ Hölscher, Tonio; Krömker, Susanne; Mara, Hubert (2020). "Der Kopf Sabouroff in Berlin: Zwischen archäologischer Beobachtung und geometrischer Vermessung". Gedenkschrift für Georgios Despinis (in German). Athens, Greece: Benaki Museum.
^ Voronoi Cells & Geodesic Distance - Sabouroff head on YouTube.Hölscher et al. cf. doi: 10.11588/heidok.00027985에 의해 기술된 GigaMesh 소프트웨어 프레임워크를 사용한 분석.
^ Bock, Martin; Tyagi, Amit Kumar; Kreft, Jan-Ulrich; Alt, Wolfgang (2009). "Generalized Voronoi Tessellation as a Model of Two-dimensional Cell Tissue Dynamics". Bulletin of Mathematical Biology. 72 (7): 1696–1731. arXiv:0901.4469v1. Bibcode:2009arXiv0901.4469B. doi:10.1007/s11538-009-9498-3. PMID 20082148. S2CID 16074264.
^ Hui Li (2012). Baskurt, Atilla M; Sitnik, Robert (eds.). "Spatial Modeling of Bone Microarchitecture". Three-Dimensional Image Processing (3Dip) and Applications Ii. 8290: 82900P. Bibcode:2012SPIE.8290E..0PL. doi:10.1117/12.907371. S2CID 1505014.
^ ^a ^b Sanchez-Gutierrez, D.; Tozluoglu, M.; Barry, J. D.; Pascual, A.; Mao, Y.; Escudero, L. M. (2016-01-04). "Fundamental physical cellular constraints drive self-organization of tissues". The EMBO Journal. 35 (1): 77–88. doi:10.15252/embj.201592374. PMC 4718000. PMID 26598531.
^ Feinstein, Joseph; Shi, Wentao; Ramanujam, J.; Brylinski, Michal (2021). Ballante, Flavio (ed.). Bionoi: A Voronoi Diagram-Based Representation of Ligand-Binding Sites in Proteins for Machine Learning Applications. Protein-Ligand Interactions and Drug Design. Methods in Molecular Biology. Vol. 2266. New York, NY: Springer US. pp. 299–312. doi:10.1007/978-1-0716-1209-5_17. ISBN 978-1-0716-1209-5. PMID 33759134. S2CID 232338911. Retrieved 2021-04-23.
^ Springel, Volker (2010). "E pur si muove: Galilean-invariant cosmological hydrodynamical simulations on a moving mesh". MNRAS. 401 (2): 791–851. arXiv:0901.4107. Bibcode:2010MNRAS.401..791S. doi:10.1111/j.1365-2966.2009.15715.x. S2CID 119241866.
^ Kasim, Muhammad Firmansyah (2017-01-01). "Quantitative shadowgraphy and proton radiography for large intensity modulations". Physical Review E. 95 (2): 023306. arXiv:1607.04179. Bibcode:2017PhRvE..95b3306K. doi:10.1103/PhysRevE.95.023306. PMID 28297858. S2CID 13326345.
^ Steven Johnson (19 October 2006). The Ghost Map: The Story of London's Most Terrifying Epidemic — and How It Changed Science, Cities, and the Modern World. Penguin Publishing Group. p. 187. ISBN 978-1-101-15853-1. Retrieved 16 October 2017.
^ Mulheran, P. A.; Blackman, J. A. (1996). "Capture zones and scaling in homogeneous thin-film growth". Physical Review B. 53 (15): 10261–7. Bibcode:1996PhRvB..5310261M. doi:10.1103/PhysRevB.53.10261. PMID 9982595.
^ Pimpinelli, Alberto; Tumbek, Levent; Winkler, Adolf (2014). "Scaling and Exponent Equalities in Island Nucleation: Novel Results and Application to Organic Films". The Journal of Physical Chemistry Letters. 5 (6): 995–8. doi:10.1021/jz500282t. PMC 3962253. PMID 24660052.
^ Fanfoni, M.; Placidi, E.; Arciprete, F.; Orsini, E.; Patella, F.; Balzarotti, A. (2007). "Sudden nucleation versus scale invariance of InAs quantum dots on GaAs". Physical Review B. 75 (24): 245312. Bibcode:2007PhRvB..75x5312F. doi:10.1103/PhysRevB.75.245312. ISSN 1098-0121. S2CID 120017577.
^ Miyamoto, Satoru; Moutanabbir, Oussama; Haller, Eugene E.; Itoh, Kohei M. (2009). "Spatial correlation of self-assembled isotopically pure Ge/Si(001) nanoislands". Physical Review B. 79 (165415): 165415. Bibcode:2009PhRvB..79p5415M. doi:10.1103/PhysRevB.79.165415. ISSN 1098-0121. S2CID 13719907.
^ Löbl, Matthias C.; Zhai, Liang; Jahn, Jan-Philipp; Ritzmann, Julian; Huo, Yongheng; Wieck, Andreas D.; Schmidt, Oliver G.; Ludwig, Arne; Rastelli, Armando; Warburton, Richard J. (2019-10-03). "Correlations between optical properties and Voronoi-cell area of quantum dots". Physical Review B. 100 (15): 155402. arXiv:1902.10145. Bibcode:2019PhRvB.100o5402L. doi:10.1103/physrevb.100.155402. ISSN 2469-9950. S2CID 119443529.
^ "GOLD COAST CULTURAL PRECINCT". ARM Architecture.
^ Lopez, C.; Zhao, C.-L.; Magniol, S; Chiabaut, N; Leclercq, L (28 February 2019). "Microscopic Simulation of Cruising for Parking of Trucks as a Measure to Manage Freight Loading Zone". Sustainability. 11 (5), 1276.
^ Singh, K.; Sadeghi, F.; Correns, M.; Blass, T. (December 2019). "A microstructure based approach to model effects of surface roughness on tensile fatigue". International Journal of Fatigue. 129: 105229. doi:10.1016/j.ijfatigue.2019.105229. S2CID 202213370.
^ Niu, Hanlin; Savvaris, Al; Tsourdos, Antonios; Ji, Ze (2019). "Voronoi-visibility roadmap-based path planning algorithm for unmanned surface vehicles" (PDF). The Journal of Navigation. 72 (4): 850–874. doi:10.1017/S0373463318001005. S2CID 67908628.
^ Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. (April 2004). "Coverage control for mobile sensing networks". IEEE Transactions on Robotics and Automation. 20 (2): 243–255. doi:10.1109/TRA.2004.824698. ISSN 2374-958X. S2CID 2022860.
^ Teruel, Enrique; Aragues, Rosario; López-Nicolás, Gonzalo (April 2021). "A Practical Method to Cover Evenly a Dynamic Region With a Swarm". IEEE Robotics and Automation Letters. 6 (2): 1359–1366. doi:10.1109/LRA.2021.3057568. ISSN 2377-3766. S2CID 232071627.
^ Mitchell, Tom M. (1997). Machine Learning (International ed.). McGraw-Hill. p. 233. ISBN 978-0-07-042807-2.
^ Shenwai, Tanushree (2021-11-18). "A Novel Deep Learning Technique That Rebuilds Global Fields Without Using Organized Sensor Data". MarkTechPost. Retrieved 2021-12-05.
^ Ghostarchive 및 Wayback Machine에서 아카이브:
^ "School zones". Victorian Government Department of Education and Training. Retrieved 2020-08-24.
^ Rong, Guodong; Tan, Tiow Seng (2006). "Jump flooding in GPU with applications to Voronoi diagram and distance transform" (PDF). In Olano, Marc; Séquin, Carlo H. (eds.). Proceedings of the 2006 Symposium on Interactive 3D Graphics, SI3D 2006, March 14-17, 2006, Redwood City, California, USA. ACM. pp. 109–116. doi:10.1145/1111411.1111431.
^ "Shadertoy".

레퍼런스

Aurenhammer, Franz; Klein, Rolf; Lee, Der-Tsai (2013). Voronoi Diagrams and Delaunay Triangulations. World Scientific. ISBN 978-9814447638.
Bowyer, Adrian (1981). "Computing Dirichlet tessellations". Comput. J. 24 (2): 162–166. doi:10.1093/comjnl/24.2.162.
de Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2000). "7. Voronoi Diagrams". Computational Geometry (2nd revised ed.). Springer. pp. 47–163. ISBN 978-3-540-65620-3. Fortune의 알고리즘에 대한 설명이 포함됩니다.
Klein, Rolf (1989). "Abstract Voronoi diagrams and their applications". Computational Geometry and its Applications. Lecture Notes in Computer Science. Vol. 333. Springer. pp. 148–157. doi:10.1007/3-540-50335-8_31. ISBN 978-3-540-52055-9.
Lejeune Dirichlet, G. (1850). "Über die Reduktion der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen". Journal für die Reine und Angewandte Mathematik. 1850 (40): 209–227. doi:10.1515/crll.1850.40.209. S2CID 199546675.
Okabe, Atsuyuki; Boots, Barry; Sugihara, Kokichi; Chiu, Sung Nok (2000). Spatial Tessellations — Concepts and Applications of Voronoi Diagrams (2nd ed.). Wiley. ISBN 0-471-98635-6.
Reem, Daniel (2009). "An algorithm for computing Voronoi diagrams of general generators in general normed spaces". Proceedings of the Sixth International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2009). pp. 144–152. doi:10.1109/ISVD.2009.23. ISBN 978-1-4244-4769-5.
Reem, Daniel (2011). "The geometric stability of Voronoi diagrams with respect to small changes of the sites". Proceedings of the 27th Annual ACM Symposium on Computational Geometry (SoCG): 254–263. arXiv:1103.4125. Bibcode:2011arXiv1103.4125R. doi:10.1145/1998196.1998234. ISBN 9781450306829. S2CID 14639512.
Voronoï, Georges (1908a). "Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier mémoire. Sur quelques propriétés des formes quadratiques positives parfaites" (PDF). Journal für die Reine und Angewandte Mathematik. 1908 (133): 97–178. doi:10.1515/crll.1908.133.97. S2CID 116775758.
Voronoï, Georges (1908b). "Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs" (PDF). Journal für die Reine und Angewandte Mathematik. 1908 (134): 198–287. doi:10.1515/crll.1908.134.198. S2CID 118441072.
Watson, David F. (1981). "Computing the n-dimensional Delaunay tessellation with application to Voronoi polytopes". Comput. J. 24 (2): 167–172. doi:10.1093/comjnl/24.2.167.

외부 링크

Weisstein, Eric W. "Voronoi diagram". MathWorld.
CGAL의 Voronoi 다이어그램, 계산기하 알고리즘 라이브러리

[1] Burrough, Peter A.; McDonnell, Rachael; McDonnell, Rachael A.; Lloyd, Christopher D. (2015). "8.11 Nearest neighbours: Thiessen (Dirichlet/Voroni) polygons". Principles of Geographical Information Systems. Oxford University Press. pp. 160–. ISBN 978-0-19-874284-5.

[2] Longley, Paul A.; Goodchild, Michael F.; Maguire, David J.; Rhind, David W. (2005). "14.4.4.1 Thiessen polygons". Geographic Information Systems and Science. Wiley. pp. 333–. ISBN 978-0-470-87001-3.

[3] Sen, Zekai (2016). "2.8.1 Delaney, Varoni, and Thiessen Polygons". Spatial Modeling Principles in Earth Sciences. Springer. pp. 57–. ISBN 978-3-319-41758-5.

[4] Aurenhammer, Franz (1991). "Voronoi Diagrams – A Survey of a Fundamental Geometric Data Structure". ACM Computing Surveys. 23 (3): 345–405. doi:10.1145/116873.116880. S2CID 4613674.

[5] Okabe, Atsuyuki; Boots, Barry; Sugihara, Kokichi; Chiu, Sung Nok (2000). Spatial Tessellations – Concepts and Applications of Voronoi Diagrams (2nd ed.). John Wiley. ISBN 978-0-471-98635-5.

[6] Boyd, Stephen; Vandenberghe, Lieven (2004). Convex Optimization. Exercise 2.9: Cambridge University Press. p. 60.{{cite book}}: CS1 유지보수: 위치(링크)

[Tran09-7] Tran, Q. T.; Tainar, D.; Safar, M. (2009). Transactions on Large-Scale Data- and Knowledge-Centered Systems. p. 357. ISBN 9783642037214.

[Reem_alg-8] 2009년을 맞이합니다.

[Reem_geo_stable-9] 2011년 리엠

[10] 보로노 1908a와 보로노 1908b.

[berg2008-11] Berg, Mark; van Kreveld, Marc; Overmars, Mark; Schwarzkopf, Otfried (2008). Computational Geometry (Third ed.). Springer-Verlag. ISBN 978-3-540-77974-2. 7.4 최단점 보로노이 다이어그램.알고리즘에 대한 설명을 포함합니다.

[12] 에는 가장 먼 점의 Voronoi 다이어그램을 계산하는 간단한 알고리즘이 포함되어 있습니다Skyum, Sven (18 February 1991). "A simple algorithm for computing the smallest enclosing circle". Information Processing Letters. 37 (3): 121–125. doi:10.1016/0020-0190(91)90030-L..

[13] Biedl, Therese; Grimm, Carsten; Palios, Leonidas; Shewchuk, Jonathan; Verdonschot, Sander (2016). "Realizing farthest-point Voronoi diagrams". Proceedings of the 28th Canadian Conference on Computational Geometry (CCCG 2016).

[14] 를 클릭합니다Edelsbrunner, Herbert (2012) [1987]. "13.6 Power Diagrams". Algorithms in Combinatorial Geometry. EATCS Monographs on Theoretical Computer Science. Vol. 10. Springer-Verlag. pp. 327–328. ISBN 9783642615689..

[15] Sunil Arya, Sunil; Malamatos, Theocharis; Mount, David M. (2002). "Space-efficient approximate Voronoi diagrams". Proceedings of the thiry-fourth annual ACM symposium on Theory of computing. pp. 721–730. doi:10.1145/509907.510011. ISBN 1581134959. S2CID 1727373.

[Hoelscher20a-16] Hölscher, Tonio; Krömker, Susanne; Mara, Hubert (2020). "Der Kopf Sabouroff in Berlin: Zwischen archäologischer Beobachtung und geometrischer Vermessung". Gedenkschrift für Georgios Despinis (in German). Athens, Greece: Benaki Museum.

[Hoelscher20b-17] Voronoi Cells & Geodesic Distance - Sabouroff head on YouTube.Hölscher et al. cf. doi: 10.11588/heidok.00027985에 의해 기술된 GigaMesh 소프트웨어 프레임워크를 사용한 분석.

[18] Bock, Martin; Tyagi, Amit Kumar; Kreft, Jan-Ulrich; Alt, Wolfgang (2009). "Generalized Voronoi Tessellation as a Model of Two-dimensional Cell Tissue Dynamics". Bulletin of Mathematical Biology. 72 (7): 1696–1731. arXiv:0901.4469v1. Bibcode:2009arXiv0901.4469B. doi:10.1007/s11538-009-9498-3. PMID 20082148. S2CID 16074264.

[19] Hui Li (2012). Baskurt, Atilla M; Sitnik, Robert (eds.). "Spatial Modeling of Bone Microarchitecture". Three-Dimensional Image Processing (3Dip) and Applications Ii. 8290: 82900P. Bibcode:2012SPIE.8290E..0PL. doi:10.1117/12.907371. S2CID 1505014.

[Sanchez-Gutierrez_77–88-20] Sanchez-Gutierrez, D.; Tozluoglu, M.; Barry, J. D.; Pascual, A.; Mao, Y.; Escudero, L. M. (2016-01-04). "Fundamental physical cellular constraints drive self-organization of tissues". The EMBO Journal. 35 (1): 77–88. doi:10.15252/embj.201592374. PMC 4718000. PMID 26598531.

[21] Feinstein, Joseph; Shi, Wentao; Ramanujam, J.; Brylinski, Michal (2021). Ballante, Flavio (ed.). Bionoi: A Voronoi Diagram-Based Representation of Ligand-Binding Sites in Proteins for Machine Learning Applications. Protein-Ligand Interactions and Drug Design. Methods in Molecular Biology. Vol. 2266. New York, NY: Springer US. pp. 299–312. doi:10.1007/978-1-0716-1209-5_17. ISBN 978-1-0716-1209-5. PMID 33759134. S2CID 232338911. Retrieved 2021-04-23.

[22] Springel, Volker (2010). "E pur si muove: Galilean-invariant cosmological hydrodynamical simulations on a moving mesh". MNRAS. 401 (2): 791–851. arXiv:0901.4107. Bibcode:2010MNRAS.401..791S. doi:10.1111/j.1365-2966.2009.15715.x. S2CID 119241866.

[23] Kasim, Muhammad Firmansyah (2017-01-01). "Quantitative shadowgraphy and proton radiography for large intensity modulations". Physical Review E. 95 (2): 023306. arXiv:1607.04179. Bibcode:2017PhRvE..95b3306K. doi:10.1103/PhysRevE.95.023306. PMID 28297858. S2CID 13326345.

[Johnson2006-24] Steven Johnson (19 October 2006). The Ghost Map: The Story of London's Most Terrifying Epidemic — and How It Changed Science, Cities, and the Modern World. Penguin Publishing Group. p. 187. ISBN 978-1-101-15853-1. Retrieved 16 October 2017.

[MulheranBlackman1996-25] Mulheran, P. A.; Blackman, J. A. (1996). "Capture zones and scaling in homogeneous thin-film growth". Physical Review B. 53 (15): 10261–7. Bibcode:1996PhRvB..5310261M. doi:10.1103/PhysRevB.53.10261. PMID 9982595.

[PimpinelliTumbek2014-26] Pimpinelli, Alberto; Tumbek, Levent; Winkler, Adolf (2014). "Scaling and Exponent Equalities in Island Nucleation: Novel Results and Application to Organic Films". The Journal of Physical Chemistry Letters. 5 (6): 995–8. doi:10.1021/jz500282t. PMC 3962253. PMID 24660052.

[FanfoniPlacidi2007-27] Fanfoni, M.; Placidi, E.; Arciprete, F.; Orsini, E.; Patella, F.; Balzarotti, A. (2007). "Sudden nucleation versus scale invariance of InAs quantum dots on GaAs". Physical Review B. 75 (24): 245312. Bibcode:2007PhRvB..75x5312F. doi:10.1103/PhysRevB.75.245312. ISSN 1098-0121. S2CID 120017577.

[MiyamotoMoutanabbir2009-28] Miyamoto, Satoru; Moutanabbir, Oussama; Haller, Eugene E.; Itoh, Kohei M. (2009). "Spatial correlation of self-assembled isotopically pure Ge/Si(001) nanoislands". Physical Review B. 79 (165415): 165415. Bibcode:2009PhRvB..79p5415M. doi:10.1103/PhysRevB.79.165415. ISSN 1098-0121. S2CID 13719907.

[Löbl_Zhai_Jahn_Ritzmann_p.-29] Löbl, Matthias C.; Zhai, Liang; Jahn, Jan-Philipp; Ritzmann, Julian; Huo, Yongheng; Wieck, Andreas D.; Schmidt, Oliver G.; Ludwig, Arne; Rastelli, Armando; Warburton, Richard J. (2019-10-03). "Correlations between optical properties and Voronoi-cell area of quantum dots". Physical Review B. 100 (15): 155402. arXiv:1902.10145. Bibcode:2019PhRvB.100o5402L. doi:10.1103/physrevb.100.155402. ISSN 2469-9950. S2CID 119443529.

[30] "GOLD COAST CULTURAL PRECINCT". ARM Architecture.

[31] Lopez, C.; Zhao, C.-L.; Magniol, S; Chiabaut, N; Leclercq, L (28 February 2019). "Microscopic Simulation of Cruising for Parking of Trucks as a Measure to Manage Freight Loading Zone". Sustainability. 11 (5), 1276.

[32] Singh, K.; Sadeghi, F.; Correns, M.; Blass, T. (December 2019). "A microstructure based approach to model effects of surface roughness on tensile fatigue". International Journal of Fatigue. 129: 105229. doi:10.1016/j.ijfatigue.2019.105229. S2CID 202213370.

[33] Niu, Hanlin; Savvaris, Al; Tsourdos, Antonios; Ji, Ze (2019). "Voronoi-visibility roadmap-based path planning algorithm for unmanned surface vehicles" (PDF). The Journal of Navigation. 72 (4): 850–874. doi:10.1017/S0373463318001005. S2CID 67908628.

[34] Cortes, J.; Martinez, S.; Karatas, T.; Bullo, F. (April 2004). "Coverage control for mobile sensing networks". IEEE Transactions on Robotics and Automation. 20 (2): 243–255. doi:10.1109/TRA.2004.824698. ISSN 2374-958X. S2CID 2022860.

[35] Teruel, Enrique; Aragues, Rosario; López-Nicolás, Gonzalo (April 2021). "A Practical Method to Cover Evenly a Dynamic Region With a Swarm". IEEE Robotics and Automation Letters. 6 (2): 1359–1366. doi:10.1109/LRA.2021.3057568. ISSN 2377-3766. S2CID 232071627.

[36] Mitchell, Tom M. (1997). Machine Learning (International ed.). McGraw-Hill. p. 233. ISBN 978-0-07-042807-2.

[37] Shenwai, Tanushree (2021-11-18). "A Novel Deep Learning Technique That Rebuilds Global Fields Without Using Organized Sensor Data". MarkTechPost. Retrieved 2021-12-05.

[38] Ghostarchive 및 Wayback Machine에서 아카이브:

[39] "School zones". Victorian Government Department of Education and Training. Retrieved 2020-08-24.

[40] Rong, Guodong; Tan, Tiow Seng (2006). "Jump flooding in GPU with applications to Voronoi diagram and distance transform" (PDF). In Olano, Marc; Séquin, Carlo H. (eds.). Proceedings of the 2006 Symposium on Interactive 3D Graphics, SI3D 2006, March 14-17, 2006, Redwood City, California, USA. ACM. pp. 109–116. doi:10.1145/1111411.1111431.

[41] "Shadertoy".

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[19]

[18]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

권한 관리
국립도서관	프랑스. (데이터) 독일. 이스라엘 미국
다른.	대상 용어의 적용 면 SUDOC(프랑스) 1

Search

보로노이 도표

네임스페이스

더

목차

가장 간단한 경우

형식적 정의

일러스트

특성.

역사와 연구

예