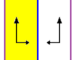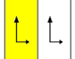평면 대칭군 목록

이 글은 유클리드 평면의 이산대칭군 계급을 요약한 것이다.대칭 그룹은 다음과 같은 세 가지 이름 체계로 여기서 명명된다.국제 표기법, 오비폴드 표기법 및 Coxeter 표기법.평면의 대칭군에는 다음과 같은 세 가지 종류가 있다.

• 로제트 그룹 2개 제품군 – 2D 포인트 그룹
• 7단계 그룹 – 2D 라인 그룹
• 17개의 벽지 그룹 – 2D 공간 그룹.

로제트 그룹

이산 2차원 점군에는 두 개의 패밀리가 있으며, 이들 패밀리는 그룹 내 회전군 순서인 매개변수 n으로 지정된다.

가족	인틀 (svifold)	쇤.	지오 콕시터	주문	예
순환 대칭	n (n•)	Cn	n [n]+	n	C1, [ ]+ (•)	C2, [2](+2•)	C3, [3]+ (3•)	C4, [4]+ (4•)	C5, [5]+ (5•)	C6, [6]+ (6•)
치측 대칭	nm (*n•)	Dn	n [n]	2n	D1, [ ] (*•)	D2, [2](*2•)	D3, [3] (*3•)	D4, [4] (*4•)	D5, [5] (*5•)	D6, [6] (*6•)

프리제 그룹

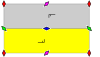
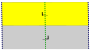
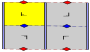
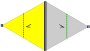
주기적인 방향을 가진 7개의 프리제 그룹, 2차원 선 그룹은 5개의 공칭적인 이름으로 주어진다.쇤파리 표기법은 7개 분음부의 무한 한계로 주어진다.황색 지역은 각각에 있는 무한한 기본 영역을 나타낸다.

[1,∞], IUC (svifold) 지오 쇤플라이스 콕시터 기본 도메인 예 p1m1 (*∞•) p1 C∞v [1,∞] 몸을 옆으로 비키다 p1 (∞•) p1 C∞ [1,∞]+ 깡충깡충 뛰다 [2,∞+], IUC (svifold) 지오 쇤플라이스 콕시터 기본 도메인 예 p11m (∞*) 페이지 1 C∞h [2,∞+] 펄쩍 뛰다 p11g (∞×) 페이지 g1 S2∞ [2+,∞+] 스텝을 밟다

[2,∞], IUC (svifold) 지오 쇤플라이스 콕시터 기본 도메인 예 p2mm (*22∞) p2 D∞h [2,∞] 회전 점프 p2mg (2*∞) p2g D∞d [2+,∞] 빙글빙글 도는 옆구리 p2 (22∞) p2 D∞ [2,∞]+ 회전 깡충깡충 뛰기

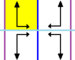
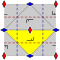
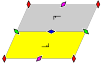
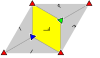
배경화면 그룹

유한한 기본 영역을 가진 17개의 벽지 그룹은 국제 표기법, 오비폴드 표기법, 콕시터 표기법에 의해 주어지며, 평면의 5개의 브라바리스 격자로 분류된다: 사각형, 사선(병렬), 육각형(동삼각형), 직사각형(중심방형), 롬빅(중심 직사각형).

반사 대칭이 없는 p1과 p2 그룹은 모든 등급에서 반복된다.관련 순수반사 Coxeter 그룹은 사선을 제외한 모든 클래스와 함께 주어진다.

사각형 [4,4], IUC (오르브) 지오 콕시터 도메인 콘웨이명 p1 (°) p1 단항성 p2 (2222) p2 [4,1+,4]+ [1+,4,4,1+]+ 등방성 들먹이다 (22×) pg2g [4+,4+] 디글라이드 pmm (*2222) p2 [4,1+,4] [1+,4,4,1+] 디스커픽 cmm (2*22) c2 [(4,4,2+)] 디르옴빅 p4 (442) p4 [4,4]+ 사차이성 p4g (4*2) pg4 [4+,4] 테트라기로 p4m (*442) p4 [4,4] 테트라스코픽

직사각형 [∞h,2,∞v], IUC (오르브) 지오 콕시터 도메인 콘웨이명 p1 (°) p1 [∞+,2,∞+] 단항성 p2 (2222) p2 [∞,2,∞]+ 등방성 pg(h) (××) pg1 h: [∞,+ (2)2]+ 모노글라이드 pg(v) (××) pg1 v: [(synchrones,2),reason]++ 모노글라이드 pgm (22*) pg2 h: [((,2),∞]+ 디지로 pmg (22*) pg2 v: [message, (2,message)]+ 디지로 pm(h) (**) p1 h: [∞,+ 2, 2] 모노스코스 pm(v) (**) p1 v: [csv,2,csv]+ 모노스코스 pmm (*2222) p2 [∞,2,∞] 디스커픽

롬빅 [∞h,2+,∞v], IUC (오르브) 지오 콕시터 도메인 콘웨이명 p1 (°) p1 [∞+,2+,∞+] 단항성 p2 (2222) p2 [∞,2+,∞]+ 등방성 cm(h) (*×) c1 h: [∞,+ 2+, 2] 모노롬빅 cm(v) (*×) c1 v: [csv,2+,csv]+ 모노롬빅 들먹이다 (22×) pg2g [((∞,2)+)[2]] 디글라이드 cmm (2*22) c2 [∞,2+,∞] 디르옴빅 평행사변형(불변형) p1 (°) p1 단항성 p2 (2222) p2 등방성

육각형/삼각형 [6,3], / [3[3]], IUC (오르브) 지오 콕시터 도메인 콘웨이명 p1 (°) p1 단항성 p2 (2222) p2 [6,3]Δ 등방성 cmm (2*22) c2 [6,3]⅄ 디르옴빅 p3 (333) p3 [1+,6,3+] [3[3]]+ 삼중수소성 p3m1 (*333) p3 [1+,6,3] [3[3]] 트리스코픽 p31m (3*3) h3 [6,3+] 트리지로 p6 (632) p6 [6,3]+ 육방성 p6m (*632) p6 [6,3] 헥사스코픽

배경화면 부분군 관계

17개 벽지 그룹^[2] 간의 부분군 관계

		o	2222	××	**	*×	22×	22*	*2222	2*22	442	4*2	*442	333	*333	3*3	632	*632
		p1	p2	pg	pm	cm	들먹이다	pmg	pmm	cmm	p4	p4g	p4m	p3	p3m1	p31m	p6	p6m
o	p1	2
2222	p2	2	2	2
××	pg	2		2
**	pm	2		2	2	2
*×	cm	2		2	2	3
22×	들먹이다	4	2	2			3
22*	pmg	4	2	2	2	4	2	3
*2222	pmm	4	2	4	2	4	4	2	2	2
2*22	cmm	4	2	4	4	2	2	2	2	4
442	p4	4	2								2
4*2	p4g	8	4	4	8	4	2	4	4	2	2	9
*442	p4m	8	4	8	4	4	4	4	2	2	2	2	2
333	p3	3												3
*333	p3m1	6		6	6	3								2	4	3
3*3	p31m	6		6	6	3								2	3	4
632	p6	6	3											2			4
*632	p6m	12	6	12	12	6	6	6	6	3				4	2	2	2	3

참고 항목

• 구면 대칭군 목록
• 오비폴드 표기법#쌍곡면 - 쌍곡 대칭 그룹

메모들

참조

• The Symmetries of Things 2008, John H. Conway, Hidi Burgiel, Chaim Goodman-Strass, ISBN978-1-56881-220-5(다면체, 유클리드 및 쌍곡선 기울기에 대한 Orbifold 표기법)
• 2003년 Quaternions와 Octonion에서는 John Horton Conway와 Derek A.스미스 ISBN 978-1-56881-134-5
• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[2]
  • (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380–407, MR 2,10]
  • (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559–591]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3–45]
• Coxeter, H. S. M. & Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.
• N.W. 존슨: 기하학과 변환, (2018) ISBN 978-1-107-10340-5장 12: 유클리드 대칭군

외부 링크

• 오비폴드 표기법상의 "콘웨이의 원고"(이 원본에서 변경된 표기법, 현재 x는 오픈 도트 대신, o는 클로즈드 도트 대신 사용)
• 17개의 벽지 그룹