지수화
Exponentiation| bn | |
|---|---|
기보법 | |
| 기저 대역 지수 n |

| 산술연산 | ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
수학에서 지수화는 밑과 지수 또는 거듭제곱의 두 수를 포함하는 연산입니다. 지수화는 b로n 표기되며, 여기서 b는 밑, n은 거듭제곱이며, 이것은 "b(높임)에서 n의 거듭제곱"으로 발음됩니다.[1] n이 양의 정수일 때, 지수화는 기저의 반복된 곱에 해당합니다. 즉n, b는 n개의 기저를 곱한 곱입니다.[1]
지수는 일반적으로 밑면 오른쪽에 위첨자로 표시됩니다. 이n 경우 b는 "n번째 거듭제곱으로 상승", "b(상승)", "b(상승)", "b의 n번째 거듭제곱", "b(n번째 거듭제곱)" 또는 "[2]b(n번째)"라고 합니다.
위에서 언급한 기본 사실로부터 시작하여, 임의의 양의 n{\n에 ,b {\n}}는b {\ n 발생이며, 모두 서로 곱한 것이며, 지수화의 다른 여러 속성이 직접적으로 뒤따릅니다. 특히:[nb 1]
즉, 하나의 지수로 상승된 기저에 다른 지수로 상승된 동일한 기저를 곱하면 지수가 더해집니다. 지수들이 추가하는 이 기본 규칙으로부터, 우리는 의 b≠ 0 {\ b에 대하여 b\n}이 1과 같아야 한다는 것을 도출할 수 있습니다. 0 다음과 같습니다. For any , . Dividing both sides by gives .
= displaystyle b^{1}= b}라는 사실도 같은 규칙에서 도출할 수 있습니다. 예를 들어 ( 1 3 = b × × = b 1+ 1 + = b 3 {\displaystyle (b^{1})^{3} = b^{1}\times b^{1}\times b^{1} = b^{1+1} = b^{3}}입니다. 양변의 세제곱근을 취하면 b 1 = b {\displaystyle b^{1} = b}가 나옵니다.
곱하기를 통해 지수가 더해지는 규칙을 사용하여 음의 정수 지수의 속성을 유도할 수도 있습니다. - 의 의미가 무엇인지 생각해 보십시오. exponents add' 규칙을 준수하려면 b - × 1 = - + =b 0 1}\times b^{1}= b^{-1+1}= b^{0}=1}이어야 합니다. 양변을 b 1 {\displaystyle b^{1}}로 나누면 b - 1 = 1 / b 1 {\displaystyle b^{-1}= 1/b^{1}}, 1 = b {\displaystyle b^{-1} = b} 위의 결과를 사용하여b - = / b {\ b^{-1} = 1/로 간단히 쓸 수 있습니다. 유사한 인수를 사용하여 b - n = 1 / b {\displaystyle b^{-n} = 1/b^{n}입니다.
분수 지수의 속성도 같은 규칙을 따릅니다. 예를 들어, 을(를) 고려하여 = b b^{r}= {\sqrt {b}}과 같은 지수가 있는지 묻습니다. 제곱근의 정의로부터, × b = {\displaystyle {\sqrt {b}}\times {\sqrt {b}}= b}입니다. 따라서 지수 r은 × = b b}\times b^{r}= b}가 되어야 합니다. 지수를 곱하면 br + r = b {\display b^{r+r}= b}가 됩니다. The on the right-hand side can also be written as , giving . Equating the exponents on both sides, we have . Therefore, , = 1 / 2 {\displaystyle {\sqrt {b}} = b^{1/2}}.
지수화의 정의는 임의의 실수 또는 복소 지수를 허용하도록 확장될 수 있습니다. 정수 지수에 의한 지수화는 행렬을 포함한 다양한 대수 구조에 대해서도 정의될 수 있습니다.
지수화는 복합 관심, 인구 증가, 화학 반응 역학, 파동 행동 및 공개 키 암호학과 같은 응용 분야와 함께 경제, 생물학, 화학, 물리학 및 컴퓨터 과학을 포함한 많은 분야에서 광범위하게 사용됩니다.
어원
지수(exponent)라는 용어는 "내미는 것"을 의미하는 현재의 지수(exponentre)의 입자인 라틴어 지수(latin exponentem)에서 유래했습니다.[3] 거듭제곱()은 그리스 수학자 유클리드가 키오스의 히포크라테스를 따라 선의 제곱을 위해 사용한 고대 그리스 δύν αμ ις를 잘못 번역한 것입니다.
역사
고대
모래 계산기
모래 계산기에서 아르키메데스는 10의 거듭제곱을 조작하는 데 필요한 지수 10·10 = 10의 법칙을 증명했습니다. 그리고 나서 그는 우주에 포함될 수 있는 모래 알갱이의 수를 추정하기 위해 10의 거듭제곱을 사용했습니다.
이슬람 황금기
말과 카 ʿ바("사각형"과 "큐브형")
9세기에 페르시아의 수학자 무함마드 이븐 무사 알콰리즈미 ī는 정사각형을 مَال(mal, "소유물", "재산")이라는 용어로 사용했습니다. "그 시대와 그 이전 시대의 대부분의 수학자들처럼, 제곱수는 땅의 면적, 특히 그에 따른 재산을 묘사하는 것으로 생각했습니다." 그리고 كَعْبَة(카ʿ바, 큐브)는 정육면체를 의미하는 كَعْبَة, 이후 이슬람 수학자들은 15세기까지 수학적 표기법으로 각각 문자 m īm(m)과 kāf(k)를 나타냈으며, 이는 아부 알 하산 이븐 알 ī 알 칼라사드 ī의 연구에서 볼 수 있습니다.
15세기~18세기
지수 소개
니콜라스 추케(Nicolas Chuquet)는 15세기에 지수 표기법의 한 형태를 사용했는데, 예를 들어 12는2 12x를2 나타냅니다.[11] 이것은 나중에 16세기에 헨리쿠스 그라마테우스와 마이클 스티펠에 의해 사용되었습니다. 16세기 후반에 Jost Bürgi는 지수에 로마 숫자를 사용하였는데, 예를 들어 4x의3 경우 와 같은 방식이었습니다.[12]
"익스폰던트"; "사각형" 및 "큐브"
지수라는 단어는 1544년 마이클 스티펠에 의해 만들어졌습니다.[13][14] 16세기에 Robert Recorde는 정사각형, 정육면체, 젠지젠치(네 번째 거듭제곱), 황고체(다섯 번째), 젠지큐브(여섯 번째), 두 번째 황고체(여 일곱 번째), 젠지젠치(여 여덟 번째)라는 용어를 사용했습니다.[9] 바이쿼드레이트는 네 번째 전력을 지칭하는 데에도 사용되었습니다.
현대 지수 표기법
1636년, 제임스 흄은 본질적으로 현대적인 표기법을 사용했고, L'Algèbre de Vietè에서 그는 A를3 위해 A를iii 썼습니다.[15] 17세기 초, 르네 데카르트가 "La Géométrie"라는 제목의 텍스트에서 현대 지수 표기법의 첫 번째 형태를 소개했습니다. 거기서, 그 표기법은 책 I에 소개되어 있습니다.[16]
나는 ... a, 즉 a를 스스로 곱하는 것; 그리고2 a를 다시3 한 번 a에 곱하는 것, 즉 무한대로 지정합니다.
— René Descartes, La Géométrie
일부 수학자(데카르트와 같은)는 2보다 큰 거듭제곱에 대해서만 지수를 사용했으며, 제곱을 반복 곱하기로 표현하는 것을 선호했습니다. 따라서 그들은 다항식을 예를 들어 ax + bx + cx3 + d로 적습니다.
"지수"
Samuel Jake는 1696년에 지수라는 용어를 도입했습니다.[6] involution이라는 용어는 용어 인덱스와 동의어로 사용되었지만 사용이[17] 감소했기 때문에 더 일반적인 의미와 혼동되어서는 안 됩니다.
가변 지수, 비-정수 지수
1748년 레온하르트 오일러는 다음과 같은 글을 써서 가변 지수, 그리고 암묵적으로 비-정수 지수를 도입했습니다.
지수 자체가 변수인 지수 또는 거듭제곱을 고려합니다. 이런 종류의 양은 대수함수가 아님이 분명한데, 지수가 일정해야 하기 때문입니다.[18]
용어.
b = b · b라는 표현은 한 변의 길이가 b인 정사각형의 넓이가 b이기 때문에 "b의 제곱" 또는 "b의 제곱"이라고 합니다. ("b to second power"라고도 할 수 있는 것은 사실이지만, "b의 제곱"과 "b의 제곱"은 전통과 편의에 의해 너무 깊이 뿌리 박혀 있어서 "b to second power"가 이상하거나 어설프게 들리는 경향이 있습니다.)
마찬가지로, b = b · b · b는 한 변의 길이가 b인 정육면체의 부피가 b이기 때문에 "b의 정육면체" 또는 "b 정육면체"라고 불립니다.
지수가 양의 정수인 경우, 이 지수는 기본의 복사본을 몇 개 곱했는지 나타냅니다. 예를 들어 3 = 3 · 3 · 3 · 3 = 243 입니다. 지수가 5이기 때문에 밑 3은 곱셈에서 5번 나타납니다. 여기서 243은 3의 5제곱, 즉 3의 5제곱을 5제곱으로 올리는 것입니다.
"높아진"이라는 단어는 보통 생략되고, 때때로 "힘"도 있으므로 3은5 "3에서 5까지" 또는 "3에서 5까지"로 간단히 읽을 수 있습니다. 따라서 지수 b는n "b to n", "b to n", "b to n", "b to n", 또는 가장 간단히 "b to n"으로 표현할 수 있습니다.
중첩57 지수가 3인 공식(3이(57)5 아닌 3을 의미함)7은 힘의 탑 또는 간단히 탑이라고 합니다.[19] 예를 들어 를 쓰는 것은 ( d를 쓰는 것과 같습니다 동일한 아이디어는 더 많은 수준이 추가될 때 계속 적용됩니다. {\ b를 b ( f) b 등을 의미합니다. For example, can be computed as , which can be computed as , which is equal to , which is equal to 10.
정수 지수
정수 지수를 사용한 지수화 연산은 기본 산술 연산에서 직접 정의할 수 있습니다.
양의 지수
반복 곱셈으로서의 지수의 정의는 유도를 사용하여 공식화할 수 있으며,[20] 연관 곱셈이 있는 즉시 이 정의를 사용할 수 있습니다.
기본 케이스는
그리고 재발은
곱셈의 연관성은 임의의 양의 정수 m과 n에 대하여,
그리고.
영지수
정의에 따르면 0이 아닌 숫자가 0으로 증가하면 1이 됩니다.[21][1]
이것은 공식을 적용할 수 있는 영 지수의 유일한 정의입니다.
지수가 0이 되도록. 모든 대수 구조에서 항등식을 갖는 곱셈으로 사용될 수 있습니다.
직관적으로 은 b의 복사본의 빈 곱으로 해석될 수 있습니다. 따라서, 0 ={\displaystyle b^{0}=1}은 빈 제품에 대한 일반적인 관례의 특별한 경우입니다.
0인0 경우는 더 복잡합니다. 정수의 거듭제곱만 고려되는 상황에서 값 1은 일반적으로 0에0 할당되지만, 그렇지 않은 경우 값을 할당할지 여부와 할당할 값의 선택은 상황에 따라 달라질 수 있습니다.
음의 지수
음의 지수를 사용한 지수화는 임의의 정수 n과 0이 아닌 b에 대해 성립하는 다음 항등식으로 정의됩니다.
- - n = b n {\displaystyle b^-n} = {\frac {1} {b^{n}}}.
0을 음의 지수로 높이는 것은 정의되지 않지만 경우에 따라 무한대로 해석될 수 ∞ {\\infty}).
음의 지수를 사용한 이 지수의 정의는 동일성 + n = ⋅ {\ b^{m+n} = b^{m}\cdot b^{n}}를 음의 지수로 확장할 수 있는 유일한 정의입니다(대례 m = - n {\displaystyle m=-n}).
동일한 정의는 연관 곱셈과 1로 표시된 곱셈 항등식(예를 들어, 주어진 차원의 제곱 행렬)을 갖는 곱셈 모노이드, 즉 대수 구조의 가역 요소에 적용됩니다. 특히, 이러한 구조에서 가역 요소 x의 역수는 으로 x- 로 표시됩니다 {\ x
신원 및 속성
지수 규칙이라고도 불리는 다음 ID는 베이스가 0이 아닌 경우 모든 정수 지수에 대해 유지됩니다.[1]
덧셈과 곱셈과 달리 지수화는 교환적이지 않습니다. For example, 23 = 8 ≠ 32 = 9. 또한 덧셈과 곱셈과 달리 지수화는 연관성이 없습니다. 예를 들어 (2) = 8 = 64인 반면 2 = 2 = 512입니다. 괄호가 없으면 위첨자 표기법에서 연속 지수화를 위한 기존의 작업 순서는 상향식[22][23][24][25](또는 오른쪽 연관식)이 아니라 하향식(또는 왼쪽 연관식)입니다. 그것은,
일반적으로, 그것은 다른 것입니다.
합의 거듭제곱
합의 거듭제곱은 일반적으로 이항 공식에 의해 합의 거듭제곱으로부터 계산될 수 있습니다.
그러나 이 공식은 섬머가 통근하는 경우(즉, ab = ba)에만 해당되며, 이는 섬머가 통근하는 구조에 속할 경우를 의미합니다. 그렇지 않으면 a와 b가 같은 크기의 정사각형 행렬이면 이 공식을 사용할 수 없습니다. 따라서 컴퓨터 대수학에서는 지수 기저가 통근하지 않을 때 정수 지수를 포함하는 많은 알고리즘을 변경해야 합니다. 일부 범용 컴퓨터 대수 시스템은 비 commuting 기저를 갖는 지수화를 위해 다른 표기법(때로는 ^ 대신 ^^)을 사용하며, 이를 비가환 지수화라고 합니다.
조합해석
음이 아닌 정수 n과 m의 경우, n의m 값은 m개 원소 집합에서 n개 원소 집합까지의 함수 수이다(기본 지수 참조). 이러한 함수는 n-요소 집합의 m-튜플(또는 n-문자 알파벳의 m-문자 단어)로 나타낼 수 있습니다. m과 n의 특정 값에 대한 몇 가지 예는 다음 표에 나와 있습니다.
| nm | 집합m {1, ..., n}에서 가능한 요소의 m-쌍 |
|---|---|
| 05 = 0 | 없음. |
| 14 = 1 | (1, 1, 1, 1) |
| 23 = 8 | (1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2) |
| 32 = 9 | (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) |
| 41 = 4 | (1), (2), (3), (4) |
| 50 = 1 | () |
특정베이스
10의 거듭제곱
기본 10(십진수) 수 체계에서 10의 정수 거듭제곱은 숫자 1 다음에 지수의 부호와 크기에 의해 결정되는 숫자 0으로 기록됩니다. 예를 들어 10 = 1000 및 10 = 0.0001입니다.
밑이 10인 지수화는 과학적 표기법에서 크거나 작은 수를 나타내는 데 사용됩니다. 예를 들어, 299792458m/s(진공에서의 빛의 속도, 초당 미터)는 2.99792458×10m8/s로 표기한 다음 2.998×10m8/s로 근사할 수 있습니다.
10의 거듭제곱에 기반한 SI 접두사는 작거나 큰 양을 설명하는 데에도 사용됩니다. 예를 들어, 접두사 킬로는 10 = 1000을 의미하므로 1킬로미터는 1000미터입니다.
2의 거듭제곱
2의 첫 번째 음의 거듭제곱은 일반적으로 사용되며, 예를 들어 반과 사분의 일과 같은 특별한 이름이 있습니다.
2의 거듭제곱은 집합 이론에 등장하는데, n개의 원소를 가진 집합은 모든 부분집합의 집합인 거듭제곱 집합을 가지며, 이것은n 2개의 원소를 가진 집합입니다.
2의 정수 거듭제곱은 컴퓨터 과학에서 중요합니다. 양의 정수 거듭제곱 2는 n비트 정수 이진수에 대해 가능한 값의 수를 제공합니다. 예를 들어, 바이트는 2 = 256개의 다른 값을 가질 수 있습니다. 이진수 체계는 임의의 수를 2의 거듭제곱의 합으로 표현하고, 0과 1의 수열로 표시하며, 1은 2의 거듭제곱을 나타내고, 1은 합에 나타나는 2의 거듭제곱을 나타내고, 지수는 이 1의 위치에 의해 결정됩니다. 음이 아닌 지수는 점의 왼쪽에 있는 1의 순위입니다(0부터 시작). 음의 지수는 점의 오른쪽에 있는 순위에 의해 결정됩니다.
한 사람의 힘
1의 모든 거듭제곱은 1 = 1과 같습니다. 이것은 n이 음수여도 사실입니다.
숫자의 첫 번째 거듭제곱은 숫자 그 자체입니다: n = n.
0의 거듭제곱
지수 n이 양수(n > 0)이면 0의 n번째 거듭제곱은 0 = 0입니다.
지수 n이 음수(n < 0)인 경우n 0의 n번째 거듭제곱은 정의되지 않습니다. 0은 -n > 0과 / 0- {\1/이 같아야 하며, 위에 1 / {\이 됩니다.
식0 0은 1로 정의되거나 정의되지 않은 상태로 유지됩니다.
음의 1의 거듭제곱
만약 n이 짝수 정수이면 (-1) = 1입니다. 음수에 다른 음수를 곱하면 부호가 취소되므로 양수가 나오기 때문입니다.
n이 홀수 정수이면 (-1) = -1입니다. 왜냐하면 -1쌍을 제거하고 남은 -1개가 있기 때문입니다.
이 때문에 -1의 거듭제곱은 순서를 번갈아 표현하는 데 유용합니다. 복소수 i의 거듭제곱에 대한 유사한 논의는 복소수의 § n번째 근을 참조하십시오.
대지수
한 수보다 큰 수의 거듭제곱 수열의 한계가 발산합니다. 즉, 수열은 무한히 증가합니다.
- bn → ∞ as n → ∞ when b > 1
이것은 "b가 1보다 클 때 n이 무한대인 경향이 있기 때문에 n의 거듭제곱에 대한 b는 + ∞의 경향이 있다"고 읽을 수 있습니다.
절대값이 1보다 작은 숫자의 거듭제곱은 0인 경향이 있습니다.
- bn → 0 as n → ∞ when b < 1
한 사람의 어떤 힘도 항상 하나입니다.
- bn = 1 for all n if b = 1
-1의 거듭제곱은 n이 짝수와 홀수를 번갈아 가면서 1과 -1 사이에서 교대하므로 n이 커짐에 따라 제한이 없습니다.
bn < –1인 경우, b는 n이 짝수와 홀수를 번갈아 가면서 점점 더 큰 양수와 음수를 번갈아 가며, 따라서 n이 커짐에 따라 제한되는 경향이 없습니다.
지수가 무한대인 경향이 있기 때문에 지수가 1인 경향이 있는 동안 지수 수가 달라지는 경우, 한계가 반드시 위의 것들 중 하나일 필요는 없습니다. 특히 중요한 경우는
- (1 + 1/n)n → e as n → ∞
기타 한계, 특히 불확정 형태를 취하는 표현의 한계는 아래 § 권한 한계에 설명되어 있습니다.
멱함수
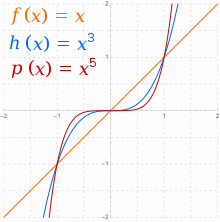

= n {\ f(x) = cx^{}} 형태의 실수 함수, 여기서 c ≠ 0 {\displaystyle c\n 0 때로는 멱함수라고도 합니다.[26] 이 정수이고 ≥ 1 ngeq 1}인 경우 n n} 와 n} 홀수의 두 기본 패밀리가 합니다 In general for , when is even will tend towards positive infinity with increasing , and also towards positive infinity with decreasing . 고른 멱함수 계열의 모든 그래프는 인 모양이 = x 2 {\ y = cx^{2}}이며, n {\displaystyle n}이 증가할수록 중간에서 더 평평해집니다. 이와 같은 대칭성(( - ) =(x ) {\displaystyle f (-x) = f (x )})을 갖는 함수를 짝수 함수라고 합니다.
n이(가) 홀수인 경우 의점근 동작이 의 x 에서 의 x 로 돌아갑니다 > 0 c의 경우 ) = c n {\ fx) = cx^{n}} 또한 x {\displaystyle x}가 증가하면 양의 무한대로, x {\displaystyle x}가 감소하면 음의 무한대로 향하는 경향이 있습니다. 홀수 멱함수 계열의 모든 그래프는 일반적인 y = c x 3 {\displaystyl y = cx^{3}, 이 증가함에 따라 중간에서 더 평평해지고 = 1{\ = 1}에 대해 직선에서 모든 평탄도를 잃게 됩니다. 이러한 대칭성을 갖는 함수(f ( - x ) = - f ( x ) {\displaystyle f (-x) = - f (x )}를 홀수 함수라고 합니다.
< 의 경우각 경우에 반대 점근적 동작이 참입니다.[27]
십진법의 거듭제곱표
| n | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
유리 지수

x가 음이 아닌 실수이고 n이 양의 정수이면 / x 또는 x 는 x의 고유한 양의 실수 n번째 루트, 즉 y가 = 가 되도록 한 양의 실수 y를 나타냅니다 displaystyle y^{n}= x.
x가 양의 실수이고, {\ {가 유리수이고, p와 q > 0의 정수인 경우, p/ 는 다음과 같이 정의됩니다.
The equality on the right may be derived by setting and writing
r이 양의 유리수이면 정의상 0 = 0입니다.
이 모든 정의는 항등식( r) = x {\displaystyle (x^{r})^{s} = x^{rs}}를 유리 지수로 확장하는 데 필요합니다.
반면, 이러한 정의를 양의 실수가 아닌 기저로 확장하는 데는 문제가 있습니다. 예를 들어, 음수인 실수는 n이 홀수이면 음수이고, n이 짝수이면 실수가 없습니다. 후자의 경우, 복잡한 n번째 루트 가 x {\ x에 대해 선택하는 것 중 하나는 항등식( a = {\displaystyle (x^{a})^{b} = x^{ab}}에 대해 만족할 수 없습니다. 예를들면,
이러한 문제를 처리하는 방법에 대한 자세한 내용은 § 실수 지수 및 § 복소수의 정수가 아닌 거듭제곱을 참조하십시오.
실수 지수
양의 실수의 경우, 실제 거듭제곱에 대한 지수는 연속성에 의해 유리제곱을 실수로 확장하거나(합리적 지수의 § 한계, 아래) 기저와 지수 함수의 로그로 확장하거나(로그를 통한 §제곱, 아래) 두 가지 동등한 방법으로 정의할 수 있습니다. 결과는 항상 양의 실수이며, 정수 지수에 대해 위에 표시된 항등식과 성질은 실수 지수에 대한 이러한 정의와 함께 참으로 유지됩니다. 두 번째 정의는 복소 지수로 간단히 일반화하기 때문에 더 일반적으로 사용됩니다.
반면, 음수인 실수의 실제 거듭제곱에 대한 지수는 비실수일 수 있고 여러 값을 가질 수 있기 때문에 일관성 있게 정의하기가 훨씬 더 어렵습니다(음의 기저를 가진 § 실수 지수 참조). 이러한 값 중 하나를 선택할 수 있는데, 이 값을 주값이라 부르지만, 주값을 선택할 수 없습니다.
참입니다. § 검정력 및 로그 항등식의 고장을 참조하십시오. 따라서 양의 실수가 아닌 기저를 갖는 지수화는 일반적으로 다가치 함수로 간주됩니다.
유리 지수의 한계

임의의 무리수는 유리수열의 극한으로 표현될 수 있으므로, 임의의 실수 지수 x를 갖는 양의 실수 b의 지수는 규칙과의[28] 연속성에 의해 정의될 수 있습니다.
여기서 극한은 r의 유리수 값만을 인수합니다. 이 한계는 모든 양의 b와 모든 실수 x에 대해 존재합니다.
예를 들어, 만약 x = π, 비종단 십진법 표현 π = 3.14159... 유리수의 단조성을 사용하여 원하는 만큼 작은 로 경계를 이루는 구간을 얻을 수 있으며 bπ를 포함해야 합니다. bpi}}
따라서 구간의 상한과 하한은 π로 표시되는 동일한 극한을 갖는 두 개의 시퀀스를 형성합니다. bpi}}
이것은 모든 양의 b와 실수 x에 대한 b를 b와 x의 연속 함수로 정의합니다. 정의된 식을 참조하십시오.[29]
지수함수
지수 함수는 흔히 ↦ x, xe^{x}}로 정의되며서 ≈ 2.{\e\approx 2.718}은 오일러의 수이다. 순환 추론을 피하기 위해 여기서는 이 정의를 사용할 수 없습니다. 따라서 지수 함수의 정의는 ), exp(x)} 및 오일러 수에 대한 정의가 주어지며, 이는 양의 정수 지수를 갖는 지수화에만 의존합니다. 그런 다음 앞 절에서 주어진 지수의 정의를 사용하면 다음과 같은 증명을 얻을 수 있습니다.
지수 함수를 정의하는 데는 여러 가지 동등한 방법이 있는데, 그 중 하나는
하나는 (0 = 1, {\displaystyle \exp(0) = 1,}이며 지수 ID exp (x + y ) = exp (x ) exp ( y) {\displaystyle \exp(x+y) =\exp(x)\exp(y)}가 다음과 같이 유지됩니다.
그리고 2차 항 2 는 한계에 영향을 주지 않으므로 (x ( = exp (x + y) {\displaystyle \exp(x)\exp(y) =\exp(x+y)}를 산출합니다.
오일러의 수는 = () {\ e =\exp(1)}로 정의할 수 있습니다. x가 정수일 때 (x) = x {\displaystyle \exp(x) = e^{x}}를 exp하는 앞의 식에서 다음과 같습니다(이는 지수의 반복 multip화 정의에서 비롯됩니다). x가 실수인 경우 ( ) = x {\displaystyle \exp(x) = e^{x}}는 x가 유리인 경우 지수 항등식을 사용하고, 그렇지 않은 경우 지수 함수의 연속성을 사용하여 이전 절에 주어진 정의에서 비롯됩니다.
지수 함수를 정의하는 한계는 x의 모든 복소값에 대해 수렴하므로 (z) \expz)},, e^{z}}의 정의를 실수에서 임의의 복소 인수 z로 확장하는 데 사용할 수 있습니다. 이 확장된 지수 함수는 여전히 지수 항등식을 만족하며, 일반적으로 복소 기저 및 지수에 대한 지수를 정의하는 데 사용됩니다.
로그를 통한 전력 공급
e를x 지수 함수로 정의하면 모든 양의 실수 b에 대해 지수 함수와 로그 함수로 b를x 정의할 수 있습니다. 구체적으로, 자연로그 ln(x)가 지수 함수 e의x 역수라는 것은 다음을 의미합니다.
모든 b > 0에 대하여. 아이덴티티) y= 보존을 위해}xy개가 있어야 합니다.
x bx\ln b}}는 임의의 양의 실수 b에 대한 대안적인 정의로 사용될 수 있습니다. 이는 유리 지수와 연속성을 사용하여 위에서 제시한 정의와 일치하며, 모든 복소 지수로 바로 확장할 수 있는 이점이 있습니다.
양의 실수 기저를 갖는 복소 지수
b가 양의 실수일 경우, 기저 b와 복소 지수 z를 갖는 지수는 복소 인수를 갖는 지수 함수에 의해 정의됩니다(위의 § 지수 함수 끝 참조).
여기서 b ln b}는 b의 자연로그를 나타냅니다.
이것은 아이덴티티를 만족시킵니다.
일반적으로( b는 가 아니므로 는z 정의되지 않았습니다. 복소수의 지수에 의미를 부여하면 일반적으로 다음과 같은 것을 갖습니다(복소수의 비-정수의 거듭제곱, 아래 § 참조).
z가 실수이거나 t가 정수가 아닌 이상.
의 극 형태를 z의 실수부와 허수부로 표현할 수 있습니다. 즉,
여기서 삼각 계수의 절대값은 1입니다. 결과는 다음과 같습니다.
복소수의 정수가 아닌 거듭제곱
앞 절에서 정수가 아닌 지수를 사용한 지수는 양의 실수 기저에 대해서만 정의되었습니다. 다른 기저의 경우, n번째 근의 겉보기에 단순한 경우, 즉 지수 1에서 n은 양의 정수입니다. n번째 근에는 일반적으로 정수가 아닌 지수를 사용하는 지수 이론이 적용되지만 복잡한 로그를 사용할 필요가 없으므로 이해하기 쉽기 때문에 이 경우를 먼저 고려해야 합니다.
복소수의 n번째 근
0이 아닌 모든 복소수 z는 극형으로 다음과 같이 쓰여질 수 있습니다.
여기서ρ \rho}은 의 절대값이고 θdisplaystyle \theta}은(는) 인수입니다. 인수는 최대 2 π의 정수 배로 정의됩니다. 즉θ {\displaystyle \theta}가의 인수인경우 θ + 2 kπ {\displaystyle \theta + 2k\pi}도 모든정수 k {\displaystyle k}에 대해 한복소수의 인수입니다.
두 복소수 곱의 극형은 절대값을 곱하고 인수를 더하면 얻어집니다. 복소수의 n번째 근의 극성 형태는 절대값의 n번째 근을 취하고 그 인수를 n으로 나누면 구할 수 있습니다.
θ{\displaystyle\theta}에 의 π {\displaystyle 2\pi}이() 추가되면 복소수는 변경되지 않지만 n번째 루트의 인수에 2i π / n {\displaystyle 2i\pi / n}이(가) 추가되어 새 n번째 루트가 제공됩니다. 이것은 n번 할 수 있으며 복소수의 n번째 근을 제공합니다.
n번째 뿌리 중 하나를 주근으로 선택하는 것이 일반적입니다. 일반적인 선택은π< θ ≤ π,\pi <\theta \leq \pi,} 즉, 실수부가 가장 큰 n번째 루트를 선택하고, 두 개일 경우 양의 허수부를 갖는 루트를 선택하는 것입니다. 따라서 주 n번째 근은 라디칼의 음의 실수 값을 제외하고 전체 복소 평면에서 연속 함수가 됩니다. 이 함수는 양의 실제 라디칼에 대한 일반적인 n번째 근과 같습니다. 음의 실수 라디칼과 홀수 지수의 경우, 일반적인 n번째 근은 실수이지만 주 n번째 근은 실수가 아닙니다. 분석적 연속은 주 n번째 근이 양이 아닌 실수 없이 일반적인 n번째 근을 복소 평면으로 확장하는 고유한 복소 미분 가능 함수임을 보여줍니다.
인수를 증가시켜 복소수를 0 주위로 이동시킨 경우, π 증가 후 2\pi,} 복소수는 초기 위치로 되돌아오고, n번째 루트는 순환 치환됩니다(이들은e π/ n^{2i\pi / n}을 ). 이것은 전체 복소 평면에서 연속되는 n번째 근 함수를 정의할 수 없음을 보여줍니다.
단결의 뿌리

그런 다음 통일의 n번째 근은 w = 1과 같은 복소수이며, 여기서 n은 양의 정수입니다. 이산 푸리에 변환 또는 대수 방정식의 대수 솔루션(라그랑주 분해능)과 같은 수학의 다양한 영역에서 발생합니다.
통일성의 n번째 루트는 {\displaystyle \=e^{\ {2\pii}{n}}의 ω = π의 n번째 거듭제곱으로, 즉 1 = ω 0 = ω n, ω = ω 1, ω 2, ω n - 1입니다. {\displaystyle 1=\omega ^{n}=\omega ^{n},\omega =\omega ^{1},\omega ^{2},\omega ^{n-1},\omega ^{n-1}입니다.이러한 생성 속성을 갖는 단일성의 n번째 루트는 단일성의 원시 n번째 루트라고 불리며, k개의 코프림이 n인 \omega^{k}e^{\frac {2k\pii}{n}}에서 k 의 형태를 갖습니다. 유니티의 고유한 원시 제곱근은 유니티의 원시 네 번째 루트는 및
통일의 n번째 근은 복소수 z의 모든 n번째 근을 통일의 n번째 근을 가진 z의 주어진 n번째 근의 곱으로 표현할 수 있습니다.
기하학적으로, 통일성의 n번째 근은 실수 1 위에 하나의 꼭짓점이 있는 정규 n-곤의 꼭짓점에 있는 복소 평면의 단위 원 위에 놓여 있습니다.
epii}{n}}의 e π는 가장 작은 양의 논법을 가진 통일성의 원시 n근이므로 통일성의 원시 n근이라고 하며, 때로는 통일성의 원시 n근이라고도 하며, 이 용어는 주값 / n 1즉 1과 혼동될 수 있습니다.[30][31][32]
복소 지수
기저로 지수화를 정의하면 z w 에 대해 일반적으로 무한히 많은 가능한 값이 있다는 점을 제외하고는 앞 절에서 설명한 것과 유사한 어려움이 발생합니다 따라서 실제 및 양이 아닌 z 값에 대해 연속적이지 않은 주 값이 정의됩니다. 또는 z는 다중값 함수로 정의됩니다.
모든 경우에 복소 로그를 사용하여 복소 지수를 정의합니다.
서 z\log z}는 사용되는 복소 로그의 변형, 즉 함수 또는 다음과 같은 다중 값 함수입니다.
정의 영역의 모든 z에 대하여.
본원가치
복소수 로그의 주요 값은 0이 아닌 모든 복소수 z에 대하여, 일반적으로 표시되는 고유한 연속 함수{\입니다.
그리고 z의 주장은 만족합니다.
복소 로그의 주값은 = 0{\displaystyle z = 0,}에 대해 정의되지 않으며, z의 음의 실수 값에서 불연속적이며, 다른 곳에서는 복소 미분이 가능합니다. z가 실수이고 양수인 경우, 복소수 로그의 주값은 자연 로그( z = ln z. {\ \log z =\ln z.})입니다.
z의 주값은 = z, {\ z^{w}=e^{w\log z}}로 정의되며, 여기서 로그 z {\displaystyle \log z}는 로그의 주값입니다.
함수( w → w {\는 z가 실수이고 양이 아닌 점의 근방을 제외하고는 동형입니다.
z가 실수이고 양수인 경우 {\ z의 주값은 위에서 정의한 일반적인 값과 같습니다. = /n, {\displaystyle w = 1/n,} 여기서 n은 정수입니다. 이 주값은 위에서 정의한 것과 동일합니다.
다치함수
컨텍스트에서 z z}및 z^{w}의 주 값이 z의 음의 실수 값에서 불연속적으로 발생하는 문제가 있습니다. 이 경우에는 이러한 함수를 다가치 함수로 간주하는 것이 유용합니다.
z \log z}가 다중 값 로그(일반적으로 해당 기본 값)의 값 중 하나를 나타내는 경우 다른 값은 2ik π + 로그 z, {\displaystyle 2ik\pi +\log z,}이며 k는 임의의 정수입니다. 마찬가지로 가 지수의 한 값일 경우 다른 값은 다음과 같습니다.
여기서 k는 임의의 정수입니다.
k의 다른 값은 w가 유리수 즉, dw가 정수가 되는 정수가 아닌 이상 z의 다른 값을 제공합니다. 이는 지수 함수의 주기성, 구체적으로 a - b {\displaystyle a-b가 2 π i의 정수 배인 경우에만 = {\ e^{a}= e^{b}인 경우에 기인합니다. {\displaystyle 2\pi i}
= m {\ w = {\frac {m}{n}}이(가) n > 0, {\displaystyle n> 0,}인 경우 z w {\displaystyle z^{w}}는 정확히 n 값을 갖습니다. =인 경우 displaystyle m = 1,} 이 값은 복소수의 § n번째 근에 설명된 값과 동일합니다. w가 정수라면 § 정수 지수 값과 일치하는 값은 하나뿐입니다.
는 z ≠ {\ z\n에 대해 동형입니다.의 그래프가 모든 점의 근방에서 각각의 동형 함수를 정의하는 여러 장의 시트로 구성된다는 점에서. z가 0을 중심으로 원을 따라 연속적으로 변하는 경우, 회전한 후 {\ z의 값이 시트에서 변경되었습니다.
연산
의 표준 x+ 는 z와 w의 표준 형식에서 계산할 수 있습니다. 이것은 하나의 공식으로 설명할 수 있지만 계산을 여러 단계로 나누는 것이 더 명확합니다.
- z의 극형. = +ib {\displaystyle z = a+ib}가 z의 표준 형식(a와 b는 실수)이면 해당 극 형식은 여기서 ρ = a2 + b 2 {\displaystyle \rho = {\}+b^{2 a2 (a, b)에서 {\displaystyle \theta \operatorname {atan2}(a, b)}(이 함수의 정의는 a2 참조).
- z의 로그. 이 로그의 주값은 z = ρ + i θ, {\displaystyle \log z =\ln \rho + i\theta,}이며, 여기서 ln {\displaystyle \ln }은 자연 로그를 나타냅니다. 로그의 다른 값들은 임의의 정수 k에 2 π 2ik\pi}을 더하여 얻어집니다.
- 의 표준 형식 w\log z.} c와 d real이 있는 w = c + di {\displaystyle w= c+di}인 경우 w log z {\displaystyle w\log z}의 값은 = 에 해당하는 주값. {\ k = 0.}
- 최종 결과. ID + = y}=e^{x}e^{y}} 및 y ln x = xy, {\displaystyle e^{y\ln x}= x^{y}}를 사용하면 다음을 얻을 수 있습니다. 값에 = 0 {\displaystyle k = 0}을 사용합니다.
예
-
i의 극 형식은 = π / 2, {\ i=e^{i\pi /2}}이며 로그 i {\displaystyle \logi}의 값은 다음과 같습니다.다음은의 모든 값은 실수이며, 주 1은
마찬가지로 -2의 극 형태는 = 2 π입니다. {\displaystyle -2 = 2e^{i\pi}} 따라서 위에서 설명한 방법은 값을 제공합니다.이 경우 모든 값은 동일한 인수 2, 4\ln 2,} 및 다른 절대값을 갖습니다.
두 예 에서 의 모든 값은 동일한 인수를 가집니다. 더 일반적으로, 이것은 w의 실수 부분이 정수인 경우에만 해당됩니다.
검정력 및 로그 항등식의 고장
양의 실수에 대한 거듭제곱과 로그에 대한 일부 항등식은 복소수에 대해 실패합니다. 아무리 복소수의 거듭제곱과 복소수를 단일 값 함수로 정의하더라도 말입니다. 예:
- 항등식 로그(b) = x ⋅ 로그 b는 b가 양수이고 x가 실수일 때마다 유지됩니다. 그러나 복소 로그의 주 분기에 대해서는
로그의 어느 분기를 사용하든 동일성의 유사한 고장이 존재합니다. (이 결과를 사용하는 경우에만) 말할 수 있는 최선의 방법은 다음과 같습니다.
로그를 다중 값 함수로 고려해도 이 ID는 유지되지 않습니다. z ⋅ 로그의 값을 포함하는 log(w)의 가능한 값이 적절한 부분 집합이었습니다. log(w)와 m의 주값에 log(w)를 사용하면 n은 임의의 정수로서 가능한 양변의 값은 다음과 같습니다.
- 항등식 (bc) = bc 및 (b/c) = b/c는 b와 c가 양의 실수이고 x가 실수일 때 유효합니다. 그러나 주요 가치의 경우 다음과 같습니다. 그리고.반면, x가 정수일 때 항등식은 0이 아닌 모든 복소수에 대해 유효합니다. 지수화가 다중 값 함수로 간주되는 경우 가능한 값(-1 ⋅ -1)은 {1, -1}입니다. ID가 유지되지만 {1} = {(-1 ⋅ -1)}이라고 말하는 것이 잘못되었습니다.
- 항등식 (e) = e는 실수 x와 y를 의미하지만, 복소수에 대한 참값을 가정하면 1827년 클라우젠에 의해 발견된 다음과 같은 역설이 나타납니다. 임의의 정수 n에 대하여, 우리는 다음을 갖습니다.
- + 의 ) = e {\displaystyle \left(e^{1+2\piin}\right)^{1+2\iin} =e\qquad} ((( + 2 π의 경우) {\displaystyle (1+\piin)} -양쪽의 거듭제곱)
- + in- 4 2n 2 e displaystyle 1+4\pi in-4\pi 2}}= e\qquad ((x) y = y {\displaystyle \left(e^{x}\right) 사용)}xy 및 지수 확장)
- - π 2n = e e^{1}e^{4\piin}e^{-4\pi {2}}=e\qquad } (ex+ y = ex {\displaystyle e^x+y}=e^{x}e^{y} 사용)
- - 2n 1 {\displaystyle e^{-4\pi ^{2}n^2}} = 1\qquad }iding)
따라서 지수를 확장할 때 복소 로그 값이 다중 이기 에 로그 z\log \exp z=z}가 잘못되었다고 암묵적으로 가정합니다. 즉, 잘못된 아이덴티티(e) = e를 아이덴티티로 대체해야 합니다.다중값 함수 간의 진정한 동일성입니다.
비합리성과 초월성
만약 b가 양의 실수 대수적 수이고, x가 유리수라면, b는x 대수적 수이다. 이것은 대수적 확장 이론에서 비롯됩니다. 이것은 b가 임의의 대수적 수일 경우에도 성립하며, 이 경우 (다치x 함수로서) b의 모든 값은 대수적입니다. 만약 x가 무리수이고(즉, 유리수가 아니고), b와 x가 모두 대수적이라면, 겔폰드-슈나이더 정리는 b가 0 또는 1인 경우를 제외하고 b의x 모든 값은 초월수라고 주장합니다.
즉, x가 무리수이고 가 ∉{0, 1 }일 경우 b\n 에서 b, x, b 중x 적어도 하나는 초월수입니다.
대수학에서의 정수적 거듭제곱
양의 정수 지수를 반복 곱셈으로 사용하는 지수의 정의는 곱셈으로 표시되는 임의의 연관 연산에 적용될 수 있습니다.[nb 2] x의0 정의는 곱셈 항등식의 존재를 더 필요로 합니다.[34]
곱셈적으로 표시되는 연관 연산과 함께 집합으로 구성된 대수 구조이며, 1로 표시되는 곱셈 항등식은 모노이드(monoid)입니다. 이러한 모노이드에서 원소 x의 지수는 다음에 의해 유도적으로 정의됩니다.
- 이 아닌 정수 에대해 x n+ 1 = x x n {\displaystyle x^{+1} = xx^{n}}.
n이 음의 정수이면 x 은 x가 곱셈 역수를 가지는 경우에만 정의됩니다.[35] 이 경우 x의 역수는 x로−1 표시되며, x는n( 1 )- 으로 정의됩니다 {\
정수 지수를 사용한 지수화는 대수 구조에서 x와 y, m과 n의 정수에 대해 다음과 같은 법칙을 따릅니다.
이러한 정의는 수학의 많은 영역에서 널리 사용되며, 특히 군, 고리, 장, 정방행렬(고리를 형성하는)에 사용됩니다. 그들은 또한 함수 구성 아래 모노이드를 형성하는 집합에서 자신으로의 함수에도 적용됩니다. 여기에는 구체적인 예로서 기하학적 변환 및 임의의 수학적 구조의 내형화가 포함됩니다.
반복될 수 있는 연산이 여러 개 있을 때는 지수 앞에 기호를 위첨자에 넣어 반복되는 연산을 표시하는 것이 일반적입니다. 예를 들어, f가 값이 곱해질 수 있는 실수 함수일 경우, {\ f는 곱셈에 대한 지수를 나타내고, ∘ n circ n}은 함수 조성에 대한 지수를 나타낼 수 있습니다. 그것은,
그리고.
Commonly, is denoted while is denoted
단체로
곱셈 그룹은 곱셈으로 표시되는 연관 연산이 있고 항등원 요소가 있으며 모든 요소가 역을 갖는 집합입니다.
따라서 G가 군이면 x 은 모든 ∈ G {\x\in G}와 모든 정수 n에 대해 정의됩니다.
그룹의 요소에 대한 모든 거듭제곱들의 집합은 부분군을 형성합니다. 특정 원소 x의 모든 거듭제곱으로 이루어진 군(또는 부분군)은 x에 의해 생성된 순환군입니다. 만약 x의 모든 거듭제곱이 서로 다르다면, 군은 정수의 Z 와 동형입니다. 그렇지 않으면 순환군은 유한하고(유한 수의 원소를 포함한다), 원소의 개수는 x의 차수입니다. 만약 x의 차수가 n이라면, n = 0 = {\ x} = x^{0} = 1,} 이며, x에 의해 생성된 순환군은 (지수 0 또는 1과 상관없이 시작하는) x의 n개의 첫 번째 거듭제곱으로 구성됩니다.
원소의 순서는 군론에서 기본적인 역할을 합니다. 예를 들어, 유한 그룹의 원소 순서는 항상 그룹의 원소 수(그룹의 순서)의 약수입니다. 군 원소의 가능한 순서는 군의 구조에 대한 연구(Sylow 정리 참조)와 유한 단순 군의 분류에서 중요합니다.
위첨자 표기법은 공액(conjugation)에도 사용됩니다. 즉, g = hgh, 여기서 g와 h는 그룹의 원소입니다. 위첨자는 정수가 아니므로 이 표기법은 지수화와 혼동할 수 없습니다. 이 표기법의 동기는 결합이 지수화 법칙의 일부, 즉( k = k 를 따르는 것입니다.} ^{hk}}및 ( k . {\displaystyle(gh)^{k} g^{kh^{k}}
반지속에
환에서 0이 아닌 일부 원소는 일부 정수 n에 대해 = displaystyle x^{n}=0}을 만족하는 경우가 발생할 수 있습니다. 그런 요소는 전혀 효력이 없다고 합니다. 교환환에서, nilpotent 원소들은 고리의 nilradical이라고 불리는 이상을 형성합니다.
nilradical이 0 이상으로 감소하는 경우(, ≠ 0일 경우 x\n)은(는) 0 x^{n}\n을 의미합니다.모든 양의 정수 n에 대하여 교환환은 감소한다고 합니다. 아핀 대수 집합의 좌표 고리는 항상 축소된 고리이기 때문에, 축소된 고리는 대수기하학에서 중요합니다.
보다 일반적으로, 교환환 R에서 아이디얼 I이 주어졌을 때, I에 힘을 갖는 R의 원소들의 집합은 아이디얼 I의 라디칼이라고 불립니다. 닐라디칼은 제로 이상의 라디칼입니다. 급진적 이상은 자신의 급진성과 동등한 이상입니다. k 필드 위의 다항식 [ ] k에서, 아핀 대수 집합에서 0인 모든 다항식의 집합인 경우에만 아이디얼은 라디칼입니다(이는 힐베르트의 널스텔렌사츠의 결과입니다).
행렬 및 선형 연산자
A가 정방행렬이면, 자신이 n번인 A의 곱을 행렬 거듭제곱이라고 합니다. A 0{\ A을 항등 행렬로 정의하고, A가 이면A - = ( -){\ An} =\left (A^{-1}\
행렬 파워는 종종 이산 동적 시스템의 맥락에서 나타나며, 여기서 행렬 A는 일부 시스템의 상태 벡터 x에서 시스템의 다음 상태 Ax로의 전환을 표현합니다.[37] 예를 들어, 이것은 마르코프 체인의 표준 해석입니다. A A는 두 번의 시간 단계를 거친 후의 시스템 상태입니다. 는 n번의 시간 단계를 거친 후의 시스템 상태입니다. 행렬 파워 은 현재 상태와 미래의 n 단계에서 상태 사이의 전이 행렬입니다. 따라서 매트릭스 파워를 계산하는 것은 동적 시스템의 진화를 해결하는 것과 같습니다. 많은 경우 행렬의 거듭제곱은 고유값과 고유 벡터를 사용하여 쉽게 계산할 수 있습니다.
행렬 외에도 보다 일반적인 선형 연산자를 지수화할 수도 있습니다. 미적분학의 도함수 연산자 / x{\ ddx}가 그 예인데 이 연산자는 f ) f(x)}에 작용하여 새로운( / d) (x) = (x) {\displaystyle (d/dx) f (x)}를 제공하는 선형 연산자입니다. 미분 연산자의 n번째 거듭제곱은 n번째 도함수입니다.
이러한 예는 선형 연산자의 이산 지수에 대한 것이지만 많은 상황에서 연속 지수를 사용하여 그러한 연산자의 거듭제곱을 정의하는 것도 바람직합니다. 이것이 반집단의 수학 이론의 출발점입니다.[38] 이산 지수를 사용하는 컴퓨팅 행렬 파워가 이산 동적 시스템을 해결하는 것처럼, 연속 지수를 사용하는 컴퓨팅 행렬 파워도 연속적인 동적 시스템을 사용하는 시스템을 해결합니다. 열 방정식, 슈뢰딩거 방정식, 파동 방정식, 그리고 시간 진화를 포함한 다른 편미분 방정식을 풀기 위한 접근법들이 그 예입니다. 미분 연산자를 정수가 아닌 거듭제곱으로 지수화하는 특별한 경우를 분수 미분이라고 하는데, 이것은 분수 적분과 함께 분수 미분학의 기본 연산 중 하나입니다.
유한장
장은 곱셈, 덧셈, 뺄셈, 나눗셈이 정의되고 곱셈이 연상되고 0이 아닌 모든 요소가 곱셈 역을 갖는 특성을 만족하는 대수 구조입니다. 이는 0의 양이 아닌 거듭제곱을 제외하고 정수 지수를 사용한 지수가 잘 정의되어 있음을 의미합니다. 일반적인 예로는 복소수, 실수, 유리수의 분야가 있는데, 이들은 모두 무한대입니다.
유한장은 유한한 수의 원소가 있는 장입니다. 이 원소의 수는 소수이거나 소수입니다. 즉, = {\displaystyle q = p^{k}}의 형태를 가지며, p는 소수이고, k는 양의 정수입니다. 그러한 모든 q에 대하여, q 요소가 있는 필드가 있습니다. q 요소가 있는 필드는 모두 동형이며, 일반적으로 요소가 있는 필드가 하나인 것처럼 작업할 수 있습니다. F. \ {F
하나는.
모든 ∈ F q. xF}_{q}에 대하여
A primitive element in is an element g such that the set of the q − 1 first powers of g (that is, ) equals the set of the nonzero elements of F}_{q}에는p-1 p-1)} 원시 가 있으며 여서 φ \varphi }는 오일러의 토티엔트 함수입니다.
_ 신입생의 꿈의 아이덴티티
는 지수 p에 대하여 참입니다. Fq에서 = x {\ x^{p}=x}와 같이 {\displaystyle \mathbb {F}_{q}} 다음은 지도입니다.
는 에 대해 선형이며, 필드 오토모피즘이며, 이를 프로베니우스 오토모피즘이라고 합니다. = p , {\q = p^{k}}인 경우 F q {\displaystyle \mathbb {F} _{q} 필드는 F의 k번째 거듭제곱인 k개의 자기동형을 갖습니다. 즉, 의 갈루아 군은 프로베니우스 오토모피즘에 의해 생성된 순서 k의 순환군입니다.
디피-헬만 키 교환은 보안 통신에 널리 사용되는 유한 필드의 지수화 응용 프로그램입니다. 지수화는 계산적으로 저렴하지만, 역연산인 이산 로그는 계산적으로 비싸다는 사실을 이용합니다. 좀 더 정확하게 말하면, 가 의 원시 요소인 경우{\_{ {\ g는 q가 크더라도 임의의 e에 대해 제곱함으로써 지수로 효율적으로 계산될 수 있습니다. q가 충분히 클 경우 ge 에서 e를 검색할 수 있는 알려진 계산적으로 실용적인 알고리즘은 없습니다.
집합의 거듭제곱
The Cartesian product of two sets S and T is the set of the ordered pairs such that and This operation is not properly commutative nor associative, but has these properties up to canonical isomorphisms, that allow identifying, 예를 들어(( (( z (, 및( z y,
이를 통해 집합 S의 n번째 전력 S을 S의 모든 n-튜플 집합으로 정의할 수 있습니다.
S가 어떤 구조를 부여받았을 때, {\ S도 비슷한 구조를 자연스럽게 부여받는 경우가 많습니다. 이 경우 일반적으로 "데카르트 곱" 대신 "직접 곱"이라는 용어가 사용되며 지수화는 제품 구조를 의미합니다. 예를 들어 서 R 은 실수를 나타냅니다)은 의 n개 사본의 데카르트 곱과 벡터 공간, 위상 공간, 링 등의 직접 곱을 나타냅니다.
지수로 설정합니다.
S의 요소 중 n-튜플( 은{ n의 함수로 간주할 수 있습니다 이는 다음과 같은 표기법으로 일반화됩니다.
두 집합 S와 T가 주어졌을 때, T부터 S까지의 모든 함수의 집합은 S로 표시됩니다 이 지수 표기는 다음과 같은 표준 동형에 의해 정당화됩니다(첫 번째는 Currying 참조).
여기서× 는 데카르트 곱을 ⊔ {\\sqcup}는 서로소 결합을 나타냅니다.
일반적으로 아벨 군, 벡터 공간 또는 모듈의 직접 합에 대한 집합의 다른 연산에 대한 지수로 집합을 사용할 수 있습니다. 직접 합과 직접 곱을 구별하기 위해 직접 합의 지수는 괄호 사이에 배치됩니다. 예를 들어, {\^{\은 실수의 무한한 수열의 벡터 공간을 나타내고, ( 은 유한한 수의 0이 아닌 수열의 벡터 공간을 나타냅니다. 후자는 정확히 1과 같은 0이 아닌 요소를 가진 서열로 구성된 기초를 가지고 있지만, 전자의 하멜 염기는 명시적으로 설명할 수 없습니다(그들의 존재는 존의 보조정리를 포함하기 때문에).
여기서 2는 집합{ 1 을 나타낼 수 있습니다 따라서 S 2는 S에서{0 까지의 함수의 집합인 S의 멱집합을 나타냅니다.각 함수를 1의 역상으로 매핑하여 S의 부분집합들의 집합으로 식별할 수 있습니다.
이것은 S = S, 여기서 X는 X의 기수라는 의미에서 기수의 지수화와 일치합니다.
범주론에서는
집합의 범주에서 집합 X와 Y 사이의 형태소는 X에서 Y까지의 함수입니다. 앞 절의 Y로 표시된 X부터 Y까지의 함수의 집합도 Y)로 표시할 수 있습니다. {\X,Y)} ( ≅ ST × (S^{T})^을(를) 다시 쓸 수 있습니다.
이것은 "힘 T에 대한 팽창"이 "T가 있는 직접적인 제품"에 대한 오른쪽 인접임을 의미합니다.
이것은 유한한 직접 곱이 존재하는 범주에서 지수의 정의로 일반화됩니다. 이러한 범주에서, X → {\ X X^{T}}는 존재한다면, 함수 Y → T × Y에 오른쪽으로 인접합니다. {\displaystyle Y\to T\times Y} 범주를 데카르트 닫힌 범주라고 합니다. 직접 곱이 존재하고, 모든 T에 Y → X × Y {\Y\ X\times 가 오른쪽 인접을 갖는 경우.
반복 지수화
자연수의 지수화가 반복적인 곱셈에 의해 동기 부여되는 것처럼 반복적인 지수화에 기초하여 연산을 정의할 수 있습니다. 이 연산을 하이퍼-4 또는 테트라테이션이라고도 합니다. 테트라테이션을 반복하면 또 다른 작업이 일어나며, 하이퍼 오퍼레이션이라는 개념이 생겨납니다. 이 연산 순서는 아커만 함수와 크누스의 위쪽 화살표 표기법으로 표현됩니다. 지수화가 덧셈보다 더 빠르게 성장하는 곱셈보다 더 빠르게 성장하는 것처럼 테테이션도 지수화보다 더 빠르게 성장합니다. (3, 3)에서 평가한 함수의 덧셈, 곱셈, 지수화 및 사분화 수율은 각각 6, 9, 27 및 7625597484987(= 3 = 3)입니다.
힘의 한계
0에서 0의 거듭제곱은 불확정 형태 0인0 여러 한계의 예를 제공합니다. 이 예제의 한계는 존재하지만 다른 값을 가지므로 2변수 함수 x가y 점 (0, 0)에서 한계가 없음을 보여줍니다. 이 기능에 한계가 있는 지점을 고려할 수 있습니다.
좀 더 정확하게, D = { (x, ∈ R 2 : x > 0 } {\displaystyle D=\{(x, y)\in \mathbf {R} ^{2}:x > 에 정의된 함수 f (, y) = x^{y}를 생각해 보십시오. 그렇다면 D는 확장된 실수선 R = [- ∞, + ∞]에 속하는 x, y를 갖는 R의 부분집합(즉, 모든 쌍(x, y)의 집합)으로 볼 수 있습니다. 함수 f가 한계를 가지는 점을 포함하는 제품 토폴로지)를 부여합니다.
실제로 f는 (0, 0), (+ ∞, 0), (1, + ∞) 및 (1, - ∞)을 제외한 D의 모든 축적 지점에서 한계를 갖습니다. 따라서 불확정 형태로 남아 있는 0, (+∞), 1, 1을 제외하고 0 ≤ x ≤ + ∞, - ∞ ≤ y ≤ + ∞일 때마다 연속성으로 거듭제곱 x를 정의할 수 있습니다.
연속성에 의한 이 정의에 따라 다음을 얻을 수 있습니다.
- x+∞ = +∞ and x−∞ = 0, when 1 < x ≤ +∞.
- x+∞ = 0 and x−∞ = +∞, when 0 ≤ x < 1.
- 0 < y ≤ + ∞일 때 0 = 0 및 (+ ∞) = + ∞입니다.
- 0 = + ∞ 및 (+ ∞) = 0, -∞ ≤ y < 0일 때.
이러한 거듭제곱은 x의 양의 값에 대해 x의y 한계를 취함으로써 얻어집니다. 이 방법은 x < 0인 쌍(x, y)이 D의 누적점이 아니므로 x < 0인 경우 x의 정의를y 허용하지 않습니다.
반대로 n이 정수일 때 거듭제곱 x는n 음수를 포함한 x의 모든 값에 대해 이미 의미가 있습니다. 이것은 n이 홀수일 때 음수 n에 대해 위에서 얻은 0 = + ∞의 정의를 문제로 만들 수 있습니다. 이 경우 x → + ∞는 양수 값을 통해 0이 되는 경향이 있지만 음수 값은 아니기 때문입니다.
정수 지수를 사용한 효율적인 계산
반복된 곱셈을 사용하는 계산 b는n n - 1 곱셈 연산이 필요하지만 다음 예에서 보여주듯이 그보다 더 효율적으로 계산할 수 있습니다. 2를100 계산하려면 이진법으로 작성된 지수 100에 호너의 규칙을 적용합니다.
- .
그런 다음 호너의 규칙을 오른쪽에서 왼쪽으로 읽으며 다음 항들을 순서대로 계산합니다.
| 22 = 4 |
| 2 (22) = 23 = 8 |
| (23)2 = 26 = 64 |
| (26)2 = 212 = 4096 |
| (212)2 = 224 = 16777216 |
| 2 (224) = 225 = 33554432 |
| (225)2 = 250 = 1125899906842624 |
| (250)2 = 2100 = 1267650600228229401496703205376 |
이 일련의 단계는 99가 아닌 8 곱셈만 필요합니다.
일반적으로 를 계산하는 데 필요한 곱셈 연산 수는에 의한를 사용하여 ♯ + ⌊2 n ⌋ - n+\lfloor \log _{2}n\rfloor -1,}로 줄일 수 서 ♯ n {\displaystyle \sharp n}은 n의 이진 표현에서 1의 수를 나타냅니다. 일부 지수(100은 그 중에 없음)의 경우, 최소 덧셈-체인 지수를 계산하고 사용함으로써 곱셈 수를 더 줄일 수 있습니다. b에n 대한 최소 곱셈 시퀀스(지수에 대한 최소 길이 덧셈 체인)를 찾는 것은 어려운 문제이며, 현재 효율적인 알고리즘은 알려져 있지 않지만(서브셋 합 문제 참조), 많은 합리적으로 효율적인 휴리스틱 알고리즘을 사용할 수 있습니다.[40] 그러나 실제 계산에서 제곱에 의한 지수화는 충분히 효율적이며 구현하기가 훨씬 쉽습니다.
반복 함수
함수 구성은 오른쪽에 쓰여진 함수의 코드 도메인이 왼쪽에 쓰여진 함수의 도메인에 포함되도록 함수에 정의되는 이진 연산입니다. ∘ f, circ f,}로 표시되며 다음과 같이 정의됩니다.
f 의 정의역에 있는 모든 x 에 대하여.
함수 f의 도메인이 코드 도메인과 동일한 경우 함수를 임의의 시간으로 구성할 수 있으며, 이는 일반적으로 함수의 n번째 반복이라고 하는 합성 아래 함수의 n번째 거듭제곱을 정의합니다. 는 일반적으로 f의 n번째 반복을 나타냅니다. 예를 들어, 3 ) 는 ((를 의미합니다 f
함수의 코드 도메인에서 곱셈이 정의되면 함수에 대한 곱셈, 즉 점별 곱셈을 정의하여 또 다른 지수를 유도합니다. 함수 표기법을 사용할 때 일반적으로 함수의 인수를 둘러싸는 괄호 앞에 함수 반복의 지수를 배치하고 괄호 뒤에 점별 곱셈의 지수를 배치하여 두 종류의 지수를 구별합니다. ( ) = f(), } (x) = f (f (x)),} 및 f (x ) 2 = f (x ) ⋅f (x ). {\displaystyle f (x)^{2} = f (x)\cdot f (x ).함수 표기법을 사용하지 않을 때는 지수 앞에 조성 기호를 배치하여 명확화를 수행하는 경우가 많습니다. 를 들어 f f f, {\ f^{\3} f\circ f,} 및 f 3 f f f. {\displaystyle f^{3} f\cdot f\cdot f.} 역사적인 이유로, 반복된 곱셈의 지수는 특정 함수, 일반적으로 삼각 함수의 인수 앞에 배치됩니다. So, and both mean and not which, in any case, is rarely considered. 역사적으로 이러한 표기법의 여러 변형이 다른 저자에 의해 사용되었습니다.[42][43][44]
여기서 지수- 은 존재하는 경우 항상 역함수를 나타냅니다. So - x =sin - () = arcsin x . {\displaystyle \sin^{-1}x =\sin^{-1}(x) =\arcsin x.} 곱셈 역분수의 경우 일반적으로 1 / sin x. {\displaystyle 1/\sin(x) = {\frac {1}{\sin x}}와 같이 사용됩니다.
프로그래밍 언어로
프로그래밍 언어는 일반적으로 위첨자를 지원하지 않기 때문에 지수 함수를 infix 연산자 또는 함수 응용 프로그램으로 표현합니다. 지수화에 대한 가장 일반적인 연산자 기호는 캐럿(carette)입니다.^). ASCII의 원래 버전에는 위쪽 화살표 기호가 포함되어 있었습니다.↑)는 지수화를 위한 것이었지만 1967년에 캐럿으로 대체되었기 때문에 캐럿은 프로그래밍 언어에서 일반적인 것이 되었습니다.[45] 주석에는 다음이 포함됩니다.
x ^ y: AWK, BASIC, J, MATLAB, Wolfram Language (Mathematica), R, Microsoft Excel, Analytica, TeX (및 파생형), TI-BASIC, bc (정수 지수의 경우), Haskell (음이 아닌 정수 지수의 경우), Lua 및 대부분의 컴퓨터 대수 시스템.x ** y. 포트란 문자 집합에 다음 이외의 소문자 또는 문장 부호가 포함되지 않았습니다.+-*/()&=.,'그래서 사용된**지수화[46][47](사용된 초기 버전)의 경우a xx b대신...)[48] 많은 다른 언어들이 그 뒤를 이었습니다. Ada, Z shell, KornShell, Bash, COBOL, CoffeeScript, Fortran, FoxPro, Gnuplot, Groovy, JavaScript, OCaml, F#, Perl, PHP, PL/I, Python, Rexx, Ruby, SAS, Seed7, Tcl, ABAP, Mercury, Haskell (for floating-point exponents), Turing, VHDL.x ↑ y: 알골 참조 언어, 코모도어 BASIC, TRS-80 레벨 II/III BASIC.[49][50]x ^^ y: 해스켈(소수 기저, 정수 지수의 경우), D.x⋆y: APL.
infix 지수 연산자가 있는 대부분의 프로그래밍 언어에서, 그것은 올바른 연관성, 즉, a^b^c 로 해석됩니다. a^(b^c).[51]왜냐하면[51]. (a^b)^c 와 동등합니다. a^(b*c) 따라서 유용하지 않습니다. 일부 언어에서는 왼쪽으로 연결되며, 특히 알골, 매트랩 및 마이크로소프트 엑셀 공식 언어에서 사용됩니다.
다른 프로그래밍 언어들은 함수 표기법을 사용합니다.
다른 것들은 표준 라이브러리의 일부로서 지수화만 제공합니다.
pow(x, y): C, C++(인)math도서관).Math.Pow(x, y): 다#.math:pow(X, Y): 어랑.Math.pow(x, y): 자바.[Math]::Pow(x, y): 파워쉘.
Rust와 같이 유형 안전을 우선시하는 일부 정적 유형 언어에서는 다양한 방법을 통해 지수화가 수행됩니다.
x.pow(y)위해서x그리고.y정수로서x.powf(y)위해서x그리고.y부동소수점으로x.powi(y)위해서x물에 띄워서y정수로서
참고 항목
| 산술식 | 다항식 | 대수식 | 닫힌 형식 표현식 | 해석식 | 수학식 | |
|---|---|---|---|---|---|---|
| 일정한 | 네. | 네. | 네. | 네. | 네. | 네. |
| 기초연산 | 네. | 덧셈, 뺄셈, 곱셈만 | 네. | 네. | 네. | 네. |
| 유한합 | 네. | 네. | 네. | 네. | 네. | 네. |
| 유한곱 | 네. | 네. | 네. | 네. | 네. | 네. |
| 유한 계속 분수 | 네. | 아니요. | 네. | 네. | 네. | 네. |
| 변수 | 아니요. | 네. | 네. | 네. | 네. | 네. |
| 정수 지수 | 아니요. | 네. | 네. | 네. | 네. | 네. |
| 정수 n근 | 아니요. | 아니요. | 네. | 네. | 네. | 네. |
| 유리 지수 | 아니요. | 아니요. | 네. | 네. | 네. | 네. |
| 정수 요인 | 아니요. | 아니요. | 네. | 네. | 네. | 네. |
| 무리수 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 지수함수 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 로그 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 삼각함수 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 역삼각함수 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 쌍곡선함수 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 역쌍곡선함수 | 아니요. | 아니요. | 아니요. | 네. | 네. | 네. |
| 대수적 해가 아닌 다항식의 근 | 아니요. | 아니요. | 아니요. | 아니요. | 네. | 네. |
| 정수가 아닌 자의 감마 함수 및 계승 | 아니요. | 아니요. | 아니요. | 아니요. | 네. | 네. |
| 베셀 함수 | 아니요. | 아니요. | 아니요. | 아니요. | 네. | 네. |
| 특수함수 | 아니요. | 아니요. | 아니요. | 아니요. | 네. | 네. |
| 무한합(급수)(급수 포함) | 아니요. | 아니요. | 아니요. | 아니요. | 수렴만 | 네. |
| 무한곱 | 아니요. | 아니요. | 아니요. | 아니요. | 수렴만 | 네. |
| 무한연속분수 | 아니요. | 아니요. | 아니요. | 아니요. | 수렴만 | 네. |
| 제한. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네. |
| 도함수 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네. |
| 적분 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네. |
메모들
참고문헌
- ^ a b c d e Nykamp, Duane. "Basic rules for exponentiation". Math Insight. Retrieved 2020-08-27.
- ^ Weisstein, Eric W. "Power". mathworld.wolfram.com. Retrieved 2020-08-27.
- ^ https://www.etymonline.com/word/exponent
- ^ a b Rotman, Joseph J. (2015). Advanced Modern Algebra, Part 1. Graduate Studies in Mathematics. Vol. 165 (3rd ed.). Providence, RI: American Mathematical Society. p. 130, fn. 4. ISBN 978-1-4704-1554-9.
- ^ Szabó, Árpád (1978). The Beginnings of Greek Mathematics. Synthese Historical Library. Vol. 17. Translated by A.M. Ungar. Dordrecht: D. Reidel. p. 37. ISBN 90-277-0819-3.
- ^ a b O'Connor, John J.; Robertson, Edmund F., "Etymology of some common mathematical terms", MacTutor History of Mathematics Archive, University of St Andrews
- ^ Ball, W. W. Rouse (1915). A Short Account of the History of Mathematics (6th ed.). London: Macmillan. p. 38.
- ^ 아르키메데스. (2009). 샌드 레코너. T에서. 히스(Ed.), 아르키메데스의 작품: 서론 장과 함께 현대 표기법으로 편집 (Cambridge Library Collection - Mathematics, pp. 229-232). 캠브리지: 캠브리지 대학 출판부. doi:10.1017/CBO9780511695124.017
- ^ a b Quinion, Michael. "Zenzizenzizenzic". World Wide Words. Retrieved 2020-04-16.
- ^ O'Connor, John J.; Robertson, Edmund F., "Abu'l Hasan ibn Ali al Qalasadi", MacTutor History of Mathematics Archive, University of St Andrews
- ^ Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. The Open Court Company. p. 102.
- ^ Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. London: Open Court Publishing Company. p. 344.
- ^ 수학 단어 중 일부의 초기 알려진 사용법
- ^ Stifel, Michael (1544). Arithmetica integra. Nuremberg: Johannes Petreius. p. 235v.
- ^ Cajori, Florian (1928). A History of Mathematical Notations. Vol. 1. The Open Court Company. p. 204.
- ^ Descartes, René (1637). "La Géométrie". Discourse de la méthode [...]. Leiden: Jan Maire. p. 299.
Et aa, ou a2, pour multiplier a par soy mesme; Et a3, pour le multiplier encore une fois par a, & ainsi a l'infini
(그리고 a, 또는 a는2 a를 스스로 곱하기 위해; 그리고 a에3 a를 한 번 더 곱하기 위해, 그리고 a는 무한대로). - ^ 이러한 의미에서 OED가 가장 최근에 사용한 것은 1806년("involution". Oxford English Dictionary (Online ed.). Oxford University Press.구독 또는 참여기관 회원가입 필요)부터입니다.
- ^ Euler, Leonhard (1748). Introductio in analysin infinitorum (in Latin). Vol. I. Lausanne: Marc-Michel Bousquet. pp. 69, 98–99.
Primum ergo considerandæ sunt quantitates exponentiales, seu Potestates, quarum Exponens ipse est quantitas variabilis. Perspicuum enim est hujusmodi quantitates ad Functiones algebraicas referri non posse, cum in his Exponentes non nisi constantes locum habeant.
- ^ Kauffman, Louis; J. Lomonaco, Samuel; Chen, Goong, eds. (2007-09-19). "4.6 Efficient decomposition of Hamiltonian". Mathematics of Quantum Computation and Quantum Technology. CRC Press. p. 105. ISBN 9781584889007. Archived from the original on 2022-02-26. Retrieved 2022-02-26.
- ^ Hodge, Jonathan K.; Schlicker, Steven; Sundstorm, Ted (2014). Abstract Algebra: an inquiry based approach. CRC Press. p. 94. ISBN 978-1-4665-6706-1.
- ^ Achatz, Thomas (2005). Technical Shop Mathematics (3rd ed.). Industrial Press. p. 101. ISBN 978-0-8311-3086-2.
- ^ Robinson, Raphael Mitchel (October 1958) [1958-04-07]. "A report on primes of the form k · 2n + 1 and on factors of Fermat numbers" (PDF). Proceedings of the American Mathematical Society. University of California, Berkeley, California, USA. 9 (5): 673–681 [677]. doi:10.1090/s0002-9939-1958-0096614-7. Archived (PDF) from the original on 2020-06-28. Retrieved 2020-06-28.
- ^ Bronstein, Ilja Nikolaevič; Semendjajew, Konstantin Adolfovič (1987) [1945]. "2.4.1.1. Definition arithmetischer Ausdrücke" [Definition of arithmetic expressions]. Written at Leipzig, Germany. In Grosche, Günter; Ziegler, Viktor; Ziegler, Dorothea (eds.). Taschenbuch der Mathematik [Pocketbook of mathematics] (in German). Vol. 1. Translated by Ziegler, Viktor. Weiß, Jürgen (23 ed.). Thun, Switzerland / Frankfurt am Main, Germany: Verlag Harri Deutsch (and B. G. Teubner Verlagsgesellschaft, Leipzig). pp. 115–120, 802. ISBN 3-87144-492-8.
- ^ Olver, Frank W. J.; Lozier, Daniel W.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010). NIST Handbook of Mathematical Functions. National Institute of Standards and Technology (NIST), U.S. Department of Commerce, Cambridge University Press. ISBN 978-0-521-19225-5. MR 2723248.[1]
- ^ Zeidler, Eberhard [in German]; Schwarz, Hans Rudolf; Hackbusch, Wolfgang; Luderer, Bernd [in German]; Blath, Jochen; Schied, Alexander; Dempe, Stephan; Wanka, Gert; Hromkovič, Juraj; Gottwald, Siegfried (2013) [2012]. Zeidler, Eberhard [in German] (ed.). Springer-Handbuch der Mathematik I (in German). Vol. I (1 ed.). Berlin / Heidelberg, Germany: Springer Spektrum, Springer Fachmedien Wiesbaden. p. 590. doi:10.1007/978-3-658-00285-5. ISBN 978-3-658-00284-8. (xii+635 pages)
- ^ Hass, Joel R.; Heil, Christopher E.; Weir, Maurice D.; Thomas, George B. (2018). Thomas' Calculus (14 ed.). Pearson. pp. 7–8. ISBN 9780134439020.
- ^ a b Anton, Howard; Bivens, Irl; Davis, Stephen (2012). Calculus: Early Transcendentals (9th ed.). John Wiley & Sons. p. 28. ISBN 9780470647691.
- ^ Denlinger, Charles G. (2011). Elements of Real Analysis. Jones and Bartlett. pp. 278–283. ISBN 978-0-7637-7947-4.
- ^ Tao, Terence (2016). "Limits of sequences". Analysis I. Texts and Readings in Mathematics. Vol. 37. pp. 126–154. doi:10.1007/978-981-10-1789-6_6. ISBN 978-981-10-1789-6.
- ^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). Introduction to Algorithms (second ed.). MIT Press. ISBN 978-0-262-03293-3. Wayback Machine의 온라인 리소스 아카이브 2007-09-30
- ^ Cull, Paul; Flahive, Mary; Robson, Robby (2005). Difference Equations: From Rabbits to Chaos (Undergraduate Texts in Mathematics ed.). Springer. ISBN 978-0-387-23234-8. 페이지 351에 정의됨
- ^ "통합의 원리", 수학세계.
- ^ Steiner, J.; Clausen, T.; Abel, Niels Henrik (1827). "Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen" [Problems and propositions, the former to solve, the later to prove]. Journal für die reine und angewandte Mathematik. 2: 286–287.
- ^ Bourbaki, Nicolas (1970). Algèbre. Springer.Bourbaki, Nicolas (1970). Algèbre. Springer.I.2
- ^ Bloom, David M. (1979). Linear Algebra and Geometry. Cambridge University Press. p. 45. ISBN 978-0-521-29324-2.
- ^ 1장 초등 선형대수, 8E, 하워드 안톤
- ^ Strang, Gilbert (1988), Linear algebra and its applications (3rd ed.), Brooks-ColeStrang, Gilbert (1988), Linear algebra and its applications (3rd ed.), Brooks-Cole5장.
- ^ E. Hille, R. S. Phillips: 함수 분석 및 부분군. 미국수학학회, 1975
- ^ Nicolas Bourbaki, Topologie genérale, V.4.2.
- ^ Gordon, D. M. (1998). "A Survey of Fast Exponentiation Methods" (PDF). Journal of Algorithms. 27: 129–146. CiteSeerX 10.1.1.17.7076. doi:10.1006/jagm.1997.0913.
- ^ Peano, Giuseppe (1903). Formulaire mathématique (in French). Vol. IV. p. 229.
- ^ Herschel, John Frederick William (1813) [1812-11-12]. "On a Remarkable Application of Cotes's Theorem". Philosophical Transactions of the Royal Society of London. London: Royal Society of London, printed by W. Bulmer and Co., Cleveland-Row, St. James's, sold by G. and W. Nicol, Pall-Mall. 103 (Part 1): 8–26 [10]. doi:10.1098/rstl.1813.0005. JSTOR 107384. S2CID 118124706.
- ^ [2]Herschel, John Frederick William (1820). "Part III. Section I. Examples of the Direct Method of Differences". A Collection of Examples of the Applications of the Calculus of Finite Differences. Cambridge, UK: Printed by J. Smith, sold by J. Deighton & sons. pp. 1–13 [5–6]. Archived from the original on 2020-08-04. Retrieved 2020-08-04. (NB. 여기서 허셜은 그의 1813년 작품을 언급하며 한스 하인리히 뷔르만의 오래된 작품을 언급합니다.)
- ^ Cajori, Florian (1952) [March 1929]. A History of Mathematical Notations. Vol. 2 (3rd ed.). Chicago, USA: Open court publishing company. pp. 108, 176–179, 336, 346. ISBN 978-1-60206-714-1. Retrieved 2016-01-18.
- ^ Richard Gilam, Unicode Demystified: A Practical Programmer's Guide to Encoding Standard, 2003, ISBN 0170522, 페이지 33
- ^ Backus, John Warner; Beeber, R. J.; Best, Sheldon F.; Goldberg, Richard; Herrick, Harlan L.; Hughes, R. A.; Mitchell, L. B.; Nelson, Robert A.; Nutt, Roy; Sayre, David; Sheridan, Peter B.; Stern, Harold; Ziller, Irving (1956-10-15). Sayre, David (ed.). The FORTRAN Automatic Coding System for the IBM 704 EDPM: Programmer's Reference Manual (PDF). New York, USA: Applied Science Division and Programming Research Department, International Business Machines Corporation. p. 15. Archived (PDF) from the original on 2022-07-04. Retrieved 2022-07-04. (2+51+1페이지)
- ^ 브라이스 카르나한, 제임스 O. Wilkes, MTS 애플리케이션을 통한 디지털 컴퓨팅 및 FORTRAN IV 소개, 1968, 페이지 2-2, 2-6
- ^ Backus, John Warner; Herrick, Harlan L.; Nelson, Robert A.; Ziller, Irving (1954-11-10). Backus, John Warner (ed.). Specifications for: The IBM Mathematical FORmula TRANSlating System, FORTRAN (PDF) (Preliminary report). New York, USA: Programming Research Group, Applied Science Division, International Business Machines Corporation. pp. 4, 6. Archived (PDF) from the original on 2022-03-29. Retrieved 2022-07-04. (29페이지)
- ^ Daneliuk, Timothy "Tim" A. (1982-08-09). "BASCOM - A BASIC compiler for TRS-80 I and II". InfoWorld. Software Reviews. Vol. 4, no. 31. Popular Computing, Inc. pp. 41–42. Archived from the original on 2020-02-07. Retrieved 2020-02-06.
- ^ "80 Contents". 80 Micro. 1001001, Inc. (45): 5. October 1983. ISSN 0744-7868. Retrieved 2020-02-06.
- ^ Robert W. Seebesta, 프로그래밍 언어의 개념, 2010, ISBN 0136073476, 페이지 130, 324






![{\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividend}}}{\scriptstyle {\text{divisor}}}}\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{numerator}}}{\scriptstyle {\text{denominator}}}}\end{matrix}}\right\}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d5d22ff59234f0d437be740306e8dd905991e1e)



![{\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)







![{\displaystyle {\begin{aligned}b^{n+m}&=\underbrace {b\times \dots \times b} _{n+m{\text{ times}}}\\[1ex]&=\underbrace {b\times \dots \times b} _{n{\text{ times}}}\times \underbrace {b\times \dots \times b} _{m{\text{ times}}}\\[1ex]&=b^{n}\times b^{m}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b3910691105e0b2f80e2656b6dc0037980fea92)



 의미가 무엇인지 생각해 보십시오. exponents add' 규칙을 준수하려면 b -
의미가 무엇인지 생각해 보십시오. exponents add' 규칙을 준수하려면 b -































 다음과 같이 정의됩니다.
다음과 같이 정의됩니다. 





![{\displaystyle \left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f09aec126692a109ddd2b003c78002512678e923)
















![{\displaystyle \left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc4ae73419a2cabb0133293dc1bfa19d743b1d9)






 .
. 



 그래프가 모든 점의 근방에서 각각의 동형 함수를 정의하는 여러 장의 시트로 구성된다는 점에서.
그래프가 모든 점의 근방에서 각각의 동형 함수를 정의하는 여러 장의 시트로 구성된다는 점에서.  표준
표준 



























![{\displaystyle k[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37c2b680cd4b215ac5c3c548a0e596d534526cab)

 두 번의 시간 단계를 거친 후의 시스템 상태입니다.
두 번의 시간 단계를 거친 후의 시스템 상태입니다. 
 현재 상태와
현재 상태와 



 꿈
꿈








 n번째 전력
n번째 전력  모든
모든 

 공간
공간





















