실제 변수의 함수

함수
x ↦ f (x)
도메인 및 코도메인의 예
$(\displaystyle X}$ → ${\displaystyle \mathbb{B}}$ ${\$ $\},$ $\displaystyle \mathb {B} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathb{B} ^{n}}$ → $(\displaystyle X}$ $(\displaystyle X}$ → ${\displaystyle \mathbb{Z}}$ ${\$ $\displaystyle \mathb {Z} }$ → $(\displaystyle X}$ $(\displaystyle X}$ → ${\displaystyle \mathbb{R}}$ ${\$ $\},$ ${\displaystyle \mathb {R} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathb{R} ^{n}}$ → $(\displaystyle X}$ $(\displaystyle X}$ → ${\displaystyle \mathbb{C}}$ ${\$ ${\displaystyle \mathb {C} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathb{C} ^{n}}$ → $(\displaystyle X}$
클래스/속성
상수 아이덴티티 선형 다항식 이성적 대수학 분석적 부드러움 연속 측정 가능 주입식 굴욕적인 비주사적
시공
제한 구성 λ 반비례
일반화
부분적 다중값 암묵적
v t

수학적 분석과 기하학, 응용수학, 공학 및 자연과학 분야의 응용에서 실제 변수의 함수는 실제 숫자$$R {\$displaystyle$$$\$mathb$ {$R}$또는 양의 $길이$의$$간격이 $포함$된 R {\displaystyle$$$\mathb$ {$R}$의 하위 집합인 함수다. 고려되고 연구되는 대부분의 실제 기능들은 어떤 구간에서는 서로 다른 것이다. 그러한 함수들이 가장 널리 고려되는 것은 실제 변수들의 실제 가치 함수, 즉 코도메인이 실수의 집합인 실제 변수의 함수들이다.

그럼에도 불구하고, 실제 변수의 함수의 코도메인은 어떤 집합이 될 수 있다. 그러나 종종 $R{\displaystyle \mathbb{}}$ ${\$_벡터$$ 공간의 구조가 reals 위에 있는 것으로 가정한다. 즉, 코도메인은 유클리드 공간, 좌표 벡터, 주어진 크기의 실제 숫자의 행렬 집합 또는 복잡한 숫자 또는 쿼터니온과 같은 $R{\displaystyle \mathbb{}}$ ${\$ -algebra일$$ 수 있다. $코도메인$의$구조$ R {\displaystyle $\mathb {R}$-벡터$$ 공간은 함수에 $R{\displaystyle \mathbb{}}$ ${\$-벡터$$ 공간의 구조를 유도한다. 코도메인의 구조가 $R{\displaystyle \mathbb{}}$ ${\$ -algebra인$$ 경우 함수도 마찬가지다.

실제 변수의 함수의 이미지는 코도메인의 곡선이다. 이 맥락에서 곡선을 정의하는 함수를 곡선의 모수 방정식이라고 한다.

실제 변수의 함수의 코도메인이 유한차원 벡터 공간인 경우, 함수를 실제 함수의 시퀀스로 볼 수 있다. 이것은 종종 어플리케이션에서 사용된다.

실함수

실제 함수는 $R{\displaystyle \mathbb{}}$ ${\$의 하위 집합에서 $R{\displaystyle \mathbb{}}$, ${\displaystyle \mathb {R}$에 이르는$$ 함수인데, 여기서$$ $R{\displaystyle \mathbb{}}$ ${\$은 평소와 같이 실수 집합을 나타낸다. 즉, 실제 함수의 도메인은 부분 $집합{\displaystyle \mathbb{}}$ R ${\$이고$,$ 그 $코드명$은 R. ${\displaystyle \mathb$ {R$}.}$ 도메인에는$$ 양 길이의 간격이 포함되어 있다고 일반적으로 가정한다.

기본 예시

일반적으로 사용되는 많은 실제 함수의 경우, 도메인은 전체 실수 집합이며, 함수는 도메인의 모든 지점에서 연속적이고 차별화된다. 어떤 사람은 이러한 기능들이 어디에서나 정의되고, 지속적이며, 차별화 된다고 말한다. 다음의 경우에 해당한다.

• 상수함수와 선형함수를 포함한 모든 다항함수
• 사인 및 코사인 함수
• 지수함수

어떤 기능은 어디에서나 정의되지만, 어떤 지점에서는 연속되지 않는다. 예를 들어,

• Hubiside 스텝 기능은 어디서나 정의되지만 0에서 연속되는 것은 아니다.

어떤 기능은 어디에서나 정의되고 지속되지만, 어디에서나 다를 수 있는 것은 아니다. 예를 들어,

• 절대적 가치는 어디에서나 정의되고 지속되며, 0을 제외한 모든 곳에서 차별성이 있다.
• 입방근은 어디에서나 정의되고 지속되며, 0을 제외한 모든 곳에서 차별성이 있다.

많은 공통 기능은 어디에서나 정의되는 것이 아니라, 정의되는 모든 곳에서 지속적이고 차별화된다. 예를 들면 다음과 같다.

• 합리적 함수는 두 다항 함수의 몫이며, 분모의 0에서 정의되지 않는다.
• 접선 함수는 $\pi {\displaystyle \frac{}{}}$ ${\displaystyle \frac{2}{}}$+ ${\displaystyle k}$ ${\displaystyle \pi }$, ${\displaystyle {\frac {\pi }{2}}+k\pi ,}$에 대해 정의되지 않음. 여기서$$ k는 정수임.
• 로그 함수는 변수의 양의 값에 대해서만 정의된다.

일부 함수는 전체 영역에서 연속적이며, 어떤 지점에서는 구별할 수 없다. 다음의 경우에 해당한다.

• 제곱근은 변수의 음수가 아닌 값에 대해서만 정의되며, 0에서는 다를 수 없다(변수의 모든 양의 값에 대해 다를 수 있다).

일반적 정의

실제 변수의 실제 값 함수는 변수 x로 대표되는 실제 숫자를 입력으로 가져가는 함수로서, 일반적으로 f(x)로 표기되는 또 다른 실수 값인 함수의 값을 생성한다. 단순성을 위해 이 글에서 실제 변수의 실제 가치 함수는 단순히 함수라고 할 것이다. 모호성을 방지하기 위해 발생할 수 있는 다른 유형의 기능이 명시적으로 지정될 것이다.

어떤 함수는 변수의 모든 실제 값에 대해 정의되지만(한 함수는 변수의 값이 정의된 모든 곳에 있다고 말함) 변수의 값이 항상 양의 길이의 간격을 포함하도록 되어 있는 함수의 영역인 ℝ의 부분집합 X에서 취해지는 경우에만 정의되는 다른 함수가 있다. 즉, 실제 변수의 실제 값 함수는 함수다.

$\displaystyle f:X\to \mathb {R} }$

도메인 X가 양의 길이의 간격을 포함하는 ℝ의 하위 집합이 되도록 한다.

한 변수에 포함된 함수의 간단한 예는 다음과 같다.

$\displaystyle f:X\to \mathb {R} }$

${\displaystyle X=\{x\in \mathb {R} \,:\,x\geq 0\}$

${\displaystyle f(x)={\sqrt{x}}$

x의 제곱근이다.

이미지

함수 $f{\displaystyle (}$ ${\displaystyle x}$) ${\displaystyle f(x)}$의 이미지는 변수 x가 f의 전체 도메인에서 실행될 때 f의 모든 값의 집합이다$$. 연결된 도메인이 있는 연속(정의의 경우 아래 참조) 실제 값 함수의 경우 이미지는 구간이거나 단일 값이다. 후자의 경우 함수는 상수함수다.

주어진 실수 y의 프리이미지는 y = f(x) 등식의 해법 집합이다.

도메인

몇 개의 실제 변수의 함수의 영역은 때때로 명시적으로 정의되는 subset의 부분집합이다. 실제로 함수 f의 영역 X를 부분 집합 Y ⊂ X로 제한하면 공식적으로 다른 함수인 f to Y의 제한, 즉 f로 _Y 표시된다. 실제로 f와 f를 _Y 식별하고 첨자를 생략하는 것은 해롭지 않은 경우가 많다.

반대로, 예를 들어 연속성이나 분석적 연속성에 의해 주어진 함수의 영역을 자연스럽게 넓히는 것이 가능할 때도 있다. 이것은 실제 변수의 함수의 영역을 명시적으로 정의할 가치가 없다는 것을 의미한다.

대수구조

산술 연산은 다음과 같은 방법으로 함수에 적용할 수 있다.

• 모든 실제 숫자 r에 대해 상수 함수$({\displaystyle x}$) ${\displaystyle \mapsto }$ ${\displaystyle r}$ ${\displaystyle (x)\mapsto r}$은$($는) 정의된 모든 곳에 있다.
• 모든 실제 숫자 r과 모든 함수 ${\displaystyle f}$에 대해 $r{\displaystyle }$ f${\displaystyle }$:${\displaystyle }$( ${\displaystyle x}$) ${\displaystyle \mapsto }$ ${\displaystyle r}$ ${\displaystyle f}$( x${\displaystyle }$) ${\displaystyle rf:(x)\mapsto rf(x)}$는 f와 동일한 도메인을$$ 가지고 있다(또는 r = 0이면 어디에나 정의된다).
• If f and g are two functions of respective domains X and Y such that X∩Y contains an open subset of ℝ, then ${\displaystyle f+g:(x)\mapsto f(x)+g(x)}$ and ${\displaystyle f\,g:(x)\mapsto f(x)\,g(x)}$ are functions that have a domain containing X∩Y.

그것은 어느 곳에나 정의되어 있는 n 변수의 기능과 주어진 지점의 일부 인접 지역에서 정의되어 있는 n 변수의 함수는 둘 다 실제에 걸쳐 교감 알제브라를 형성하는 것을 따른다.

${\displaystyle 1}$ ${\displaystyle /}$ f : (${\displaystyle x}$)${\displaystyle \mapsto }$ 1${\displaystyle }$/ ${\displaystyle f}$( x${\displaystyle }$)${\displaystyle }$, ${\displaystyle$1$/f:(x)\mapsto$1$/f(x)$를 유사하게 정의할 수 있는데, 이는$$ f(x) ≠ 0이 ℝ의 열린 부분집합이 포함된 f의 영역에 있는 점(x)의 집합이 있는 경우에만 함수다. 이 제약조건은 위의 두 알헤브라가 밭이 아니라는 것을 암시한다.

연속성 및 한계

19세기 2부까지는 수학자들에 의해 연속적인 기능만 고려되었다. 그 당시, 위상학적 공간과 위상학적 공간 사이의 연속적 지도의 공식적 정의보다 다소 오래 전에 하나 또는 여러 개의 실제 변수의 기능에 대해 연속성의 개념이 정교하게 설명되었다. 수학에서는 실제 변수의 연속적인 기능이 어디에나 존재하기 때문에 위상학적 공간 사이의 연속적인 지도라는 일반적인 개념과는 무관하게 이 개념을 정의할 가치가 있다.

연속성을 정의하기 $위해서$는 d${\displaystyle (x}$ ,${\displaystyle y}$) =${\displaystyle x}$ - ${\displaystyle y}${\$displaystyle d(x,y)= x-y$}의 두 개의 실제 변수에 대한 도처에 정의된 함수인 of의 거리 함수를 고려하는 것이 유용하다.

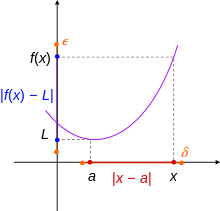
A기능 f점 내부의 도메인에 있는{\displaystyle},, 모든 긍정적인 실수 ε, 아직은 긍정적인 실수가 f())− f(를)<>모든 x에 ε{\displaystyle f())-f(를)<>\varepsilon}{\displaystyle)}가 d(x,)<>φ.{\displayst φ 연속적입니다.yle d(x,a$다시$ 말하면$,$${\displaystyle (은}$ $f{\displaystyle }$ (${\displaystyle }$)$$. {\$displaystyle$ f$(a$)를 중심으로 하는 $길이{\displaystyle }$ 2ε의 간격에 포함된$$ ${\displaystyle a}$을 중심으로 하는 반지름 φ의 간격의 f에 의해 이미지를 가질 수 있을 만큼 충분히 작게 선택할 수 있다$.$$}$ 함수는$$ 도메인의 모든 지점에서 연속되는 경우 연속적이다.

실제 변수의 실제 값 함수의 한계는 다음과 같다.^[1] 함수 f의 도메인 X의 위상학적 폐쇄에 한 점을 두어라. 함수, f는 x가 a를 향하는 경우 한계 L을 가진다.

${\displaystyle L=\lim _{x\to a}f(x),}$

다음 조건이 충족되는 경우: 모든 양의 실수 > > 0에 대해 다음과 같은 양의 실수 Δ > 0이 있다.

$[\displaystyle f(x)-L <\varepsilon }$

다음과 같은 도메인 내의 모든 x에 대해

$d(x,a)를 표시한다.$

한계가 존재한다면 그것은 독특하다. a가 도메인의 내부에 있는 경우, 기능이 a에서 연속적인 경우에만 한계가 존재한다. 이 경우 우리는 다음과 같은 조치를 취하였다.

${\displaystyle f(a)=\lim _{x\to a}f(x).}$

a가 f 도메인의 경계에 있을 때, 그리고 f가 a에 한계가 있을 경우, 후자 공식은 f의 도메인을 "연속성에 의해 확장"할 수 있게 한다.

미적분학.

실제 변수 각각에 대해 여러 함수를 수집할 수 있다.

${\displaystyle y_{1}=f_{1}=f_{1}(x)\\n2}=f_{2}(x)\dots, y_{n}=f_{n}(x)}$

x에 의해 파라메트릭된 벡터로:

${\displaystyle \mathbf {y} =(y_{1},y_{2},\ldots,y_{n})=[f_{1}(x), f_{2}(x),\ldots,f_{n}(x)]}}$

벡터 y의 파생상품은 i = 1, 2, ..., n:에 대한 f_i(x)의 벡터 파생상품이다.

${\dplaystyle {\frac {d\mathbf {y}}{dx}}{dx}=\left\frac {dy_{1}:{dx}}, {\frac {dy_{dx}},\ldots, {\frac {dy_{dx}}\rig)}$

또한 위치 벡터 r = r(x)로 x에 의해 파라메트리된 공간 곡선을 따라 선 통합을 수행할 수 있으며, 변수 x에 대해 통합한다.

${\displaystyle \int_{a}^{b}\mathbf {y}(x)\cdot d\mathbf {r} =\int_{a}^{b}\mathbf {y}(x)\cdot {\d\mathbf {r}{d}}}}}{dx}dx}dx}dx}x}x}dxx}$

여기서 ·는 도트 제품이고, x = a와 x = b는 곡선의 시작과 끝점이다.

정리

통합과 파생상품의 정의로 부품별 미적분 통합의 기본 정리, 테일러의 정리 등 핵심 정리들을 공식화할 수 있다. 통합과 파생상품의 혼합을 평가하는 것은 적분 부호 아래의 정리 분화를 이용하여 할 수 있다.

암묵함수

실제 변수의 실제 값 암묵적 함수는 "y = f(x)" 형식으로 작성되지 않는다. 대신, 매핑은 공간² to에서 ℝ의 0 요소(일반적인 0:

${\displaystyle \phi :\mathb {R}^{2}\to \{0\}}}$

그리고

$\phi(x,y)=0}$

변수들의 방정식이다. 암묵적 함수는 다음과 같은 경우에 함수를 나타내는 더 일반적인 방법이다.

${\displaystyle y=f(x)}$

그러면 우리는 항상 다음을 정의할 수 있다.

$\phi(x,y)=y-f(x)=0}$

그러나 역이 항상 가능한 것은 아니다. 즉, 모든 암묵적 함수가 이 방정식의 형태를 갖는 것은 아니다.

dimensional의ⁿ 1차원 공간 곡선

공식화

함수 r₁ = r₁(t), r₂ = r₂(t), ..., r_n = r_n(t) 모든 공통 변수 t를 고려할 때, 다음과 같이 한다.

${\displaystyle {\begin{aligned}r_{1}:\mathbb {R} \rightarrow \mathbb {R} &\quad r_{2}:\mathbb {R} \rightarrow \mathbb {R} &\cdots &\quad r_{n}:\mathbb {R} \rightarrow \mathbb {R} \\r_{1}=r_{1}(t)&\quad r_{2}=r_{2}(t)&\cdots &\quad r_{n}=r_{n}(t)\\\end{aligned}}}$

또는 함께 고려:

${\displaystyle \mathbf {r} :\mathb {R} \rightarrow \mathb {R} ^{n}\...\quad \mathbf {r} =\mathbf {r}(t)}$

파라메트리된 엔투플이

${\displaystyle \mathbf {r}(t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]}$

1차원 공간 곡선을 묘사한다.

원곡선에 접선

r(t = c) = a = (a₁, a₂, a, ..., a_n) 어떤 상수 t = c에 대해 해당 지점에서 곡선에 대한 1차원 접선 라인의 방정식은₁ t:에 대한 r(t), r₂(t), ..., r_n(t) 및 r:

${\displaystyle {\frac {r_{1}(t)-a_{1}}{dr_{1}(t)/dt}}={\frac {r_{2}(t)-a_{2}}{dr_{2}(t)/dt}}=\cdots ={\frac {r_{n}(t)-a_{n}}{dr_{n}(t)/dt}}}$

정규 평면 대 곡선

r = a에서 접선 라인에 정규적인 n차원 하이퍼 평면의 방정식은 다음과 같다.

${\displaystyle (p_{1}-a_{1}){\frac {dr_{1}(t)}{dt}}+(p_{2}-a_{2}){\frac {dr_{2}(t)}{dt}}+\cdots +(p_{n}-a_{n}){\frac {dr_{n}(t)}{dt}}=0}$

또는 도트 제품 측면에서:

${\dapsestyle(\mathbf {p} -\mathbf {a} )\cdot {\d\mathbf {r}(t)}{dt}=0}$

여기서 p = (p₁, p₂, p, ..., p_n)는 공간 곡선이 아닌 평면의 점이다.

운동학과의 관계

dr(t)/dt의 물리적 및 기하학적 해석은 r(t) 경로를 따라 이동하는 점 모양의 입자의 "속도"로서, r을 시간 t에 의해 파라메트리된 공간 위치 벡터 좌표로 처리하며, 순간 이동 방향에서 모든 t에 대한 공간 곡선에 접하는 벡터다. t = c에서 공간 곡선은 접선 벡터 dr(t)/dt를 가지며, t = c에서 공간 곡선에 대한 하이퍼플레인 또한 t = c에서 접선까지 정규 분포를 이룬다. 이 평면의 벡터(p - a)는 dr(t)/dt에 대해 정상이어야 한다.

마찬가지로 dr²(t)/dt는² 입자의 "가속"이며, 곡률 반경을 따라 지시된 곡선에 정상인 벡터다.

행렬 값 함수

행렬은 또한 단일 변수의 함수가 될 수 있다. 예를 들어, 2d 단위의 회전 행렬:

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\end{bmatrix}}cos \theta \\cos \theta \\nd{bmatrix}}}}}}}$

원점에 대한 회전 각도의 매트릭스 값 함수. 마찬가지로 특수 상대성에서는 순수 부스트(회전 없음)에 대한 로렌츠 변환 매트릭스:

${\displaystyle \Lambda (\beta )={\begin{bmatrix}{\frac {1}{\sqrt {1-\beta ^{2}}}}&-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&0&0\\-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&{\frac {1}{\sqrt {1-\beta ^{2}}}}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}}$

부스트 파라미터 β = v/c의 함수로서, v는 기준 프레임 사이의 상대 속도(연속 변수)이고 c는 빛의 속도, 상수다.

바나흐와 힐베르트의 공간과 양자역학

이전 섹션을 일반화하면 실제 변수의 함수 출력은 바나흐 공간이나 힐버트 공간에 위치할 수도 있다. 이러한 공간에서는 분할과 곱셈과 한계가 모두 정의되므로 파생적 개념과 적분 개념은 여전히 적용된다. 특히 양자역학에서는 케트나 오퍼레이터의 파생물을 취하게 되는 경우가 많다. 예를 들어, 일반적인 시간에 의존하는 슈뢰딩거 방정식에서 다음과 같은 현상이 발생한다.

${\displaystyle i\hbar {\frac {\partial t}{\partial t}\psi = {\hat {H}\psi }$

여러 다른 힐버트 공간의 요소가 될 수 있는 파동 함수의 파생물을 취한다.

실제 변수의 복합 값 함수

실제 변수의 복합 값 함수는 이완, 실제 값 함수의 정의, 코도메인을 실제 숫자로 제한하고 복잡한 값을 허용함으로써 정의할 수 있다.

f(x)가 이처럼 복잡한 가치 함수인 경우, 다음과 같이 분해될 수 있다.

f(x) = g(x) + ih(x),

여기서 g와 h는 실제 값 함수다. 즉, 복합적인 가치 함수에 대한 연구는 실제 가치 함수의 쌍에 대한 연구로 쉽게 감소한다.

실제 변수 함수 집합의 카디널리티

The cardinality of the set of real-valued functions of a real variable, ${\displaystyle \mathbb {R} ^{\mathbb {R} }=\{f:\mathbb {R} \to \mathbb {R} \}}$, is ${\displaystyle \beth _{2}=2^{\mathfrak {c}}}$, which is strictly larger than the cardinality of the continuum (i.e., set of all 실제 수). 이 사실은 산술적으로 쉽게 증명된다.

Furthermore, if ${\displaystyle X}$ is a set such that ${\displaystyle 2\leq \mathrm {card} (X)\leq {\mathfrak {c}}}$, then the cardinality of the set ${\displaystyle X^{\mathbb {R} }=\{f:\mathbb {R} \to X\}}$ is also ${\displaystyle 2^{\mathfrak {c}}}$, since

However, the set of continuous functions ${\displaystyle C^{0}(\mathbb {R} )=\{f:\mathbb {R} \to \mathbb {R} :f\ \mathrm {continuous} \}}$ has a strictly smaller cardinality, the cardinality of the continuum, ${\displaystyle {\mathfrak {c}}}$. 이것은 연속 함수가 그것의 도메인의 밀집된 부분 집합에 대한 그것의 값에 의해 완전히 결정된다는 사실에서 온다.^[2] 따라서 리얼스에 대한 연속적인 실질 가치 함수 집합의 카디널리티는 합리적 변수의 실제 가치 함수 집합의 카디널리티보다 크지 않다. 기본 산술 기준:

On the other hand, since there is a clear bijection between ${\displaystyle \mathbb {R} }$ and the set of constant functions ${\displaystyle \{f:\mathbb {R} \to \mathbb {R} :f(x)\equiv x_{0}\}}$, which forms a subset of ${\displaystyle C^{0}(\mathbb {R} )}$, ${\displaystyle \mathrm{c}\mathrm{a}\mathrm{r}\mathrm{d}(}$${\displaystyle C^{}}$ ${\displaystyle {0\mathrm{}}^{}}$( ${\displaystyle R\mathbb{}}$)${\displaystyle \ge }$ ${\displaystyle c\mathfrak{}}$ ${\$도 유지되어야 한다$$. 따라서 $c{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{a}}$ r ${\displaystyle \mathrm{d}(}$ C ${\displaystyle 0\mathbb{}{}^{}}$( R${\displaystyle }$)${\displaystyle }$= ${\displaystyle c\mathfrak{}}$ ${\$

참고 항목

• 실분석
• 여러 실제 변수의 함수
• 복합분석
• 여러 복잡한 변수의 함수

참조

• F. Ayres, E. Mendelson (2009). Calculus. Schaum's outline series (5th ed.). McGraw Hill. ISBN 978-0-07-150861-2.
• R. Wrede, M. R. Spiegel (2010). Advanced calculus. Schaum's outline series (3rd ed.). McGraw Hill. ISBN 978-0-07-162366-7.
• N. Bourbaki (2004). Functions of a Real Variable: Elementary Theory. Springer. ISBN 354-065-340-6.

외부 링크

• 다변량 미적분학
• L. A. 탤먼(2007) 다변량 함수에 대한 가변성