실용수

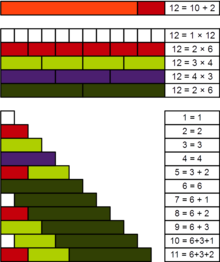
정수론에서 실용적인 번호나panarithmic number[1]은 긍정적인 정수 n{n\displaystyle}가 모든 작은 양의 정수가 될 수 있는으로 금액의 별개의 제수의 n{n\displaystyle}. 예를 들면, 예를 들어 12는 실용적인 숫자 때문에 모든 숫자에서 1-11이 될 수 있게 표현으로 금액의 제수 1,.2,3, 4, 6: 이러한 구분자 자체뿐만 아니라 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, 11 = 6 + 3 + 2가 있다.

실수의 순서(OEIS의 순서 A005153)가 시작된다.

피보나찌는 리베르 아바시(1202)에서 이집트 분수로 합리적으로 숫자를 표현하는 문제와 관련하여 실용적인 숫자를 사용했다.피보나찌는 공식적으로 실제 숫자를 정의하지는 않지만, 실제 분모가 있는 분수에 대한 이집트 분수 확대 표를 제시한다.^[2]

"실용수"라는 명칭은 스리니바산(1948년) 때문이다.그는 "화폐, 가중치, 조치의 세분화에는 보통 10의 권력으로 대체될 만큼 불편해야 할 4, 12, 16, 20, 28과 같은 숫자들이 포함된다"고 지적했다.테와트(1954년)와 시에르피에스키(1955년).이러한 특성화를 통해 숫자는 원시 요인화를 검토하여 실제적인지 여부를 판단할 수 있다.짝수 짝수 하나, 두 사람의 힘 하나하나가 실용적이다.

실제 수치는 또한 많은 특성에서 소수와 유사한 것으로 나타났다.^[3]

실수의 특성화

스리니바산(1948)에 의한 본래의 특성화에서는 실수는 부족수가 될 수 없으며, 그 중 하나가 부족이 1이 아니면 모든 구분자(1과 그 자체 포함)의 합이 2배 이하라고 명시되어 있다.If the ordered set of all divisors of the practical number ${\displaystyle n}$ is ${\displaystyle {d_{1},d_{2},...,d_{j}}}$ with ${\displaystyle d_{1}=1}$ and ${\displaystyle d_{j}=n}$, then Srinivasan's statement can be expressed by the inequality

. 즉, 모든 디비저의 순서 1< d <.. . . j{\$daystyle {d_{1}<d_{2}<...$실제$숫자의 <d_{$j}}}은(는) 완전한 하위 숫자여야 한다.

이러한 부분적 특성화는 원시적 요인화에서 숫자가 실제적인지를 판단하는 것이 간단하다는 것을 보여준 스튜어트(1954)와 시에르피에스키(1955)에 의해 확장되고 완성되었다.prime factorization $n{\displaystyle }$= ${\displaystyle {}_{}^{}}$ ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {{\alpha \mathrm{}}_{}}_{}^{}}$ 1${\displaystyle }$.${\displaystyle }$. . . ${\displaystyle {}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {{\alpha k}_{}}_{}^{}}${\$displaystyle$ n$=p_{1}^{\alpha _{1}}...$P_{k}^{\alpha_{k}}}(정렬된 주문 p1<>에서 소수 수열이야, p2<⋯<>안 k와{\displaystyle p_{1}<>p_{2}<>\dots <, p_{k}})실용적이다 만일 각의 주요 요소 p 나는{\displaystyle p_{나는}}은 작은 만큼에 대한 p나는 − 1{\displaystyle p_{나는}-1} 한 표현으로 금액의 smaller 제수.이것이 사실이 되려면 첫 번째 $p{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$}가 2와 같아야$$ 하며, 2 ~ k 사이의 모든 i에 대해 각 연속 $p{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 불평등에 따라야 한다$$.

${\displaystyle p_{i}\leq 1+\sigma (p_{1}^{\alpha _{1}}p_{2}^{\alpha _{2}}\dots p_{i-1}^{\alpha _{i-1}})=1+\prod _{j=1}^{i-1}{\frac {p_{j}^{\alpha _{j}+1}-1}{p_{j}-1}},}$

where ${\displaystyle \sigma (x)}$ denotes the sum of the divisors of x. For example, 2 × 3² × 29 × 823 = 429606 is practical, because the inequality above holds for each of its prime factors: 3 ≤ σ(2) + 1 = 4, 29 ≤ σ(2 × 3²) + 1 = 40, and 823 ≤ σ(2 × 3² × 29) + 1 = 1171.

위에 언급된 조건은 숫자가 실용적이기 위해 필요하며 충분하다.한 방향에서, 이 조건은 $p{\displaystyle {}_{}}$ -${\displaystyle {}_{}1}$ ${\displaystyle p_{i}-$$1$을$$n ${\displaystyle n$}의 디비저의 합으로$$ 나타낼 수 있도록 하기 위해 필요하다$.$ 왜냐하면 불평등이 진실되지 않으면 더 작은 디비저를 모두 합해도 $p{\displaystyle {}_{}}$ ${\displaystyle i_{}}$- ${\displaystyle 1}$ ${\displaystyp_{i}-1}$에 도달할 수 없을 만큼 작은 합을 제공하기 때문이다.$$. 다른 방향에서는 유도로 볼 수 있는 바와 같이 조건도 충분하다.보다 강력하게, $n{\displaystyle }$ ${\displaystyle n}$의 인자화가 위의 조건을 만족한다면$$, $다음{\displaystyle }$ 단계 순서에 따라 m ${\displaystyle \le \sigma }$ ${\displaystyle (n}$ )$${\$displaystyle m$\leq $\sigma$ (n$)}$을(를$)$$$n {\$displaystyn}$의 디비저의 합으로 나타낼 수 있다$$.^[4]

• By induction on ${\displaystyle j\in [1,\alpha _{k}]}$, it can be shown that ${\displaystyle p_{k}^{j}\leq 1+\sigma (n/p_{k}^{\alpha _{k}-(j-1)})}$. Hence ${\displaystyle p_{k}^{\alpha _{k}}\leq 1+\sigma (n/p_$$\{$$k}$ .
• Since the internals ${\displaystyle [qp_{k}^{\alpha _{k}},qp_{k}^{\alpha _{k}}+\sigma (n/p_{k})]}$ cover ${\displaystyle [1,\sigma (n)]}$ for ${\displaystyle 1\leq q\leq \sigma (n/p_{k}^{\alpha _{k}})}$, there$q{\displaystyle }$ ${\displaystyle q}$과(와) 일부 $r{\displaystyle }$∈${\displaystyle }$[${\displaystyle 0,}$ ${\displaystyle \sigma }$($n$/ ${\displaystyle p_{}}$ ${\displaystyle k{}_{}}$) ${\displaystyle ]}$ ${\displaystyle r\in[0,\p_{k}}]$이며, $m{\displaystyle }$= ${\displaystyle {}_{}^{}}$ ${\displaystyle k_{}^{}}$ $α$ ${\displaystyle {k_{}}_{}^{}}$+ ${\displaystyle r}$ ${\displaystym m=qp_{k}^{\c$
• Since ${\displaystyle q\leq \sigma (n/p_{k}^{\alpha _{k}})}$ and ${\displaystyle n/p_{k}^{\alpha _{k}}}$ can be shown by induction to be practical, we can find a representation of q as a sum of divisors of ${\displaystyle n/p_{k}^{\alpha _{k}}}$.
• $r{\displaystyle }$ ${\displaystyle \le }$(${\displaystyle n}$/ ${\displaystyle p{}_{}}$ $){\displaystyle r\leq \sigma (n/p_{k}})$, $그리고{\displaystyle }$ n${\displaystyle }$/ ${\displaystyle p_{}}$ k ${\$n/$p_{k}}}}$ 유도에 의해 실용적으로 보일 수 있기$$ 때문에${\displaystyle }$n / ${\displaystyle p{}_{}}$ ${\displaystyle k_{}}$ ${\$의 divors 합으로 r을 찾을 수 있다.
• r을 나타내는 칸막이와 q를 나타내는 칸막이의 $각각에$ p k ${\displaystyle {{\alpha }_{}}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\$을 나타내는 칸막이와 함께 n {\$displaystyle n$의 칸막이의 합으로 m을 표현한다$.$

특성.

• 유일한 홀수 실제 숫자는 1이다. $왜냐하면{\displaystyle }$ n ${\displaystyle$$$n}이$$(가) 2보다 큰 홀수일 경우, $2$는$$n {\$displaystyn$}의 구별되는 구분수의 합으로 표현할 수 없기 때문이다$.$ 더 강하게, Srinivasan(1948)은 1과 2를 제외한 모든 실제 숫자는 4 또는 6(또는 둘 다)로 나눌 수 있다고 관찰한다.
• 두 개의 실제 숫자의 산물도 실제 숫자다.^[5]보다 강하게 두 개의 실제 숫자 중 최소 공통 배수는 또한 실제 숫자다.동등하게, 모든 실제 숫자의 집합은 곱셈으로 닫힌다.
• 스튜어트와 시에르피에스키에 의한 위의 특징에서 n ${\displaystyle n}$이(가) $실제{\displaystyle }$ 숫자이고 $d{\displaystyle }$ ${\displaystyle$ $d$$}$이(가) 그 부차수 중 하나라면 n${\displaystyle }n{\displaystyle }$ ${\displaystyle d}$ ${\displaystyn\cdot d}$도 실제 숫자여야 함을$$ 알 수 있다.
• 모든 실제 숫자의 집합에는 원시적인 실제 숫자의 집합이 있다.원시적인 실제 숫자는 실용적이고 사각형이 없거나 실용적이며, 요인화 지수가 1보다 큰 주요 인자로 나누면 더 이상 실용적이지 않다.원시 실제 번호의 순서(OEIS의 순서 A267124)가 시작된다.

다른 등급의 숫자에 대한 관계

다른 몇 가지 주목할 만한 정수 집합은 실제 숫자로만 구성된다.

• $n{\displaystyle }$ ${\displaystyle$ n}을(를$)$ 가진 위의 속성에서 $실제$ 숫자와 d {\$displaystyle d$$}$ 칸막이 중$$ 하나($즉{\displaystyle }$, ${\displaystyle d}$n {\$displaystyd$n})를 가진 경우 $n{\displaystyle d}$ d$${\$displaystyle n\cdot$ d$}$도 실제 숫자여야 하므로$$ 3의 모든 전력이 6배만큼 실제 숫자가 되어야 한다.2의
• 2의 모든 힘은 실용적인 숫자다.^[6]두 개의 힘은 그들의 주요 인자화 측면에서 실용적인 숫자의 특성화를 사소한 것으로 만족시킨다. 즉, 그들의 인자화에서 유일한 프라임인₁ p는 필요에 따라 2와 같다.
• 짝수 하나하나가 실제 수이기도 하다.^[6]이는 짝수 완전수는 반드시 ${\displaystyle {2k}^{}}$- ${\displaystyle 1^{}}$( ${\displaystyle {2k}^{}}$- $){\displaystyle 2^{k-1}(2^{k}-1)}$의 형태를 가져야 한다는 Leonhard Euler의 결과에 따른 것이다$.$이 인자의 홀수 부분은 짝수 부분의 분수의 합계와 같으므로, 그러한 숫자의 모든 홀수 주요 인자는 최대 짝수 부분의 분수의 합이 되어야 한다.따라서 이 숫자는 실제 숫자의 특성화를 만족시켜야 한다.
• 모든 영장류($일부{\displaystyle }$ $i{\displaystyle }$ ${\displaystyle$ $i$$}$ prime의$$ 제품, 일부 i ${\displaystyle$ i$\})$는 실용적이다.^[6]처음 두 개의 영장류인 두 개와 여섯 개의 영장류인 경우, 이것은 분명하다.각 연속 primorial}는 양쪽 두 달력에서 윤년은 작은 primorial과 내가 1{\displaystyle p_{i-1}− 다음 작은 총리, p}에 의해 나는{\displaystyle p_{나는}소수 p증가함으로써. 베르트랑 공준까지 형성된다, 나는;2p나는 − 1{\displaystyle p_{나는}<, 2p_{i-1}}그래서 각각의 연속적인 전성기 < p. 사실원추리의 r은 이전 원추리의 점괘 중 하나보다 적다.유도에 의해, 모든 영장류는 실제 숫자의 특성화를 만족시키는 것을 따른다.원초성은 정의상 사각형이 없는 것이기 때문에 그것은 또한 원시적인 실제 수이다.
• 원형을 일반화하려면 첫 $번째{\displaystyle }$ k ${\displaystyle k}$ 프리타임의$$ 0이 아닌 힘의 산물인 숫자도 실용적이어야 한다.여기에는 라마누잔의 고도로 복합적인 숫자(어떤 작은 양의 정수보다 더 많은 분수를 가진 숫자)뿐만 아니라 요인 번호도 포함된다.^[6]

실제 수 및 이집트 분수

폼의 m/m<>로 n{\displaystyle m/n}만약 n{n\displaystyle}실용적이다, 다음 중 합리적인 숫자였을 것이다;n{\displaystyle m<, n}를 합으로 ∑ 표시할 수 있는 것은/dn{\textstyle\sum d_{나는}/n}n{n\displaystyle}의 제가 거기{\displaystyle d_{나는}각 d}은 뚜렷한 인자다. 각각의 정확...에서이 합계는 단위 분수로 단순화되므로, 이러한 합은 $m{\displaystyle /n}$ ${\displaystyle m/n}$을(를) 이집트 분수로 나타낸다$$.예를 들어.

피보나찌는 그의 1202년 저서 "리베르 아바시^[2]"에서 합리적인 수의 이집트 분수를 찾기 위한 몇 가지 방법을 열거하고 있다.이 중 첫째는 숫자 자체가 이미 단위분수인지 시험하는 것이지만, 둘째는 위에서 설명한 바와 같이 분모의 분수의 합으로서 분자의 표현을 검색하는 것이다.이 방법은 실제적인 분모에 대해서만 성공이 보장된다.피보나찌는 실제 숫자 6, 8, 12, 20, 24, 60 및 100을 분모로 하는 분수에 대한 이러한 표현 표들을 제공한다.

Vose(1985)는 모든 합리적인 숫자 $x{\displaystyle /y}$ ${\displaystyle$ x$/y}$이(가) $O{\displaystyle (\sqrt{\mathrm{로그}}}$ ${\displaystyle \sqrt{}}$ y${\displaystyle }$) ${\displaystyle O({\sqrt {\log y})}$개의$$ 항으로 이집트 분수를 나타낸다는$$ 것을 보여주었다.증명에는 $n{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$보다 작은 모든 숫자를 O${\displaystyle (}로그{\displaystyle \sqrt{{}_{}}}$ n ${\displaystyle \sqrt{i_{}}}$- 1${\displaystyle \sqrt{{}_{}}}$)의$$합으로 쓸 수 있는$$ 속성과 함께$$ $n{\displaystyle {}_{}}$ i ${\displaystyle n_{i-1}}$의 구별되는$$ divisors of n ${\$$n_}}}}$의 순서를 찾는 것이 포함된다.그래서 나는}1<> 베<나는{\displaystyle n_{i-1}< n;y<, n_{나는}−와 그리고 나서, i,)나는}{\displaystyle xn_{나는}ny{이\displaystyle}에 의해 지수 q{\displaystyle q}이고 나머지 r{r\displaystyle}을 주고 나뉘어 져 있다. 선택된다{\displaystyle 나는}그것은 x 이런 선택에서 Y을 따르 )nq${\displaystyle \frac{i_{}}{}}$+ ${\displaystyle r\frac{}{}}$ y ${\displaystyle \frac{i_{}}{}}$ ${\$${i$$\}\}\}\}\}.$ 이 공식의 오른쪽에 있는 두 숫자 모두를 ${\displaystyle n_{}}$ i ${\$i}}}}의 구분합으로 확장하면 원하는 이집트 분율 표현이 된다$$.테넌바움 &, 요코타는 x/y{\displaystyle x/y}모든 합리적인 수가 가장 큰 분모는 O(}{\displaystyle O({\frac{y\log ^{2}y{\log \log 이집트 일부 표현이다 보여 주는 것이 실용적인 숫자의 다른 순서와 관련된 연쇄 반응은 비슷한 기술을 사용하(1990년).y}$})}$.

Zhi-Wei Sun의 2015년 9월 추정에 따르면,^[7] 모든 양의 이성적인 숫자는 모든 분모가 실제적인 숫자인 이집트 분수를 나타낸다.그 추측이 데이비드 엡스타인(2021년)에 의해 증명되었다.

소수점이 있는 유사점

실제 숫자에 관심을 갖는 한 가지 이유는 그들의 많은 성질이 소수들의 성질과 비슷하기 때문이다.실제로, Goldbach의 추측과 쌍둥이 원시 추측과 유사한 이론들은 실제 숫자로 알려져 있다: 모든 양의 짝수 정수는 두 개의 실제 숫자의 합이며$,$ 실제 숫자의 세 쌍이 $무한히$한다$(x$ - 2, $x$x +$2$^[8]멜피는 또한 실용적인 피보나치 숫자들이 무한히 많다는 것을 보여주었다; 무한히 많은 피보나치 프리임의 존재에 대한 유사한 문제가 열려있다.하우스만${\displaystyle \&}$샤피로(1984)는 프리타임에 대한$$ Legendre의 추측과 유사한 결과인$$모든 양의 $real{\displaystyle }$ x ${\displaystyle$ [x$^{2},${\$displaystyle$$[x^{$2}},${\displaystyle }$[$x+1)^{2}]$ 간격에 항상 실제 숫자가 존재한다는 것을 보여주었다.짧은 간격의 실제 숫자에 대한 이 결과는 ${\displaystyle {만약}_{}}$ s n ${\$가 실제 숫자의 순서라면$$, 충분히 $큰{\displaystyle }$ n$${\$displaystyle n}$과 $적절한{\displaystyle }$ A ${\displaystyle A}$에 대해 증명하는 멜피에 의해 결과적으로 개선되었다$.$

Let ${\displaystyle p(x)}$ count how many practical numbers are at most ${\displaystyle x}$. Margenstern (1991) conjectured that ${\displaystyle p(x)}$ is asymptotic to ${\displaystyle cx/\log x}$${\displaystyle n}$ for some constant ${\displaystyle c}$, a formula which resem소수 정리를 블링하여, 실제 숫자가 정수에 밀도 0을 가지고 있다는 이전의 Erdds & Loxton(1979) 주장을 강화한다.테넨바움(1986)의 추정치를 개선한 결과, 사이아스(1997)는 p${\displaystyle }$( ${\displaystyle x}$) ${\디스플레이$ 스타일 $p(x)}$의 크기가 $x{\displaystyle /\log }$ ${\displaystyle x}$ ${\디스플레이$ 스타일 $x/\log$ x$}$인 것을 발견했고$,$ 와인가트너(2015)는 마겐스턴의 추측을 입증했다.우리는^[10] 가지고 있다.

$여기$서 c${\displaystyle }$= 1${\displaystyle \mathrm{.33607...}}$$c=1.33607...$$}$ 따라서$$^[11] 실제 숫자는 소수보다 약 33.6% 더 많다.상수 $요인{\displaystyle }$ c ${\displaystyle c}$의 정확한^[12] 값은 여기서 $\gamma {\displaystyle }$ ${\displaystyle \gamma}$은(는) 오일러-마스케로니 상수이고 $p{\displaystyle }$ ${\displaystyp p}$은(는) 프라임으로 실행된다$$.

산술적 수열의 소수들과 마찬가지로, 두 개의 $자연수$인 ${\$$displaystyle$ $a}$과 $q를$주어$,$ 우리는 다음과^[13] 같이 한다.

The constant factor ${\displaystyle c_{q,a}}$ is positive if, and only if, there is more than one practical number congruent to ${\displaystyle a{\bmod {q}}}$. If ${\displaystyle \gcd(q,a)=\gcd(q,b)}$, then ${\displaystyle c_{q,a}=c_{q,b}}$. For의 예로서, 실제 숫자의 약 38.26%는 마지막 소수 자릿수가 0인 반면, 2, 4, 6, 8의 마지막 자릿수는 각각 15.43%의 동일한 상대 주파수로 발생한다.

메모들

참조

외부 링크

• 주세페 멜피가 집계한 실제 숫자 표.
• PlanetMath의 실제 수.
• Weisstein, Eric W., "Practical Number", MathWorld