도함수
Derivative| 에 대한 일련의 기사의 일부 |
| 미적분학. |
|---|
도함수는 함수의 입력에 대한 함수의 출력 변화의 민감도를 측정하는 미적분학의 기본 도구입니다. 선택한 입력 값에서 단일 변수의 함수가 존재할 때, 그 점에서 함수의 그래프에 대한 접선의 기울기입니다. 접선은 해당 입력 값에 가까운 함수의 최상의 선형 근사치입니다. 이러한 이유로 도함수는 종속변수의 순간 변화율과 독립변수의 순간 변화율의 비율로 설명되는 경우가 많습니다.[1] 도함수를 찾는 과정을 미분이라고 합니다.
미분에는 여러 가지 다른 표기법이 있는데, 가장 일반적으로 사용되는 것은 라이프니츠 표기법과 소수 표기법입니다. 라이프니츠 표기법은 고트프리트 빌헬름 라이프니츠의 이름을 따서 두 미분의 비율로 표기하고, 프라임 표기법은 프라임 마크를 붙여 표기합니다. 상위 표기법은 반복되는 미분을 나타내며, 일반적으로 미분에 위첨자를 추가하여 라이프니츠 표기법으로 표시하고, 소수 표기법에는 소수 표기법을 추가하여 표시합니다. 예를 들어, 시간에 대한 움직이는 물체의 위치에 대한 첫 번째 도함수는 물체의 속도, 두 번째 도함수는 물체의 가속도, 시간이 지남에 따라 속도가 어떻게 변하는지입니다.
도함수는 여러 실제 변수의 함수로 일반화될 수 있습니다. 이 일반화에서 도함수는 그래프가 (적절한 번역 후) 원래 함수의 그래프와 가장 좋은 선형 근사인 선형 변환으로 재해석됩니다. Jacobian 행렬은 독립 변수와 종속 변수의 선택에 의해 주어진 기초에 대해 이러한 선형 변환을 나타내는 행렬입니다. 독립 변수에 대한 편미분으로 계산할 수 있습니다. 여러 변수의 실제 값 함수의 경우, 자코비안 행렬은 기울기 벡터로 줄어듭니다.
정의.
한도로
실제 변수 {\의 함수는 도메인의 지점에서 구별할 수 있습니다. 도메인에 이(가) 포함된 열린 간격및 한계가 있는 경우
If the function is differentiable at , that is if the limit exists, then this limit is called the derivative of at . Multiple notations for the derivative exist.[4] The derivative of at can be denoted , read as " prime of "; or it can be denoted , read as "the derivative of with respect to at " or " by (or over) at ". 아래의 § 표기법을 참조하십시오. 가 도메인의 모든 점에서 도함수를 갖는 함수인 경우, 함수는 x 를 x 에서 {\ f 도함수의 값에 매핑하여 정의할 수 있습니다 이 함수는 로 작성되며, f의 도함수 또는 도함수라고 합니다 함수 는 도메인의 전부는 아니지만 최대 점에서 도함수를 갖는 경우가 있습니다. {\가 정의되고 다른 에서는정의되지 마다 {\displaystyle f'(의값이 f'( {\displaystyle f'(a와 동일한 함수를 f의 도함수라고도 합니다 여전히 함수입니다. 그러나 도메인이 f의 도메인보다 작을 수 있습니다[5]
예를 들어, 를 제곱 함수라고 하자: ) = {\displaystyle f(x) = x^{2}}. 그렇다면 도함수의 정의에서 몫은
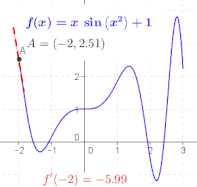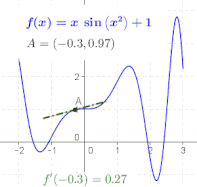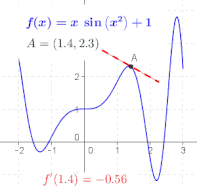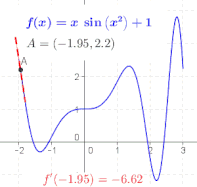
도함수의 정의에서 비율은 함수 의 그래프에서 두 점 구체적으로 점 ( f( 및 + (+ + h,a + 를 통과하는 선의 기울기입니다 h가 , 이 점들은 서로 가까워지고, 이 선의 기울기는 에서 f의 그래프에 대한 접선의 기울기인 극한값에 가까워집니다 즉, 도함수는 접선의 기울기입니다.[7]
무한소 사용
도함수 ( 를 생각하는 한 가지 방법은 함수 의 출력의 무한소 변화와 입력의 무한소 변화의 비율입니다.[8] 이러한 직관을 엄격하게 하기 위해서는 극소량을 조작하는 규칙 체계가 필요합니다.[9] 초실수의 체계는 무한대와 무한대의 극소량을 다루는 방법입니다. 하이퍼리얼은 임의의 유한한 항에 1+ + ⋯ + 1cdots + 1} 형태보다 큰 수를 포함하는 실수의 확장입니다. 그러한 숫자들은 무한하고, 그들의 역수는 무한소입니다. 초실수를 미적분학의 기초에 적용하는 것을 비표준 분석이라고 합니다. 이것은 미분학과 적분학과 같은 미적분학의 기본 개념을 무한소의 관점에서 정의할 수 있는 방법을 제공하므로 라이프니츠 표기법의 에 정확한 의미를 부여합니다. f( 의 도함수는
연속성 및 차별화 가능성
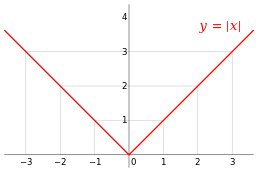
가 에서 미분 가능한 경우 도 에서 연속적이어야 합니다[11] 예를 들어, choose a point and let be the step function that returns the value 1 for all less than , and returns a different value 10 for all greater than or equal to . 함수 는 a에서 도함수를 가질 수 없습니다 가 음수이면+ 가 단계의 낮은 부분에 있습니다. 에서+ h a까지의 할선은 매우 가파릅니다. 가 0이 되면 기울기가 무한대가 됩니다. h가 양수이면+ a가 스텝의 높은 부분에 있으므로 a에서+ 까지의 할선은 기울기가 0입니다. 결과적으로 할선들은 어떤 하나의 기울기에도 접근하지 않으므로 차분계수의 한계가 존재하지 않습니다. 그러나 어떤 함수가 한 지점에서 연속적이라고 해도 그 지점에서 구별할 수 없을 수 있습니다. 예를 들어, ) = xdisplaystyle f(x) = x }가 부여하는 절대값 함수는 x = 0 {\displaystyle x = 0}에서 연속적이지만 여기서 구별할 수는 없습니다. If is positive, then the slope of the secant line from 0 to is one; if is negative, then the slope of the secant line from to is .[12] 그래프에서 = {\displaystyle x = 0}의 에서 " kink" 또는 "커스프"로 볼 수 있습니다. 매끄러운 그래프를 가진 함수라도 접선이 수직인 지점에서는 미분할 수 없습니다. 예를 들어, = {\ f(x) = x^{1/3}}에서 f = 1/ 3}로 표시되는 함수는 x = 0 {\displaystyle x = 0}에서 구별할 수 없습니다. 요약하면, 도함수를 갖는 함수는 연속적이지만, 도함수를 갖지 않는 연속적인 함수가 존재합니다.[11]
실제로 발생하는 대부분의 함수는 모든 점 또는 거의 모든 점에 도함수가 있습니다. 미적분학의 역사 초기에 많은 수학자들은 연속함수가 대부분의 점에서 미분 가능하다고 가정했습니다.[13] 온화한 조건(예를 들어, 함수가 모노톤 또는 립시츠 함수인 경우)에서는 이것이 사실입니다. 그러나 1872년 바이에르스트라스는 어디에서나 연속적이지만 어디에서도 미분할 수 없는 함수의 첫 번째 예를 발견했습니다. 이 예는 현재 Weierstrass 함수로 알려져 있습니다.[14] 1931년, 스테판 바나흐는 어떤 점에서 도함수를 갖는 함수들의 집합이 모든 연속 함수들의 공간에 대한 미미한 집합이라는 것을 증명했습니다. 비공식적으로, 이것은 임의의 연속 함수가 한 점에서 도함수를 갖는 경우는 거의 없다는 것을 의미합니다.[15]
표기법
함수의 도함수에 대한 하나의 일반적인 기호는 라이프니츠 표기법입니다. 그것들은 1675년 고트프리트 빌헬름 라이프니츠에 의해 소개된[16]두 미분 와 의 몫으로 쓰여집니다.[17] 방정식 = (x ) {\displaystyle y = f(x)}를 종속 변수와 독립 변수 사이의 함수 관계로 볼 때 여전히 일반적으로 사용됩니다. 첫 번째 도함수는 로 표시되며, "x x에 대한 y의 도함수"로 읽힙니다.[18] 이 도함수는 = x ) 함수에 미분 연산자를 적용하는 것으로 번갈아 취급될 수 있습니다 {\textstyle {\frac {dy}{dx}}={\frac {d}{dx}f(x).상위 도함수는 f (x {\displaystyle y f (x) {\displaystyle y f (x)}의 {\n}번째 에 n {^{n}}} 표기법을 사용하여 표현됩니다. 이것은 도함수 연산자의 여러 응용에 대한 약어입니다. 예를 들어, d x 2 =d (d d x f (x)). {\textstyle {\frac {d^{2}y}{dx^{2}}={\frac {d}{dx}}{\Bigl(}{\frac {d}}{dx}f(x){\Bigr )}}. 일부 대안과 달리, 라이프니츠 표기법은 분모에 미분을 위한 변수의 명시적인 지정을 포함하며, 이는 여러 상호 관련된 양으로 작업할 때 모호성을 제거합니다. The derivative of a composed function can be expressed using the chain rule: if and then [20][21]
미분을 위한 또 다른 일반적인 표기법은 함수 의 기호에 소수 표기법을 사용하는 것입니다 이것은 조셉 루이 라그랑주 때문에 소수 표기법이라고 알려져 있습니다.[22] The first derivative is written as , read as " prime of ", or , read as " prime".[23] 마찬가지로 두 번째 도함수와 세 번째 도함수는 각각 ″ {\displaystyle 와 ‴ {\displaystyle f'''}로 표기할 수 있습니다. 여기서 더 높은 도함수의 수를 나타내기 위해 위첨자에 로마 숫자를 사용하는 저자도 있고, 또는 (와 같이 괄호 안에 숫자를 넣는 저자도 있습니다 f[25] The latter notation generalizes to yield the notation for the -th derivative of .[19]
뉴턴 표기법이나 점 표기법에서는 시간 도함수를 나타내기 위해 기호 위에 점을 둡니다. 가 t의 함수인 경우 첫 번째 와 두 번째 도함수는 각각 ˙ {\dot {및 ¨ {\ {\dot {y}}로 적을 수 있습니다. 이 표기법은 시간 또는 호 길이에 대한 도함수에만 사용됩니다. 일반적으로 물리학과 미분기하학의 미분 방정식에 사용됩니다.[26] 그러나 점 표기법은 고차 도함수(4차 이상)에 대해 관리할 수 없으며 여러 개의 독립 변수를 다룰 수 없습니다.
또 다른 표기법은 D-notation으로, 미분 연산자를 기호 로 나타냅니다 D 첫 번째[19] 도함수는 ( 로 표기되고 상위 도함수는 위첨자로 표기되므로, n번째 도함수는 입니다 D이 표기법은 때때로 오일러 표기법이라고 불리는데, 레온하르트 오일러는 이 표기법을 사용하지 않은 것으로 보이며, 루이 프랑수아 앙투안 아르보가스트가 이 표기법을 도입했습니다.[27] 편미분을 나타내기 위해 에 의해 미분된 변수는 첨자로 표시됩니다. 예를 들어 x {\displaystyle x}에 대한 편미분 u = f ( {\displaystyle u = f (x,y)} 함수가 주어지면 D x u {\displaystyle D_{x}u} 또는 D x f (x,y )로 쓸 수 있습니다 Higher partial derivatives can be indicated by superscripts or multiple subscripts, e.g. and =∂∂f ( y)) {\x}^{2}f(x,y={\frac { }{l x}}{\Bigl(}{\frac { x}}{l x}f(x,y){\Bigr )}}}입니다.
계산규칙
원칙적으로, 함수의 도함수는 차이계수를 고려하고 그 극한을 계산함으로써 정의로부터 계산될 수 있습니다. 일단 몇 개의 단순 함수의 도함수가 알려지면, 다른 함수의 도함수는 더 단순한 함수로부터 더 복잡한 함수의 도함수를 얻기 위한 규칙을 사용하여 더 쉽게 계산됩니다. 도함수를 구하는 이 과정을 미분이라고 합니다.[29]
기본적인 기능에 대한 규칙
다음은 가장 일반적인 기본 함수의 도함수에 대한 규칙입니다. 서 는 실수이고, e는 수학 상수 약 2.71828입니다.[30]
- 거듭제곱의 도함수:
- 지수, 자연 로그 및 일반 기저를 갖는 로그의 함수:
- x (a) {\displaystyle {\fra{d}{dxa^{x}=a^{x}\ln(a)}, a > 0 display a>0}의 경우
- (x ) 1 x {\displaystyle {\fra{d}{dxn(x) = {\frac {1}{x}}, x > 0 displaystyle x>0}
- ( 1x (a) {\displaystyle {\fra{d}{dx}}\log _{}(x) = {\frac {1x\(a)}}, x의 경우 a> 0 {\displaystyle x,a>0}
- 삼각 함수:
- 역삼각함수:
- ( ) = 11 - x 2 {\displaystyle {\fra{d}{dx}\arcsn(x) = {\frac {1}{\sqrt {1-x^{2}}}, - 1 < 1 displaystyle -1<x<1}}
- (x ) - 11 - x 2 {\displaystyle {\fra{d}{dx}}\arccs(x) = -{\frac {1}{\sqrt {1-x^{2}}}, - 1 < x < 1 displaystyle -1<x<1}
결합함수에 대한 규칙
f와 g가 함수임을 감안하면, 기본 함수의 도함수로부터 함수의 도함수를 도출하기 위한 가장 기본적인 규칙은 다음과 같습니다.[31]
- 상수 규칙: 가 일정하면 모든 x에 대해
- 합 규칙:
- for all functions and and all real numbers and .
- 제품 규칙:
- for all functions and . As a special case, this rule includes the fact whenever is a constant, 규칙에 의해 α ' = ⋅ f = 0 {\displaystyle \alpha 'f = 0\cdot f = 0}이기 때문입니다.
- 몫 규칙:
- g' ' g - f' g' g 2 {\displaystyle \frac {f}{g}\riht)' ={\frac {f'g-fg'}{g^{2}} 모든 함수 f {\displaystyle f} 및 g {\displaystyle g}에 대해 g가 0인 경우.
- 합성 함수에 대한 연쇄 규칙: 만약 () = h((x ) ) {\displaystyle f (x) = h (g (x))}이면,
계산예
= + sin (x 2) - ln (x) x + 7 {\displaystyle f(x) = x^{4}+\sin \left(x^{2}\right)-\ln(x)e^{x}+7}로 주어진 함수의 도함수는
고차 도함수
차수가 높다는 것은 함수가 반복적으로 미분된다는 것을 의미합니다. 가 미분 가능한 함수임을 감안할 때, 의 도함수는 f로 표시되는 첫 번째 도함수입니다 의 도함수는 ″ {\displaystylef'}로 표시되는 2차 도함수이고, f ″ {\displaystyle f'}의는 f ‴ {\displaystyle f'}로표시되는 3차입니다. 이 과정을 계속함으로써 존재하는 경우, the -th derivative as the derivative of the -th derivative or the derivative of order . As has been discussed above, the generalization of derivative of a function may be denoted as .[32] k개의 연속 도함수를 갖는 함수를 배 미분이라고 합니다. 번째 도함수가 연속적이라면, 함수는 미분가능성 클래스 k C라고 합니다[33] 무한히 많은 도함수를 갖는 함수를 무한히 미분가능하거나 매끄러운 함수라고 합니다.[34] 무한히 미분 가능한 함수의 한 예는 다항식입니다. 이 함수를 미분하면 상수 함수가 반복적으로 나오고, 이 함수의 무한히 뒤따르는 도함수는 모두 0입니다.[35]
그 응용 중 하나에서 고차 도함수는 물리학에서 특정한 해석을 가질 수 있습니다. 함수가 그 시간에 물체의 위치를 나타낸다고 가정하고, 그 함수의 첫 번째 도함수는 시간에 대한 물체의 속도입니다. 함수의 두 번째 도함수는 시간에 대한 물체의 가속도이고,[29] 세 번째 도함수는 저크입니다.[36]
더 높은 차원에서
벡터값 함수
실수 변수의 벡터 값 y 는 일부 벡터 공간 의 벡터로 실수를 보냅니다 벡터 값 함수는 좌표 함수 y {\nt)}, 즉 (1(t), y 2(t), …, y (t) {\displaystyle \mathbf {y} (y_{1}(t),y_{2}(t),\,y_{n}(t)}입니다. 여기에는 예를 들어 2 또는 3 의 파라미터 곡선이 포함됩니다 좌표 함수는 실수 값 함수이므로 위의 도함수 정의가 이에 적용됩니다. 의 도함수는 접선 벡터라고 불리는 벡터로 정의되며, 그 벡터의 좌표는 좌표 함수의 도함수입니다. 즉,[37]
편미분
함수는 두 개 이상의 변수에 따라 달라질 수 있습니다. 여러 변수의 함수에 대한 부분 도함수는 해당 변수 중 하나에 대한 도함수이며, 다른 변수는 일정하게 유지됩니다. 편미분은 벡터 미적분학과 미분기하학에서 사용됩니다. 일반 도함수와 마찬가지로 여러 가지 표기법이 존재합니다. 변수 에 대한 함수 ( y f (의 부분 도함수는 다음과 같이 다양하게 표시됩니다.
여러 가지 가능성 [38]중에서 방향의 함수 변화율로 생각할 수 있습니다.[39] 여기서 ∂는 편미분 기호라고 불리는 반올림된 것입니다. 문자 d와 구별하기 위해 ∂는 "dee" 대신 "der", "del", "partial"로 발음되기도 합니다. 예를 들어, ( y) = + y + y 2 {\ f(x, y) = x^{2}+xy+y^{2}라고 하면, x {\displaystyle x} 및 y {\displaystyle y} 변수에 대한 함수 f {\displaystyle f}의 편미분은 각각 다음과 같습니다.
이것은 여러 실제 변수의 함수에 대한 연구의 기초가 됩니다. ( 가 그러한 실수 함수라고 하자. 에 대한 모든 편미분 f 가 점 1 {\에서 정의되면 이러한 편미분은 벡터를 정의합니다.
방향 도함수
가 의 실수 값 함수인 경우 f의 편미분은 좌표축 방향의 변화를 측정합니다. For example, if is a function of and , then its partial derivatives measure the variation in in the and direction. 그러나 = displaystyle y = x}을 따라 f {\ f의 을 직접 측정하지는 않습니다. 방향 도함수를 사용하여 측정합니다. Choose a vector , then the directional derivative of in the direction of at the point is:[43]
의 모든 편미분이 에서 연속적인 경우 이들은 v 으로 의 방향미분을 다음 공식으로 결정합니다.
도함수, 미분 및 자코비안 행렬
가 부터 의 열린 부분 집합의 함수일 때 선택한 방향에서 f 의 방향 도함수는 해당 지점 및 해당 방향에서 f에 대한 최상의 선형 근사치입니다. 그러나 > n>일 때 방향 도함수는 f 의 동작을 완전히 파악할 수 없습니다 전체 도함수는 모든 방향을 한 번에 고려하여 완전한 그림을 제공합니다. 즉, 에서 시작하는 임의의 벡터 에 대하여 선형 근사 공식은 다음과 같습니다.[44]
도함수가 에 존재하는 경우 의 모든 편도함수와 방향 도함수는 에 존재하며 모든 에 대하여 is the directional derivative of in the direction . If is written using coordinate functions, so that m}}, 그러면 편미분을 행렬로 사용하여 전체 도함수를 표현할 수 있습니다. 이 행렬은 에서 f의 야코비안 행렬이라고 합니다[46]
일반화
도함수의 개념은 다른 많은 설정으로 확장될 수 있습니다. 공통적인 스레드는 점에서의 함수의 도함수가 점에서의 함수의 선형 근사의 역할을 한다는 것입니다.
- 도함수의 중요한 일반화는 복소수 에서 C 까지의 함수와 같은 복소수 변수의 복소수 함수에 관한 것입니다 그러한 함수의 도함수의 개념은 정의에서 실제 변수를 복잡한 변수로 대체함으로써 얻어집니다.[47] 복소수 를 + y x로 써서 와 가 식별되면 C 에서 로의 미분 가능한 함수는 2 에서 까지의 함수로서 확실히 미분 가능합니다. (그것의 편미분이 모두 존재한다는 의미에서), 그러나 일반적으로 그 반대는 사실이 아닙니다: 복소 도함수는 실수 도함수가 복소 선형이고 이것이 코시-리만 방정식이라고 불리는 부분 도함수 사이의 관계를 부과하는 경우에만 존재합니다 – 홀로모픽 함수를 참조하십시오.[48]
- 또 다른 일반화는 미분 가능한 매니폴드 또는 매끄러운 매니폴드 사이의 기능에 관한 것입니다. 직관적으로 이러한 다양체 M은 접선 공간이라고 하는 벡터 공간에 의해 각 x 근처에 근사할 수 있는 공간입니다. 원형의 예는 3 의 매끄러운 표면입니다 (미분 가능한) 맵 의 도함수(또는 미분 → N {\ f between manifolds, at a point in , is then a linear map from the tangent space of at to the tangent space of at . 도함수는 M과 N의 접선 다발 사이의 지도가 됩니다 이 정의는 미분기하학에서 사용됩니다.[49]
- 미분은 또한 일반화가 Gateaux 도함수와 Fréchet 도함수인 Banach 공간과 같은 벡터 공간 사이의 지도에 대해 정의될 수 있습니다.[50]
- 고전 도함수의 한 가지 단점은 매우 많은 함수들이 미분할 수 없다는 것입니다. 그럼에도 불구하고 약도함수라는 개념을 사용하여 모든 연속함수와 다른 많은 함수를 미분할 수 있도록 도함수의 개념을 확장하는 방법이 있습니다. 이 아이디어는 연속 함수를 분포 공간이라고 불리는 더 큰 공간에 내장하고 함수가 "평균적으로" 미분 가능하도록 요구하는 것입니다.[51]
- 도함수의 성질은 대수학과 위상수학에서 많은 유사한 대상의 도입과 연구에 영감을 주었습니다; 미분대수학이 그 예입니다. 여기서는 링, 이상, 필드 등과 같은 추상 대수학의 몇 가지 주제를 도출하는 것으로 구성됩니다.[52]
- 미분의 이산 등가물은 유한 차이입니다. 미분적분학에 대한 연구는 시간 척도 미적분학의 유한한 차이의 미분적분학과 통합됩니다.[53]
- 산술 도함수는 소인수분해에 의해 정수에 대해 정의되는 함수를 포함합니다. 이것은 제품 규칙과 유사한 것입니다.[54]
참고 항목
메모들
- ^ Stewart 2002, 페이지 129–130.
- ^ Stewart 2002, p. 127; Stranger et al. 2023, p. 220.
- ^ 고닉 2012, 83쪽.
- ^ 고닉 2012, 페이지 88; Strang et al. 2023, 페이지 234.
- ^ Gonick 2012, 83쪽; Strang et al. 2023, 232쪽.
- ^ 고닉 2012, 77-80쪽.
- ^ Thompson 1998, 페이지 34, 104; Stewart 2002, 페이지 128.
- ^ Thompson 1998, 84–85쪽.
- ^ Keisler 2012, pp. 902–904.
- ^ Keisler 2012, p. 45; Henle & Kleinberg 2003, p. 66.
- ^ a b 고닉 2012, 156쪽.
- ^ 고닉 2012, 149쪽.
- ^ 자셰크 1922년, 야르니크 1922년, 리클릭 1923년
- ^ 2018년 데이비드.
- ^ Hewitt & Stromberg 1965에서 인용된 바나흐 1931.
- ^ 아포스톨 1967, 172쪽.
- ^ 카조리 2007, 204쪽
- ^ Moore & Siegel 2013, 110페이지
- ^ a b c Varberg, Purcell & Rigdon 2007, 페이지 125–126.
- ^ Varberg, Purcell & Rigdon 2007, 페이지 119.
- ^ 극한의 관점에서 미적분학의 공식화에서 다양한 저자들은 du 기호에 다양한 의미를 부여했습니다. 일부 저자는 du에 의미를 부여하지 않고 du/dx 기호의 일부로만 지정합니다. 다른 사람들은 dx를 독립 변수로 정의하고 du = dx ⋅f'(x)로 du를 정의합니다. 비표준 분석에서 du는 무한소로 정의됩니다. 함수 u의 외부 도함수로도 해석됩니다. 자세한 내용은 미분(무한소)을 참조하십시오.
- ^ 슈워츠먼 1994, 171쪽.
- ^ Moore & Siegel 2013, p. 110; Goodman 1963, p. 78–79.
- ^ Varberg, Purcell & Rigdon 2007, p. 125–126; Cajori 2007, p. 228.
- ^ Choudary & Niculescu 2014, p. 222; Apostol 1967, p. 171.
- ^ Evans 1999, 63쪽; Kreyszig 1991, 1쪽.
- ^ 카조리 1923.
- ^ Apostol 1967, p. 172; Varberg, Purcell & Rigdon 2007, p. 125–126.
- ^ a b 아포스톨 1967, 160쪽.
- ^ Varberg, Purcell & Rigdon 2007. 멱함수는 p. 133, 삼각함수는 p. 115–116, 자연로그는 p. 326, 가 {\ e인 지수는 p. 338–339,가 a인 지수는 p. 343, 가 a인 지수는 p 344를 참조하십시오 삼각함수의 역함수는 369입니다.
- ^ 상수 규칙과 합 규칙은 각각 Apostol 1967, 페이지 161, 164를 참조하십시오. 곱 규칙, 몫 규칙 및 연쇄 규칙은 각각 Varberg, Purcell & Rigdon 2007, 페이지 111–112, 119를 참조하십시오.
- ^ Apostol 1967, p. 160; Varberg, Purcell & Rigdon 2007, p. 125–126.
- ^ 워너 1983, 5쪽.
- ^ Debnath & Shah 2015, 40쪽.
- ^ Carothers 2000, p. 176.
- ^ Stewart 2002, p. 193.
- ^ a b 스튜어트 2002, 893쪽.
- ^ Stewart 2002, 947쪽; Christopher 2013, 682쪽.
- ^ 스튜어트 2002, 949쪽.
- ^ Silverman 1989, 216쪽; Bhardwaj 2005, 6.4쪽 참조.
- ^ Mathai & Haubold 2017, 페이지 52.
- ^ Gbur 2011, pp. 36–37.
- ^ Varberg, Purcell & Rigdon 2007, 페이지 642.
- ^ a b c Davvaz 2023, p. 266.
- ^ Lee 2013, 72쪽.
- ^ Davvaz 2023, p. 267.
- ^ 루소스 2014, 303쪽.
- ^ Gbur 2011, pp. 261–264.
- ^ 그레이, Abbena & Salamon 2006, 826쪽.
- ^ Azegami 2020. Gateaux 도함수는 p. 209를 참조하고, Fréchet 도함수는 p. 211을 참조하십시오.
- ^ 푸나로 1992, 페이지 84–85.
- ^ 콜친 1973, 페이지 58, 126.
- ^ 게오르기예프 2018, 8페이지
- ^ 1961년 바보.
참고문헌
- Apostol, Tom M. (June 1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra, vol. 1 (2nd ed.), Wiley, ISBN 978-0-471-00005-1
- Azegami, Hideyuki (2020), Shape Optimization Problems, Springer, doi:10.1007/978-981-15-7618-8, ISBN 978-981-15-7618-8
- Banach, Stefan (1931), "Uber die Baire'sche Kategorie gewisser Funktionenmengen", Studia Math., 3 (3): 174–179, doi:10.4064/sm-3-1-174-179.
- Barbeau, E. J. (1961). "Remarks on an arithmetic derivative". Canadian Mathematical Bulletin. 4 (2): 117–122. doi:10.4153/CMB-1961-013-0. Zbl 0101.03702.
- Bhardwaj, R. S. (2005), Mathematics for Economics & Business (2nd ed.), Excel Books India, ISBN 9788174464507
- Cajori, Florian (1923), "The History of Notations of the Calculus", Annals of Mathematics, 25 (1): 1–46, doi:10.2307/1967725, hdl:2027/mdp.39015017345896, JSTOR 1967725
- Cajori, Florian (2007), A History of Mathematical Notations, vol. 2, Cosimo Classics, ISBN 978-1-60206-713-4
- Carothers, N. L. (2000), Real Analysis, Cambridge University Press
- Choudary, A. D. R.; Niculescu, Constantin P. (2014), Real Analysis on Intervals, Springer India, doi:10.1007/978-81-322-2148-7, ISBN 978-81-322-2148-7
- Christopher, Essex (2013), Calculus: A complete course, p. 682, ISBN 9780321781079, OCLC 872345701
- Courant, Richard; John, Fritz (December 22, 1998), Introduction to Calculus and Analysis, Vol. 1, Springer-Verlag, doi:10.1007/978-1-4613-8955-2, ISBN 978-3-540-65058-4
- David, Claire (2018), "Bypassing dynamical systems: A simple way to get the box-counting dimension of the graph of the Weierstrass function", Proceedings of the International Geometry Center, Academy of Sciences of Ukraine, 11 (2): 53–68, arXiv:1711.10349, doi:10.15673/tmgc.v11i2.1028
- Davvaz, Bijan (2023), Vectors and Functions of Several Variables, Springer, doi:10.1007/978-981-99-2935-1, ISBN 978-981-99-2935-1
- Debnath, Lokenath; Shah, Firdous Ahmad (2015), Wavelet Transforms and Their Applications (2nd ed.), Birkhäuser, doi:10.1007/978-0-8176-8418-1, ISBN 978-0-8176-8418-1
- Evans, Lawrence (1999), Partial Differential Equations, American Mathematical Society, ISBN 0-8218-0772-2
- Eves, Howard (January 2, 1990), An Introduction to the History of Mathematics (6th ed.), Brooks Cole, ISBN 978-0-03-029558-4
- Funaro, Daniele (1992), Polynomial Approximation of Differential Equations, Springer, doi:10.1007/978-3-540-46783-0, ISBN 978-3-540-46783-0
- Gbur, Greg (2011), Mathematical Methods for Optical Physics and Engineering, Cambridge University Press, ISBN 978-1-139-49269-0
- Georgiev, Svetlin G. (2018), Fractional Dynamic Calculus and Fractional Dynamic Equations on Time Scales, Springer, doi:10.1007/978-3-319-73954-0, ISBN 978-3-319-73954-0
- Goodman, A. W. (1963), Analytic Geometry and the Calculus, The MacMillan Company
- Gonick, Larry (2012), The Cartoon Guide to Calculus, William Morrow, ISBN 978-0-06-168909-3
- Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), Modern Differential Geometry of Curves and Surfaces with Mathematica, CRC Press
- Henle, James M.; Kleinberg, Eugene M. (2003), Infinitesimal Calculus, Dover Publications, ISBN 978-0-486-42886-4
- Hewitt, Edwin; Stromberg, Karl R. (1965), Real and abstract analysis, Springer-Verlag, Theorem 17.8, doi:10.1007/978-3-662-29794-0, ISBN 978-3-662-28275-5
- Jašek, Martin (1922), "Funkce Bolzanova" (PDF), Časopis pro Pěstování Matematiky a Fyziky (in Czech), 51 (2): 69–76
- Jarník, Vojtěch (1922), "O funkci Bolzanově" (PDF), Časopis pro Pěstování Matematiky a Fyziky (in Czech), 51 (4): 248–264여기 영어 Jarník, Vojtěch (1922), "O funkci Bolzanově" (PDF), Časopis pro Pěstování Matematiky a Fyziky (in Czech), 51 (4): 248–264버전을 보세요.
- Keisler, H. Jerome (2012) [1986], Elementary Calculus: An Approach Using Infinitesimals (2nd ed.), Prindle, Weber & Schmidt, ISBN 978-0-871-50911-6
- Kolchin, Ellis (1973), Differential Algebra And Algebraic Groups, Academic Press, ISBN 978-0-08-087369-5
- Kreyszig, Erwin (1991), Differential Geometry, New York: Dover, ISBN 0-486-66721-9
- Larson, Ron; Hostetler, Robert P.; Edwards, Bruce H. (February 28, 2006), Calculus: Early Transcendental Functions (4th ed.), Houghton Mifflin Company, ISBN 978-0-618-60624-5
- Lee, John M. (2013), Introduction to Smooth Manifolds, Springer, doi:10.1007/978-0-387-21752-9, ISBN 978-0-387-21752-9
- Mathai, A. M.; Haubold, H. J. (2017), Fractional and Multivariable Calculus: Model Building and Optimization Problems, Springer, doi:10.1007/978-3-319-59993-9, ISBN 978-3-319-59993-9
- Moore, Will H.; Siegel, David A. (2013), A Mathematical Course for Political and Social Research, Princeton University Press, ISBN 978-0-691-15995-9
- Roussos, Ioannis M. (2014), Improper Riemann Integral, CRC Press, ISBN 978-1-4665-8807-3
- Rychlík, Karel (1923), Über eine Funktion aus Bolzanos handschriftlichem Nachlasse
- Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, Mathematical Association of American, ISBN 9781614445012
- Silverman, Richard A. (1989), Essential Calculus: With Applications, ISBN 9780486660974
- Stewart, James (December 24, 2002), Calculus (5th ed.), Brooks Cole, ISBN 978-0-534-39339-7
- Strang, Gilbert; et al. (2023), Calculus, volume 1, OpenStax, ISBN 978-1-947172-13-5
- Thompson, Silvanus P. (September 8, 1998), Calculus Made Easy (Revised, Updated, Expanded ed.), New York: St. Martin's Press, ISBN 978-0-312-18548-0
- Varberg, Dale E.; Purcell, Edwin J.; Rigdon, Steven E. (2007), Calculus (9th ed.), Pearson Prentice Hall, ISBN 978-0131469686
- Warner, Frank W. (1983), Foundations of Differentiable Manifolds and Lie Groups, Springer, ISBN 978-0-387-90894-6





 정의되고,
정의되고, 














































 함수임을 감안하면, 기본 함수의 도함수로부터 함수의 도함수를 도출하기 위한 가장 기본적인 규칙은 다음과 같습니다.
함수임을 감안하면, 기본 함수의 도함수로부터 함수의 도함수를 도출하기 위한 가장 기본적인 규칙은 다음과 같습니다.


































 점
점










 선택하여 이 근사치의 오차가 가능한 한 작습니다.
선택하여 이 근사치의 오차가 가능한 한 작습니다. 



 (를) f
(를) f
 C
C  써서
써서