교환환

추상대수의 한 분야인 환 이론에서, 교환환이란 곱셈 연산이 교환적인 환이다.교환환 연구는 교환대수라고 불린다.보완적으로, 비가환 대수는 곱셈이 가환적일 필요가 없는 비가환의 연구이다.

대수 구조 → 고리 이론 링 이론
기본 개념 반지. • 서브링 • 이상적 • 비율 링 • 소수점 이상 • 분수의 총 고리 • 링 제품 • 연상 대수의 자유곱 • 대수의 텐서 곱 링 동형사상 • 커널 • 내부 자기동형성 • 프로베니우스 내형성 대수 구조 • 모듈 • 연관 대수 • 등급 링 • 인볼루티브 링 • 링의 카테고리 • 초기 $링{\displaystyle \mathbb{}}$Z ${\displaystyle \mathbb${$Z}$ • 단자 $링{\displaystyle \mathrm{}}$ 0 $=$ ${\displaystyle {\mathrm{}}_{}}$1 {\$displaystyle$ 0=\$mathbb {Z} _{1}}$ 관련 구조 • 필드 • 유한 필드 • 비연관 링 • 리 링 • 조던 링 • 세미닝 • 세미필드
가환 대수 교환환 • 통합 도메인 • 통합 폐쇄 도메인 • GCD 도메인 • 고유한 인수 분해 영역 • 주요 이상 영역 • 유클리드 도메인 • 필드 • 유한 필드 • 컴포지션 링 • 다항식 링 • 정식 파워 시리즈 링 대수적 수론 • 대수적 수 필드 • 정수의 고리 • 대수적 독립성 • 초월수 이론 • 초월도 p-adic 수 이론과 소수점 • 직접 한계/역 한계 • $제로링{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ 1$(\$ • 정수 $모듈$로 Zn${\displaystyle }$/ ${\displaystyle p^{}}$ n$$ { $displaystyle \mathbb {Z}$ /$p^{n}\mathbb {Z} }$ • Prüfer $p-ring{\displaystyle \mathbb{}}$Z ( ${\$ ) ( \ $displaystyle$ \$mathbb$ { Z } ( $p^$ { \ infty$}$ ) } • Base-p 원 $링{\displaystyle \mathbb{}}$T ${\display\mathbb$ {T$}$} • Base-p $정수{\displaystyle \mathbb{}}$Z {\$displaystyle \mathbb {Z} }$ • $p-adic$은${\displaystyle }$Z [${\displaystyle 1}$ ${\displaystyle /}$ $]{ displaystyle \mathbb {Z} [1/$p]} • Base-p 실수$R{\displaystyle \mathbb{}}$ {\style $\mathbb {R} 표시}$ • p-adic $정수{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {}_{}}$p \$style \mathbb {Z} _{p}$ • p-adic $숫자{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {}_{}}$ ${$style $\mathbb {Q}_{p}$ 표시 • p-adic $솔레노이드{\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {}_{}}$p \$style \mathbb {T}$ _${p}$ 대수기하학 • 아핀 품종
비가환 대수 비가환환 • 분할 링 • 반잠수 링 • 심플링 • 정류자 비가환 대수 기하학 자유 대수 클리포드 대수 • 기하학 대수 연산자 대수
v t

대수 구조
그룹라이크 그룹. 세미그룹 / 모노이드 랙 앤 쿼들 준군 및 루프 아벨 군 마그마 리 그룹 군론
반지 같은 울리다 Rng 세미링 니어링 교환환 통합 도메인 들판 분할링 리 링 링 이론
격자 모양 격자 반격자 보완 격자 총주문량 헤이팅 대수 부울 대수 격자 지도 격자 이론
모듈형 모듈 연산자가 있는 그룹 벡터 공간 선형 대수
대수적 대수학 어소시에이티브 비관련성 구성 대수 리 대수 등급부 바이알게브라 홉프 대수
v t

정의와 첫 번째 예시

정의.

링은 2개의 바이너리 연산, 즉 링의 임의의 두 요소를 세 번째 요소로 결합하는 연산을 갖춘 $세트{\displaystyle }$ R$(\displaystyle$ R$)$입니다.이들은 덧셈과 곱셈이라고 불리며 일반적으로$+\displaystyle$ $+\}"$ 및 ${\displaystyle "\backslash }$$displaystyle \$$cdot$$"$ ($a{\displaystyle }$ ${\displaystyle +}$ \ $displaystyle$$$a +$b$$)$로 표시됩니다.이 두 가지 연산이 링을 형성하려면 링이 추가 그룹 아래에 아벨리안이어야 합니다.는 곱셈 아래의 모노이드로서 잘 알려져 있습니다.즉, ${\displaystyle 곱셈}$은 덧셈 위에 분산되어 있습니다.즉${\displaystyle ,}$ a${\displaystyle (b}$+${\displaystyle }$c )$=$ ($a)$ a$\cdot \left(b+c\right$)=\$left(a\cdot$ b$\right$)+$left(a\cdot$c\$right$입니다.덧셈 및 곱셈의 식별 요소는 각각 0$(\displaystyle$ 0$)$ $및$ 1$(\displaystyle$1)로 $표시$됩니다.

곱셈이 가환인 경우.

$링{\displaystyle }$ R$(\displaystyle$ R$)$을 교환환이라고 합니다.이 문서의 나머지 부분에서는 특별히 명기되어 있지 않는 한 모든 링은 치환됩니다.

첫 번째 예

$중요$한 예이며, 어떤 의미에서는 중요한 것은 덧셈과 곱셈의 두 가지 연산이 있는 $Z의$$$링이다.정수의 곱은 교환 연산이므로, 이것은 교환환이다.보통 독일어 자흘렌(숫자)의 약자로 Z$\$로 표기됩니다.

필드는 0${\displaystyle 1}$1 { $displaystyle$0 \ $not = 1$ } 및$$ 0 이외의 모든 $요소{\displaystyle }$a { $displaystyle$ a$$} 가$$ 반전되는 $교환환$입니다.즉, a${\displaystyle =}$ ${\displaystyle 1}$ { $displaystyle$a \ $cdot$ b $= 1$ 의 곱셈 $역b{\displaystyle }${ $displaystyle$ b$}$ 가$$ 됩니다.따라서 정의상 어떤 필드도 교환환입니다.유리, 실수 및 복소수가 필드를 형성합니다.

R$${\$displaystyle$ R$}$이 주어진 가환환일 $경우{\displaystyle }$ 변수$$X ${\displaystyle$ X$}의$ $계수$가 R {\$displaystyle$ R$\$left[X\$right$인 모든 다항식 집합이${\displaystyle }$다항식 링을 형성합니다.여러 변수에 대해서도 마찬가지입니다.

V$${\$displaystyle$$$V$}$이(가) 위상 공간인 $경우{\displaystyle }$$,$ 예를 들어 일부 ${\displaystyle {}^{}}$n {\$displaystyle \mathbb {$R$} ^{$n$\}\}$의 부분 집합이면 V {\$displaystyle$ V$}$의 실수 $또는{\displaystyle }$ 복소수 연속 함수가 교환환을 형성합니다.V {\$displaystyle$ V$}$의 경우처럼 두 가지 개념이 정의되어 있는 경우, 미분 가능 함수 또는 완전 형상 함수에 대해서도 마찬가지입니다.

나눗셈성

0이 아닌 모든 요소가 곱셈적으로 반전되는 필드와는 대조적으로 링의 나눗셈성 개념은 더욱 풍부합니다.$링{\displaystyle }$R의 $요소{\displaystyle }$ a$({$$displaystyle$ R$})$는 곱셈 역수를 가지고 있는 경우 단위라고 불립니다.또 다른 특정 유형의 요소는 0 제수입니다. 즉, 링에 0이 아닌 $요소{\displaystyle }$$b{\displaystyle }$(\$displaystyle$$$$=0$가 존재하는 요소 ${\displaystyle a}$$(\displaystyle$ a$).$ R(\$displaystyle$ R$)$에$$0이 아닌 제수가 없는 $경우{\displaystyle }$, 이 요소는 적분(또는 도메인)이라고 합니다.어떤 양의 $n$에 ${\displaystyle {대해}^{}}$ n $= 0$을 만족하는$$ $요소{\displaystyle {}^{}}$ a$(\$$displaystyle$a$^{n$}=$0)$를 nilpotent라고 합니다.

현지화

링의 국부화는 일부 요소가 반전 불가능하게 되는 과정입니다. 즉, 곱셈 반전이 링에 추가됩니다.구체적으로는 S$(\displaystyle$ S$)$가 R$(\$${\displaystyle \mathrm{displaystyle}}$ R$)($$즉{\displaystyle }$, S$(\displaystyle$ s,$t\in$S$)$의 곱셈폐쇄 서브셋인 ${\displaystyle \mathrm{경우}}$$,$ S(\$displaystyle$ S$)$에서의$R$(\$displaystyle$ S) 또는 S$(\$$displaystyle$S)의 링 분모에 $대한{\displaystyle }$ 부분집합.$isplaystyle$ S$.$ 보통 S${\displaystyle {}^{}}$- ${\displaystyle {}^{}}$ R$(\displaystyle$ S$^{-1}R)$로 $표시$됨)은 기호로 구성됩니다.

유리수에서 흔히 볼 수 있는 취소와 유사한 특정 규칙이 적용됩니다.실제로 이 $언어$에서 Q$(\$는$$0이 아닌 모든 $정수$에서 Z$(\displaystyle$\mathbb ${Z})$의 현지화입니다.이 구조는 Z$(\$가 아닌 모든 $통합{\displaystyle }$ 도메인$R$(\$displaystyle \$displaystyle {Z$$$$})에 적용됩니다.로컬라이제이션$R$ { ${\displaystyle 0^{}}$ ${\displaystyle {\}}^{}}$ )${\displaystyle {}^{}}$- 1 $(\displaystyle \left$\ { $0\right\}\right)^{-1}R$$)$은 $ientR$이라고 하는 $필드$입니다.

이상과 모듈

다음 개념의 대부분은 반드시 가환환에 대해서도 존재하지만 정의와 특성은 일반적으로 더 복잡하다.예를 들어, 교환환의 모든 이상은 자동으로 양면이기 때문에 상황은 상당히 단순해집니다.

모듈

$링{\displaystyle }$ R$({displaystyle$R$\})$의 경우$,$ R({$displaystyle$R$})$ - $모듈$ M({$displaystyle$ M$})$은 필드에 대한 벡터 공간과 같습니다.즉, 모듈 내의 요소를 추가할 수 있으며 벡터 공간과 동일한 공리를 적용하여$R의 요소$를 곱할 수 있습니다.

모듈 연구는 벡터 공간보다 훨씬 더 중요합니다.기본값이 없는 모듈, 즉 요소가 선형 독립적인 스패닝 세트를 포함하지 않는 모듈이 있기 때문입니다.기반이 있는 모듈을 프리 모듈이라고 하며 프리 모듈의 서브모듈은 프리 모듈일 필요가 없습니다.

유한 타입의 모듈은 유한 스패닝세트를 가진 모듈입니다.유한 유형의 모듈은 선형 대수학에서 유한 차원 벡터 공간의 역할과 유사하게 교환환 이론에서 기본적인 역할을 한다.특히 노에테리안 고리(이하 § 노에테리안 고리 참조)는 유한형 모듈의 모든 서브모듈이 유한형인 링으로 정의할 수 있다.

이상

$링{\displaystyle }$ $R$의 이상$($$Ideplaystyle$ R$)$은$R$의 $하위{\displaystyle }$ 모듈, 즉$R$에 $포함$된 모듈입니다. 더 자세히 설명하자면, $I{\displaystyle }$($I)$는 R$($R$)$의 $모든{\displaystyle }$ $디스플레이 스타일$$$$R$에 대해 $비어$ 있지$$$$ 않은 부분 집합입니다.$I$의 $displaystyle$ i$}$와 j$($$displaystyle$ $i$$)$는 $모두{\displaystyle }$$I$에 있습니다$.$ ${\displaystyle \mathrm{다양}}$한 어플리케이션에서 링의 이상을 이해하는 것은 특히 중요하지만 일반적으로 모듈을 학습함으로써 진행됩니다.

모든 링에는 0의 이상$(\$\})과$$R$\$displaystyle R$(\displaystyle$ R$)$의 2가지 이상이 있습니다.R$(\displaystyle$ R$)$이 필드일 $경우{\displaystyle }$ 이 두 가지 이상이 정확히 유일한 이상입니다.R$${\$displaystyle$ R$}$의 하위 $집합{\displaystyle }$ F $=$ {$f_$j}${\displaystyle {\_\{}_{}}$j$\$ J}($여기$서$$J {\$displaystyle$ J$}$는 일부$$ 색인 집합)의 F = {$f_{j}$ j$\in$ J$}$에 대해$$F$${\$displaystyle$ F$}$에 의해 $생성$되는 이상은 $Fstyle$을 $포함$하는 최소값입니다$.$양이온

주요 이상 영역

F$(\displaystyle$ F$)$가 단일 $요소{\displaystyle }$r(\$displaystyle$ r$)$로 구성되어 $있는{\displaystyle }$$$경우 F(\$displaystyle$ F$)$에 의해 생성되는 이상은$r$(\$displaystyle$rs$)$의 배수, 즉 $임의$의 ${\displaystyle \mathrm{요소}}$ r(\$displaystyle$ s$)$의 형태 요소 rs(\$displaystyle$rs$$$)$로 구성되어 있습니다. 이러한 이상을 주체 ID라고 합니다.eal. 모든 이상이 주 아이디얼인 경우$,$ R(\$displaystyle$ R$)$을 주 아이디얼 링이라고 합니다.두 가지 중요한 $경우$는 Z$(\$와 $(\displaystyle$$$k$\backslash$$left[X\$right$])$입니다$.$이들 2개는 추가 도메인이기 때문에 주요 이상 도메인이라고 불립니다.

일반적인 고리와는 달리, 주요 이상 영역의 경우, 개별 원소의 특성은 고리 전체의 특성과 강하게 관련된다.예를 들어, 임의의 주요 이상 $영역{\displaystyle }$R(\$displaystyle$ R$)$은 고유한 인수분해 도메인(UFD)입니다. 즉, 모든 요소는 환원 불가능한 요소의 산물이며, 이는 (인자의 순서 변경까지) 고유한 방식으로 이루어집니다.여기서 도메인 내의 요소 a는 곱으로 표현할 수 있는 유일한 방법이 있다면 환원 불가능이라고 불린다.

b$(\displaystyle$$b$) 또는 c(\$displaystyle$ c$)$가 $하나$의 단위입니다.예를 들어, 필드 이론에서 중요한 $것$은 필드$k$에 대해 k${\displaystyle }$[${\displaystyle }$X $]$ \ $displaystyle$$k$$$\$left$ [ X \ $right$$]$의 환원 불가능한 다항식입니다.Z$(\$가 UFD라는 $사실$은 자연수가 소수 거듭제곱의 곱으로 고유하게 분해될 수 있다는 점에서 보다 원론적으로 설명할 수 있다.그것은 또한 산수의 기본 정리라고도 알려져 있다.

$요소$$a$가$$제품$$ $b$를$$분할할 $때$마다 요소 a는 소수$$ 요소이고$,$ $요소 a$는 $소수{\displaystyle }$ $요소$b$$$또는$ $c$를 분할합니다. 도메인에서 소수 $요소$는 축소할 수 없음을 의미합니다.그 반대는 고유한 인수분해 영역에서는 참이지만 일반적으로는 거짓입니다.

계수 링

이상의 정의는 "분할" I($디스플레이{\displaystyle }$ $스타일$ I$)$ "아웃"이 다른 링인 요인 링 $(디스플레이 스타일$ R$)$ / $(디스플레이 스타일$ I$):$ I$(디스플레이 스타일$ I$)$의 코셋 세트입니다.

${\displaystyle 및}{\displaystyle }$( a${\displaystyle }$+${\displaystyle I}$) (${\displaystyle b}$ +${\displaystyle I}$ ) $=$ +$$ \ $displaystyle$ \ left ($a$ +$I$ \ $right )\ left ( b$ +$I$ \ right )=$$$ab$ +$I$ 예를 들어 링${\displaystyle Z}$ / $Z$\$displaystyle \mathbb {Z} /n\mathbb${Z} $$($Z$n \displaystyle \$mathbb {Z} _{$n})$$ ($여기$서$$n {$displaystyle$ n$\}$은 정수)는 $모듈러{\displaystyle }$산술의 기본입니다.

이상이 링 전체보다 확실히 작다면 적절하다.어떤 적절한 이상에도 엄밀하게 포함되지 않은 이상을 최대라고 합니다.$이상적$인 m$($$displaystyle$ m$)$은$$R(\displaystyle R$)$ $/$ m(\$displaystyle$ m$)$이 필드인 $경우$에만 최대입니다.제로 고리를 제외하고, (정체성을 가진) 모든 고리는 적어도 하나의 최대 이상을 가지고 있다. 이는 조른의 보조 법칙에 따른 것이다.

노에테르 고리

반지는 (이 개념을 개발한 에미 노이더에게 경의를 표하여) 노이더리안이라고 불리는데, 만약 모든 상승 사슬이 이상에 대해

즉, 어떤 $지수{\displaystyle }$ n$\displaystyle$n을 넘어 일정하게 된다. 따라서, 모든 이상은 완전히 많은 요소에 의해 생성되거나, 완전히 생성된 모듈의 하위 모듈이 완전히 생성된다.

노이더리언이 되는 것은 매우 중요한 미세성 조건이며 기하학에서 자주 발생하는 많은 연산 하에서 그 조건이 보존됩니다.예를 들어$R$이 $Noetherian$인 $경우{\displaystyle }$ 다항식 $링{\displaystyle }$R [${\displaystyle {}_{}{}_{}}$ ${\displaystyle {X2\mathrm{}}_{}}$ ${\displaystyle ...,}$ $](\$$displaystyle$ R$$$\left [X_{1$}, $X_{2},\dots, X_n}\right)$도 ${\displaystyle {\mathrm{마찬가지}}^{}}$입니다$($힐버트 정리).$(\displaystyle$ I$\backslash )$

Noetherian이 아닌 링 $(\displaystyle$ R$)$은 Noetherian 서브링의 결합입니다.노에테르 근사라고 알려진 이 사실은 특정 정리를 노에테르 고리가 아닌 고리로 확장할 수 있게 해준다.

아르티니아 고리

반지는 (에밀 아르틴의 이름을 따서) 아르티니아라고 불리는데, 만약 모든 이상의 하강 사슬이

결국 움직이지 않게 됩니다.대칭으로 보이는 두 조건에도 불구하고, 노에테르 고리는 아르티니아 고리보다 훨씬 더 일반적입니다.예를 들어$,$ Z(\$displaystyle \mathbb {Z})$는 Noetherian입니다. 모든 이상은 하나의 요소로 생성될 수 있지만 Artian은 아닙니다.

$$체인{\displaystyle \mathbb{}}$$

Z

$${\displaystyle z\mathbb{}}$$

2

$${\displaystyle \mathrm{Z}z\mathbb{}}$$

4 Z

$${\displaystyle \mathrm{z}}$$

$${\displaystyle 8\mathbb{}}$$

Z

$$...$$

{

$$displaystyle$$

\

$$mathbb$$

{Z

$$}$$

\

$$suetneq$$

\ 4

$$\mathbbbbb {Suet$$

}사실 홉킨스 가족은...레비츠키 정리, 모든 아르티니아 반지는 노에테리안이야좀 더 정확히 말하면, 아르티니아 고리는 크룰 치수가 0인 노에테르 고리로 특징지을 수 있다.

교환환의 스펙트럼

프라임 아이디얼

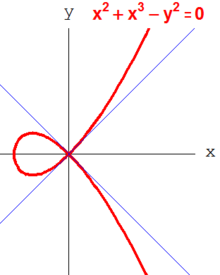
앞에서 설명한 바와 같이$,$ $Z{\displaystyle \mathbb{}}$ ${\displaystyle$ \$mathbb${Z$}}$는 고유한 인수분해 영역이다.이것은 19세기에 대수학자들이 깨달은 것처럼 더 일반적인 고리에 대해서는 사실이 아니다.예를 들어,

6을 곱으로 표기하는 방법에는 두 가지가 있습니다.소수가 아닌 소수가 이 문제를 회피할 수 있는 방법을 제공한다.가장 중요한 이상은 적절한(즉, R(\$displaystyle$ R$)$ $이상{\displaystyle }$p(\$displaystyle$ p$)$입니다. 즉, 2개의 링 $요소{\displaystyle }$중 b$(\$$displaystyle$ a$)$와 b$(\displaystyle$ b$)$의 ${\displaystyle 곱}$이${\displaystyle }$p$(\displaystyle$ p$)$에 $있을{\displaystyle }$ 때마다 적어도 1개가 이미 들어가 있습니다.$.$ {\$displaystyle$p.}($$정의상 어떤 이상에도 반대 결론이 적용됩니다.)따라서, 만약 소수가 주원소라면, 소수에 의해 동등하게 생성된다.단${\displaystyle ,}$ Z${\displaystyle \sqrt{}}$[ - $],$ \$displaystyle \mathbb {Z}$ \$left[{\sqrt${-$5}}\right]$와 $같은{\displaystyle \mathbb{}}$ 링에서는 주 아이디얼이 될 필요가 없습니다.이로 인해 링 이론에서 소수 원소의 사용이 제한됩니다.그러나 대수적 수론의 주춧돌은 어떤 데데킨드 고리$Z$[ - 5 $]$ \$displaystyle \mathbb {Z}$ \left$[{\sqrt${-$5}}\$right]} $포함$)에서 보다 일반적으로 어떤 이상(예를 들어 6에 의해 생성된 이상)도 고유하게 분해된다는 사실이다.

어떤 최대 이상도 프라임 아이디얼 또는 더 간단히 프라임 아이디얼입니다.또한 이상$I는 인자$ $링{\displaystyle }$ R$/I가$필수$$ 영역인 경우에만 소수입니다.이상이 소수임을 증명하거나 링에 제로디비서가 없다는 것을 증명하는 것은 매우 어려울 수 있습니다.$또{\displaystyle }$ 다른 표현 방법은 R ${\displaystyle p}$p \ $displaystyle$R \ $setminus p$is$$${\displaystyle }$is ic ic that that that that that라고 하는 것입니다.${\displaystyle {\mathrm{현지화}}^{}}({\displaystyle {}^{}}$ ${\displaystyle {Rp}^{}}$p${\displaystyle {}^{}}$) - ${\displaystyle {}^{}}$R ( \ $displaystyle \$left ($R$ \ $setminus$p \ $right )^{ -$1 R } local$$ 、 ${\displaystyle R_{}}$ p \$displaystyle$ R _ { $p$} :: ::::::::::::::::::::::::::::::::::::::::::::::이 링에는 ${\displaystyle {pR}_{}}$ p$\$라는 최대 아이디얼이 1개밖에 없습니다.이러한 링을 로컬이라고 부릅니다.

스펙트럼

${\displaystyle Spec}$ R$${\$displaystyle {Spec$$R$로 ${\displaystyle \text{나타나는}}$ 링$R{\displaystyle }$ {\$displaystyle$ R$\}$^{[nb 1]}의 스펙트럼은 R$$${\$$displaystyle$R$\}$의 모든 주요 이상 집합이며, R$${\$displaystyle$ R$\}$의 대수적 특성을 반영하는 토폴로지를 갖추고 있습니다.

$여기$서 f$\displaystyle$f는$$ 링 요소입니다.f$\displaystyle$f를$$ f mod p 값(즉, 잔류 필드 R/p의 f 이미지)을 취하는 함수로 $해석$하면, 이 서브셋은 f가 0이 아닌 궤적이 됩니다.스펙트럼은 또한 국소화와 인자 고리가 상호 보완적이라는 직관을 정밀하게 한다. 자연 지도 R → R_f → R / fR은 Zariski 토폴로지로 문제의 고리의 스펙트럼을 끝낸 후 각각 상호 보완적인 개방 및 폐쇄 이머에 대응한다.오른쪽의 R = Z와 같은 기본 링에서도 Zariski 토폴로지는 실수 집합의 토폴로지와는 상당히 다르다.

스펙트럼에는 mSpec(R)으로 표시되는 최대 이상 세트가 포함되어 있습니다.대수적으로 닫힌 필드 k의 경우, mSpec(k₁[T_n, ..., T] / (f_m, ..., f)는₁ 집합과 함께 분사됩니다.

따라서, 최대 이상은 교환환 연구의 초기 동기인 다항식의 해 집합의 기하학적 특성을 반영한다.그러나, 고리의 기하학적 특성의 일부로서 최대값이 아닌 이상을 고려하는 것은 몇 가지 이유로 유용하다.예를 들어, 최소 소수 이상(즉, 더 작은 이상을 엄격하게 포함하지 않는 이상)은 사양 R의 환원 불가능한 구성요소에 해당한다.Noetherian 링 R의 경우 Spec R에는 환원 불가능한 성분이 매우 많습니다.이것은 1차 분해의 기하학적 재현이며, 그에 따라 어떤 이상도 많은 1차 이상들의 산물로 분해될 수 있다.이 사실은 데데킨드 고리의 주요 이상으로 분해하는 궁극적인 일반화이다.

아핀 방식

스펙트럼의 개념은 교환대수와 대수기하학의 공통적인 기초이다.대수기하학에서는 사양 R에 $시프{\displaystyle \mathcal{}}$ O$(다양$한 열린 부분 집합에서 로컬로 정의된 함수를 수집하는 엔티티$)$를 부여하여 진행합니다.공간과 다발의 기준점을 아핀 스킴이라고 합니다.아핀 스킴이 주어졌을 때, 기본 링$R$은 O의 전역 섹션(\$displaystyle\mathcal {O$으로 복구할 수 있다. 또한, 링과 아핀 스킴 간의 일대일 대응은 링 동형과도 호환된다. 즉, f : R → S는 반대 방향의 연속 맵을 발생시킨다.

상기 두 범주의 결과적 등가성은 기하학적 방식으로 고리의 대수적 특성을 적절히 반영한다.

다양체가 R의 열린ⁿ 부분 집합에 의해 국소적으로 주어지는 사실과 유사하게, 아핀 체계는 대수 기하학의 연구 대상인 체계에 대한 국소 모델이다.그러므로, 교환환에 관한 몇 가지 개념은 기하학적 직관에서 비롯된다.

치수

고리 R의 크럴 치수(또는 치수) Dim R은 대략적으로 R의 독립 원소를 세어 고리의 "크기"를 측정한다.필드 k 위의 대수의 치수는 다음 4가지 특성에 의해 공리화될 수 있다.

• 치수는 로컬 특성입니다. dim R = sup_{p ∊ Spec R} dim_p R.
• 치수는 영가원소와는 무관하다. I µ R이 영가원소라면 dim R = dim R / I이다.
• 치수는 유한 확장 시 일정하게 유지된다. S가 R-모듈로 최종 생성되는 R 대수라면 Dim S = Dim R이다.
• 치수는 dim k[X₁, ..., X_n] = n으로 보정됩니다.이 공리는 n개의 변수에서 다항식 고리를 n차원 공간의 대수적 유사체로 간주함으로써 동기 부여된다.

차원은 임의의 링 R에 대해 주요 이상 사슬의 길이 n의 최고값으로 정의된다.

예를 들어, 필드는 0차원입니다. 유일한 주요 이상은 0 이상이기 때문입니다.체인은 (0) ( (p)형식이므로 정수는 1차원입니다.여기서 p는 소수입니다.Noetherian이 아닌 링 및 Noetherian이 아닌 링의 경우 치수는 무한할 수 있지만 Noetherian의 국소 링은 한정된 치수를 가집니다.위의 네 가지 공리들 중에서, 처음 두 가지는 정의의 기본적인 결과이고, 나머지 두 가지는 교환 대수학에서 중요한 사실, 상승 정리 그리고 크룰의 주요 이상 정리에 달려 있다.

링 동형사상

링 동형사상 또는 더 구어체로 간단히 지도는 다음과 같이 지도 f:R → S이다.

이러한 조건들은 f(0) = 0을 보장한다. 다른 대수 구조들과 마찬가지로, 링 동형사상은 그러므로 문제의 대수적 물체의 구조와 양립할 수 있는 지도이다.이러한 상황에서 S의 s에 R의 r을 곱할 수 있다는 것을 이해함으로써 S를 R 대수라고도 한다.

f의 커널과 이미지는 ker (f) = {r r R, f(r) = 0} 및 im (f) = f(R) = {f(r), r ∈ R}로 정의됩니다.커널은 R의 이상이고 이미지는 S의 서브링입니다.

고리의 동형사상은 만약 그것이 비사적이라면 동형사상이라고 불린다.중국의 나머지 정리라고 알려진 환 동형사상의 예는 다음과 같다.

여기서 n = pp₁₂...p는_k 쌍으로 구별되는 소수들의 곱이다.

교환 고리는 고리 동형사상과 함께 범주를 형성합니다.링 Z는 이 범주의 초기 객체이다. 즉, 모든 교환 링 R에 대해 고유한 링 동형사상 Z → R이 존재한다. 이 맵을 통해 정수 n은 R의 요소로 간주될 수 있다.예를 들어, 이항 공식은

이 맵을 사용하여 이항 계수를 R의 요소로 해석함으로써 어떤 교환환 R의 두 요소 a와 b에 대해서도 유효하다.

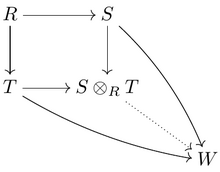
두 개의 R-대수 S와 T가 주어졌을 때, 그 텐서 곱은

다시 가환 R-대수가 됩니다.경우에 따라 텐서 곱은 S가 R과 관련된 것처럼 Z와 관련된 T-대수를 찾는 역할을 할 수 있다.예를들면,

유한 생성

R-대수 S는 s의 어떤 원소가 s의_i 다항식으로 표현될 수 있도록 s, ..., s가_1n 완전히 많으면 (대수로서) finally generated라고 불린다.동등하게, S는 다음 식과 동형이다.

보다 강력한 조건은 S가 R-모듈로서 최종적으로 생성된다는 것입니다.즉, 임의의 s는 일부 유한 집합₁ s, ..., s의_n R-선형 조합으로 표현될 수 있습니다.

로컬 링

링이 m으로 표시되는 단일 최대 아이디얼을 갖는 경우 링은 로컬이라고 불립니다.(로컬이 아닌) 임의의 링 R에 대해서, 로컬라이제이션은

p는 국소적인 이상이다.이 현지화는 사양 R의 기하학적 특성 "주변 p"를 반영합니다.교환대수의 몇 가지 개념과 문제는 R이 국소적인 경우로 축소될 수 있으며, 국소 링은 특히 깊이 연구된 링 클래스가 된다.R의 잔류 필드는 다음과 같이 정의된다.

임의의 R-모듈 M은 M/mM에서 주어진 k-벡터 공간을 산출합니다.Nakama의 약어는 이 구절이 중요한 정보를 보존하고 있음을 나타냅니다.완전히 생성된 모듈 M은 M/mM이 0인 경우에만 0입니다.

일반 로컬링

k-벡터 공간 m/m은² 코탄젠트 공간의 대수적 화신이다.비공식적으로 m의 원소는 p점에서 소실되는 함수로 생각할 수 있는 반면² m은 적어도 2개의 차수와 함께 소실되는 함수를 포함한다.노에테르 로컬 링 R에 대해 부등식은

는 true를 유지하며, 코탄젠트(또는 동등한 탄젠트) 공간이 적어도 규격 R 공간의 치수를 갖는다는 생각을 반영합니다.이 추정치에서 등식이 참일 경우 R은 일반 로컬링이라고 불립니다.Noetherian 로컬 링은 링(접선 원뿔의 함수 링)인 경우에만 규칙적입니다.

k 위의 다항식 고리와 동형이다.대체로, 정규 국소 링은 다항식 링과 다소 ^[1]유사합니다.일반 지역 링은 UFD ^[2]링입니다.

이산 평가링은 임의의 요소 r에 정수를 할당하는 기능을 갖추고 있다.r의 평가라고 불리는 이 숫자는 비공식적으로 0 또는 r의 극 차수로 간주될 수 있다.이산 평가 링은 정확히 1차원 정규 국소 링입니다.예를 들어 리만 표면상의 홀모픽 함수의 세균 고리는 이산 밸류에이션 링이다.

완전한 교차로

크럴의 주요 이상 정리에 의해, 고리의 차원 이론의 기초적인 결과, 고리의 차원

링 R은 최소 r - n이다. 링 R이 이 최소 경계에 도달하는 방식으로 표시될 수 있는 경우 완전한 교차 링이라고 한다.이 개념은 로컬 링에 대해서도 주로 연구되고 있습니다.일반 로컬 링은 완전한 교차 링이지만 그 반대는 아닙니다.

링 R은 R에 관련된 환원링, 즉 모든 nilpotent 원소를 분할하여 얻은 환이 완전교차라면 집합이론 완전교차이다.2017년 현재, 3차원 공간의 곡선이 설정 이론상 완전 ^[3]교차점인지 여부는 일반적으로 알려져 있지 않다.

코헨-맥컬리 링

로컬 링 R의 깊이는 최대_i 정규 시퀀스에 포함되는 요소의 수, 즉 모든 a가 0이 아닌_n 제수인 시퀀스₁ a, ..., µm입니다.

어떤 지역 노에테르 조직에서도 불평등은

홀드(holds). 평등이 일어나는 로컬 링을 코헨-맥컬리 링이라고 합니다.로컬 완전 교차 링과 포트리오리 정규 로컬 링은 Cohen-Macaulay이지만 그 반대는 아닙니다.Cohen-Macaulay는 정규 링의 바람직한 특성(예: 보편적으로 현수 링이라는 특성, 즉 소수의 (co) 치수가 잘 동작한다는 의미)을 결합하지만, 또한 일반 국소 ^[4]링보다 인용률에서 더 강력하다.

가환환 구성 중

주어진 링으로 새로운 링을 만드는 방법은 여러 가지가 있습니다.이러한 구성의 목적은 종종 링의 특정 특성을 개선하여 링을 보다 쉽게 이해할 수 있도록 하는 것입니다.예를 들어, 분수 영역에서 일체적으로 닫힌 적분 영역을 정규 영역이라고 합니다.이것은 바람직한 속성입니다.예를 들어 일반 1차원 링은 반드시 규칙적입니다.링을^{[clarification needed]} 정규화하는 것을 정규화라고 합니다.

완료

만약 내가 교환환 R의 이상이라면, I의 거듭제곱은 R을 위상환으로 볼 수 있는 0의 위상 근방을 형성한다.이 토폴로지를 I-adic 토폴로지라고 부릅니다.다음으로 이 토폴로지에 관해 R을 완료할 수 있습니다.형식적으로 I-adic 완성은 링 Rⁿ/I의 역한계이다.예를 들어, k가 필드인 경우, k[X] 위의 하나의 변수에 있는 형식 멱급수환인 k[X]는 K[X]의 I-adic 완성이며, 여기서 I는 X에 의해 생성된 주 아이디얼이다.이 고리는 디스크의 대수적 유사체 역할을 합니다.마찬가지로 p-adic 정수의 고리는 주 아이디얼(p)에 대한 Z의 완성이다.자신의 완성도와 동형인 링을 완전이라고 부릅니다.

완전한 국소 고리는 헨젤의 보조합(lema)을 충족하며, 대략적으로 말하면 잔기장 k에서 R까지 (다양한 문제의) 해법을 확장할 수 있다.

호몰로지 개념

가환환의 몇 가지 더 깊은 측면이 호몰로지 대수의 방법을 사용하여 연구되었다.Hochster(2007)는 이 분야의 활발한 연구에 대한 몇 가지 미해결 질문을 열거하고 있다.

투영 모듈 및 Ext 펑터

투영 모듈은 자유 모듈의 직접 합계가 되도록 정의할 수 있습니다.R이 로컬인 경우 최종 생성된 투영 모듈은 실제로 무료이며, 투영 모듈과 벡터 ^[5]번들 간의 유추에 콘텐츠를 제공합니다.퀴렌-수슬린 정리는 k[T₁, ..., T_n] (k a field)에 대해 최종적으로 생성된 투영 모듈은 자유롭다고 주장하지만, 일반적으로 이 두 개념은 다르다.로컬 노이더 링은 글로벌 치수가 유한한 경우에만 규칙적이다(예를 들어 n). 즉, 최종적으로 생성된 R-모듈은 최대 n개의 길이의 투영 모듈에 의한 분해능을 가진다.

이 문장과 기타 관련 문장의 증명은 Ext 펑터 등의 호몰로지 메서드의 사용에 의존합니다.이 펑터는 펑터의 파생 펑터입니다.

후자의 펑터는 M이 투영적인 경우에는 정확하지만, 그렇지 않은 경우에는 정확하지 않다. 즉, R-모듈의 주관적 지도 E → F의 경우, 지도 M → E로 확장될 필요가 없다.로 확장될 필요가 없다.Ext 함수가 높을수록 홈 함수의 부정확성을 측정합니다.호몰로지 대수학에서 이 표준 구조의 중요성은 잔기장 k를 갖는 국소 노에테르 고리 R이 규칙적이라는 사실에서 확인할 수 있다.

충분히 큰 n에 대해 사라집니다.또한 Betti 수치로 알려진 이러한 Ext-groups의 치수는 R이 국소 완전 교차 ^[6]링인 경우에만 n에서 다항식으로 증가한다.이러한 고려사항의 주요 논거는 Koszul 복합체이며, 이는 규칙적인 시퀀스의 관점에서 로컬 링 R의 잔류 필드 k의 명시적인 자유 분해능을 제공한다.

평탄도

텐서 곱은 가환환의 맥락에서 관련된 또 다른 비정밀 함수이다: 일반적인 R 모듈 M의 경우, 함수는

정확할 뿐입니다.정확히 말하면, M은 플랫이라고 불립니다.R이 로컬인 경우 최종적으로 제시된 플랫모듈은 유한 랭크가 없기 때문에 투사적입니다.호몰로지 대수학의 관점에서 정의되었음에도 불구하고, 평탄성은 기하학적 함의를 가지고 있다.예를 들어 R대수 S가 평면일 경우 파이버의 치수는

(R의 소수 이상 p의 경우)는 "예상" 치수, 즉 Dim S - dim R + dim (R/p)를 가진다.

특성.

웨더번의 정리에 따르면, 모든 유한 나눗셈 고리는 가환이며, 따라서 유한장입니다.제이콥슨에 의한 링의 교환성을 보증하는 또 다른 조건은 다음과 같습니다.R의 모든 요소 r에 대해 r =^[7] r이 되는ⁿ 정수 n > 1이 존재합니다.만약 r² = r이 모든 r에 대해 링을 부울링이라고 부릅니다.링의 교환성을 보증하는 보다 일반적인 조건도 ^[8]알려져 있습니다.

일반화

계단식 치환환

등급환 R = _i∊Zδ_i R은 등급환 a 및 b에 대해 등급환이라고 한다.

R이_i 차분에 의해 연결되어 있는 경우, 즉, 제품 규칙의 추상적인 형태가 유지되도록 한다.

R을 교환 미분 등급 대수(cdga)라고 합니다.예를 들어, 다지관상의 미분 형태의 복합체는 외부 곱에 의해 주어지는 곱셈과 함께 cdga이다.cdga의 코호몰로지는 단계별 교환환이며, 코호몰로지 링이라고도 합니다.등급링의 광범위한 예는 이러한 방식으로 발생합니다.예를 들어, 라자드 고리는 복잡한 다양체의 코보디즘 클래스의 고리이다.

Z/2(Z가 아닌)에 의한 등급 부여에 관한 등급 부여-환환(graded-commative ring)을 슈퍼대칭환이라고 한다.

관련 개념은 거의 가환환입니다.즉, R은 관련된 등급링과 같은 방식으로 필터링됩니다.

가환적입니다.한 예로 와일 대수와 미분 연산자의 더 일반적인 고리가 있다.

단순 가환환

단순환이란 단순환의 범주에 속하는 단순물체이다.이들은 (접속형) 유도 대수기하학을 위한 구성 블록입니다.밀접하게_∞ 관련되어 있지만 보다 일반적인 개념은 E-링입니다.

교환 링의 적용

• 정칙함수
• 대수적 K이론
• 위상 K 이론
• 분할된 전력 구조
• 위트 벡터
• 헤케 대수(와일스의 페르마의 마지막 정리 증명에 사용)
• 퐁텐의 생리가 울리다
• 군집 대수
• (가환군의) 컨볼루션 대수
• 프레셰 대수

「 」를 참조해 주세요.

• 거의 링, 교환 링의 특정 일반화
• 나눗셈성(링 이론): 0의 소자(예: 이중수)
• 이상과 모듈: 이상, 모리타 등가의 급진
• 고리 동형사상: 적분요소: 케일리-해밀턴 정리, 적분폐역, 크럴 고리, 크럴-아키즈키 정리, 모리-나가타 정리
• 소수점: 소수 회피 보조군, 제이콥슨 래디컬, 링의 Nilradical, 스펙트럼:콤팩트 공간, 연결 고리, 교환 대수에 대한 미적분, 바나흐-스톤 정리
• 로컬 호출음:고렌슈타인 국소환(와일스의 페르마의 마지막 정리 증명에도 사용):이원성(수학), 에벤 매틀리스, 이원화 모듈, 포페스쿠 정리, 아르탱 근사 정리.

메모들

인용문

레퍼런스

추가 정보