복소수

이 문서는 확인을 위해 추가 인용이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주시기 바랍니다. 소스가 없는 재료는 문제가 발생하여 제거될 수 있습니다.출처 찾기: "복잡한 번호" – 뉴스, 신문, 책, 학자, JSTOR (2022년 7월) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

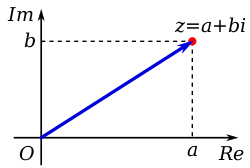
복소수(a數, ) 또는 복소수(number數, )는 수학에서 실수를 확장하는 수 체계의 요소로, 허수 단위라고 하며, 방정식 i2 = -1을 만족시킨다.위의 방정식을 만족시키는 실수가 없기 때문에 르네 데카르트는 i를 허수라고 불렀습니다.$복소수{\displaystyle }$a +$$ {\$displaystyle$ a$+bi$의 경우, a를 실수부라고 하고, b를 허수부라고 합니다.복소수 집합은 기호 ${$ 또는 C 중 하나로 표시됩니다.역사적인 명명법 "상상"에도 불구하고, 복소수는 수학 과학에서 실수만큼 "실제"로 간주되고 자연계의 ^[1][a]과학적 설명의 많은 측면에서 기본적입니다.

복소수는 실수로 해가 없는 경우에도 모든 다항식 방정식에 대한 해를 허용합니다.더 정확하게 말하면, 대수의 기본 정리는 실수 또는 복소수 계수를 갖는 모든 상수 다항식 방정식이 복소수인 해를 갖는다고 주장합니다.예를 들어$,{\displaystyle }$ ${\displaystyle \mathrm{실수}}$의 제곱이 음수일 수 없기 때문에 방정식${\displaystyle }$(${\displaystyle \mathrm{x}{}^{}}$+ ${\displaystyle {1\mathrm{}}^{}}$ ) 2$=$- ${\displaystyle 9}$ \ \ \ \ $displaystyle$($x$ + $1$$)^{2$}=-$9}$은 실제 해가 없지만$,{\displaystyle }$ 두 ${\displaystyle 개}$의$비실체$ 복소${\displaystyle }$해 - ${\displaystyle 1}$ + 3$$${\displaystyle i}$와 - 1${\displaystyle }$- 3$$i \$$$displaystyle$ - 1 - $3$i를 가지고 있습니다.

복소수의 더하기, 빼기 및 곱하기는 연관, 교환 및 분배 법칙과 결합된 $규칙{\displaystyle {}^{}}$ $=$ -$$ {{$displaystyle$ i$^{2$}=-$1}$을 사용하여 자연스럽게 정의할 수 있습니다.0이 아닌 모든 복소수에는 곱셈 역수가 있습니다.이렇게 하면 복소수가 실수를 하위 필드로 갖는 필드가 됩니다.복소수는 또한 {1, i}를 기준으로 2차원의 실제 벡터 공간을 형성합니다.

이 표준 기준은 복소수를 복소수 평면이라고 하는 데카르트 평면으로 만듭니다.이를 통해 복소수와 그 연산에 대한 기하학적 해석이 가능하며, 역으로 복소수의 기하학적 특성과 구조를 표현할 수 있습니다.예를 들어, 실수는 복소 평면의 수평 축으로 식별되는 실수 선을 형성합니다.절대값 1의 복소수는 단위 원을 형성합니다.복소수의 덧셈은 복소수 평면에서의 변환이고 복소수에 의한 곱셈은 원점을 중심으로 한 유사성입니다.복소 켤레는 실제 축에 대한 반사 대칭입니다.복소수 절대값은 유클리드 노름입니다.

요약하면, 복소수는 대수적으로 닫힌 장, 실수에 대한 교환 대수, 2차원의 유클리드 벡터 공간인 풍부한 구조를 동시에 형성합니다.

정의.

복소수는 a + bi 형식의 수이며, 여기서 a와 b는 실수이고, i는 i = -1을 만족하는² 불확정치입니다.예를 들어, 2 + 3i는 ^[3]복소수입니다.

이런 식으로, 복소수는 i + 1 = 0 관계가² 부과되는 단일 불확정 i에서 실수 계수를 갖는 다항식으로 정의됩니다.이 정의에 따라 다항식에 대한 덧셈과 곱셈을 사용하여 복소수를 추가하고 곱셈할 수 있습니다.i + 1 = 0 관계는² 모든 정수 k에 대해 유지되는 등식^4k i = 1, i^4k+1 = i^4k+2, i = -1^4k+3 및 i = -i를 유도합니다. 이것들은 복소수의 추가와 곱셈으로 인해 발생하는 다항식을 i에서 실수 계수 a, b와 함께 a + b의 형태로 다시 감소시킬 수 있습니다.

실수 a는 복소수 a + bi의 실수 부분이라고 불리고 실수 b는 그것의 가상 부분이라고 불립니다.강조하기 위해 가상 부분에는 인수 i가 포함되지 않습니다. 즉, 가상 부분은 ^[4][5]b가 아니라 b입니다.

공식적으로, 복소수는 다항식 i² + 1에 의해 생성된 이상에 의해 불확정 i에서 다항식 링의 몫 링으로 정의됩니다(아래 ^[6]참조).

표기법

실수 a는 가상 부분이 0인 복소수 a + 0i로 간주될 수 있습니다.순수 가상 수 bi는 실수 부분이 0인 복소수 0 + bi입니다.다항식과 마찬가지로 a + 0i는 a이고 bi는 0 + bi는 b로 쓰는 것이 일반적입니다.또한, 가상 부분이 음수일 때, 즉 b = - b < 0일 때, a + (-b)i 대신에 - bi를 쓰는 것이 일반적입니다. 예를 들어, b = -4의 경우, 3 + (-4)i 대신에 3 - 4i를 쓸 수 있습니다.

불확정 i와 실수의 곱은 실수 계수를 가진 다항식에서 교환적이기 때문에, 다항식 a + bi는 + ib로 쓸 수 있습니다.예를 들어 b가 ^[7]라디칼인 경우 식으로 표시되는 가상 부분에 대해 이 방법이 유용합니다.

복소수 z의 실제 부분은 Re(z), Re(z)({mathcal {Re}}(z) 또는 R(z)({mathfrak {R}}(z)로 표시되며, 복소수 z의 가상 부분은 Im(z), Im(z)(z)({mathcal {I})로 표시된다.예를$$ 들면,

모든 복소수의 집합은 C${$흑판 굵기) 또는 C(직립 굵기)로 표시됩니다.

일부 분야, 특히 전자기학과 전기 공학에서 i는 ^[8][9]전류를 나타내는 데 자주 사용되기 때문에 i 대신 j가 사용됩니다.이 경우 복소수는 + bj 또는 + jb로 기록됩니다.

시각화

따라서 복소수 z는 실수의 순서쌍$({\displaystyle \mathrm{\Delta }}$(${\displaystyle z),\mathrm{\Delta }}$ (${\displaystyle z)}$) \$displaystyle$(\$Re (z),$ \$Im (z)}$으로 식별될 수 있으며, 이는 다시 2차원 공간에서 점의 좌표로 해석될 수 있습니다.가장 가까운 공간은 적절한 좌표를 가진 유클리드 평면이며, 이를 장-로버트 아르간드의 이름을 딴 복소 평면 ^[10][b][11]또는 아르간드 다이어그램이라고 합니다.좌표가 투영될 수 있는 또 다른 두드러진 공간은 구면의 2차원 표면이며, 구면은 리만 구라고 불립니다.

데카르트 복소면

두 개의 임의의 실수 값을 포함하는 복소수의 정의는 복소수 평면에서 데카르트 좌표의 사용을 즉시 제안합니다.수평(실제) 축은 일반적으로 실제 부분을 표시하는 데 사용되며, 오른쪽으로 값이 증가하고, 가상 부분은 수직(상상) 축을 표시하고 위쪽으로 값이 증가합니다.

차트화된 숫자는 좌표화된 점 또는 원점에서 이 점까지의 위치 벡터로 볼 수 있습니다.따라서 복소수 z의 좌표 값은 데카르트, 직사각형 또는 대수적 형태로 표현될 수 있습니다.

특히, 덧셈과 곱셈의 연산은 복소수를 위치 벡터로 볼 때 매우 자연스러운 기하학적 특성을 취합니다. 덧셈은 벡터 덧셈에 해당하는 반면, 곱셈(아래 참조)은 크기를 곱하고 실제 축으로 만드는 각도를 추가하는 것에 해당합니다.이와 같이 볼 때, 복소수를 i로 곱하는 것은 원점에 대해 반시계방향으로 위치 벡터를 4분의 1 회전(90°) 회전시키는 것에 해당합니다.

극복합체 평면

계수와 인수

복소 평면의 좌표에 대한 대안적인 옵션은 원점(O)에서 점 z의 거리와 시계 반대 방향으로 양의 실축과 선분 Oz 사이에 있는 각도를 사용하는 극좌표계입니다.이는 극 형태로 이어집니다.

${\displaystyle z=re^{i\varphi}=r(\cos \varphi +i\sin \varphi )}$

복소수의, 여기서 r은 z의 절대값이고, ${{displaystyle \varphi}$는 z의 인수입니다.

복소수 z = x + yi의^[12] 절대값(또는 계수 또는 크기)은

z가 실수인 경우(즉, y = 0인 경우), r = x입니다. 즉, 실수의 절대값은 복소수로서 절대값과 같습니다.

피타고라스 정리에 따르면, 복소수의 절대값은 복소수 평면에서 복소수를 나타내는 점의 원점까지의 거리입니다.

z의 인수(많은 응용 분야에서 "위상" ^[11]θ라고 함)는 양의 실수 축을 갖는 반지름 Oz의 각도이며, argz로 기록됩니다.계수와 마찬가지로, 인수는 x + yi^[13] 직사각형 형식에서 찾을 수 있습니다. 즉, 가상의 실제 부분에 대한 몫에 역접선을 적용하면 됩니다.반각 항등식을 사용함으로써, 아크탄의 단일 분기는 arg 함수의 범위(-θ, θ)를 커버하기에 충분하며, 더 미묘한 케이스 바이 케이스 분석을 피할 수 있습니다.

일반적으로 위에서 설명한 대로 구간의 주 값(-π, π)이 선택됩니다.arg 값이 음수인 경우 2µ를 더하면 범위(-π, π] 또는 [0, 2µ]의 값을 얻을 수 있습니다.이 글에서는 φ의 값을 라디안으로 표현하고 있습니다.그것은 2θ의 정수 배수만큼 증가할 수 있으며, 양의 실제 축의 광선과 원점에서 z까지의 범위에서 소숫점으로 보이는 동일한 각도를 제공합니다.따라서 arg 함수는 때때로 다중값으로 간주됩니다.복소수 0에 대한 극각은 불확실하지만 극각 0의 임의 선택은 일반적입니다.

φ의 값은 an2의 결과와 같습니다.

계수와 인수의 조합이 평면에서 점의 위치를 완전히 지정하기 때문에, r과 π는 복소수를 나타내는 또 다른 방법인 극형을 제공합니다.극형으로부터 원래의 직사각형 좌표를 복구하는 것은 삼각형이라고 불리는 공식에 의해 이루어집니다.

오일러의 공식을 사용하여 다음과 같이 쓸 수 있습니다.

cis 함수를 사용하여, 이것은 때때로 다음과 같이 축약됩니다.

전자 공학에서 종종 진폭 r과 위상 π를 갖는 위상을 나타내기 위해 사용되는 각도 표기법에서는 다음과 같이 기록됩니다^[14].

복잡한 그래프

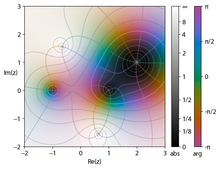
복잡한 기능을 시각화할 때는 복잡한 입력과 출력이 모두 필요합니다.각 복소수는 2차원으로 표현되기 때문에 복소수 함수를 시각적으로 그래프화하려면 투영에서만 가능한 4차원 공간의 인식이 필요합니다.이 때문에 복잡한 기능을 시각화하는 다른 방법이 설계되었습니다.

도메인 색상에서 출력 치수는 각각 색상과 밝기로 표시됩니다.도메인으로서의 복소수 평면의 각 점은 일반적으로 복소수의 인수를 나타내는 색상과 크기를 나타내는 밝기로 장식됩니다.어두운 점은 0 근처에 모듈리를 표시하고 밝은 점은 원점에서 더 멀리 떨어져 있으며, 눈금은 불연속적일 수 있지만 단조로운 것으로 가정됩니다.색상은 빨간색, 노란색, 녹색, 청록색, 파란색에서 자홍색에 이르기까지 0~2도에 대해 π/3 단계로 다양합니다.이러한 그림을 컬러 휠 그래프라고 합니다.이것은 정보를 잃지 않고 기능을 시각화할 수 있는 간단한 방법을 제공합니다.그림은 ±1, (2 + i)의 0과${\displaystyle \sqrt{}}$±${\displaystyle \sqrt{2}}$-${\displaystyle \sqrt{\mathrm{2i}}}$의${\displaystyle }$극을 보여줍니다$.$ \$pm \sqrt${-$2-2i}.$

역사

일반적인 입방 방정식의 라디칼(삼각함수가 없는)에서의 해는, 그 세 근이 모두 실수일 때, 음의 수의 제곱근을 포함하며, 이는 합리적인 근 검정의 도움을 받아 인수 분해하여 수정할 수 없는 상황입니다.입방체가 환원 불가능한 경우; 이것은 소위 카수스 환원 불가능한 경우("환원 불가능한 경우")입니다.이 난제는 이탈리아 수학자 제롤라모 카르다노가 1545년경 ^[15]아르스 마그나에서 복소수를 구상하도록 유도했지만, 비록 그의 이해는 초보적이었지만, 그는 나중에 복소수를 "^[16]쓸데없는 만큼 미묘하다"고 묘사했습니다.카다노는 가상의 숫자를 사용했지만, 그것들을 "정신적 고문"^[17]이라고 묘사했습니다.이는 그래픽 복합 평면을 사용하기 전의 것입니다.카르다노와 다른 이탈리아 수학자들, 특히 스키피오네 델 페로는 1500년대에 일반적으로 하나의 실제 해와 가상의 숫자를 포함하는 두 개의 해를 가진 입방 방정식을 풀기 위한 알고리즘을 만들었습니다.그들이 가상의 숫자가 있는 답을 무시했기 때문에, 카르다노는 그것들이 ^[18]쓸모없다는 것을 알았습니다.

일반 다항식 문제에 대한 연구는 궁극적으로 대수의 근본적인 정리로 이어졌는데, 이는 복소수와 함께 1도 이상의 모든 다항식 방정식에 대한 해가 존재한다는 것을 보여줍니다.따라서 복소수는 모든 다항식이 근을 갖는 대수적으로 닫힌 필드를 형성합니다.

많은 수학자들이 복소수의 발전에 기여했습니다.복소수의 덧셈, 뺄셈, 곱셈, 그리고 근 추출에 대한 규칙은 이탈리아 수학자 라파엘 봄벨리에 ^[19]의해 개발되었습니다.복소수에 대한 보다 추상적인 형식주의는 아일랜드 수학자 윌리엄 로언 해밀턴에 의해 더욱 발전되었으며, 그는 이 추상화를 쿼터니언 ^[20]이론으로 확장했습니다.

음의 제곱근에 대한 최초의 일시적인 언급은 기원후 1세기에 그리스 수학자 알렉산드리아의 헤로의 작업에서 발생할 수 있는데, 그는 그의 스테레오메트리에서 81 - 144라는 용어에 도달하기 위한 불가능한 피라미드의 부피를 분명히 오류가 있다고 생각했다헤로는 ${\displaystyle \sqrt{\mathrm{오늘날}}}$ -63 ${\displaystyle =}$ ${\displaystyle 3}$ ${\displaystyle i\sqrt{\mathrm{}}}$7 \ $displaystyle${\ sqrt {-$63$}= $3i sqrt {7$로 단순화할 것이라고 $계산$했습니다. 음의 양은 헬레니즘 수학에서 생각되지 않았고 단지 양 ${\displaystyle \sqrt{144}}$ ${\displaystyle \sqrt{-}}$ ${\displaystyle \sqrt{81}}$ = ${\displaystyle 37\sqrt{\mathrm{}}}$. \ $displaystyle {sqrt${-$81$}=$3i sqrt$sqrt {$7}$로 대체했을 뿐입니다.$}$^[21]

복소수를 주제로 연구하려는 추진력은 16세기에 이탈리아 수학자들(니콜로 폰타나 타르탈리아와 제롤라모 카르다노)에 의해 입방 다항식과 사차 다항식의 근에 대한 대수적 해법이 발견되었을 때 처음으로 나타났습니다.이러한 공식이 실제 솔루션에만 관심이 있더라도 때때로 음수의 제곱근의 조작이 필요하다는 것을 곧 깨달았습니다(그러나 훨씬 ^[22]나중에 증명되었습니다).사실, 이 세 뿌리가 ^[c]모두 실재하고 구별되는 경우 복소수의 사용은 피할 수 없다는 것은 나중에 증명되었습니다.그러나 일반 공식은 0이 아닌 복소수에 대한 3개의 입방근의 존재로 인한 모호성을 처리하기 위해 여전히 사용될 수 있습니다.라파엘 봄벨리는 처음으로 입방 방정식의 역설적인 해결책을 명시적으로 다루었고 복잡한 산술을 위한 규칙을 개발하여 이러한 문제를 해결하려고 노력했습니다.

이러한 양에 대한 "상상적"이라는 용어는 1637년 르네 데카르트에 의해 만들어졌는데,^[23] 그는 그들의 비현실성을 강조하기 위해 고심했습니다.

때때로 상상 속에서만, 그것은 내가 각 방정식에서 말한 만큼 상상할 수 있지만, 때때로 우리가 상상하는 것과 일치하는 양이 존재하지 않습니다.
[... quelquefois seule imaginer i'est-a-dire l'on peut toujours an autant quaidit quaque quéquéqué, mais qu'ill'y quéquén'y quéquén'on quéimaginage는 quene에 해당하는 오쿠네 quite quécelle qué에 해당합니다.]

또 다른 혼란의 원인은 방정식 - 12 = - 1 = - 1 \ \ \ displaystyle {\ sqrt {-1}^ {2}= displaysqrt {-1}= - 1이 음이 아닌 실수와 b에 유효한 대수적 동일성 a = a \ sqrt {b}= displaystyle {-1}와 변덕스럽게 일치하지 않는 것처럼 보인다는 것이다a, b 양의 값과 음의 값 중 하나를 사용한 플렉스 수 계산.a와 b가 모두 음수인 경우에 이 동일성을 잘못 사용하고, $관련\frac{\mathrm{}}{}$ $\frac{\sqrt{동일성}}{}$ 1 $=$ $\sqrt{\frac{1}{}}$ a ${\${1}{\sqrt {a}}=$sqsqrt {frac {1}{a$ 심지어는 레온하르트 오일러도 마찬가지입니다.이러한 어려움은 결국 이러한 ^{[citation needed]}실수를 방지하기 위해 $({${-$1}})$대신$$ 특수 기호를 사용하는 관례로 이어졌습니다.그럼에도 불구하고, 오일러는 오늘날 우리보다 훨씬 더 일찍 학생들에게 복소수를 소개하는 것이 당연하다고 생각했습니다.그의 초등 대수 교과서인 대수학의 요소에서, 그는 이 숫자들을 거의 동시에 소개하고 내내 자연스러운 방식으로 사용합니다.

18세기에 복소수는 삼각함수를 포함하는 계산을 단순화하기 위해 복소수의 공식적인 조작이 사용될 수 있다는 것이 주목받으면서 더 광범위하게 사용되었습니다.예를 들어, 1730년에 아브라함 드 모브레는 각도의 정수 배수의 삼각함수와 그 각도의 삼각함수의 거듭제곱과 관련된 항등식을 다음과 같은 드 모브레의 공식으로 다시 표현할 수 있다고 언급했습니다.

1748년 오일러는 더 나아가 오일러의 복소해석 ^[24]공식을 얻었습니다.

복잡한 멱급수를 공식적으로 조작함으로써 이 공식이 삼각형 동일성을 훨씬 더 단순한 지수 동일성으로 줄이는 데 사용될 수 있다는 것을 관찰했습니다.

복소수의 개념은 덴마크-노르웨이 수학자 카스파르 베셀에 의해 1799년에 ^[25]처음 기술되었다.^[26]

베셀의 회고록은 코펜하겐 아카데미의 회의록에 등장했지만 대부분 주목받지 못했습니다.1806년에 장-로버트 아르간드는 독자적으로 복소수에 대한 팜플렛을 발행했고 ^[27]대수학의 기본 정리에 대한 엄격한 증명을 제공했습니다.카를 프리드리히 가우스는 1797년에 근본적으로 위상학적인 증명을 발표했지만 당시 "-^[28]1의 제곱근의 진정한 형이상학"에 대해 의문을 표명했습니다.1831년이 되어서야 그는 이러한 의심을 극복하고 ^[29]복소수에 대한 논문을 평면의 점으로 출판하여 현대의 표기법과 ^[30]용어를 확립했습니다.

만약 누군가가 이전에 이 주제를 잘못된 관점에서 생각했고 따라서 신비한 어둠을 발견했다면, 이것은 대부분 어설픈 용어 때문입니다.+1, -1$,{\displaystyle \sqrt{}}$ $,$ -1({$displaystyle {sqrt$ {-$1}})$의 양의, 음의, 상상의(또는 불가능한) 단위가 아닌 직접, 역의, 또는 측면 단위가 있었다면 그러한 어둠에 대한 이야기는 거의 없었을 것입니다.

19세기 초, 다른 수학자들은 복소수의 기하학적 표현을 독립적으로 발견했습니다.부에,^[31][32] 모레이,^{[33] [34][35][36]}워렌, 프랑세즈 그리고 그의 형제 벨라비스.^[37][38]

영국의 수학자 G.H.Hardy는 가우스가 1831년 ^[39]논문을 발표하기 전에 노르웨이의 닐스 헨리크 아벨과 칼 구스타프 제이콥 야코비와 같은 수학자들이 반드시 그것들을 일상적으로 사용했음에도 불구하고 가우스가 "정말 자신 있고 과학적인 방법으로" 복소수를 사용한 최초의 수학자라고 언급했습니다.

오거스틴-루이 코시와 베른하르트 리만은 복합 분석의 기본적인 아이디어를 높은 완성도의 상태로 가져왔고, 코시의 경우 1825년경에 시작되었습니다.

이론에서 사용되는 일반적인 용어는 주로 창시자들에 의한 것입니다.cos φ + i는 방향 인자 φ에 $있고{\displaystyle }$, r $=$ ${\displaystyle \sqrt{{a\mathrm{}}^{}}}$2 + ${\displaystyle \sqrt{{}^{}}}$ {$displaystyle$ r = {\$sqrt {a^{2}$ + $b^{2$}라고 하는 Argand계수;^[d][40] 코시 (1821)는 cos φ + is in을 축소된 형태 (l'expression reduite)^[41]라고 불렀고, 명백하게 인수라는 용어를 도입했다; 가우스는 i를 $-1({$sqrt {-^[f]$1$^[e]에 사용했고, a + bi에² 대한 용어 복소수를 도입했으며,^[g] a + b를 표준이라고 불렀습니다².종종 φ에서 cos φ + i에 사용되는 표현 방향 계수는 Hankel(1867)^[45]에 의한 것이고, 계수에 대한 절대값은 Weierstrass에 의한 것입니다.

일반 이론에 대한 후기 고전 작가들에는 리하르트 데데킨트, 오토 ld더, 펠릭스 클라인, 앙리 푸앵카레, 헤르만 슈바르츠, 카를 바이어슈트라스 등이 있습니다.복잡한 다변량 미적분학의 중요한 작업(체계화 포함)은 20세기 초에 시작되었습니다.중요한 결과는 1927년 빌헬름 비팅거에 의해 달성되었습니다.

관계 및 운영

평등

복소수는 실수와 유사한 정의를 갖습니다. 두 개의 복소수₁ a₂ + b와₁₂ a + b는 실수와 가상 부분이 모두 동일한 경우에만 동일합니다. 즉₁, a₂ = a와₁ b₂ = b입니다.극형으로 작성된 0이 아닌 복소수는 크기가 같고 인수가 2π의 정수 배수로 다를 경우에만 동일합니다.

주문

실수와 달리, 복소수의 자연스러운 순서는 없습니다.특히, 덧셈 및 곱셈과 호환되는 복소수에는 선형 순서가 없습니다.따라서 복소수는 정렬된 필드의 구조를 갖지 않습니다.이에 대한 한 가지 설명은 순서가 지정된 필드의 모든 제곱합이 0이 아니며² i² + 1 = 0은 제곱합이 아니라는 것입니다.따라서, 복소수는 자연스럽게 2차원 평면에 존재하는 것으로 생각됩니다.

켤레

복소수 z = x + yi의 복소 공역은 x - yi로 주어집니다.그것은 z 또는 z*^[46]로 표시됩니다.복소수에 대한 이 단항 연산은 기본 연산 덧셈, 뺄셈, 곱셈 및 나눗셈만 적용하여 표현할 수 없습니다.

기하학적으로, z는 실제 축에 대한 z의 "반사"입니다.두 번 짝짓기를 하면 원래 복소수가 나옵니다.

이 작전을 혁명으로 만드는 거지반사는 실제 부분과 z의 크기를 모두 변경하지 않고 남습니다. 즉,

${\displaystyle 그리고\stackrel{}{}}$ z${\displaystyle \stackrel{}{}¯}$ $=$ ${\displaystyle z}$. \$displaystyle$\displaystyle \displaystyle {\$overline {z}$ = $z.$

가상 부분과 복소수 z의 인수는 켤레 아래에서 부호를 바꿉니다.

인수 및 크기에 대한 자세한 내용은 극성 양식의 섹션을 참조하십시오.

복소수 z = x + yi와 그 공역의 곱을 절대 제곱이라고 합니다.이것은 항상 음이 아닌 실수이며 각각의 크기의 제곱과 같습니다.

이 속성은 분수의 분자와 분모를 주어진 분모의 공역으로 확장하여 복소수 분모를 갖는 분수를 실제 분모를 갖는 동등한 분수로 변환하는 데 사용될 수 있습니다.이 과정은 분모의 단순한 표현에서 뿌리를 제거하는 방법과 유사하기 때문에 분모의 "합리화"라고 불리기도 합니다(최종 표현의 분모가 비합리적인 실수일 수도 있지만).

복소수 z의 실제 부분과 가상 부분은 다음과 같은 활용을 사용하여 추출할 수 있습니다.

또한 복소수는 자신의 공역과 같은 경우에만 실제입니다.

켤레는 기본적인 복잡한 산술 연산에 걸쳐 분포합니다.

컨쥬전은 선에 대한 반사보다 더 일반적인 반사를 연구하는 기하학의 한 분야인 반전 기하학에도 사용됩니다.전기 회로의 네트워크 분석에서, 복소 공역은 최대 전력 전달 정리를 찾을 때 등가 임피던스를 찾는 데 사용됩니다.

덧셈과 뺄셈

두 개의 $복소수{\displaystyle }$ a $=$ +$$ {$displaystyle$ a ${\displaystyle =}$$x+yi}$와 b $=$ +$$ {$displaystyle$ b =$u$+vi$}$는 실제 부분과 가상 부분을 별도로 추가하여 가장 쉽게 추가할 수 있습니다.즉, 다음과 같습니다.

마찬가지로, 뺄셈은 다음과 같이 수행될 수 있습니다.

$복소수{\displaystyle }$ a $=$ + ${\displaystyle y}$ $({displaystyle$ a=$x+yi})$와 실수 r의 곱셈은 다음과 같이 별도로 r과 실수 및 가상 부분을 곱하여 수행할 수 있습니다.

특히, 뺄셈은 (-1을 곱한) 부분 끝을 부정하고 결과를 분 끝에 추가함으로써 수행될 수 있습니다.

복소평면에서 복소수의 시각화를 이용하여, 덧셈은 다음과 같은 기하학적 해석을 갖습니다. 복소평면에서 점으로 해석되는 두 복소수 a와 b의 합은 3개의 꼭짓점 O로부터 평행사변형을 만들어 얻은 점이며, a와 b로 표시된 화살표의 점은 (만약 그것들이 아니다면)선 위에 t).동등하게, 이 점들을 각각 A, B, 그리고 평행사변형 X의 네 번째 점이라고 부르는 것은 삼각형 OAB와 XBA가 합동입니다.

곱셈과 제곱

분배 속성의 규칙, (더하기와 곱하기의) 교환 속성 및 정의 속성² i = -1은 복소수에 적용됩니다.따라서

특히,

역수와 나눗셈

공액을 사용하여 0이 아닌 $복소수{\displaystyle }$ z $=$ + ${\displaystyle y}$ i$({displaystyle$ z=$x+yi})$의 역수를 실제 성분과 가상 성분으로 나눌 수 있습니다.

이것은 임의의 $복소수{\displaystyle }$ w$=$ + ${\displaystyle \mathrm{vi}}${\$displaystyle$ w ${\displaystyle =}$$u$+vi$}$를 0이 아닌 $복소수{\displaystyle }$ z $=$ + ${\displaystyle y}${\$displaystyle$ z = $x+yi}$로 나눗셈하는 데 사용할 수 있습니다.

극형에서의 곱셈과 나눗셈

곱셈, 나눗셈 및 지수 공식은 데카르트 좌표의 해당 공식보다 극성 형태가 더 간단합니다.삼각형 항등식 때문에, 두₁ 개의 복소수 z = r(cos φ₁₂₂ + i sin φ₁)과₂ z = r₂(cos φ + i sin φ)이₁ 주어집니다.

우리는 도출할 수 있습니다.

즉, 절대값이 곱되고 인수가 추가되어 제품의 극성 형태가 생성됩니다.예를 들어 i를 곱하면 i² = -1을 반환하는 시계 반대 방향으로 1/4 회전하는 것에 해당합니다.오른쪽 그림은 다음의 곱셈을 보여줍니다.5 + 5i의 실수 부분과 가상 부분이 같기 때문에, 그 숫자의 인수는 45도 또는 π/4(라디안)입니다.반면에, 빨간색과 파란색 삼각형의 원점에 있는 각도의 합은 각각 아크탄(1/3)과 아크탄(1/2)입니다.따라서, 공식은홀드. 아크탄 함수는 매우 효율적으로 근사할 수 있기 때문에, 이와 같은 공식(마친 유사 공식이라고 함)은 π의 고정밀 근사에 사용됩니다.

마찬가지로, 나눗셈은 다음과 같습니다.

제곱근

a + bi의 제곱근은 ± (${\displaystyle \pi }$+ π${\displaystyle }$i$$) \${\displaystyle \mathrm{pm}}$ $(\gamma$+\$deltai)$이며$,$ 여기서

그리고.

여기서 sgn은 시그넘 함수입니다.이는 ${\displaystyle \pm (}$π${\displaystyle }$+ ${\displaystyle \pi }$i$$) \$displaystyle \pm(\gamma$+\$deltai)}$을${\displaystyle }$제곱하여 + ^[47][48]bi를 구하면 알 수 있습니다.$여기{\displaystyle \sqrt{{}^{}}}$ a ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$+ ${\displaystyle \sqrt{{}^{}}}$2 ${\displaystyle \sqrt{{표시\mathrm{}}^{}}}$ $스타일({sqrt {a^{2}+b^{2$})$a$ + bi의 계수라고 하며, 제곱근 기호는 음이 아닌 실수 부분이 있는 제곱근을 나타내며, 주 제곱근이라고도 합니다. $또한{\displaystyle \sqrt{{}^{}{}^{}}}$ + ${\displaystyle b2\sqrt{}\sqrt{{}^{}}}$= $¯,$ ${\sqrt {a^{2}+b^{2$} $표시$$}}}={zsqrt {z}},},$ 여기서 z = a + bi입니다.^[49]

지수함수

지수 ${\displaystyle \mathrm{함수}}$exp : ${\displaystyle C\mathbb{}}$→${\displaystyle C\mathbb{}}$ ; ${\displaystyle z}$ ${\displaystyle \mapsto }$ $⁡$ \ $displaystyle$ \$exp$\sigma $\mathbb {C} \to$ \$mathbb {C};z\mapsto \exp$z}는$$ 멱급수를 통해 모든 복소수 z에 대해 정의할 수 있습니다.

수렴 반경이 무한합니다.

지수 함수의 1에서의 값은 오일러의 수이다.

z가 실제인 경우 exp${\displaystyle }$⁡ $=$ ${\displaystyle {ez}^{}}$ ${\displaystyle {}^{}}${\$displaystyle$ \$exp$ z=$e^{$$z$}를 ${\displaystyle \mathrm{사용}}$합니다.해석적 연속성을 통해 z의 모든 복소수 값에 대해 이 동일성을 확장할 수 있으며, 따라서 기저 e를 사용하여 복소수 지수를 정의할 수 있습니다$$.

함수 방정식

지수 함수는 함수 $방정식{\displaystyle {}^{}}$ ${\displaystyle {ez}^{}}$+ $=$ ${\displaystyle {ez}^{}}$.$$\ $displaystyle$ e$^{z+t$}= e$^{z}e^{t}$를 만족합니다.이는 두 구성원의 검정력 시리즈 확장을 비교하거나 방정식의 제한에서 실제 인수까지 분석 연속성을 적용하여 증명할 수 있습니다$$.

오일러 공식

오일러의 공식은 임의의 실수에 대해 다음과 같이 말합니다.

따라서 함수 방정식은 x와 y가 실수라면 다음과 같은 것을 의미합니다.

이것은 지수 함수를 실제 부분과 가상 부분으로 분해하는 것입니다.

복소 로그

실제의 경우, 자연 로그는 지수 ${\displaystyle \mathrm{함수}}$의 역${\displaystyle {}^{}}$: R +${\displaystyle {}^{}\to }$ ${\displaystyle R}$; ${\displaystyle x}$ $⁡$ ln $ln$ \$displaystyle$\displaystyle \displaystyle \$dathbb {R}^{+}\to \mathbb {R};x\mapsto \desx}$로 정의될 수 있습니다.이를 복소 영역으로 확장하기 위해 오일러의 공식에서 시작할 수 있습니다.이는 ${\displaystyle {\mathbb{}}^{}}$ $∈$ C × \$displaystyle$z\$in \mathbb${C$}^{\$times$$}가$$ 극형으로 쓰인다는 것을 의미합니다.

$r{\displaystyle ,}$ ${\displaystyle \phi \mathbb{}}$∈ R$,$ \$displaystyle$ r, \$varphi \in \mathbb {R},$ 다음으로$$복소수 로그는 적절한 역수를 갖습니다.

그러나 코사인과 사인은 주기적인 함수이므로 2µ에서 µ의 정수 배수를 추가해도 z는 변경되지 않습니다.예를 들어, e^iπ3iπ = e = -1이므로 iπ와 3iπ 모두 -1의 자연 로그에 대해 가능한 값입니다.

따라서 복소수 로그를 다중값 함수로 정의하지 않을 경우

분기 절단을 사용하고 코도메인을 제한하여, 결과적으로 목적 함수를 생성해야 합니다.

$만약{\displaystyle }$ z ${\displaystyle {}_{}}$ ${\displaystyle C\mathbb{}\setminus }$ ( - ${\displaystyle {\mathrm{R}}_{}}$ ${\displaystyle {}_{}}$ 0 )$$\$displaystyle$ z$\in \mathbb {C}$ \$setminus \left(-\mathbb {R}_{\geq$ 0$}\$right)}가$$ 양의 실수(양의 실수 또는 비실수)가 아니라면, 복소수 로그의 결과 주 값은 - π < φ>로 구할 수 있습니다.이 함수는 음수 실수 외부의 분석 함수이지만, 어떤 음수 $실수{\displaystyle }$z∈ -${\displaystyle {\mathbb{}}^{}}$+ \$displaystyle$z\$in -\mathbb {R$에서 연속적인 함수로 연장할 수 없습니다. 여기서 주 값은 lnz = ln(-z) + ^[h]iπ입니다.

지수화

만약 x > 0이 실수이고 z가 복잡하다면, 지수는 다음과 같이 정의됩니다.

여기서 ln은 자연 로그를 나타냅니다.

이 공식을 x의 복소수 값으로 확장하는 것은 당연해 보이지만 복소수 로그가 실제로 함수가 아니라 다중값 함수라는 사실로 인해 발생하는 몇 가지 어려움이 있습니다.

따라서 만약 z가 위와 같다면, 그리고 그것이 다른 복소수라면, 지수는 다중값 함수입니다.

정수 및 분수 지수

앞의 공식에서 t가 정수이면 사인과 코사인은 k와 독립적입니다.따라서, 만약 지수 n이 정수라면, z는ⁿ 잘 정의되고, 지수 공식은 드 모이브르의 공식으로 단순화됩니다.

복소수 z의 n번째 근은 다음과 같습니다.

0 ≤ k ≤ n - 1에 대하여. (${\displaystyle \text{exception 25:}}$서$${$n}{$r}}은 양의 실수 r의 일반적인 (양의) n번째 근이다.)사인과 코사인은 주기적이기 때문에 k의 다른 정수 값은 다른 값을 제공하지 않습니다.

양의 실수 r의 n번째 근이 c = r을 만족하는ⁿ 양의 실수 c가 되도록 선택되는 반면, 복소수의 특정 복소수 n번째 근을 구별하는 자연스러운 방법은 없습니다.따라서 n번째 근은 z의 n-값 함수입니다.이것은 양의 실수의 경우와 반대로, 사람이 가지고 있다는 것을 의미합니다.

왼쪽은 n개의 값으로 구성되고 오른쪽은 단일 값이기 때문입니다.

특성.

필드 구조

복소수의 $집합{\displaystyle \mathbb{}}$ C${$는 ^[50]필드입니다.간단히 말해서, 이것은 다음과 같은 사실을 의미합니다: 첫째, 임의의 두 개의 복소수를 더하고 곱하여 또 다른 복소수를 산출할 수 있습니다.둘째, 임의의 복소수 z에 대하여, 그 덧셈 역수 -z 또한 복소수이고, 셋째, 모든 0이 아닌 복소수는 상호 복소수입니다.또한, 이러한 연산은 많은 법칙들을 만족시킵니다. 예를 들어, 임의의 두 복소수₁ z와₂ z에 대한 덧셈과 곱셈의 교환성의 법칙:

이 두 법칙과 필드에 대한 다른 요구 사항은 위의 공식으로 증명할 수 있습니다. 실수 자체가 필드를 형성한다는 사실을 사용합니다.

실제와 달리, ${displaystyle$ \$mathbb {C}$는 순서 필드가 아닙니다. 즉, 덧셈 및 곱셈과 호환되는 관계₁ z < z를₂ 정의할 수 없습니다.실제로, 임의의 순서 필드에서, 임의의 원소의 제곱은 반드시 양수이므로, i² = -1은${\displaystyle }$C에 $대한{\displaystyle \mathbb{}}$ 순서의 존재를 배제합니다$.$ \$displaystyle \mathbb {C}.}$

수학적 주제 또는 구성의 기본 필드가 복소수 필드인 경우, 주제의 이름은 일반적으로 해당 사실을 반영하도록 수정됩니다.예를 들어, 복소 분석, 복소 행렬, 복소 다항식 및 복소 리 대수입니다.

다항식의 해

임의의 복소수(계수라고_n 함)가₀ 주어졌을 때 a, ..., a, 방정식

는 하나 이상의 복잡한 솔루션 z를 가지고 있으며, 단, 더 높은 계수₁ a, ..., a_n 중 적어도 하나는 ^[6]0이 아닙니다.이것은 카를 프리드리히 가우스와 장 르 론 달랑베르의 대수학의 기본 정리입니다.이 때문에, ${$를 대수적으로 닫힌 필드라고 합니다.이 성질은 유리수 Q(다항식 x2 - 2는 유리수가 아니기 때문에 유리수를 갖지 않는다.)나 실수 R(다항식 x2 + a는 > 0에 대한 실수를 갖지 않는다,x의 제곱은 임의의 실수 x)에 대해 양수이기 때문이다.

리우빌의 정리와 같은 분석 방법이나 와인딩 수와 같은 위상학적 방법 또는 갈루아 이론과 홀수 차수의 실수 다항식이 적어도 하나의 실수 근을 가지고 있다는 사실을 결합한 증명에 의해 이 정리의 다양한 증명이 있습니다.

이러한 사실 때문에, 대수적으로 닫힌 필드에 대해 유지되는 정리는 C$.$ {\$displaystyle \mathbb {C}$에 적용됩니다. 예를 들어, 비어 있지 않은 복소 사각 행렬은 적어도 하나의 (복소) 고유값을 가집니다.

대수적 특성화

$필드{\displaystyle \mathbb{}}$ C${$에는 다음과 같은 세 가지 속성이 있습니다.

• 첫째, 특성이 0입니다.즉, 임의의 수의 합계(모두 1)에 대해 1 + 1 + 1 + 1 ≠ + 1 ⋯ 0을 의미합니다.
• 둘째, C의${\displaystyle }기본{\displaystyle \mathbb{}}$ 필드인 Q${$$displaystyle \mathbb {Q}$에 $대한{\displaystyle \mathbb{}}$ 초월도는 연속체의 카디널리티입니다$.$
• 셋째, 대수적으로 닫혀 있습니다(위 참조).

예를 들어, p-adic 수의 Qp(displaystyle \mathbb {Q}_{p})의 대수적 폐색은 이 세 가지 속성을 만족시키기 때문에, 이 두 개의 필드는 (필드로서, 위상 필드로서가 아님) 동형이다.[52]$또한{\displaystyle \mathbb{}}$, C${$는 복소 푸이수 급수의 장과 동형입니다.그러나 동형을 지정하려면 선택의 공리가 필요합니다.이 대수적 특성화의 또 다른 결과는 C${$가 C${$와 동형인 많은 적절한 하위 필드를 포함한다는 $것$입니다.

위상 분야로서의 특성화

$C{$displaystyle $\mathbb {C}$의 이전 특성은${\displaystyle }$C의 $대수적{\displaystyle \mathbb{}}$ 측면만을 설명합니다$. 즉$, 분석 및 위상과 같은 영역에서 중요한 근접성과 연속성의 특성은 다루지 않습니다.C${$displaystyle $\mathbb {C}$를 위상 필드(즉, 수렴 개념을 허용하는 위상이 장착된 필드)로 설명하면 위상 특성이 고려됩니다.${$는 다음 세 가지 조건을 만족하는 0이 아닌 원소의 부분 집합 P(즉, 양의 실수 집합)를 포함합니다.

• P는 덧셈, 곱셈 및 취역에서 닫힙니다.
• x와 y가 P의 개별 요소이면 x - y 또는 y - x가 P에 있습니다.
• S가 P의 비어 있지 않은 부분 집합이라면${\displaystyle ,}$ C의 $일부{\displaystyle \mathbb{}}$ x에 대해 S + P = x + P입니다$.$ {\$displaystyle \mathbb {C}$

$게다가{\displaystyle \mathbb{}}$, C$displaystyle \mathbb$ ${$$C}$는 C의 $임의$의 0이 아닌 x에 대해 x*가 P에 있는 것과 같은 사소하지 않은 인볼루시브 오토모픽 x ↦ x*(즉, 복소 켤레)를 가지고 있습니다$.$

이러한 속성을 가진 모든 필드 F는 집합 B(x, p) = {yp - (y - x)(y - x)* ∈ P }를 기본으로 함으로써 위상을 부여할 수 있습니다. 여기서 x는 필드에 걸쳐 있고 p는 P에 걸쳐 있습니다.이 위상에서 F는 위상 필드로서$$C.{{$displaystyle \mathbb {C}$와 동형입니다.

유일하게 연결된 국소 콤팩트 위상 필드는 R(displaystyle \mathbb {R} 및 C({displaystyle \mathbb {C})이다. 이는 C(displaystyle \mathbb {C})가 0이 아닌 복소수이기 때문에 R(displaystyle \mathbb {R})와 구별될 수 있기 때문에 위상 필드로서 C(c)의 또 다른 특성을 제공한다0이 아닌 실수는 연결되지 않습니다.^[53]

형식 구문

주문된 쌍으로 구성

윌리엄 로완 해밀턴은 복소수의^[54] $집합{\displaystyle \mathbb{}}$ C$(\displaystyle$\$mathbb$$${C$})$를 실수의 순서쌍(a, b)의 집합 $({2}})$로 정의하는 접근법을 도입했으며, 여기에는 덧셈과 곱셈에 대한 다음과 ^[50]같은 규칙이 부과됩니다.

그런 다음 (a, b)를 + bi로 표현하는 것은 단지 표기법의 문제입니다.

계수장으로서의 건설

이 낮은 수준의 구조는 복소수의 구조를 정확하게 설명하지만, 다음과 같은 동등한 정의는 C${$의 대수적 특성을 더 즉시 드러냅니다.이 특성화는 필드와 다항식의 개념에 의존합니다.필드는 예를 들어 합리적인 숫자에서 익숙한 대로 동작하는 덧셈, 뺄셈, 곱셈 및 나눗셈 연산이 부여된 집합입니다.예를 들어, 분배 법칙.

필드의 세 가지 요소 x, y 및 z에 대해 고정해야 합니다.실수의 $집합{\displaystyle \mathbb{}}$ R${$은 필드를 형성합니다.실수 계수를 갖는 다항식 p(X)는 다음과 같은 형식의 표현입니다.여기서₀ a, ..., a는_n 실수입니다.일반적인 다항식의 덧셈과 곱셈은 고리 구조를 가진 모든 다항식의 $집합{\displaystyle \mathbb{}}$R [$]{\displaystyle \mathbb {R}$ [$X]$를 제공합니다.이 고리는 실수 위의 다항식 고리라고 불립니다.

복소수 집합은 몫환${\displaystyle }R{\displaystyle \mathbb{}}$ [${\displaystyle X}$]${\displaystyle }$/ (${\displaystyle {X\mathrm{}}^{}}$2 +${\displaystyle 1}$)$$. {\$displaystyle \mathbb {R}$ [$X]/(X^{2}+1)}$로 정의됩니다.$$^[6] 이 확장 필드는 -1의 두 제곱근, 즉 (의) X와 -X의 코셋을 포함합니다. () 1과 X의 코셋은 R${\displaystyle }$[${\displaystyle X]/}$ (${\displaystyle {}^{}}$2 + ${\displaystyle 1}$)$$\$style \mathbb {R}$ [$X]$ / ($X^{2}$ + $1)$의 기저를 형성합니다.즉, 확장 필드의 각 요소는 이 두 요소의 선형 조합으로 고유하게 작성될 수 있습니다.마찬가지로, 확장 필드의 요소는 실수의 순서쌍(a, b)으로 작성될 수 있습니다.X + 1은 R$,$ \$displaystyle \mathbb {R}$에 $비해{\displaystyle \mathbb{}}$ 환원할 수 없으므로 생성되는² 이상은 최대입니다.

X² = -1 관계 R${\displaystyle }$[$],$ \$displaystyle \mathbb {R}$ [$X],}$ 모듈의$$ 덧셈 및 곱셈 공식은 순서쌍으로 정의된 복소수의 덧셈 및 곱셈 공식에 해당합니다.따라서 $C$의 두 정의는 ($필드로서$$)$ 동형입니다$.$

이 접근법에서 $C$${$$displaystyle \mathbb$$${C}가 R{$displaystyle{\displaystyle \mathbb{}}$ \$mathbb {R}$의 대수적 확장이므로 C${$ \$mathbb {C}$는 R$.{displaystyle \mathbb {R}$의 대수적 폐쇄입니다.

복소수 행렬 표현

복소수 a + bi는 다음과 같은 형태의 2 × 2 행렬로 나타낼 수 있습니다.

여기서 항목 a와 b는 실수입니다.이러한 두 행렬의 합과 곱이 다시 이 형태이기 때문에, 이 행렬들은 고리 2 × 2 행렬의 하위 고리를 형성합니다.

간단한 계산 결과 지도는 다음과 같습니다.

복소수 필드에서 이러한 행렬의 고리까지의 고리 동형입니다.이 동형성은 복소수의 절대값의 제곱을 해당 행렬의 행렬식과 연관시키고 복소수의 공액을 행렬의 전치와 연관시킵니다.

복소수의 곱셈에 대한 기하학적 설명은 복소수와 그러한 행렬 사이의 이 대응 관계를 사용하여 회전 행렬로 표현될 수도 있습니다.벡터(x, y)에 대한 행렬의 작용은 x + iy를 + ib로 곱한 것에 해당합니다.특히, 행렬식이 1이면 행렬이 다음과 같은 형태를 갖는 실수 t가 있습니다.

이 경우 벡터에 대한 행렬의 작용과 ${\displaystyle \mathrm{복소수}}$ ${\displaystyle \cos }$+ ${\displaystyle \mathrm{is}}$ \$displaystyle \cost+i\sint}$에서의 곱셈은 모두 각도 t의 회전입니다.

복소해석학

복소 변수의 함수에 대한 연구는 복소 분석으로 알려져 있고 응용 수학뿐만 아니라 수학의 다른 분야에서 엄청난 실용적인 사용을 가지고 있습니다.종종 실제 분석 또는 짝수 이론에서 진술에 대한 가장 자연스러운 증명은 복잡한 분석의 기술을 사용합니다(예를 들어 소수 정리 참조).일반적으로 2차원 그래프로 표현되는 실제 함수와 달리, 복잡한 함수는 4차원 그래프를 가지고 있으며 3차원 그래프를 컬러 코딩하여 4차원을 제안하거나 복잡한 함수의 동적 변환을 애니메이션화하여 유용하게 설명할 수 있습니다.

복잡한 지수 함수 및 관련 함수

(실제) 분석에서 수렴 급수와 연속 함수의 개념은 복잡한 분석에서 자연스러운 유사점을 가집니다.복소수의 수열은 실제 부분과 가상 부분이 수렴하는 경우에만 수렴한다고 합니다.이는 실수의 절대값이 복소수의 절대값으로 대체되는 한계의 (ε, δ)-정의와 같습니다.더 추상적인 $관점$에서, C${$는 미터법을 부여받습니다.

삼각 부등식을 포함하는 완전한 미터법 공간입니다. 임의의 두 개의₁ 복소수 z와 z에₂ 대해.

실제 분석에서와 마찬가지로, 이 수렴 개념은 많은 기본 함수를 구성하는 데 사용됩니다: 지수 함수 expz, 또한 e는^z 무한 급수로 정의됩니다.

실제 삼각함수 사인과 코사인, 쌍곡선함수 sinh와 코사인을 정의하는 시리즈는 또한 변화 없이 복잡한 인수로 이어집니다.탄젠트와 같은 다른 삼각 함수와 쌍곡선 함수의 경우 정의 급수가 모든 복잡한 값에 대해 수렴하지 않기 때문에 상황이 약간 더 복잡합니다.따라서 사인, 코사인 및 지수의 관점에서 또는 분석 연속법을 사용하여 동일하게 정의해야 합니다.

오일러의 공식은 다음과 같습니다.

임의의 실수 φ에 대하여, 특히.그것이 오일러의 정체입니다.실수의 상황과는 달리, 방정식의 복소해 z의 무한대가 있습니다.임의의 복소수 ≠ 0에 대하여.이러한 해 z(w의 복소 로그라고 함)가 다음을 만족한다는 것을 알 수 있습니다. 여기서 arg는 위에 정의된 인수이고 (실제) 자연 로그에서.arg는 최대 2µ의 배수에서만 고유한 다중값 함수이므로 로그도 다중값 함수입니다.로그의 주 값은 종종 가상 부분을 간격(-π, π)으로 제한하여 취합니다.

복소 지수^ω z는 다음과 같이 정의됩니다.

및 는 다중값입니다. 단, π가 정수인 경우는 예외입니다.π = 1 / n의 경우, 일부 자연수 n에 대해, 이것은 위에서 언급한 n번째 근의 비고유성을 복구합니다.

실수와 달리 복소수는 일반적으로 수정되지 않은 검정력 및 로그 동일성을 만족시키지 않으며, 특히 단일 값 함수로 순진하게 취급될 때는 검정력 및 로그 동일성의 실패를 참조하십시오.예를 들어, 그들은 만족하지 못합니다.

방정식의 양쪽은 여기에 주어진 복잡한 지수의 정의에 의해 다중값이고 왼쪽의 값은 오른쪽의 값의 부분 집합입니다.

완전 동형 함수

함수 f: ${$→$$ ${$가 코시-리만 방정식을 만족하는 경우 완전 동형이라고 합니다.예를 들어, $임의$의 R${$ - 선형$$ $맵{\displaystyle \mathbb{}}$ C${$→$$ ${$는 다음과 같은 형식으로 쓸 수 있습니다.

복소 계수 a와 b를 갖는.이 지도는 b = 0인 경우에만 완전 동형입니다.두 번째 $합계{\displaystyle }$ ${\displaystyle bz\stackrel{}{}}$ $¯$ {\$displaystyle$ b${\overline {z}}$는 실제 미분 가능하지만 코시-리만 방정식을 만족시키지는 못합니다.

복잡한 분석을 통해 실제 분석에서는 명확하지 않은 몇 가지 특징을 확인할 수 있습니다.예를 들어$,$ $임의$로 작은 C{displaystyle $\mathbb {C}$의 열린 부분 집합에 동의하는 두 개의 완전 동형 함수 f와 g는 반드시 모든$$ 곳에서 일치합니다.완모형 함수 f와 함께 f(z)/(z - ⁿz₀)로 국소적으로 작성될 수 있는 함수인 복모형 함수는 여전히 완모형 함수의 일부 특징을 공유합니다.z = 0에서 sin(1/z)과 같은 다른 함수에는 필수 특이점이 있습니다.

적용들

복소수는 신호 처리, 제어 이론, 전자기학, 유체 역학, 양자 역학, 지도 제작 및 진동 분석을 포함한 많은 과학 분야에 적용됩니다.이러한 응용 프로그램 중 일부는 아래에 설명되어 있습니다.

기하학.

모양들

평면에서 세 개의 비공선 $점{\displaystyle }$u,${\displaystyle v}$, ${displaystyle$$$u,$$$v$,$w$}는$$ 삼각형 $u,$의 모양을 결정합니다. 복소 평면에서 점들을 찾는 이 삼각형의 모양은 다음과 같이 복잡한 연산으로 표현할 수 있습니다.

삼각형의 모양$S{\displaystyle }$({$displaystyle$ S$})$는 복잡한 평면이 변환 또는 확장(아핀 변환)에 의해 변환될 때 모양의 직관적 개념에 해당하고 유사성을 설명할 때 동일하게 유지됩니다.따라서 각${\displaystyle }$삼각형 {${\displaystyle u,v}$, $}{displaystyle$\{$u, v$, $w\}$은(^[55]는) 동일한 모양을 가진 삼각형의 유사성 클래스에 있습니다.

프랙탈 기하학

만델브로트 집합은 복잡한 평면에 형성된 프랙탈의 일반적인 예입니다.이는 무한히 반복될 때 시퀀스 ${\displaystyle {fc}_{}z)}$ $=$ ${\displaystyle {z\mathrm{}}^{}}$ 2${\displaystyle {}^{}}$+$$({$displaystyle f_{c}(z$)=z$^{2}+c$}가$$ 발산되지 않는 모든 $위치{\displaystyle }$c{$displaystyle$c}를$$ 표시함으로써 정의됩니다.마찬가지로 Julia 집합은 c${displaystyle$ c$}$가 일정하게 유지되는 $경우$를 제외하고 동일한 규칙을 가집니다.

삼각형

모든 삼각형에는 고유한 Steiner 타원이 있습니다. 즉, 삼각형 내부의 타원이며 삼각형의 세 변의 중간점에 접합니다.삼각형의 슈타이너 타원의 초점은 마르덴의 ^[56][57]정리에 따라 다음과 같이 구할 수 있습니다.복소 평면에서 삼각형의 꼭짓점을 a = x_AA + yi, b = x_B + yi_B 및 c = x_C + yi로_C 나타냅니다.입방정식${\displaystyle }$(${\displaystyle x}$-${\displaystyle a}$) (${\displaystyle x}$ ${\displaystyle -b}$) (${\displaystyle x}$ ${\displaystyle -c}$ ) $= 0$ {\$displaystyle$ ($x-a)(x-b)(x-c)=$0$\}$을 쓰고 그 도함수를 취하여 (직류) 도함수를 0으로 동일시합니다.마르덴의 정리에 따르면 이 방정식의 해는 스타이너 타원의 두 초점의 위치를 나타내는 복소수입니다.

대수적 수론

위에서 언급한 바와 같이, (복잡한 계수에서) 모든 일정하지 않은 다항식은 C${displaystyle$ \$mathbb {C$의 해를 갖습니다. Fortori, 방정식이 합리적인 계수를 갖는 경우에도 마찬가지입니다.이러한 방정식의 근은 대수적 수라고 불립니다 – 대수적 수 이론의 주요 연구 대상입니다.모든 대수적 숫자를 포함하는 Q${$의 대수적 폐쇄인 Q${\$ \mathbb {Q$\}\}$와 $비교$하면 C${$는 기하학적 용어로 쉽게 이해할 수 있는 장점이 있습니다.이러한 방식으로, 대수적 방법은 기하학적 질문을 연구하는 데 사용될 수 있고 그 반대도 마찬가지입니다.대수적 방법, 더 구체적으로 단일성의 뿌리를 포함하는 수 필드에 필드 이론의 기계를 적용하면 나침반과 직선만 사용하여 정규 노나곤을 구성할 수 없음을 보여줄 수 있습니다.

또 다른 예는 가우스 정수입니다. 즉, x + iy 형식의 숫자입니다. 여기서 x와 y는 정수이며, 제곱합을 분류하는 데 사용할 수 있습니다.

해석수론

해석적 수 이론은 해석적 방법이 사용될 수 있는 복소수로 간주될 수 있다는 사실을 이용하여 종종 정수 또는 유리수를 연구합니다.이는 복소수 값 함수에서 숫자 이론 정보를 인코딩함으로써 수행됩니다.예를 들어, 리만 제타 함수 ω(s)는 소수의 분포와 관련이 있습니다.

부적절한 적분

적용된 필드에서 복소수는 복소수 함수를 통해 특정 실제 값의 부적절한 적분을 계산하는 데 종종 사용됩니다.이를 위한 몇 가지 방법이 있습니다. 등고선 통합 방법을 참조하십시오.

동역학 방정식

미분방정식에서, 일차 미분방정식 또는 방정식 시스템의 특성방정식의 모든 복소근 r을 찾은 다음, f(t) = ert 형식의 기저함수의 관점에서 시스템을 풀려고 시도하는 것이 일반적이다.마찬가지로, 차분 방정식에서, 차분 방정식의 특성 방정식의 복소근 r은 다음과 같다uation 시스템은 f(t) = r^t 형식의 기본 함수 측면에서 시스템을 해결하기 위해 사용됩니다.

선형대수학

고유 분해는 행렬 검정력과 행렬 지수를 계산하는 데 유용한 도구입니다.그러나 행렬이 실제(예: 회전 행렬)인 경우에도 복잡한 숫자를 사용해야 하는 경우가 많습니다.

복소수는 종종 원래 실수로 생각된 개념을 일반화합니다.예를 들어, 공역 전치 행렬은 전치 행렬을 일반화하고, 에르미트 행렬은 대칭 행렬을 일반화하며, 단일 행렬은 직교 행렬을 일반화합니다.

응용수학

제어 이론

제어 이론에서, 시스템은 종종 라플라스 변환을 사용하여 시간 영역에서 복잡한 주파수 영역으로 변환됩니다.그런 다음 시스템의 0과 극이 복잡한 평면에서 분석됩니다.근 궤적, 나이키스트 플롯 및 니콜스 플롯 기법은 모두 복잡한 평면을 사용합니다.

루트 궤적 방법에서는 0과 극이 왼쪽 또는 오른쪽 절반 평면에 있는지, 즉 실제 부분이 0보다 크거나 작은지가 중요합니다.선형 시간 불변(LTI) 시스템에 다음과 같은 극이 있는 경우

• 오른쪽 반평면에서는 불안정할 겁니다
• 왼쪽 반평면에 모두 안정적일 겁니다
• 가상 축에서, 그것은 한계 안정성을 가질 것입니다.

오른쪽 절반 평면에 0이 있는 시스템은 비최소 위상 시스템입니다.

신호 분석

복소수는 주기적으로 변화하는 신호를 편리하게 설명하기 위해 신호 분석 및 기타 필드에 사용됩니다.실제 물리적 양을 나타내는 실제 함수의 경우, 종종 사인과 코사인 측면에서 해당하는 복잡한 함수가 실제 부분이 원래 양인 것으로 간주됩니다.주어진 주파수의 사인파의 경우 해당 z의 절대값 z는 진폭이고 인수 argz는 위상입니다.

푸리에 분석을 사용하여 주어진 실제 값 신호를 주기 함수의 합으로 작성하는 경우, 이러한 주기 함수는 종종 형식의 복소수 값 함수로 작성됩니다.

그리고.

여기서 θ는 각 주파수를 나타내며 복소수 A는 위에서 설명한 대로 위상과 진폭을 인코딩합니다.

이러한 사용은 또한 디지털 신호 처리 및 디지털 이미지 처리로 확장되어 디지털 버전의 푸리에 분석(및 웨이블릿 분석)을 사용하여 디지털 오디오 신호, 스틸 이미지 및 비디오 신호를 전송, 압축, 복원 및 처리합니다.

AM 라디오의 진폭 변조의 두 측면 대역과 관련된 또 다른 예는 다음과 같습니다.

물리학에서

전자기학 및 전기공학

전기 공학에서 푸리에 변환은 다양한 전압과 전류를 분석하는 데 사용됩니다.그런 다음 저항, 콘덴서 및 인덕터의 처리는 후자의 두 가지에 대해 가상의 주파수 의존 저항을 도입하고 임피던스라고 불리는 하나의 복잡한 숫자로 세 가지를 모두 결합함으로써 통일될 수 있습니다.이 접근법은 위상 미적분학이라고 불립니다.

전기 공학에서, 가상의 단위는 일반적으로 전류를 나타내기 위해 사용되는 I 또는 더 구체적으로, 일반적으로 순간 전류를 나타내기 위해 사용되는 i와 혼동을 피하기 위해 j로 표시됩니다.

AC 회로의 전압이 진동하므로 다음과 같이 표현할 수 있습니다.

측정 가능한 수량을 얻기 위해 실제 부품을 사용합니다.

복소수 값 신호 V(t)는 실제 값 측정 가능한 신호 v(t)의 분석적 표현이라고 합니다.

유체 역학

유체 역학에서 복잡한 함수는 2차원에서 잠재적 흐름을 설명하는 데 사용됩니다.

양자역학

복소수 필드는 양자 역학의 수학적 공식에 내재되어 있으며, 여기서 복잡한 힐버트 공간은 편리하고 아마도 가장 표준적인 공식에 대한 컨텍스트를 제공합니다.양자역학의 원래 기초 공식인 슈뢰딩거 방정식과 하이젠베르크의 행렬 역학은 복소수를 사용합니다.

상대성 이론

특수 상대성 이론과 일반 상대성 이론에서 시공간 연속체의 시간 성분을 가상으로 받아들인다면 시공간에 대한 메트릭의 일부 공식은 더 단순해집니다. (이 접근법은 더 이상 고전 상대성 이론에서 표준이 아니지만 양자장 이론에서 필수적인 방식으로 사용됩니다.)복소수는 상대성 이론에 사용되는 텐서의 일반화인 스피너에 필수적입니다.

일반화 및 관련 개념

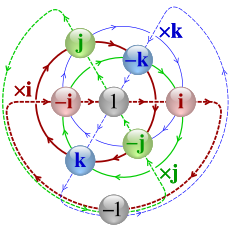
실수의 R${$$}$ $필드$를 C${$로 확장하는 과정은 케일리-딕슨 구조로 알려져 있습니다.그것은 더 높은 차원으로 운반될 수 있으며, (실제 벡터 공간으로서) 각각 4차원과 8차원인 $H${\$displaystyle \mathbb$ {H$}$와 8차원의 $옥타니언{\displaystyle \mathbb{}}$ O${\$를 산출합니다.이러한 맥락에서 복소수는 ^[59]이진수라고 불립니다.

실제에 구조를 적용하는 것이 순서의 속성을 잃는 것처럼, 실수와 복소수에서 익숙한 속성은 각 확장과 함께 사라집니다.쿼터니언은 교환성을 잃습니다. 즉, 일부 쿼터니언 x, y의 경우 x·y ≠ y·x이며, 일부 쿼터니언 x, y, z의 경우 추가적으로 옥타니언의 곱셈이 연관성이 없습니다. (x·y)·z ≠ x·(y·z).

실수, 복소수, 쿼터 및 옥타니언은 모두 R${$에 $대한{\displaystyle \mathbb{}}$ 정규 분할 대수입니다. 후르비츠의 정리에 따르면, 케일리-딕슨 구조의 다음 단계인 세브란스는 이러한 구조를 갖지 못합니다.

케일리-딕슨 구조는 기저 (1, i)와 관련하여 R$({$$displaystyle \mathbb${R$}$ - 대수적$$ 공간)으로 $생각$되는 C$,$ \$displaystyle \mathbb${C$}$의 정규 표현과 밀접한 $관련$이 있습니다.이는 다음을 의미합니다: ${$ - 선형$$ 맵

일부 고정 복소수의 경우 w는 2 × 2 행렬로 나타낼 수 있습니다(기준이 선택되면).기저 (1, i)에 대하여, 이 행렬은즉, 위의 복소수 행렬 표현 섹션에서 언급된 것.이것은 2×2 실수 행렬에서 C${$의 선형 표현이지만, 유일한 것은 아닙니다.임의 행렬는 제곱이 항등식 행렬의 음수라는 특성을 갖습니다. J² = -I.그리고나서또한 $필드{\displaystyle \mathbb{}}$ C$,$ \$displaystyle$\$mathbb {C$$}$와 동형이며 $R2$에${\displaystyle {}^{}}대한{\displaystyle {\mathbb{}}^{}}$ 대체 복소 구조를 제공합니다$.$$$ 이것은 선형 복합 구조의 개념에 의해 일반화됩니다.

초복소수는 $또한{\displaystyle \mathbb{}}$ R$,$ \$displaystyle \mathbb {R},$ $C$$,$ \$displaystyle \mathbb {C},$ $H$$,$ \$displaystyle \mathbb {H$$}$$$및 O$.$ $예$를 들어, 이 개념은 분할복소수를 포함합니다$.$(복소수의 경우 R$[$ /${\displaystyle }$(${\displaystyle {x2\mathrm{}}^{}}$- $)$ \$style \mathbb {R}$ [$x]$ /${\displaystyle }$(${\displaystyle {x2\mathrm{}}^{}}$+ 1$)$ \style \$mathbb$ {R} [x] / (x2 + 1) $$\style \mathbb ${R}$ [$x]$ / ($x^{2}+1)$의 원소.이 링에서 방정식² a = 1은 4개의 해를 갖습니다.

R${$$}$ $필드$는 일반적인 절대값 메트릭과 관련하여 합리적인 숫자의 $필드$인 Q$,$ {\$displaystyle \mathbb {Q$$}$ 필드입니다.Q{displaystyle \mathbb {Q}에 대한 다른 메트릭 선택은 (소수 p에 대한) p-adic 숫자의 필드 Qp({displaystyle \mathbb {Q}_{p})로 이어지며, 이는 R(displaystyle \mathbbb {R})과 유사하다,${\displaystyle }$오스트로우스키 정리에 의한$$ ${\displaystyle \mathbb$ {$Q} _{p}}.$$Qp${\displaystyle $\mathbb$$${$Q} _{p$}}의 $대수적{\displaystyle \stackrel{}{{\mathbb{}}_{}}}$ ${\displaystyle \stackrel{}{{}_{}}}$ Q p $¯$ ${\displaystyle$${Q$$} _$${$$p$}}은$$ 여전히 규범을 가지고 있지만 ($C${\displaystyle \$mathbb$ {C$\}$와는 달리) 이와 관련하여 완전하지 않습니다.${\displaystyle \stackrel{}{{}_{}}}$ $¯$ ${{\mathbb${C}$_{p}}$의 $완성{\displaystyle \stackrel{}{{\mathbb{}}_{}}}$ ${\displaystyle {}_{}}${\$displaystyle \mathbb$${$C} $_{p}}$는 대수적으로 닫힌 것으로 밝혀졌습니다.비유적으로, 그 필드는 p-adic 복소수라고 불립니다.

$필드{\displaystyle \mathbb{}}$ R$,$ {\$displaystyle \mathbb {R},}$ ${\displaystyle {}_{}}$, {\$displaystyle \mathbb {Q}_$${p}$ 및 C$,$ {\$displaystyle \mathbb {C}$를 $포함$한 유한 필드 확장을 로컬 필드라고 합니다.

참고 항목

• 대수면
• 복소수를 이용한 원운동
• 복합기 시스템
• 복소기하학
• 이중복소수
• 아이젠슈타인 정수
• 오일러 항등식
• 기하학적 대수(복잡한 평면을 2차원 스피너 $부분공간{\displaystyle {\mathcal{}}_{}^{}}$ ${\displaystyle {G2}_{\mathrm{}}^{}}$+$displaystyle {mathcal$ {G$}$_$\{$$2$}^{+}로 포함)
• 단위복소수

숫자 체계 복잡한 ${\displaystyle :\;\mathbb {C} 표시$ 진짜 ${\displaystyle}:\;\mathbb {R}$ 합리적인 ${\displaystyle :\;\mathbb {Q} 표시$ 정수 ${\displaystyle :\;\mathbb {Z} 표시$ 자연의 ${\displaystyle}:\;\mathbb {N}$ 0: 0 하나: 1 소수 합성수 음의 정수 분수 유한소수 이진수(유한 이진수) 반복 소수 비합리적 대수적 무리수 초월론 상상의

메모들

레퍼런스

인용된 작품

진일보한 내용

• Penrose, Roger (2005). The Road to Reality: A complete guide to the laws of the universe. Alfred A. Knopf. ISBN 978-0-679-45443-4.
• Derbyshire, John (2006). Unknown Quantity: A real and imaginary history of algebra. Joseph Henry Press. ISBN 978-0-309-09657-7.
• Needham, Tristan (1997). Visual Complex Analysis. Clarendon Press. ISBN 978-0-19-853447-1.

수학적

히스토리컬