카탈루냐 수

조합수학에서 카탈루냐 숫자는 다양한 계수 문제에서 발생하는 자연수의 연속이며, 종종 재귀적으로 정의된 사물을 포함한다. 그들은 프랑스-벨기에 수학자 외젠 샤를 카탈란 (1814–1894)의 이름을 따서 지어졌다.

n번째 카탈로니아 숫자는 이항계수의 관점에서 직접 표현할 수 있다.

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}=\prod \limits _{k=2}^{n}{\frac {n+k}{k}}\qquad {\text{for }}n\geq 0.}$

n = 0, 1, 2, 3, ...의 첫 번째 카탈로니아 번호는

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ... (시퀀스 A000108 in OEIS)

특성.

C에_n 대한 대체 표현은

$C$ ${\displaystyle n_{}}$=${\displaystyle }$( ${\displaystyle \genfrac{}{}{0ex}{}{}{}}$)${\displaystyle }$-${\displaystyle }$( ${\displaystyle \genfrac{}{}{0ex}{}{}{}}$+ ${\displaystyle \genfrac{}{}{0ex}{}{1}{}}$) ${\$ 선택 n$}-{2n \n$ 선택 ${\displaystyle \mathrm{n}}$$+1}:$ $n$ ${\displaystyle \ge }$ 0${\displaystyle ,}$ ${\displaysty n\geq 0,}$

이는${\displaystyle }$(${\displaystyle \genfrac{}{}{0ex}{}{}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{+}{}\genfrac{}{}{0ex}{}{1}{}}$) =${\displaystyle \frac{n}{}}$ +${\displaystyle \frac{}{}\frac{1}{}}$ ( ${\displaystyle \genfrac{}{}{0ex}{}{}{}}$)$${\$displaystyle {\tbinom {2n}{n+1}={\tfrac {n}{n+$1}{$n+1}{\tbinom${n$}{$n}{$n$에 따라 위에 제공된 표현과 동일하다. 이 표현식은 C가_n 정수라는 것을 보여주는데, 이는 주어진 첫 번째 공식에서 바로 알 수 있는 것이 아니다. 이 표현은 공식의 정확성을 증명하는 근거가 된다.

카탈루냐의 숫자는 재발 관계를 만족시킨다.

${\displaystyle C_{0}=1\qad {\dext{and}\quad C_{n+1}=\sum _{i=0}^{n_{n-i}C_{n-i}\quad {\text{}n\geq 0}$

그리고

${\displaystyle C_{0}=1\quad {\text{nand}\quad C_{n+1}={\frac {2(n+1)}{n+2}}C_{n}.}$

점증상으로는 카탈루냐인들의 수가 증가하면서

n번째 카탈로니아 숫자와 오른쪽의 표현은 n이 무한에 가까워질 때 1을 향해 경향이 있다는 점에서. 이것은 중심 이항계수의 점증적 성장을 사용하거나, $!$ {\$displaystyle$ n$!}$에 대한 스털링의 근사치를 사용하거나$,$ 또는 생성함수를 통해 증명할 수 있다.

유일하게_n 홀수인 카탈로니아 숫자 C는^k n = 2 - 1이며, 다른 모든 숫자는 짝수다. 카탈루냐의 주요 숫자는 C₂ = 2와 C₃ = 5이다.^[1]

카탈로니아 숫자들은 필수적인 표현을 가지고 있다.

${\displaystyle C_{n}={\frac {1}{1}{2\pi }\int _{0}x^{n}{\sqrt{4-x}}{x}}}\x.\}$

조합식 응용 프로그램

카탈로니아 숫자에 의해 해결책이 제시된 조합에는 많은 계산상의 문제들이 있다. 책 Enumerative Compinatorics: 제2권 콤비네이터 리차드 P. 스탠리는 카탈로니아 숫자에 대한 66가지 다른 해석을 설명하는 일련의 연습을 포함하고 있다. 다음은 사례₃ C = 5와₄ C = 14의 예와 함께 몇 가지 예들이다.

• C는_n 길이가 2n인 Dyck 단어의^[2] 수입니다. Dyck 워드는 문자열의 초기 세그먼트가 X보다 더 많은 Y를 가지지 않도록 n X와 n Y로 구성된 문자열이다. 예를 들어, 길이 6의 Dyck 단어들은 다음과 같다.

• 기호 X를 개방 괄호로, Y를 근접 괄호로 다시 삽입하면 C는_n 정확하게 일치하는 n쌍의 괄호를 포함하는 식 수를 카운트한다.

• C는_n n + 1 요인을 완전히 괄호화할 수 있는 여러 가지 방법의 수(또는 매트릭스 체인 곱셈 문제에서처럼 이진 연산자의 n개 응용 프로그램을 연결하는 방법의 수)이다. 예를 들어 n = 3의 경우 다음과 같은 네 가지 요인에 대한 다섯 가지 상이한 괄호가 있다.

• 이진 연산자의 연속적인 적용은 내부 노드를 설명하는 각각의 정확하게 일치하는 브래킷을 사용하여 완전한 이진 트리의 단위로 나타낼 수 있다. C는_n 잎이 n + 1인 완전 이진수 또는 내부 노드가 총 n개인 경우:

또한 Dyck 워드의 첫 번째 X에 대해 정확하게 일치하는 닫힘 Y의 내부에는 왼쪽 하위 트리에 대한 설명이 포함되며, 외부에는 오른쪽 하위 트리가 설명된다.

• C는_n 정점이 n + 1인 비 이형 정렬(또는 평면) 트리의 수입니다.^[3] 일반 트리를 이진 트리로 인코딩하는 것을 참조하십시오.
• C는_n 대각선 위로 통과하지 않는 n × n 제곱 셀을 가진 격자의 가장자리를 따라 있는 단조 격자 경로의 수입니다. 단조로운 경로는 왼쪽 하단 모서리에서 시작하여 오른쪽 상단 모서리에서 마무리되며, 전체적으로 오른쪽 또는 위를 가리키는 가장자리로 구성된다. 그러한 경로를 세는 것은 Dyck 단어들을 세는 것과 같다: X는 "오른쪽으로 이동"을 의미하고 Y는 "위로 이동"을 의미한다.

다음 도표는 사례 n = 4를 나타낸다.

이는 카탈루냐 요소를 열 높이로 나열하여 나타낼 수 있다.^[4]

• n + 2면이 있는 볼록한 다각형은 교차하지 않는 선 세그먼트(폴리곤 삼각형의 일종)와 정점을 연결하여 삼각형으로 자를 수 있다. 형성된 삼각형의 수는 n이고 이를 달성할 수 있는 다른 방법의 수는 C이다_n. 다음의 육각형은 사례 n = 4를 나타낸다.

• C_n is the number of stack-sortable permutations of {1, ..., n}. A permutation w is called stack-sortable if S(w) = (1, ..., n), where S(w) is defined recursively as follows: write w = unv where n is the largest element in w and u and v are shorter sequences, and set S(w) = S(u)S(v)n, with S being the identity for one-element sequences.
• C는_n 순열 패턴 123(또는 길이 3의 다른 패턴 중 하나)을 피하는 {1, ..., n}의 순열 수입니다. 즉, 3개월 증가되는 순열이 없는 순열 수입니다. n = 3의 경우, 이러한 순열은 132, 213, 231, 312 및 321이다. n = 4의 경우 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312, 4321이다.
• C는_n 세트 {1, ..., n}의 비교차 파티션 수입니다. fortiori, C는_n n번째 벨 번호를 절대 초과하지 않는다. C는_n 또한 모든 블록의 크기가 2인 집합 {1, ..., 2n}의 비교차 파티션 수입니다. 이 두 가지 사실의 결합은 위그너 반원법칙의 2도 이상의 자유적 누적치가 모두 0이라는 수학적 유도에 의한 증거에 이용될 수 있다. 이 법칙은 자유 확률 이론과 무작위 행렬 이론에서 중요하다.
• C는_n 높이 n의 계단 모양을 직사각형 n개로 바둑판식으로 배열하는 방법의 수입니다. 대각선을 가로지르고 가장자리만 보면 완전한 이진수가 나온다. 다음 그림은 사례 n = 4를 나타낸다.

• C는_n 모두 수평선 위에 머무르는 n개의 업스트로크, n개의 다운스트로크로 "산맥 범위"를 형성하는 방법의 수입니다. 산은 결코 지평선 아래로 내려가지 않는다는 것이 산맥의 해석이다.

• C는_n 표준 Young tableaux의 숫자로, 도표는 2 by n 직사각형이다. 즉, 숫자 1, 2, ..., 2n을 2 by n 직사각형으로 배열하여 각 행과 각 열이 증가하도록 하는 방법의 수입니다. 이와 같이, 이 공식은 후크 길이 공식의 특별한 사례로 도출될 수 있다.
• C는_n n개의 라벨이 없는 품목에 대한 반주문 수입니다.^[5]

• 무한 완벽한 이진 결정 트리와 n - 1표를 부여하면, $C{\displaystyle {}_{}}$ ${\displaystyle n_{}}${\$displaystyle C_{n}$는 어떤 노드에서든 원하는 방식으로 표를 분할할 수 있다는 점에서 가능한 투표 결과의 수입니다$$.
• ${\displaystyle C_{}}$ ${\displaystyle n_{}}$ ${\$는 $1{\displaystyle \mathrm{}}$ ${\displaystyle$ 1$}$ 로 $시작$하는 길이$$n 시퀀스의 수입니다$$. $0{\displaystyle \mathrm{}}$ ${\displaystyle 0$$\}$ $또는$ 1 ${\displaystyle$ 1}만큼 증가하거나 임의의 수만큼 감소할 수 있다($최소{\displaystyle \mathrm{}}$ 1 ${\displaystystyle$ 1$}).$ For ${\displaystyle n=4}$ these are ${\displaystyle 1234,1233,1232,1231,1223,1222,1221,1212,1211,1123,1122,1121,1112,1111}$. Compared to the similar representation of the Bell numbers, only ${\displaystyle 1213}$ is missing.

공식 증명

이 공식의 이유를 설명하는 방법에는 여러 가지가 있다.

${\displaystyle C_{n}={\frac {1}{n+1}{2n \선택 n}}$

위에 나열된 결합 문제를 해결한다. 아래의 첫 번째 증거는 발생 함수를 사용한다. 다른 증거들은 주관적인 증거들의 예들이다; 그것들은 정확한 공식에 도달하기 위해 말 그대로 어떤 종류의 물체의 모음을 세는 것을 포함한다.

첫 번째 증거

우리는 우선 위에 열거된 모든 결합적 문제들이 세그너의 재발[6] 관계를 만족시키는 것을 관찰한다.

${\displaystyle C_{0}=1\text{n1}\quad C_{n+1}=\sum _{i=0}^{n}C_{n-i}\c_{n-i}\quad{}}}}}}}}}}}$

예를 들어, 길이 2 2의 모든 Dyck 단어 w는 양식에 독특한 방법으로 쓰여질 수 있다.

w = Xw₁Yw₂

(아마도₂ 비어 있을 것이다) Dyck 단어 w와₁ w.

카탈루냐 번호의 생성 함수는 다음과 같이 정의된다.

${\displaystyle c(x)=\sum _{n=0}^{\nft }C_{n}x^{n}.}$

위에 제시된 재발 관계는 관계에 의해 함수 생성 형태로 요약될 수 있다.

${\displaystyle c(x)=1+xc(x)^{2};}$

즉, 이 방정식은 양쪽을 권력 계열로 확장함으로써 재발 관계에서 따온 것이다. 한편, 재발 관계는 카탈로니아 숫자를 고유하게 결정하며, 다른 한편에서는 발생 함수 관계를 대수적으로 해결하여 산출할 수 있다.

${\displaystyle c(x)={\frac {1\pm {\sqrt{1-4x}}{2x}}.}$

마이너스 부호를 선택하면 분수는 0에서 검정력 시리즈를 가지므로 계수가 카탈로니아 숫자여야 한다. 이 해결책은 만족한다.

${\displaystyle \lim_{x\to 0^{+}c(x)=C_{0}=1.}$

제곱근 용어는 ID를 사용하여 파워 시리즈로 확장할 수 있다.

${\displaystyle {\sqrt {1+y}}=\sum _{n=0}^{\infty }{{\frac {1}{2}} \choose n}y^{n}=\sum _{n=0}^{\infty }{\frac {(-1)^{n+1}}{4^{n}(2n-1)}}{2n \choose n}y^{n}}$

이것은 뉴턴의 일반화된 이항 정리의 특별한 경우로서, 일반 정리와 마찬가지로, 그것은 그것의 테일러 시리즈를 생산하기 위한 파생상품을 계산함으로써 증명될 수 있다.

y = -4x 제공 설정

${\displaystyle {\sqrt{1-4x}=\sum _{n=0}^{\inflit }{\frac {-1}{2n:1}} \n \선택 n}x^{n}}}}$

그리고 이 파워 시리즈를 c(x)의 표현으로 대체하고, 합계 지수 n을 1로 바꾸면, 확장은 다음과 같이 단순화된다.

${\displaystyle \sum _{n=1}^{\inflat }{1}{1}{2n-1)}{2n \n 선택 n}x^{n-1}.}$

$N{\displaystyle }$= ${\displaystyle n}$ -${\displaystyle 1}$ ${\displaystyle N=n-1$}을$($를) 다음과 같이 하십시오.

${\displaystyle \sum _{N=0}^{\inflat }{\frac {1}{1}{2N+1)}{2N+2 \{2N+2 \선택 N+1}x^{}엔}$

$그리고{\displaystyle \frac{\mathrm{}}{}}$ 1 ${\displaystyle \frac{2\mathrm{}}{}}$( ${\displaystyle \frac{2}{}}$ ${\displaystyle \frac{\mathrm{N}}{}}$+ 1${\displaystyle \frac{}{}}$)${\displaystyle \frac{}{}}$( 2 ${\displaystyle \genfrac{}{}{0ex}{}{N}{}}$+ ${\displaystyle \genfrac{}{}{0ex}{}{2}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{}{}}$+ ${\displaystyle \genfrac{}{}{0ex}{}{1}{}}$)${\displaystyle }$= C ${\displaystyle N_{}}$ ${\${1}{$1}{2N+1)}{2N+2$ \{2N+2 \선택 $N+1}=C_이기$ 때문이다.${{N}}($위의 '재발 방지' 참조)

우리는 가지고 있다.

${\displaystyle c(x)=\sum _{n=0}^{\n}{2n \선택 n}{\frac {x^{n}}{n+1}.}$

두 번째 교정쇄

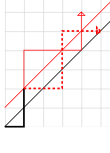
우리는 n × n 그리드의 대각선에서 시작하고 끝나는 경로의 수를 계산한다. 그러한 모든 길은 올바른 걸음과 높은 걸음걸이가 있다. 2n 단계 중 위 또는 오른쪽을 선택할 수 있으므로, 이 유형의 단조$$ 경로에는 총${\displaystyle }$(${\displaystyle \genfrac{}{}{0ex}{}{}{}}$) ${\${\$tbinom {2n}{n}}}$개가 있다. 나쁜 경로는 주 대각선을 가로지르고 다음으로 높은 대각선(그림에서 빨간색)을 건드려도 된다.

더 높은 대각선이 표시된 후 경로의 부분은 빨간색 점선으로 표시된 것처럼 대각선을 중심으로 플립된다. 이것은 모든 올바른 단계를 상향으로 바꾸고, 반대로 상향으로 바꾼다. 반영되지 않은 경로의 구간에는 오른쪽 단계보다 한 단계 더 높은 단계가 있으므로, 나쁜 경로의 나머지 구간은 위쪽 단계보다 한 단계 더 많은 오른쪽 단계가 있다. 경로의 이 부분이 반영되면, 그것은 올바른 단계보다 한 단계 더 높은 단계를 갖게 될 것이다.

아직 2n단계가 남아있기 때문에 n+1단계가 있고 n -1단계가 있다. 따라서 (n,n)에 도달하는 대신, 반사 후의 모든 나쁜 경로는 (n - 1, n + 1)로 끝난다. 왜냐하면 (n - 1) × (n + 1) 그리드의 모든 단조로운 경로가 더 높은 대각선을 충족시키기 때문에, 그리고 반사 과정이 되돌릴 수 있기 때문에, 반사되는 것은 따라서 원래의 그리드의 나쁜 경로와 새로운 그리드의 단조로운 경로 사이의 바이어싱이 된다.

따라서 불량 경로의 수는 다음과 같다.

${\displaystyle {n-1+n+1 \n-1}={2n 선택 n-1}={2n 선택 \n+1}$

그리고 원래 그리드의 총 단조 경로 수에서 불량 경로 수를 제거하여 카탈로니아 경로(즉, 양호한 경로)의 수를 구한다.

${\displaystyle C_{n}={2n \선택 n}-{2n \선택 n+1}={\frac {1}{n+1}:{2n \선택 n}}$

Dyck 단어의 경우, N X와 N Y의 (비 Dyck) 시퀀스로 시작하여 Dyck 조건을 위반하는 첫 번째 Y 이후의 모든 X와 Y를 교환한다. 이 Y 이후 Xs보다 Y가 정확히 하나 더 많다는 점에 유의하십시오.

세 번째 교정쇄

이 주관적 증거는 C에_n 대한 공식의 분모에 나타나는 n + 1 용어에 대한 자연적인 설명을 제공한다. 이 증명의 일반화된 버전은 루카비카 요제프(2011년) 논문에서 확인할 수 있다.^[7]

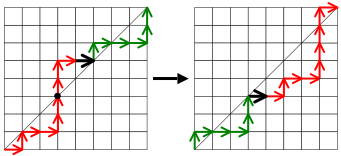
단조로운 경로가 주어진 경우 경로의 초과도는 대각선 위의 수직 가장자리 수로 정의된다. 예를 들어, 그림 2에서 대각선 위의 가장자리는 빨간색으로 표시되므로 이 경로의 초과도는 5이다.

초과가 0이 아닌 단조로운 경로의 경우, 다음 알고리즘을 적용하여 초과가 시작했던 경로보다 1보다 적은 새로운 경로를 구축한다.

• 왼쪽 아래에서 시작하여 대각선 위로 처음 이동할 때까지 경로를 따라 이동하십시오.
• 대각선에 다시 닿을 때까지 경로를 계속 따라가십시오. X로 도달한 첫 번째 가장자리를 나타낸다.
• X 이전에 발생한 경로의 일부를 X 이후 발생하는 부분과 교환한다.

그림 3에서 검은 점은 경로가 대각선을 처음 가로지르는 지점을 나타낸다. 검은색 가장자리는 X이며, 오른쪽 상단 모서리에 빨간색 부분의 마지막 격자점을, 왼쪽 하단 모서리에 녹색 부분의 첫 번째 격자점을 배치하고, 그에 따라 X를 배치하여 두 번째 다이어그램에 나타난 새로운 경로를 만든다.

초과가 3에서 2로 줄었다. 사실 알고리즘은 대각선에서 시작하는 첫 번째 수직 단계(검은 점으로 표시된 지점에서)가 대각선 위에서 아래로 통과하는 고유한 수직 에지이기 때문에 대각선의 동일한 면에 다른 모든 수직 에지가 있기 때문에 우리가 대각선에 공급하는 경로에 대해 초과도가 1 감소한다.

또한 이 과정이 되돌릴 수 있다는 것도 어렵지 않다: 초과도가 n보다 작은 경로 P를 고려할 때, 알고리즘을 적용할 때 정확히 하나의 경로가 있다. 실제로 원래 대각선으로 끝나는 첫 번째 수평 단계였던 (검은색) 에지 X는 대각선에서 시작하는 마지막 수평 단계가 되었다. 또는 원래 알고리즘을 반전시켜 대각선 아래를 통과하는 첫 번째 에지를 찾으십시오.

이는 초과 n의 경로 수가 초과 n - 1의 경로 수와 같으며, 초과 n - 2의 경로 수와 같으며, 따라서 0으로 감소함을 의미한다. 즉, 모든 단조 경로의 집합을 0과 n 사이의 가능한 초과에 해당하는 n + 1 균일한 크기의 클래스로 분할했다. $){\$이(가) 있기 때문에 원하는 $공식{\displaystyle {}_{}}$ ${\displaystyle {Cn}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \frac{1n}{}}$ ${\displaystyle \frac{+}{}}$ ${\displaystyle \frac{1}{}}$( ${\displaystyle \genfrac{}{}{0ex}{}{}{}}$) .$${\$displaystyle \textstyle C_{n}={\frac${1$}{n+1$}{$2n \$n$\}$을 얻는다.$}$

그림 4는 n = 3에 대한 상황을 보여준다. 20개의 가능한 단일 경로 각각이 테이블의 어딘가에 나타난다. 첫 번째 열에는 대각선 위에 완전히 놓여 있는 초과 3의 모든 경로가 표시된다. 오른쪽 열은 알고리즘의 연속 적용 결과를 보여주며, 초과도는 한 번에 한 단위씩 감소한다. 다섯 개의 행, 즉 C₃ = 5가 있고 마지막 열에는 대각선보다 높지 않은 모든 경로가 표시된다.

Using Dyck words, start with a sequence from ${\displaystyle \textstyle {\binom {2n}{n}}}$. Let ${\displaystyle X_{d}}$ be the first X that brings an initial subsequence to equality, and configure the sequence as ${\displaystyle (F)X_{d}(L)}$. The new sequence is ${\di$$splaystyle LXF}$.

네 번째 교정쇄

이 증거는 C와_n C 사이의_n+1 관계를 설정하기 위해 카탈로니아 숫자의 삼각측량 정의를 사용한다.

n + 2 변과 삼각형을 가진 다각형 P의 경우, 옆면 중 하나를 기준으로 표시하고 2n + 1 전체 가장자리 중 하나의 방향을 정한다. 주어진 베이스에 대해 그러한 (4n + 2)C_n 표시 삼각형이 있다.

다각형 Q에 n + 3 변이 있고 (다른) 삼각형이 있는 경우, 다시 한 변을 기준으로 표시한다. 밑면이 아닌 다른 면 중 하나를 표시하십시오(내측 삼각형 가장자리가 아님). 주어진 베이스에는 (n + 2)C와_{n + 1} 같이 표시된 삼각형이 있다.

이 두 개의 표시된 삼각형 사이에는 간단한 편차가 있다. 옆면이 표시된 Q의 삼각형을 접거나(두 가지 방법으로, 그리고 밑부분을 접을 수 없는 두 개의 삼각형을 빼거나), 반대로 P의 방향 가장자리를 삼각형으로 확장하여 새로운 면을 표시할 수 있다.

그러므로

${\$$$$C_{n}=(n+2)C_$$n+1}$1.

${\displaystyle \frac{\mathrm{4n}}{}}$- ${\displaystyle \frac{}{}}$+ 1 ${\displaystyle {\mathrm{C}}_{}}$ -${\displaystyle {}_{}}$1${\displaystyle {}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$. ${\$1}$C_{n-1}=C_{n}.$$}$

왜냐하면${\displaystyle }$(${\displaystyle \mathrm{2n})!}$=${\displaystyle }$( ${\displaystyle \mathrm{2n})!}$( ${\displaystyle \mathrm{2n}}$- ${\displaystyle 1)!}$= ${\displaystyle {}^{}!}$( ${\displaystyle \mathrm{2n}}$- ${\displaystyle 1)!}$ ($2n)! (2n)!$ ($2n$)!!(2n-1$)!!$$=2^{n}n!(2n-1)!!$$}$

그때

${\displaystyle {\frac {(2n)!}}{n!}=2^{n}(2n-1)!!=(4n-2)!!!!!}$

$C{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle 1}$ ${\displaystyle C_{1}=1$}을(를$)$ 사용하여 반복을 적용하면 결과가 나온다$$.

다섯 번째 교정쇄

이 증거는 카탈로니아 숫자의 Dyck 단어 해석에 기초하므로, C는_n 대괄호 n쌍을 정확하게 일치시키는 방법의 수입니다. 우리는 c와 그 역("["와 "]이 교환되는 곳)으로 c와^' (아마 빈) 정확한 문자열을 나타낸다. c는 c = [ c₁ ] c로₂ 고유하게 분해될 수 있으므로, 닫는 괄호를 즉시 배치할 수 있는 지점을 합하면 재귀적 정의를 제공한다.

${\displaystyle C_{0}=1\text{n1}\quad C_{n+1}=\sum _{i=0}^{n}C_{n-i}\c_{n-i}\quad{}}}}}}}}}}}$

b는 길이 2n의 균형 잡힌 문자열을 의미하도록 한다. 즉, 길이가 "["와 "]"의 수가 ${\displaystyle {같으므로}_{}Bn\genfrac{}{}{0ex}{}{\mathrm{}}{}}$ ${\displaystyle =}$ (${\displaystyle \genfrac{}{}{0ex}{}{}{}}$) {\$displaystyle \textstyle B_{$n}={$2n \선택$ n$\}\}\}\}.$ 이전과 같이 모든 균형 잡힌 문자열은 [ c ] 또는 [ ] c^' [b]로 고유하게 분해될 수 있다.

${\displaystyle B_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}.}$

잘못된 균형 문자열은 c ]로 시작하고, 나머지 문자열은 ]보다 한 개 더 많으므로

${\displaystyle B_{n+1}-C_{n+1}=\sum _{i=0}^{n}{2i+1 \선택 i}C_{n-i}}}$

또한 이 정의에서 다음과 같은 내용을 확인할 수 있다.

${\displaystyle B_{n+1}-C_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}-\sum _{i=0}^{n}C_{i}\,C_{n-i}=\sum _{i=0}^{n}(2B_{i}-C_{i})C_{n-i}.}$

그러므로

${\displaystyle 2B_{i}-C_{i}={2i+1 \선택 i}={\frac {2i+1}{i+1}{i+1}{i}}}$

${\displaystyle C_{i}=B_{i}\왼쪽(2-{\frac {2i+1}{i+1}{i+1}\오른쪽),}$

${\displaystyle C_{i}={\frac {1}{i+1}:{\binom {2i}{i}}}.}$

여섯 번째 교정쇄

이 증거는 카탈루냐 숫자에 대한 다이크어 해석에 기초하고 드보레츠키와 모츠킨의 사이클 보조기를 사용한다.^[8][9]

우리는 X와 Y가 지배하는 순서를 왼쪽에서 오른쪽으로 읽으면 X의 수가 Y의 수보다 항상 엄격히 더 많으면 X와 Y가 지배하는 순서를 부른다. 주기적^[10] 보조정리기는 $${\$displaystyle$m} X$$ 및 $n{\displaystyle }${\$displaystyle$n$}$ Y의$$ 모든 시퀀스가 ${\displaystyle \mathrm{정확히}}$ m -${\displaystyle }$n$${\$displaystyle m_n}$을를 지배하는 주기적 순열을 갖는다고 명시한다. 이를 보려면 $m{\displaystyle }$ + ${\displaystyle m+n}$ X와$$ Y의 지정된 순서를 원으로 정렬하십시오. XY 쌍을 반복적으로 제거하면 정확히 ${\displaystyle m}$- n ${\displaystyle m-n}$ X가$$ 남는다. 이 X들 각각은 어떤 것이 제거되기 전에 지배적인 순환 순열의 시작이었다.

For example, consider ${\displaystyle XXYXY}$. This is dominating, but none of its cyclic permutations ${\displaystyle XYXYX}$, ${\displaystyle YXYXX}$, ${\displaystyle XYXXY}$ and ${\displaystyle YXXYX}$ are.

특히 $m{\displaystyle }$= ${\displaystyle \mathrm{n}}$+ 1 ${\displaystyle m=n+1$}이$($가) 되면 정확히 하나의 지배적인 순환 순열이 있다. 그것에서 선행 X를 제거하면(주요 시퀀스는 X로 시작해야 함) Dyck 시퀀스가 남는다. Since there are ${\displaystyle \textstyle {2n+1 \choose n}}$ in total, and each one belongs to an equivalence class of size 2n+1 (because n, m and 2n+1 are pairwise coprime), we have ${\displaystyle \textstyle {\frac$${1}{2n+1}}{2n+1 \choose n}={\frac {1}{n+1}}{2n \choose n}=C_{n}}$ distinct cycles of ${\displaystyle n+1}$ X's and ${\displaystyle n}$ Y's, each of which corresponds to exactly one Dyck sequence, hence ${\displaystyle \textstyle C_{n}}$ counts Dyck sequences.

행클 매트릭스

(i, j) 항목이 카탈로니아 번호 C인_i+j−2 n×n 행클 행렬은 n의 값에 관계없이 1이 결정된다. 예를 들어, n = 4의 경우

${\displaystyle \det{bmatrix}1&&2&5\\1&2&5&144\2&144\5&144\5&144&#4226\end{bmatrix}=1.}$

더욱이 (i, j) 항목이 카탈로니아 번호 C로_i+j−1 채워지도록 인덱싱이 "변형"된 경우, n의 값에 관계없이 결정 요소는 여전히 1이다. 예를 들어, n = 4의 경우

${\displaystyle \det{bmatrix}1&2&5&144\\2&144\\5&14&42\\5&14&42&nd\14&42&#429\end{bmatrix}=1.}$

이 두 조건을 종합하면 카탈로니아 숫자를 고유하게 정의한다.

카탈루냐-한켈 매트릭스 고유의 또 다른 특징은 2에서 시작하는 n×n 서브매트릭스의 결정 요인이 n + 1을 갖는다는 것이다.

${\displaystyle \det{bmatrix}2\end{bmatrix}=2}$

${\displaystyle \det{bmatrix}2&5\5\14\end{bmatrix}=3}$

${\displaystyle \det{bmatrix}2&#5&14\5&144\\14&42\\14&42&#14&#8226\end{bmatrix}=4}$

${\displaystyle \det{bmatrix}2&#5&1442\\5&1442\\\14429\429\429&1430\end{bmatrix}=5}$

기타의

역사

카탈로니아 수열은 18세기에 레오나르드 오일러에 의해 설명되었는데, 그는 다각형을 삼각형으로 나누는 다양한 방법의 수에 관심이 있었다. 이 순서는 하노이 탑 퍼즐을 탐험하는 동안 괄호화된 표현과 연관성을 발견한 외젠 찰스 카탈란의 이름을 따서 명명되었다. 다이크 단어에 대한 반성계수법(두 번째 증거)은 1887년 데시레 안드레에 의해 발견되었다.

"카탈란 숫자"라는 이름은 존 리오르단으로부터 유래되었다.^[11]

1988년, 1730년까지 몽골의 수학자 밍간투에 의해 중국에서 카탈로니아 숫자 순서가 사용되었다는 사실이 밝혀졌다.^[12][13] 이때 그는 1774년 제자인 첸지신이 완성했으나 60년 후에 출판한 《게위안미 루제파》[원분할의 정밀한 비율을 얻기 위한 빠른 방법]를 쓰기 시작했다. 피터 J. 라르콤베(1999)는 1700년대 초 중국에 3개의 무한 시리즈를 가져온 피에르 자르투스의 자극 등 밍간투 작품의 특징 일부를 스케치했다.

예를 들어, 밍은 죄(2α)와 죄(4α)의 직렬 확장을 죄(α)의 관점에서 표현하기 위해 카탈로니아 수열을 사용했다.

일반화

음이 아닌 정수의 2-모수 시퀀스$({\displaystyle \frac{2}{}}$ m${\displaystyle \frac{}{}}$)${\displaystyle \frac{}{}}$!${\displaystyle \frac{}{}}$( ${\displaystyle \frac{2}{}}$ ${\displaystyle \frac{n}{}}$)${\displaystyle \frac{}{}}$!${\displaystyle \frac{}{}}$( m${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{n}{}}$)${\displaystyle \frac{}{}}$! ${\displaystyle \frac{m}{}}$! n ! ${\$$n!}}}$은 카탈루냐 숫자의 일반화다. 이 숫자들은 Ira Gesel에 따라 슈퍼 카탈란 숫자로 명명된다. 이것들은 슈뢰더-히파르쿠스 숫자와 혼동해서는 안 되며,때로는슈퍼카탈란 숫자라고도 한다.

$m{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle m=1}$의 경우$,$ 이것은 일반적인 카탈로니아 숫자의 두 배에 불과하며, ${\displaystyle m}$= n ${\displaystyle m=n}$의 경우$,$ 이 숫자들은 조합 설명이 쉽다. 그러나 다른 조합설명은 $m{\displaystyle }$= 2,${\displaystyle 3}$ ${\displaystyle m=2,3}$ 및$$ $4{\displaystyle \mathrm{}}$ ${\displaystyle 4}$에 대해서만 알려져^[14] 있으며$,$^[15] 일반적인 조합 해석을 찾는 것은 개방적인 문제다.

세르게이 포민과 네이선 리딩은 어떤 유한 결정학적 콕시터 그룹, 즉 그 그룹의 완전한 상호교합적 요소의 수와 관련된 일반화된 카탈로니아 숫자를 부여했다. 관련 루트 시스템의 관점에서 보면, 그것은 양의 뿌리의 포셋에 있는 반체인(또는 순서 이상)의 수이다. 고전적인 카탈루냐 번호 $C{\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$는 A$$ {\$displaystyle A_{n}$의 루트 시스템에 해당한다$.$ 고전적 재발 관계는 일반화된다: Coxeter 다이어그램의 카탈로니아 번호는 모든 적절한 하위 직경의 카탈로니아 숫자의 합계와 같다.^[16]

카탈로니아 K-폴드 콘볼루션은 다음과 같다.^[17]

${\displaystyle \sum _{i_{1}+\cdots +i_{m}=n \atop i_{1},\ldots ,i_{m}\geq 0}C_{i_{1}}\cdots C_{i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2)(n+m/2+3)\cdots (n+m)}}C_{n+m/2}},&m{\text{짝수,}\\[5pt]{\dfrac {m(n+1)(n+2)\cdots (n+1)\cdots (n+1){n+(m+3)/2+1)\cdots (n+m)}}}}}}{n+m+m+m)}}}}}}}}}}}}}}C_{n+(m-1)/2},&m{\text{ 홀수.}}}\end{case}}$

카탈로니아 숫자들은 하우스도르프 순간 문제의 해결책이다.^[18]

참고 항목

메모들

참조

• 스탠리, 리처드 P(2015), 카탈루냐 숫자. 케임브리지 대학 출판부, ISBN 978-1-107-42774-7
• Conway and Guy (1996) The Book of Numbers. 뉴욕: 코페르니쿠스 96-106쪽.
• Gardner, Martin (1988), Time Travel and Other Mathematical Bewilderments, New York: W.H. Freeman and Company, pp. 253–266 (Ch. 20), ISBN 0-7167-1924-X
• Koshy, Thomas (2008), Catalan Numbers with Applications, Oxford University Press, ISBN 978-0-19-533454-8
• 코시, 토마스&정구앙 가오(2011) "카탈란 숫자의 일부 불분명한 특성", 수학적 가제트 95:96–102.
• Larcombe, P.J. (1999). "The 18th century Chinese discovery of the Catalan numbers" (PDF). Mathematical Spectrum. 32: 5–7.
• Stanley, Richard P. (1999), Enumerative combinatorics. Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, ISBN 978-0-521-56069-6, MR 1676282
• Egecioglu, Omer (2009), A Catalan–Hankel Determinant Evaluation (PDF)
• Gheorghiciuc, Irina; Orelowitz, Gidon (2020), Super-Catalan Numbers of the Third and Fourth Kind, arXiv:2008.00133

외부 링크

• Stanley, Richard P. (1998), Catalan addendum to Enumerative Combinatorics, Volume 2 (PDF)
• Weisstein, Eric W. "Catalan Number". MathWorld.
• 데이비스, 톰: 카탈로니아 숫자. 여전히 더 많은 예.
• 울프람 시위 프로젝트의 "세 가지 카탈루냐 숫자 해석의 동일성" [1]
• Wikiversity에서 파티션 관련 숫자 삼각형 관련 학습 자료