로그
Logarithm
| 연산 | ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
수학에서 로그는 지수화의 역함수입니다.즉, 밑 b에 대한 숫자 x의 로그값이 x를 생성하기 위해 b를 올려야 하는 지수임을 의미합니다.예를 들어, 1000 = 10이므로 1000의 로그 밑수 10은 3이거나 로그 (1000) = 3입니다.밑 b에 대한 x의 로그를 logb (x), 괄호가 없는 경우, logb x, 또는 명시적 밑이 없는 경우에도 log x, 혼동이 가능하지 않은 경우, 또는 큰 O 표기와 같이 밑이 중요하지 않은 경우로 표시됩니다.
로그 밑 10은 십진법 또는 보통 로그라고 불리며 과학과 공학에서 일반적으로 사용됩니다.자연 로그는 숫자 e ≈ 2.718을 기본으로 합니다. 매우 단순한 도함수 때문에 수학과 물리학에서 널리 사용됩니다.이진 로그는 밑이 2인 것을 사용하며 컴퓨터 과학에서 자주 사용됩니다.
로그는 1614년 존 네이피어(John Napier)에 의해 계산을 단순화하는 수단으로 도입되었습니다.[1]탐색기, 과학자, 엔지니어, 측량사 등이 빠른 속도로 도입하여 높은 정확도의 계산을 보다 쉽게 수행할 수 있게 되었습니다.로그 테이블을 사용하면 지루한 다자리 곱셈 단계를 테이블 조회 및 간단한 추가로 대체할 수 있습니다.이것은 제품의 로그가 요인들의 로그의 합이기 때문에 가능합니다.
로그 스케일은 광범위한 양을 더 작은 범위로 줄입니다.예를 들어, 데시벨(dB)은 비율을 로그로 표현하는 데 사용되는 단위로, 대부분 신호 전력 및 진폭(음압이 일반적인 예임)에 대해 사용됩니다.화학에서 pH는 수용액의 산도에 대한 로그 척도입니다.로그는 과학 공식과 알고리즘의 복잡성과 프랙탈이라고 불리는 기하학적 객체의 측정에서 일반적입니다.그것들은 음악 간격의 빈도 비율을 설명하는 데 도움이 되고, 소수를 세는 공식이나 근사 인자에 나타나고, 정신 물리학의 일부 모델에 정보를 주고, 법의학적 회계 처리에 도움이 될 수 있습니다.
지수화의 역수인 로그의 개념은 다른 수학적 구조로도 확장됩니다.그러나 일반 설정에서는 로그가 다중 값 함수인 경향이 있습니다.예를 들어, 복소수 로그는 복소수 지수 함수의 다중 값 역수입니다.마찬가지로 이산 로그는 유한 그룹에서 지수 함수의 다중 값 역수입니다. 공개 키 암호학에서 사용됩니다.
동기
덧셈, 곱셈, 지수화는 가장 기본적인 산술 연산 중 세 가지입니다.덧셈의 역은 뺄셈이고 곱셈의 역은 나눗셈입니다.마찬가지로 로그는 지수화의 역연산입니다.지수화(exponentiation)는 어떤 지수인 특정한 거듭제곱(exponent)에 밑인 b를 올려 x 값을 주는 것입니다.
밑 b의 로그는 입력 x에서 출력 y를 제공하는 역연산입니다.즉, b가 양수일 경우 = y =\는 x = =에 해당합니다.(b가 양수가 아닌 경우 지수와 로그를 모두 정의할 수 있지만 여러 값을 사용할 수 있으므로 정의가 훨씬 복잡합니다.)
로그를 도입한 주요한 역사적 동기 중 하나는 공식입니다.
정의.
b가 ≠ 1인 양의 실수 b가 주어지면, 밑 b에 대한 양의 실수 x의 로그는 x를 산출하기 위해 b를 올려야 하는 지수입니다.즉, 밑 b에 대한 x의 로그는 = b}= 한 실수입니다
로그는 "logb x"("x의 로그에서 밑 b로의 로그", "x의 밑 b의 로그" 또는 가장 일반적으로 "x의 밑 b의 로그"로 발음됨)로 표시됩니다.
이와 동등하고 한 정의는 함수 로그가 함수 ↦ b x x b}}의 역함수라는 것입니다
예
- 로그 16 = 4이므로 2 = 2 × 2 × 2 = 16.
- 로그는 음수일 수도 있습니다. 2 = - 1 _-1 의 {\ { 1 2 2. } {\}} {\ {\frac {2}}}.
- 로그 150은 대략 2. 176으로 2와 3 사이에 위치하며, 150은 10 = 100과 10 = 1000 사이에 위치합니다.
- b = b 및 b = 1이므로 b = 1을 기록하고 1 = 0을 기록합니다.
로그 항등식
로그 아이덴티티 또는 로그 법칙이라고 불리는 몇 가지 중요한 공식은 로그를 서로 연관시킵니다.[4]
곱, 몫, 거듭제곱, 근
곱의 로그는 곱해지는 숫자의 로그의 합이고, 두 숫자의 비율의 로그는 로그의 차이입니다.숫자의 p번째 거듭제곱의 로그는 숫자 자체의 로그의 p배입니다. p번째 뿌리의 로그는 숫자의 로그를 p로 나눈 것입니다.다음 표에는 이러한 ID가 예제와 함께 나열되어 있습니다.각 항등식은 왼쪽에서 로그 정의 = x x= 또는 = y y=로 대체한 후 도출할 수 있습니다.
| 공식 | 예 | |
|---|---|---|
| 제품. | ||
| 몫 | ||
| 힘 | ||
| 뿌리 |
베이스변경
로그 로그b x는 다음 공식을 사용하여 임의의 기저 k에 대한 x와 b의 로그로부터 계산할 수 있습니다.[nb 2]
일반적인 과학 계산기는 로그를 밑수 10과 e로 계산합니다.[5]임의의 밑 b에 대한 로그는 이전 공식에 의해 다음 두 로그 중 하나를 사용하여 결정할 수 있습니다.
숫자 x와 그것의 로그 = 로그 x를 알 수 없는 밑 b에 대해, 밑은 다음과 같이 주어집니다.
정의 방정식 = = x= _{=를 1 의 거듭제곱으로 취하는 것에서 알 수 있습니다
특정염기

베이스에 대한 모든 선택들 중에서, 세 가지가 특히 일반적입니다.이들은 b = 10, b = e(비합리적인 수학 상수 ≈ 2.71828), b = 2(이진 로그)입니다.수학적 분석에서 로그 밑 e는 아래에 설명된 분석적 특성 때문에 널리 사용됩니다.반면, 10진법 체계에서 수동 계산에 사용하기 쉬운 로그는 10진법입니다.[6]
다음 표에는 이러한 베이스 및 로그가 사용되는 필드에 대한 일반적인 표기법이 나와 있습니다.많은 학문 분야에서 로그b x 대신 로그 x를 작성하는데, 이는 의도된 베이스가 컨텍스트에서 결정될 수 있는 경우입니다."ISO 표기법" 열에는 국제 표준화 기구(ISO 80000-2)가 제안한 지정이 나열되어 있습니다.[10]표기 로그 x는 세 개의 기본 모두(또는 기본이 불확실하거나 중요하지 않은 경우)에 사용되었기 때문에 의도된 기본은 종종 문맥 또는 규율에 따라 추론되어야 합니다.컴퓨터 과학에서 log는 보통2 log를 가리키고 수학에서 log는 보통 log를e 가리킵니다.[11]다른 맥락에서 log는 종종 log를10 의미합니다.[12]
| 베이스 b | 로그b x의 이름 | ISO 표기법 | 기타 표기법 | 사용처 |
|---|---|---|---|---|
| 2 | 이항 로그 | lb x[13] | ld x, log x, lg x,[14] log2 x | 컴퓨터과학, 정보이론, 생물정보학, 음악이론, 사진학 |
| e | 자연대수 | lnx[nb3] | 로그 x (수학[18] 및 많은 프로그래밍 언어에서[nb 4]), loge x | 수학,물리학,화학, 통계학, 경제학, 정보이론 그리고 공학 |
| 10 | 평대수 | lg x | log x, log10 x (공학, 생물학, 천문학) | 다양한 엔지니어링 분야(데시벨 참조 및 아래 참조), 로그 테이블, 휴대용 계산기, 분광학 |
| b | 밑 b에 대한 대수 | 로그b x | 수학의 |
역사
17세기 유럽의 로그의 역사는 대수적 방법의 범위를 넘어 분석의 영역을 확장하는 새로운 함수의 발견을 목격했습니다.로그의 방법은 1614년 존 네이피어(John Napier)에 의해 미리피 로그룸 캐논리스 디스크립티오(Description of the Wonderful Canonis Description of Logms)라는 제목의 책에서 제안되었습니다.[19][20]네이피어의 발명 이전에, 1600년경 Jost Bürgi에 의해 광범위하게 개발된, 원형해부술 또는 진행표의 사용과 같은 비슷한 범위의 다른 기술들이 있었습니다.[21][22]네이피어는 중세 라틴어에서 로그를 뜻하는 용어인 "logarithmus"를 만들었는데, 이는 문자 그대로 "비율, 비율, 단어" + 산술 "숫자"에서 유래한 것입니다.
어떤 수의 공통 로그는 10의 거듭제곱 지수이며, 이 지수는 그 수와 같습니다.[23]어떤 수를 그렇게 많은 숫자를 필요로 한다고 말하는 것은 일반적인 대수를 대략적으로 암시하는 것이며 아르키메데스는 "숫자의 순서"라고 불렀습니다.[24]최초의 실제 로그는 곱셈을 덧셈으로 바꾸는 휴리스틱 방법이었고, 따라서 빠른 계산을 용이하게 했습니다.이러한 방법 중 일부는 삼각형 항등식에서 파생된 표를 사용했습니다.[25]이러한 방법을 전립선비대증이라고 합니다.
자연 로그로 알려진 함수의 발명은 프라하에 거주하는 벨기에 예수회 사람인 Gégoire de Saint-Vincent에 의해 직사각형 쌍곡선의 직교를 수행하려는 시도에서 시작되었습니다.아르키메데스는 기원전 3세기에 포물선의 사각형을 썼지만, 쌍곡선을 위한 사각형은 1647년 생뱅센트가 그의 결과를 발표할 때까지 모든 노력을 피했습니다.로그가 인수의 기하학적 진행과 값의 산술적 진행 사이에서 제공하는 관계는 A를 유도했습니다. A. de Sarasa는 자연 로그의 동의어인 "하이퍼볼릭 로그"라는 용어를 유도하면서, 생뱅센트의 직교와 프로스타파헤레시스의 로그 전통의 연결을 만듭니다.곧 크리스티아안 호이겐스와 제임스 그레고리가 새로운 기능을 인정했습니다.1675년 라이프니츠에 의해 로그라는 표기법이 채택되었고, 다음 해에 그는 그것을 적분 ∫ 연결했습니다
오일러가 복잡한 자연로그에 대한 그의 현대적인 개념을 개발하기 전에, 로저 코츠는 그가 1714년에 다음을[27] 보여주었을 때 거의 동등한 결과를 가지고 있었습니다.
로그 테이블, 슬라이드 규칙 및 기록 응용프로그램

계산기와 컴퓨터가 사용 가능해지기 전에 어려운 계산을 단순화함으로써, 로그는 과학, 특히 천문학의 발전에 기여했습니다.그들은 측량술, 천체 항해술, 그리고 다른 영역에서의 발전에 매우 중요했습니다.로그라 불리는 피에르시몽 라플라스
- "...[a]수개월의 노동을 며칠로 줄임으로써 천문학자의 수명을 두 배로 늘리고 긴 계산과 분리할 수 없는 오류와 혐오감을 덜어주는 훌륭한 책략."[28]
함수 f(x) = b가 로그 x의 역함수이기 때문에, 이것을 대수 반대라고 부릅니다.요즘에는 이 함수를 지수 함수라고 더 흔히 부릅니다.
로그 테이블
로그의 실용적인 사용을 가능하게 한 주요 도구는 로그표였습니다.[30]그러한 최초의 표는 네이피어의 발명 직후인 1617년 헨리 브릭스에 의해 작성되었지만 10을 기본으로 사용하는 혁신과 함께 작성되었습니다.Briggs의 첫 번째 표는 정확도 14자리의 1부터 1000까지의 범위에 있는 모든 정수의 공통 로그를 포함하고 있습니다.이어서 범위가 증가하는 표를 작성했습니다.이 표들은 특정 범위, 특정 정밀도에 있는 임의의 숫자 x에 대한 로그10 x의 값을 나열했습니다.Base-10 로그는 계산에 보편적으로 사용되었으며, 따라서 10의 인자별로 다른 수는 정수별로 다른 로그를 가지고 있으므로 공통 로그라는 이름이 붙었습니다.x의 공통 로그는 정수 부분과 특성 및 가수로 알려진 분수 부분으로 분리될 수 있습니다.로그 테이블에는 십진점에서 숫자를 세어 쉽게 특성을 확인할 수 있기 때문에 가수만 포함하면 됩니다.[31]10 · x의 특징은 1 더하기 x의 특징이며, 그들의 사마귀는 같습니다.따라서 3자리 로그 테이블을 사용하여 로그 값 3542는 다음과 같이 근사화됩니다.
보간을 통해 더 높은 정확도를 얻을 수 있습니다.
로그는x 단조 함수이기 때문에 10의 값은 같은 표에서 역방향 조회를 통해 결정할 수 있습니다.
계산
두 개의 양수 c와 d의 곱과 몫은 로그의 합과 차이로 일상적으로 계산되었습니다.제품 cd 또는 몫 c/d는 동일한 표를 통해 합 또는 차이의 대수를 찾는 데서 나왔습니다.
눈에 띄는 정밀도를 요구하는 수동 계산의 경우, 두 로그의 조회를 수행하고, 합 또는 차이를 계산하고, 대수를 조회하는 것은 삼각형 항등식에 의존하는 초기 방법에 의한 곱셈을 수행하는 것보다 훨씬 빠릅니다.
거듭제곱과 근의 계산은 곱셈이나 나눗셈, 조회로 줄어듭니다.
그리고.
삼각 함수의 공통 로그를 포함하는 표를 통해 삼각 함수 계산이 용이해졌습니다.
슬라이드 규칙
또 다른 중요한 응용 프로그램은 계산에 사용되는 대수적으로 분할된 척도 쌍인 슬라이드 규칙이었습니다.비슬라이딩 로그 눈금, 군터의 법칙은 네이피어의 발명 직후에 발명되었습니다.윌리엄 오트레드는 슬라이드 규칙(서로에 대해 이동 가능한 로그 눈금 쌍)을 만들기 위해 이 규칙을 강화했습니다.숫자는 로그 간의 차이에 비례하는 거리에서 슬라이딩 눈금에 배치됩니다.상위 스케일을 적절히 슬라이딩하면 다음과 같이 로그를 기계적으로 추가할 수 있습니다.

예를 들어, 하위 척도의 1에서 2까지의 거리와 상위 척도의 1에서 3까지의 거리를 더하면 6이 산출되며, 이 값은 하위 부분에서 판독됩니다.슬라이드 규칙은 1970년대까지 엔지니어와 과학자들에게 필수적인 계산 도구였습니다. 이는 정밀도를 희생하면서도 표를 기반으로 하는 기술보다 훨씬 빠른 계산을 가능하게 하기 때문입니다.[32]
분석속성
로그를 더 깊이 연구하려면 함수의 개념이 필요합니다.함수는 주어진 한 숫자가 다른 숫자를 만들어내는 규칙입니다.[33]예를 들어 임의의 실수 x로부터 b의 x번째 거듭제곱을 생성하는 함수를 들 수 있습니다. 여기서 밑 b는 고정된 숫자입니다.이 함수는 f(x) = b로 표기됩니다. b가 양수이고 1과 같지 않을 때, f는 실수에서 양의 실수로의 함수로 간주될 때 가역적임을 아래에서 보여줍니다.
존재
b를 1과 같지 않은 양수라고 하고 f(x) = b라고 합니다.
이것은 어떤 연속적인 엄밀하게 단조로운 함수가 그 영역과 범위 사이에서 객관적이라는 실제 분석의 표준 결과입니다.이 사실은 중간값 정리에서 따온 것입니다.[34]이제 f는 엄밀하게 증가하고(b > 1일 경우), 또는 엄밀하게 감소하고([35]0 < b < 1일 경우), 연속적이고, R \을 가지며 범위 > _을 갖습니다따라서 f는 \에서 > 0 까지의 사영입니다즉, 각각의 양의 실수에 , x = {\b^{x}=인 실수 x가 정확히 하나 있습니다
b: > → {\ _colon이(가) 역오프를 나타내도록 합니다.즉, 로그는 b = y b}=인 실수 x입니다이 함수를 기저 로그 함수 또는 로그 함수(또는 그냥 로그)라고 합니다.
제품 공식에 의한 특징
함수 로그b x 는 또한 본질적으로 제품 공식에 의해 특징지어질 수 있습니다.
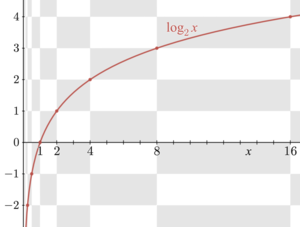
로그 함수의 그래프

위에서 논의한 바와 같이, 함수 로그는 지수 x↦ {\ x b와 반대입니다 따라서, 그들의 그래프는 오른쪽과 같이 x와 y coordin수를 교환할 때(또는 대각선 x = y에서 반사할 때) 서로 대응됩니다. f 의 그래프에 있는 점 (t, u = b)는 점 (u, t = log u)를 로그의 그래프에서 또는 그 반대입니다.결과적으로, b가 1보다 클 경우, x가 무한대로 커지면b 로그 (x)는 무한대로 갈라집니다 (어떤 주어진 수보다도 커집니다.이 경우 logb(x)는 증가 함수입니다.b < 1의 경우 로그b(x)는 대신 무한대를 차감하는 경향이 있습니다.x가 0에 가까워지면 로그b x는 b > 1에 대해 마이너스 무한대로 이동합니다(각각 b < 1에 대해 무한대를 더한 값).
도함수 및 항도함수

함수의 분석 속성은 그 역으로 전달됩니다.[34]따라서 f(x) = b가 연속적이고 미분 가능한 함수이므로 논리도 마찬가지입니다.대략 연속 함수는 그래프에 뾰족한 "모퉁이"가 없으면 구별할 수 있습니다.또한, f(x)의 도함수가 지수함수의 성질에 의해 ln(b) b로x 평가될 때, 연쇄법칙은 로그b x의 도함수가 다음과[35][37] 같이 주어진다는 것을 암시합니다.
ln(x)의 도함수는 1/x이며, 이는 ln(x)가 x = 1에 대한 값이 0인 1/x의 유일한 도함수임을 의미합니다.이것은 자연 로그를 "자연"으로 인정하도록 동기를 부여한 매우 간단한 공식입니다. 이것은 또한 상수 e의 중요성에 대한 주요한 이유 중 하나입니다.
일반화된 함수 인수 f(x)를 갖는 도함수는
자연 로그의 적분 표현

등식(1)은 적분을 두 부분으로 나누고 등식(2)은 변수의 변화(w = x/t)입니다.아래 그림에서 분할은 영역을 노란색 부분과 파란색 부분으로 나누는 것에 해당합니다.왼쪽 파란색 영역을 요소 t만큼 수직으로 축소하고 같은 요소만큼 수평으로 축소해도 크기가 변경되지 않습니다.적절히 이동하면 영역이 함수 f(x) = 1/x의 그래프에 다시 들어맞습니다.따라서 t에서 tu까지의 f(x)의 적분인 왼쪽 파란색 영역은 1에서 u까지의 적분과 같습니다.이것은 더 기하학적인 증명으로 (2) 등식을 정당화합니다.

거듭제곱 공식 ln(t) = rln(t)도 유사한 방법으로 유도할 수 있습니다.
자연수의 역수에 대한 합은
대수의 초월성
대수적이지 않은 실수를 초월수라고 합니다. 예를 들어, π와 e는 그러한 수이지만, -{\ 그렇지 않습니다.거의 모든 실수는 초월적입니다.로그는 초월 함수의 한 예입니다.겔폰드-슈나이더 정리는 로그가 보통 초월적인, 즉 "어려운" 값을 취한다고 주장합니다.[44]
계산

로그는 로그 (1000) = 3과 같이 계산하기 쉬운 경우가 있습니다. 일반적으로 로그는 멱급수 또는 산술 geometric 평균을 사용하여 계산하거나 고정된 정밀도를 제공하는 미리 계산된 로그 표에서 가져올 수 있습니다.방정식을 대략 푸는 반복적인 방법인 뉴턴의 방법은 로그를 계산하는 데에도 사용될 수 있는데, 이는 그 역함수인 지수 함수가 효율적으로 계산될 수 있기 때문입니다.[47]룩업 테이블을 사용하여 CORDIC와 유사한 방법을 사용하여 덧셈 및 비트 시프트의 연산만을 사용하여 로그를 계산할 수 있습니다.[48][49]또한 이항 로그 알고리즘은 x의 거듭된 제곱에 기초하여 lb(x)를 재귀적으로 계산하고 관계를 이용합니다.
멱급수
테일러 급수

0 < z ≤ 2를 만족하는 임의의 실수 z에 대하여, 다음 공식이 성립합니다.[nb 5][50]
예를 들어, z = 1.5일 때 세 번째 근사값은 0.4167로 ln(1.5) = 0.405465보다 약 0.011 큽니다.이 영상 시리즈는 합의 수가 충분히 많은 경우 임의의 정밀도로 ln(z)에 근사합니다.따라서 기초 미적분학에서 ln(z)는 이 급수의 극한입니다.이는 z = 1에서 자연 로그의 테일러 급수입니다.ln(z)의 테일러 급수는 그 이후 z가 작을 때 ln(1 + z)에 특히 유용한 근사치를 제공합니다.
역 쌍곡 접선
또 다른 시리즈는 역 쌍곡 탄젠트 함수를 기반으로 합니다.
밀접하게 관련된 방법을 사용하여 정수의 로그를 계산할 수 있습니다.위의 급수에 = n+ z={\을 넣으면 다음과 같습니다.
산술-기하학 평균 근사치
산술-기하학 평균은 자연 로그의 고정밀 근사치를 산출합니다.1982년에 사사키와 카나다는 소수점 400자리에서 1000자리 사이의 정밀도가 특히 빠르다는 것을 보여주었고 테일러 급수 방법은 일반적으로 정밀도가 덜 필요할 때 더 빠르다는 것을 보여주었습니다.그들의 작업에서 ln(x)는 (칼 프리드리히 가우스로 인해) 다음 공식에 의해 2(또는−p p 정밀 비트)의 정밀도로 근사됩니다.[51][52]
여기서 M(x, y)는 x와 y의 산술 기하학적 평균을 나타냅니다.x와 y의 평균 (x + y)/2 (산술평균)과 기하평균)을 반복하여 계산한 다음 두 숫자가 다음 x와 y가 되도록 합니다.두 수는 M(x, y)의 값인 공통 한계로 빠르게 수렴합니다. m은 다음과 같이 선택됩니다.
필요한 정밀도를 확보할 수 있습니다.m이 크면 M(x, y) 계산이 더 많은 단계를 밟게 되지만(초기 x와 y가 더 멀리 떨어져 있으므로 수렴하는 데 더 많은 단계가 필요함) 더 많은 정밀도를 얻을 수 있습니다.상수 π 및 ln(2)은 빠른 수렴 직렬로 계산할 수 있습니다.
파인만 알고리즘
Los Alamos National Laboratory에서 Manhattan Project를 연구하는 동안 Richard Feynman은 long division과 비슷한 로그를 계산하는 비트 처리 알고리즘을 개발했고 나중에 Connection Machine에서 사용되었습니다.알고리즘은 모든 실수 1 < x < 2가 1 + 2 형태의−k 서로 다른 인자들의 곱으로 표현될 수 있다는 사실을 사용합니다.알고리즘은 P = 1, k = 1부터 순차적으로 해당 제품 P를 구축합니다: P · (1 + 2) < x이면 P를 P · (1 + 2)로 바꿉니다.그러면 는 상관없이 1씩 증가합니다.알고리즘은 k가 원하는 정확도를 줄 수 있을 정도로 크면 중지됩니다.log(x)는 인자 1 + 2가−k 제품 P에 포함된 k에 해당하는 log(1 + 2−k)의 항의 합이므로, 모든 k에 대해 log(1 + 2−k) 표를 사용하여 단순 덧셈으로 log(x)를 계산할 수 있습니다.로그 표에는 임의의 밑수를 사용할 수 있습니다.[53]
적용들

로그는 수학의 안과 밖에 많은 응용을 가지고 있습니다.이러한 현상 중 일부는 규모 불변성의 개념과 관련이 있습니다.예를 들어, 노틸러스 껍질의 각 챔버는 상수 계수에 의해 축척된 다음 챔버의 근사 복사본입니다.이로 인해 로그 나선이 생성됩니다.[54]앞자리의 분포에 대한 벤포드의 법칙은 척도 불변성으로도 설명될 수 있습니다.[55]로그는 자기 유사성과도 연결됩니다.예를 들어 로그는 문제를 두 개의 유사한 작은 문제로 나누고 해결책을 패치하여 해결하는 알고리즘의 분석에 나타납니다.[56]자체 유사 기하학적 형상, 즉 부분이 전체 그림과 비슷한 형상의 치수도 로그를 기반으로 합니다.로그 척도는 절대적인 차이가 아닌 값의 상대적인 변화를 정량화하는 데 유용합니다.또한 로그 함수 로그(x)는 큰 x에 대해 매우 느리게 증가하기 때문에 로그 스케일은 대규모 과학 데이터를 압축하는 데 사용됩니다.로그는 Tsiolkovsky 로켓 방정식, Fenske 방정식 또는 Nernst 방정식과 같은 다양한 과학 공식에서도 발생합니다.
로그 눈금

과학적 양은 종종 로그 눈금을 사용하여 다른 양의 로그로 표현됩니다.예를 들어 데시벨은 로그 스케일 양과 관련된 측정 단위입니다.이 값은 전력 비율의 공통 로그의 10배 또는 전압 비율의 공통 로그의 20배인 비율의 공통 로그를 기반으로 합니다.전기 신호를 전송할 때 전압 레벨의 손실을 정량화하고,[57] 음향학에서 소리의 전력 레벨을 설명하고,[58] 분광법과 광학 분야에서 빛의 흡광도를 설명하는 데 사용됩니다.(의미 있는) 신호와 관련하여 원하지 않는 노이즈의 양을 설명하는 신호 대 노이즈 비율도 데시벨 단위로 측정됩니다.[59]유사한 맥락에서, 최대 신호 대 잡음비는 일반적으로 로그를 사용하여 음향 및 영상 압축 방법의 품질을 평가하는 데 사용됩니다.[60]
지진의 강도는 지진에서 방출된 에너지의 공통 로그를 취함으로써 측정됩니다.모멘트 규모 척도 또는 리히터 규모 척도에서 사용됩니다.예를 들어, 5.0 지진의 경우 32배(10배1.5)의 에너지를 방출하고 6.0의 경우 4.0의 에너지를 1000배(10배3) 방출합니다.[61]겉보기 등급은 항성의 밝기를 대수적으로 측정합니다.[62]화학에서 십진 로그의 음수인 십진대수는 문자 p로 표시됩니다.[63]예를 들어, pH는 수소 이온(H가 물에서 취하는 수소 이온의+
형태)의 활성의 십진대 대수입니다.[64]중성수에서의 하이드로늄 이온의 활성은 10−7 mol·L이므로−1 pH는 7.식초는 일반적으로 약 3의 pH를 가집니다.4의 차이는 활성의 10의4 비율에 해당하며, 즉 식초의 하이드로늄 이온 활성은 약 10−3 mol·L입니다−1.
세미로그(로그-선형) 그래프는 시각화에 로그 스케일 개념을 사용합니다. 일반적으로 수직 축인 한 축은 로그 스케일로 조정됩니다.예를 들어 오른쪽 차트는 100만에서 1조로 급격한 증가를 100만에서 100만으로 증가하는 것과 동일한 공간(수직 축)으로 압축합니다.이러한 그래프에서 f(x) = a · b 형태의 지수 함수는 기울기가 b의 로그와 같은 직선으로 나타납니다. 로그 로그 그래프는 양 축을 로그로 축척하므로 f(x) = a · x 형태의 함수는 지수 k와 기울기가 같은 직선으로 표시됩니다.이는 멱법칙을 시각화하고 분석할 때 적용됩니다.[65]
심리학
로그는 인간의 인식을 설명하는 여러 법칙에서 발생합니다.[66][67]힉의 법칙은 개인이 대안을 선택하는 데 걸리는 시간과 선택한 수 사이의 로그 관계를 제안합니다.[68]피츠의 법칙에 따르면 목표 지역으로 빠르게 이동하는 데 필요한 시간은 목표 지역까지의 거리와 크기의 로그 함수입니다.[69]심리물리학에서 웨버-페크너 법칙은 자극과 감각 사이의 로그 관계를 제안합니다. 예를 들어, 사람이 들고 다니는 물체의 실제 무게 대 지각된 무게와 같은 것입니다.[70] (그러나 이 "법칙"은 스티븐스의 거듭된 법칙과 같은 최근의 모델보다는 덜 현실적입니다.)[71]
심리학적 연구에 따르면 수학 교육을 거의 받지 않은 사람들은 대수적으로 양을 추정하는 경향이 있는데, 즉 그들은 숫자를 그 대수에 따라 표시되지 않은 선에 위치시켜 100에서 1000만큼 10이 100에 가깝게 위치한다는 것을 발견했습니다.교육을 늘리면 이는 일부 환경에서 선형 추정치(1000을 10배 멀리 배치)로 이동되는 반면, 로그는 표시할 숫자를 선형으로 표시하기 어려울 때 사용됩니다.[72][73]
확률이론과 통계학


로그는 확률 이론에서 발생합니다. 큰 수의 법칙은 공정한 동전의 경우 동전 던지기의 수가 무한대로 증가하면 앞면의 관측 비율이 2분의 1에 근접한다는 것을 지시합니다.이 비율의 약 1/2은 반복 로그의 법칙으로 설명됩니다.[74]
로그는 로그 정규 분포에서도 발생합니다.랜덤 변수의 로그가 정규 분포를 가질 때 변수는 로그 정규 분포를 갖는다고 합니다.[75]로그 정규 분포는 변수가 많은 독립적인 양의 랜덤 변수의 곱으로 형성되는 경우(예: 난류 연구) 많은 분야에서 발견됩니다.[76]
로그는 모수 통계 모형의 최대 우도 추정에 사용됩니다.이러한 모형의 경우 우도 함수는 추정해야 하는 모수 하나 이상에 따라 달라집니다.우도 함수의 최대치는 우도의 로그의 최대치와 같은 모수-값에서 발생합니다(로그 우도). 로그는 증가 함수이기 때문입니다.로그 우도는 특히 독립 확률 변수에 대한 곱셈 우도에 대해 더 쉽게 최대화할 수 있습니다.[77]
Benford의 법칙은 건물의 높이와 같은 많은 데이터 집합에서 숫자의 발생을 설명합니다.Benford의 법칙에 따르면, 데이터 표본에서 한 항목의 첫 번째 소수점 자리가 d일 확률(1부터 9까지)은 측정 단위에 관계없이 log10 (d + 1) - log10 (d)와 같습니다.[78]따라서 약 30%의 데이터가 1을 첫 번째 숫자로, 18%는 2로 시작할 것으로 예상할 수 있습니다.감사인들은 분식회계를 적발하기 위해 벤포드의 법칙에서 벗어난 것을 조사합니다.[79]
로그 변환은 경험적 분포를 가정된 분포에 가깝게 만들기 위해 사용되는 데이터 변환의 한 유형입니다.
계산 복잡도
알고리즘 분석(Algorithm analysis of algorithm)은 컴퓨터 과학의 한 분야로 알고리즘의 성능을 연구하는 학문입니다.[80]로그는 문제를 더 작은 문제로 나누고 하위 문제의 해결책을 결합하는 알고리즘을 설명하는 데 유용합니다.[81]
예를 들어, 정렬된 목록에서 숫자를 찾기 위해 이진 검색 알고리즘은 중간 항목을 확인하고 여전히 숫자를 찾을 수 없는 경우 중간 항목 이전 또는 이후의 절반으로 진행합니다.이 알고리즘은 평균적으로 로그2(N) 비교가 필요하며, 여기서 N은 목록의 길이입니다.[82]마찬가지로 병합 정렬 알고리즘은 결과를 병합하기 전에 목록을 반으로 나누고 먼저 정렬하여 정렬되지 않은 목록을 정렬합니다.병합 정렬 알고리즘은 일반적으로 N · log(N)에 비례하는 시간이 필요합니다.[83]로그의 밑수는 다른 밑수를 사용할 때 결과가 상수 인자만큼만 변하기 때문에 여기서는 지정하지 않습니다.상수 인자는 일반적으로 표준 균일 비용 모델 하에서 알고리즘 분석에서 무시됩니다.[84]
만약 f(x)가 x의 로그에 (정확히 또는 대략적으로) 비례한다면 함수 f(x)는 대수적으로 증가한다고 합니다. (그러나 유기체 성장에 대한 생물학적 설명은 지수 함수에 대해 이 용어를 사용합니다.)[85]예를 들어, 임의의 자연수 N은 로그2 N + 1 비트 이하의 이진 형태로 표현될 수 있습니다.즉, N을 저장하는 데 필요한 메모리 양은 N에 따라 대수적으로 증가합니다.
엔트로피와 혼돈
엔트로피는 대체로 어떤 계의 무질서에 대한 척도입니다.통계적 열역학에서, 어떤 물리계의 엔트로피 S는 다음과 같이 정의됩니다.
랴푸노프 지수는 로그를 사용하여 동적 시스템의 혼돈 정도를 측정합니다.예를 들어 타원형 당구대에서 움직이는 입자의 경우 초기 조건을 조금만 변경해도 입자의 경로가 매우 달라집니다.초기 상태의 작은 측정 오류가 예측 가능하게 크게 다른 최종 상태로 이어지기 때문에 이러한 시스템은 결정론적인 방식으로 혼란스럽습니다.[87]결정론적으로 혼란스러운 계의 적어도 하나의 랴푸노프 지수는 양입니다.
프랙탈스

로그는 프랙탈 차원의 정의에서 발생합니다.[88]프랙탈은 작은 부분들이 적어도 전체 전역 구조를 대략적으로 재현한다는 점에서 자체적으로 유사한 기하학적 물체입니다.시에르핀스키 삼각형(사진)은 각각의 변이 원래 길이의 절반인 세 개의 복사본으로 덮일 수 있습니다.이것은 이 구조의 하우스도르프 차원을 ln(3)/ln(2) ≈ 1.58로 만듭니다.로그 기반 차원의 또 다른 개념은 문제의 프랙탈을 커버하는 데 필요한 상자의 수를 계산함으로써 얻어집니다.
음악
로그는 음악적 음색과 간격과 관련이 있습니다.동일한 기질에서 주파수 비율은 두 톤 사이의 간격에만 의존하며, 개별 톤의 특정 주파수 또는 음정에는 의존하지 않습니다.예를 들어, A 노트의 주파수는 440Hz이고 B-flat의 주파수는 466Hz입니다.A와 B-flat 사이의 간격은 반음역이고, B-flat과 B(주파수 493Hz) 사이의 간격은 반음역입니다.따라서 주파수 비율은 다음과 같습니다.
| 간격 (두 톤이 동시에 재생됨) | 1/12톤 ⓘ | 세미톤 ⓘ | 메이저 3분의 1. ⓘ | 장3 ⓘ | 트리톤 ⓘ | 옥타브 ⓘ |
| 도수비 r | ||||||
| 해당 개수의 세미톤 | ||||||
| 해당센트수 |
수론
자연로그는 수론에서 중요한 주제인 소수(2, 3, 5, 7, 11, ...)를 세는 것과 밀접하게 연결되어 있습니다.임의의 정수 x에 대하여, x보다 작거나 같은 소수의 양은 π(x)로 표시됩니다.소수 정리는 π(x)가 대략 다음과 같이 주어진다고 주장합니다.
n 요인의 로그, n! = 1 · 2 · ...· n, 가 준
일반화
복소수

방정식을 푸는 모든 복소수 a.
는 z 의 복소수 로그(complex logms)라고 하며, 이때 z 는 복소수로 간주됩니다.복소수는 일반적으로 z = x + iy로 표현되는데, 여기서 x와 y는 실수이고 i는 허수 단위이며 제곱은 -1입니다.이러한 숫자는 오른쪽에 표시된 것처럼 복소 평면의 한 점으로 시각화할 수 있습니다.극형은 그 절대값, 즉 원점까지의 (양의, 실수의) 거리 r, 그리고 실수 (x) 축 Re와 원점과 z 둘 다를 지나는 선 사이의 각도에 의해 0이 아닌 복소수 z를 부호화합니다.이 각도를 z의 인수라고 합니다.
z의 절대값 r은 다음과 같이 주어집니다.
사인과 코사인의 기하학적 해석과 2 π에서의 주기성을 사용하면 임의의 복소수 z는 다음과 같이 나타낼 수 있습니다.
임의의 정수 k에 대하여.분명히 z의 인수는 고유하게 지정되지 않습니다. φ와 φ의 = φ + 2k π 모두 모든 정수 k에 대해 z의 유효한 인수입니다. φ에 2k π 라디안 또는 k ⋅ 360°를 더하는 것은 원점에서 k번씩 시계 반대 방향으로 "winding"에 해당하기 때문입니다.결과적인 복소수는 k = 1에 대한 오른쪽에 있는 것처럼 항상 z가 됩니다. φ을 편리하게 선택된 하나의 턴(예: -π < φ ≤ π 또는 0 ≤ φ < 2 π)에 속하도록 요구함으로써 가능한 z의 인수 중 하나를 대문자 A로 Arg(z)로 나타내는 소위 주 인수로 정확히 선택할 수 있습니다.z의 인수가 유일하게 결정되는 이러한 영역을 인수 함수의 분기라고 합니다.

오일러 공식은 삼각함수 사인과 코사인을 복소 지수와 연결합니다.
이 공식과 주기성을 사용하면 다음과 같은 항등식이 성립합니다.[95]
여기서 ln(r)은 고유한 실수 자연 로그이고, a는k z의 복소수 로그이고, k는 임의의 정수입니다.따라서, e의 a번째k 거듭제곱이 z와 같은 모든 복소수 값 a인k z의 복소수 로그는 무한히 많은 값입니다.
k를 사용하여 π + 2k φ이 주요 인수에 대해 정의된 구간 내에 있다고 하면, a를 로그의 주요 값이라고 하며, 다시 L을 대문자로 표시합니다.양의 실수 x의 주요 인수는 0이므로 로그(x)는 실수이고 실수(자연적) 로그와 같습니다.그러나 위의 곱과 거듭제곱의 로그 공식은 복소수 로그의 주 값으로 일반화되지 않습니다.[96]
오른쪽 그림은 로그(z)를 보여주며 z의 인수를 구간(- π, π)에 국한합니다.이런 식으로 복소수 로그의 해당 분기는 음의 실수 x 축을 따라 불연속성을 갖는데, 이는 거기서 색상의 점프에서 볼 수 있습니다.이 불연속성은 경계를 넘을 때, 즉 연속적으로 인접한 분지의 대응하는 k-값으로 변하지 않는 것과 같은 분지의 다른 경계로 점프하는 것에서 발생합니다.이러한 위치를 분기 컷(branch cut)이라고 합니다.인수의 범위 제한을 삭제하면 관계가 "z의 인수"가 되고 결과적으로 "z의 로그"가 다중값 함수가 됩니다.
다른 지수함수의 역수
지수화는 수학의 많은 영역에서 발생하며, 그 역함수는 종종 로그(log)라고 불립니다.예를 들어, 행렬의 로그는 행렬 지수의 (다중 값) 역함수입니다.[97]다른 예로는 p-adic 지수의 역함수인 p-adic 로그가 있습니다.둘 다 실제 경우와 유사한 테일러 급수를 통해 정의됩니다.[98]미분기하학의 맥락에서 지수 맵은 다양체 점의 접선 공간을 해당 점의 이웃에 매핑합니다.그 역을 로그(또는 로그) 맵이라고도 합니다.[99]
유한 그룹의 맥락에서 지수화는 하나의 그룹 요소 b에 그 자신을 반복적으로 곱함으로써 주어집니다.이산 로그는 방정식을 푸는 정수 n입니다.
로그와 같은 역함수에는 이중 로그 ln(x)), 슈퍼 또는 하이퍼-4 로그(컴퓨터 과학에서는 반복 로그라고 불리는 약간의 변형), 램버트 W 함수 및 로짓이 포함됩니다.이들은 각각 f(w) = we의 이중 지수 함수인 테트레이션과 로지스틱 함수의 역함수입니다.
관련개념
항등식 log(cd) = log(c) + log(d)는 곱셈 하에서 양의 실수와 덧셈 하에서 실수 사이의 군 동형을 표현합니다.로그 함수는 이 그룹들 사이의 유일한 연속 동형입니다.[104]동형 사상에 의해, 실수의 Haar 측도(Lebegue 측도) dx는 양의 실수의 Haar 측도 dx/x에 해당합니다.[105]음이 아닌 실수는 곱셈을 가질 뿐만 아니라 덧셈을 가지며 확률 반올림이라고 불리는 반올림을 형성합니다. 이것은 사실 반올림입니다.그런 다음 로그는 덧셈에 곱셈을 적용하고(로그 곱셈), 로그 덧셈(LogSumExp)에 덧셈을 적용하여 확률 반올림과 로그 반올림 사이의 반올림에 대한 동형화를 제공합니다.
로그 원 형태 df/f는 복소 분석과 대수 기하학에서 로그 극을 가진 미분 형태로 나타납니다.[106]
폴리로그 대수는 다음과 같이 정의된 함수입니다.
참고 항목
메모들
- ^ x와 b에 대한 제한은 "Analytic properties" 섹션에서 설명합니다.
- ^ 증명: 로그를 ID = 로그 b , {\x = b^{\x} 로 하면 x = k ( x )= ⋅ 가됩니다 {\ \x=\}\^{\x}\=\cdot \ 수식은 에 대해 해결합니다.
- ^ 어떤 수학자들은 이 표기법을 못마땅해 했습니다.폴 할모스(Paul Halmos)는 1985년 자서전에서 어떤 수학자도 사용한 적이 없다고 말한 "어린 ln 표기법"을 비판했습니다.[15]그 표기법은 수학자인 어빙 스트링햄에 의해 발명되었습니다.[16][17]
- ^ 예를 들어 C, Java, Haskell 및 BASIC.
- ^ 동일한 열은 z - 1 < 1을 만족하는 복소수 z에 대한 복소수 로그의 주 값을 나타냅니다.
- ^ 양의 실수 부분을 갖는 복소수 z에 대한 복소수 로그의 주 값은 동일한 열에 의해 결정됩니다.
- ^ 2 π에서 360도 사이의 변환에 대해서는 라디안을 참조하십시오.
참고문헌
- ^ Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614; a lecture, University of California Libraries, Cambridge : University Press
- ^ Remmert, Reinhold. (1991), Theory of complex functions, New York: Springer-Verlag, ISBN 0387971955, OCLC 21118309
- ^ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8제1장
- ^ 이 섹션의 모든 설명은 Shailesh Shirali 2002, 섹션 4(Douglas Downing 2003, p. 275) 또는 Kate & Bhapkar 2009, p. 1-1에서 확인할 수 있습니다.
- ^ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5p. 21.
- ^ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-9Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, NY: Barron's, ISBN 978-0-7641-1972-917장 275쪽
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0p. 20개
- ^ Van der Lubbe, Jan C. A. (1997), Information Theory, Cambridge University Press, p. 3, ISBN 978-0-521-46760-5
- ^ Allen, Elizabeth; Triantaphillidou, Sophie (2011), The Manual of Photography, Taylor & Francis, p. 228, ISBN 978-0-240-52037-7
- ^ 수량 및 단위 – 파트 2: 수학 (ISO 80000-2:2019); EN ISO 80000-2
- ^ Goodrich, Michael T.; Tamassia, Roberto (2002), Algorithm Design: Foundations, Analysis, and Internet Examples, John Wiley & Sons, p. 23,
One of the interesting and sometimes even surprising aspects of the analysis of data structures and algorithms is the ubiquitous presence of logarithms ... As is the custom in the computing literature, we omit writing the base b of the logarithm when b = 2.
- ^ Parkhurst, David F. (2007), Introduction to Applied Mathematics for Environmental Science (illustrated ed.), Springer Science & Business Media, p. 288, ISBN 978-0-387-34228-3
- ^ Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
- ^ 각주 1 참조
- ^ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4
- ^ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, p. xiii
- ^ Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, p. 59, ISBN 978-0-12-370478-8
- ^ 정리 3.29 참조
- ^ Napier, John (1614), Mirifici Logarithmorum Canonis Descriptio [The Description of the Wonderful Canon of Logarithms] (in Latin), Edinburgh, Scotland: Andrew Hart 속편... Constructio는 사후에 출판되었습니다: Napier, John (1619), Mirifici Logarithmorum Canonis Constructio [The Construction of the Wonderful Rule of Logarithms] (in Latin), Edinburgh: Andrew Hart Ian Bruce는 두 책의 주석이 달린 번역본(2012)을 17centurymaths.com 에서 이용할 수 있게 했습니다.
- ^ Hobson, Ernest William (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
- ^ Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), "Jost Bürgi's method for calculating sines", Historia Mathematica, 43 (2): 133–147, arXiv:1510.03180, doi:10.1016/j.hm.2016.03.001, MR 3489006, S2CID 119326088
- ^ O'Connor, John J.; Robertson, Edmund F., "Jost Bürgi (1552 – 1632)", MacTutor History of Mathematics Archive, University of St Andrews
- ^ 윌리엄 가드너 (1742) 로그표
- ^ Pierce, R. C. Jr. (January 1977), "A brief history of logarithms", The Two-Year College Mathematics Journal, 8 (1): 22–26, doi:10.2307/3026878, JSTOR 3026878
- ^ Enrique Gonzales-Velasco (2011) 수학 여행 – 창의적인 역사 속의 에피소드, §2.4 쌍곡 로그, 페이지 117, Springer ISBN 978-0-387-92153-2
- ^ Florian Cajori (1913) "지수와 로그 개념의 역사", 미국 수학 월간지 20: 5, 35, 75, 107, 148, 173, 205.
- ^ Stillwell, J. (2010), Mathematics and Its History (3rd ed.), Springer
- ^ Bryant, Walter W. (1907), A History of Astronomy, London: Methuen & CoBryant, Walter W. (1907), A History of Astronomy, London: Methuen & Co44쪽
- ^ Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (10th ed.), New York: Dover Publications, ISBN 978-0-486-61272-0Abramowitz, Milton; Stegun, Irene A., eds. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (10th ed.), New York: Dover Publications, ISBN 978-0-486-61272-0섹션 4.7., 페이지 89
- ^ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0섹션2
- ^ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4p. 264
- ^ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, sections 1, 13, ISBN 978-0-691-14134-3
- ^ Devlin, Keith (2004), Sets, functions, and logic: an introduction to abstract mathematics, Chapman & Hall/CRC mathematics (3rd ed.), Boca Raton, Fla: Chapman & Hall/CRC, ISBN 978-1-58488-449-1Devlin, Keith (2004), Sets, functions, and logic: an introduction to abstract mathematics, Chapman & Hall/CRC mathematics (3rd ed.), Boca Raton, Fla: Chapman & Hall/CRC, ISBN 978-1-58488-449-1또는 기능의 참조를 참조합니다.
- ^ a b Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4757-2698-5, ISBN 978-0-387-94841-6, MR 1476913제III.Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2nd ed.), Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4757-2698-5, ISBN 978-0-387-94841-6, MR 14769133절
- ^ a b Lang 1997, 섹션 IV.2
- ^ Dieudonné, Jean (1969), Foundations of Modern Analysis, vol. 1, Academic Press, p. 84 항목 (4.3.1)
- ^ "Calculation of d/dx(Log(b,x))", Wolfram Alpha, Wolfram Research, retrieved 15 March 2011
- ^ Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0p. 386
- ^ "Calculation of Integrate(ln(x))", Wolfram Alpha, Wolfram Research, retrieved 15 March 2011
- ^ 아브라모위츠 & 스테건, eds. 1972, p. 69
- ^ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, MR 1009558제III.Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-60842-4, MR 10095586절
- ^ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5섹션 11.5 및 13.8
- ^ Nomizu, Katsumi (1996), Selected papers on number theory and algebraic geometry, vol. 172, Providence, RI: AMS Bookstore, p. 21, ISBN 978-0-8218-0445-2
- ^ Baker, Alan (1975), Transcendental number theory, Cambridge University Press, ISBN 978-0-521-20461-3Baker, Alan (1975), Transcendental number theory, Cambridge University Press, ISBN 978-0-521-20461-3p. 10개
- ^ Muller, Jean-Michel (2006), Elementary functions (2nd ed.), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0Muller, Jean-Michel (2006), Elementary functions (2nd ed.), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0섹션 4.2.2(p. 72) 및 5.5.2(p. 95)
- ^ Hart; Cheney; Lawson; et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John WileyHart; Cheney; Lawson; et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John Wiley섹션 6.3, 페이지 105-11
- ^ Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), "Table driven Newton scheme for high precision logarithm generation", IEE Proceedings - Computers and Digital Techniques, 141 (5): 281–92, doi:10.1049/ip-cdt:19941268, ISSN 1350-2387Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), "Table driven Newton scheme for high precision logarithm generation", IEE Proceedings - Computers and Digital Techniques, 141 (5): 281–92, doi:10.1049/ip-cdt:19941268, ISSN 1350-2387개요에 대한 섹션
- ^ Meggitt, J.E. (April 1962), "Pseudo Division and Pseudo Multiplication Processes", IBM Journal of Research and Development, 6 (2): 210–26, doi:10.1147/rd.62.0210, S2CID 19387286
- ^ Kahan, W. (20 May 2001), Pseudo-Division Algorithms for Floating-Point Logarithms and Exponentials
- ^ a b 아브라모위츠 & 스테건, eds. 1972, 페이지 68
- ^ Sasaki, T.; Kanada, Y. (1982), "Practically fast multiple-precision evaluation of log(x)", Journal of Information Processing, 5 (4): 247–50, retrieved 30 March 2011
- ^ Ahrendt, Timm (1999), "Fast Computations of the Exponential Function", Stacs 99, Lecture notes in computer science, vol. 1564, Berlin, New York: Springer, pp. 302–12, doi:10.1007/3-540-49116-3_28, ISBN 978-3-540-65691-3
- ^ Hillis, Danny (15 January 1989), "Richard Feynman and The Connection Machine", Physics Today, 42 (2): 78, Bibcode:1989PhT....42b..78H, doi:10.1063/1.881196
- ^ Maor 2009, 페이지 135
- ^ Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly, ISBN 978-0-596-10164-0Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly, ISBN 978-0-596-10164-06장 64절
- ^ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3p. 21, 섹션 1.3.2
- ^ Bakshi, U.A. (2009), Telecommunication Engineering, Pune: Technical Publications, ISBN 978-81-8431-725-1Bakshi, U.A. (2009), Telecommunication Engineering, Pune: Technical Publications, ISBN 978-81-8431-725-1섹션 5.2
- ^ Maling, George C. (2007), "Noise", in Rossing, Thomas D. (ed.), Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5Maling, George C. (2007), "Noise", in Rossing, Thomas D. (ed.), Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5섹션 23.0.2
- ^ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, New York: John Wiley & Sons, p. 98, ISBN 978-0-470-31983-3
- ^ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-384-8
- ^ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th ed.), Boston: Cengage Learning, ISBN 978-0-547-15669-94.Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th ed.), Boston: Cengage Learning, ISBN 978-0-547-15669-94절
- ^ Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, Cambridge Planetary Science, Cambridge University Press, ISBN 978-0-521-53551-9Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, Cambridge Planetary Science, Cambridge University Press, ISBN 978-0-521-53551-9섹션 8.3, 페이지 231
- ^ Nørby, Jens (2000). "The origin and the meaning of the little p in pH". Trends in Biochemical Sciences. 25 (1): 36–37. doi:10.1016/S0968-0004(99)01517-0. PMID 10637613.
- ^ IUPAC (1997), A. D. McNaught, A. Wilkinson (ed.), Compendium of Chemical Terminology ("Gold Book") (2nd ed.), Oxford: Blackwell Scientific Publications, doi:10.1351/goldbook, ISBN 978-0-9678550-9-7
- ^ Bird, J.O. (2001), Newnes engineering mathematics pocket book (3rd ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6Bird, J.O. (2001), Newnes engineering mathematics pocket book (3rd ed.), Oxford: Newnes, ISBN 978-0-7506-4992-6섹션34
- ^ Goldstein, E. Bruce (2009), Encyclopedia of Perception, Encyclopedia of Perception, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8Goldstein, E. Bruce (2009), Encyclopedia of Perception, Encyclopedia of Perception, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8pp. 355-56
- ^ Matthews, Gerald (2000), Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, ISBN 978-0-415-04406-6Matthews, Gerald (2000), Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, ISBN 978-0-415-04406-6p. 48개
- ^ Welford, A.T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156Welford, A.T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156p. 61
- ^ Paul M. Fitts (June 1954), "The information capacity of the human motor system in controlling the amplitude of movement", Journal of Experimental Psychology, 47 (6): 381–91, doi:10.1037/h0055392, PMID 13174710, S2CID 501599에 Paul M. Fitts (June 1954), "The information capacity of the human motor system in controlling the amplitude of movement", Journal of Experimental Psychology, 47 (6): 381–91, doi:10.1037/h0055392, PMID 13174710, S2CID 501599재인쇄된.
- ^ Banerjee, J.C. (1994), Encyclopaedic dictionary of psychological terms, New Delhi: M.D. Publications, p. 304, ISBN 978-81-85880-28-0, OCLC 33860167
- ^ Nadel, Lynn (2005), Encyclopedia of cognitive science, New York: John Wiley & Sons, ISBN 978-0-470-01619-0Nadel, Lynn (2005), Encyclopedia of cognitive science, New York: John Wiley & Sons, ISBN 978-0-470-01619-0레몬의 심리물리학과 인식: 개요
- ^ Siegler, Robert S.; Opfer, John E. (2003), "The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity" (PDF), Psychological Science, 14 (3): 237–43, CiteSeerX 10.1.1.727.3696, doi:10.1111/1467-9280.02438, PMID 12741747, S2CID 9583202, archived from the original (PDF) on 17 May 2011, retrieved 7 January 2011
- ^ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), "Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures", Science, 320 (5880): 1217–20, Bibcode:2008Sci...320.1217D, CiteSeerX 10.1.1.362.2390, doi:10.1126/science.1156540, PMC 2610411, PMID 18511690
- ^ Breiman, Leo (1992), Probability, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-296-4Breiman, Leo (1992), Probability, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-296-4섹션 12.9
- ^ Aitchison, J.; Brown, J.A.C. (1969), The lognormal distribution, Cambridge University Press, ISBN 978-0-521-04011-2, OCLC 301100935
- ^ Jean Mathieu and Julian Scott (2000), An introduction to turbulent flow, Cambridge University Press, p. 50, ISBN 978-0-521-77538-0
- ^ Rose, Colin; Smith, Murray D. (2002), Mathematical statistics with Mathematica, Springer texts in statistics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95234-5Rose, Colin; Smith, Murray D. (2002), Mathematical statistics with Mathematica, Springer texts in statistics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95234-5섹션 11.3
- ^ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, RI: American Mathematical Society, pp. 36–40, ISBN 978-0-8218-3919-5Tabachnikov, Serge (2005), Geometry and Billiards, Providence, RI: American Mathematical Society, pp. 36–40, ISBN 978-0-8218-3919-5섹션 2.1
- ^ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), "The Effective Use of Benford's Law in Detecting Fraud in Accounting Data" (PDF), Journal of Forensic Accounting, V: 17–34, archived from the original (PDF) on 29 August 2017, retrieved 28 May 2018
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-01-2쪽
- ^ Harel, David; Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, New York: Addison-Wesley, ISBN 978-0-321-11784-7Harel, David; Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, New York: Addison-Wesley, ISBN 978-0-321-11784-7p. 143
- ^ Knuth, Donald (1998), The Art of Computer Programming, Reading, MA: Addison-Wesley, ISBN 978-0-201-89685-5Knuth, Donald (1998), The Art of Computer Programming, Reading, MA: Addison-Wesley, ISBN 978-0-201-89685-5섹션 6.2.1, 페이지 409-26
- ^ Donald Knuth 1998, 섹션 5.2.4, 페이지 158-68
- ^ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, p. 20, ISBN 978-3-540-21045-0
- ^ Mohr, Hans; Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4Mohr, Hans; Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-419장 298쪽
- ^ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8제III절
- ^ Sprott, Julien Clinton (2010), "Elegant Chaos: Algebraically Simple Chaotic Flows", Elegant Chaos: Algebraically Simple Chaotic Flows. Edited by Sprott Julien Clinton. Published by World Scientific Publishing Co. Pte. Ltd, New Jersey: World Scientific, Bibcode:2010ecas.book.....S, doi:10.1142/7183, ISBN 978-981-283-881-0Sprott, Julien Clinton (2010), "Elegant Chaos: Algebraically Simple Chaotic Flows", Elegant Chaos: Algebraically Simple Chaotic Flows. Edited by Sprott Julien Clinton. Published by World Scientific Publishing Co. Pte. Ltd, New Jersey: World Scientific, Bibcode:2010ecas.book.....S, doi:10.1142/7183, ISBN 978-981-283-881-0섹션 1.9
- ^ Helmberg, Gilbert (2007), Getting acquainted with fractals, De Gruyter Textbook, Berlin, New York: Walter de Gruyter, ISBN 978-3-11-019092-2
- ^ Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4873-9Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4873-9제5장
- ^ Bateman, P.T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3, OCLC 492669517Bateman, P.T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3, OCLC 492669517정리 4.1
- ^ P. T. Bateman & Diamond 2004, 정리 8.15
- ^ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3제4장
- ^ Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3정의 1.6.3
- ^ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), "Introduction to complex analysis", London: Hilger, Providence, RI: AMS Bookstore, Bibcode:1974aitc.book.....W, ISBN 978-0-8218-4399-4Nevanlinna, Rolf Herman; Paatero, Veikko (2007), "Introduction to complex analysis", London: Hilger, Providence, RI: AMS Bookstore, Bibcode:1974aitc.book.....W, ISBN 978-0-8218-4399-4섹션 5.9
- ^ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, Singapore: World Scientific, ISBN 978-981-02-0246-0Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, Singapore: World Scientific, ISBN 978-981-02-0246-0섹션 1.2
- ^ Wilde, Ivan Francis (2006), Lecture notes on complex analysis, London: Imperial College Press, ISBN 978-1-86094-642-4Wilde, Ivan Francis (2006), Lecture notes on complex analysis, London: Imperial College Press, ISBN 978-1-86094-642-4정리 6.1
- ^ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, Philadelphia, PA: SIAM, ISBN 978-0-89871-646-7Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, Philadelphia, PA: SIAM, ISBN 978-0-89871-646-711장
- ^ Neukirch, Jürgen (1999), Algebraische Zahlentheorie, Grundlehren der mathematischen Wissenschaften, vol. 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR 1697859, Zbl 0956.11021Neukirch, Jürgen (1999), Algebraische Zahlentheorie, Grundlehren der mathematischen Wissenschaften, vol. 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR 1697859, Zbl 0956.11021제II.5절
- ^ Hancock, Edwin R.; Martin, Ralph R.; Sabin, Malcolm A. (2009), Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings, Springer, p. 379, ISBN 978-3-642-03595-1
- ^ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (3rd ed.), London: CRC Press, ISBN 978-1-58488-508-5
- ^ Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, Cambridge University Press, ISBN 978-0-521-39231-0
- ^ Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996), "On the Lambert W function" (PDF), Advances in Computational Mathematics, 5: 329–59, doi:10.1007/BF02124750, ISSN 1019-7168, S2CID 29028411, archived from the original (PDF) on 14 December 2010, retrieved 13 February 2011
- ^ Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Learning from data: concepts, theory, and methods, Wiley series on adaptive and learning systems for signal processing, communications, and control, New York: John Wiley & Sons, ISBN 978-0-471-68182-3Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Learning from data: concepts, theory, and methods, Wiley series on adaptive and learning systems for signal processing, communications, and control, New York: John Wiley & Sons, ISBN 978-0-471-68182-3p. 357
- ^ Bourbaki, Nicolas (1998), General topology. Chapters 5–10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, MR 1726872Bourbaki, Nicolas (1998), General topology. Chapters 5–10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, MR 1726872V.4.1절
- ^ Ambartzumian, R.V. (1990), Factorization calculus and geometric probability, Cambridge University Press, ISBN 978-0-521-34535-4Ambartzumian, R.V. (1990), Factorization calculus and geometric probability, Cambridge University Press, ISBN 978-0-521-34535-4섹션 1.4
- ^ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, vol. 20, Basel, Boston: Birkhäuser Verlag, CiteSeerX 10.1.1.178.3227, doi:10.1007/978-3-0348-8600-0, ISBN 978-3-7643-2822-1, MR 1193913Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, vol. 20, Basel, Boston: Birkhäuser Verlag, CiteSeerX 10.1.1.178.3227, doi:10.1007/978-3-0348-8600-0, ISBN 978-3-7643-2822-1, MR 1193913섹션2
- ^ Apostol, T.M. (2010), "Logarithm", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
외부 링크
 Wikimedia Commons의 로그 관련 매체
Wikimedia Commons의 로그 관련 매체 Wiktionary에서 로그의 사전적 정의
Wiktionary에서 로그의 사전적 정의 로그에 대한 교훈은 Wik variety 에서 찾을 수 있습니다.
로그에 대한 교훈은 Wik variety 에서 찾을 수 있습니다.- Weisstein, Eric W., "Logarithm", MathWorld
- Khan Academy: 로그, 무료 온라인 마이크로 강의
- "Logarithmic function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Colin Byfleet, Educational video on logarithms, retrieved 12 October 2010
- Edward Wright, Translation of Napier's work on logarithms, archived from the original on 3 December 2002, retrieved 12 October 2010
{{citation}}: CS1 maint : URL(링크) 부적합 - Glaisher, James Whitbread Lee (1911), , in Chisholm, Hugh (ed.), Encyclopædia Britannica, vol. 16 (11th ed.), Cambridge University Press, pp. 868–77






![{\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividend}}}{\scriptstyle {\text{divisor}}}}\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{numerator}}}{\scriptstyle {\text{denominator}}}}\end{matrix}}\right\}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d5d22ff59234f0d437be740306e8dd905991e1e)



![{\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5582d567e7e7fbcdb728291770905e09beb0ea18)











![{\textstyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ca3b6cc8ff1c0192fb0e9206d32b14aec60e02)











![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=10^{{\frac {1}{d}}\log _{10}c}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cee4c3ee52a4b250c30c38836d4d58a006ce74c)



























![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55acf246da64ba711e1717eb43ad81792220ab32)



![{\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)


![\log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)






![\log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)


















