복합 로그
Complex logarithm수학에서 복합 로그는 자연 로그에서 0이 아닌 복잡한 숫자로 일반화하는 것이다. 이 용어는 다음 중 하나를 말하며, 이 중 관련성이 강하다.
- 0이 아닌 복잡한 숫자 z의 복잡한 로그, ew = z에 대한 모든 복잡한 숫자로 정의된다.[1][2] 그러한 숫자 w는 로그 z로 표시된다.[1] z가 z = re로iθ 극형으로 주어지는 경우, 여기서 r과 θ은 r > 0의 실제 숫자인 경우 ln(r)+ iθ는 z의 하나의 로그이며, z의 모든 복잡한 로그는 정수 k에 대한 ln(r) + i(θ + 2kk) 형식의 정확한 숫자다.[1][2] 이러한 로그는 복잡한 평면에서 수직선을 따라 균등하게 간격을 두고 있다.
- A complex-valued function , defined on some subset of the set of nonzero complex numbers, satisfying for all in \displaystyle U}. 이런 복잡한 로그 기능은 실제 로그 함수 ln:R을;0→ R{\displaystyle \ln \colon \mathbb{R}_{>0}\to \mathbb{R}}, 진짜 지수 함수의 역이며, 따라서))x. 복잡한 로그 기능 수 있는 모든 긍정적인 진짜 번호를 eln x충족과 유사합니다. constru 가치 함수와 관련된 명시적 공식, 1/ 통합 또는 분석 연속성 프로세스에 의해 cced.
C^*}에 정의된 연속적인 복합 로그 함수는 없다 이를 처리하는 방법에는 가지, 관련 리만 표면, 복합 지수 함수의 부분 invers 등이 포함된다. 기본값은 특정한 복합 로그 함수를 정의한다. : → C 음의 실제 축을 따라 계속되는 것을 제외하고 연속하는 것은 (real) natur의 분석적 연속이다.알 로그
복합 지수함수 반전 문제

함수가 역수를 가지려면 구별되는 값을 구별되는 값에 매핑해야 한다. 즉, 주입해야 한다. 그러나 복잡한 지수함수는w 주입되지 않는데, 왜냐하면w+2kπi w에 i k를 더하면 ew = e = w와 정수 k가 반시계방향 θ 라디안을 회전시키는 효과가 있기 때문이다. 그래서 포인트는
수직선을 따라 균등하게 간격을 두고, 모두 지수함수에 의해 동일한 숫자에 매핑된다. 이것은 지수함수가 표준적인 의미에 역함수가 없다는 것을 의미한다.[3][4] 이 문제에는 두 가지 해결책이 있다.
하나는 지수함수의 도메인을 2ii의 정수배수로 다른 두 개의 숫자를 포함하지 않는 영역으로 제한하는 것이다. 이는 자연적으로 로그 z의 분기의 정의로 이어지며, 로그 z의 분기는 각 도메인에서 각 숫자의 로그 하나를 골라내는 특정한 기능이다. 이는 [-1, 1]에 대한 아크신 x의 정의와 유사하며, 죄악의 제한에 대한 역행으로 [-π/2, π/2] 구간에 대한 θ의 정의와 유사하다: 죄악의 θ = x를 가진 실수의 θ은 무한히 많지만, [-π/2, π/2]에 있는 실수의 θ은 임의로 선택한다.
불변성을 해결하는 또 다른 방법은 로그선을 복합 평면의 영역이 아닌 무한대1 방식으로 구멍이 뚫린 복합 평면을 덮는 리만 표면의 함수로 보는 것이다.
가지들은 복잡한 숫자로 평가될 수 있다는 장점이 있다. 반면 리만 표면의 기능은 로그의 모든 분기를 패키징하고 정의의 일부로서 임의의 선택을 요구하지 않는다는 점에서 우아하다.
원금값
정의
0이 아닌 각 복합수 z에 대해 주 값 Log z는 가상 부분이 구간(-through, π)[2]에 있는 로그다. ew = 0을 만족하는 복잡한 숫자가 없기 때문에 Log 0 식이 정의되지 않은 상태로 남아 있다.[1]
비양성 실수가 아닌 복잡한 숫자의 경우, 복합 로그의 기본값은 자연 로그의 분석적 연속성이다. 음의 복잡한 숫자에 대해서는 음의 실수를 양의 가상 부분을 가진 복잡한 숫자의 한계로 표현함으로써 더 나아가서 주값을 얻는다.
특정한 로그가 지정되지 않은 상태에서 표기 로그 z가 나타날 경우, 일반적으로 주값을 의도한다고 가정하는 것이 가장 좋다. 특히, 이것은 z가 양의 실수일 때 ln z의 실제 값과 일치하는 값을 제공한다. Log 표기법상의 대문자화는 z의 다른 로그와 주값을 구별하기 위해 일부 저자에[2] 의해 사용된다.
기본 값 계산
0이 아닌 콤플렉스 숫자 z = x + 이 = z = reiθ, 여기서 r= = 2+ y }은 z의 절대값이고, θ은 그 주장이다. 절대값은 현실이고 긍정적이다. 인수는 2㎛의 정수배수까지 정의된다. 주값은 구간(- (-, y])에 속하는 값으로, atan2(y,x)로 표현된다.
이는 복합 로그의 주요 값에 대한 다음과 같은 공식으로 이어진다.
예를 들어 Log(-3i) = ln 3 - -i/2, Log(-3) = ln 3 + πi.
역함수로서의 주 값
Log z를 설명하는 또 다른 방법은 앞의 절에서와 같이 복합 지수함수의 제한에 대한 역행으로 설명된다. 수평 스트립 S는 복잡한 숫자 w = x+yi로 구성되며, -π < y ≤ π π은 2πi의 정수 배수로 다른 두 숫자를 포함하지 않는 지역의 예이므로 지수함수를 S로 제한하는 것은 역수를 가진다. In fact, the exponential function maps S bijectively to the punctured complex plane , and the inverse of this restriction is . The conformal mapping section below ex이 지도의 기하학적 성질을 보다 상세하게 평지하다.
특성.
ln에 의해 충족되는 모든 정체성이 복잡한 숫자로 확장되는 것은 아니다. 모든 zLog z ≠ 0에 대한 e = z(Log z가 z의 로그임을 의미함)는z 사실이지만, Log e = z라는 ID는 스트립 S 밖에 있는 z에 대해 실패한다. 이러한 이유로, 항상 로그(Log)를w ID의z 양쪽에 적용하여 z = w를 추론할 수는 없다. 또한, Log(z12) = Log1 z + Log z는2 실패할 수 있다: 양면이 2πi의 정수 배수로 변할 수 있다.[1] 예를 들어,
그렇지만
Log z 함수는 각 음수 실수에 불연속적이지만 {\의 다른 모든 곳에서 연속된다 불연속성에 대해 설명하려면 z가 음수 실수에 근접할 때 Arg z가 어떻게 되는지 고려한다. z가 위에서 a에 접근하면 π에 접근하게 되는데, 이 또한 π은 Arg a 자체의 값이기도 하다. 그러나 z가 아래로부터 a에 접근하면 Arg z는 -time에 접근한다. 그래서 z가 음의 실제 축을 가로지르면서 Arg z "점프"는 2㎛, Log z는 2㎛이 점프한다.
복합 로그의 분기
모든 에 연속되는 함수 L(z)을 만들기 위해 각 비제로 콤플렉스 숫자의 로그를 선택하는 다른 방법이 있는가? 답은 no이다 그 이유를 알아보려면 0이 0에서 2㎛로 증가할 때 L(eiθ)를 평가하여 단위 원을 따라 그러한 로그 함수를 추적한다고 상상해 보십시오. L(z)이 연속적인 경우 L(eiθ) – iθ도 마찬가지지만, 후자는 e의iθ 두 로그의 차이가 있으므로 이산형 2 의 값을 취하므로 일정하다 특히 L(e2πi) – 2πi = L(e0) – 0은 L(e2πi) = L(1) = L(e0)와 모순된다.
복잡한 숫자에 정의된 연속 로그를 얻으려면, 따라서 복잡한 평면의 작은 부분집합 U로 도메인을 제한할 필요가 있다. 목표 중 하나는 함수를 구별할 수 있는 것이기 때문에, 함수가 그 영역의 각 지점의 근방에 정의되어 있다고 보는 것이 타당하다. 즉, U는 공개 집합이어야 한다. 또한 U의 서로 다른 구성요소의 함수 값이 서로 관련이 없을 수 있으므로 U가 연결되어 있다고 가정하는 것이 타당하다. 이 모든 것은 다음과 같은 정의에 동기를 부여한다.
- 로그 z의 분기는 L(z)이 U의 각 z에 대해 z의 로그가 되도록 복잡한 평면의 연결된 오픈 서브셋 U에 정의된 연속 함수 L(z)이다.[2]
예를 들어, 기본값은 연속되는 오픈 세트의 분기를 정의하는데, 이는 복합 평면에서 0과 모든 음의 실수를 제거하여 얻은 C - 0{\-\ 0이다.
다른 예: 메르카토르 시리즈
u < 1에 대해 국지적으로 균일하게 수렴하므로, 설정 z = 1+u는 1을 중심으로 한 반경 1의 열린 디스크에 로그 z의 분기를 정의한다.(실제 이것은 1에서 차이를 구별하고 값을 비교함으로써 알 수 있듯이, Log z의 제한에 불과하다.)
분기가 고정되면 혼동이 발생하지 않을 경우 "log z"로 표기할 수 있다. 가지마다 특정 복합수의 로그에 대해 다른 값을 부여할 수 있지만, "log z"가 정확하고 모호하지 않은 의미를 가지려면 분기를 미리 고정(또는 주 분기를 이해해야 함)해야 한다.
나뭇가지 절단
단위 원을 포함하는 위의 인수는 0 주위에 감기는 닫힌 곡선을 포함하는 열린 집합 U에 로그 z의 분기가 없다는 것을 나타내기 위해 일반화된다. 하나는 "log z가 0에 분기점을 가지고 있다"고 말한다. 0 주위에 감기는 닫힌 곡선을 포함하지 않기 위해 U는 일반적으로 어떤 방향에서 0(포함)에서 무한대로 가는 복잡한 평면에서 광선이나 곡선의 보완물로 선택된다. 이 경우 곡선을 가지 절단이라고 한다. 예를 들어, 주가지에는 음의 실제 축을 따라 가지 절단부가 있다.
만일 L(z) 함수가 분기 컷의 지점에서 정의되도록 확장된다면, 거기서 반드시 불연속적일 것이다. 기껏해야 음의 실수의 Log z처럼 "한 면에" 연속적으로 존재할 것이다.
복합 로그의 파생 모델
오픈 세트 U에 있는 로그 z의 각 분기 L(z)는 지수함수의 제한, 즉 이미지 L(U)에 대한 제한의 역이다. 지수함수는 비바니싱 파생상품과 함께 홀로모르픽(즉, 복잡다양한)이기 때문에 역함수 정리의 복잡한 아날로그가 적용된다. U에서는 L(z)이 홀모픽이고 U에서는 L(z) = 각 z에 대해 1/z임을 보여준다.[2] 이를 증명하는 또 다른 방법은 극좌표에서 Cauchy-Remann 방정식을 확인하는 것이다.[2]
통합을 통한 분기 구성
real > 함수는 으로구성할수
통합 범위가 1이 아닌 양수로 시작되면 공식은 다음과 같아야 한다.
대신에
복합 로그에 대한 아날로그를 개발함에 있어 추가적인 복잡성이 있다: 복합 적분 정의는 경로 선택을 필요로 한다. 다행히 통합이 홀모픽이라면 (끝점을 고정하고 있는 동안) 경로를 변형시켜 적분 값을 변경하지 않으며, 단순하게 연결된 영역 U("구멍이 없는 지역")에서는 U 내부의 a에서 z까지의 어떤 경로도 U 내부의 다른 경로로 연속적으로 변형될 수 있다. 이 모든 것은 다음과 같은 결과를 초래한다.
- U가 0을 포함하지 않고 단순히 된C {\ {C의 열린 부분 집합인 경우 U에서 시작점 a를 선택하고 a의 로그 b를 선택한 다음 정의함으로써 U에 정의된 로그 z의 분기를 구성할 수 있다.
- U의 각 z에 [5]대해
등각 지도로서의 복잡한 로그
Any holomorphic map satisfying for all is a conformal map, which means that if two curves passing through a point a of U form an angle α (in the sense that the tangent lines to the curves at a form an 각도 α), 그러면 두 곡선의 영상이 f(a)에서 동일한 각도 α를 형성한다. 로그 z의 분기는 홀로모르픽이고, 그 파생상품 1/z는 결코 0이 아니기 때문에, 그것은 순응 지도를 정의한다.
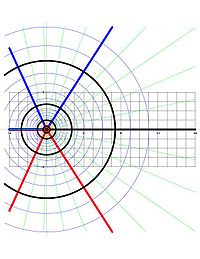
예를 들어 w = Log 는 C - 0 0에서 Imz < π>에 의해 정의된 수평 스트립까지의 매핑으로 간주되는 다음과 같은 특성을 가지며, 이는 극성 형태의 공식에 직접적인 영향을 미친다.
- 0에 중심을 둔 z-평면의[6] 원은 - ii를 + ii에 연결하는 w-평면의 수직 세그먼트에 매핑되며, 여기서 a는 원의 반지름의 실제 로그다.
- z 면의 0에서 방출되는 광선은 w 면의 수평선에 매핑된다.
위와 같은 z-평면의 각 원과 광선은 직각으로 만난다. Log(로그)에 따른 이들의 영상은 w-플레인에서 수직 세그먼트와 수평선(존중)이며, 이들 역시 직각에서 만난다. 이것은 Log의 순응적 성질을 보여주는 삽화다.
관련 리만 표면
건설
로그 z의 다양한 분기는 의 연속 함수 Cglued → \colon \\mathb {을(를) 제공하기 위해 접착할 수 없다. Compare, for example, the principal branch Log(z) on with imaginary part θ in (−π,π) and the branch L(z) on whose imaginary part θ lies in (0,2π). 이것들은 위쪽 반쪽 면에서는 일치하지만 아래쪽 반쪽 면에서는 그렇지 않다. 따라서 이 가지들의 도메인을 위쪽 절반 면의 복사본을 따라 접착하는 것이 타당하다. 결과적으로 접착된 도메인이 연결되었지만, 하단 반면의 복사본이 2개 있다. 이 두 권의 사본은 주차장의 두 단계로 시각화할 수 있으며, 0을 중심으로 시계 반대 방향으로 360° 이동하여 (로그 레벨의) 양의 실제 축을 먼저 교차시킨 다음, 음의 실제를 교차하면 하단 면의 로그 레벨에서 하단 면의 L 레벨까지 도달할 수 있다. (L 레벨의) 축을 하단 면의 L 레벨로 한다.
상상의 θ이 있는 가지를 (π,3π), (2π,4π), 그 밖의 방향에서는 상상의 θ이 있는 가지를 (-2π,0), (-3π,-π), (- by,-π) 등으로 붙이면 된다. 최종 결과는 연결된 표면으로, 위아래로 모두 무한히 많은 층을 가진 나선형 주차장으로 볼 수 있다. 이것은 로그 z와 연관된 Riemann 표면 R이다.[7]
R에 대한 점은 θ이 z의 인수의 가능한 값인 쌍(z,csi)으로 생각할 수 있다. 이런 식으로 을 C× R × R { \mathb {R} \ 약에 삽입할 수 있다
리만 표면의 로그 함수
가지들의 영역은 그들의 값이 합의된 오픈 세트를 따라 접착되었기 때문에, 가지들은 잘 정의된 단일 함수 : R→ 를) 부여하기 위한 접착제로[8] R의 각 지점(z,c)을 ln z + iθ에 매핑한다. 호환 가능한 홀모픽 함수를 접착하여 원래의 분기 로그를 확장하는 이 과정을 분석적 연속이라고 한다.
R에서 까지 Spiral을 "평탄하게" 하여 (z,cs)를 z로 보내는 "투영 지도"가 있다. z z {에 대해 "직접 위" z에 놓여 있는 R의 포인트(z,cs)를 모두 가져가고 이 모든 지점에서 로그를R 평가하면, z의 모든 로그가 얻어진다.
로그 z의 모든 분기 접착
Instead of gluing only the branches chosen above, one can start with all branches of log z, and simultaneously glue every pair of branches and along the largest open subset of L과1 L이2 동의하는 이것은 전과 동일한 Riemann 표면 R과 기능 로그를R 산출한다. 이러한 접근방식은 시각화하기는 다소 어렵지만 특정 분기를 선택할 필요가 없다는 점에서 더욱 자연스럽다.
만일 U′이 C의 이미지 U에 대해 객관적으로 투영하는 R의 공개 서브셋이라면, U′에 대한 로그R 제한은 U에 정의된 로그 z의 한 가지 분기에 해당한다. 로그 z의 모든 분기는 이와 같이 발생한다.
범용 커버로서의 리만 표면
The projection map realizes R as a covering space of . In fact, it is a Galois covering with deck transformation group isomorphic to , generated by the homeomorphism sending (z,θ) to (z,θ+2π).
복합다지관으로서 R은 로그로R 를) 갖는 바이홀모픽이다.(역지도가 z를 (ez,Im z)로 보낸다. 이것은 R이 단순히 연결되어 있음을 보여주므로, 은 C의 범용 표지 입니다
적용들
- 기초가 복잡한 숫자인 지수를 정의하려면 복합 로그가 필요하다. 즉, a와 b가 ≠ 0의 복잡한 숫자라면, 원금 값을 사용하여 ab = e를b Log a 정의할 수 있다. 또한 a의 다른 로그에 의한 로그 a를 대체하여 e형식의2πinb 인자에 따라 다른b a의 다른 값을 얻을 수 있다.[1][9] 식 a는b b가 정수인 경우에만 단일 값을 갖는다.[1]
- 삼각함수는 e의iz 합리적 함수로 표현할 수 있기 때문에 역삼각함수는 복잡한 로그의 관점에서 표현할 수 있다.
- mapping w = Log z는 0에 중심을 둔 원을 수직 직선 세그먼트로 변환하기 때문에, 환율을 포함하는 엔지니어링 애플리케이션에 유용하다.[citation needed]
일반화
다른 베이스에 대한 로그
실제 숫자와 마찬가지로 복잡한 숫자 b와 x에 대해 정의할 수 있다.
b와 x에서 정의된 로그 분기의 선택에 따라 값이 달라진다(로그 b ≠ 0). 예를 들어, 기본값을 사용하면
홀로모르프 함수의 로그
If f is a holomorphic function on a connected open subset U of , then a branch of log f on U is a continuous function g on U such that eg(z) = f(z) for all z in U. Such a function g is necessarily holomorphic with g′(z) = f′(z)/f(z) for all z in U.
U가 의 간단히 연결된 개방형 서브셋이고 f가 U에서 기점 a를 선택하고, f(a)의 logarithm b를 선택하고, 정의하면 U에 정의된 로그 f의 분기를 구성할 수 있다.
U의 각 z에 [2]대해
메모들
참조
- Ahlfors, Lars V. (1966). Complex Analysis (2nd ed.). McGraw-Hill.
- Conway, John B. (1978). Functions of One Complex Variable (2nd ed.). Springer.
- Kreyszig, Erwin (2011). Advanced Engineering Mathematics (10th ed.). Berlin: Wiley. ISBN 9780470458365.
- Lang, Serge (1993). Complex Analysis (3rd ed.). Springer-Verlag.
- Moretti, Gino (1964). Functions of a Complex Variable. Prentice-Hall.
- Sarason, Donald (2007). Complex Function Theory (2nd ed.). American Mathematical Society.
- Whittaker, E. T.; Watson, G. N. (1927). A Course of Modern Analysis (Fourth ed.). Cambridge University Press.







 제외하고 연속하는 것은 (
제외하고 연속하는 것은 (