삼각함수의 역함수
수학 에서 역삼각형 함수 (때로는 아르쿠스 함수 ,[1] [2] [3] [4] [5] 항삼각형 함수 [6] 사이클로메트릭 함수 라고도[7] [8] [9] 삼각형 함수 의 역함수 입니다.구체적으로 사인 함수, 코사인 함수 , 접선 함수, 코탄젠트 함수, 시컨트 함수 및 코탄젠트 함수의 역수이며 [10] 역삼각형 함수는 공학 , 내비게이션 , 물리학 , 기하학 에서 널리 사용됩니다.
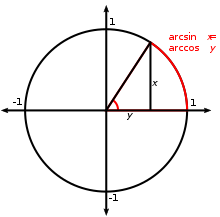
표기법 반지름이 1인 원의 경우, 아크신과 아크코는 문제의 양에 의해 결정되는 실제 아크의 길이입니다. 역삼각형 함수에 대한 몇 가지 표기법이 있습니다. 가장 일반적인 규칙은 arc-prefix를 사용하여 역삼각형 함수의 이름을 짓는 것입니다: arcsin(x ), arcos(x ), arctan(x ) 등. [6] 이 표기법은 다음과 같은 기하학적 관계에서 비롯됩니다. 라디안으로 측정할 때 θ 라디안의 각도는 길이가 r θ인 호 에 해당하고, 여기서 r 은 원의 반지름입니다. 따라서 단위 원 에서 "코사인이 x 인 원호"는 "코사인이 x 인 각도"와 같으며, 이는 원의 원호 길이가 라디안의 각도 측정과 같기 때문입니다.[11] 컴퓨터 프로그래밍 언어에서 역삼각형 함수는 종종 sin , acos , atan 과 같은 축약된 형태로 불립니다.[12]
1813년 존 허셜 에 의해 소개된 sin−1 (x ), cos−1 (x ), tan−1 (x ) 등의 표기법은 영어 소스에서도 종종 사용되는데,[13] [14] [6] 성립 된[−1] sin(x ), cos[−1] (x ), tan[−1] (x ) 보다 훨씬 더 많습니다 – 각 역삼각형의 다중값 버전을 정의하는 데 유용한 (예를 들어) 역함수 의 표기법과 일치하는 규약 tan 1 x arctan k Z } {\displaystyle \tan ^{-1}(x arctan(x +\pi k\mid k\in \mathbb {Z} \}~.} sin(x ) 과 같은 표현에 대한 일반적인 의미론과 논리적으로 충돌하는 것처럼 보일 수 있습니다.함수 구성이 아닌 경우, 따라서 역수 (multiplic 역수 )와 역수 함수에 대한 표기법 사이에 혼동이 발생할 수 있습니다.
이러한 혼란은 각 역삼각함수가 (cos(x ) = sec(x ))와 같은 고유한 이름을 가지고 있기 때문에 다소 완화됩니다. 그럼에도 불구하고 일부 저자들은 애매모호하기 때문에 사용하지 말 것을 권고하고 있습니다.[6] [16] 소수의 저자들이 사용하는 또 다른 불안정한 관습은 "-1 " 위첨자와 함께 대문자 첫 글자를 사용하는 것입니다: Sin−1 (x ), Cos−1 ( [17] x ),Tan−1 (x ) 등. 비록 이것이 sin−1 (x ), cos−1 −1 ( x ) 등으로 표현되어야 하는 역수 와 혼동을 피하기 위한 것이기는 하지만, 특히−1 Mathematica , MAGMA )이 매우 동일한 대문자 표현을 사용하기 때문에, 이것은 다시 모호성의 또 다른 주요 원천을 만듭니다. 표준 trig 함수의 경우 ns인 반면, 다른 함수들(Python , SymPy , NumPy , Matlab , MALE 등)은 소문자를 사용합니다.
따라서 2009년부터 ISO 80000-2 표준은 역함수에 대한 "arc" 접두사만을 지정했습니다.
기본개념 1 , Sec( θ), Csc( θ) 로 표시된 점은 원점에서 해당 점까지의 선분의 길이를 나타냅니다.Sin(θ), Tan( θ ), 1 은 x축에서 시작하는 선까지의 높이이고 Cos( θ ), 1 , Cot( θ ) 은 원점에서 시작하는 x축을 따르는 길이입니다.주값 6개의 삼각 함수 중 어느 것도 일대일 이 아니기 때문에 역함수를 가지려면 이 함수들을 제한해야 합니다. 따라서 역함수의 결과 범위 는 원래 함수의 도메인의 적절한(즉 , 엄격한) 부분 집합입니다.
예 를 들어, 제곱근 함수 y {\displaystyle sqrt {x}}} x , displaystyle 함수 아크신 ( x ) displaystyle arcsin(x)} sin ( y ) . displaystyle \sin(y x.} x {\di -1 ≤ x ≤ 1인 splaystyle {\ -1 \ leq x\leq 1,} 수 y {\displaystyle } . sin 0 ) = 0 , {\displaystyle \sin( 0 = 0,} sin ( π = , {\displaystyle \sin(\pi = sin π = 0 , {\displaystyle = 0,} yle \sin(2\pi)=0,} 하나의 값만 원하는 경우 함수는 주 분기 로 제한될 수 있습니다. 이 제한을 사용하면 도메인의 각 displaystyle x} ( x ) displaystyle \arcsin(x)} 해당 주 값 이라는 단일 값으로만 평가됩니다. 이러한 속성은 모든 역삼각형 함수에 적용됩니다.
주요 역들은 다음 표에 나열되어 있습니다.
이름. 통상적인 표기법 정의. 실제 {\displaystyle x} 통상적인 원금의 범위 (레이디언즈 ) 통상적인 원금의 범위 (degrees ) 아크신 y = 호신 ( x ) {\displaystyle y=\arcsin(x)} x = sin (y ) − 1 ≤ x ≤ 1 {\displaystyle -1\leq x\leq 1} − π 2 ≤ y ≤ π 2 {\displaystyle -{\frac {\pi}{2}}\leq \leq {\frac {\pi}{2}} − 90 ∘ ≤ y ≤ 90 ∘ {\displaystyle -90^{\circ}\leq y\leq 90^{\circ}} 아크코신 y = 아코코 ( x ) {\displaystyle y=\arccos(x)} x = cos (y ) − 1 ≤ x ≤ 1 {\displaystyle -1\leq x\leq 1} 0 ≤ y ≤ π {\displaystyle 0\leq \leq \pi } 0 ∘ ≤ y ≤ 180 ∘ {\displaystyle 0^{\circ}\leqy\leq 180^{\circ}} 아크탄젠트 y = 아크탄 ( x ) {\displaystyle y=\arctan(x)} x = tan (y )모든 실수 − π 2 < y < π 2 {\displaystyle -{\frac {\pi}{2}}<y<\frac {\pi}{2}}} − 90 ∘ < y < 90 ∘ {\displaystyle -90^{\circ}<y<90^{\circ}} 활강제의 y = 아궁이 ( x ) {\displaystyle y=\operator name {arccot}(x)} x = cot (y )모든 실수 0 < y < π {\displaystyle 0<y<\pi} 0 ∘ < y < 180 ∘ {\displaystyle 0^{\circ}<y<180^{\circ}} 호상의 y = 아크섹 ( x ) {\displaystyle y=\operator name {arcsec}(x)} x = sec (y ) x ≥ 1 {\displaystyle {\left\vert x\right\vert}\geq 1} 0 ≤ y < π 2 아니면 π 2 < y ≤ π {\displaystyle 0\leqy<{\frac {\pi}{2}}{\text{또는 }}{\frac {\pi}{2}}<y\leq \pi } 0 ∘ ≤ y < 90 ∘ 아니면 90 ∘ < y ≤ 180 ∘ {\displaystyle 0^{\circ }\leq y<90^{\circ }{\text{ or }}}<y\leq 180^{\circ }} 호각류의 y = arccsc ( x ) {\displaystyle y=\operator name {arccsc}(x)} x = csc (y ) x ≥ 1 {\displaystyle {\left\vert x\right\vert}\geq 1} − π 2 ≤ y < 0 아니면 0 < y ≤ π 2 {\displaystyle -{\frac {\pi}{2}}\leqy<0{\text{또는 }}}0<y\leq{\frac {\pi}{2}} − 90 ∘ ≤ y < 0 ∘ 아니면 0 ∘ < y ≤ 90 ∘ {\displaystyle -90^{\circ }\leq y<0^{\circ }{\text{ or }}{\circ }<y\leq 90^{\circ }
참고: 접선 함수가 이 도메인에서 음이 아니기 때문에 일부 저자는 호의 범위를 (0 ≤ 2 또는 3 2 ){\ 스타일 (0\leqy<{\frac {\pi}{2}}{\text }}\pi \leqy<\frac \pi}{2})} . 이것은 몇몇 계산들을 더 일관성 있게 만듭니다. 예를 들어, 이 범위를 사용하면 tan ( arcsec x )) x 2 1 {\displaystyle \tan(\operator {arcsec}(x)) = {\ sqrt {x^{2}-1}} 0 ≤ y π 2 또는 π y π ) {\textstyle (0\leq y<{\frac pi }{2}}{\ 또는 frac pi }{2}}<y\leq )} 경우 arcsec x = 1 {\displaystyle \tan(\operatorname }( x)) 합니다 접선 0≤ y π , textstyle leq <{\pi}{2}}, \ pi π π . textstyle {\frac }{2}}<y\leq .} π y ≤ π textstyle (-\pi < y\leq -{\frac pi }{2}}) 또는 y ≤ π {\textstyle 0<y\leq {\frac {\pi}{2}}). }
x {\displaystyle x} 복소수 일 수 있으면y {\displaystyle }
아래 표에는 역삼각형 함수의 이름과 도메인이 라디안 단위의 일반적인 주 값 의 범위 와 함께 표시됩니다.
이름. 기호. 도메인 이미지/범위 역 기능. 도메인 이미지 주요 가치 사인의 죄악의 {\displaystyle \sin} : {\displaystyle :} R {\displaystyle \mathbb {R}} → {\displaystyle \to} [ − 1 , 1 ] {\displaystyle [-1,1]} 호신 {\displaystyle \arcsin} : {\displaystyle :} [ − 1 , 1 ] {\displaystyle [-1,1]} → {\displaystyle \to} [ − π 2 , π 2 ] {\displaystyle \left[-{\tfrac {\pi}{2}},{\tfrac {\pi}{2}}\right]} 코사인 cos {\displaystyle \cos} : {\displaystyle :} R {\displaystyle \mathbb {R}} → {\displaystyle \to} [ − 1 , 1 ] {\displaystyle [-1,1]} 아코코 {\displaystyle \arccos} : {\displaystyle :} [ − 1 , 1 ] {\displaystyle [-1,1]} → {\displaystyle \to} [ 0 , π ] {\displaystyle [0,\pi ]} 접선의 태닝한 {\displaystyle \tan} : {\displaystyle :} π Z + ( − π 2 , π 2 ) {\displaystyle \pi \mathbb {Z} +\left(-{\tfrac {\pi}{2}}, {\tfrac {\pi}{2}}\right)} → {\displaystyle \to} R {\displaystyle \mathbb {R}} 아크탄 {\displaystyle \arctan} : {\displaystyle :} R {\displaystyle \mathbb {R}} → {\displaystyle \to} ( − π 2 , π 2 ) {\displaystyle \left (-{\tfrac {\pi}{2}},{\tfrac {\pi}{2}}\right)} 공태음의 간이 침대 {\displaystyle \cot} : {\displaystyle :} π Z + ( 0 , π ) {\displaystyle \pi \mathbb {Z} +(0,\pi )} → {\displaystyle \to} R {\displaystyle \mathbb {R}} 아궁이 {\displaystyle \operator name {arccot}} : {\displaystyle :} R {\displaystyle \mathbb {R}} → {\displaystyle \to} ( 0 , π ) {\displaystyle (0,\pi )} 부항의 초 {\displaystyle \sec} : {\displaystyle :} π Z + ( − π 2 , π 2 ) {\displaystyle \pi \mathbb {Z} +\left(-{\tfrac {\pi}{2}}, {\tfrac {\pi}{2}}\right)} → {\displaystyle \to} R ∖ ( − 1 , 1 ) {\displaystyle \mathbb {R} \set마이너스(-1,1)} 아크섹 {\displaystyle \operator name {arcsec}} : {\displaystyle :} R ∖ ( − 1 , 1 ) {\displaystyle \mathbb {R} \set마이너스(-1,1)} → {\displaystyle \to} [ 0 , π ] ∖ { π 2 } {\displaystyle [\,0,\;\pi \,]\;\setminus \left\{\tfrac {\pi}{2}}\right\}} 공변의 csc {\displaystyle \csc} : {\displaystyle :} π Z + ( 0 , π ) {\displaystyle \pi \mathbb {Z} +(0,\pi )} → {\displaystyle \to} R ∖ ( − 1 , 1 ) {\displaystyle \mathbb {R} \set마이너스(-1,1)} arccsc {\displaystyle \operator name {arccsc}} : {\displaystyle :} R ∖ ( − 1 , 1 ) {\displaystyle \mathbb {R} \set마이너스(-1,1)} → {\displaystyle \to} [ − π 2 , π 2 ] ∖ { 0 } {\displaystyle \left[-{\tfrac {\pi}{2}}, {\tfrac {\pi}{2}\right]\set마이너스 \{0\}
기호 R , {\displaystyle \mathbb {R} infty,\infty )} 나타내고 …, 2 , 1, 0 1, , …} displaystyle mathbb ldots,\, -2, -1,\, 0, 2,\, dots \} 정수 의 집합을 나타냅니다. π {\displaystyle pi
π Z := { π n : n ∈ Z } = { … , − 2 π , − π , 0 , π , 2 π , … } . {\displaystyle \pi \mathbb {Z} ~:=~\{\pin\;:\n\in \mathbb {Z} \} ~=~\{\ldots,\,-2\pi,\,-\pi,\,0,\pi,\,2\pi,\,\,\ldots \}
기호 displaystyle setminus \,} 들어 1 , ) , 1 1 ] displaystyle mathbb setminus 1, infty, -1 cup infty ]} R {\displaystyle \mathbb {R}( , 없는 점들의 집합입니다. {\displaystyle (-1 , 1 ) ,1). }
민코프스키 합 표기법 π Z 0 , ) {\ textstyle \mathbb {Z} (0 ,\ pi )}, 2 2 {\displaystyle \mathbb {Z} {\bigl (}{-{\tfrac {\pi }{2}}, tfrac {\pi }{2}}, tfrac pi bigr }}}이(가 .
cotangent cot {\displaystyle \cot} coscant csc {\displaystyle \csc} cot {\ displaystyle \,\cot \,} csc {\ displaystyle \,\csc \,} 이들은 sin 0 , {\displaystyle \sin \theta \neq 0,}, 정수 , {\displaystyle n,} displaystyle \pin} 모든 실수 θ {\ theta}
π Z + ( 0 , π ) = ⋯ ∪ ( − 2 π , − π ) ∪ ( − π , 0 ) ∪ ( 0 , π ) ∪ ( π , 2 π ) ∪ ⋯ = R ∖ π Z {\displaystyle {\begin{aligned}\pi \mathbb {Z} +(0,\pi)&=\cdots \cup (-2\pi,-\pi)\cup (-\pi,0)\cup (\pi,2\pi)\cup \cdots \&=\mathbb {R} \setminus \pi \mathbb {Z} \end{aligned}}
접선 {\displaystyle \tan} 및 접선 {\displaystyle \sec} 도메인 : 접선 {\ displaystyle \,\tan 초 {\ displaystyle \,\sec \,} θ ≠ 0 {\displaystyle theta neq 0,} 각도 {\ theta
π Z + ( − π 2 , π 2 ) = ⋯ ∪ ( − 3 π 2 , − π 2 ) ∪ ( − π 2 , π 2 ) ∪ ( π 2 , 3 π 2 ) ∪ ⋯ = R ∖ ( π 2 + π Z ) {\displaystyle {\begin{aligned}\pi \mathbb {Z} +\left (-{\tfrac {\pi}{2}}, {\tfrac {\pi}{2}\right)&=\cdots \cup {\bigl(}{-{\tfrac {3\pi}{2}}, {-{\tfrac {\pi}{2}}, {\bigr )}\cup {\bigl(}{-{\tfrac {\pi}{2}, {\tfrac {\pi}{2}}, {\bigr )}\cup {\bigl(}, {\tfrac {\pi}}, {\bigr )}, {\bigl(})}, {\tfrac {3\pi }{2}}{\bigr )}\cup \cdots \&=\mathbb {R} \setminus \left ({\tfrac {\pi }{2}}+\pi \mathbb {Z} \right)\\end{aligned}}
기본 삼각방정식의 해 각 삼각 함수는 인수의 실제 부분에서 주기적이며, 2 각 . {\displaystyle 2\pi :}
사인과 코사인은 π k 2 {\textstyle \pi-{\frac {\pi}{2}}( k {\displaystyle k} 2 textstyle 2\pi k+{\frac {\pi }} k textstyle 2\pi k+{\frac {\pi}{ 2 k 2 {\ textstyle pi k+{\ \pi}{2}}. 코사인과 secant는 2 π k, displaystyle \pik,} 2 . displaystyle pik +\ pi..} k k . {\displaystyle 2\pi+2\pi} 탄젠트는 π k 2 {\textstyle 2\pi-{\ frac {\pi}{2}} k 2 {\textstyle 2\pi+{\frac {\pi}{2}}, textstyle 2\pi 2 {\pi }{2}} 2 . textstyle pi k frac {3 }{2}} 코탄젠트는 π k , {\displaystyle 2\pik} , {\displaystyle 2\pik+\pi} k {\displaystyle 2\pik+\pi} k . {\displaystyle 2\pik+2\pi} 이 {\displaystyle k}
다음 표는 6개의 표준 삼각 함수를 포함하는 등호를 풀기 위해 역삼각 함수를 사용하는 방법을 보여줍니다. 아래의 관련 식이 잘 {\ \theta {\ r {\ displaystyle s {\ displaystyle x } "일부 k Z displaystyle k\in \mathbb {Z 일부 정수 . displaystyle .}" .
기호 ⟺ {\ displaystyle \,\iff \,} 논리적으로 동일합니다 . "LHS ⟺ {\ displaystyle \,\iff \,} 모두 참이거나, 그렇지 않으면 (b) 왼손 측과 오른손 측이 모두 거짓임을 나타냅니다. 옵션 (c)은 없습니다. 예를 들어, LHS 문이 참일 수 도 있고 RHS 문이 동시에 참일 수도 없습니다. false), 그렇지 않았다면 "LHS ⟺ {\ displaystyle \,\iff \,}
등식 만일의 경우에만 해결책 죄악의 θ = y {\displaystyle \sin \theta =y} ⟺ {\displaystyle \iff} θ = {\displaystyle \theta =\,} ( − 1 ) k {\displaystyle (-1)^{k} 호신 ( y ) {\displaystyle \arcsin(y)} + {\displaystyle +} π k {\displaystyle \pick} 일부 k Z {\displaystyle k\in \mathbb {Z} csc θ = r {\displaystyle \csc \theta =r} ⟺ {\displaystyle \iff} θ = {\displaystyle \theta =\,} ( − 1 ) k {\displaystyle (-1)^{k} arccsc ( r ) {\displaystyle \operator name {arccsc}(r)} + {\displaystyle +} π k {\displaystyle \pick} 일부 k Z {\displaystyle k\in \mathbb {Z} cos θ = x {\displaystyle \cos \theta = x} ⟺ {\displaystyle \iff} θ = {\displaystyle \theta =\,} ± {\displaystyle \pm \,} 아코코 ( x ) {\displaystyle \arccos(x)} + {\displaystyle +} 2 {\displaystyle 2} π k {\displaystyle \pick} 일부 k Z {\displaystyle k\in \mathbb {Z} 초 θ = r {\displaystyle \sec \theta =r} ⟺ {\displaystyle \iff} θ = {\displaystyle \theta =\,} ± {\displaystyle \pm \,} 아크섹 ( r ) {\displaystyle \operator name {arcsec}(r)} + {\displaystyle +} 2 {\displaystyle 2} π k {\displaystyle \pick} 일부 k Z {\displaystyle k\in \mathbb {Z} 태닝한 θ = s {\displaystyle \tan \theta = s} ⟺ {\displaystyle \iff} θ = {\displaystyle \theta =\,} 아크탄 ( s ) {\displaystyle \arctan(들)} + {\displaystyle +} π k {\displaystyle \pick} 일부 k Z {\displaystyle k\in \mathbb {Z} 간이 침대 θ = r {\displaystyle \cot \theta =r} ⟺ {\displaystyle \iff} θ = {\displaystyle \theta =\,} 아궁이 ( r ) {\displaystyle \operator name {arccot}(r)} + {\displaystyle +} π k {\displaystyle \pick} 일부 k Z {\displaystyle k\in \mathbb {Z}
여기서 처음 4가지 솔루션은 다음과 같이 확장된 형태로 작성할 수 있습니다.
등식 만일의 경우에만 해결책 죄악의 θ = y {\displaystyle \sin \theta =y} ⟺ {\displaystyle \iff} θ = 호신 ( y ) + 2 π h {\displaystyle \theta =\;\;\,\arcsin(y)+2\pih} 아니면 θ = − 호신 ( y ) + 2 π h + π {\displaystyle \theta =-\arcsin(y)+2\pi h+\pi } 일부 h Z {\displaystyle h\in \mathbb {Z}} csc θ = r {\displaystyle \csc \theta =r} ⟺ {\displaystyle \iff} θ = arccsc ( y ) + 2 π h {\displaystyle \theta =\;\;\,\operator name {arccsc}(y)+2\pih} 아니면 θ = − arccsc ( y ) + 2 π h + π {\displaystyle \theta =-\operator name {arccsc}(y)+2\pi h+\pi } 일부 h Z {\displaystyle h\in \mathbb {Z}} cos θ = x {\displaystyle \cos \theta = x} ⟺ {\displaystyle \iff} θ = 아코코 ( y ) + 2 π k {\displaystyle \theta =\;\;\,\arccos(y)+2\pick} 아니면 θ = − 아코코 ( y ) + 2 π k {\displaystyle \theta =-\arccos(y)+2\pick} 일부 k Z {\displaystyle k\in \mathbb {Z} 초 θ = r {\displaystyle \sec \theta =r} ⟺ {\displaystyle \iff} θ = 아크섹 ( y ) + 2 π k {\displaystyle \theta =\;\;\,\operator name {arcsec}(y)+2\pick} 아니면 θ = − 아크섹 ( y ) + 2 π k {\displaystyle \theta =-\operator name {arcsec}(y)+2\pick} 일부 k Z {\displaystyle k\in \mathbb {Z}
예를 들어 cos 1 {\displaystyle \cos \theta } k 2 ( 1 k ) {\displaystyle \theta pi +2\pi pi -\ 2\ pi (1 )} k Z {\displaystyle \in \mathbb {Z} .} sin 1 {\displaystyle \sin \theta pm } 2 k k {\textstyle \theta frac {\pi}{2}}+\pi k = 일부 ∈ {\ frac pi}{2}}+\ k+1)}, displaystyle \in \mathbb {Z},} k {\displaystyle } = 1 {\displaystyle \sin \theta = } 경우 θ = 1인 경우 {\displaystyle \sin = -1.} sec θ 1 {\displaystyle sec = -1} csc θ = 1 {\displaystyle \csc \theta = pm } c θ = 1 {\displaystyle \cos \the a -1} s 1 , {\displaystyle \sin \the a pm 1,} 방금 풀린 식(즉 , sin {\displaystyle \sin } csc {\displaystyle csc \theta pm 1} cos {\displaystyle \cos 1 {\displaystyle \sec \theta -1}) k {\ displaystyle } displaystyle theta }( r , s , x , {\displaystyle r, s, x,} 및 {\displaystyle y}).
"플러스 또는 마이너스" 기호에 대한 자세한 예시 및 설명 ± cos x {\displaystyle \cos \theta } sec {\displaystyle \sec \theta x} " 기호 \,\pm,\,} sec x {\ displaystyle cos \theta x} cos x {\ displaystyle sec \theta x} 우리 -1 ≤ x ≤ displaystyle x } 사이 displaystyle x} cos x {\displaystyle \theta} . {\displaystyle \cos \theta .} . {\displaystyle \theta .}
θ = ± 아코코 x + 2 π k 어느 정도는 k ∈ Z {\displaystyle \,\theta =\pm \arccos x+2\pik\,\mathbb {Z} quad {\text{일부}} 이것은 (적어도) 다음 문장 중 하나가 참이라는 속설입니다.
일부 정수 대해 = ar c cos π {\ displaystyle \,\t h eta arccos x+2\pik\,}, ,} 아니면 θ = k ar c cos x 2 π {\displaystyle \,\t h eta arccos 2\pik\,}. {\displaystyle .} 위에서 언급한 바와 같이 arccos x {\displaystyle \,\arccos pi \,}( x cos {\displaystyle cos \pi -1} ) 정수 {\displaystyle } . {\displaystyle } + 2 π {\displaystyle \theta = \pi +2\pi } 정수 displaystyle k} 1 displaystyle +1} θ = π 2 π ( 1 K ) {\displaystyle \theta = pi +2\pi (1 )). 그러나 x 1 {\displaystyle x\neq -1} 정수 {\displaystyle k} 고유 . {\displaystyle \theta .} arccos x {\displaystyle \,\arccos 0\,}( 정의상 cos 0 1 {\displaystyle cos 1 arccos x {,\pm \arccos 0\,}( se + arccos x 0 {\displaystyle \,+\arccos \,} arccos x 0 {\displaystyle \,-\arccos -0 \,} arccos x {\displaystyle \,\pm arccos 0 arccos 0 {\displaystyle \,\arccos arccos x , {\displaystyle \,\arccos pi,\,} arccos x {\displaystyle \,\arccos \ neq \,} arccos x displaystyle \,\arccos neq ,\,} cos {\displaystyle \cos \theta x}
θ = ± 아코코 x + 2 π k 어느 정도는 k ∈ Z {\displaystyle \,\theta =\pm \arccos x+2\pik\,\mathbb {Z} quad {\text{일부}} 이전과 마찬가지로 (1)과 (2) 중 하나의 진술이 참이라고 말하는 축약어입니다. 그러나 이번에는 arccos x 0 {\displaystyle \,\arccos x\neq 0\,} 0 arccos x , {\displaystyle \,0<\arccos x<\pi,\,,} 하나(둘 다 아님)입니다. θ {\displaystyle theta 예를 들어 x {\displaystyle 0} displaystyle \theta} 것 은 {\displaystyle \,-\pi \leq \theta \leq \pi \,}( 그리고나서 아코코 x = 아코코 0 = π 2 {\displaystyle \arccos x=\arccos 0={\frac {\pi}{2}} 그리고 이 특정한 경우 k {\displaystyle 0 } (+ displaystyle \,+\,} displaystyle \,-,} θ = ± 아코코 x + 2 π k = ± ( π 2 ) + 2 π ( 0 ) = ± π 2 . {\displaystyle \theta ~=~\pm \arccos x+2\pik~~=~\pm \left ({\frac {\pi}{2}}\right)+2\pi (0)~=~\pm {\frac {\pi}{2}}} 즉 displaystyle theta ( {\displaystyle \,\pi /2\,} 2일 . {\displaystyle \,-\pi /2.} {\displaystyle \theta} θ {\displaystyle theta 각도 {\displaystyle 축( 2 {\displaystyle \theta pi }) x {\displaystyle x} 2 {\displaystyle \theta pi 2})
방정식 변환 위의 방정식은 반사 및 이동 항등식을 사용하여 변환할 수 있습니다.[18]
이동 및 반사에 의한 방정식 변환 인수: _ {\displaystyle {\ 밑줄 − θ {\displaystyle -\theta} π 2 ± θ {\displaystyle {\frac {\pi}{2}}\pm \theta } π ± θ {\displaystyle \pi \pm \theta } 3 π 2 ± θ {\displaystyle {\frac {3\pi}{2}}\pm \theta } 2 k π ± θ , {\displaystyle 2k\pi \pm \theta,} ( k ∈ Z ) {\displaystyle (k\in \mathbb {Z} )} 죄악의 _ = {\display style \sin {\\ 밑줄 {\;~~~}}=} − 죄악의 θ {\displaystyle -\sin \theta} − cos θ {\displaystyle {\phantom {-}}\cos \theta} ∓ 죄악의 θ {\displaystyle \mp \sin \theta} − cos θ {\displaystyle -\cos \theta} ± 죄악의 θ {\displaystyle \pm \sin \theta} csc _ = {\display style \csc {\밑줄 {\;~~~~\"}=} − csc θ {\displaystyle -\csc \theta } − 초 θ {\displaystyle {\phantom {-}}\sec \theta} ∓ csc θ {\displaystyle \mp \csc \theta } − 초 θ {\displaystyle -\sec \theta} ± csc θ {\displaystyle \pm \csc \theta } cos _ = {\display style \cos {\ 밑줄 {\;~~~}}=} − cos θ {\displaystyle {\phantom {-}}\cos \theta} ∓ 죄악의 θ {\displaystyle \mp \sin \theta} − cos θ {\displaystyle -\cos \theta} ± 죄악의 θ {\displaystyle \pm \sin \theta} − cos θ {\displaystyle {\phantom {-}}\cos \theta} 초 _ = {\display style \sec {\ 밑줄 {\;~~~}}=} − 초 θ {\displaystyle {\phantom {-}}\sec \theta} ∓ csc θ {\displaystyle \mp \csc \theta } − 초 θ {\displaystyle -\sec \theta} ± csc θ {\displaystyle \pm \csc \theta } − 초 θ {\displaystyle {\phantom {-}}\sec \theta} 태닝한 _ = {\display style \tan {\밑줄 {\;~~~}}=} − 태닝한 θ {\displaystyle -\tan \theta} ∓ 간이 침대 θ {\displaystyle \mp \cot \theta } ± 태닝한 θ {\displaystyle \pm \tan \theta } ∓ 간이 침대 θ {\displaystyle \mp \cot \theta } ± 태닝한 θ {\displaystyle \pm \tan \theta } 간이 침대 _ = {\display style \cot {\ 밑줄 {\;~~~}}=} − 간이 침대 θ {\displaystyle -\cot \theta} ∓ 태닝한 θ {\displaystyle \mp \tan \theta} ± 간이 침대 θ {\displaystyle \pm \cot \theta } ∓ 태닝한 θ {\displaystyle \mp \tan \theta} ± 간이 침대 θ {\displaystyle \pm \cot \theta }
이러한 공식은 특히 다음과 같은 의미를 갖습니다.
죄악의 θ = − 죄악의 ( − θ ) = − 죄악의 ( π + θ ) = − 죄악의 ( π − θ ) = − cos ( π 2 + θ ) = − cos ( π 2 − θ ) = − cos ( − π 2 − θ ) = − cos ( − π 2 + θ ) = − cos ( 3 π 2 − θ ) = − cos ( − 3 π 2 + θ ) cos θ = − cos ( − θ ) = − cos ( π + θ ) = − cos ( π − θ ) = − 죄악의 ( π 2 + θ ) = − 죄악의 ( π 2 − θ ) = − 죄악의 ( − π 2 − θ ) = − 죄악의 ( − π 2 + θ ) = − 죄악의 ( 3 π 2 − θ ) = − 죄악의 ( − 3 π 2 + θ ) 태닝한 θ = − 태닝한 ( − θ ) = − 태닝한 ( π + θ ) = − 태닝한 ( π − θ ) = − 간이 침대 ( π 2 + θ ) = − 간이 침대 ( π 2 − θ ) = − 간이 침대 ( − π 2 − θ ) = − 간이 침대 ( − π 2 + θ ) = − 간이 침대 ( 3 π 2 − θ ) = − 간이 침대 ( − 3 π 2 + θ ) {\displaystyle {\begin{aligned}\sin \theta &=-\sin (-\theta )&=-\sin(\pi +\theta )&={\phantom {-}\sin(\pi -\theta )\&=-\cos \left ({\frac {\pi }{2}+\theta \right) &={\phantom {-}}\cos \left ({\frac {\pi}{2}-\theta \right)&=-\cos \left (-{\pi}{2}-\theta \right)\" \&={\phantom {-}}\cos \left(-{\frac {\pi}{2}}+\theta \right)&=-\cos \left({\frac {3\pi}{2}-\theta \right)-&=-\cos \left(-{\frac {3\pi}{2}+\theta \right)\\\[0.3ex]\cos \theta &={\phantom {-}\cos (-\theta )&=-\cos (\pi +\theta )&={\cos {-}\cos (\pi -\theta )\&&={\phantom {-}\sin \left({{\pi }{2}}+\theta \right) &&={\phantom {-}}\sin \left ({\frac {\pi}{2}-\theta \right)&=-\sin \left (-{\pi}{2}-\theta \right)\&=-\sin \left (-{\frac {\pi}{2}}+\theta \right)&=-\sin \left ({\frac {3\pi}{2}-\theta \right) &={\phantom {-}}\sin \left (-{\frac {3\pi}{2}}+\theta \right)\[0.3ex]\tan \theta &=-\tan (-\theta )&={\tan {-}\tan (\pi +\theta )&=-\tan (\pi -\theta )\\&\tan \left ({\frac {2}+\theta \right) &&={\phantom {-}}\cot \left ({\frac {\pi}{2}-\theta \right) &&={\phantom{-}}\cot \left (-{\frac {\pi}{2}-\theta \right)\&=-\cot \left (-{\frac {\pi}{2}}+\theta \right) &={\phantom {-}}\cot \left ({\frac {3\pi}{2}-\theta \right)&=-\cot \left (-{\frac {3\pi}{2}}+\theta \right)\[0.3ex]\end{aligned}}
여기 csc displaystyle sin \left \csc ,} 스와핑 sec displaystyle cos left sec ,} 스왑 cot displaystyle tan left arrow } csc , sec 및 cot , {\displaystyle \csc ,\sec {\text{ }\cot ,}
따라서 예를 들어, sin cos , textstyle \sin \left frac {\pi }{2}-\theta \right cos \theta,} cos x displaystyle \cos \theta x} x , textstyle \sin \left frac {\pi }{2}-\theta \right x}, φ = x {\displaystyle \;\sin varphi = x\;}( 여기 φ = π 2 θ {\textstyle varphi : = {\frac {\pi }}-\theta }) 사용 φ = 일부 k개 ∈ Z π displaystyle \varphi = (- 1)^{k}\arcsin(x)+\pi {\text{ k\in mathbb }
π 2 − θ = ( − 1 ) k 호신 ( x ) + π k 어느 정도는 k ∈ Z {\displaystyle {\frac {\pi}{2}}-\theta ~=~(-1)^{k}\arcsin(x)+\pik\quad {\text{일부}}}\n\mathbb {Z}} 여기서 ( 1 k 1 {\displaystyle (-1)^{k 1)^{-k} 사용 k {\displaystyle k} cos x {\displaystyle \;\cos \theta x\;} θ = ( − 1 ) h + 1 호신 ( x ) + π h + π 2 어느 정도는 h ∈ Z . {\displaystyle \theta ~=~(-1)^{h+1}\arcsin(x)+\pi h+{\frac {\pi}{2}}\quad {\text{일부}}}h\in \mathbb {Z} .} x arcos x {\displaystyle \;\arcsin frac {\pi }}-\arcos x\;} x displaystyle \;\arcos \;} arcos x {\displaystyle {\displaystyle \;\arcsin .\;}
동일한 삼각함수 아래 표는 θ {\displaystyle \theta} {\displaystyle \varphi}
등식 만일의 경우에만 솔루션(일부 k Z {\displaystyle k\in \mathbb {Z}) ) 또한 에 대한 해결책. − 죄악의 θ = 죄악의 φ {\displaystyle {\phantom {-}}\sin \theta =\sin \varphi} ⟺ {\displaystyle \iff} θ = ( − 1 ) k φ + 2 π k + π {\displaystyle \theta ={\phantom {\quad }}(-1)^{k}\varphi +{\phantom {2}}\pik{\phantom {+\pi}} − csc θ = csc φ {\displaystyle {\phantom {-}}\csc \theta =\csc \varphi } − cos θ = cos φ {\displaystyle {\phantom {-}}\cos \theta =\cos \varphi } ⟺ {\displaystyle \iff} θ = − 1 ± φ + 2 π k + π {\displaystyle \theta = {\phantom {-1\quad }}\pm \varphi +2\pik{\phantom {+\pi}} − 초 θ = 초 φ {\displaystyle {\phantom {-}}\sec \theta =\sec \varphi } − 태닝한 θ = 태닝한 φ {\displaystyle {\phantom {-}}\tan \theta =\tan \varphi } ⟺ {\displaystyle \iff} θ = ( − 1 ) k + 1 φ + 2 π k + π {\displaystyle \theta = {\phantom {(-1)^{k+1}}\varphi +{\phantom {2}}\pik{\phantom {+\pi}} − 간이 침대 θ = 간이 침대 φ {\display style {\phantom {-}}\cot \theta =\cot \varphi } − 죄악의 θ = 죄악의 φ {\displaystyle -\sin \theta =\sin \varphi } ⟺ {\displaystyle \iff} θ = ( − 1 ) k + 1 φ + 2 π k + π {\displaystyle \theta = (-1)^{k+1}\varphi +{\phantom {2}}\pik{\phantom {+\pi}} − csc θ = csc φ {\displaystyle -\csc \theta =\csc \varphi } − cos θ = cos φ {\displaystyle -\cos \theta =\cos \varphi } ⟺ {\displaystyle \iff} θ = − 1 ± φ + 2 π k + π + π {\display style \theta = {\phantom {-1\quad }}\pm \varphi +2\pi +\pi {\phantom {+\pi}} − 초 θ = 초 φ {\displaystyle -\sec \theta =\sec \varphi } − 태닝한 θ = 태닝한 φ {\displaystyle -\tan \theta =\tan \varphi } ⟺ {\displaystyle \iff} θ = − 1 − φ + 2 π k + π {\displaystyle \theta = {\phantom {-1\quad }}-\varphi +{\phantom {2}}\pik{\phantom {+\pi}} − 간이 침대 θ = 간이 침대 φ {\displaystyle -\cot \theta =\cot \varphi } − 죄악의 θ = 죄악의 φ − cos θ = cos φ {\displaystyle {\begin{aligned}{\phantom{-}}\left \sin \theta \right &=\left \sin \varphi \right \{\phantom{-}}\left \cos \theta \right &=\left \cos \varphi \right \end{aligned}} ⟺ {\displaystyle \iff} θ = − 1 ± φ + 2 π k + π {\display style \theta = {\phantom {-1\quad }}\pm \varphi +{\phantom {2}}\pik{\phantom {+\pi}} − 태닝한 θ = 태닝한 φ csc θ = csc φ 초 θ = 초 φ 간이 침대 θ = 간이 침대 φ {\디스플레이 스타일 {\begin {aligned}{\phantom {-}}\left \tan \theta \right &=\left \tan \varphi \right \\\left \csc \teta \right &=\left \csc \varphi \right \\\left \sec \sec \theta \right &=\left \sec \varphi \right \right \end{align}}
삼각함수와 역삼각함수의 관계 역삼각형 함수의 삼각형 함수는 아래 표와 같습니다. 그들을 도출하는 빠른 방법은 길이 1의 한 변과 길이 x , displaystyle x} 피타고라스 정리 와 삼각형 비율의 정의를 적용하는 것입니다. 주의할 점은 호와 호의 경우, 다이어그램 {\displaystyle } 절대값 사용과 부호(sgn ) 연산을 통해 결과를 수정해야 한다는 것입니다.
θ {\displaystyle \theta} 죄악의 ( θ ) {\displaystyle \sin(\theta )} cos ( θ ) {\displaystyle \cos(\theta )} 태닝한 ( θ ) {\displaystyle \tan(\theta )} 도표 호신 ( x ) {\displaystyle \arcsin(x)} 죄악의 ( 호신 ( x ) ) = x {\displaystyle \sin(\arcsin(x))=x} cos ( 호신 ( x ) ) = 1 − x 2 {\displaystyle \cos(\arcsin(x)) ={\sqrt {1-x^{2}}}} 태닝한 ( 호신 ( x ) ) = x 1 − x 2 {\displaystyle \tan(\arcsin(x)) ={\frac {x}{\sqrt {1-x^{2}}}}} 아코코 ( x ) {\displaystyle \arccos(x)} 죄악의 ( 아코코 ( x ) ) = 1 − x 2 {\displaystyle \sin(\arccos(x)) ={\sqrt {1-x^{2}}}} cos ( 아코코 ( x ) ) = x {\displaystyle \cos(\arccos(x))=x} 태닝한 ( 아코코 ( x ) ) = 1 − x 2 x {\displaystyle \tan(\arccos(x)) ={\frac {\sqrt {1-x^{2}}}{x}} 아크탄 ( x ) {\displaystyle \arctan(x)} 죄악의 ( 아크탄 ( x ) ) = x 1 + x 2 {\displaystyle \sin(\arctan(x)) ={\frac {x}{\sqrt {1+x^{2}}}}} cos ( 아크탄 ( x ) ) = 1 1 + x 2 {\displaystyle \cos(\arctan(x)) ={\frac {1}{\sqrt {1+x^{2}}}}} 태닝한 ( 아크탄 ( x ) ) = x {\displaystyle \tan(\arctan(x))=x} 아궁이 ( x ) {\displaystyle \operator name {arccot}(x)} 죄악의 ( 아궁이 ( x ) ) = 1 1 + x 2 {\displaystyle \sin(\operator name {arccot}(x)) ={\frac {1}{\sqrt {1+x^{2}}}}} cos ( 아궁이 ( x ) ) = x 1 + x 2 {\displaystyle \cos(\operator name {arccot}(x)) ={\frac {x}{\sqrt {1+x^{2}}}}} 태닝한 ( 아궁이 ( x ) ) = 1 x {\displaystyle \tan(\operator name {arccot}(x)) ={\frac {1}{x}} 아크섹 ( x ) {\displaystyle \operator name {arcsec}(x)} 죄악의 ( 아크섹 ( x ) ) = x 2 − 1 x {\displaystyle \sin(\operator name {arcsec}(x)) ={\frac {\sqrt {x^{2}-1}}{x}} cos ( 아크섹 ( x ) ) = 1 x {\displaystyle \cos(\operator name {arcsec}(x)) ={\frac {1}{x}} 태닝한 ( 아크섹 ( x ) ) = sgn ( x ) x 2 − 1 {\displaystyle \tan(\operator name {arcsec}(x)) =\operator name {sgn}(x){\sqrt {x^{2}-1}} arccsc ( x ) {\displaystyle \operator name {arccsc}(x)} 죄악의 ( arccsc ( x ) ) = 1 x {\displaystyle \sin(\operator name {arccsc}(x)) ={\frac {1}{x}} cos ( arccsc ( x ) ) = x 2 − 1 x {\displaystyle \cos(\operator name {arccsc}(x)) ={\frac {\sqrt {x^{2}-1}}{x}} 태닝한 ( arccsc ( x ) ) = sgn ( x ) x 2 − 1 {\displaystyle \tan(\operator name {arccsc}(x)) ={\frac {\operatorname {sgn}(x)}{\sqrt {x^{2}-1}}}}:
역삼각함수 사이의 관계 직교 평면에 그래프로 표시된 호(x )(빨간색) 및 호(x )(파란색) 함수의 일반적인 주 값입니다. 직교 평면에 그래프로 표시된 아크탄(x ) 및 아크코트(x ) 함수의 일반적인 주 값입니다. 직교 평면에 그래프로 표시된 arsec(x ) 및 arccsc(x ) 함수의 주 값입니다. 상보각:
아코코 ( x ) = π 2 − 호신 ( x ) 아궁이 ( x ) = π 2 − 아크탄 ( x ) arccsc ( x ) = π 2 − 아크섹 ( x ) {\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi}{2}}-\arcsin(x)\[0.5em]\operatorname {arccot}(x)&={\frac {\pi}{2}-\arctan(x)\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}-\operatorname {arcsec}(x)\end{aligned}} 부정적 인수:
호신 ( − x ) = − 호신 ( x ) 아코코 ( − x ) = π − 아코코 ( x ) 아크탄 ( − x ) = − 아크탄 ( x ) 아궁이 ( − x ) = π − 아궁이 ( x ) 아크섹 ( − x ) = π − 아크섹 ( x ) arccsc ( − x ) = − arccsc ( x ) {\displaystyle {\begin{aligned}\arcsin (-x)&=-\arcsin(x)\\\arccos (-x)&=\pi -\arccos(x)\\arctan (-x)&=-\arctan(x)\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccsec}(-x)&=\pi -\operatorname {arcsc}(-x)&=-\operatorname {arcsc}(x)\end{aligned}} 역수 인수:
아코코 ( 1 x ) = 아크섹 ( x ) 호신 ( 1 x ) = arccsc ( x ) 아크탄 ( 1 x ) = π 2 − 아크탄 ( x ) = 아궁이 ( x ) , 한다면 x > 0 아크탄 ( 1 x ) = − π 2 − 아크탄 ( x ) = 아궁이 ( x ) − π , 한다면 x < 0 아궁이 ( 1 x ) = π 2 − 아궁이 ( x ) = 아크탄 ( x ) , 한다면 x > 0 아궁이 ( 1 x ) = 3 π 2 − 아궁이 ( x ) = π + 아크탄 ( x ) , 한다면 x < 0 아크섹 ( 1 x ) = 아코코 ( x ) arccsc ( 1 x ) = 호신 ( x ) {\displaystyle {\begin{aligned}\arccos \left ({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left ({\frac {1}{x}\right)&=\operatorname {arccsc}(x)\[0.3em]\arctan \left ({\frac {1}{x}\right)&={\frac {2}}-\arctan(x)=\operatorname {arccot}(x),{\text{if}}x>0\[0.3em]\arctan \left ({\frac {1}{x}\right)&=-{\frac {\pi}{2}-\a rctan(x)=\operatorname {arccot}(x)-\pi \,{\text{if }}x<0\[0.3em]\operatorname {arccot}\left ({\frac {1}{x}\right)&={\frac {\pi}{2}-\operatorname {arccot}(x)=\arctan(x)\,{\text{if }x>0\[0.3em]\operatorname {arccot} \left ({\frac {1}{x}\right)&={\frac {3\pi}{2}-\operatorname {arccot}(x)=\pi +\arctan(x)\,{\text{if }}x<0\[0.3em]\operatorname {arccot} 이름 {arcsec} \left ({\frac {1}{x}\right)&=\arccos(x)\\[0.3em]\operator name {arccsc} \left ({\frac {1}{x}\right)&=\arcsin(x)\end{aligned}} 사인 테이블의 조각만 있는 경우 유용한 ID:
아코코 ( x ) = 호신 ( 1 − x 2 ) , 한다면 0 ≤ x ≤ 1 , 당신이 얻는 것은 아코코 ( 1 − x 2 1 + x 2 ) = 호신 ( 2 x 1 + x 2 ) , 한다면 0 ≤ x ≤ 1 호신 ( 1 − x 2 ) = π 2 − sgn ( x ) 호신 ( x ) 아코코 ( x ) = 1 2 아코코 ( 2 x 2 − 1 ) , 한다면 0 ≤ x ≤ 1 호신 ( x ) = 1 2 아코코 ( 1 − 2 x 2 ) , 한다면 0 ≤ x ≤ 1 호신 ( x ) = 아크탄 ( x 1 − x 2 ) 아코코 ( x ) = 아크탄 ( 1 − x 2 x ) 아크탄 ( x ) = 호신 ( x 1 + x 2 ) 아궁이 ( x ) = 아코코 ( x 1 + x 2 ) {\displaystyle {\begin{aligned}\arccos(x)&=\arcsin \left ({\sqrt {1-x^{2}}\right),{\text{if}},0\leq x\leq 1{\text{, 여기서 }}\\arccos &\leq ({\frac {1-x^{2},{1+x^{2} }}\right)=\arcsin \left ({\frac {2x}{1+x^{2 }}\right),{{\text{if}},0\leq x\leq 1\\\rft ({\sqrt {1-x^{2}}\right)={\frac {\pi}{2}}-\operatorname {sgn}(x)\arcsin(x)\\\arccos(x)&={\frac {1}{2}\right)\rft(2x^{2}-,{\text{if}}},0\leq x\leq 1\\arcsin(x)&={\frac {1}{2}\right)\rft(1-2x^{2}\right)\rft(1-2x^{2}\right)\,,,{\text{if}}},0\leq x\leq 1\leqsin(x)&&{\frac {1}\right},\arcos \left(1-2x^{2}\right)\,,, {\text{if}}0\leq x\leq 1\\\arcsin(x)&=\arctan \left ({\frac {x}{\sqrt {1-x^{2}}}\right)\\arccos(x)&=\arctan \left ({\frac {\sqrt {1-x^{2}}{x}\right)\\arcsin \left ({\frac {x}{\sqrt {1+x^{2}}\right)\\arcsin \leq x(x)&=\arcsin \leq. }}}}\right)\" \\operator name {arccot}(x)&=\arccos \left ({\frac {x}{\sqrt {1+x^{2 }}}}\right)\end{aligned}} 복소수의 제곱근이 여기서 사용될 때마다 양의 실수 부분(또는 제곱이 음의 실수인 경우 양의 허수 부분)을 갖는 근을 선택합니다.
위의 표에서 바로 이어지는 유용한 형태는
arc t an x arc c os + x 2 ), 약 x 0 \arctan \left (x\ri g ht)=\arccos \l ef t ({\sqrt {\frac {1}{ 1 + x^{2 }}}}\right),{{\text{if}}}x\geq0 cos arctan x )) 11 x 2 cos arccos 11 displaystyle \left arctan \left(x\right))\right sqrt frac {1}{1 x^{2 }}}}=\cos \left(\arccos \left ({\sqrt {\frac {1}{1+x^{2 }}}}\right)\right
반각 공식 에서 tan ( 2 sin 1 cos {\display \tan \left tfrac {\theta}{2}\right tfrac {\sin(\theta )}{1+\cos(\theta )}},
호신 ( x ) = 2 아크탄 ( x 1 + 1 − x 2 ) 아코코 ( x ) = 2 아크탄 ( 1 − x 2 1 + x ) , 한다면 − 1 < x ≤ 1 아크탄 ( x ) = 2 아크탄 ( x 1 + 1 + x 2 ) {\displaystyle {\begin{aligned}\arcsin(x)&=2\arctan \left ({\frac {x}{1+{\sqrt {1-x^{2}}}\right)\[0.5em]\arccos(x)&=2\arctan \left ({\frac {\sqrt {1-x^{2}}{1+x}}\right),{\text{if }}-1<x\leq 1\[0.5em]\arctan(x)&=2\arctan \left ({\frac {x}{1+{\sqrt {1+x^{2}}\right)\,{\text{if }}-1<x\leq 1\[0.5em]\arctan(x)&=2\arctan \left ({\frac {x}{1+{x}}{1+x}{2}}\rft. }}}}}\right)\end{aligned}} 아크탄젠트 덧셈 공식 아크탄 ( u ) ± 아크탄 ( v ) = 아크탄 ( u ± v 1 ∓ u v ) ( 모드의 π ) , u v ≠ 1 . {\displaystyle \arctan(u)\pm \arctan(v)=\arctan \left ({\frac {u\pm v}{1\mp uv}}\right){\pmod {\pi}},,,,\quad uv\neq 1\.} 이는 접선 덧셈 공식 에서 유도됩니다.
태닝한 ( α ± β ) = 태닝한 ( α ) ± 태닝한 ( β ) 1 ∓ 태닝한 ( α ) 태닝한 ( β ) , {\displaystyle \tan(\alpha \pm \beta )={\frac {\tan(\alpha )\pm \tan(\beta )}{1\mp \tan(\alpha )\tan(\tan(\beta )}}\,} 허용함으로써
α = 아크탄 ( u ) , β = 아크탄 ( v ) . {\displaystyle \alpha =\arctan(u)\,,,\quad \beta =\arctan(v)\,} 미적분학에서 역삼각함수의 도함수 복소수 z 값에 대한 도함수 는 다음과 같습니다.
d d z 호신 ( z ) = 1 1 − z 2 ; z ≠ − 1 , + 1 d d z 아코코 ( z ) = − 1 1 − z 2 ; z ≠ − 1 , + 1 d d z 아크탄 ( z ) = 1 1 + z 2 ; z ≠ − i , + i d d z 아궁이 ( z ) = − 1 1 + z 2 ; z ≠ − i , + i d d z 아크섹 ( z ) = 1 z 2 1 − 1 z 2 ; z ≠ − 1 , 0 , + 1 d d z arccsc ( z ) = − 1 z 2 1 − 1 z 2 ; z ≠ − 1 , 0 , + 1 {\displaystyle {\begin{aligned}{\frac {d}{dz}}\arcsin(z)&{}={\frac {1}{\sqrt {1-z^{2}}}\;&z&{}\neq -1,+1\{\frac {d}{dz}}\arccos(z)&{}=-{\frac {1}{\sqrt {1-z^{2}}}\;&z&{}\neq -1,+1\{\frac {d}{dz}\arctan(z)&{}={\frac {1}{1+z^{2}}\frac {1} }}\;&z&{}\neq -i,+i\{\frac {d}{dz}}\operator name {arccot}(z)&{}=-{\frac {1}{1+z^{2 }}\;&z&{}\neq -i,+i\{\frac {d}{dz}}\operatorname {arcsec}(z)&{}={\frac {1}{z^{2}}}}\;&z&{}}\neq -1,0,+1\{\frac {d}{ dz}\operatorname {arccsc}(z)&{{}=-{\frac {1}{z^{2}}}\;&z&{{}\frac {1}{z^{2}}}\;&z&{{}\neq -1,0,+1\end{align}}}\operatorname {arccsc}(z)&{z}=-{\frac {1}{z^{2}}}}}\;&z&{}\neq -1,0,+1\end{align}}} x 의 실수 값에 대해서만:
d d x 아크섹 ( x ) = 1 x x 2 − 1 ; x > 1 d d x arccsc ( x ) = − 1 x x 2 − 1 ; x > 1 {\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsec}(x)&{}={\frac {1}{ x {\sqrt {x^{2}-1}}}\;& x >1\{\frac {d}{dx}}\operatorname {arccsc}(x)&{{}=-{\frac {1}{ x {\sqrt {x^{2}-1}}\;& x >1\end{aligned}} 샘플 파생의 경우: x ) {\displaystyle \theta \arcsin(x)} 아크 .
d 호신 ( x ) d x = d θ d 죄악의 ( θ ) = d θ cos ( θ ) d θ = 1 cos ( θ ) = 1 1 − 죄악의 2 ( θ ) = 1 1 − x 2 {\displaystyle {\frac {d\arcsin(x)) {dx}}={\frac {d\theta}{{d\sin(\theta)}}={\frac {d\theta}{\cos(\theta)\,d\theta}}={\frac {1}{\cos(\theta)}={\frac {1}{\sqrt {1-\sin ^{2}(\theta)}}={\frac {1}{\sqrt {1-x^{2}}}}}}{\frac {1}} 수식을 정적분식 도함수를 적분하고 값을 한 점에 고정하면 역삼각형 함수에 대한 식을 정적분으로 얻을 수 있습니다.
호신 ( x ) = ∫ 0 x 1 1 − z 2 d z , x ≤ 1 아코코 ( x ) = ∫ x 1 1 1 − z 2 d z , x ≤ 1 아크탄 ( x ) = ∫ 0 x 1 z 2 + 1 d z , 아궁이 ( x ) = ∫ x ∞ 1 z 2 + 1 d z , 아크섹 ( x ) = ∫ 1 x 1 z z 2 − 1 d z = π + ∫ − x − 1 1 z z 2 − 1 d z , x ≥ 1 arccsc ( x ) = ∫ x ∞ 1 z z 2 − 1 d z = ∫ − ∞ − x 1 z z 2 − 1 d z , x ≥ 1 {\displaystyle {\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}\, dz\;,& x &{}\leq 1\\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}\, dz\;,& x &{}\\req 1\\int _0}^{x}=\int _{0}^{x}}{\frac {1}{z^{2}+1}}, dz\;,\\\operatorname {arccot}(x)&{}=\int _x}^{\infty}{\frac {1}{z^{2}+1}, dz\;,\operatorname {arcsec}(x)&{}=\in. t_{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}\, dz=\pi +\int _{-x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}\, dz\;,&x&{}\geq 1\\\\operatorname {arccsc}(x)&{}=\int _x}^{\infty}{\frac {1}{z{\sqrt {z^{2}-1}}\, dz=\int _{-\infty}^{-x}{\frac {1}{z{\sqrt {z^{2}-1}}}, dz;,&x&{}\geq 1\\\end{aligned}}} x 가 1일 때 도메인이 제한된 적분은 부적절한 적분 이지만 여전히 잘 정의되어 있습니다.
무한급수 사인 함수 및 코사인 함수와 마찬가지로 역삼각형 함수도 다음 과 같이 멱급수 를 사용하여 계산할 수 있습니다. 아크사인의 경우 급수는 도함수인 11 z 2 {\ textstyle {\tfrac {1}{\sqrt {1-z^{2}}} 이항급수 로 확장하고 항 단위로 적분하여 유도할 수 있습니다(위와 같이 적분 정의를 사용). 아크탄젠트에 대한 급수는 도함수 11 z 2 {\ textstyle {\frac {1}{1 ^{2}}}} 기하급수 로 확장하고 위의 적분 정의를 적용함으로써 유사하게 유도할 수 있습니다(라이프니즈 급수 참조).
호신 ( z ) = z + ( 1 2 ) z 3 3 + ( 1 ⋅ 3 2 ⋅ 4 ) z 5 5 + ( 1 ⋅ 3 ⋅ 5 2 ⋅ 4 ⋅ 6 ) z 7 7 + ⋯ = ∑ n = 0 ∞ ( 2 n − 1 ) ! ! ( 2 n ) ! ! z 2 n + 1 2 n + 1 = ∑ n = 0 ∞ ( 2 n ) ! ( 2 n n ! ) 2 z 2 n + 1 2 n + 1 ; z ≤ 1 {\displaystyle {\begin{aligned}\arcsin(z)&=z+\left ({\frac {1}{2}}\right){\frac {z^{3}}+\left ({\frac {1\cdot 3}{2\cdot 4}\right){\frac {z^{5}}{5}+\left ({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right){\frac {z^{7}}+\cdot \[5pt]&=\sum _{n=0}^{\infty}{\frac {(2n-1)!!! }{(2n)!! }}{\frac {z^{2n+1}}{2n+1}}\[5pt]&=\sum _{n=0}^{\infty}}{\frac {(2n)! }{(2^{n}n!) ^{2}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad z \leq 1\end{aligned}}} 아크탄 ( z ) = z − z 3 3 + z 5 5 − z 7 7 + ⋯ = ∑ n = 0 ∞ ( − 1 ) n z 2 n + 1 2 n + 1 ; z ≤ 1 z ≠ i , − i {\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{{\frac {z^{5}}{5}}-{\frac {z^{7}}+\cdots =\sum _{n=0}^{\infty}{\frac {(-1)^{n}z^{2n+1}\,;\qquad z \leq 1\qquad z\neq i,-i} 다른 역삼각형 함수에 대한 급수는 위에 주어진 관계에 따라 이들의 용어로 주어질 수 있습니다. 예 arccos 2 ( x ) {\displaystyle \arccos(x pi /2-\arcsin(x)}, arccsc x 1 {\displaystyle \operatorname {arccsc}(x arcsin(1/x)} . 또 다른 시리즈는 다음과 같습니다.[19]
2 ( 호신 ( x 2 ) ) 2 = ∑ n = 1 ∞ x 2 n n 2 ( 2 n n ) . {\displaystyle 2\left(\arcsin \left ({\frac {x}{2}}\right)^{2}=\sum _{n=1}^{\infty}{\frac {x^{2n}}{n^{2}{\binom {2n}}}}} 레온하르트 오일러 는 테일러 급수보다 더 빨리 수렴하는 아크탄젠트 급수 를 발견했습니다.
아크탄 ( z ) = z 1 + z 2 ∑ n = 0 ∞ ∏ k = 1 n 2 k z 2 ( 2 k + 1 ) ( 1 + z 2 ) . {\displaystyle \arctan(z)={\frac {z}{1+z^{2}}\sum _{n=0}^{\infty}}\sum _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2}}}}} [20] (n = 0에 대한 합의 항은 빈 제품 이므로 1도 마찬가지입니다.)
또는 다음과 같이 나타낼 수 있습니다.
아크탄 ( z ) = ∑ n = 0 ∞ 2 2 n ( n ! ) 2 ( 2 n + 1 ) ! z 2 n + 1 ( 1 + z 2 ) n + 1 . {\displaystyle \arctan(z)=\sum _{n=0}^{\infty}{\frac {2^{2n}(n!) ^{2}}}{(2n+1)! }}}{\frac {z^{2n+1}}{{(1+z^{2})^{n+1}}}}}. 아크탄젠트 함수에 대한 또 다른 시리즈는 다음과 같이 제공됩니다.
아크탄 ( z ) = i ∑ n = 1 ∞ 1 2 n − 1 ( 1 ( 1 + 2 i / z ) 2 n − 1 − 1 ( 1 − 2 i / z ) 2 n − 1 ) , {\displaystyle \arctan(z)=i\sum _{n=1}^{\infty}{\frac {1}{2n-1}}\left ({\frac {1}{(1+2i/z) ^{2n-1}}-{\frac {1}{(1-2i/z)^{2n-1}}\right}),} 여기서 i 1 {\displaystyle sqrt {-1}} 허수 단위 입니다.
아크탄젠트의 연속 분수 아크탄젠트의 멱급수에 대한 두 가지 대안은 다음과 같은 일반화된 연속 분수 입니다.
아크탄 ( z ) = z 1 + ( 1 z ) 2 3 − 1 z 2 + ( 3 z ) 2 5 − 3 z 2 + ( 5 z ) 2 7 − 5 z 2 + ( 7 z ) 2 9 − 7 z 2 + ⋱ = z 1 + ( 1 z ) 2 3 + ( 2 z ) 2 5 + ( 3 z ) 2 7 + ( 4 z ) 2 9 + ⋱ {\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}}{{\cfrac {(3z)^{2}}{5-3z^{2}}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}}}}}}{{\frac {1+{\cfrac {(2z)^{2}}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{(4z)^{9+\ddots}}}}}}}}}}}. 이 중 두 번째는 절단된 복소 평면에서 유효합니다. -i에서 무한대에 있는 지점까지, 가상의 축을 따라 내려가는 두 개의 컷이 있고 i에서 무한대에 있는 지점까지, 같은 축을 따라 올라가는 두 개의 컷이 있습니다. -1에서 1 사이의 실수에 가장 적합합니다. 부분 분모는 홀수 자연수이고, 부분 분자(첫 번째 이후)는 단지 (nz )이며,2 각 완벽한 제곱은 한 번 나타납니다. 첫 번째는 레온하르트 오일러 에 의해 개발되었고, 두 번째는 칼 프리드리히 가우스 가 가우스 초기하학 시리즈 를 사용하여 개발되었습니다.
역삼각함수의 부정적분 z 의 실수 값과 복소수 값의 경우:
∫ 호신 ( z ) d z = z 호신 ( z ) + 1 − z 2 + C ∫ 아코코 ( z ) d z = z 아코코 ( z ) − 1 − z 2 + C ∫ 아크탄 ( z ) d z = z 아크탄 ( z ) − 1 2 ln ( 1 + z 2 ) + C ∫ 아궁이 ( z ) d z = z 아궁이 ( z ) + 1 2 ln ( 1 + z 2 ) + C ∫ 아크섹 ( z ) d z = z 아크섹 ( z ) − ln [ z ( 1 + z 2 − 1 z 2 ) ] + C ∫ arccsc ( z ) d z = z arccsc ( z ) + ln [ z ( 1 + z 2 − 1 z 2 ) ] + C {\displaystyle {\begin{aligned}\int \arcsin(z)\, dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}+C\\\int \arccos(z)\, dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}+C\\int \arctan(z), dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+ C\\\int \operator name {arccot}(z)\, dz&{}=z\,\operator name {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+ C\\\int \operatorname {arcsec}(z)\, dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right]+ C\\\int \operatorname {arccsc}(z)\, dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}\right]+ C\end{aligned}} real x ≥ 1의 경우:
∫ 아크섹 ( x ) d x = x 아크섹 ( x ) − ln ( x + x 2 − 1 ) + C ∫ arccsc ( x ) d x = x arccsc ( x ) + ln ( x + x 2 − 1 ) + C {\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\, dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+ C\\\int \operatorname {arccsc}(x)\, dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+ C\end{aligned}} -1과 1사이가 아닌 모든 실수 x 에 대해:
∫ 아크섹 ( x ) d x = x 아크섹 ( x ) − sgn ( x ) ln x + x 2 − 1 + C ∫ arccsc ( x ) d x = x arccsc ( x ) + sgn ( x ) ln x + x 2 − 1 + C {\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\, dx&{}=x\,\operatorname {arcsec}(x)\ln \left x+{\sqrt {x^{2}-1}}\right +C\int \operatorname {arccsc}(x)\, dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left x+{\sqrt {x^{2}-1}\right +C\end{aligned}}} 절대값은 호각함수와 호각함수의 음과 양의 값을 모두 보상하기 위해 필요합니다. 기호 함수는 x의 양과 음의 값에 대한 두 개의 다른 해를 생성하는 두 함수 의 도함수에서 절대값으로 인해 또한 필요합니다. 역 쌍곡선 함수 의 로그 정의를 사용하여 이를 더욱 단순화할 수 있습니다.
∫ 아크섹 ( x ) d x = x 아크섹 ( x ) − 아궁이 같은 ( x ) + C ∫ arccsc ( x ) d x = x arccsc ( x ) + 아궁이 같은 ( x ) + C {\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\, dx&{}=x\,\operatorname {arcsec}(x)+C\int \operatorname {arcsc}(x)\, dx&{}=x\,\operatorname {arcsc}(x)+C\\end{aligned}} arcosh 함수의 인수에서 절대값은 그래프의 음의 반을 생성하여 위에 표시된 시그넘 로그 함수와 동일합니다.
이러한 모든 유도체는 위에 제시된 단순한 유도체 형태와 부품별 통합 을 이용하여 유도할 수 있습니다.
예 ∫ ud uv du {\displaystyle intu uv-\int v\,du}( 부품별 통합 ) 사용 , 설정
u = 호신 ( x ) d v = d x d u = d x 1 − x 2 v = x {\displaystyle {\begin{aligned}u&=\arcsin(x)&dv&=dx\du&={\frac {dx}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}} 그리고나서
∫ 호신 ( x ) d x = x 호신 ( x ) − ∫ x 1 − x 2 d x , {\displaystyle \int \arcsin(x)\, dx= x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}\, dx,} w 1 x 2 ,dw 2 x x {\displaystyle 1-x^{2},\dw 2x\, } 치환 으로 최종 결과를 산출합니다.
∫ 호신 ( x ) d x = x 호신 ( x ) + 1 − x 2 + C {\displaystyle \int \arcsin(x)\, dx= x\arcsin(x)+{\sqrt {1-x^{2}}}+C} 복소평면으로 확장 관계 tan x 리만 표면 입니다. 가운데 주황색 시트는 아크탄 x 위의 파란색 시트와 아래의 녹색 시트는 각각 2 π와 -2 π만큼 변위됩니다. 역삼각형 함수는 분석 함수 이므로 실수선에서 복소면까지 확장할 수 있습니다. 이렇게 하면 여러 시트와 분기점 이 있는 기능이 발생합니다. 확장을 정의하는 한 가지 가능한 방법은 다음과 같습니다.
아크탄 ( z ) = ∫ 0 z d x 1 + x 2 z ≠ − i , + i {\displaystyle \arctan(z)=\int _{0}^{z}{\frac {dx}{1+x^{2 }}}\quad z\neq -i,+i} 여기서 가상 축에서 분기점(-i 및 +i) 사이에 엄격하게 놓여 있지 않은 부분은 주 시트와 다른 시트 사이의 분기 절단 입니다. 적분 경로는 분기 절단선과 교차하면 안 됩니다. 분기 절단이 아닌 z 의 경우 0에서 z 로의 직선 경로가 이러한 경로입니다. 분기 절단의 z 의 경우 경로는 위쪽 분기 절단의 경우 Re[x] > 0 에서, 아래쪽 분기 절단의 경우 Re[x] < 0 에서 접근해야 합니다.
아크신 함수는 다음과 같이 정의될 수 있습니다.
호신 ( z ) = 아크탄 ( z 1 − z 2 ) z ≠ − 1 , + 1 {\displaystyle \arcsin(z)=\arctan \left ({\frac {z}{\sqrt {1-z^{2}}}\right)\quad z\neq -1,+1} 여기서 (제곱근 함수는 음의 실수축을 따라 절단되고) -1과 +1 사이에 엄격하게 놓여 있지 않은 실수축의 부분은 아크신의 주판과 다른 판 사이에 절단된 가지입니다.
아코코 ( z ) = π 2 − 호신 ( z ) z ≠ − 1 , + 1 {\displaystyle \arccos(z)={\frac {\pi}{2}}-\arcsin(z)\quad z\neq -1,+1} 아크신과 동일한 절단면을 갖는 것,
아궁이 ( z ) = π 2 − 아크탄 ( z ) z ≠ − i , i {\displaystyle \operatorname {arccot}(z)={\frac {\pi}{2}}-\arctan(z)\quad z\neq -i,i} 아크탄과 동일한 절단면을 갖는 것,
아크섹 ( z ) = 아코코 ( 1 z ) z ≠ − 1 , 0 , + 1 {\displaystyle \operatorname {arcsec}(z)=\arccos \left ({\frac {1}{z}\right)\quad z\neq -1,0,+1} -1과 +1 사이의 실제 축 부분이 아크초의 주 시트와 다른 시트 사이의 절단일 때,
arccsc ( z ) = 호신 ( 1 z ) z ≠ − 1 , 0 , + 1 {\displaystyle \operatorname {arccsc}(z)=\arcsin \left ({\frac {1}{z}\right)\quad z\neq -1,0,+1} arcsec와 같은 컷을 가지고 있습니다.
로그 양식 이러한 함수는 복잡한 로그 를 사용하여 나타낼 수도 있습니다.이것은 그들의 영역 을 복잡한 평면 까지 자연스러운 방식으로 확장합니다. 함수의 주 값에 대한 다음의 식별 정보는 분기 컷(branch cut)에서도 정의된 모든 위치에 적용됩니다.
호신 ( z ) = − i ln ( 1 − z 2 + i z ) = i ln ( 1 − z 2 − i z ) = arccsc ( 1 z ) 아코코 ( z ) = − i ln ( i 1 − z 2 + z ) = π 2 − 호신 ( z ) = 아크섹 ( 1 z ) 아크탄 ( z ) = − i 2 ln ( i − z i + z ) = − i 2 ln ( 1 + i z 1 − i z ) = 아궁이 ( 1 z ) 아궁이 ( z ) = − i 2 ln ( z + i z − i ) = − i 2 ln ( i z − 1 i z + 1 ) = 아크탄 ( 1 z ) 아크섹 ( z ) = − i ln ( i 1 − 1 z 2 + 1 z ) = π 2 − arccsc ( z ) = 아코코 ( 1 z ) arccsc ( z ) = − i ln ( 1 − 1 z 2 + i z ) = i ln ( 1 − 1 z 2 − i z ) = 호신 ( 1 z ) {\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left ({\sqrt {1-z^{2}}+iz\right)=i\ln \left ({\sqrt {1-z^{2}}-iz\right) &{}=\operator name {arccsc} \left ({\frac {1}{z}\right) \\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi}{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left ({\frac {1}{z}\right) \\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left ({\frac {i-z}{i+z}\right)=-{\frac {i}{2}\ln \left ({\frac {1+iz}{1-iz}\right) &{}=\operator name {arccot} \left ({\frac {1}{z}\right) \\[10pt]\operator name {arccot}(z)&{}=-{\frac {i}{2}\ln \left ({\frac {z+i}{z-i}\right)=-{\frac {i}{2}\ln \left ({\frac {iz+1}{iz+1}\right) &{}=\arctan \left ({\frac {1}{z}}\right) \\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}+{\frac {1}{z}\right)={\frac {\pi}{2}}-\operatorname {arcsc}(z)&{}=\arcccos \left ({\frac {1}{z}\right) \\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left ({\sqrt {1-{\frac {1}{z^{2}}}}+{\frac {i}{z}}\right)=i\ln \left ({\sqrt {1-{\frac {1}{z^{2}}}-{\frac {i}{z}\right) &{}=\arcsin \left ({\frac {1}{z}}\right)\end{aligned}} 일반화 모든 역삼각형 함수는 직각 삼각형의 각도를 출력하기 때문에 오일러 공식 을 사용하여 복소 평면에서 직각 삼각형을 형성함으로써 일반화할 수 있습니다. 대수학적으로, 이것은 우리에게 다음을 제공합니다.
c e i θ = c cos ( θ ) + i c 죄악의 ( θ ) {\displaystyle ce^{i\theta}=c\cos(\theta)+ic\sin(\theta)} 아니면
c e i θ = a + i b {\displaystyle ce^{i\theta}=a+ib} 여기서 {\displaystyle a} b {\displaystyle b} c {\displaystyle c} 여기서 θ {\displaystyle \theta} .
e ln ( c ) + i θ = a + i b ln c + i θ = ln ( a + i b ) θ = 임 ( ln ( a + i b ) ) {\displaystyle {\begin{aligned}e^{\ln(c)+i\theta}&=a+ib\\ln c+i\theta &=\ln(a+ib)\ \\theta &=\operator name {Im} \left(\ln(a+ib)\right)\end{aligned}} 아니면
θ = − i ln ( a + i b c ) {\displaystyle \theta =-i\ln \left ({\frac {a+ib}{c}}\right)} 단순히 허수 부분을 취하는 것은 실제 값 displaystyle a} 및 displaystyle b} , {\displaystyle a} b {\displaystyle b} 빗변의 길이는 각도를 변경하지 않으므로 ln a bi ) {\displaystyle \ln(a bi)} 방정식 displaystyle c} 최종 방정식에서, 우리는 복소 평면에서 삼각형의 각도는 각 변의 길이를 입력함으로써 구할 수 있음을 알 수 있습니다. 세 변 중 하나를 1로, 나머지 한 변을 입력 z {\displaystyle z} . 역삼각함수는 오직 하나의 입력만을 필요로 하기 때문에, 우리는 피타고라스 정리 관계를 이용하여 삼각형의 마지막 변을 다른 두 변의 항으로 넣어야 합니다.
a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2 }=c^{2}} 아래 표는 위의 식들에 값을 대입하고 단순화한 θ {\displaystyle \theta}
a b c − i ln ( a + i b c ) θ θ a , b ∈ R 호신 ( z ) 1 − z 2 z 1 − i ln ( 1 − z 2 + i z 1 ) = − i ln ( 1 − z 2 + i z ) 임 ( ln ( 1 − z 2 + i z ) ) 아코코 ( z ) z 1 − z 2 1 − i ln ( z + i 1 − z 2 1 ) = − i ln ( z + z 2 − 1 ) 임 ( ln ( z + z 2 − 1 ) ) 아크탄 ( z ) 1 z 1 + z 2 − i ln ( 1 + i z 1 + z 2 ) = − i ln ( 1 + i z 1 + z 2 ) 임 ( ln ( 1 + i z ) ) 아궁이 ( z ) z 1 z 2 + 1 − i ln ( z + i z 2 + 1 ) = − i ln ( z + i z 2 + 1 ) 임 ( ln ( z + i ) ) 아크섹 ( z ) 1 z 2 − 1 z − i ln ( 1 + i z 2 − 1 z ) = − i ln ( 1 z + 1 z 2 − 1 ) 임 ( ln ( 1 z + 1 z 2 − 1 ) ) arccsc ( z ) z 2 − 1 1 z − i ln ( z 2 − 1 + i z ) = − i ln ( 1 − 1 z 2 + i z ) 임 ( ln ( 1 − 1 z 2 + i z ) ) {\displaystyle {\begin{aligned}&a&b&c&-i\ln \left ({\frac {a+ib}{c}\right)&\theta &\theta _{a, b\in \mathbb {R} }\\\arcsin(z)\ \\{\sqrt {1-z^{2}}&&-i\ln \left ({\frac {\sqrt {1-z^{2}}+iz}{1}\right) &=-i\ln \left ({\sqrt {1-z^{2}}+iz\right)\left(\ln \left ({\sqrt {1-z^{2}}+iz\right)\right)\\\arccos(z)\ \\z&{\sqrt {1-z^{2}}}&1&-i\ln \left ({\frac {z+i{1-z^{2}}}\right) &=-i\ln \left(z+{\sqrt {z^{2}- 1}}\right)&\operator name {Im} \left(\ln \left(z+{\sqrt {z^{2}-1}}\right)\\arctan(z)\\&z&{\sqrt {1+z^{2}) }}&-i\ln\left ({\frac {1+iz}{\sqrt {1+z^{2 }}})\right)&=-i\ln\left ({\frac {1+iz}{\sqrt {1+z^{2 }}}\right)&\operator name {Im}\left(\ln \left(1+iz\right)\right)\" \\operatorname {arccot}(z)\ \\z&1&{\sqrt {z^{2}+1}}&-i\ln \left ({\frac {z+i}{\sqrt {z^{2}+1}}\right)&=-i\ln \left ({\frac {z+i}{\sqrt {z^{2}+1}}\right)&\left(\ln \left(z+i\right)\right)\right)\left(\ln \left(z+i\right)\right). \\operatorname {arcsec}(z)\ \&1&{\sqrt {z^{2}-1}}&z&-i\ln \left ({\frac {1+i{\sqrt {z^{2}-1}}{{z}}\right)&=-i\ln \left ({\frac {1}{z}+{\sqrt {1}{z^{2}-1}\right)\left(\ln \left ({\frac {1}{z}}+{\sqrt {1}{z^{2}}\right)\right) \\operatorname {arccsc}(z)\ \\{\sqrt {z^{2}-1}}&&&z&-i\ln \left ({\frac {\sqrt {z^{2}-1}}+i}{z}\right) &=-i\ln \left ({\sqrt {1-{\frac {1}{z^{2}}}+{\frac {i}{z}\right) &\operatorname {Im} \left(\ln \left ({\sqrt {1-{\frac {1}{z^{2}}}}+{\frac {i}{z}\right)\\end{aligned}} 자연로그 및 제곱근 함수의 주분점을 역삼각함수의 일반적인 주분점 과 일치시키기 위해서는 단순화된 공식의 특정 형태가 중요합니다. 맨 오른쪽 열 두 개에 주어진 공식은 Im (ln z ) {\displaystyle \operatorname {Im} \left(\ln \right)\in (-\pi,\pi ]} Re (z) 0 {\displaystyle \operatorname {Re} \left({\sqrt {z})\right)\geq 0} . Im ln z 0 , {\displaystyle \operatorname {Im} \left(\l n z\right)\in[0,2\pi )} Im (z) 0 {\displaystyle \operatorname {Im} \left({\sqrt {z}\right)\geq 0} ≥ . Re ( θ ) π displaystyle {Re theta >\ pi ( θ displaystyle operatorname }(\
이러한 의미에서 모든 역삼각함수는 복소값 로그함수의 특정한 경우로 간주될 수 있습니다. 이러한 정의는 임의의 복소 값 {\displaystyle z} , 출력으로 쌍곡선 각도를 허용하고 역 쌍곡선 함수를 추가로 정의하는 데 사용할 수 있습니다. 관계의 기본적인 증명은 삼각 함수의 지수 형태로 확장을 통해 진행될 수도 있습니다.
증명 예시 죄악의 ( ϕ ) = z ϕ = 호신 ( z ) {\displaystyle {\begin{aligned}\sin(\phi)&=z\\\phi &=\arcsin(z)\end{aligned}} 사인의 지수 정의 를 사용하고 ξ = ei {\displaystyle \xi ^{i\phi}}
z = e i ϕ − e − i ϕ 2 i 2 i z = ξ − 1 ξ 0 = ξ 2 − 2 i z ξ − 1 ξ = i z ± 1 − z 2 ϕ = − i ln ( i z ± 1 − z 2 ) {\displaystyle {\begin{aligned}z&={\frac {e^{i\phi}}-e^{-i\phi}}{2i}}\[10mu]2iz&=\xi -{\frac {1}{\xi}}\[5mu]0 &=\xi ^{2}-2iz\xi -1\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}\right)\end{aligned}} (양의 분기가 선택됨)
ϕ = 호신 ( z ) = − i ln ( i z + 1 − z 2 ) {\displaystyle \phi =\arcsin(z)=-i\ln \left(iz+{\sqrt {1-z^{2}}}\right)} 복소평면 역삼각함수 의 색상환 그래프 호신 ( z ) {\displaystyle \arcsin(z)} 아코코 ( z ) {\displaystyle \arccos(z)} 아크탄 ( z ) {\displaystyle \arctan(z)}
arccsc ( z ) {\displaystyle \operator name {arccsc}(z)} 아크섹 ( z ) {\displaystyle \operator name {arcsec}(z)} 아궁이 ( z ) {\displaystyle \operator name {arccot}(z)}
적용들 직각 삼각형의 각도 찾기 A {\displaystyle A} 직각 삼각형 입니다.역삼각형 함수는 삼각형의 변의 길이를 알 때 직각 삼각형 의 나머지 두 개의 각도를 결정하는 데 유용합니다. 사인과 코사인의 오른쪽 삼각형 정의를 떠올리면 다음과 같습니다.
θ = 호신 ( 반대로 저급한 용법 ) = 아코코 ( 인접한 저급한 용법 ) . {\displaystyle \theta =\arcsin \left ({\frac {\text{opposite}}{\text{hypotenuse}}\right)=\arcos \left ({\frac {\text{adjacent}}{\text{hypotenuse}}\right)} 피타고라스 정리 : a 2 b 2 2 {\displaystyle a^{2} b^{2 = h^{2}}. 여기 {\displaystyle } 아크탄젠트는 이 상황에서 도움이 되는데, 이 경우에는 길이가 필요 없기 때문입니다.
θ = 아크탄 ( 반대로 인접한 ) . {\displaystyle \theta =\arctan \left ({\frac {\text{opposite}}{\text{adjacent}}\right),} 예를 들어 지붕이 20피트나 떨어져 8피트가 떨어진다고 가정합니다. 지붕은 수평과 각도 θ을 이루며, 여기서 θ은 다음과 같이 계산될 수 있습니다.
θ = 아크탄 ( 반대로 인접한 ) = 아크탄 ( 증가 달려. ) = 아크탄 ( 8 20 ) ≈ 21.8 ∘ . {\displaystyle \theta =\arctan \left ({\frac {\text{opposite}}{\text{run}}\right)=\arctan \left ({\frac {\text{rise}}{\text{run}}\right)=\arctan \left ({\frac {8}{20}\right)\approx 21.8 ^{\circ}\",} 컴퓨터과학과공학과에서 아크탄젠트의 두 논항 변형
2 함수의 2개 인수는 y 와 x 가 주어졌을 때 y / x 의 아크탄젠트를 계산하지만 (- π, π)의 범위를 갖습니다.즉, atan2(y , x )는 평면의 양의 x축과 그 위의 점 (x , y) 사이의 각도이며, 반시계 방향 각도(상부 반평면 , y > 0)는 양의 부호이고, 시계 방향 각도(하부 반평면, y < 0)는 음의 부호입니다. 그것은 많은 컴퓨터 프로그래밍 언어로 처음 소개되었지만, 지금은 과학과 공학의 다른 분야에서도 흔히 볼 수 있습니다.
표준 아크탄 함수의 경우, 즉 (-)의 범위를 갖습니다. π / 2 π 2
2번에 ( y , x ) = { 아크탄 ( y x ) x > 0 아크탄 ( y x ) + π y ≥ 0 , x < 0 아크탄 ( y x ) − π y < 0 , x < 0 π 2 y > 0 , x = 0 − π 2 y < 0 , x = 0 미정의 y = 0 , x = 0 {\displaystyle \operatorname {atan2}(y,x)={\begin{case}\arctan \left ({\frac {y}{x}}\right)&\quad x>0\\\\arctan \left ({\frac {y}{x}\right)+\pi &\quad y\geq 0,\;x<0\\arctan \left ({\frac {y}{x}\right)-\pi &\quad y<0,\x<0\frac {\pi}{2}&\pi>0,\;x=0\{\frac {2}}&\{\pi}\quad y<0,\x=0\{\text{undefined}}&\x=0\end{case}}}\pi &x=0\end} 또한 복소수 x + iy 의 인수 의 주 값과 같습니다 .
위 함수의 이 제한된 버전은 다음과 같이 접선 반각 공식을 사용하여 정의될 수도 있습니다.
2번에 ( y , x ) = 2 아크탄 ( y x 2 + y 2 + x ) {\displaystyle \operator name {atan2}(y,x)=2\arctan \left ({\frac {y}{{\sqrt {x^{2}+y^{2} }}}}+x}}\right)} x > 0 또는 y ≠ 0인 경우.그러나 x ≤ 0이고 y = 0이 주어지면 실패하므로 식을 계산에 사용하기에 적합하지 않습니다.
위의 인수 순서 (y , x )가 가장 일반적인 것으로 보이며, 특히 C 프로그래밍 언어 와 같은 ISO 표준 에서 사용되지만, 몇몇 저자들은 반대의 규약 (x , y )을 사용할 수 있으므로 어느 정도 주의가 필요합니다. 이러한 변형은 atan2 에 자세히 설명되어 있습니다.
위치 매개변수가 있는 아크탄젠트 함수 많은 응용에서 방정식 x tan y ) {\displaystyle } y tan(y)} {\displaystyle \infty <\infty
y = 아크탄 η ( x ) := 아크탄 ( x ) + π rni ( η − 아크탄 ( x ) π ) . {\displaystyle y=\arctan _{\eta}(x): =\arctan(x)+\pi \,\operatorname {rni} \left ({\frac {\eta -\arctan(x)}{\pi}}\right)\,} 함수 rni {\displaystyle \operatorname {rni}}은(
수치정확도 0 과 π에 가까운 각도의 경우 아크코신은 조건 이 좋지 않으며, π/2와 π/2에 가까운 각도의 경우 아크신과 유사합니다.따라서 컴퓨터 응용 프로그램은 이러한 함수에 대한 입력의 안정성과 계산의 민감도를 고려하거나 대체 방법을 사용해야 합니다.[23]
참고 항목 메모들 ^ 명확하게 설명하기 위해 "LHS displaystyle iff 왼손잡이 를 줄인)와 RHS는 모두 개별적으로 참이거나 거짓일 수 있습니다. 예를 들어 θ {\displaystyle \theta displaystyles} tan s arctan ( s 일부 k Z {\displaystyle \theta \,\iff \, \theta =\arctan(들)+\pik\quad {\text{ for some }}}, k\in {Z}}, tan θ = s {\displaystyle \tan \theta = s}" θ {\displaystyle theta {\displaystyles} 예를 들어 θ 0 {\displaystyle \theta 0} 0 displaystyle s 0} 참 tan tan displaystyle tan s} ) {\displaystyle \theta 0} s 2 {\displaystyle 2} tan tan 0 s displaystyle \theta tan s} s 2 {\displaystyle 2}) {\displaystyle \theta } s 0 거짓 displaystyle neq .} k displaystyle mathbb } arctan s k {\displaystyle \theta arctan(s)+\pi " RHS 문은 참 또는 거짓일 수도 있습니다(이전과 마찬가지로 RHS 문이 참인지 거짓인지 여부는 θ {\displaystyle \theta} s {\displaystyles} 논리적 동일성 기호 ⟺ {\ displaystyle \,\iff \,} 참 이고, 또한 (b) LHS 문이 거짓이면 RHS 문도 거짓임 을 의미합니다. 마찬가지 로 ⟺ {\ displaystyle \,\iff \,} 참 이고, 또한 (d) RHS 문이 거짓이면 LHS 문도 거짓임 을 의미합니다. 참고문헌 ^ Taczanowski, Stefan (1 October 1978). "On the optimization of some geometric parameters in 14 MeV neutron activation analysis". Nuclear Instruments and Methods ScienceDirect . 155 (3): 543–546. Bibcode :1978NucIM.155..543T . doi :10.1016/0029-554X(78)90541-4 . ^ Hazewinkel, Michiel (1994) [1987]. Encyclopaedia of Mathematics Kluwer Academic Publishers / Springer Science & Business Media . ISBN 978-155608010-4 ^ Ebner, Dieter (25 July 2005). Preparatory Course in Mathematics (PDF) (6 ed.). Department of Physics, University of Konstanz . Archived (PDF) from the original on 26 July 2017. Retrieved 26 July 2017 . ^ Mejlbro, Leif (11 November 2010). Stability, Riemann Surfaces, Conformal Mappings - Complex Functions Theory (PDF) (1 ed.). Ventus Publishing ApS / Bookboon . ISBN 978-87-7681-702-2 the original (PDF) on 26 July 2017. Retrieved 26 July 2017 . ^ Durán, Mario (2012). Mathematical methods for wave propagation in science and engineering . Vol. 1: Fundamentals (1 ed.). Ediciones UC. p. 88. ISBN 978-956141314-6 ^ a b c d Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). "Chapter II. The Acute Angle [14] Inverse trigonometric functions" . Written at Ann Arbor, Michigan, USA. Trigonometry . Vol. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. - Berwick & Smith Co., Norwood, Massachusetts, USA. p. 15. Retrieved 12 August 2017 . […] α = arcsin m : It is frequently read "arc-sine m " or "anti-sine m ," since two mutually inverse functions are said each to be the anti-function of the other. […] A similar symbolic relation holds for the other trigonometric functions . […] This notation is universally used in Europe and is fast gaining ground in this country. A less desirable symbol, α = sin-1 m , is still found in English and American texts. The notation α = inv sin m is perhaps better still on account of its general applicability. […] ^ Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in German). Vol. 1 (3rd ed.). Berlin: J. Springer .^ Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis Dover Publications, Inc. / The Macmillan Company . ISBN 978-0-48643480-3 . Retrieved 13 August 2017 .^ Dörrie, Heinrich (1965). Triumph der Mathematik . Translated by Antin, David. Dover Publications . p. 69. ISBN 978-0-486-61348-2 ^ Weisstein, Eric W. "Inverse Trigonometric Functions" . mathworld.wolfram.com . Retrieved 29 August 2020 . ^ Beach, Frederick Converse; Rines, George Edwin, eds. (1912). "Inverse trigonometric functions". The Americana: a universal reference library ^ Cook, John D. (11 February 2021). "Trig functions across programming languages" . johndcook.com (blog). Retrieved 10 March 2021 . ^ Cajori, Florian (1919). A History of Mathematics The Macmillan Company . p. 272 .^ Herschel, John Frederick William (1813). "On a remarkable Application of Cotes's Theorem" . Philosophical Transactions . Royal Society, London. 103 (1): 8. doi :10.1098/rstl.1813.0005 ^ "Inverse trigonometric functions" . Wiki. Brilliant Math & Science (brilliant.org) . Retrieved 29 August 2020 .^ Korn, Grandino Arthur; Korn, Theresa M. (2000) [1961]. "21.2.-4. Inverse Trigonometric Functions". Mathematical handbook for scientists and engineers: Definitions, theorems, and formulars for reference and review Dover Publications, Inc. p. 811 . ISBN 978-0-486-41147-7 ^ Bhatti, Sanaullah; Nawab-ud-Din; Ahmed, Bashir; Yousuf, S. M.; Taheem, Allah Bukhsh (1999). "Differentiation of Trigonometric, Logarithmic and Exponential Functions". In Ellahi, Mohammad Maqbool; Dar, Karamat Hussain; Hussain, Faheem (eds.). Calculus and Analytic Geometry (1 ed.). Lahore : Punjab Textbook Board. p. 140. ^ 아브라모위츠 & 스테건 1972 , 페이지 73, 4.3.44^ Borwein, Jonathan; Bailey, David; Gingersohn, Roland (2004). Experimentation in Mathematics: Computational Paths to Discovery A. K. Peters . p. 51 . ISBN 978-1-56881-136-9 ^ Hwang Chien-Lih (2005), "An elementary derivation of Euler's series for the arctangent function", The Mathematical Gazette , 89 (516): 469–470, doi :10.1017/S0025557200178404 , S2CID 123395287 ^ S. M. Abrarov and B. M. Quine (2018), "A formula for pi involving nested radicals", The Ramanujan Journal , 46 (3): 657–665, arXiv :1610.07713 doi :10.1007/s11139-018-9996-8 , S2CID 119150623 ^ 시변 각도 교차 ± {\displaystyle \pm \pi /2} ^ Gade, Kenneth (2010). "A non-singular horizontal position representation" (PDF) . The Journal of Navigation . Cambridge University Press . 63 (3): 395–417. Bibcode :2010JNav...63..395G . doi :10.1017/S0373463309990415 .
외부 링크













































![[-1, 1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)

![{\displaystyle \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2052f9d4a9c6a14f6db2e4bcd2606bce26d720d)


![[0,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)











![{\displaystyle [\,0,\;\pi \,]\;\;\;\setminus \left\{{\tfrac {\pi }{2}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c913c2c78d11f57ccd118976bfb4b0595e5a2e0e)


![{\displaystyle \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e84fda7925743a03ffa0aec3fbed76a2967a3012)


 도메인은
도메인은
































































![{\displaystyle {\begin{aligned}\sin \theta &=-\sin(-\theta )&&=-\sin(\pi +\theta )&&={\phantom {-}}\sin(\pi -\theta )\\&=-\cos \left({\frac {\pi }{2}}+\theta \right)&&={\phantom {-}}\cos \left({\frac {\pi }{2}}-\theta \right)&&=-\cos \left(-{\frac {\pi }{2}}-\theta \right)\\&={\phantom {-}}\cos \left(-{\frac {\pi }{2}}+\theta \right)&&=-\cos \left({\frac {3\pi }{2}}-\theta \right)&&=-\cos \left(-{\frac {3\pi }{2}}+\theta \right)\\[0.3ex]\cos \theta &={\phantom {-}}\cos(-\theta )&&=-\cos(\pi +\theta )&&={\phantom {-}}\cos(\pi -\theta )\\&={\phantom {-}}\sin \left({\frac {\pi }{2}}+\theta \right)&&={\phantom {-}}\sin \left({\frac {\pi }{2}}-\theta \right)&&=-\sin \left(-{\frac {\pi }{2}}-\theta \right)\\&=-\sin \left(-{\frac {\pi }{2}}+\theta \right)&&=-\sin \left({\frac {3\pi }{2}}-\theta \right)&&={\phantom {-}}\sin \left(-{\frac {3\pi }{2}}+\theta \right)\\[0.3ex]\tan \theta &=-\tan(-\theta )&&={\phantom {-}}\tan(\pi +\theta )&&=-\tan(\pi -\theta )\\&=-\cot \left({\frac {\pi }{2}}+\theta \right)&&={\phantom {-}}\cot \left({\frac {\pi }{2}}-\theta \right)&&={\phantom {-}}\cot \left(-{\frac {\pi }{2}}-\theta \right)\\&=-\cot \left(-{\frac {\pi }{2}}+\theta \right)&&={\phantom {-}}\cot \left({\frac {3\pi }{2}}-\theta \right)&&=-\cot \left(-{\frac {3\pi }{2}}+\theta \right)\\[0.3ex]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56b92e80450bbbbb81122c562038255732fca3fc)



















































![{\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec43798232f580abb074cf15f3d77692edd36af0)

![{\displaystyle {\begin{aligned}\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)\\[0.3em]\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)\\[0.3em]\arctan \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=-{\frac {\pi }{2}}-\arctan(x)=\operatorname {arccot}(x)-\pi \,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {\pi }{2}}-\operatorname {arccot}(x)=\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&={\frac {3\pi }{2}}-\operatorname {arccot}(x)=\pi +\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecb0a376d9148e3cf65ea6e6ed5fb37752a581c7)



![{\displaystyle {\begin{aligned}\arcsin(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)\\[0.5em]\arccos(x)&=2\arctan \left({\frac {\sqrt {1-x^{2}}}{1+x}}\right)\,,{\text{ if }}-1<x\leq 1\\[0.5em]\arctan(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1+x^{2}}}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dd6a9370a877ca5e198e28b7582bd06b377bdc3)









![{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0f778db7f760db059cf12f13ee5c2bf239fbb2f)






![{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3e2dde92bb82231c4326e45ce8b50e7298688bb)












![{\displaystyle {\begin{aligned}\arcsin(z)&{}=-i\ln \left({\sqrt {1-z^{2}}}+iz\right)=i\ln \left({\sqrt {1-z^{2}}}-iz\right)&{}=\operatorname {arccsc} \left({\frac {1}{z}}\right)\\[10pt]\arccos(z)&{}=-i\ln \left(i{\sqrt {1-z^{2}}}+z\right)={\frac {\pi }{2}}-\arcsin(z)&{}=\operatorname {arcsec} \left({\frac {1}{z}}\right)\\[10pt]\arctan(z)&{}=-{\frac {i}{2}}\ln \left({\frac {i-z}{i+z}}\right)=-{\frac {i}{2}}\ln \left({\frac {1+iz}{1-iz}}\right)&{}=\operatorname {arccot} \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccot}(z)&{}=-{\frac {i}{2}}\ln \left({\frac {z+i}{z-i}}\right)=-{\frac {i}{2}}\ln \left({\frac {iz-1}{iz+1}}\right)&{}=\arctan \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arcsec}(z)&{}=-i\ln \left(i{\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {1}{z}}\right)={\frac {\pi }{2}}-\operatorname {arccsc}(z)&{}=\arccos \left({\frac {1}{z}}\right)\\[10pt]\operatorname {arccsc}(z)&{}=-i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}+{\frac {i}{z}}\right)=i\ln \left({\sqrt {1-{\frac {1}{z^{2}}}}}-{\frac {i}{z}}\right)&{}=\arcsin \left({\frac {1}{z}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13b511be341b52fcd0c0660f3a4b1e5a164bfcb1)


 인접한 면,
인접한 면,  반대 면,
반대 면,  빗변입니다.여기서 θ
빗변입니다.여기서 θ 





![{\displaystyle {\begin{aligned}z&={\frac {e^{i\phi }-e^{-i\phi }}{2i}}\\[10mu]2iz&=\xi -{\frac {1}{\xi }}\\[5mu]0&=\xi ^{2}-2iz\xi -1\\[5mu]\xi &=iz\pm {\sqrt {1-z^{2}}}\\[5mu]\phi &=-i\ln \left(iz\pm {\sqrt {1-z^{2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed03e8cf773fa44cc78823d65f7d82f41276fb96)

















