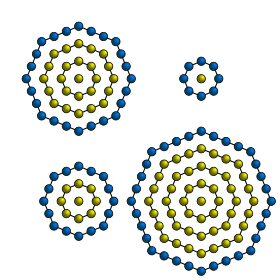
중심팔각수

가운데 팔각수는 가운데에 점이 있는 팔각형(八角形)과 그 밖의 모든 점들이 연속 팔각형으로 중앙점을 둘러싸고 있는 것을 나타내는 중심형상이다.^[1]중심 팔각수는 홀수 제곱수와 같다.^[2]따라서 n번째 홀수 제곱수와 t번째 중심 팔각수는 공식에 의해 주어진다.

${\displaystyle (2n-1)^{2}=4n^{2}-4n+1(2t+1)^{2}=4t^{2}=4t^{2}+4t+1.}$

처음^[2] 몇 개의 중심 팔각수는

1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089, 1225

중심 8각수로 라마누잔의 타우함수를 계산하면 홀수가 나오는 반면, 다른 숫자에 대해서는 짝수가 나온다.^[2]

참고 항목

• 팔각수

참조