중심 다곤수

중심 다각형 번호는 각각 중앙 점으로 형성되는 일련의 구상적 숫자로, 변의 수가 일정한 점의 다각적 층으로 둘러싸여 있다.폴리곤 층의 각 면은 이전 층의 각 면보다 한 개의 점을 더 포함하고 있으므로, 두 번째 폴리곤 층부터 중심 k-곤 숫자의 각 층은 이전 층보다 더 많은 k개의 점을 포함한다.

예

시리즈에서 각 중심 k-곤 숫자는 이전의 삼각형 숫자 + 1의 k배이다.$이$는 k ${\displaystyle \frac{n}{}}$( ${\displaystyle \frac{n}{}}$+ ${\displaystyle \frac{1}{}}$) ${\displaystyle \frac{\mathrm{}}{}}$+ ${\displaystyle 1}$ ${\displaystyle {\frac {kn(n+1)}{2$라는 표현으로 공식화할 수 있다.$}}+1$ 여기서 n은 시리즈 순위(초기 1의 경우 0으로 시작함)입니다.예를 들어, 시계열의 각 중심 정사각형 숫자는 이전의 삼각형 숫자에 1을 더한 값의 4배이다.이는 ${\displaystyle \frac{\mathrm{4n}(n}{}}$+ ${\displaystyle \frac{1}{}}$) ${\displaystyle 2}$+ 1 ${\displaystyle {\frac {4n(n+1)}{2$라는 표현으로 공식화할 수 있다.$}}+1}$.

이 시리즈는 다음과 같이 구성되어 있다.

• 중심 삼각형 숫자 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, ... (OEIS: A005448)
• 중심 정사각형 번호 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, ... (OEIS: A001844)
• 중심 오각형 번호 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, ... (OEIS: A005891)
• 중심 육각형 번호 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, ...(OEIS: A003215), 즉 연속 큐브의 차이(예³: n - 1)를 정확히 나타낸다.³
• 중심 헵탄수 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, ... (OEIS: A069099)
• 중심 팔각형 숫자 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, ... (OEIS: A016754)는 정확히 홀수 제곱이다.
• 중심 비각형 번호 1, 10, 28, 55, 91, 136, 136, 190, 253, 325, 406, 496, 595, ... (OEIS: A060544), 6을 제외한 모든 완전한 숫자를 포함한다.
• 중심 십각형 숫자 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, ... (OEIS: A062786)
• 중심 암각형 번호 1, 12, 34, 67, 111, 166, 232, 309, 397, 496, 606, 727, ... (OEIS: A069125)
• 중심 도각형 번호 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, ...(OEIS: A003154) 역시 항성 번호로 되어 있다.

등등.

다음 도표는 중심적인 다각형 숫자와 그 기하학적 구조의 몇 가지 예를 보여준다.이 도표를 다각형 숫자의 도표와 비교하십시오.

중심적인 삼각형의 번호를 붙이다	중심적인 정사각형의 번호를 붙이다	중심적인 오각형의 번호를 붙이다	중심적인 육각형의 번호를 붙이다

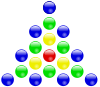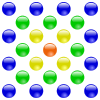중심 제곱수

1		5		13		25

중심 육각수

1		7		19		37

공식

위의 도표에서 볼 수 있듯이 n번째 중심 k-곤 번호는 중심점을 중심으로 (n-1)번째 삼각형 숫자의 k 복사본을 배치하여 얻을 수 있으므로 n번째 중심 k-곤 번호는 다음과 같이 수학적으로 나타낼 수 있다.

${\displaystyle C_{k,n}={\frac {kn}{2}}(n-1)+1.}$

n번째와 (n+1)번째 연속 중심 k-gonal 수의 차이는 k(2n+1)이다.

n번째 중심 k-곤 번호는 n번째 정규 k-곤 번호 플러스(n-1)와 같다.²

정규 다곤수의 경우와 마찬가지로 첫 번째 중심 k-곤수는 1이다.따라서 어떤 k에 대해서도 1은 k-곤과 중심 k-곤이다.k-곤과 중심 k-곤 둘 다 되는 다음 숫자는 다음 공식을 사용하여 찾을 수 있다.

${\displaystyle {\frac {k^{2}}:{2}}(k-1)+1}$

10은 삼각형과 중심형, 25는 정사각형과 중심형이라는 것을 알 수 있다.

소수 p는 다각형 숫자일 수 없는 반면(즉, 각 p는 두 번째 p-곤 숫자임), 많은 중심 다각형 숫자는 소수다.실제로 k ≥ 3, k ≠ 8, k ≠ 9이면 primes(분야콥스키 추측)인 중심 k-gonal 숫자가 무한히 많다.(중점 팔각수 역시 모두 정사각형 수이고, 중심 비각수 역시 모두 삼각수(3과 같지 않음)이므로 둘 다 소수일 수는 없다.)

왕복 합

중심 k-곤 숫자에 대한 왕복선의 합은 다음과^[1] 같다.

${\displaystyle {\frac {2\pi }{k{\sqrt {1-{\frac {8}{k}}}}}}\tan \left({\frac {\pi }{2}}{\sqrt {1-{\frac {8}{k}}}}\right)}$, if k ≠ 8

${\displaystyle \frac{{}^{}}{}}$π ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\$ k = 8인 경우

참조

• Neil Sloane & Simon Plouffe (1995). The Encyclopedia of Integer Sequences. San Diego: Academic Press.: 그림 M3826
• Weisstein, Eric W. "Centered polygonal number". MathWorld.
• F. Tapson (1999). The Oxford Mathematics Study Dictionary (2nd ed.). Oxford University Press. pp. 88–89. ISBN 0-19-914-567-9.