온도

온도
단백질 알파나선 세그먼트의 열진동.진폭은 온도에 따라 증가합니다.
공통 기호	T
SI 단위	K
기타 유닛	°C, °F, °R, °Rö, °Ré, °N, °D, °L, °W
집약적?	네.
파생상품 기타 수량	${\displaystyle \frac{p}{}}$ V ${\displaystyle \frac{}{}}$ ${\displaystyle \frac{R}{}}$({$displaystyle {pV}$ {$nR$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{\text{q}}_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{d}{}}$S ({$displaystyle {dq_{\text{rev}})$ {$d$$스}}}$
치수	$디스플레이 스타일Theta }}}$

열역학
고전적인 카르노 히트 엔진
나뭇가지 고전적인 통계 화학의 양자 열역학 평형/비평형
법률 제로스 첫번째 둘째 셋째
시스템들 폐쇄형 시스템 오픈 시스템 격리 시스템 주 상태 방정식 이상 기체 실가스 상황 위상(매터) 평형 볼륨 제어 인스트루먼트 과정 이소바릭 아이소코리 등온 단열성 등엔트로픽 이센탈픽 준정전성 폴리트로픽 자유 확장 가역성 불가역성 내복원성 사이클 히트 엔진 히트 펌프 열효율
시스템 속성 주의: 이탤릭체로 표시된 켤레 변수 속성도 집약적이고 광범위한 속성 프로세스 기능 일하다. 열 국가 기능 온도/엔트로피(개요) 압력/볼륨 화학 퍼텐셜/입자수 증기 품질 속성 감소
재료 특성 속성 데이터베이스 비열 용량 ${\displaystyle c=}$ ${\displaystyle T}$ $\displaystyle \partial S\$ ${\displaystyle N}$ ${\displaystyle\partial T}$ 압축성 $\displaystyle \displays =-}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ $(\displaystyle\displayp)$ 열팽창 $\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ ${\displaystyle\partial T}$
방정식 카르노의 정리 클라우시우스 정리 기본 관계 이상기체의 법칙 맥스웰 관계 온사저 호혜 관계 브리지만 방정식 열역학 방정식 표
가능성 자유 에너지 자유 엔트로피 내부 에너지 ${\displaystyle U(S,V)}$ 엔탈피 ${\displaystyle H(S,p)=U+pV}$ 헬름홀츠 자유 에너지 ${\displaystyle A(T,V)=U-TS}$ 깁스 자유 에너지 ${\displaystyle G(T,p)=H-TS}$
역사 문화 역사 일반 엔트로피 가스 법칙 "영구 운동" 기계 철학 엔트로피와 시간 엔트로피와 생명 브라운 래칫 맥스웰의 악마 열사 역설 로슈미트의 역설 시너제틱스 이론들 열량론 Vis viva ('생체력') 열의 기계적 등가 동력 주요 출판물 실험적인 질문 ~에 대해서열 균형에 대하여 이종 물질 의 리플렉션 불의 원동력 타임라인 열역학 히트 엔진 예체능 교육 맥스웰의 열역학 표면 에너지 분산으로서의 엔트로피
과학자 베르누이 볼츠만 브리지만 카라테오도리 카르노 클라피론 클라우시우스 돈더 듀헴 깁스 폰 헬름홀츠 줄 루이스 마시외 맥스웰 폰 메이어 네른스트 온사게 플랑크 랭킨 스미톤 스틸 태트 톰슨 톰슨 판 데르 발스 워터스톤
다른. 핵생성 자가 조립 자기 조직화 질서와 무질서
카테고리
v t

온도는 물질이 얼마나 뜨거운지를 나타내는 물리량 또는 시스템의 원자 또는 분자당 평균 변환 운동 에너지 측정값입니다.이는 물질의 몰 열 에너지 중 감지 가능한 부분입니다. 온도 차이는 에너지가 뜨거운 물체에서 차가운 물체로 흐르기 때문에 열 전달이 발생할 수 있습니다.

온도는 온도계로 측정한다.이는 정의를 위해 다양한 기준점과 온도 측정 물질에 의존해 온 다양한 온도 척도로 보정된다.가장 일반적인 척도는 섭씨 척도(단위 °C로 "기존 "섭씨"로 불림), 화씨 척도(단위 °F로 불림), 켈빈 척도(단위 K로 불림)이며, 켈빈 척도는 주로 과학적 목적으로 사용되며 국제 단위계(SI)에서 정의한 1차 온도 척도이다.

이론적으로 가장 낮은 온도는 절대 영도이며, 이 절대 온도에서는 더 이상의 열에너지를 물체에서 추출할 수 없습니다.실험적으로, 열역학 제3법칙에서 인정된, 매우 가까이 접근할 수 있을 뿐, 도달할 수 없습니다.

온도는 물리, 화학, 지구과학, 천문학, 의학, 생물학, 생태학, 재료과학, 야금, 기계공학, 지리학 등 자연과학의 모든 분야에서 중요하다.

영향들

많은 물리적 프로세스는 온도와 관련되어 있으며, 그 중 일부는 다음과 같습니다.

• 상(고체, 액체, 기체 또는 플라즈마), 밀도, 용해성, 증기 압력, 전기 전도율, 경도, 내마모성, 열 전도율, 내식성, 강도를 포함한 재료의 물리적 특성
• 화학 반응이^[1] 일어나는 속도와 정도
• 물체 표면에서 방출되는 열복사의 양과 특성
• 공기 온도는 모든 살아있는 유기체에 영향을 미친다
• 절대^[2] 온도의 제곱근에 비례하는 음속

스케일

이 섹션은 확인을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.( 2021년 1월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다)

온도 눈금은 0도로 선택된 점과 온도 증분 단위의 크기 등 두 가지 방식으로 다릅니다.

일반적으로 사용되는 척도

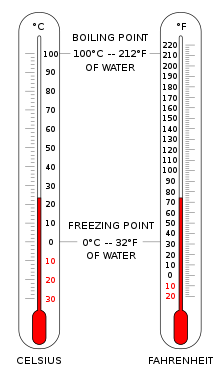
섭씨 눈금(°C)은 세계 대부분의 일반적인 온도 측정에 사용됩니다.이는 역사적으로 발전한 경험적 척도로, 0°C를 해수면의 대기압에서 물의 어는 점으로, 100°C를 물의 끓는점으로 정의했다.100도의 간격 때문에, ^[3]그것은 섭씨 눈금이라고 불렸습니다.국제 단위계의 켈빈 표준화 이후 켈빈 척도의 동등한 고정점 측면에서 켈빈을 재정의하였으며, 섭씨 1도의 온도 증가는 1켈빈의 증가량과 동일하지만 수치적으로는 정확히 273.15의 가산 오프셋으로 차이가 난다.

화씨 눈금은 미국에서 일반적으로 사용되고 있다.물은 화씨 32도에서 얼고 해수면 대기압에서는 화씨 212도에서 끓는다.

절대 제로

절대 0도 온도에서는 열로서 물질로부터 어떤 에너지도 제거될 수 없으며, 이는 열역학 제3법칙에서 표현된다.이 온도에서 물질은 거시적인 열에너지를 포함하지 않지만 불확실성 원리에 의해 예측된 양자역학적 영점 에너지를 가지고 있지만 절대 온도의 정의에 들어가지는 않는다.실험적으로 절대 0에 근접할 수 있으며, 절대 0에 근접할 수 없습니다(실험으로 얻은 최저 온도는 100 pK).^{[citation needed]}이론적으로 절대 영도의 물체에서는 입자의 모든 고전적인 움직임이 멈췄고 그들은 이 고전적인 의미에서 완전히 정지해 있다.0 K로 정의된 절대 영점은 정확히 -273.15°C 또는 -459.67°F와 동일합니다.

절대 척도

는 볼츠만 상수, Maxwell–Boltzmann 유통에, 엔트로피의 볼츠만 통계적 기계적 정의에 대해 최희섭은 깁스 definition,[4]에서 뚜렷한 독립적으로 interparticle 잠재적 에너지를 무시하면서, 국제 협정에 의해 미세 입자 이동에 대해서는 온도 눈금과 말했다 b.으로 한정된다e는bsolute는 특정 온도계 물질 및 온도계 메커니즘의 특성과 독립적이기 때문입니다.절대 영점 이외에는 기준 온도가 없습니다.그것은 과학과 기술에 널리 사용되는 켈빈 척도로 알려져 있다.켈빈(단위 이름은 소문자 'k'로 표기)은 국제 단위계(SI)의 온도 단위입니다.열역학적 평형 상태에 있는 물체의 온도는 절대 영도에 대해 항상 양수이다.

국제적으로 합의된 켈빈 척도 외에, 켈빈 경에 의해 발명된 열역학 온도 척도도 있습니다. 또한 절대 0에서 숫자 0을 가지고 있지만, 비록 미시적 엔트로피를 포함한, 비록 깁스 통계학에서 언급되기는 하지만 거시적 열역학 개념과 직접적으로 관련이 있습니다.절대 ^[4]0에 가까운 온도 측정을 설명할 수 있도록 입자 간 위치 에너지뿐만 아니라 독립 입자 운동을 고려하는 정준 앙상블에 대한 엔트로피의 기계적 정의.이 눈금은 물의 세 배 지점에 기준 온도가 있으며, 이 수치는 앞서 국제적으로 합의된 켈빈 눈금을 사용하여 측정함으로써 정의된다.

켈빈 척도

많은 과학적 측정에서 켈빈 온도 척도를 사용합니다. 켈빈 온도 척도는 처음 켈빈 온도를 정의한 물리학자의 이름을 따서 명명된 단위 기호: K.그것은 절대적인 규모이다.0 K라는 숫자는 절대 0도 온도입니다.2019년 5월부터, 켈빈은 입자 운동 이론과 통계 역학을 통해 정의되어 왔다.국제단위계(SI)에서 켈빈의 크기는 볼츠만 상수로 정의되며, 볼츠만 상수의 값은 국제규약에 ^[5][6]의해 고정된다.

통계적 기계 대 열역학 온도 척도

2019년 5월 이후, 켈빈의 크기는 미시적 현상과 관련하여 정의되었으며, 통계 역학의 관점에서 특징지어진다.이전에는 1954년부터 국제 단위계가 켈빈의 척도와 단위를 열역학적 온도로 정의했으며, 물의 세 배 점의 신뢰할 수 있는 재현 가능한 온도를 두 번째 기준점으로 사용했다. 첫 번째 기준점은 절대 ^{[citation needed]}0에서 0 K이다.

역사적으로 물의 삼중점 온도는 정확히 273.16 K로 정의되었다.오늘날 그것은 경험적으로 측정된 양이다.해수면 대기압에서 물의 응고점은 273.15K = 0°C에 매우 가까운 온도에서 발생한다.

척도의 분류

온도계에는 다양한 종류가 있습니다.경험적, 이론적으로 분류하는 것이 편리할 수 있습니다.경험적 온도 척도는 역사적으로 더 오래된 반면, 이론적으로 기반을 둔 척도는 19세기 ^[7][8]중반에 생겨났다.

경험적 척도

경험적 기반 온도 척도는 재료의 단순한 거시적 물리적 특성 측정에 직접 의존한다.예를 들어 유리벽이 있는 모세관 안에 갇힌 수은 기둥의 길이는 온도에 따라 크게 달라지며 매우 유용한 수은-유리 온도계의 기초가 됩니다.이러한 눈금은 편리한 온도 범위 내에서만 유효합니다.예를 들어, 수은의 끓는점 이상에서는 수은 유리 온도계가 실용적이지 않습니다.대부분의 재료는 온도 상승에 따라 팽창하지만, 물과 같은 일부 재료는 특정 범위의 온도 상승에 따라 수축하므로 온도 측정 재료로는 거의 도움이 되지 않습니다.재료는 상변화 온도(예: 비등점) 근처에서는 온도계로 사용할 수 없습니다.

이러한 한계에도 불구하고, 가장 일반적으로 사용되는 실용 온도계는 경험에 기초한 종류이다.특히 열량 측정에 사용되어 열역학 발견에 크게 기여하였다.그럼에도 불구하고, 경험적 온도 측정법은 이론 물리학의 기초로 판단될 때 심각한 결점을 가지고 있다.경험적 기반 온도계는 온도계 재료의 일반적인 물리적 특성에 대한 단순한 직접 측정으로 기준을 벗어나 이론적인 물리적 추론을 사용하여 재보정할 수 있으며, 이는 적정성의 범위를 확장할 수 있다.

이론적 척도

이론적으로 기초하는 온도 척도는 이론적인 논쟁, 특히 운동 이론과 열역학의 논쟁에 직접적으로 기초한다.그것들은 실질적으로 실현 가능한 물리적 장치 및 재료에서 어느 정도 이상적으로 실현됩니다.이론적인 기반 온도 척도는 실제 경험적 기반 온도계에 대한 교정 표준을 제공하기 위해 사용됩니다.

미시적 통계 기계 척도

물리학에서 국제적으로 합의된 전통적인 온도 척도를 켈빈 척도라고 합니다.국제적으로 합의된 볼츠만 ^[5][6]상수의 값을 통해 보정되며, 온도 측정 대상인 체내의 원자, 분자, 전자 등 미세 입자의 움직임을 말한다.켈빈에 의해 발명된 열역학적 온도 척도와는 대조적으로, 현재 일반적인 켈빈 온도는 표준 물체의 기준 상태 온도와의 비교를 통해 정의되거나 거시적 열역학 측면에서 정의되지 않는다.

절대 0의 온도와는 별도로, 내부 열역학적 평형 상태의 물체의 켈빈 온도는 볼츠만 ^{[citation needed]}상수의 관점에서 정확하게 알려진 이론적 설명과 같이 적절히 선택된 물성의 측정에 의해 정의된다.이 상수는 인체 구성에서 선택된 종류의 미세한 입자를 말합니다.이런 운동에서는 입자는 상호 작용 없이 개별적으로 움직입니다.이러한 움직임은 일반적으로 입자 간 충돌에 의해 중단되지만 온도 측정의 경우 충돌 사이에 궤적의 비대화 세그먼트가 정확한 측정에 접근할 수 있도록 모션이 선택된다.이를 위해 입자간 전위 에너지는 무시된다.

이상 기체 및 이론적으로 이해되는 다른 물체에서 켈빈 온도는 적절한 기술로 측정할 수 있는 비인터랙티브하게 움직이는 현미경 입자의 평균 운동 에너지에 비례하도록 정의된다.비례 상수는 볼츠만 상수의 단순 배수입니다.만약 분자, 원자 또는 ^[9][10]전자가 물질로부터 방출되고 그 속도가 측정된다면, 그들의 속도의 스펙트럼은 종종 맥스웰-볼츠만 분포라고 불리는 이론 법칙에 거의 준거합니다. 이것은 법칙이 적용되는 ^[11]온도의 충분한 근거를 제공합니다.온도계측을 위해 페르미-디락 분포를 직접 사용하는 이와 같은 종류의 실험은 아직 성공하지 못했지만,^[12] 아마도 미래에 이루어질 것이다.

기체의 음속은 이론적으로 기체의 분자 특성, 온도와 압력, 볼츠만 상수 값으로부터 계산될 수 있습니다.알려진 분자 특성과 압력을 가진 기체의 경우, 이것은 온도와 볼츠만 상수 사이의 관계를 제공합니다.이러한 양은 세 개의 점에서의 물 샘플 상태를 정의하는 열역학 변수보다 더 정확하게 알려지거나 측정될 수 있습니다.따라서 볼츠만 상수 값을 정확히 정의된 값의 일차적인 기준으로서 음속 측정을 통해 ^[13]가스 온도를 보다 정확하게 측정할 수 있다.

이상적인 3차원 흑체로부터의 전자파 방사 스펙트럼 측정은 흑체 방사선의 최대 스펙트럼 광도의 주파수는 흑체 온도에 정비례하기 때문에 정확한 온도 측정을 제공할 수 있다.이것은 빈의 변위 법칙으로 알려져 이론적인 e가 있다.플랑크의 법칙과 보스-아인슈타인 법칙의 xplanation.

전기저항기에 의해 발생하는 노이즈 파워의 스펙트럼을 측정함으로써 정확한 온도 측정을 할 수 있습니다.저항기에는 2개의 단자가 있으며 사실상 1차원 본체입니다.이 경우에 대한 Bose-Ainstein 법칙은 소음 전력이 저항의 온도, 저항값 및 소음 대역폭에 정비례한다는 것을 나타냅니다.주어진 주파수 대역에서 노이즈 파워는 모든 주파수에서 동일한 기여를 하며 존슨 노이즈라고 합니다.저항 값이 알려진 경우 온도를 확인할 ^[14][15]수 있습니다.

거시적 열역학 척도

역사적으로, 2019년 5월까지 켈빈 척도의 정의는 켈빈에 의해 발명되었으며, 이상적인 카르노 엔진의 프로세스에서 에너지 양의 비율에 기초하여 전적으로 거시 ^{[citation needed]}열역학 측면에서 정의되었다.그 카르노 엔진은 두 온도 사이에서 작동한다. 즉, 온도를 측정해야 하는 물체의 온도와 물의 3중점 온도에서 기준되는 물체의 온도 사이에서 작동한다.그 후 삼중점의 기준 온도는 정확히 273.16 K로 정의되었다. 2019년 5월부터 이 값은 정의에 의해 고정되지 않았지만 위에서 설명한 바와 같이 볼츠만 상수를 포함하는 현미경 현상을 통해 측정되어야 한다.미시적 통계적 기계적 정의에는 기준 온도가 없습니다.

이상 기체

거시적으로 정의된 온도 척도가 기초가 될 수 있는 재료가 이상 기체이다.이상적인 기체의 부피와 질량에 의해 가해지는 압력은 기체의 온도에 정비례합니다.일부 천연 가스는 적절한 온도 범위에서 매우 이상적인 성질을 보여 온도 측정에 사용될 수 있습니다; 이것은 열역학의 발전 동안 중요했고 ^[16][17]오늘날에도 여전히 실용적으로 중요합니다.그러나 이상적인 가스 온도계는 이론적으로 열역학에는 완벽하지 않습니다.이는 절대 0의 온도에서 이상 기체의 엔트로피가 양의 반확정량이 아니기 때문에 기체가 열역학 제3법칙에 위배되기 때문입니다.실제 물질과 대조적으로 이상적인 가스는 아무리 차가워도 액상화되거나 굳지 않습니다.또는 이상적인 기체 법칙인 사고방식은 무한히 높은 온도와 제로 압력의 한계를 나타냅니다. 이러한 조건들은 구성 ^[18][19][20]분자의 비 상호작용 운동을 보장합니다.

운동 이론 접근법

켈빈의 크기는 볼츠만 상수의 값에서 도출된 운동 이론의 관점에서 정의됩니다.

운동 이론은 다양한 종의 분자와 이온과 같은 많은 미세한 입자로 구성된 거시적 시스템에 기초해, 특히 가스의 일부 물체에 대한 온도의 미시적 설명을 제공하며, 종의 입자는 모두 비슷합니다.그것은 미시적인 입자의 고전적인 역학을 통해 거시적인 현상을 설명한다.운동 이론의 등분할 정리는 자유롭게 움직이는 입자의 각 고전적 자유도가 kT_B/2의 평균 운동 에너지를 가지고 있다고 단언합니다. 여기서_B k는 볼츠만 ^{[citation needed]}상수를 나타냅니다.입자의 번역운동은 3가지 자유도를 가지며, 양자효과가 우세한 매우 낮은 온도를 제외하고, 온도가 T인 시스템에서 자유롭게 움직이는 입자의 평균 번역운동 에너지는 3kT_B/2가 될 것이다.

산소(O₂)와 같은 분자는 단일 구형 원자보다 자유도가 더 높다: 그들은 변환뿐만 아니라 회전과 진동 운동을 겪는다.가열은 분자의 평균 변환 운동 에너지의 증가로 인해 온도가 상승합니다.가열은 또한 균열을 통해 진동 및 회전 모드와 관련된 에너지를 증가시킵니다.따라서 이원자 가스는 온도를 일정량 증가시키기 위해 더 많은 에너지 입력이 필요할 것이다. 즉, 이 가스는 단원자 가스보다 더 큰 열 용량을 가질 것이다.

앞에서 기술한 바와 같이, 기체 중의 음속은 기체의 분자 특성, 온도와 압력, 볼츠만 상수 값으로부터 계산할 수 있다.볼츠만 상수 값을 정확히 정의된 값의 일차적으로 정의된 기준으로 삼으면, 소리의 속도를 측정하면 ^[13]가스의 온도를 보다 정확하게 측정할 수 있습니다.

현미경 입자가 격납벽의 작은 구멍을 통해 시스템의 대부분에서 빠져나갈 수 있다면 구성 현미경 입자의 평균 운동 에너지를 측정할 수 있습니다.속도의 스펙트럼을 측정해야 하고, 그것으로부터 평균을 계산해야 한다.탈출하여 측정된 입자가 시스템의 대부분에 남아 있는 입자와 동일한 속도 분포를 갖는 것은 아니지만 때로는 좋은 샘플이 가능합니다.

열역학적 접근법

온도는 열역학 연구의 주요 양 중 하나이다.이전에는 켈빈의 크기가 열역학적 용어로 정의되었지만, 오늘날에는 위에서 언급한 것처럼 운동 이론으로 정의된다.

열역학적 온도는 두 가지 이유로 절대적이라고 한다.하나는 그 형식적인 특성이 특정 재료의 특성과 무관하다는 것입니다.또 다른 이유는 열역학 제3법칙에 따르면 그 0은 물질의 구성 입자의 미세한 고전적 운동이 없음을 나타내는 절대적인 것이기 때문이다.그럼에도 불구하고, 열역학적 온도는 사실 전통에 의해 임의로 선택되고 특정 물질의 특성에 따라 결정되는 확실한 수치를 가지고 있습니다; 그것은 단순히 섭씨나 화씨 같은 상대적인 "도" 척도보다 덜 임의적입니다.고정점(0)이 1개인 절대 척도이므로 상대 척도와 같이 2개의 자유도가 아니라 1개의 자유도만 임의 선택에 남습니다.2019년 5월 이후 켈빈 척도의 경우, 국제 협약에 따라 분자 운동에 대한 미시적 운동 이론에 의존하여 다양한 온도 측정 장치의 작동 모드에 대한 지식을 사용하는 것이 선택되었다.수치 척도는 볼츠만 상수의 값에 대한 기존의 정의에 의해 결정되며, 볼츠만 상수는 분자 같은 입자의 평균 미시적 운동 에너지와 거시적 온도를 관련짓습니다.그 수치는 임의적이며, 켈빈과 섭씨처럼 화씨 눈금과 정렬되도록 만들어진 랭킨 눈금으로 불리는 덜 널리 사용되는 대체 절대 온도 눈금이 존재합니다.

온도의 열역학적 정의는 켈빈 때문이다.이것은 카르노 엔진이라고 불리는 이상적인 디바이스의 관점에서 프레임화 되어 있으며, 작업 주체의 상태 사이클을 가로지르는 가공의 연속적인 프로세스 사이클로 동작하는 상상을 하고 있습니다.엔진은 온수 탱크에서 열₁ Q를 흡수하여 더 적은 양의 폐열₂ Q < 0을 냉수 탱크에 전달합니다.작업 주체가 흡수하는 순 열 에너지는 열역학 작업으로 작업 저장소로 전달되며 엔진의 출력으로 간주됩니다.사이클은 너무 느리게 진행되어 사이클의 각 지점에서 작업 주체가 열역학적 평형 상태에 있는 것으로 상상됩니다.따라서 사이클의 연속적인 프로세스는 엔트로피 생성 없이 가역적으로 실행될 것으로 상상됩니다.그러면 작업체가 가열될 때 온수 저장소에서 유입되는 엔트로피의 양은 작업체가 냉각될 때 냉수 저장소로 전달되는 엔트로피의 양과 같다.저장소의 절대 또는 열역학적 온도 T와₁₂ T는 다음과^[21] 같이 정의됩니다.

${\displaystyle {T_{1}}{T_{2}}=-{\frac {Q_{1}}{Q_{2}}}.}$

(1)

열역학 제0법칙은 다른 열 저장소가 관심 물체와 동일한 온도를 갖도록 함으로써 이 정의를 사용하여 관심 물체의 절대 또는 열역학적 온도를 측정할 수 있도록 합니다.

켈빈의 절대 온도를 가정한 원작은 1848년에 출판되었다.그것은 열역학 제1법칙의 공식화 이전에 카르노의 연구에 기초했다.카르노는 열에 대한 건전한 이해와 엔트로피의 특정한 개념이 없었다.그는 '칼로리'에 대해 썼고, 온수 저장소에서 나온 모든 열량이 차가운 저장소로 전달되었다고 말했다.켈빈은 1848년 논문에서 자신의 척도는 "특정 물질의 특성과는 독립적으로" 정의되었다는 점에서 절대적이었다고 썼다.방금 언급한 정의를 설명하는 그의 최종 출판물은 1853년에 인쇄되었고,^{[22][23][24][25]} 1851년에 읽힌 논문이다.

수치 세부 사항은 이전에는 절대 온도가 273.^[26]16K로 정의된 물의 세 번째 지점에서 열 저장고 중 하나를 셀로 만드는 방식으로 결정되었다. 오늘날 수치 값은 위에서와 같이 미시적 통계 역학적 국제 정의를 통해 측정하여 대신 구한다.

고도의 가변성

열역학적 관점에서 온도는 특정 물체에 대해 하나의 광범위한 변수에 대한 미분 계수와 같기 때문에 강도 높은 변수입니다.따라서 두 개의 광범위한 변수 비율의 차원을 가지고 있다.열역학에서 두 물체는 공통 벽과의 접촉에 의해 연결된 것으로 간주되며, 이는 몇 가지 특정한 투과성 특성을 가지고 있습니다.이러한 특정 투과성은 특정 강도 변수를 참조할 수 있다.예를 들어 열에 대해서만 투과성이 있는 투과성 벽이 있습니다. 이 경우 온도 변수가 강합니다.두 물체가 매우 오랜 시간 동안 투과성 벽을 통해 연결되고 영구적인 정상 상태로 자리를 잡으면, 관련된 강도 높은 변수는 두 물체에서 동일합니다. 온열 벽의 경우, 이 문장은 ^[27][28][29]열역학 제0법칙이라고 부르기도 합니다.

특히, 물체의 내부 에너지 U, 확장 변수인 엔트로피 S, 확장 변수 및 다른 상태 변수 V, N의 함수로 U = U(S, V, N)를 표현함으로써 물체를 기술하면,^[28][29][30] 온도는 엔트로피에 대한 내부 에너지의 편도함수와 같다.

${\displaystyle T=\left({\frac U}{\partial S}}\오른쪽)_{V,N}.}$

(2)

마찬가지로, 인체의 엔트로피 S를 ^[28][30][31]내부 에너지 U 및 다른 상태 변수 V, N의 함수로 기술하는 경우, 온도의 역수는 내부 에너지에 대한 엔트로피의 편도함수와 같다.

${\displaystyle\frac{1}{T}}=\left({\frac {\partial U}}\오른쪽)_{V,N}.}$

(3)

절대 온도의 위의 정의인 방정식 (1)은 켈빈에 기인한다.물질 전달에 폐쇄된 시스템을 말하며 직접 실험 절차를 특히 강조합니다.깁스에 의한 열역학 발표는 보다 추상적인 수준에서 시작되어 물질의 전달에 개방된 시스템을 다룬다; 이 열역학 발전에서, 위의 방정식 (2)와 (3)은 사실 ^[32]온도의 대체 정의이다.

국소 열역학 평형

실제 물체는 종종 열역학적 평형에 있지 않고 균질하지 않다.고전적인 불가역 열역학 방법에 의한 연구를 위해, 물체는 보통 작은 크기의 '세포'로 개념적으로 분할된다.만약 물질에 대한 고전적인 열역학적 평형 조건이 그러한 '셀'에서 좋은 근사치까지 충족된다면, 그것은 균질하고 그것에 대한 온도가 존재한다.만약 이것이 신체의 모든 '세포'에 대해 그렇다면, 국소적인 열역학적 균형은 ^{[33][34][35][36][37]}몸 전체에 걸쳐 우세하다고 한다.

예를 들어 광범한 변수 U 또는 광범한 변수 S에 대해 시스템의 단위 부피당 밀도 또는 단위 질량당 양을 갖는 것은 타당하지만 시스템의 단위 부피당 온도 밀도 또는 단위 질량당 온도량을 말하는 것은 타당하지 않습니다.반면에, 국소 열역학 평형이 우세할 때, 한 지점의 온도에 대해 말하는 것은 이치에 맞지 않습니다.따라서, 온도는 전지구 열역학 평형이 아닌 국소 열역학 평형이 있는 매체에서 지점마다 다를 수 있다.

따라서 체내에서 국소적인 열역학적 평형이 우세할 때, 온도는 그 체내에서 공간적으로 변화하는 국소적 특성으로 간주될 수 있으며, 이는 온도가 강도 높은 변수이기 때문이다.

기본 이론

켤레 변수 열역학의

압력. 용량 (스트레스) (스트레인) 온도 엔트로피 화학 퍼텐셜 파티클 번호

온도는 ^[38]물질 상태의 품질을 측정하는 척도입니다.품질은 이를 측정하는 특정 온도 척도보다 더 추상적인 실체로 간주될 수 있으며, 일부 ^[39][40][41]저자들에 의해 고온도라고 불립니다.고온의 품질은 특정 장소에서만 물질의 상태를 말하며, 일반적으로 열역학적 평형의 안정된 상태로 유지되는 물체와는 별도로, 고온은 장소마다 다르다.특정 장소에 있는 물질이 잘 정의된 고온 또는 온도를 가질 수 있을 만큼 안정적이고 거의 균일한 상태에 있는 것은 아닙니다.열도는 1차원 다양체로 추상적으로 표현될 수 있다.모든 유효 온도 척도는 자체적인 ^[42][43]일대일 맵을 핫니스 매니폴드에 가집니다.

열접촉에 있는 두 시스템이 같은 온도에 있을 경우 두 시스템 간에 열이 전달되지 않습니다.온도차가 존재하면 열이 온열 시스템에서 냉열 시스템으로 자연스럽게 흐르면서 열 평형이 됩니다.이러한 열전달은 전도 또는 ^{[44][45][46][47][48][49][50][51]}열복사에 의해 발생합니다.

예를 들어 갈릴레오와 ^[52]뉴턴 같은 실험물리학자들은 무한히 많은 경험적 온도 척도가 있다는 것을 발견했다.그럼에도 불구하고 열역학 제0법칙은 모두 같은 품질을 측정한다고 말한다.이것은 내부 열역학적 평형 상태에 있는 물체에 대해, 정확하게 보정된 모든 종류의 온도계가, 몸의 온도를 측정하는, 1과 같은 온도를 기록한다는 것을 의미합니다.내부 열역학적 평형 상태에 있지 않은 물체의 경우 온도계의 작동 메커니즘에 따라 온도계가 다른 온도를 기록할 수 있습니다.

열역학적 평형 상태의 물체

실험 물리학에서, 뜨거움은 각각의 개별 열역학적 평형에서 주어진 두 물체를 비교할 때, 적절히 주어진 경험적 온도계와 수치 척도 측정치가 일치하는 두 물체가 주어진 두 물체 중 어느 것이 더 뜨거운지 또는 같은 ^[53]온도를 갖는다는 것을 의미합니다.이는 두 온도계가 수치 척도 판독치 사이에 선형 관계를 가질 필요는 없지만, 수치 판독치 사이의 관계는 엄격히 ^[54][55]단조로운 것이어야 한다.열량 측정, 열역학 및 특정 재료의 특성과는 별개로 열복사의 변위 법칙에 따라 열복사 욕조의 온도는 주파수 스펙트럼의 최대 주파수에 대해 보편적 상수로 비례한다.ency는 항상 긍정적이지만 0인 경향이 있는 값을 가질 수 있습니다.열복사는 처음에 열역학 평형의 공동에 대해 정의된다.이러한 물리적 사실들은 열기가 질서정연한 1차원 다양체에 존재한다는 수학적 진술을 정당화한다.이것은 열역학적 ^{[7][42][43][56][57]}평형 상태에 있는 물체에 대한 온도와 온도계의 기본 특성입니다.

얼음의 융해와 같은 1차 상변화를 겪는 시스템을 제외하고 폐쇄형 시스템은 부피의 변화 없이 외력장의 변화 없이 열을 받으면 온도가 상승한다.열역학적 평형으로부터의 이탈이 무시될 정도로 천천히 상변화를 겪는 시스템의 경우, 시스템에 잠열이 공급될 때 온도는 일정하게 유지됩니다.반대로 위상변화, 부피변화, 외력장 변화 없이 닫힌 시스템에서 발생하는 열 손실은 온도를 ^[58]낮춥니다.

정상 상태이지만 열역학적 평형 상태에 있지 않은 물체

열역학 평형 상태에 있는 물체의 경우, 온도의 개념은 모든 경험적 온도계가 두 물체 중 어느 것이 더 뜨거운지 또는 같은 온도에 있는지에 대해 일치해야 하는 것을 요구하지만, 이 요구 사항은 열역학 평형 상태에 있지 않지만 안정된 상태에 있는 물체에 대해서는 안전하지 않습니다.그러면 다른 경험적 온도계가 어떤 것이 더 뜨거운지에 대해 의견이 엇갈릴 수 있고, 만약 그렇다면, 적어도 한 물체는 절대 열역학적 온도가 명확하게 정의되어 있지 않다.그럼에도 불구하고, 누구나 몸을 준 적이 있고 어떤 적절한 경험적 온도계라도 여전히 적절한 범위의 프로세스에 대한 경험적, 절대적, 고온 및 온도의 개념을 지원할 수 있다.이것은 비균형 ^{[citation needed]}열역학에서 연구해야 할 문제이다.

시체가 정상 상태가 아닌 경우

물체가 정상 상태에 있지 않을 때, 온도의 개념은 열역학적 평형이 아닌 정상 상태에 있는 물체보다 훨씬 덜 안전해진다.이것은 또한 비평형 열역학에서 연구해야 할 문제이다.

열역학적 평형 공리론

열역학적 평형의 공리적인 처리를 위해, 1930년대부터 열역학의 제0법칙을 언급하는 것이 관례가 되었다.이러한 법칙의 관습적으로 언급된 미니멀리즘 버전은 열적으로 연결되었을 때 모든 물체는 정의상 같은 온도를 갖는다고만 가정하지만, 그 자체로 온도를 척도의 실수로 표현되는 양으로 설정하지는 않는다.이러한 법칙의 보다 물리적인 정보 버전은 경험적 온도를 열도 ^[42][57][59]다양체의 차트로 본다.제0법칙은 많은 경험적 온도 척도의 정의를 허용하는 반면, 열역학 제2법칙은 열역학 ^{[7][42][60][61][62][63]}온도라고 불리는 임의의 척도 요인까지 고유한 단일 선호 절대 온도의 정의를 선택합니다.내부 에너지가 열역학적 평형에서 균질계의 부피와 엔트로피의 함수로 간주되면, 열역학적 절대 온도는 일정한 부피에서의 엔트로피와 관련하여 내부 에너지의 부분 도함수로 나타난다.자연적, 본질적 원점 또는 늘점은 시스템의 엔트로피가 최소인 절대 0입니다.모델에 의해 설명되는 가장 낮은 절대 온도이지만, 열역학 제3법칙은 어떤 물리적 시스템에서도 절대 0에 도달할 수 없다고 가정합니다.

열용량

몸으로 또는 몸으로부터 에너지가 전달되는 것이 열과 같을 때, 몸의 상태는 변한다.주변환경이나 벽면에 따라 신체에 다양한 변화가 있을 수 있습니다.화학 반응, 압력 상승, 온도 상승, 상변화 등이 이에 해당한다.특정 조건에서의 ^[64]각 종류의 변화에 대해 열 용량은 변화의 크기에 대한 전달되는 열량의 비율입니다.

예를 들어 상변화와 화학적 변화가 없는 일정한 체적에서의 온도 상승이면 체온이 상승하고 압력이 높아진다.전달되는 열량 δQ를 관측 온도 변화 δT로 나눈 값은 일정한 체적에서 인체의 열 용량이다.

$({displaystyle C_{V}={Delta Q}{\Delta T})}$

잘 정의된 양의 물질에 대해 열 용량을 측정하는 경우, 비열은 해당 단위량의 온도를 한 단위의 온도만큼 증가시키는 데 필요한 열의 측정값입니다.예를 들어, 물의 온도를 1켈빈(섭씨 1도) 올리려면 kg당 4186줄(J/kg)이 필요합니다.

측정.

현대 과학 온도계와 온도 척도를 사용한 온도 측정은 다니엘 가브리엘 화씨(Daniel Gabriel Fahrenheit)가 온도계와 올레 크리스텐센 뢰머에 의해 개발된 척도를 채택한 18세기 초까지 거슬러 올라간다.화씨 눈금은 여전히 미국에서 비과학적인 용도로 사용되고 있습니다.

온도는 다양한 온도 척도로 보정할 수 있는 온도계를 사용하여 측정합니다.세계 대부분(벨리즈, 미얀마, 라이베리아 및 미국 제외)에서 섭씨 눈금은 대부분의 온도 측정 목적으로 사용됩니다.대부분의 과학자들은 섭씨 척도를 사용하여 온도를 측정하고 켈빈 척도를 사용하여 열역학적 온도를 측정합니다. 켈빈 척도는 0K = -273.15°C 또는 절대 0입니다.미국의 많은 공학 분야, 특히 첨단 기술과 미국 연방 사양(민간 및 군사)에서도 켈빈과 섭씨 척도를 사용합니다.미국의 다른 공학 분야도 연소 등 열역학 관련 분야에서 작업할 때 랭킨 척도(화씨 기준 이동)에 의존합니다.

단위

국제 단위계(SI)의 기본 온도 단위는 켈빈입니다.그것은 K기호를 가지고 있다.

일상 용도의 경우 섭씨 눈금을 사용하는 것이 편리합니다. 섭씨 눈금은 0°C가 물의 어는점에 매우 가깝고 100°C가 해수면에서의 끓는점에 해당합니다.액체 방울은 일반적으로 영하의 온도에서 구름에 존재하기 때문에 0°C가 얼음의 녹는점으로 더 잘 정의됩니다.이 척도에서 섭씨 1도의 온도 차이는 1켈빈 증가량과 동일하지만 눈금은 얼음이 녹는 온도(273.15K)로 상쇄됩니다.

국제 ^[65]협약에 따라, 2019년 5월까지 켈빈과 섭씨 척도는 두 가지 고정점, 즉 절대 0과 비엔나 표준 평균 해양수의 삼중점으로 정의되었다. 이는 수소와 산소 동위원소의 특정 혼합으로 특별히 제조된 물이다.절대 0은 정확히 0K와 -273.15°C로 정의되었다.이것은 물질을 구성하는 입자의 모든 고전적 번역 운동이 멈추고 고전적 모델에서 완전히 정지하는 온도입니다.하지만 양자역학적으로 제로포인트 운동은 남아있고 관련된 에너지인 제로포인트 에너지를 가지고 있습니다.물질은 접지 ^[66]상태이며 열에너지를 포함하지 않습니다.온도 273.16K와 0.01°C는 물의 삼중점 온도와 동일했다.이 정의는 다음과 같은 목적을 수행했다: 절대 0과 물의 삼중점 사이의 차이의 273.16 부분에서 켈빈의 크기가 정확히 1 부분인 것으로 고정되었다. 그것은 1 켈빈의 크기가 섭씨 척도의 1도와 정확히 동일하다는 것을 확인하였고, null p 사이의 차이를 확립하였다.273.15K(0K = -273.15°C 및 273.16K = 0.01°C)로 표시되어야 한다.2019년부터 볼츠만 ^[67]상수에 기초한 새로운 정의가 있었지만 척도는 거의 변하지 않았다.

미국에서는 화씨 눈금이 가장 널리 사용된다.이 스케일에서 물의 응고점은 32°F, 비등점은 212°F에 해당한다.미국의 화학 공학 분야에서 여전히 사용되는 랭킨 척도는 화씨 증가에 기초한 절대 척도다.

변환

다음 표는 섭씨 눈금으로 변환하기 위한 온도 변환 공식을 보여 줍니다.

온도 변환

	섭씨로부터	섭씨까지
화씨	[°F] = [°C] ×9/5 + 32	[°C] = ([°F] - 32) × 5µ9
켈빈	[K] = [°C] + 273.15	[°C] = [K] - 273.15
랭킨	[°R] = ([°C] + 273).15)×9/5	[°C] = ([°R] - 491.67) × 5µ9
딜리슬	[°De] = (100 - [°C]) × 3⁄2	[°C] = 100 - [°De] × 2⁄3
뉴턴 경이다.	[°N] = [°C] × 33°100	[°C] = [°N] × 100º33
레아우무르	[°Ré] = [°C] × 4⁄5	[°C] = [°Ré] × 5µ4
뢰머	[°Rö] = [°C] × 21º40 + 7.5	[°C] = ([°Rö] - 7.5) × 40µ21

플라즈마 물리학

플라즈마 물리학 분야는 매우 높은 온도를 수반하는 전자기적 현상을 다룬다.온도는 전자볼트(eV) 또는 킬로전자볼트(keV) 단위로 에너지로 표시하는 것이 일반적입니다.온도와 차원이 다른 에너지는 볼츠만 상수 및 온도의 $곱$으로 계산됩니다(\$displaystyle$ E$=k_{\text{B}).$$T$ 그러면 1 eV는 11605 K에 해당합니다.QCD 물질에 대한 연구에서는 정기적으로 수백 MeV의 온도, 즉 약 10¹² K에 해당하는 온도에 직면한다.

이론적 기초

역사적으로 온도의 설명에는 몇 가지 과학적 접근법이 있다: 실험실에서 측정할 수 있는 거시적 경험 변수에 기초한 고전적인 열역학 기술; 거시적 기술을 기체 입자의 운동 에너지의 확률 분포와 관련짓는 가스의 운동 이론.통계물리학과 양자역학에 기초한 미시적 설명.게다가 엄격하고 순수하게 수학적인 처리는 고전적인 열역학 및 ^[68]온도에 대한 자명한 접근을 제공해 왔다.통계물리학은 물질의 원자 거동을 설명함으로써 더 깊은 이해를 제공하고 고전적 상태와 양자적 상태를 모두 포함한 미시적 상태의 통계적 평균으로부터 거시적 특성을 도출합니다.기본적인 물리적 설명에서는 자연 단위를 사용하여 온도를 에너지 단위로 직접 측정할 수 있습니다.그러나, 현대의 단위 미터법과 같은 과학, 기술 및 상거래에 대한 실용적인 측정 시스템에서는 거시적 설명과 미시적 설명은 미시적 평균 운동 에너지로 온도를 조정하는 비례적 요소인 볼츠만 상수에 의해 상호 연관되어 있다.

통계역학의 미시적 설명은 물질의 기본 입자 또는 고전적 또는 양자역학적 발진기 집합으로 시스템을 분석하고 시스템을 미시 상태의 통계적 앙상블이라고 간주하는 모델에 기초한다.고전적인 물질 입자의 집합으로서, 온도는 고체, 액체, 기체 또는 플라스마에서 입자의 평균 운동 에너지라고 불리는 운동 에너지의 측정값입니다.고전 역학의 개념인 운동 에너지는 입자의 질량에 속도를 제곱한 것의 절반이다.이 열운동의 기계적 해석에서 재료 입자의 운동 에너지는 입자의 속도 또는 진동 운동 또는 회전 모드의 관성에 존재할 수 있다.단원자 완전 기체 및 대략 대부분의 가스 및 단순 금속에서 온도는 평균 입자 변환 운동 에너지인 3/2_B kT의 측정값이다.또한 에너지의 확률 분포 함수를 결정합니다.응집 물질, 특히 고형물에서는 이러한 순수 기계적인 설명은 종종 덜 유용하며, 발진기 모델은 양자 역학적 현상을 설명하는 더 나은 설명을 제공합니다.온도는 앙상블의 마이크로 상태의 통계적 점유율을 결정합니다.온도의 미시적 정의는 열역학 한계에서만 의미가 있으며, 이는 상태 또는 입자의 큰 앙상블이 통계 모델의 요구사항을 충족한다는 것을 의미한다.

운동 에너지는 또한 열에너지의 구성요소로 여겨진다.열 에너지는 입자의 자유도 또는 열역학 시스템의 발진기 모드에 기인하는 독립적인 구성요소로 분할될 수 있습니다.일반적으로 에너지의 재분할에 사용할 수 있는 이러한 자유도의 수는 온도, 즉 고려 중인 상호작용의 에너지 영역에 따라 달라집니다.고체의 경우, 열에너지는 주로 평형 위치에 있는 원자 또는 분자의 진동과 관련이 있습니다.이상적인 단원자 기체에서 운동 에너지는 입자의 순수 변환 운동에서만 발견됩니다.다른 시스템에서는 진동 및 회전 운동도 자유도에 기여합니다.

기체 운동 이론

맥스웰과 볼츠만은 기체 ^[69]내 온도에 대한 기본적인 이해를 제공하는 운동 이론을 개발했다.이 이론은 또한 이상적인 가스 법칙과 단원자(^[70][71][72]또는 '귀한') 가스의 관측된 열 용량을 설명합니다.

이상적인 기체 법칙은 압력(p), 체적(V), 온도(T) 사이의 관찰된 경험적 관계에 기초하고 있으며 가스의 운동 이론이 발달하기 훨씬 전에 인식되었습니다.이상 기체 법칙은 ^[73]다음과 같습니다.

${\displaystyle pV=nRT,}$

여기서 n은 가스의 몰 수이고 R = 8.314462618... JmmolkK는^−1−1[74] 기체 상수이다.

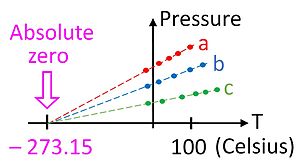
이 관계는 켈빈과 같은 절대적인 척도로 온도를 측정할 때만 유지되기 때문에 온도 척도에 절대 0이 있다는 첫 번째 힌트를 줍니다.이상적인 가스 법칙은 가스 온도계를 사용하여 이 절대 눈금으로 온도를 측정할 수 있게 해줍니다.켈빈 단위의 온도는 1입방미터 용기 내 가스 1몰의 압력(pascal)을 가스 상수로 나눈 값으로 정의할 수 있습니다.

가스 온도계는 특별히 편리한 장치는 아니지만 모든 온도계를 교정할 수 있는 중요한 이론적 근거를 제공합니다.실용적으로는 온도가 0이 되기 훨씬 전에 기체가 응축되어 액체가 되기 때문에 절대 영점 온도를 측정하기 위해 가스 온도계를 사용할 수 없다.그러나 그림과 같이 이상적인 가스 법칙을 사용하여 절대 0으로 추정할 수 있습니다.

운동 이론은 압력이 개별 원자가 벽에 부딪히는 힘에 의해 발생하며 모든 에너지가 변환 운동 에너지라고 가정합니다.정교한 대칭 인수를 사용하여 ^[75]볼츠만은 이상적인 기체에서 입자의 속도에 대해 현재 맥스웰-볼츠만 확률 분포 함수라고 불리는 것을 추론했다.이 확률 분포 함수로부터, 단원자 이상 기체의^[71][76] (입자당) 평균 운동 에너지는 다음과 같다.

$\displaystyle E_{\text{k}=mv_{\text{2}^{2}=mvfrac{3}{{2}k_{\text{B}}T,}$

볼츠만 상수에서 k_B 는 이상적인 기체 상수를 Avogadro 수로 나눈 $값$이며, ${\text{vrms}}_{}$ $=\sqrt{}$ $\sqrt{{v2\mathrm{}}^{}}$ $\sqrt{{}^{}}$ $=$ $\sqrt{v,}$ $v {\$ ${\text{\$text${\text$}}= $rt$ {\$rangle$}} = rt {\$rangle$ v, v$\rangle$}}} 은$$ 제곱 평균 ^[77]속도입니다.온도와 평균 분자 운동 에너지 사이의 이러한 정비례는 등분할 정리의 특별한 경우이며, 완벽한 기체의 고전적인 한계에서만 유지됩니다.대부분의 물질에 대해서는 정확하게 유지되지 않습니다.

열역학 제0법칙

다른 방법으로는 고립된 두 물체가 물질에 침투하지 않는 단단한 물리적 경로로 서로 연결되면, 뜨거운 물체에서 차가운 물체로 에너지가 자발적으로 전달됩니다.결국, 그들은 열전달이 정지된 상호 열평형 상태에 도달하고, 물체의 각각의 상태 변수는 ^[78][79][80]변하지 않는 상태가 된다.

열역학 제0법칙의 한 가지 설명은 만약 두 개의 시스템이 각각 세 번째 시스템과 열평형 상태에 있다면,^[81][82][83] 그들은 또한 서로 열평형 상태에 있다는 것입니다.

이 문장은 온도를 정의하는 데 도움이 되지만 그것만으로는 정의를 완료하지 않습니다.경험적 온도는 열역학계의 뜨거움을 나타내는 수치 척도입니다.이러한 뜨거움은 1차원 다지관에 존재하며 고온과 저온 사이를 연장하는 것으로 정의할 수 있다.때때로 제0법칙은 경험적 ^[59]온도의 완전한 정의를 제공하기 위해 고유한 보편적 열도 다양체의 존재와 그 위에 있는 수치 척도를 포함한다고 명시된다.경험적 온도 측정에 적합하기 위해서는 재료는 다른 모든 관련 좌표를 고정할 때 열도와 압력이나 부피와 같이 쉽게 측정되는 상태 변수 사이에 단조로운 관계를 가져야 한다.이상적인 가스는 절대 켈빈 눈금과 일치하는 온도 눈금을 제공할 수 있습니다.켈빈 척도는 열역학 제2법칙에 기초해 정의된다.

열역학 제2법칙

열역학 제0법칙을 고려하거나 정의하는 것에 대한 대안으로,^{[citation needed]} 엔트로피를 다루는 열역학 제2법칙의 관점에서 온도를 정의하는 것은 열역학에서의 역사적 발전이었다.두 번째 법칙은 어떤 과정이든 우주의 엔트로피가 변화하거나 순증하는 결과를 초래하지 않는다고 말한다.이것은 확률로 이해할 수 있다.

예를 들어, 일련의 동전 던지기에서 완벽한 순서는 모든 동전 던지기 앞면이 나오거나 모든 동전 던지기 뒷면이 나오는 시스템입니다.이는 결과가 항상 100% 동일함을 의미합니다.반대로, 많은 혼합(무질서한) 결과가 가능하며, 토스할 때마다 그 수가 증가합니다.결국 50%의 앞면과 50%의 뒷면의 조합이 지배적이기 때문에 50/50과는 크게 다른 결과를 얻을 가능성은 점점 낮아지고 있습니다.따라서 시스템은 자연스럽게 최대 무질서 또는 엔트로피 상태로 진행됩니다.

온도는 두 시스템 사이의 열 전달을 좌우하며 우주가 엔트로피를 최대화하는 경향이 있기 때문에 온도와 엔트로피 사이에 어떤 관계가 있을 것으로 예상된다.열 엔진은 열에너지를 기계적 에너지로 변환하여 작업 성능을 높이기 위한 장치입니다.Carnot 열 엔진의 분석은 필요한 관계를 제공합니다.에너지 절약 및 에너지가 전체 사이클에 걸쳐 변화하지 않는 상태 함수이므로, 열 엔진에서 전체 사이클에 걸쳐 발생하는 작업은 순열, 즉_H 고온 > 0에서 시스템에 투입되는 열의 합과 저온 ^[84]q < 0에서 방출되는 폐열의 합과 같습니다_C.

효율은 작업을 열 입력으로 나눈 값입니다.

${\displaystyle {\text{efficiency}}=paramfrac {w_{\text{cy}}{q_{\text{\text}H}}}} = flac {q_{\text{}H}}+q_{\text{C}} {q_{\text{H}}}=1-{\frac {q_{\text{C}} {q_{\text{H}}}}}},}$

(4)

여기서_cy w는 사이클당 실행되는 작업입니다.효율은 q/q에만_CH 의존합니다.q와_H q는 각각 온도_C T와_H T에서의 열전달에 대응하므로_C q /q는_H 다음_C 온도의 일부 함수가 되어야 합니다.

$\ displaystyle \ frac { q _ \ text \C}} {q_{\text{H}}}=f\left(T_{\text{})H}}, T_{\text{C}}\right).}$

(5)

Carnot의 정리는 동일한 열 저장고 사이에서 작동하는 모든 가역 엔진은 동등하게 ^{[citation needed]}효율적이라는 것입니다.따라서 T와₃ T 사이에서 작동하는₁ 열 엔진은 T와 T 사이₂, 그리고₁ T와 T 사이₃ 두₂ 번째 사이클로 구성된 것과 동일한 효율성을 가져야 합니다.이 경우는 다음과 같습니다.

$({displaystyle q_{13}=syslogfrac {q_{1}q_{2}}} {q_{3}}})$

그 의미는

${\displaystyle q_{13}=f\left(T_{1}, T_{3}\right)=f\left(T_{1}, T_{2}\right)f\left(T_{3}\right)}$

첫 번째 함수는 T와₂ 독립적이기 때문에 이 온도는 오른쪽에서 취소되어야 한다. 즉, f(T₁₁, T₃₃)는 g(T₁)/g(T₃)(즉, f(T, T₂) = f(T₁, T)f(T₂, T₃) = g(T₁)/G₂(T₂₃₁₃)/T(T)의 형식이다.온도 척도는 이제 다음과 같은 특성으로 선택할 수 있습니다.

$\ displaystyle \ frac { q _ \ text \C}} {q_{\text{H}}}}} = flac {T_{\text{}C}}{T_{\text{H}}}}}}}.$

(6)

(6)을 (4)로 다시 치환하면 온도 측면에서 효율성에 대한 관계가 나타납니다.

${\displaystyle {text {efficiency}}=1-{\frac {q_{\text}C}} {q_{\text{H}}}}=1-{\frac {T_{\text{}C}}{T_{\text{H}}}}}}}.$

(7)

T = 0 K의 경우_C 효율은 100%이며 0 K 이하에서는 100% 이상입니다.효율이 100%를 초과하면 열역학 제1법칙에 위반되므로 0K가 가능한 최소 온도임을 의미합니다.실제로 거시적 시스템에서 지금까지 측정된 최저 온도는 20nK였으며, 이는 1995년 NIST에서 달성되었다.(5)의 오른쪽을 중간에서 뺀 후 정렬하면^[21][84] 다음과 같이 됩니다.

$\ displaystyle \ frac { q _ \ text \H}}{T_{\text{H}}}}}}+{\frac {q_{\text{\text}C}}{T_{\text{C}}}}=0,}$

여기서 마이너스 기호는 시스템에서 열이 배출됨을 나타냅니다.이 관계는 상태 함수 S의 존재를 시사하며, 그 변화는 다음과 같이 정의되면 완전한 사이클 동안 특징적으로 사라진다.

${\displaystyle dS=syslogfrac {dq_{\text{rev}}}{T}},}$

(8)

여기서 첨자는 리버서블 공정을 나타냅니다.이 함수는 앞에서 설명한 시스템의 엔트로피에 해당합니다.재배열(8)은 엔트로피와 열의 가상의 무한소 준역성 요소의 관점에서 온도에 대한 공식을 제공한다.

${\displaystyle T=syslogfrac {dq_{\text{rev}}{dS}}.}$

(9)

엔트로피 S(E)가 에너지 E의 함수인 상수 체적 시스템의 경우, dE = dq_rev 및 (9)는 다음과 같다.

${\displaystyle T^{-1}=black {d}{dE}}S(E),}$

(10)

즉, 온도의 역수는 일정한 부피에서 에너지에 대한 엔트로피의 증가율이다.

통계역학으로부터의 정의

통계역학에서는 시스템의 기본 자유도에 따라 온도를 정의합니다.Eq.(10)는 온도의 정의 관계입니다.여기서 $엔트로피{\displaystyle }$S(\$displaystyle$S)는$$ 주어진 매크로 상태(마이크로캐논컬 앙상블에 지정된)에 있는 시스템의 마이크로 상태 수의 로그로 정의됩니다.

${\displaystyle S=k_{\mathrm {B}}\ln(W)}$

${\displaystyle {여기}_{}}$서$$K(\$displaystyle k_{\mathrm {B}})$는 볼츠만 상수이고 W는 시스템의 에너지 E(퇴행)를 가진 미세 상태의 수입니다.

온도가 다른 두 시스템을 순수하게 열 연결하면 열이 높은 온도 시스템에서 낮은 온도 시스템으로 흐릅니다. 열역학적으로 이는 열역학 제2법칙에 의해 이해됩니다.시스템 1에서 시스템 2로 에너지 ${\displaystyle \delta }$ E$(\displaystyle \Delta$ E$)$ 전달$$ 후 엔트로피의 총 변화는 다음과 같습니다.

$\displaystyle \Delta S=-(dS/dE)_{1}\cdot \Delta E+(dS/dE)_{2}\cdot \Delta E=\left({\frac {1}{}){T_{2}}-{\frac {1}{T_{1}}\right)\Delta E}$

따라서 > $(\$의 긍정적입니다.$T_{2}}:$

통계역학의 관점에서 복합시스템1 + 시스템2의 마이크로스테이트의 총수는 ${\displaystyle {N1\mathrm{}}_{}{}_{}}$ $({$입니다.이 로그의 합계(볼츠만 상수 곱하기)는 엔트로피의 합계이며, 따라서 고온에서 저온으로의 열 흐름은 e에 영향을 미칩니다.ntropy는 결과 매크로 상태에 더 많은 마이크로 상태가 있기 때문에 다른 시나리오보다 가능성이 더 높다(더 가능성이 더 높다).

단립자 통계에서 일반화된 온도

양자점처럼 입자가 적은 시스템으로도 온도의 정의를 확장할 수 있습니다.일반화된 온도는 단일/이중 점유 시스템을 가진 페르미온의 작은 시스템(10개 미만이라도) 간에 열 및 입자 교환의 경우 통계 역학에서 주어진 구성 공간 앙상블 대신 시간 앙상블을 고려하여 구한다.에르고딕성과 정통성의 ^[86]가설 하에서 얻은 유한 양자 그랜드 정준합은 ^[85]1/2 점유 ^[87]시스템의 평균 점유 시간 ${\displaystyle {1\mathrm{}}_{}}$ 1$(\displaystyle$ \$tau$ _${1})$과 ${\displaystyle {2\mathrm{}}_{}}$2(\$displaystyle \tau$ _${2})$의 비율로 일반화 온도를 표현할 수 있다.

${\displaystyle T=black {E-E_{\text}F}}\left(1+{\frac {3}{2)N}}\오른쪽)}{k_{\text{B}}\ln \left(2{\frac_{2}}{\tau_{1}}\right}}}}},$

여기서_F E는 페르미 에너지이다.이 일반화 온도는 N이 무한대가 되면 상온으로 변합니다.

마이너스 온도

절대 0을 참조하지 않는 경험적 온도 척도에서 음의 온도는 사용된 척도의 0점보다 1 낮습니다.예를 들어 드라이아이스의 승화 온도는 -78.5°C로 -109.3°^[88]F에 해당합니다.절대 켈빈 척도에서 이 온도는 194.6 K입니다.어떤 물체도 유한한 실행 가능한 과정에 의해 정확히 0K(이상적으로 가장 차가운 물체의 온도)로 만들 수 없습니다. 이것은 열역학 ^[89][90][91]제3법칙의 결과입니다.

물체의 국제 운동 이론 온도는 음의 값을 취할 수 없습니다.그러나 열역학적 온도 척도는 그렇게 제한되지 않습니다.

물질의 물체에 대해서는 미시적 자유도의 관점에서 개념적으로 정의될 수 있다. 즉, 입자 스핀, 서브시스템은 전신의 온도와는 다른 온도이다.신체가 내부 열역학적 평형 상태에 있을 때, 몸 전체와 하위 시스템의 온도는 동일해야 한다.두 온도는 외부에서 가해진 힘장을 통한 작업에 의해 에너지가 신체의 다른 부분과 별도로 서브시스템으로 전달되거나 서브시스템에서 전달될 수 있을 때 달라질 수 있습니다. 그러면 몸 전체가 내부 열역학적 평형 상태에 있지 않습니다.이러한 스핀 서브시스템이 도달할 수 있는 에너지의 상한이 있습니다.

서브시스템이 가상 열역학적 평형의 일시적인 상태라고 생각하면 열역학적 척도로 음의 온도를 얻을 수 있다.열역학적 온도는 내부 에너지와 관련하여 하위 시스템의 엔트로피 유도체의 역수입니다.서브시스템의 내부 에너지가 증가함에 따라 엔트로피는 일정 범위에서 증가하지만, 결국 최대치에 도달하고 가장 높은 에너지 상태가 채워지기 시작하면서 감소하기 시작합니다.에너지 함수로서의 엔트로피의 기울기가 0으로 감소하여 음으로 변하기 때문에 최대 엔트로피 지점에서 온도 함수는 특이점의 동작을 나타낸다.서브시스템의 엔트로피가 최대치에 도달하면 열역학적 온도가 양의 무한대로 이동하고 기울기가 음으로 변하면 음의 무한대로 전환됩니다.이러한 음의 온도는 어떤 양온도보다 뜨겁다.시간이 지남에 따라 서브시스템이 정온인 신체의 나머지 부분에 노출되면 에너지는 음온 서브시스템에서 정온 시스템으로 ^[92]열로 전달됩니다.운동 이론 온도는 그러한 서브시스템에 대해 정의되어 있지 않다.

예

다양한 척도의 온도 비교

	온도		피크 방사 파장[93] 흑체 방사선의
	켈빈	섭씨
절대 제로 (정의에 따라 정의됨)	0 K	−273.15 °C	정의할 수 없습니다.
블랙홀의 블랙홀 온도: 궁수자리 A*[94]라는 우리 은하의 중심	15 FK	-273.1499999999985°C	2.5×10km8(1.7AU)
최저 온도 달성한[95]	100pK	-273.14999999900°C	29000km
가장 춥다 보스-아인슈타인 응축수[96]	450 pK	-273.1499999955°C	6400km
1밀리켈빈 (정의에 따라 정의됨)	0.001 K	-273.149°C	2.89777m (라디오, FM 대역)[97]
우주 마이크로파 배경 (2013년 측정)	2.7260 K	- 270.424 °C	0.00106301 m (밀리파장 마이크로파)
물.삼중점 (정의에 따라 정의됨)	273.16 K	0.01°C	10608.3 nm (장파장 IR)
물 끓는점[A]	373.1339K	99.9839°C	7766.03 nm (중파장 IR)
철융점	1811 K	1538 °C	1600 nm (원적외선)
백열등[B]	2500 K	2,200°C 이하	1160 nm (근적외선)[C]
태양의 가시[D][98] 표면	5778 K	5505 °C	501.5 nm (녹색-청색 조명)
번개 채널[E]	28kK	28000°C	100 nm (원 자외선)
태양핵[E]	16 MK	1600만 °C	0.18 nm(X선)
열핵무기 (피크 온도)[E][99]	350 MK	3억 5천만 °C	8.3×10−3 nm (광선)
Sandia 국립 연구소' Z머신[E][100]	2 GK	20억 °C	1.4×10−3 nm (광선)[F]
고질량 별의 마지막[E][101] 날 핵	3 GK	30억 °C	1×10−3 nm (광선)
쌍성 중성자별[E][102] 시스템을 병합하는 중	350 GK	3,500억 °C	8×10−6 nm (광선)
상대론적 헤비 이온 충돌기[E][103]	1 TK	1조 °C	3×10−6 nm (광선)
CERN의 양성자와 핵충돌[E][104]	10 TK	10조 °C	3×10−7 nm (광선)
Universe 5.391×10s−44 빅뱅[E] 이후	1.417×1032 K (플랭크 온도)	1.417×1032 °C	1.616×10−27 nm (플랭크 길이)[105]

「 」를 참조해 주세요.

주 및 참고 자료

인용 인용 문헌 목록

• C.J. 애드킨스(1968/1983)Equilibrium Thermodynamics, (제1판 1968), 제3판 1983, 캠브리지 대학 출판부, 영국 캠브리지, ISBN 0-521-25445-0.
• H.A. 부크달(1966년)고전 열역학의 개념, 캠브리지 대학 출판부, 캠브리지.
• 제인스, E.T.(1965년)깁스 vs 볼츠만 엔트로피, 미국 물리학 저널, 33(5), 391~398.
• 미들턴, W.E.K. (1966년)온도계의 역사와 도량형에서의 사용, 볼티모어, 존스 홉킨스 프레스.
• Miller, J (2013). "Cooling molecules the optoelectric way". Physics Today. 66 (1): 12–14. Bibcode:2013PhT....66a..12M. doi:10.1063/pt.3.1840. Archived from the original on 2016-05-15. Retrieved 2013-07-25.
• 파팅턴, J.R. (1949년)물리 화학에 관한 고급 논문, 제1권, 기본 원리. The Properties of Gas, Longmans, Green & Co, London, 페이지 175–177.
• 피퍼드, A.B.(1957/1966)물리고등학생을 위한 고전 열역학 요소, 1957년 초판, 1966년 전재, 케임브리지 대학 출판부, 케임브리지 영국.
• 퀸, TJ(1983년)온도, 학술 출판사, 런던, ISBN 0-12-569680-9.
• Schoolley, J.F. (1986년)온도계, CRC 프레스, 보카 라톤, ISBN 0-8493-5833-7.
• 로버츠, J.K., 밀러, A.R.(1928/1960).열과 열역학, (초판 1928), 제5판, Blackie & Son Limited, Glasgow.
• 톰슨, W. (켈빈 경) (1848년)카르노의 열 동력 이론에 기초하고 레그놀트의 관측으로 계산한 절대 온도 측정 척도, Proc. 캠브, 필 Soc. (1843/1863) 1, 5번: 66-71.
• Thomson, W. (Lord Kelvin) (March 1851). "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam". Transactions of the Royal Society of Edinburgh. XX (part II): 261–268, 289–298.
• 트루즈델, C.A.(1980년)열역학의 비극적 역사, 1822–1854, 뉴욕 스프링어, ISBN 0-387-90403-4.
• 노스웨스트 주 츠초글(2000년)평형 및 정상 상태 열역학의 기초, 암스테르담 엘세비어, ISBN 0-444-50426-5.
• Zeppenfeld, M.; Englert, B.G.U.; Glöckner, R.; Prehn, A.; Mielenz, M.; Sommer, C.; van Buuren, L.D.; Motsch, M.; Rempe, G. (2012). "Sysiphus cooling of electrically trapped polyatomic molecules". Nature. 491 (7425): 570–573. arXiv:1208.0046. Bibcode:2012Natur.491..570Z. doi:10.1038/nature11595. PMID 23151480. S2CID 4367940.

추가 정보

• 장, 하석(2004년).발명의 온도: 측정 및 과학적 진보.옥스퍼드:옥스퍼드 대학 출판부ISBN 978-0-19-517127-3.
• 제만스키, 마크 월도(1964).온도가 매우 낮고 매우 높습니다.프린스턴, 뉴저지: 밴 노스트랜드.

외부 링크

• 지구 표면 온도의 현재 지도