가스

기체는 물질의 네 가지 기본 상태 중 하나입니다. 다른 것은 고체, 액체 및 플라즈마입니다.^[1]

순수한 기체는 개별 원자(예: 네온과 같은 비활성 기체), 한 종류의 원자(예: 산소)로 만들어진 원소 분자, 또는 다양한 원자(예: 이산화탄소)로 만들어진 화합물 분자로 구성될 수 있습니다. 공기와 같은 가스 혼합물에는 다양한 순수 가스가 포함되어 있습니다. 기체와 액체 및 고체를 구별하는 것은 개별 기체 입자의 방대한 분리입니다. 이 분리는 보통 무색의 기체를 인간 관찰자에게 보이지 않게 만듭니다.

물질의 기체 상태는 액체 상태와 플라스마 상태 사이에서 발생하며,^[2] 후자는 기체의 고온 경계를 제공합니다. 온도 척도의 하단을 제한하는 것은 점점 더 주목을 받고 있는 퇴행성 양자 가스입니다^[3].^[4] 매우 낮은 온도로 과냉각된 고밀도 원자 가스는 통계적 행동에 의해 보스 가스 또는 페르미 가스로 분류됩니다. 이러한 이국적인 물질 상태의 포괄적인 목록은 물질 상태 목록을 참조하십시오.

원소기체

STP에서 안정적인 이원자핵분자기체는 수소(H₂), 질소(N₂), 산소(O₂)와 불소(F₂), 염소(Cl₂) 등 두 가지 할로겐뿐입니다. 헬륨(He), 네온(Ne), 아르곤(Ar), 크립톤(Kr), 크세논(Xe), 라돈(Rn)과 같은 단원자 비활성 기체와 함께 묶으면 이러한 기체를 "원소 가스"라고 부릅니다.

어원

가스라는 단어는 17세기 초 플랑드르의 화학자 얀 침례 반 헬몬트에 의해 처음 사용되었습니다.^[5] 그는 공기 이외에 알려진 최초의 가스인 이산화탄소를 발견했습니다.^[6] 반 헬몬트의 단어는 단순히 고대 그리스 단어 χάος '혼돈'의 음성 표기인 것으로 보입니다. 네덜란드어의 g는 "loch"의 ch처럼 발음됩니다. 이 경우 반 헬몬트는 파라셀수스의 작품에서 처음으로 입증된 확립된 연금술 사용을 따랐을 뿐입니다. 파라셀수스의 용어에 따르면 혼돈은 '초미립수'와 같은 것을 의미했습니다.^[7]

다른 이야기는 반 헬몬트의 용어가 유령이나 영혼을 의미하는 "가스트"에서 유래했다는 것입니다.^[8] 그 이야기는 옥스포드 영어 사전의 편집자들에 의해 전혀 신뢰를 받지 못합니다.^[9] 이와는 대조적으로, 프랑스계 미국인 역사가 자크 바르준은 반 헬몬트가 발효로 인한 거품을 의미하는 독일어 게슈트에서 이 단어를 차용했다고 추측했습니다.^[10]

물리적 특성

대부분의 기체는 직접 관찰하기 어렵기 때문에 압력, 부피, 입자의 수(화학자들은 이들을 몰별로 그룹화), 온도 등 4가지 물리적 특성이나 거시적 특성을 이용하여 설명합니다. 이 네 가지 특징은 로버트 보일, 자크 찰스, 존 돌턴, 조셉 게이뤼삭, 아메데오 아보가드로 등의 과학자들에 의해 다양한 환경에서 다양한 기체에 대해 반복적으로 관찰되었습니다. 그들의 상세한 연구는 궁극적으로 이상 기체 법칙에 의해 표현되는 이러한 특성들 사이의 수학적 관계로 이어졌습니다(아래의 단순화된 모델 섹션 참조).

기체 입자는 서로 광범위하게 분리되어 있으며, 결과적으로 액체나 고체보다 분자 간 결합이 약합니다. 이러한 분자간 힘은 가스 입자들 사이의 정전기적 상호작용에서 비롯됩니다. 서로 다른 가스 입자의 비슷한 전하를 띤 영역은 서로를 끌어당기는 반면, 서로 다른 가스 입자의 반대 전하를 띤 영역은 서로를 끌어당깁니다. 영구적으로 전하를 띤 이온을 포함하는 가스를 플라스마라고 합니다. 극성 공유 결합을 가진 기체 화합물은 영구 전하 불균형을 포함하기 때문에 화합물의 순전하는 중성을 유지하지만 상대적으로 강한 분자 간 힘을 경험합니다. 분자의 비극성 공유 결합에 걸쳐 일시적이고 무작위로 유도된 전하가 존재하고 이들에 의해 유발된 정전기 상호작용을 반데르발스 힘이라고 합니다. 이러한 분자간 힘의 상호작용은 각 기체에 고유한 많은 물리적 특성을 결정하는 물질 내에서 다양합니다.^[11][12] 이온결합과 공유결합에 의해 형성된 화합물의 끓는점을 비교하면 이러한 결론을 얻을 수 있습니다.^[13]

다른 물질 상태에 비해 가스는 밀도와 점도가 낮습니다. 압력과 온도는 특정 부피 내에서 입자에 영향을 미칩니다. 이러한 입자 분리 및 속도의 변화를 압축성이라고 합니다. 이러한 입자 분리 및 크기는 다음 굴절률 목록에서 볼 수 있듯이 기체의 광학적 특성에 영향을 미칩니다. 마지막으로, 가스 입자들은 그들 자신을 모든 용기에 균질하게 분배하기 위해 서로 흩어지거나 확산됩니다.

기체의 거시적 관점

기체를 관찰할 때 일반적으로 기준 또는 길이 척도의 프레임을 지정합니다. 더 큰 길이 척도는 가스의 거시적 또는 전체적 관점에 해당합니다. 이 영역(부피라고 함)은 가스 입자를 많이 샘플링할 수 있을 정도의 크기여야 합니다. 이 표본 크기에 대한 결과적인 통계 분석은 해당 지역 내의 모든 가스 입자의 "평균" 행동(즉, 속도, 온도 또는 압력)을 생성합니다. 반대로 길이 척도가 작으면 미시적 또는 입자적 관점에 해당합니다.

거시적으로 측정된 가스 특성은 가스 입자 자체(속도, 압력 또는 온도) 또는 주변 환경(부피)에 대한 것입니다. 예를 들어, 로버트 보일은 그의 경력의 작은 부분을 위해 공압 화학을 공부했습니다. 그의 실험 중 하나는 기체의 압력과 부피의 거시적 특성과 관련이 있습니다. 그의 실험은 J. Boyle이라는 글자 모양의 시험관처럼 보이는 J-튜브 압력계를 사용했습니다. J. Boyle은 수은 기둥으로 시험관의 닫힌 끝에 불활성 가스를 가두어 입자의 수와 온도를 일정하게 만들었습니다. 그는 기체의 압력이 증가하면, 컬럼에 수은을 더 많이 첨가함으로써 갇힌 기체의 부피가 감소하는 것을 관찰했습니다(이것을 역관계라고 합니다). 또한 Boyle이 각 관측치의 압력과 부피를 곱했을 때 생성물은 일정했습니다. 이 관계는 보일이 관찰한 모든 가스에 대해 유지되었으며(PV=k), 이 분야에서 그의 업적을 기리기 위해 명명된 법칙으로 이어졌습니다.

가스 특성을 분석하는 데 사용할 수 있는 많은 수학적 도구가 있습니다. 기체가 극단적인 조건에 노출됨에 따라 이 도구들은 비자성 흐름에 대한 오일러 방정식에서 나비에로 더 복잡해집니다.–점근 효과를 완전히 설명하는 스톡 방정식^[14]. 이러한 방정식은 해당 가스 시스템의 조건에 맞게 조정됩니다. 보일의 실험실 장비는 대수학을 사용하여 그의 분석 결과를 얻을 수 있게 해주었습니다. 그의 결과는 그가 가스들이 "이상적인" 방식으로 행동하는 비교적 낮은 압력의 상황에서 가스를 연구하고 있었기 때문에 가능했습니다. 이러한 이상적인 관계는 사용 중인 재료의 다양한 비행 조건에 대한 안전 계산에 적용됩니다. 오늘날 사용되는 첨단 기술 장비는 가스가 더 이상 "이상적인" 방식으로 작동하지 않는 보다 이국적인 작동 환경을 안전하게 탐색할 수 있도록 설계되었습니다. 통계학과 다변수 미적분학을 포함한 이 고급 수학은 우주 차량 재진입과 같은 복잡한 동적 상황에 대한 해결책을 가능하게 합니다. 이 적재 조건에서 재료 특성이 적절한지 확인하기 위해 촬영된 우주왕복선 재진입체의 분석이 그 예입니다. 이 비행 체제에서는 가스가 더 이상 이상 이상적으로 작동하지 않습니다.

압력.

식에서 압력을 나타내는 기호는 "p" 또는 "P"로, SI 단위의 파스칼입니다.

가스 용기를 설명할 때 압력(또는 절대 압력)이란 가스가 용기 표면에 작용하는 단위 면적당 평균 힘을 말합니다. 이 부피 내에서 가스 입자가 용기와 충돌할 때까지 직선으로 이동하는 것을 시각화하는 것이 더 쉬운 경우가 있습니다(기사 상단의 그림 참조). 이 충돌 동안 기체 입자가 용기 안으로 전달하는 힘은 입자의 운동량 변화입니다.^[15] 충돌 중에는 속도의 정상적인 구성 요소만 바뀝니다. 벽에 평행하게 이동하는 입자는 운동량을 바꾸지 않습니다. 따라서 표면의 평균 힘은 이러한 모든 가스 입자 충돌로 인한 선운동량의 평균 변화여야 합니다.

압력은 용기 벽에 충격을 주는 입자가 작용하는 모든 정상적인 힘 성분의 합을 벽의 표면적으로 나눈 값입니다.

온도

방정식에서 온도를 나타내는 기호는 켈빈의 SI 단위를 갖는 T입니다.

기체 입자의 속도는 절대 온도에 비례합니다. 갇힌 기체 입자가 극도로 차가운 질소를 첨가해 속도를 줄이면 영상 속 풍선의 부피가 줄어들게 됩니다. 모든 물리계의 온도는 [기체]계를 구성하는 입자(분자 및 원자)의 운동과 관련이 있습니다.^[16] 온도는 통계 역학에서 분자에 저장된 평균 운동 에너지의 척도입니다. 이 에너지를 저장하는 방법은 분자 자체의 자유도(에너지 모드)에 의해 결정됩니다. 기체나 액체(흡열 과정)에 추가된 열(운동) 에너지는 병진운동, 회전운동, 진동운동을 일으킵니다. 반면에 고체는 결정 격자 구조가 병진 운동과 회전 운동을 모두 막아주기 때문에 추가적인 진동 모드를 자극함으로써 내부 에너지를 증가시킬 수 있을 뿐입니다. 이러한 가열된 가스 분자는 평균 또는 평균 속도가 높을수록 속도 범위(속도의 넓은 분포)가 커집니다. 이 분포의 분산은 다른 입자와의 반복적인 충돌로 인해 개별 입자의 속도가 일정하게 변하기 때문입니다. 속도 범위는 맥스웰-볼츠만 분포로 설명할 수 있습니다. 이 분포를 사용하면 고려 중인 입자 시스템에 대해 열역학적 평형에 가까운 이상적인 가스를 의미합니다.

비부피

식에서 특정 부피를 나타내는 기호는 킬로그램당 입방 미터의 SI 단위인 "v"입니다.

방정식에서 부피를 나타내는 데 사용되는 기호는 SI 단위가 입방 미터인 "V"입니다.

열역학적 분석을 수행할 때 일반적으로 집중적이고 광범위한 특성을 말합니다. 기체의 양에 의존하는 성질(질량 또는 부피)을 광범위한 성질이라고 하고, 기체의 양에 의존하지 않는 성질을 집중적인 성질이라고 합니다. 비부피는 평형 상태에 있는 계 전체에서 동일한 기체의 질량 단위가 차지하는 부피의 비율이기 때문에 집중 특성의 한 예입니다.^[17] 1000개의 원자는 어떤 온도와 압력에서도 다른 1000개의 원자와 같은 공간을 차지합니다. 이 개념은 기체에 비해 압축성이 없는 철과 같은 고체의 경우 시각화하기가 더 쉽습니다. 그러나 볼륨 자체(특정하지 않음)는 광범위한 속성입니다.

밀도

식에서 밀도를 나타내기 위해 사용되는 기호는 ρ(rho)로 세제곱미터당 킬로그램의 SI 단위입니다. 이 용어는 특정 부피의 역수입니다.

기체 분자는 용기 안에서 자유롭게 움직일 수 있기 때문에 일반적으로 질량은 밀도에 의해 특징지어집니다. 밀도는 물질의 단위 부피당 질량의 양 또는 특정 부피의 역수입니다. 기체의 경우 압력이나 부피에 의해 제약을 받을 때 입자가 자유롭게 함께 더 가까이 이동하기 때문에 밀도가 광범위하게 변할 수 있습니다. 이러한 밀도 변화를 압축성이라고 합니다. 압력과 온도와 마찬가지로 밀도는 기체의 상태 변수이며 어떤 과정에서도 밀도의 변화는 열역학 법칙에 의해 지배됩니다. 정전기 가스의 경우 밀도는 전체 용기에서 동일합니다. 따라서 밀도는 스칼라 양입니다. 밀도는 고정된 기체 덩어리가 갇혀 있는 용기의 크기에 반비례한다는 것을 운동이론으로 증명할 수 있습니다. 고정된 질량의 경우 부피가 커짐에 따라 밀도가 감소합니다.

기체의 미시적인 모습

만약 어떤 사람이 강력한 현미경으로 기체를 관찰할 수 있다면, 어떤 확실한 모양이나 부피가 없는 입자들의 집합체가 다소 무작위적인 움직임을 보이는 것을 볼 수 있을 것입니다. 이 가스 입자들은 다른 입자나 용기의 측면과 충돌할 때만 방향을 바꿉니다. 기체에 대한 이 미시적인 관점은 통계역학에 의해 잘 설명되지만, 많은 다른 이론에 의해 설명될 수 있습니다. 이러한 충돌이 완벽하게 탄성이라고 가정하는 기체의 운동 이론은 인력과 반발력의 분자 간 힘을 설명하지 않습니다.

기체운동론

운동 이론은 기체의 분자 구성과 운동을 고려하여 거시적인 특성에 대한 통찰력을 제공합니다. 운동량과 운동 에너지의 정의를 시작으로,^[18] 정육면체의 운동량과 기하학적 관계의 보존을 사용하여 온도와 압력의 거시적인 계 특성을 분자당 운동 에너지의 미시적 특성과 연관시킬 수 있습니다. 이론은 이 두 특성에 대한 평균 값을 제공합니다.

기체의 운동 이론은 계(고려되는 기체 입자의 집합)가 온도 변화에 어떻게 반응하는지, 그에 상응하는 운동 에너지 변화를 설명하는 데 도움이 될 수 있습니다.

예: 고정된 수의 기체 입자를 포함하는 고정된 크기(일정한 부피)의 밀폐된 용기가 있다고 상상해보세요. 절대영도(원자나 분자가 열에너지를 갖지 않는 이론적 온도, 즉 움직이지 않거나 진동하지 않는 온도)에서 시작해서 용기를 가열함으로써 계에 에너지를 추가하기 시작합니다. 에너지가 내부의 입자로 전달될 수 있도록 말입니다. 일단 내부 에너지가 0점 에너지 이상이 되면, 열 에너지라고도 알려진 운동 에너지가 0이 아닌 기체 입자들이 용기 주위를 움직이기 시작할 것입니다. 상자가 더 가열됨에 따라(에너지가 더 많이 추가됨에 따라) 개별 입자는 시스템의 총 내부 에너지가 증가함에 따라 평균 속도가 증가합니다. 모든 입자의 평균 속도가 높을수록 입자와 용기 사이뿐만 아니라 입자 자체 사이에서 충돌이 발생하는 속도(즉, 시간 단위당 더 많은 수의 충돌)가 증가합니다.

거시적이고 측정 가능한 압력의 양은 개별 분자가 작은 힘을 발휘하는 표면과의 이러한 미세 입자 충돌의 직접적인 결과이며, 각각은 특정 영역 내에서 가해지는 총 힘에 기여합니다. (위 섹션 "기체의 거시적 관점"의 "압력"을 읽어 보십시오.)

마찬가지로, 거시적으로 측정 가능한 온도의 양은 입자가 보여주는 전반적인 운동 에너지, 즉 운동 에너지의 양을 정량화한 것입니다. (위 섹션 "기체의 거시적 관점"에서 "온도"를 읽어 보십시오.)

열운동과 통계역학

기체의 운동 이론에서 운동 에너지는 순수하게 계 내 입자의 속도 분포에 따른 선형 번역으로 구성된다고 가정합니다. 그러나 실제 기체 및 기타 실제 물질에서는 점질량과 유사하게 작용하는 단일 원자에 비해 분자의 구조가 더 복잡하기 때문에 계의 운동 에너지를 정의하는 운동이 단순 선형 번역보다 훨씬 더 복잡합니다. 실제 열역학계에서 양자 현상은 열 운동을 결정하는 데 큰 역할을 합니다. 분자의 무작위 열 운동(운동 에너지)은 번역, 회전 및 진동을 포함한 가능한 운동의 유한 집합입니다. 가능한 운동의 이 유한한 범위는 시스템의 유한한 분자 집합과 함께 시스템 내의 유한한 수의 미세 상태로 이어집니다. 우리는 모든 미세 상태 집합을 앙상블이라고 부릅니다. 원자 시스템이나 분자 시스템에 따라, 우리는 잠재적으로 세 가지 다른 종류의 앙상블을 가질 수 있습니다: 마이크로캐노니컬 앙상블, 캐노니컬 앙상블 또는 그랜드 캐노니컬 앙상블. 앙상블 내에서 미시 상태의 특정 조합은 시스템의 거시 상태(온도, 압력, 에너지 등)를 진정으로 정의하는 방법입니다. 그러기 위해서는 먼저 파티션 함수를 사용하여 모든 마이크로 상태를 계산해야 합니다. 통계역학과 분배함수의 사용은 모든 물리화학에서 중요한 도구입니다. 왜냐하면 그것은 온도, 압력, 열용량, 내부에너지, 엔탈피, 엔트로피와 같은 우리가 측정할 수 있는 거시적인 변수들과 계의 미시적인 상태 사이의 연결의 열쇠이기 때문입니다. 몇 가지 예를 들어보겠습니다. (읽기: 파티션 함수 의미 및 의의)

분할 함수를 사용하여 분자 또는 분자 시스템의 에너지를 찾는 것은 때때로 계산을 크게 단순화하는 등분할 정리에 의해 근사화될 수 있습니다. 그러나 이 방법은 모든 분자 자유도가 동일하게 채워지므로 분자 내 에너지 저장에 동일하게 활용된다고 가정합니다. 그것은 내부 에너지가 온도에 따라 선형적으로 변한다는 것을 의미하지만, 그렇지 않습니다. 이는 낮은 온도에서 특정 자유도가 도달할 수 없기 때문에(일명 "동결") 열 용량이 온도에 따라 변한다는 사실을 무시합니다. 분자의 내부 에너지가 증가함에 따라 추가적인 자유도 내에서 에너지를 저장하는 능력도 증가합니다. 에너지를 유지할 수 있는 자유도가 증가함에 따라 물질의 몰 열용량이 증가합니다.^[19]

브라운 운동

브라운 운동은 유체에 매달린 입자의 무작위 운동을 설명하는 데 사용되는 수학적 모델입니다. 분홍색과 녹색 입자를 사용한 가스 입자 애니메이션은 이러한 행동이 가스 밖으로 확산되는 결과(엔트로피)를 보여줍니다. 이러한 사건들은 입자 이론으로도 설명됩니다.

개별 기체 입자(원자 또는 분자)를 관찰하는 것은 현재 기술의 한계(또는 그 이상)에 있기 때문에 이론적 계산만으로 어떻게 움직이는지에 대한 제안을 할 수 있지만 브라운 운동은 많은 기체 분자의 마찰력으로 인해 부드러운 드래그를 수반하기 때문에 브라운 운동과 다른 운동입니다. 개별(또는 여러) 가스 분자와 입자의 강력한 충돌에 의해 작동합니다. 따라서 입자(일반적으로 수백만 또는 수십억 개의 원자로 구성됨)는 들쭉날쭉한 경로로 움직이지만 개별 가스 분자를 조사했을 때 예상만큼 들쭉날쭉하지는 않습니다.

분자간 힘 - 실제기체와 이상기체의 주요 차이

두 개 이상의 분자 또는 원자 사이의 힘을 인력 또는 반발력이라고 합니다. 분자 간 힘은 분자가 서로 물리적으로 근접할 때 경험합니다. 이러한 힘은 분자 시스템을 적절하게 모델링하는 데 매우 중요하며, 이는 어떤 시스템에서도 분자의 미시적 행동을 정확하게 예측하기 위해서는 물리적 조건의 광범위한 변화에 걸쳐 기체(및 액체)의 물리적 특성을 정확하게 예측하는 데 필요합니다.

물리학 전반에 걸쳐 가장 두드러진 분자간 힘 중 하나인 물리화학 연구에서 비롯된 것이 반데르발스 힘입니다. 반데르발스 힘은 점도, 유속 및 기체 역학과 같은 유체의 거의 모든 물리적 특성을 결정하는 데 중요한 역할을 합니다(물리적 특성 섹션 참조). "진짜 가스"를 모델링하는 것이 "이상적인 가스"보다 수학적으로 어려운 이유는 가스 분자 사이의 반데르발스 상호작용 때문입니다. 이러한 근접 의존적 힘을 무시하면 실제 기체를 이상 기체처럼 취급할 수 있어 계산이 크게 간단해집니다.

두 기체 분자 사이의 분자 간 인력과 반발력은 그들 사이의 거리에 따라 달라집니다. 결합된 인력과 반발력은 분자 시스템의 전위 에너지를 설명하는 모든 원자간 전위 중 가장 광범위하게 연구된 것 중 하나인 Lennard-Jones 전위에 의해 잘 모델링됩니다. 분자 사이의 Lennard-Jones 퍼텐셜은 런던 분산력에 의한 장거리 인력과 전자-전자 교환 상호작용에 의한 단거리 반발력(Pauli exclusion principle)으로 구분될 수 있습니다.

두 분자가 상대적으로 멀리 떨어져 있을 때(높은 위치 에너지를 가지고 있음을 의미함) 약한 인력을 경험하여 서로를 향해 움직이게 하여 위치 에너지를 낮춥니다. 그러나 분자가 너무 멀리 떨어져 있다면, 그들은 아무런 의미도 없는 인력을 경험하지 못할 것입니다. 또한 분자가 너무 가까이 접근하면 충돌하고 인력보다 훨씬 강한 반발력(하드구로 모델링)을 경험하기 때문에 근접으로 인한 인력은 무시됩니다.

너무 멀지도 않고 너무 가깝지도 않은 거리에서 두 분자가 서로 가까워질 때, 그들의 인력은 그들의 위치 에너지의 크기가 증가함에 따라 증가하고, 그들의 전체 내부 에너지는 낮아집니다.^[20] 분자가 더 가까워지는 인력은 물리적으로 가까워지는 데 걸리는 시간 동안 분자가 근접한 상태를 유지할 때만 발생할 수 있습니다. 따라서 분자가 저속으로 움직일 때 인력이 가장 강합니다. 이것은 가스 온도가 낮을 때 분자 사이의 인력이 상당하다는 것을 의미합니다. 그러나 이 차가운 가스를 등온적으로 작은 부피로 압축하여 분자를 근접하게 만들고 압력을 높이면 충돌이 일어나는 속도가 크게 증가하기 때문에 반발력이 인력 위에 우세하기 시작할 것입니다. 따라서 낮은 온도와 낮은 압력에서 인력은 지배적인 분자 간 상호작용입니다.

만약 두 분자가 교차하지 않는 경로를 따라 임의의 방향으로 빠른 속도로 움직이고 있다면, 그들은 런던-분산의 매력적인 힘에 의해 영향을 받을 만큼 가까운 곳에서 충분한 시간을 보내지 않을 것입니다. 두 분자가 충돌하면 너무 빨리 움직이고 운동 에너지는 어떤 매력적인 위치 에너지보다 훨씬 크므로 충돌할 때만 반발력을 경험하게 됩니다. 따라서 분자 사이의 인력은 고속으로 인해 고온에서 무시될 수 있습니다. 고온 및 고압에서 반발력은 분자 간 상호 작용이 지배적입니다.

이상적인 가스 모델에서 다음과 같은 일반화를 통해 이러한 인력과 반발, 실제 가스를 유발하는 위와 같은 효과를 설명합니다.^[21]

• 낮은 온도와 낮은 압력에서 실제 가스가 차지하는 부피는 이상적인 가스 법칙에 의해 예측된 부피보다 작습니다.
• 고온 및 고압에서 실제 기체가 차지하는 부피는 이상 기체 법칙에 의해 예측된 부피보다 큽니다.

수학적 모형

(기체에 대한) 상태 방정식은 기체의 상태 특성을 대략적으로 설명하거나 예측하는 데 사용되는 수학적 모델입니다. 현재 모든 조건에서 모든 기체의 특성을 정확하게 예측하는 상태 방정식은 단 하나도 없습니다. 따라서 특정 온도와 압력 범위의 기체에 대해 훨씬 더 정확한 상태 방정식이 많이 개발되었습니다. 가장 널리 논의되는 "가스 모델"은 "완벽한 가스", "이상적인 가스" 및 "진짜 가스"입니다. 이러한 각 모델에는 주어진 열역학 시스템의 분석을 용이하게 하기 위한 고유한 가정이 있습니다.^[22] 각 연속 모델은 적용되는 적용 범위의 온도 범위를 확장합니다.

이상적이고 완벽한 가스

이상적이거나 완벽한 기체에 대한 상태 방정식은 이상적인 기체 법칙이고 다음과 같습니다.

${\displaystyle PV=nRT,}$

여기서 P는 압력, V는 부피, n은 가스의 양(몰 단위), R은 보편 가스 상수, 8.314 J/(mol K), T는 온도입니다. 이런 식으로 쓰여지면 분자의 수 n을 강조하기 때문에 "화학자의 버전"이라고 불리기도 합니다. 다음과 같이 쓸 수도 있습니다.

${\displaystyle P=\rhoR_{s}T,}$

$여기$서 ${\displaystyle {Rs}_{}}$ ${\displaystyle R_{s}}$는 특정 가스에 대한 특정 가스 상수(단위 J/(kg K)이며 ρ = m/V는 밀도입니다. 이 표기법은 "가스 역학자의" 버전으로, 화학 반응 없이 가속을 수반하는 가스 흐름의 모델링에 더 실용적입니다.

이상적인 기체 법칙은 기체의 비열을 가정하지 않습니다. 가장 일반적인 경우, 비열은 온도와 압력의 함수입니다. 특정 응용 분야에서 압력 의존성이 무시될 경우(온도 의존성도 무시될 수 있음), 때로는 정확한 가정이 과학 저자 및/또는 분야에 따라 다를 수 있지만 가스가 완벽한 가스라고 할 수 있습니다.

이상 기체의 경우, 이상 기체 법칙은 비열에 대한 제한 없이 적용됩니다. 이상적인 가스는 압축률 Z가 1로 설정되어 있다는 가정하에 이 공압비가 일정하게 유지된다는 가정하에 단순화된 "실제 가스"입니다. 압축률 계수가 1이면 4개의 상태 변수가 이상 기체 법칙을 따라야 합니다.

이 근사는 실제 솔루션이 어디에 있어야 하는지에 대한 "볼-파크" 범위를 생성하는 데 더 간단한 모델을 사용할 수 있지만 엔지니어링 분야의 응용 프로그램에 더 적합합니다. "이상적인 가스 근사치"가 적합한 예로는 제트 엔진의 연소실 내부가 있습니다.^[23] 방출량 계산을 위해 기본 반응과 화학적 해리를 유지하는 것도 유용할 수 있습니다.

리얼가스

아래에 나열된 각 가정은 문제 해결의 복잡성을 가중시킵니다. 압력이 증가함에 따라 기체의 밀도가 증가함에 따라 분자 간 힘이 기체 행동에 더 큰 역할을 하게 되고, 이로 인해 이상적인 기체 법칙은 더 이상 "합리적인" 결과를 제공하지 않게 됩니다. 엔진 온도 범위의 상단(예: 연소기 섹션 – 1300K)에서 복합 연료 입자는 회전 및 진동을 통해 내부 에너지를 흡수하여 특정 열이 이원자 분자 및 비활성 가스의 열과 달라집니다. 그 온도의 두 배 이상에서 가스 입자의 전자 여기 및 해리가 발생하기 시작하여 압력이 더 많은 수의 입자(가스에서 플라즈마로의 전이)로 조정됩니다.^[24] 마지막으로, 모든 열역학적 과정은 고정된 분포에 따라 속도가 변하는 균일한 기체를 설명하는 것으로 추정되었습니다. 비평형 상황을 사용한다는 것은 솔루션을 활성화하기 위해 흐름 필드를 어떤 방식으로든 특성화해야 한다는 것을 의미합니다. 이상 기체 법칙의 경계를 확장하려는 첫 번째 시도 중 하나는 방정식을 pV = 상수로 조정한 다음 비열비, γ와 같은 다른 값을 통해 변화시킴으로써 다양한 열역학 과정에 대한 적용 범위를 포함하는 것이었습니다.

실제 가스 효과에는 더 큰 범위의 가스 거동을 설명하기 위해 수행된 조정이 포함됩니다.

• 압축성 효과(Z는 1.0과 다를 수 있음)
• 가변 열 용량(온도에 따라 특정 열이 다름)
• 반데르발스 힘(압축성과 관련하여 다른 상태 방정식을 대체할 수 있음)
• 비평형 열역학적 효과
• 분자 해리 및 가변 조성의 기본 반응에 대한 문제.

대부분의 애플리케이션에서 이러한 상세한 분석은 과도합니다. 실제 가스 효과가 상당한 영향을 미치는 예로는 극도로 높은 온도와 압력이 존재하는 우주왕복선 재진입이나 1990년 르두부트 화산 폭발의 이미지와 같은 지질학적 사건 동안 생성된 가스가 있습니다.

영구가스

영구 가스는 임계 온도가 인간이 거주할 수 있는 정상 온도 범위 미만이므로 이 범위 내에서 압력으로 액화할 수 없는 가스에 사용되는 용어입니다. 역사적으로 이러한 가스는 액화가 불가능하고 따라서 영구적으로 가스 상태를 유지할 것으로 생각되었습니다. 이 용어는 주변 온도 저장 및 고압에서의 가스 수송과 관련이 있습니다.^[25]

역사적 연구

보일의 법칙

보일의 법칙은 아마도 상태 방정식의 첫 번째 표현이었을 것입니다. 1662년 로버트 보일은 J자 모양의 유리관을 사용하여 일련의 실험을 수행했으며, 이 유리관은 한쪽 끝에 밀봉되어 있습니다. 수은을 튜브에 첨가하여 튜브의 짧고 밀봉된 끝에 고정된 양의 공기를 가두었습니다. 그런 다음 튜브에 추가 수은을 첨가하면서 가스의 부피를 주의 깊게 측정했습니다. 가스의 압력은 튜브의 짧은 끝에 있는 수은 수준과 길고 열린 끝에 있는 수은 수준의 차이에 의해 결정될 수 있습니다. 보일의 장비의 이미지는 보일이 기체를 연구하는 동안 사용했던 이국적인 도구들 중 일부를 보여줍니다.

이러한 실험을 통해 보일은 일정한 온도로 유지된 기체가 가하는 압력이 기체의 부피에 반비례한다는 사실에 주목했습니다.^[26] 예를 들어, 부피가 절반으로 줄어들면 압력이 두 배로 증가하고, 부피가 두 배로 늘어나면 압력이 절반으로 감소합니다. 압력과 부피 사이의 역 관계가 주어지면, 온도가 일정한 한 압력(P)과 부피(V)의 곱은 주어진 질량의 제한된 기체에 대한 상수(k)입니다. 공식으로 명시하면 다음과 같습니다.

${\displaystyle PV=k}$

고정된 양의 기체의 전후 부피와 압력은 상수 k와 같으므로 다음과 같은 방정식으로 연관될 수 있습니다.

${\displaystyle \qquad P_{1}V_{1}=P_{2}V_{2}.}$

찰스의 법칙

1787년, 프랑스의 물리학자이자 풍선 선구자인 자크 샤를은 산소, 질소, 수소, 이산화탄소, 그리고 공기가 같은 80 켈빈의 간격에 걸쳐 같은 정도로 팽창한다는 것을 발견했습니다. 그는 압력이 일정한 이상적인 기체의 경우 부피는 온도에 정비례한다고 언급했습니다.

${\displaystyle {\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}$

Gay-Lussac's law

1802년 조셉 루이스 게이뤼삭은 유사하지만 더 광범위한 실험 결과를 발표했습니다.^[27] 게이뤼삭은 찰스의 초기 업적에 대해 그를 기리기 위해 그 법의 이름을 붙였습니다. 게이뤼삭 자신도 1809년에 발견한 압력을 기술한 법으로 인정받고 있습니다. 이상 기체가 용기의 측면에 가하는 압력은 온도에 비례한다고 명시하고 있습니다.

${\displaystyle {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}\,}$

Avogadro's law

1811년 아메데오 아보가드로는 같은 부피의 순수한 기체가 같은 수의 입자를 함유하고 있음을 확인했습니다. 그의 이론은 1858년 또 다른 이탈리아 화학자 스타니슬라오 칸니차로가 비이상적인 예외를 설명할 수 있을 때까지 일반적으로 받아들여지지 않았습니다. 한 세기 전 가스에 대한 그의 연구를 위해, 그의 이름을 붙인 물리 상수(아보가드로 상수)는 원소 탄소-12 1몰당 원자의 개수(6.022×10몰²³⁻¹)입니다. 표준 온도와 압력(이상적인 기체 법칙)에서 이 특정한 수의 기체 입자는 22.40리터를 차지하며, 이를 몰 부피라고 합니다.

아보가드로의 법칙에 따르면 이상기체가 차지하는 부피는 부피 속의 물질의 양에 비례합니다. 이는 STP에서 22.4 dm³/mol(몰당 리터)인 기체의 몰 부피를 발생시킵니다. 관계는 다음과 같습니다.

여기서 n은 기체의 물질의 양(분자의 수를 아보가드로 상수로 나눈 값)입니다.

돌턴의 법칙

1801년, 존 돌턴은 이상적인 기체 법칙 관계를 가진 그의 연구로부터 편압의 법칙을 발표했습니다. 반응하지 않는 기체의 혼합물의 압력은 모든 구성 기체의 압력의 합과 같습니다. 수학적으로 이것은 n종에 대해 다음과 같이 나타낼 수 있습니다.

압력 = 압력 + 압력 + ... + 압력_n

돌턴의 저널 이미지는 그가 자신이 따라온 길을 기록하기 위해 속기로 사용한 공생을 묘사합니다. 반응성이 없는 "탄성 유체"(기체)를 혼합할 때 그가 관찰한 주요 저널에는 다음과 같은 것들이 있었습니다.^[28]

• 액체와 달리 더 무거운 기체는 혼합 시 바닥으로 떠내려가지 않았습니다.
• 가스 입자의 정체성은 최종 압력을 결정하는 데 아무런 역할을 하지 않았습니다(그들은 그들의 크기가 무시할 수 있는 것처럼 행동했습니다).

특별주제

압축성

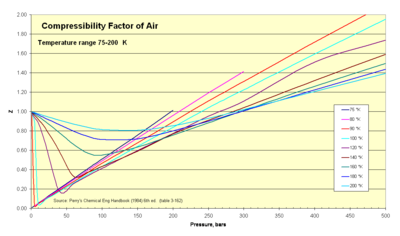
열역학자들은 이 계수(Z)를 사용하여 실제 가스의 압축성 효과를 설명하기 위해 이상적인 가스 방정식을 변경합니다. 이 인자는 실제 볼륨과 이상적인 특정 볼륨의 비율을 나타냅니다. 설계 목적으로 이상적인 가스 법칙의 유용한 범위를 확장하기 위해 "지문 요인" 또는 수정이라고도 합니다. 일반적으로 이 Z 값은 통일성에 매우 가깝습니다. 압축률 이미지는 매우 추운 온도 범위에서 Z가 어떻게 변화하는지 보여줍니다.

레이놀즈 수

유체역학에서 레이놀즈 수는 점성력(μ/L)에 대한 관성력(v ρ)의 비율입니다. 이는 유체 역학에서 가장 중요한 무차원 수치 중 하나이며, 일반적으로 다른 무차원 수치와 함께 동적 유사성을 결정하는 기준을 제공하는 데 사용됩니다. 이와 같이, 레이놀즈 수는 모델링 결과(설계)와 본격적인 실제 조건 사이의 연결고리를 제공합니다. 또한 흐름을 특성화하는 데 사용할 수 있습니다.

점성

물리적 성질인 점성은 인접한 분자들이 서로 얼마나 잘 붙는지를 나타내는 척도입니다. 고체는 이러한 끈적한 분자간 힘의 세기로 인해 전단력을 견딜 수 있습니다. 유사한 부하를 받으면 유체가 지속적으로 변형됩니다. 기체는 액체보다 점도가 낮지만 여전히 관찰 가능한 특성입니다. 만약 기체에 점도가 없다면, 그것들은 날개의 표면에 달라붙지 않고 경계층을 형성할 것입니다. 슐리렌 이미지의 델타 날개에 대한 연구는 가스 입자가 서로 달라붙는 것을 보여줍니다(경계층 섹션 참조).

난류

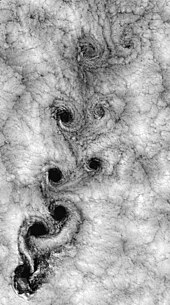
유체 역학에서 난류 또는 난류 흐름은 혼란스럽고 확률적인 특성 변화를 특징으로 하는 흐름 체계입니다. 여기에는 낮은 운동량 확산, 높은 운동량 대류, 그리고 시공간에서의 압력과 속도의 급격한 변화가 포함됩니다. 로빈슨 크루소 제도 주변의 위성 날씨 전망은 한 가지 예를 보여줍니다.

경계층

입자들은 사실상 물체의 표면에 "붙어 붙게" 될 것입니다. 이 입자층을 경계층이라고 합니다. 물체의 표면에서는 표면의 마찰로 인해 본질적으로 정적입니다. 경계층이 있는 물체는 물체에 접근할 때 나머지 분자들이 "보는" 물체의 새로운 모양입니다. 이 경계층은 표면에서 분리되어 본질적으로 새로운 표면을 생성하고 흐름 경로를 완전히 변경할 수 있습니다. 이것의 고전적인 예는 정지하는 에어포일입니다. 델타 날개 이미지는 가스가 선행 가장자리를 따라 오른쪽에서 왼쪽으로 흐를 때 경계층이 두꺼워지는 것을 명확하게 보여줍니다.

최대 엔트로피 원리

총 자유도 수가 무한대에 가까워지면 시스템은 가장 높은 다중도에 해당하는 매크로 상태에서 발견됩니다. 이 원리를 설명하기 위해 냉동 금속 바의 피부 온도를 관찰합니다. 피부 온도의 열화상 이미지를 사용하여 표면의 온도 분포를 기록합니다. 온도에 대한 이러한 초기 관찰은 "미세 상태"를 나타냅니다. 미래의 시간에 피부 온도를 두 번째로 관찰하면 두 번째 미세 상태가 생성됩니다. 이 관찰 과정을 계속함으로써 바 표면의 열 이력을 설명하는 일련의 미세 상태를 생성할 수 있습니다. 이 일련의 역사적인 미시 상태의 특성화는 이들을 모두 단일 그룹으로 성공적으로 분류하는 거시 상태를 선택함으로써 가능합니다.

열역학적 평형

에너지 전달이 시스템에서 멈추면 이 조건을 열역학적 평형이라고 합니다. 일반적으로 이 조건은 시스템과 주변 환경이 동일한 온도에 있다는 것을 의미하므로 열이 더 이상 전달되지 않습니다. 또한 외부 힘이 균형을 이루고(부피가 변하지 않음) 계 내의 모든 화학 반응이 완료되었음을 의미합니다. 이러한 이벤트의 타임라인은 해당 시스템에 따라 다릅니다. 상온에서 녹을 수 있는 얼음 용기는 몇 시간이 걸리는 반면, 반도체에서는 장치가 켜지는 상태에서 꺼지는 상태로 전환되는 과정에서 발생하는 열 전달이 수 나노초 정도에 이를 수 있습니다.

참고 항목

• 온실가스
• 기체 목록
• 천연가스
• 화산가스
• 호흡가스
• 바람

메모들

참고문헌

• Anderson, John D. (1984). Fundamentals of Aerodynamics. McGraw-Hill Higher Education. ISBN 978-0-07-001656-9.
• John, James (1984). Gas Dynamics. Allyn and Bacon. ISBN 978-0-205-08014-4.
• McPherson, William; Henderson, William (1917). An Elementary study of chemistry.

더보기

• 필립 힐과 칼 피터슨. 추진력의 역학 및 열역학: 1992년 2판 애디슨-웨슬리 ISBN 0-201-14659-2
• 미국 항공우주국(NASA). 애니메이션 가스 연구소. 2008년 2월 접속.
• 조지아 주립 대학교. 하이퍼 피지컬. 2008년 2월 접속.
• Antony Lewis Word Web. 2008년 2월 접속.
• 미시간 주 북서부 대학 가스 상태입니다. 2008년 2월 접속.
• Lewes, Vivian Byam; Lunge, Georg (1911). "Gas" . Encyclopædia Britannica. Vol. 11 (11th ed.). p. 481–493.