조건부 대칭 불안정

조건부 대칭 불안정성, 즉 CSI는 수직에서 열적으로 안정적이고 수평에서 동적으로 안정되어 있는 동안 균일한 기준 회전 프레임에서 온도 차이에 노출되는 유체의 대류적 불안정성의 한 형태다. 이 경우의 불안정성은 언급된 두 축에 관해서만 경사면에서 발생하며, 따라서 CSI 구역에서 공기 소포가 거의 포화상태로 횡방향 및 수직방향으로 이동하면 이른바 "경사대류"를 발생시킬 수 있는 것이다. 이 개념은 주로 기상학에서 따뜻한 전선 앞과 같이 다른 안정된 지역에서 강렬한 강수대의 메소스케일 형성을 설명하기 위해 사용된다.^[1][2] 해양학에도 같은 현상이 적용된다.

원리

정수 안정성

상승 중 극적으로 변화된 온도가 환경과 같거나 차가운 경우 특정 고도에서 공기 입자는 안정적일 것이다. 마찬가지로 하강 중에 온도가 같거나 따뜻하면 안정적이다. 온도가 같은 경우에는 입자가 새로운 고도에 머무르고, 다른 경우에는 초기 레벨4로 되돌아간다.

오른쪽의 도표에서 노란색 선은 대류를 수반하지 않는 환경(안정 공기) 아래 처음에는 온도가 유지되는 상승된 입자를 나타낸다. 그 다음 애니메이션에서는 표면 온난화가 일어나고 상승된 입자가 환경(안정되지 않은 공기)보다 따뜻하게 유지된다. 정수 안정성 측정은 등가 전위 온도의 수직 변동을 기록하는 것이다($$^[3]${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$

• 만약 ${\displaystyle e_{}}$ e ${\${e$}$이 고도와 함께 감소하면$$ 기단이 불안정해진다.
• $\theta {\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$가 동일한 상태로$$ 유지되면 고도는 중립 기단으로 이어진다.
• ${\displaystyle {altitude}_{}}$ e ${\$ 고도에 따라 증가하면$$ 안정적인 기단으로 이어진다.

관성 안정성

같은 방법으로 공기 입자의 횡방향 변위는 절대 vorticity $\eta {\displaystyle }$ ${\displaystyle \eta }$을(를) 변화시킨다$.$ 이는 행성 vorticity, $f{\displaystyle }$ ${\displaystyle f}$ 및$$$\zeta {\displaystyle }$ ${\displaystyle \zeta$ 소포의 측위성(또는 상대적) vorticity의 합에 의해 주어진다.^[3][4]

${\displaystyle \eta =\왼쪽[{\frac {\fract v}-{\pract x}-{\fract u}{\preased y}\right]+f=\f=\f\qquad \qquad \qquad }}}}$

위치:

• ${\displaystyle v}$ ${\displaystyle v}$ 및$$ $u{\displaystyle }$ ${\displaystyle u}$은(는) 각각 경맥과 영역 지반영양 속도다.
• ${\displaystyle }$$x{\displaystyle }$ ${\displaystyle x}$ 및 y$$ ${\displaystyle y}$은(는) 영역 및 경맥 좌표에 해당한다.
• ${\displaystyle f}$ ${\displaystyle f}$은(는) 코리올리스 파라미터로, 기준 프레임의 회전으로 발생하는 국부 수직 주위의 vorticity 성분을 설명한다.
• ${\displaystyle \zeta }$ ${\displaystyle \zeta}$은(는) 국부 수직 주위의 상대적 vorticity이다. 지압속 컬의 수직 성분을 취함으로써 발견된다.

${\displaystyle \eta }$ ${\displaystyle \eta }$은(는) 이동이 이루어지는 조건에 따라 양수, null 또는 음수일 수 있다$$. 절대 소용돌이는 시냅스 눈금에서는 거의 항상 양성이므로, 대기는 일반적으로 횡방향 이동에 안정되어 있다고 생각할 수 있다. 관성 안정성은 $\eta {\displaystyle }$ ${\displaystyle \eta }$이(가) 0에 가까울$$ 때만 낮다. $f{\displaystyle }$ ${\displaystyle f}$은(는) 항상 양의 값이기$$ 때문에${\displaystyle }\eta {\displaystyle }$ ${\displaystyle 0}$ ${\displaystyle \eta \leq$ 0$}$은(는) 강한 제트 스트림의 반발성 측이나 고도 기압 능선에서만 만족시킬 수 있으며$$, 방정식의 변위 방향의 파생 속도가 유의한 음의 값을 제공한다.^[5]

각운동량의 변화는 안정성을 나타낸다.^[3][5][6]

• ${\displaystyle \mathrm{\Delta }}$ ${\displaystyle {}_{}}$ ${\displaystyle g_{}}$= ${\displaystyle 0}$ ${\displaystyle \Delta M_{g}=0$ 그러면 이 입자는 탄력이 변하지 않았기 때문에 새로운 위치에 남게 된다.
• > ${\displaystyle \Delta M_{g}>0$ 입자의 운동량이 환경보다 크기 때문에 원래 위치로 되돌아간다.
• < 0 ${\displaystyle \Delta M_{g}<0$ 이 입자는 운동량이 환경보다 작기 때문에 변위를 계속한다.

비스듬한 움직임

그러나 어떤 안정된 정수 및 관성 조건에서 입자가 공기량 또는 풍력을 변화시킬 때 기울어진 변위는 불안정할 수 있다. 오른쪽의 그림은 그런 상황을 보여준다. 공기 입자의 변위는 왼쪽에서 오른쪽으로 증가하는 운동 모멘트 라인(${\displaystyle M_{}}$ g ${\$과 높이에 따라 증가하는 등가 전위 온도(${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$에 대해 이루어진다.

횡방향 움직임 A

수평 가속도($표면{\displaystyle {}_{}}$ ${\displaystyle M_{}}$ g$${\$displaystyle \scriptstyle M_{g$는 입자가 이동하는 $환경$의 ${\displaystyle M_{}}$ g$${\$displaystyle \scriptstyle M_{g}$ 증가/감소 때문에 발생한다. 이 경우 입자는 새로운 환경에 적응하기 위해 가속 또는 감속한다. Spipule A는 수평 가속을 거치며, 그것이 차가운 공기로 이동할 때 긍정적인 부력을 주고, 그것이 더 ${\displaystyle {작은}_{}}$ M$$g {\$displaystyle \scriptstyle M_${g$}$의 지역으로 이동할 때 감속한다$.$ 입자는 상승하여 결국 새로운 환경보다 차가워진다. 이때 그녀는 부력이 마이너스여서 하강하기 시작한다. 그렇게 하면 $M{\displaystyle {}_{}}$ ${\displaystyle g_{}}$ ${\$이 증가하여$$ 입자가 원래 위치로 되돌아간다.^[5][6]

수직 변위 B

${\displaystyle {}_{}}$ 경우 수직 이동은 입자가 따뜻한 공기와 마주칠 때 부력을 발생시키고( ${\displaystyle {negative}_{}}$ e ${\$ 높이에 따라 증가$$) 입자가 더 큰 ${\displaystyle {표면}_{}}$으로 이동할 때 수평 가속도를 발생시킨다$($M g ${\$ M_${g}).$ $입자$가 아래로 내려가면서 ${\displaystyle M_{}}$ g ${\$$스타일 \scriptstyle M_{g}}$은(는) 환경에 맞게 감소하고$$ 입자는 B로 되돌아간다.^[5][6]

경사 변위 C

C 케이스만 불안정해 수평 가속도는 수직 상향 교란과 결합되어 비스듬한 변위를 허용한다. 실제로 입자의$$ $\theta {\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$는 환경의$$ $\theta {\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$보다 크다. 입자의 운동량은 환경의 운동량보다 적다. 따라서 사선 변위는 양의 부력을 생성하고 이를 보강하는 사선 변위 방향에서 가속을 발생시킨다.^[5]

따라서 안정적이지 않은 상황에서 조건부 대칭 불안정성을 갖는 조건은 다음과 같다.^[3][5][6]

• $\theta {\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$의 기울기가 $M{\displaystyle {}_{}}$ ${\displaystyle g_{}}$ ${\$보다 크다$$.
• 측면으로 이동된 공기는 거의 포화상태다.

잠재적 효과

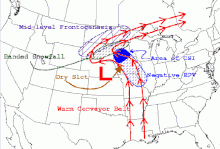
CSI는 대개 수직 상승 운동의 넓은 영역에 내장되어 있다. 이상적인 상황은 높이와 함께 증가하는 풍속과 함께 남쪽에서 오는 지리적 흐름이다. 환경이 잘 뒤섞여 포화상태에 가깝다. 유량이 단방향이기 때문에 바람의 u 성분이 0과 같게 설정될 수 있으며, 이는 기단의 온도 구배와 수직으로 대칭적인 유량을 형성한다. 이러한 유형의 흐름은 일반적으로 서쪽에 찬 공기가 있는 바로클린 대기에서 발견된다.^[6]

오른쪽의 이미지는 따뜻한 전선 근처의 음의 등가 잠재성( ${\displaystyle }$ ( ${\displaystyle \eta \leq 0$과 관련된 CSI와 함께 겨울의 그러한 상황을 보여준다. 앞쪽, 저기압 지역, CSI 부근을 따라 띠 모양의 눈이 형성된다.

경사대류

입자가 CSI 구역에서 상승할 경우, 그것은 식을 것이고 포화상태에서 수증기가 응축되어 비스듬한 대류에 의해 구름과 강수량을 줄 것이다. 예를 들어 따뜻한 전선 앞에서는 온화한 공기가 차가운 질량을 극복하기 때문에 공기량이 안정적이다. 지리적 균형은 어떤 입자도 그것을 향해 우울의 중심에서 수직으로 움직이게 한다. 그러나 CSI 층에서 시놉틱 스케일 상승 가속도에 의한 상향 경사 변위는 강우량의 평행 대역을 생성한다.^[6][7]

조건부 대칭 불안정성은 정수 대류와 유사하게 수직에서 얇거나 매우 클 수 있는 층에 영향을 미친다. 층의 두께는 지역 내 대류 강수량의 증가를 결정한다.^[6] 운동이 포화상태에 가까운 영역에 있기 때문에, 이 입자는 제한된 볼록 가용 전위 에너지(CAPE)를 제공하는 습한 단극성 착수에 매우 가깝게 유지된다. 경사진 대류 구역에서 상승 속도는 초당 수십 센티미터에서 초당 몇 미터까지 다양하다.^[6] 이는 대개 적외선 버스의 상승 속도 제한치(즉, 5 m/s)보다 낮으며, 이는 번개를 주고 CSI로 발생을 제한한다.^[6] 그러나 다음과 같은 경우에는 가능하다.^[6]

• 메소스케일 대류 시스템의 후행 강수 영역.
• 겨울 대류는 낮은 대류권과 차가운 대류권이 위쪽으로 움직이는 얼음 결정의 이온화를 돕고 있기 때문이다.
• 성숙 허리케인의 심화가 진행되는 동안 안벽에서는 대칭적으로 중립적인 지역이고 일반적으로 번개 활동이 없는 지역이기 때문에 드물지만.

경사 대류 대역은 다음과 같은 몇 가지 특성을 가진다.^[6]

1. 그들은 평행하다.
2. 열풍과 평행하다.
3. 그들은 일반 순환과 함께 움직인다.
4. 밴드 사이의 공간은 CSI 층의 두께에 비례한다.

침하

반대로 입자가 아래로 미끄러지면 따뜻해지고 상대적으로 포화도가 낮아져 구름이 흩어진다. 경사 대류에 의해 고도가 높은 곳에서 생성되는 눈 또한 하강 흐름에서 승화하여 가속할 것이다. 그것은 20m/s에 이르는 하강 속도를 줄 수 있다.^[6] 이 효과는 스팅 제트기의 지상으로 하강하는 것과 관련이 있다.^[8]

참조

외부 링크

• David M. Schultz; Philip N. Schumacher (December 14, 1998). "The Use and Misuse of Conditional Symmetric Instability". National Severe Storms Laboratory. Retrieved August 23, 2019.
• "Slantwise convection". COMET Courses. UCAR. Retrieved August 23, 2019. Interactive course that needs a login