음온

이 기사의 리드 섹션은 기사의 길이에 비해 너무 길 수도 있다. 기사의 본문으로 일부 자료를 옮겨서 도움을 주십시요. 레이아웃 가이드 및 리드 섹션 지침을 읽고 섹션에 모든 필수 세부 정보가 포함되도록 하십시오. 기사의 토크 페이지에서 이 문제를 논의하십시오. (2021년 9월)

특정 시스템은 음의 열역학적 온도를 달성할 수 있다. 즉, 켈빈 또는 랭킨 눈금에서 음의 양으로 표시할 수 있다. 이는 비열역학 섭씨 또는 화씨 척도에서 음수로 표현되는 온도와 구별되어야 하며, 그럼에도 불구하고 절대 영도보다 높다.

절대 온도(켈빈) 척도는 평균 운동 에너지의 척도로 느슨하게 이해할 수 있다. 보통 시스템 온도는 양적이다. 그러나 특히 고립된 시스템에서는 볼츠만의 엔트로피 측면에서 정의된 온도가 음이 될 수 있다.

음온의 가능성은 그가 한정된 영역에 국한된 고전적인 점의 변수에 대한 분석에서 1949년 Lars Onsager에 의해 처음 예측되었다.^[1] 구속점 vortices는 표준적인 모멘텀a가 표준적인 위치 좌표로부터 독립된 자유도가 아니기 때문에 한정된 위상 공간을 가진 시스템이다. 경계상 공간은 음의 온도를 허용하는 필수 속성이며, 그러한 온도는 고전적 시스템과 양자 시스템 모두에서 발생할 수 있다. Onsager에서 알 수 있듯이, 경계 위상 공간을 가진 시스템은 에너지가 증가함에 따라 엔트로피에서 반드시 피크를 가진다. 피크가 발생하는 값을 초과하는 에너지의 경우 에너지가 증가함에 따라 엔트로피가 감소하며, 고에너지 상태는 반드시 음의 볼츠만 온도를 가진다.

켈빈 눈금에서 정말로 음의 온도를 가진 시스템은 양의 온도를 가진 어떤 시스템보다 더 뜨겁다. 음온 시스템과 양온 시스템이 접촉하면 음온 시스템에서 양온 시스템으로 열이 흐른다.^[2][3] 그러한 시스템의 표준적인 예는 레이저 물리학의 인구 역전이다.

온도는 시스템 입자의 평균 운동 에너지로 대략 해석된다. 양온도보다 '핫터' 계통을 나타내는 음온도는 말할 것도 없고 음온의 존재는 이 해석에서 역설적으로 보일 것이다. 역설은 내부 에너지와 엔트로피 사이의 트레이드오프로서 열역학적 온도의 보다 엄격한 정의를 고려함으로써 해결되는데, 온도의 역수인 '냉동성'은 보다 근본적인 양이다. 양온의 시스템은 시스템에 에너지를 가미함에 따라 엔트로피가 증가하며, 음온의 시스템은 시스템에 에너지를 가미함에 따라 엔트로피가 감소한다.^[4]

위상 공간이 한없이 넓어진 열역학 시스템은 부정적인 온도를 달성할 수 없다: 열을 가하면 항상 엔트로피가 증가한다. 에너지가 증가함에 따라 엔트로피가 감소할 가능성은 엔트로피에서 시스템이 "포화"되어야 한다. 이것은 높은 에너지 상태의 수가 제한되어야만 가능하다. 원자나 먼지와 같은 평범한 (양자나 고전적인) 입자 체계의 경우, 높은 에너지 상태의 수는 무제한이다(원리적으로 입자 모멘텀은 무한정 증가할 수 있다). 그러나 일부 시스템(아래 예시 참조)은 보유할 수 있는 최대 에너지의 양을 가지며, 최대 에너지에 접근할 때 엔트로피가 실제로 감소하기 시작한다.^[5] 음의 온도로 시스템에 접근할 수 있는 상태의 제한된 범위는 음의 온도가 높은 에너지에서 시스템의 긴급 순서와 관련이 있다는 것을 의미한다. 예를 들어 Onsager의 포인트-피질 분석에서 음온은 대규모의 vortic 군집의 출현과 관련이 있다.^[1] 평형 통계 역학에서 이러한 자발적인 순서는 증가된 에너지가 무질서를 증가시키는 일반적인 육체적 직관에 반한다.

온도의 정의

열역학 온도 T의 정의는 가역성 열전달 Q_rev:에서 시스템 엔트로피 S의 변화에 대한 함수다.

${\displaystyle T={\frac {dQ_{\mathrm {rev}{dS}}}.}$

엔트로피는 상태함수로서, 어떤 주기적 과정에 대한 dS의 적분은 0이다. 엔트로피가 순수하게 시스템 에너지 E의 함수인 시스템의 경우, 온도는 다음과 같이 정의될 수 있다.

${\displaystyle T=\왼쪽({\frac {dS}{dE}\오른쪽)^{-1}.}$

동등하게 열역학 베타 또는 "콜드니스"는 다음과 같이 정의된다.

${\displaystyle \cHB ={\frac {1}{kT}}={\frac{1}{k}{\frac {dS}{dE},}$

여기서 k는 볼츠만 상수다.

고전적인 열역학에서 S는 온도의 측면에서 정의된다는 점에 유의한다. 이것은 여기서 반대로, S는 시스템의 가능한 미세한 부분들의 함수인 통계 엔트로피이며, 온도는 가능한 미세한 부분들 사이의 에너지 수준의 분포에 관한 정보를 전달한다. 자유도가 많은 시스템의 경우 엔트로피의 통계적 및 열역학적 정의는 일반적으로 서로 일치한다.

몇몇 학자들을 투자하는 열역학적 통계적 엔트로피의 에너지로 주가의 하향한다 작은 시스템과 시스템에 인식된 모순 해결하는 엔트로피의 대안적인 정의를 사용하여 비록 이 새로운 정의 cr 것 기온은 이 entropies에서 파생된 different,[6][7] 있는 것을 제안했다.발음하는 oeate그들의 ^[8]불일치

열 및 분자 에너지 분배

음의 온도는 제한된 수의 에너지 상태가 있는 시스템에서만 존재할 수 있다(아래 참조). 그러한 시스템에서 온도가 증가하면 입자는 점점 더 높은 에너지 상태로 이동하며, 온도가 증가함에 따라 낮은 에너지 상태와 높은 에너지 상태의 입자 수는 평등에 접근한다. (이는 상태가 제한된 시스템에 대한 통계 역학에서 온도의 정의의 결과) 이러한 시스템에 에너지를 올바른 방식으로 주입함으로써 낮은 에너지 상태보다 높은 에너지 상태에 입자가 더 많은 시스템을 만들 수 있다. 그러면 시스템은 음의 온도를 갖는 것으로 특징지어질 수 있다.

음온의 물질은 절대영도보다 춥지 않고 무한온도보다 뜨겁다. 키텔과 크로이머(462쪽)의 표현대로

저온에서 고온까지의 온도 척도:

+0 K, …, +300 K, …, +118 K, -300 K, … -0 K.

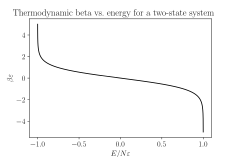
그 수량에 상응하는 역 온도 눈금, β).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em.}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/kT(어디에 k볼쯔만 상수입니다), 지속적으로 낮은 에너지 +∞,…, 0,…, −∞로 달린다. +∞에서 -∞으로 갑작스러운 점프를 피하기 때문에 β는 T보다 더 자연스런 것으로 간주된다. 비록 시스템은 여러 개의 음온 영역을 가질 수 있고 따라서 -1에서 +1까지 불연속성을 가질 수 있다.

친숙한 많은 물리적 시스템에서 온도는 원자의 운동 에너지와 연관되어 있다. 원자의 운동량에는 상한이 없기 때문에 에너지가 더해질 때 이용 가능한 에너지 상태의 수에 상한이 없으므로 음온에 도달할 수 있는 방법이 없다. 그러나 통계 역학에서 온도는 운동에너지만이 아닌 다른 자유도에 해당할 수 있다(아래 참조).

온도와 장애

시스템의 다양한 변환, 진동, 회전, 전자 및 핵 모드들 사이의 에너지 분포는 거시 온도를 결정한다. "정상" 시스템에서는 다양한 모드 간에 열 에너지가 끊임없이 교환되고 있다.

그러나 어떤 상황에서는 하나 이상의 모드를 분리할 수 있다. 실제로 격리 모드는 여전히 다른 모드와 에너지를 교환하지만, 이 교환의 시간 척도는 격리 모드 내의 교환에 비해 훨씬 느리다. 강한 외부 자기장에서 핵 스핀이 발생하는 경우를 예로 들 수 있다. 이 경우 원자가 상호작용하는 스핀 상태 사이에서 에너지는 상당히 빠르게 흐르지만, 핵 스핀과 다른 모드들 사이의 에너지 전달은 비교적 느리다. 에너지 흐름은 주로 스핀 시스템 내에 있으므로 다른 모드와 관련된 온도와 구별되는 스핀 온도를 생각해 보는 것이 타당하다.

온도의 정의는 다음과 같은 관계에 기초할 수 있다.

${\displaystyle T={\frac {dq_{\mathrm {rev}}}{d}}}{d.S}}$

이 관계를 통해 양온도는 열 에너지인 q가_rev 시스템에 추가됨에 따라 엔트로피 S가 증가하는 조건에 해당한다는 것을 알 수 있다. 이는 거시적 세계에서의 "정상적인" 조건이며, 번역, 진동, 회전, 비스핀 관련 전자 및 핵 모드의 경우 항상 그러하다. 그 이유는 이러한 종류의 모드는 무한히 많고, 시스템에 열을 더하면 정력적으로 접근할 수 있는 모드의 수가 증가하여 엔트로피가 증가하기 때문이다.

예

비상호작용 2레벨 입자

가장 간단한 예는 다소 비물리적이지만, 각각의 N 입자는 +210 또는 -210의 에너지를 가질 수 있지만, 그렇지 않으면 비 상호작용을 하는 N 입자의 시스템을 고려하는 것이다. 이는 교호작용 항이 무시할 수 있는 Ising 모델의 한계로 이해할 수 있다. 시스템의 총 에너지는

${\displaystyle E=\varepsilon \sum _{i=1}^{N}\sigma _{i}=\varepsilon j}$

여기서 σ은_i ith 입자의 부호, j는 양의 에너지를 가진 입자의 수에서 음의 에너지를 가진 입자의 수를 뺀 것이다. 기초 결합학에서 이 양의 에너지를 가진 총 마이크로스테이트 수는 이항계수:

${\displaystyle \Oomega_{E}={\binom {N}{\frac {N+j}{2}}}}}={\frac{N!}{\좌({\frac {N+j}{2)}}}\오른쪽)!\left({\frac {N-j}{2}}\오른쪽)!}}.}$

통계역학의 근본적 가정으로 이 미시적 합주곡의 엔트로피는

${\displaystyle S=k_{\text{B}\ln \오메가_{E}$

열역학 베타(β = 1/kT_B)는 연속체 한계를 적용하지 않고 중심 차이로 간주하여 해결할 수 있다.

${\displaystyle {\begin{aligned}\beta &={\frac {1}{k_{\mathrm {B} }}}{\frac {\delta _{2\varepsilon }[S]}{2\varepsilon }}\\[3pt]&={\frac {1}{2\varepsilon }}\left(\ln \Omega _{E+\varepsilon }-\ln \Omega _{E-\varepsilon }\right)\\[3pt]&={\frac {1}{2\varepsilon }}\ln \left({\frac {\left({\frac {N+j-1}{2}}\right)!\left({\frac {N-j+1}{2}}\오른쪽)!}}{\왼쪽({\frac {N+j+1}{2}}\오른쪽)!\left({\frac{N-j-1}{2}}\오른쪽)!}}\\\[3pt]&={\frac {1}{2\varepsilon }}}\ln \left({\frac {N-j+1}{N+j+1}}\오른쪽).\end{정렬}}}$

이 때문에 온도

${\displaystyle T(E)={\frac {2\barepsilon }{k_{\text{B}}}\왼쪽[\ln \left({\frac {(N+1)\varepsilon -E}{(N+1){(N+1)\varepsilon +E}\right]^{-1}.}$

이 모든 증거는 에너지가 고정되고 온도가 급발진 성질이 되는 마이크로캐논 앙상블을 가정한다. 정식 앙상블에서는 온도가 고정되어 에너지가 급발진하는 성질이다. 이 경우 다음과 같은 결과가 나온다(이러한 경우는 마이크로스테이트를 가리킨다.

${\displaystyle {\begin{aligned}Z(T)&=\sum _{i=1}^{N}e^{-\varepsilon _{i}\beta }\\[6pt]E(T)&={\frac {1}{Z}}\sum _{i=1}^{N}\varepsilon _{i}e^{-\varepsilon _{i}\beta }\\[6pt]S(T)&=k_{\text{B}}\ln(Z)+{\frac {E}{T}}\end{정렬}}$

앞의 예에 따라 레벨 2와 입자가 2인 상태를 선택한다. 이는 미세상태₁ ates = 0, , = 1, 1₂ = 1₃, 1 = 2로₄ 이어진다.

${\displaystyle{\begin{정렬}(T)&, =e^ᆱ+2e^ᆲ+e^ᆳ\\[3pt]&, =1+2e^ᆴ+e^ᆵ\\[6pt]E(T)&, ={\frac{0e^{-0\beta}+2\times 1e^{-1\beta}+2e^{-2\beta}}{Z}}\\[3pt]&, ={\frac{2e^{-\beta}+2e^{-2\beta}}{Z}}\\[3pt]&, ={\frac{2e^{-\beta}+2e^{-2\beta}}{1+2e^{-\beta}+e^{-2\beta}}}\\[6pt]S(T)&, =k_{년.텍스트{B}}\ln \좌(1+2e^{-\beta }\beta }\우)+{\frac {2e^{-\beta }{-\beta }}}}{{{+2e^{-\beta }}}}}}}{\좌우)T}}\end{정렬}}$

S, E, Z에 대한 결과 값은 모두 T에 따라 증가하며 음온 체계에 들어갈 필요가 없다.

핵 스핀스

앞의 예는 외부 자기장의 핵 스핀 시스템에 의해 대략적으로 실현된다.^[9][10] 이를 통해 핵자기 공명 분광기의 변화로 실험을 진행할 수 있다. 전자 스핀 시스템과 핵 스핀 시스템의 경우, 스핀 업과 스핀 다운에 해당하는 사용 가능한 모드는 한정된 수, 종종 단 2개뿐입니다. 자기장이 없을 때 이러한 스핀 상태는 퇴화되는데, 이는 동일한 에너지에 해당한다는 것을 의미한다. 외부 자기장을 적용하면 자기장과 정렬된 스핀 상태는 반병렬의 에너지와 다른 에너지를 가지기 때문에 에너지 레벨이 분할된다.

자기장이 없는 경우, 그러한 2회전 시스템은 원자의 절반이 스핀업 상태이고 절반은 스핀다운 상태일 때 최대 엔트로피를 가질 수 있으므로, 거의 동일한 스핀 분포로 시스템을 찾을 수 있을 것으로 예상할 수 있다. 자기장을 적용할 때, 일부 원자들은 시스템의 에너지를 최소화하기 위해 정렬하는 경향이 있을 것이고, 따라서 약간 더 많은 원자들이 낮은 에너지 상태에 있어야 한다(이 예제의 목적을 위해 우리는 스핀다운 상태가 낮은 에너지 상태라고 가정할 것이다). 무선 주파수 기법을 사용하여 스핀 시스템에 에너지를 추가할 수 있다.^[11] 이것은 원자가 스핀다운에서 스핀업으로 뒤집히게 한다.

우리가 스핀다운 상태에서 원자의 절반 이상을 가지고 시작했기 때문에, 이것은 처음에 시스템을 50/50 혼합물 쪽으로 몰아서 엔트로피가 증가하는데, 이는 양의 온도에 해당한다. 그러나 어느 순간 스팽글의 절반 이상이 스핀업 위치에 있다.^[12] 이 경우 추가 에너지를 추가하면 엔트로피가 50/50 혼합물에서 시스템을 더 멀리 이동시키기 때문에 엔트로피가 감소한다. 에너지의 추가에 따른 엔트로피 감소는 음온에 해당한다.^[13] NMR 분광학에서 이는 펄스 폭이 180° 이상인 펄스에 해당한다(특정 스핀의 경우). 고체에서는 이완이 빠르지만, 용액에서는 몇 초가 걸릴 수 있고 기체와 초인종 시스템에서는 더 오래 걸릴 수 있다; 피코켈빈 온도에서는 은과 로듐에 대해 몇 시간이 보고되었다.^[13] 핵 스핀에 대해서만 온도가 음수라는 것을 이해하는 것은 여전히 중요하다. 분자 진동, 전자 및 전자 스핀 수준과 같은 다른 자유도는 양의 온도에 있으므로 물체는 여전히 양의 지각 열을 가지고 있다. 휴식은 실제로 핵 스핀 상태와 다른 상태 사이의 에너지 교환(예를 들어 핵 오버하우저 효과를 통해 다른 스핀들과)에 의해 발생한다.

레이저스

이 현상은 또한 시스템 원자(화학 및 가스 레이저의 경우) 또는 전자(반도체 레이저의 경우)의 상당 부분이 흥분 상태에 있는 많은 라싱 시스템에서도 관찰할 수 있다. 이것을 인구 역행이라고 한다.

주파수 ν에서 발광 방사장의 단일 모드에 대한 해밀턴계는 다음과 같다.

${\displaystyle H=(h\nu -\mu )a^{\daugger }a.}$

그랜드 캐논 앙상블의 밀도 연산자는

${\displaystyle \rho ={\frac {e^{-\beta H}{Tr}{\operatorname {Tr} \left(e^{-\beta H}\오른쪽)}}.}$

시스템이 접지 상태, 수렴할 트레이스 및 밀도 연산자가 일반적으로 의미 있으려면 βH는 양의 세미데마인이트여야 한다. 따라서 hν < μ, H가 음의 세미데핀라이트라면, β 자체는 음의 온도를 의미하는 음의 것이어야 한다.^[14]

운동 자유도

부정적인 온도는 또한 운동적인 자유도에서도 달성되었다. 광학 격자를 사용하여, 상한을 운동 에너지, 상호작용 에너지 및 차가운 칼륨-39 원자의 잠재적 에너지에 두었다. 이는 페쉬바흐 공명을 사용하여 원자의 상호작용을 혐오에서 매력적으로 조정하고, 전체적인 조화 전위를 트랩에서 반트랩으로 변경하여 보스-허버드 해밀턴안을 from → - -에서 변형시킴으로써 이루어졌다. 원자를 Mott 절연체(Mott 절연체) 체제에 유지하면서 이러한 변형을 독립적으로 수행하면 낮은 엔트로피 양의 온도 상태에서 낮은 엔트로피 음의 온도 상태로 갈 수 있다. 음의 온도 상태에서 원자는 거시적으로 격자의 최대 운동량을 차지한다. 음온 앙상블은 반트래핑 조화 전위에서 평형화되고 긴 수명을 보였다.^[15]

2차원 소용돌이 운동

유한 영역에 국한된 2차원 항체 시스템은 음온 상태에서 열 평형 상태를 형성할 수 있으며,^[16][17] 실제로 음온 상태는 그의 고전적인 점 항체 분석에서 온사거에 의해 처음 예측되었다.^[1] 온사거의 예측은 2019년 보스-아인슈타인 응축수에서 양자 항진체계에 대해 실험적으로 확인되었다.^[18][19]

참고 항목

• 음저항

참조

추가 읽기

• Kittel, C.; Kroemer, H. (1980). Thermal Physics (2nd ed.). W. H. Freeman. ISBN 978-0-7167-1088-2.
• Castle, J.; Emmerich, W.; Heikes, R.; Miller, R.; Rayne, J. (1965). Science by Degrees: Temperature from Zero to Zero. Walker and Company. LCCN 64023985.
• Braun, S.; Ronzheimer, J. P.; Schreiber, M.; Hodgman, S. S.; Rom, T.; Bloch, I.; Schneider, U. (2013). "Negative Absolute Temperature for Motional Degrees of Freedom". Science. 339 (6115): 52–5. arXiv:1211.0545. Bibcode:2013Sci...339...52B. doi:10.1126/science.1227831. PMID 23288533. S2CID 8207974.
• Parihar, V.; Widom, A.; Srivastava, Y. (2006). "Thermal Time Scales in a Color Glass Condensate". Physical Review C. 73 (17901): 017901. arXiv:hep-ph/0505199. Bibcode:2006PhRvC..73a7901P. doi:10.1103/PhysRevC.73.017901. S2CID 119090586.
• Mosk, A. (2005). "Atomic Gases at Negative Kinetic Temperature". Physical Review Letters. 95 (4): 040403. arXiv:cond-mat/0501344. Bibcode:2005PhRvL..95d0403M. doi:10.1103/PhysRevLett.95.040403. PMID 16090784. S2CID 1156732.
• Schmidt, Harry; Mahler, Günter (2005). "Control of Local Relaxation Behavior in Closed Bipartite Quantum Systems". Physical Review E. 72 (7): 016117. arXiv:quant-ph/0502181. Bibcode:2005PhRvE..72a6117S. doi:10.1103/PhysRevE.72.016117. PMID 16090046. S2CID 17987338.
• Shen, Jian-Qi (2003). "Anti-shielding Effect and Negative Temperature in Instantaneously Reversed Electric Fields and Left-Handed Media". Physica Scripta. 68 (1): 87–97. arXiv:cond-mat/0302351. Bibcode:2003PhyS...68...87S. doi:10.1238/Physica.Regular.068a00087. S2CID 118894011.
• Ketterle, Wolfgang (22 Sep 2010). Towards Quantum Magnetism with Ultracold Atoms (movie). The Zurich Physics Colloquium. ETH Zurich, ITS-MMS; Switzerland. Retrieved 1 Jan 2016. Negative temperature, at about 48min. 53sec.
• Carr, Lincoln D. (2013-01-04). "Negative Temperatures?". Science. 339 (6115): 42–43. Bibcode:2013Sci...339...42C. doi:10.1126/science.1232558. PMID 23288530. S2CID 124095369.

외부 링크

• Moriarty, Philip. "−K: Negative Temperatures". Sixty Symbols. Brady Haran for the University of Nottingham.