리얼 가스

실제 가스는 분자가 공간을 차지하고 상호작용을 하는 비이상의 기체다. 결과적으로 그들은 이상적인 가스 법칙을 따르지 않는다. 실제 가스의 행동을 이해하려면 다음 사항을 고려해야 한다.

• 압축성 효과
• 가변 특정 열 용량
• 판 데르 발스 힘;
• 비흡수 열역학적 효과
• 분자 분자 분열과 가변적 구성의 기초적 반응에 관한 문제

대부분의 용도에서는 그러한 상세한 분석이 불필요하며, 이상적인 기체 근사치를 합리적인 정확도로 사용할 수 있다. 반면에, Joule–을 설명하기 위해, 실제 가스 모델은 기체의 응축 지점 근처, 임계 지점 근처, 매우 높은 압력에서 사용되어야 한다.Thomson 효과 및 다른 덜 일반적인 경우. 이상성으로부터의 편차는 압축성 인자 Z로 설명할 수 있다.

모델

반데르발스 모델

실제 가스는 종종 어금니 무게와 어금니 부피를 고려하여 모델링된다.

${\displaystyle RT=\왼쪽(p+{\frac {a}{V_{\text{m}}^{2}}\오른쪽)\왼쪽(V_{\text{m}-b\오른쪽)}$

또는 다음 중 하나:

${\displaystyle p={\frac {RT}{V_{m}-b}-{\frac {a}{V_{m}^{2}}:$

여기서 p는 압력, T는 온도, R은 이상적인 기체 상수, V는_m 어금니 체적. a와 b는 각 기체에 대해 경험적으로 결정되는 매개변수지만, 때로는 이러한 관계를 이용하여 임계 온도(T_c)와 임계 압력(p_c)에서 추정한다.

${\displaystyle {\begin}a&={\fract {27R^{2}T_{\text{c}^{2}}:{64p_{\text{c}}\\b&={\frac {RT_{\text{c}}{8p_{\text}}}{c}}\ended{aigned}}}}}}}}$

임계점에 있는 상수는 매개변수 a, b:의 함수로 표현될 수 있다.

${\displaystyle p_{c}={\frac {a}{27b^{2}}:\quad T_{c}={\frac {8a}{27bR}},\qquad V_{m,=3b,\qquad Z_{c}={\fr}}{8}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$

With the reduced properties ${\displaystyle p_{r}={\frac {p}{p_{\text{c}}}},\ V_{r}={\frac {V_{\text{m}}}{V_{\text{m,c}}}},\ T_{r}={\frac {T}{$$T_{\text{c}}}\}$ 방정식은$$ 다음과 같이 축소된 형태로 작성할 수 있다.

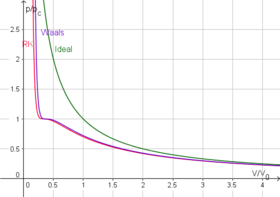
${\displaystyle p_{r}={\frac {8}{3}}{{V_{r}-{{{{{1}-{{{1}}}-{\frac {3}{V_{r}^{2}}:}$

레드리히-쿵 모형

Redlich-Kwong 방정식은 실제 가스를 모형화하는 데 사용되는 또 다른 2-모수 방정식이다. 그것은 거의 항상 반 데르 발스 방정식보다 정확하며, 종종 세 개 이상의 매개변수를 가진 일부 방정식보다 더 정확하다. 방정식은

${\displaystyle RT=\왼쪽(p+{\frac {a}{\sqrt{{T}V_{\text{m}+b\오른쪽)\왼쪽(V_{\text{m}+b\오른쪽)\왼쪽(V_{m}-b\right)}$

또는 다음 중 하나:

${\displaystyle p={\frac {RT}{V_{\text{m}-b}-{\frac {a}{\\sqrt{T}{\text}{{\m}}\reflt(V_{\text}}+b\오른쪽)}}}$

여기서 a와 b는 반 데르 발스 방정식과 동일한 매개변수가 아닌 두 개의 경험적 매개변수다. 이러한 매개변수는 다음과 같이 결정할 수 있다.

${\displaystyle {\begin{aligned}a&=0.42748\,{\frac {R^{2}{T_{\text{c}}}^{\frac {5}{2}}}{p_{\text{c}}}}\\b&=0.08664\,{\frac {RT_{\text{c}}}{p_{\text{c}}}}\end{aligned}}}$

임계점에 있는 상수는 매개변수 a, b:의 함수로 표현될 수 있다.

${\displaystyle p_{c}={\frac {({\sqrt[{3}]{2}}-1)^{7/3}}{3^{1/3}}}R^{1/3}{\frac {a^{2/3}}{b^{5/3}}},\quad T_{c}=3^{2/3}({\sqrt[{3}]{2}}-1)^{4/3}({\frac {a}{bR}})^{2/3},\qquad V_{m,c}={\frac {b}{{\sqrt[{3}]{2}}-1}},\qquad Z_{c}={\frac {1}{3}}}$

Using ${\displaystyle \ p_{r}={\frac {p}{p_{\text{c}}}},\ V_{r}={\frac {V_{\text{m}}}{V_{\text{m,c}}}},\ T_{r}={\frac {T}{$$T_{\text{c}}}}$상태 방정식은$$ 다음과 같이 축소된 형태로 작성할 수 있다.

${\$$}$$T_{R}}{V_{r}-b'}-{\frac {1}{b'{b'{\sqrt{{T_}}V_{r}\왼쪽(V_{r}+b'\오른쪽)$${\displaystyle {\}\}}^{}}$ =${\displaystyle 2}$ ${\displaystyle \text{exception 25:}}$- ${\displaystyle 1\mathrm{}\approx }$ 0.${\displaystyle 26}$ ${\displaystyle b'={\sqrt[{3}]{2}}-1\약 0.26}$

Bertelot 및 수정된 Bertelot 모델

Berthelot 방정식(D의 이름을 따서 이름. 베르테롯)^[1]은 매우 드물게 사용되며,

${\displaystyle p={\frac {RT}{V_{\text{m}-b}-{\frac {a}{TV_{\text{m}^{2}}:$

하지만 수정된 버전은 좀 더 정확하다.

${\displaystyle p={\frac {RT}{V_{\text{m}}}}\좌측[1+{\frac {9}{p}{p_{\text{c}}}}{128{\frac {T}{T}}}{\frac}{T}}{{{T}}}}}}}}}}{T_{\text{c}}}}}}}}{{\frac{6}{\frac{T^{2}}:{{T_{\text{c}^{2}}\\오른쪽)\오른쪽]}$

디에테리시 모델

이 모델(C의 이름을 딴 모델) 디에테리치^[2])는 최근 몇 년간 사용이 중단되었다.

${\displaystyle p={\frac {RT}{V_{\text{m}-b}\exp \left(-{\frac {a}{V_{\text{m})}RT}\오른쪽)}$

매개변수 a, b 및

${\displaystyle \exp \left(-{\frac {a}{V_{\text{m})}RT}}\오른쪽)=e^{-{\frac {a}{V_{\text{m}}}RT}}=1-{\frac {a}{V_{\text{m}}}RT}+\dots }$

클로스 모형

클라우시우스 방정식(Rudolf Closius의 이름을 따서 명명)은 기체를 모형화하는 데 사용되는 매우 간단한 3변수 방정식이다.

${\displaystyle RT=\왼쪽(p+{\frac {a}{T(V_{\text{m}+c)^{2}}}\오른쪽)\왼쪽(V_{\text{m}-b\오른쪽)}$

또는 다음 중 하나:

${\displaystyle p={\frac {RT}{V_{\text{m}-b}-{\frac {a}{T\왼쪽(V_{\text{m}+c\오른쪽)^{2}}:$

어디에

${\displaystyle {\begin}a&={\fract {27R^{2}T_{\text{c}}^{64p_{\text{c}}}{64p_{\c}}\b&=V_{\text{c}-{\frac{RT_{\text{c}}}{4p_{\c}}}\c&={\frac{3}RT_{\text{c}}{8p_{\text{c}}}-V_{\text{c}}\ended}}}$

여기서_c V는 중요한 볼륨이다.

처녀자리 모형

처녀 방정식은 통계 역학의 섭동적 처리에서 비롯된다.

${\displaystyle pV_{\text{m}}=RT\left[1+{\frac {B(T)}{V_{\text{m}}}{{V_{\c(T)}{{\m^{{{}}}}}{V_{\frac{D(T)}{{{{m}}}}}}}}+{{{{m^}}}}}}}}}\ldots \ldots \right]}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

또는 대안으로

${\displaystyle pV_{\text{m}}=RT\왼쪽[1+B'(T)p+C'(T)p^{2}+D'(T)p^{3}\ldots \right]}}$

여기서 A, B, C, A′, B′, C′은 온도에 따라 달라지는 상수다.

펑-로빈슨 모델

펑-로빈슨 주의 방정식(D.-Y.의 이름) Peng과 D. B^[3]. Robinson)은 실제 가스뿐만 아니라 일부 액체를 모델링하는 데 유용한 흥미로운 특성을 가지고 있다.

${\displaystyle p={\frac {RT}{V_{\text{m}-b}-{\frac {a(T)}{V_{\text{m}+b\right)\left(V_{\text}+b\ik)+b\left(V_{m-b\rig)}}}$

볼 모델

Wohl 방정식(A의 이름을 따서 명명) Wohl^[4])은 임계치 측면에서 공식화 되어 있어 실제 가스 상수를 이용할 수 없을 때는 유용하지만, 예를 들어 임계 부피 이상으로 부피가 수축될 때 압력이 급격히 감소하는 것을 보여주듯이 고밀도에는 사용할 수 없다.

${\displaystyle p={\frac {RT}{V_{\text{m}-b}-{\frac {a}{TV_{\text{m}\왼쪽(V_{\text{m}-b\오른쪽)}}}}+{\frac{c}{T^{2}V_{\text{m}^{3}}\quad }$

또는:

${\displaystyle \left(p-{\frac {c}{T^{2}V_{\text{m}}^{3}}\오른쪽)\왼쪽(V_{\text{m}-b\오른쪽)=RT-{\frac {a}{TV_{\text{m}}}}$

또는 다음 중 하나:

${\displaystyle RT=\left(p+{\frac {a}){TV_{\text{m}}(V_{\text{m}-b)}}}-{\frac {c}{T^{2}V_{\text{m}}^{3}}\오른쪽)\왼쪽(V_{\text{m}-b\오른쪽)}$

어디에

${\displaystyle a=6p_{\text{c}}T_{\text{c}V_{\text{m,c}^{2}}$

${\displaystyle }$${\displaystyle b}$${\displaystyle }$= V ${\displaystyle {m\text{,c}}_{}}$4 ${\$ b$={\frac {V_{\$${\displaystyle \frac{{}_{}}{}}$${m,c}}{4$}}{4$}}}}$$$ m,c = 4 15 R C {\$displaystyle V_{\text{m,$c}}}}}}}}}}}}}}}}}}}}}}:{c}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

$displaystyle c=4p_{\text{c}}$$T_{\text{c}}^{2}V_{\text{m,c}}^{3}\ }$, where ${\displaystyle V_{\text{m,c}},\ p_{\text{c}},\ T_{\text{c}}}$ are (respectively) the molar volume, the pressure and the temperature at the critical point.

And with the reduced properties ${\displaystyle \ p_{r}={\frac {p}{p_{\text{c}}}},\ V_{r}={\frac {V_{\text{m}}}{V_{\text{m,c}}}},\ T_{r}={\frac {T}{$$T_{\text{c}}}\{}}}$ 축소된 형태로 첫 번째 방정식을 쓸 수 있다.

${\displaystyle p_{r}={\frac {15}{4}}{\frac {T_{r}}{V_{r}-{\frac {1}:{4}-{4}}-{\frac {6}{\frac}{6}}}{\frac}}}}}{\frac {}}}}}{T_{r}V_{r}\왼쪽(V_{r}-{\frac {1}{4}}\오른쪽)}}}}{{\frac{4}{T_{r}^{2}V_{r}^{3}}}}}}}}:{3}}}}}}}}$

비티-브리지만 모델

^[5] 이 방정식은 실험적으로 결정된 5개의 상수에 기초한다. 라고 표현하고 있다.

${\displaystyle p={\frac {RT}{v^{2}}\\좌측(1-{\\frac {c}{v)T^{3}}}\오른쪽)(v+B)-{\frac {A}{v^{2}}:$

어디에

${\displaystyle {\reasoned}A&=A_{0}\왼쪽(1-{\frac {a}{v}\오른쪽)&B&=B_{0}\왼쪽(1-{\frac {b}{v}\오른쪽)\end{arged}}}$

이 방정식은 약 0.8_cr dens까지의 밀도에 대해 합리적으로 정확한 것으로 알려져 있는데, 여기서 ρ은_cr 임계점에 있는 물질의 밀도다. The constants appearing in the above equation are available in the following table when p is in kPa, v is in ${\displaystyle {\frac {{\text{m}}^{3}}{{\text{k}}\,{\text{mol}}}}}$, T is in K and R = 8.314${\displaystyle {\frac {{\text{k$$Pa}}\cdot{\text{m}^{3}{\text{k}\,{\text{mol}\cdot{\text{K}}}}}$

베네딕트-웹-루빈 모델

BWR 방정식, 때로는 BWRS 방정식이라고도 한다.

${\displaystyle p=RTd+d^{2}\왼쪽(RT(B+bd)-\왼쪽(A+ad-a\alpha d^{4}\오른쪽)-{\frac {1}{1}{{\fr}{{}}{{}}}}}}}T^{2}}}\왼쪽[C-cd\left(1+\gamma d^{2}\오른쪽)\exp \left(-\gamma d^{2}\오른쪽)}$

여기서 d는 어금니 밀도이고 a, b, c, A, B, C, α, γ은 경험적 상수다. γ 상수는 상수 α의 파생물이므로 1과 거의 동일하다는 점에 유의한다.

열역학적 팽창 작업

실제 가스의 팽창 작업은${\displaystyle {}_{}^{}}$quantity V ${\displaystyle {{}_{}}_{{}_{}}^{}}$ ${\displaystyle {V_{}}_{}^{}}$ f ${\displaystyle {{}_{}}_{}^{}R\frac{}{}}$ ${\displaystyle \frac{T}{}}$ ${\displaystyle \frac{V_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$- P ${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\displaystyle l_{}}$) ${\displaystyle d}$ ${\displaystyle V}$ ${\displaystyle \int_{V_{i}^{V_{f}}({\frac {RT}{V_{m}-{real}dV$의 양에 따라 이상적인 가스의 팽창 작업과는 다르다.

참고 항목

• 압축성인자
• 상태 방정식
• 이상적인 가스 법칙: 보일의 법칙과 게이 루삭의 법칙

참조

추가 읽기

• Kondepudi, D. K.; Prigogine, I. (1998). Modern thermodynamics: From heat engines to dissipative structures. John Wiley & Sons. ISBN 978-0-471-97393-5.
• Hsieh, J. S. (1993). Engineering Thermodynamics. Prentice-Hall. ISBN 978-0-13-275702-7.
• Walas, S. M. (1985). Fazovyje ravnovesija v chimiceskoj technologii v 2 castach. Butterworth Publishers. ISBN 978-0-409-95162-2.
• Aznar, M.; Silva Telles, A. (1997). "A Data Bank of Parameters for the Attractive Coefficient of the Peng-Robinson Equation of State". Brazilian Journal of Chemical Engineering. 14 (1): 19–39. doi:10.1590/S0104-66321997000100003.
• Rao, Y. V. C (2004). An introduction to thermodynamics. Universities Press. ISBN 978-81-7371-461-0.
• Xiang, H. W. (2005). The Corresponding-States Principle and its Practice: Thermodynamic, Transport and Surface Properties of Fluids. Elsevier. ISBN 978-0-08-045904-2.

외부 링크

• http://www.ccl.net/cca/documents/dyoung/topics-orig/eq_state.html