등가전위온도

일반적으로 teta-e (${\displaystyle {\theta }_{}}$ e${\displaystyle {}_{}}$) ${\$라고 하는 등가 전위 온도는 공기 소포의 압력 변화(즉, 대기 중 수직 이동 중) 동안 수증기가 응축되더라도 보존되는 수량이다$.$ 따라서 일반 전위 온도보다 보존이 잘 되어 불포화 수직 운동(압력 변화)에 대해서만 일정하게 유지된다.

${\displaystyle {\theta }_{}}$ ${\displaystyle e_{}}$ ${\$는 소포의 모든 수증기가 응축되어 잠열을 방출할 경우 공기 소포가 도달하는 온도로, 소포를 표준 기준 압력인 보통 해수면 대기압과 거의 동일한 1000hPa(1000mbar)로 가져왔다.

대기 안정성 추정에 사용

무압축 유체의 안정성

언덕 위에서 균형을 이룬 공처럼, 밀도가 낮은 액체 위에 놓여 있는 더 조밀한 액체는 역동적으로 불안정할 것이다: 뒤집히는 움직임(결합)은 무게중심을 낮출 수 있고, 따라서 자연적으로 일어날 것이며, 이것은 거의 항상 관찰되는 조건인 안정된 층화를 빠르게 만들어 낼 것이다. 압축 불가능한 액체의 안정성 조건은 높이에 따라 밀도가 단조롭게 감소한다는 것이다.

압축 공기의 안정성: 전위 온도

유체가 공기처럼 압축 가능한 경우, 동적 안정성의 기준은 대신 고정 기준 압력에서 유체의 밀도인 잠재적 밀도를 포함한다. 이상적인 기체의 경우(가스법 참조) 공기 기둥의 안정성 기준은 잠재적 온도가 높이에 따라 단조롭게 증가한다는 것이다.

이를 이해하려면 압력의 수직 변화가 크고 단열 온도 변화가 중요한 대기의 건조 대류를 고려하십시오. 공기 소포가 위로 이동하면 주변 압력이 떨어져 소포가 확장된다. 소포의 내부 에너지 중 일부는 기압에 맞서 팽창에 필요한 작업을 하는 데 소모되기 때문에 소포의 온도는 조금도 떨어지지 않았음에도 불구하고 떨어진다. 반대로 가라앉는 소포는 열을 가하지 않아도 압축되어 따뜻해진다.

산꼭대기의 공기는 대개 아래 계곡의 공기보다 차갑지만 배열이 불안정하지는 않다: 계곡의 공기 한 꾸러미를 어떻게든 산꼭대기까지 들어 올렸으면, 도착하였을 때는 이미 있는 공기보다 훨씬 더 차가울 것이다. 단열적인 냉방 때문에, 주변 공기보다 무거울 것이다. 원위치로 후퇴하다 마찬가지로 차가운 산꼭대기의 소포가 계곡으로 내려간다면 계곡 공기보다 따뜻하고 가벼워져 다시 산 위로 떠오를 것이다.

그러므로 온도의 높이에 따라 온도가 감소하는 한 따뜻한 공기 위에 놓여 있는 서늘한 공기는 안정적일 수 있다; 역동적으로 중요한 양은 온도가 아니라 잠재적 온도 - 공기가 기준 압력에 적응할 때 가질 수 있는 온도다. 산 주변의 공기는 압력이 낮아 상층부의 공기는 아래쪽의 따뜻한 공기보다 전위 온도가 높아 안정적이다.

물 응결의 영향: 등가 전위 온도

수증기가 충분히 상승할 경우, 수증기를 포함한 상승하는 공기는 상승된 응축 수준에 도달한다: 수증기에 포화 상태가 된다(Closius-Clapeyron 관계 참조). 공기의 소포가 계속 상승하면 수증기가 응축되어 잠열을 주변 공기로 방출하여 단열 냉각이 부분적으로 상쇄된다. 따라서 포화상태의 공기는 상승할 때 건조한 것보다 적게 냉각된다(건조 지방 소멸률보다 작은 습한 지방 소멸률에서 높이에 따라 온도가 변화한다). 이러한 포화상태의 공기는 부력을 얻을 수 있으며, 따라서 높이와 함께 잠재적 온도가 상승하더라도 더 상승할 수 있다. 포화 대류운동에 관해서도 공기열이 절대적으로 안정될 수 있는 충분한 조건은 등가 전위온도가 높이에 따라 단조롭게 증가해야 한다는 것이다.

공식

등가 전위 온도의 정의는 다음과 같다.^[1][2]

$\displaystyle \theta _{e}=T\left({\frac {p_{0}}}{p}}\오른쪽)^{R_{d}/(c_{pd}+r_{t}c)}H^{-r_{v}R_{v}/(c_{pd}+r_{t}c)}\exp \efrac[{\frac {L_{v}r_{v}}}}{(c_{pd}+r_{t}c)T}\오른쪽]}$

위치:

• ${\displaystyle T}$ ${\displaystyle T}$은(는) 압력 $p{\displaystyle }$ ${\displaystyle p}$에서 공기의 온도 [K]이다$.$
• ${\displaystyle p_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은(는) 1000 hPa로 취한 기준 압력이다.
• $[\displaystyle p}$는 지점의 압력이다.
• ${\displaystyle R_{}}$$$ ${\displaystyle d_{}}$ ${\$ 스타일 $R_{d}$ $및{\displaystyle {}_{}}$ R v ${\$ 스타일 $R_{$v}}은$($는) 건조한 공기와 수증기의 특정 가스 상수입니다.
• ${\displaystyle c_{}}$ ${\displaystyle p_{}}$ ${\displaystyle d_{}}$ ${\$ 및 $c$ ${\displaystyle c}$은(는) 각각 건조한 공기와 액체 상태의 특정 열 용량이다.
• ${\displaystyle r_{}}$ ${\displaystyle t_{}}$ ${\$ 및$$ $r{\displaystyle {}_{}}$ ${\displaystyle v_{}}$ ${\$은(는) 각각 총 수증기 혼합비, 수증기 혼합비,
• ${\displaystyle H}$ ${\displaystyle H}$은(는) 상대 습도,
• ${\displaystyle L_{}}$ ${\displaystyle v_{}}$ ${\$는 물의 증기화 잠열이다.

소포의 움직임을 따라 통합을 계산하는 것이 쉽지 않기 때문에 등가 전위 온도 계산에는 많은 대략적인 제형이 사용된다. 볼튼(1980)은 오류 추정과 함께 그러한 절차에 대한 검토를 한다. 정확도가 필요할 때 그의 최선의 근사 공식을 사용한다.

$\displaystyle \theta _{e}=\theta _{L}\exp \left[\frac {3036}{\frac){T_{L}}-1.78\오른쪽)r\왼쪽(1+0.448r\오른쪽)\오른쪽]}$

${\displaystyle \teta _{L}=T\left({p_{0}}{p-e}\오른쪽)^{\cappa _{d}\{\frac {T}{\frappa}{\frappa}{\}{\frc}{{T}}}{T_{L}}}\오른쪽)^{0.28r}$

${\displaystyle T_{L}={\frac {1}{{\frac {1}{\frac {1}{{\frac {1}{T_{d}-56}+{\frac {\log _{e}(T/T_{d}}}}}{800}}}}}}}}}}}}+56}$

위치:

• ${\displaystyle {\theta }_{}}$ ${\displaystyle L_{}}$ ${\$는 상승 응축 수준(LCL)에서 (건조) 전위 온도[K]이다$$.
• ${\displaystyle T_{}}$ ${\displaystyle L_{}}$ ${\$은(는) LCL에서 (추정) 온도[K]이다.
• ${\displaystyle T_{}}$ ${\displaystyle d_{}}$ ${\$은(는$)$ 압력 p {\$displaystyle p}$에서의 이슬점 온도$,$
• ${\displaystyle e}$ ${\displaystyle e}$은(건조한 ${\displaystyle {공기}_{}}$에 $대해{\displaystyle {}_{}}$air$$ L {\$displaystyle \theta _{L})$ 수증기 압력이다.
• ${\displaystyle {\kappa }_{}}$ ${\displaystyle d_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle d_{}}$/ c ${\displaystyle p_{}}$ ${\displaystyle d_{}}$ ${\$은(는) 일정한 압력(0.2854)에서 건조 공기의 특정 열에 대한 특정 가스 상수의 비율이다$$.
• ${\displaystyle r}$ $[\displaystyle r}$은(는) 질량당 수증기 질량의 혼합비[kg/kg]이다$$(때로는 [g/kg]^[4]에 값이 주어지며, 이 값은 1000으로 나누어야 한다).

좀 더 이론적인 공식은 이론적 설명이 중요한 홀튼(1972)과 같은 문학에서 일반적으로 사용된다.

${\displaystyle \theta _{e}\약간 \theta _{L}\exp \left[{\frac {r_{s}(T_{L}))L_{v}(T_{L})}{c_{pd}T_{L}}\오른쪽]}$

위치:

• ${\displaystyle r_{}}$ (${\displaystyle {}_{}{T}_{}}$ ${\displaystyle L_{}}$) ${\displaystyle r_{s}(T_{L})}$은(는) 온도 $T{\displaystyle {}_{}}$ ${\displaystyle L_{}}$ ${\$에서 물의 포화 혼합비$,$ 공기의 포화 수준에서의 온도,
• ${\displaystyle L_{}}$ ${\displaystyle v_{}}$( ${\displaystyle T_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle L_{v}(T_{L})}$은(는) $온도{\displaystyle {}_{}}$ T ${\displaystyle L_{}}${\$displaystyle T_{L}}}($40°C에서 2406 kJ/kg, 0°C에서)에서 및
• ${\displaystyle c_{}}$ ${\displaystyle p_{}}$ ${\displaystyle d_{}}$ ${\$는 일정한 압력(1005.7J/(kg·K)에서 건조한 공기의 특정 열이다.

$T{\displaystyle {}_{}}$ ${\displaystyle L_{}}$ ${\$의 계산을 피하는 것이 바람직한 경우, 단순화를 위해 더 간단한 공식(예: Stull 1988^[6] §13.1 페이지 546)을 사용한다$.$

$\displaystyle \theta _{e}=T_{e}\left({\frac {p_{0}}{p}}\right)^{\kappa _{d}}\approx \left(T+{\frac {L_{v}}{c_{pd}}}r\right)\left({\frac {p_{0}}{p}}\right)^{\frac {R_{d}}{c_{pd}}}}$

위치:

• ${\displaystyle T_{}}$ ${\displaystyle e_{}}$ ${\$ $$= 등가 온도
• ${\displaystyle R_{}}$ ${\displaystyle d_{}}$ ${\$ 스타일 $R_{d}$ $$= 공기에 대한 특정 가스 상수(287.04 J/(kg·K))

사용법

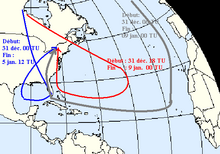
이는 기단의 특성화를 위한 시놉틱 스케일에 적용된다. 예를 들어 1998년 북미아이스톰에 대한 연구에서 갸쿰 교수(맥길 대학교, 몬트리올)와 뢰버 교수(위스콘신-밀워키 대학교)는 관련 기단이 지난주 고도 300~400hPa의 높은 북극에서 발생했으며 열대지방으로 이동하면서 지표면을 향해 내려갔다는 사실을 입증했다.암탉은 미시시피 계곡을 따라 세인트 로렌스 계곡을 향해 다시 올라갔다. 후방 궤적은 일정한 등가 전위 온도를 사용하여 평가되었다.^[7]

메소스케일에서는 등가 전위온도 불포화 대기의 정적 안정성을 측정하는 데 유용한 척도가 된다. 정상적이고 안정적인 층화 조건에서 전위 온도는 높이에 따라 증가한다.

${\displaystyle {\frac {\reason \theta_{e}{\reason z}}0}$

수직적 동작이 억제된다. 높이에 따라 등가 전위 온도가 감소할 경우,

${\displaystyle {\frac {\reason \theta_{e}{\reason z}<0}$

대기는 수직운동에 불안정하며 대류가 발생할 가능성이 높다. 포화 공기의 불안정성을 나타내는 높이에 따라 등가 전위 온도가 감소하는 상황은 매우 흔하다.

참고 항목

• 기상학
• 촉촉한 정적 에너지
• 전위 온도
• 일기예보

참고 문헌 목록

• 1989년 1월 1일, Butterworth-Heinemann이 발행한 M K Yau와 R.R. Rogers, 클라우드 물리학 단기 과정, 제3판, 304쪽. ISBN9780750632157ISBN0-7506-3215-1

참조