호킹 복사

일반상대성이론
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }=t_{\mu \nu }}$
서론 역사 수학 공식화 테스트
기본 개념 등가원칙 특수상대성이론 월드 라인 유사 리만 다양체
현상 케플러 문제 중력 렌즈 중력파 프레임 드래그 측지 효과 이벤트 호라이즌 특이점 블랙홀 시공간 시공간도 민코프스키 시공간 아인슈타인-로젠 다리
방정식 형식주의 방정식 선형 중력 아인슈타인 장 방정식 프리드만 측지학 매티슨-파페트루-딕슨 해밀턴-야코비-아인슈타인 형식주의 ADM BSSN 포스트뉴턴어 고급 이론 칼루자-클레인 이론 양자 중력
솔루션 슈바르츠실트(내부) 리스너-노르드스트롬 괴델 커 커-뉴먼 카스너 레마슈트르톨만 타우부 너트 밀른 로버트슨-워커 pp파 반스톡툼 더스트 바일루이스파파페트로우
과학자 아인슈타인 로렌츠 힐베르트 푸앵카레 슈바르츠실트 드 시터 리스너 노드스트롬 와일 에딩턴 프리드먼 밀른 즈위키 레마슈트르 괴델 휠러 로버트슨 바딘 워커 커 찬드라세카르 엘러스 펜로즈 호킹 레이쇼후리 테일러 헐스 반 스톡텀 타우브 뉴먼 야우 손 다른이들
물리 포털 카테고리
v t

호킹 복사는 상대론적 양자 효과 때문에 블랙홀의 사건 지평선 밖으로 방출되는 것으로 이론화된 열 복사이다.그것은 1974년에 ^[1]그것의 존재에 대한 이론적 주장을 개발한 물리학자 스티븐 호킹의 이름을 따서 붙여졌다.호킹 방사선은 사건의 지평선이나 국소적인 겉보기 ^[2][3]지평선을 포함하는 로렌츠 기하학의 일반적인 운동학적 효과이다.

호킹 복사는 블랙홀의 질량과 회전 에너지를 감소시키고 따라서 블랙홀의 증발을 유발하는 것으로 이론화된다.이 때문에 다른 방법으로 질량을 얻지 못하는 블랙홀은 줄어들어 결국 사라질 것으로 예상된다.가장 작은 블랙홀을 제외한 모든 블랙홀은 매우 천천히 일어날 것입니다.복사 온도는 블랙홀의 질량과 반비례하기 때문에 마이크로 블랙홀은 더 큰 블랙홀보다 더 큰 방사선을 방출하고 더 ^[4]빨리 소멸할 것으로 예측됩니다.

개요

블랙홀은 주로 작은 크기와 엄청난 중력 때문에 천체물리학적 물체이다.그것들은 아인슈타인의 1915년 일반상대성이론에 의해 처음 예측되었고, 반세기 후에 천체물리학적 증거가 쌓이기 시작했다.

블랙홀은 충분한 물질 및/또는 에너지가 빛의 속도보다 탈출 속도가 클 정도로 작은 부피로 압축될 때 형성될 수 있다.그 어떤 것도 그렇게 빨리 이동할 수 없기 때문에, 블랙홀의 질량에 비례하는 거리 내의 어떤 것도 그 거리를 벗어날 수 없습니다.빛조차 빠져나갈 수 없는 영역은 사건 지평선이다. 사건 지평선 밖의 관찰자는 사건 지평선 내의 사건을 관찰하거나 인지하거나 영향을 받을 수 없다.블랙홀의 본질은 사건의 지평선, 사건과 그 인과관계 ^{[5]: 25–36} 사이의 이론적 경계선이다.

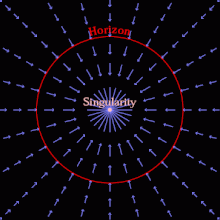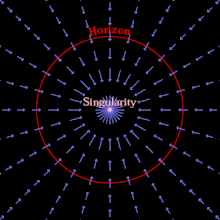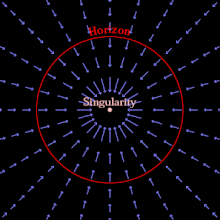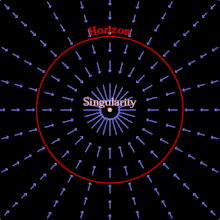
또는, 일반 상대성 이론에서 일련의 유입 좌표를 사용하여, 사람들은 사건의 지평선을 빛의 속도보다 더 빠르게 유입되는 영역으로서 개념화할 수 있다. (빛보다 더 빠르게 우주를 여행할 수 있는 것은 없지만, 우주 자체는 어떤 속도로도 유입될 수 있다.)^[6]일단 물질이 사건의 지평선 안에 있게 되면, 내부의 모든 물질은 어떠한 물질도 없는 뒤틀린 시공간을 남겨두고 무한 곡률의 장소인 중력 특이점으로 떨어질 것이다.고전적인 블랙홀은 순수한 빈 공간이며, 가장 단순한(회전하지 않고 충전되지 않은) 블랙홀은 질량과 사건의 ^{[5]: 37–43} 지평선으로 특징지어집니다.

양자 물리학에 대한 우리의 현재 이해는 사건의 지평선 주변에서 일어날 수 있는 일을 조사하는데 사용될 수 있다.1974년, 영국의 물리학자 스티븐 호킹은 이론적으로 사건 지평선에서의 중력이 열 방사선을 방출하고 에너지가 사건 지평선 안팎의 아주 작은 거리에서 더 넓은 우주로 "누출"할 만큼 강하다는 것을 보여주기 위해 곡선 시공간에서의 양자장 이론을 이용했다.실제로 이 에너지는 블랙홀 자체가 천천히 증발하는 것처럼 작용했다.^[7]

호킹 박사가 계산한 블랙홀 방사선과 흑체로부터 방출된 열 방사선의 중요한 차이점은 흑체 복사는 본질적으로 통계적이고, 그 평균만이 플랑크의 흑체 복사의 법칙이라고 알려진 것을 충족시키는 반면, 전자는 데이터에 더 잘 들어맞는다는 것이다.따라서, 열복사는 그것을 방출한 물체에 대한 정보를 포함하고 있는 반면, 호킹복사는 그러한 정보를 포함하고 있지 않고 블랙홀의 질량, 각운동량, 그리고 전하에만 의존합니다.이는 블랙홀 정보의 역설로 이어진다.

그러나 추측된 게이지-중력 이중성(AdS/CFT 대응으로도 알려져 있음)에 따르면, 특정 경우(그리고 아마도 일반적으로) 블랙홀은 0이 아닌 온도에서 양자장 이론의 해와 동등합니다.즉, (이론은 그러한 손실을 허용하지 않기 때문에) 블랙홀에서는 정보 손실이 예상되지 않으며, 블랙홀에서 방출되는 방사선은 아마도 일반적인 열 복사일 것이다.만약 이것이 맞다면, 호킹의 원래 계산은 수정될 것입니다. 하지만 어떻게 된지는 알 수 없습니다(아래 참조).

태양질량 M_☉1개의 블랙홀()의 온도는 60나노켈빈(600억분의 1 켈빈)에 불과하며, 실제로 이러한 블랙홀은 방출하는 것보다 훨씬 더 많은 우주 마이크로파 배경 방사선을 흡수할 것이다.4.5×10²² kg의 블랙홀(달의 질량 또는 약 133 μm 너비)은 2.7 K에서 평형을 이루며 ^{[citation needed]}방출되는 만큼의 방사선을 흡수할 것이다.

검출

호킹의 발견은 1973년 소련 과학자 야코프 젤도비치와 알렉세이 스타로빈스키는 그에게 회전하는 블랙홀이 입자를 만들어 내고 방출해야 한다고 확신시킨 반면, 러시아의 물리학자 블라디미르 그리보프는 심지어 회전하지 않는 블랙홀도 방사선을 방출해야 한다고 믿었다.호킹이 계산을 했을 때, 그는 놀랍게도 그것이 ^[8]사실이라는 것을 알았다.1972년, 제이콥 베켄스타인은 블랙홀이 ^[9]엔트로피를 가져야 한다고 추측했고, 같은 해에는 머리카락이 없는 이론을 제안했다.베켄슈타인의 발견과 결과는 스티븐 호킹이 칭찬한 것으로, 이 형식주의로 인해 그는 방사선에 대해 생각하게 되었다.

물리학자인 드미트리 디아코노프에 따르면, 젤도비치 모스크바 1972-1973년 세미나에서 젤도비치와 블라디미르 그리보프 사이에 논쟁이 있었다고 한다.젤도비치는 회전하는 블랙홀만이 방사선을 방출할 수 있다고 믿었고 그리보프는 회전하지 않는 블랙홀도 양자역학의 ^[10][11]법칙으로 인해 방사선을 방출한다고 믿었다.이 설명은 Vitaly Ginzburg ^[12][13]등의 Physical-Uspekhi에 실린 그리보프의 부고를 통해 확인된다.

배출 과정

호킹 방사선은 언루 효과와 블랙홀 지평선에 적용되는 등가 원리에 의해 요구됩니다.블랙홀의 사건 지평선에 가까운 곳에서, 국지적인 관측자는 빠지지 않기 위해 가속해야 합니다.가속 관찰자는 국소 가속 지평선에서 튀어나와 방향을 틀고 자유 낙하하는 입자의 열욕을 봅니다.국소 열평형 상태는 이 국소 열욕의 일관된 확장이 무한대에서 유한한 온도를 가지며, 이는 지평선에 의해 방출된 입자의 일부가 재흡수되지 않고 호킹 ^[14][15]방사선이 된다는 것을 의미한다.

슈바르츠실트 블랙홀은 측정 기준을 가지고 있다.

$(\displaystyle (\mathrm {d}s)^{2}=-\left(1-{\tfrac {2M}{r}}\right}), (\mathrm {d} t)^{2}+{\frac {1}{\left(1-{\frac {2M}{r}\right}}}}}}}}}}}}, (\leftr)^{{{{2}}}}}}}}, {\left}, {\left}}}, {\left}, {\left}}$

블랙홀은 양자장 이론의 배경 시공간이다.

필드 이론은 로컬 경로 적분에 의해 정의되므로 수평선에서의 경계 조건이 결정되면 필드 외부 상태가 지정됩니다.적절한 경계 조건을 찾으려면 수평선 바로 바깥에 있는 정지 상태의 관찰자를 고려하십시오.

${\displaystyle r=2M+{\frac {rho ^{2}}{8M}}$

가장 낮은 순서의 로컬 메트릭은 다음과 같습니다.

${\displaystyle(\mathrm {d}s)^{2}=-\leftflac\frac {rho }{4M}}\right)^{2}, (\mathrm {d} t)^{2}+(\mathrm {d} X_{\perp})^{2}=-\rho ^{2}, (\mathrm {d} \rho }^{2}+(\mathrmathrm {d})^{2}+(\rmathrmathrm {d} )$

어떤 Rindler τ).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}t/4M.메트릭은 블랙홀에 빠지지 않기 위해 가속하는 프레임을 나타냅니다.국부 가속도 α = 1/diples는 θ → 0으로 분산된다.

지평선은 특별한 경계가 아니며 물체가 빠질 수 있습니다.따라서 국소 관찰자는 일반 민코프스키 공간에서 등가의 원리에 의해 가속된다고 느낄 것이다.수평에 가까운 관찰자는 국소 온도에서 들뜬 필드를 보아야 합니다.

${{displaystyle T=beak frac {2\pi }}=beak frac {1}{2\pi \rho }}=beak frac {4\pi {2Mr\left(1-{\frac {2M}{r}}}{r}\오른쪽)}}}},}$

언루 효과입니다.

중력 적색 편이는 미터법의 시간 성분의 제곱근에 의해 주어집니다.따라서 필드 이론 상태가 일관되게 확장되려면 모든 곳에 열적 배경이 존재해야 하며, 로컬 온도는 거의 수평선 온도에 일치해야 합니다.

${\displaystyle T(r')=pi {4\pi {2Mr\left(1-{\frac {2M}{r}}\오른쪽)}}}}{\frac {1-{\frac {2M}{r'}}}}=frac {1-{\frac {2M}{r'}}}}=frac {4\pi {2Mr\left(1-{\frac {2M}{r}}}}}}}}}}}}}}.$

무한대에서 rµ로 적색 편이된 역온도는 다음과 같습니다.

${\displaystyle T(\infty)=black {1}{4\pi {blashrt {2Mr}}},$

r은 수평에 가까운 위치이고 2M에 가깝기 때문에 이것은 정말로

${\displaystyle T(\infty)=black {1}{8\pi M}}$

따라서 블랙홀 배경에서 정의된 자기장 이론은 무한대에서의 온도가 다음과 같은 열 상태에 있습니다.

$\displaystyle T_{\text{H}}=flac {1}{8\pi M}}.}$

블랙홀 온도에서 블랙홀 엔트로피 S를 계산하는 것은 간단하다.열 dQ의 양이 추가되었을 때 엔트로피의 변화는

${\displaystyle \mathrm {d} S=sq frac {mathrm {d} {T}}=8\pi M,\mathrm {d} Q.}$

유입되는 열 에너지는 총 질량을 증가시키는 역할을 합니다.

$\displaystyle \mathrm {d} S=8\pi M,\mathrm {d} M=\mathrm {d}(4\pi M^{2}).}$

블랙홀의 반지름은 플랑크 단위의 질량의 두 배이므로 블랙홀의 엔트로피는 표면적에 비례합니다.

${\displaystyle S=\pi R^{2}=syslogfrac {A}{4}}.}$

작은 블랙홀의 엔트로피가 0이라고 가정하면 적분 상수는 0입니다.블랙홀을 형성하는 것은 질량을 영역으로 압축하는 가장 효율적인 방법이며, 이 엔트로피는 또한 시공간의 모든 구체의 정보 내용에 대한 구속입니다.결과의 형태는 중력 이론의 물리적 묘사가 어떤 식으로든 경계 표면에 부호화될 수 있다는 것을 강하게 시사한다.

블랙홀 증발

입자가 빠져나갈 때, 블랙홀은 소량의 에너지를 잃고 따라서 질량의 일부를 잃게 된다(질량과 에너지는 아인슈타인의 방정식 E = mc에² 의해 관련된다).따라서 증발하는 블랙홀의 수명은 유한할 것이다.차원 분석을 통해 블랙홀의 수명은 초기 ^{[16][17]: 176–177} 질량의 입방체로 확장된다는 것을 알 수 있으며, 호킹 박사는 초기 우주에서 약 10g의¹⁵ 질량을 가진 블랙홀이 ^[18]오늘날까지 완전히 증발했을 것이라고 추정했다.

1976년 돈 페이지는 질량 ^[16]M의 무회전 무충전 슈바르츠실트 블랙홀에 대해 생성된 전력과 증발까지의 시간을 계산함으로써 이 추정치를 구체화했다.블랙홀의 이벤트 수평선 또는 엔트로피가 절반으로 줄어드는 시간을 페이지 ^[19]시간이라고 합니다.유한한 크기의 블랙홀이 완벽한 흑체가 아니라는 사실로 인해 계산이 복잡해지고, 특히 파장이 사건 지평선의 크기와 비슷해지면 주파수가 감소함에 따라 흡수 단면이 복잡하고 스핀에 의존적인 방식으로 감소합니다.페이지는 원시 블랙홀의 초기 질량이 대략 4×10¹¹ kg 이상일 경우에만 오늘날까지 생존할 수 있다고 결론지었다.1976년 당시 중성미자에 대한 이해를 이용한 페이지는 중성미자가 질량이 없고 두 가지 중성미자 맛만 존재한다고 가정하고 잘못 연구했다. 따라서 블랙홀 수명에 대한 그의 결과는 질량이 0이 아닌 중성미자의 세 가지 맛을 고려한 현대의 결과와 일치하지 않는다.2008년 우주 연령에 대한 표준 모델과 WMAP 수치를 사용한 계산에서는 질량 한계가 (5.00±0.04)이었다.×10^{11 [20]}kg

만약 블랙홀이 호킹 복사로 증발한다면,^[21] 태양질량 블랙홀은 우주의 나이보다 훨씬 긴 10년에⁶⁴ 걸쳐 증발할 것이다.질량이 100(1000억 개)인¹¹ 초대질량 블랙홀M_☉ 약 2×^[22]10년¹⁰⁰ 후에 증발할 것입니다.우주의 몇몇 괴물 블랙홀은 아마도 10개까지¹⁴ 계속 자랄 것으로 예측된다. M_☉ 은하계의 초은하단이 붕괴되는 동안.이마저도 최대 10년의^{106 [21]}기간에 걸쳐 증발할 수 있습니다.

호킹 복사 형태의 블랙홀이 방출하는 힘은 회전하지 않고 대전하지 않는 질량 M의 슈바르츠실트 블랙홀의 가장 단순한 경우로 쉽게 추정할 수 있습니다.블랙홀의 슈바르츠실트 반지름 공식, 흑체 복사의 스테판-볼츠만의 법칙, 복사 온도에 대한 위의 공식, 구체 표면적의 공식(블랙홀의 이벤트 수평선)을 조합하여 여러 방정식을 도출할 수 있다.

호킹 복사 온도는 다음과 같습니다.^[4][23][24]

${\displaystyle T_{\mathrm {H} = scfrac {hbar c^{3}} {8\pi GMk_{\mathrm {B}}}}$

순수 광자 방출(즉, 다른 입자가 방출되지 않음) 가정과 지평선이 복사 표면이라는 가정 하에 블랙홀의 베켄슈타인-호킹 광도는 다음과 같다.^[24][23]

$({displaystyle P=blac {hbar c^{6}}}{15360\pi G^{2}M^{2}}})$

여기서 P는 광도, 즉 복사 전력, θ는 감소된 플랑크 상수, c는 빛의 속도, G는 중력 상수, M은 블랙홀의 질량이다.위의 공식은 아직 반고전적 중력의 틀에서 도출되지 않았다는 것을 언급할 필요가 있다.

블랙홀이 소멸하는 데 걸리는 시간은 다음과 같습니다.^[24][23]

${\displaystyle t_{\mathrm {ev} = flac {5120\pi G^{2}M^{3}} {\hbar c^{4}} = flac {blacc^{2}}V}{\hbar G}}\times 10^{67},{\text{years}}\left({\frac {M}{M_{\odot}}\right)^{3}}$

여기서 M과 V는 블랙홀의 질량과 (슈바르츠실트) 부피이다.태양질량 M_☉1개(= 2.0×10³⁰ kg)의 블랙홀이 증발하는 데는 10년 이상이⁶⁷ 걸리며, 이는 현재 우주의 나이인¹⁰ 1.4×^[25]10년보다 더 긴 것입니다.그러나 블랙홀이 10kg일¹¹ 경우 증발 시간은 2.6×10년입니다⁹.이것이 일부 천문학자들이 원시 블랙홀의 폭발의 징후를 찾는 이유이다.

그러나 우주에는 우주 마이크로파 배경 복사가 포함되어 있기 때문에 블랙홀이 소멸하기 위해서는 현재 우주의 흑체 복사 온도 2.7K보다 더 높은 온도가 있어야 한다.한 연구에 따르면 M은 지구^[26] 질량의 0.8% 미만이어야 하며 이는 대략 달의 질량에 해당한다.

블랙홀 증발은 다음과 같은 몇 가지 중요한 결과를 초래합니다.

• 블랙홀의 증발은 블랙홀이 우주의 나머지 부분과 어떻게 열적으로 상호작용하는지를 보여줌으로써 블랙홀 열역학에 대한 보다 일관된 관점을 만들어냅니다.
• 대부분의 물체와 달리 블랙홀의 온도는 질량을 방출할 때 높아집니다.온도 상승 속도는 기하급수적이며, 가장 가능성이 높은 끝점은 감마선의 격렬한 폭발로 블랙홀이 분해되는 것이다.그러나 이 해소에 대한 완전한 설명은 양자 중력 모델을 필요로 합니다. 블랙홀의 질량이 플랑크 질량에 근접할 때 발생하며, 그 반지름 또한 플랑크 길이 2개에 근접할 것입니다.
• 가장 단순한 블랙홀 증발 모델은 블랙홀 정보의 역설로 이어집니다.이러한 모델에서는 호킹 복사가 무작위이기 때문에 블랙홀의 정보 내용은 소멸될 때 손실되는 것으로 보입니다(원래 정보와는 무관합니다).이 문제에 대한 많은 해결책이 제시되었는데, 여기에는 호킹 방사선이 누락된 정보를 포함하기 위해 교란되고, 호킹 증발은 누락된 정보를 포함하는 어떤 형태의 잔여 입자를 남기며, 이러한 조건 하에서 정보가 손실될 수 있다는 제안들이 포함되어 있다.

문제와 확장

플랑크 횡단 문제

플랑크 횡단 문제는 호킹 박사가 당초 계산한 블랙홀 지평선 부근의 플랑크 길이보다 파장이 짧아지는 양자 입자를 포함한다는 점이다.이것은 시간이 멀리서 측정될 때 멈추는 그곳의 독특한 행동 때문이다.한정된 주파수로 블랙홀에서 방출된 입자는 지평선까지 거슬러 올라가면 무한대의 주파수를 가졌을 것이고, 따라서 행성 간 파장을 가졌을 것이다.

언루 효과와 호킹 효과 모두 표면적으로 정지된 시공간에서 지평선에 걸쳐 규칙적인 다른 좌표에 대해 상대적인 빈도를 변경하는 필드 모드에 대해 설명합니다.수평선 밖에 있기 위해서는 도플러의 모드 ^{[citation needed]}전환이 끊임없이 필요한 가속이 필요하기 때문에 이것은 필연적으로 그렇습니다.

만약 이 모드가 과거로 거슬러 올라가면, 호킹 방사선의 발신 광자는 지평선에 가까워질수록 먼 거리에 있는 광자와 다른 주파수를 갖게 되는데, 이것은 블랙홀의 지평선에서 광자의 파장이 무한히 "스쿼치업"되어야 하는 것이다.최대로 확장된 외부 슈바르츠실트 솔루션에서 이 광자의 주파수는 관찰자가 갈 수 없는 과거 영역으로 다시 확장될 경우에만 규칙적인 상태를 유지합니다.그 지역은 관측할 수 없는 것으로 보이며 물리적으로 의심스럽다. 그래서 호킹 박사는 과거에 유한한 시간에 형성된 과거 영역이 없는 블랙홀 용액을 사용했다.이 경우, 모든 발신 광자의 출처를 확인할 수 있습니다. 즉, 블랙홀이 처음 형성된 바로 그 순간에 있는 미세한 점입니다.

호킹 박사가 처음에 계산한 그 작은 점에서의 양자 변동에는 모든 방출 방사선이 포함되어 있습니다.결국 방출되는 방사선을 오랜 시간에 포함하는 모드는 플랑크 길이보다 훨씬 짧은 파장을 가진 모드로 출발하는 이벤트 수평선 옆에 오래 머무르는 것에 의해 매우 큰 양의 적색편이 된다.그렇게 짧은 거리에서의 물리 법칙은 알려져 있지 않기 때문에, 어떤 사람들은 호킹의 원래 계산이 ^{[27][28][29][30]}설득력이 없다고 생각한다.

오늘날 플랑크 횡단 문제는 대부분 지평선 계산의 수학적 인공물로 여겨진다.일반 물질이 화이트 홀 용액에 떨어지는 경우에도 동일한 효과가 발생합니다.화이트 홀에 떨어진 물질은 축적되지만, 그것이 들어갈 수 있는 미래 영역은 없습니다.이 물질의 미래를 추적하면서, 그것은 화이트 홀 진화의 마지막 단일 끝점인 플랑크 횡단 지역으로 압축됩니다.이러한 유형의 분기의 이유는 외부 좌표의 관점에서 수평선에서 끝나는 모드의 주파수가 특이하기 때문이다.고전적으로 무슨 일이 일어나는지 알 수 있는 유일한 방법은 수평선을 가로지르는 다른 좌표를 확장하는 것입니다.

행성 횡단 문제를 ^{[citation needed]}다루는 호킹호에게 방사선을 주는 대체 물리 사진들이 존재한다.요점은 Unruh 방사선에 점유된 모드를 ^[14]과거로 추적할 때 유사한 Planckian 횡단 문제가 발생한다는 것이다.언루 효과에서, 온도의 크기는 일반적인 민코프스키 장 이론에서 계산될 수 있으며, 논란의 여지가 없습니다.

대형 추가 치수

이전 섹션의 공식은 중력의 법칙이 플랑크 척도까지 거의 유효할 경우에만 적용할 수 있습니다.특히 질량이 플랑크 질량 이하⁻⁸(~10 kg)인 블랙홀은 플랑크 시간 이하(~10⁻⁴³ 초)에 수명이 불가능하다.이는 일반적으로 플랑크 질량이 블랙홀 질량의 하한치임을 나타내는 것으로 보인다.

큰 추가 차원(10 또는 11)을 가진 모형에서는 플랑크 상수의 값이 근본적으로 다를 수 있으며 호킹 방사선의 공식도 수정해야 합니다.특히, 추가 차원보다 반경이 작은 마이크로 블랙홀의 수명은 Cheung(2002)^[31]의 식 9와 Car(2005)^[32]의 식 25, 26에 의해 주어진다.

$\displaystyle \sim {1} {M_{*}}\left({\frac {M_{\text{B})H}} {M_{*}}\right}^{\frac {n+3}{n+1}}}$

여기서_∗ M은 몇 TeV만큼 낮을 수 있는 낮은 에너지 척도이고, n은 큰 추가 차원의 수이다.이 공식은 현재 "새로운 플랑크 시간" ~ 10초⁻²⁶ 정도의 수명을 가진 수 TeV만큼 가벼운 블랙홀과 일치합니다.

인루프 양자 중력

블랙홀 이벤트 지평선의 양자 기하학에 대한 자세한 연구는 루프 양자 ^[33][34]중력을 이용하여 이루어졌다.루프 양자화는 자유 파라미터의 값이 다양한 상수를 상쇄하도록 설정되지 않는 한 베켄스타인-호킹 엔트로피 공식이 재현되지 않는 한 원래 베켄스타인과 호킹에 의해 발견된 블랙홀 엔트로피의 결과를 재현하지 않는다.그러나 블랙홀의 엔트로피와 방사선에 대한 양자 중력 보정은 이 이론을 바탕으로 계산되었다.

지평선 영역의 변동에 기초하여, 양자 블랙홀은 호킹의 스펙트럼에서 이탈을 나타내며, 만약 호킹이 증발하는 원시 블랙홀의 X선을 ^[35]관측한다면 관측할 수 있을 것이다.양자 효과는 호킹의 방사선 ^[36]스펙트럼 위에서 매우 뚜렷하게 나타나는 일련의 이산적이고 혼합되지 않은 주파수에서 집중된다.

실험 관찰

천문학적 탐색

2008년 6월, NASA는 원시 블랙홀의 증발에서 예상되는 감마선 섬광을 찾는 페르미 우주 망원경을 발사했다.

중이온 충돌기 물리학

추측에 근거한 대규모 추가 차원 이론이 맞다면, CERN의 강입자 충돌기는 마이크로 블랙홀을 생성하고 그 증발을 관찰할 수 있을 것입니다.CERN에서는 ^{[37][38][39][40]}이러한 미세 블랙홀이 관측되지 않았습니다.

실험적인

중력계에 대해 실험적으로 달성 가능한 조건하에서, 이 효과는 직접 관찰하기에는 너무 작다.호킹 방사선은 소리 섭동이 중력 블랙홀의 빛과 비슷하고 거의 완벽한 유체의 흐름은 ^[41]중력과 유사하다는 소닉 블랙홀을 이용한 유추로 연구될 수 있을 것으로 예측되었다.보즈-아인슈타인 ^[42][43][44]응축체를 이용한 소닉 블랙홀에서 호킹의 방사선을 관측한 것이 보고되었다.

2010년 9월, 실험 설정은 실험실의 "화이트 홀 이벤트 지평선"을 만들어 냈고, 실험자들은 호킹의 ^[45]방사선과 유사한 광학적 방사선을 방출하는 것으로 나타났다고 주장했다.그러나, 그 결과는 검증되지 ^[46][47]않고 논란의 여지가 있으며, 진정한 확인이라는 그것의 지위는 여전히 ^[48]의문으로 남아있다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

• 호킹 방사선 계산 도구
• 미니 블랙홀 A의 케이스.Barau & J. Grain은 호킹 방사선이 어떻게 충돌기에서 검출될 수 있는지를 설명합니다.