마이크로캐논 앙상블

통계역학
열역학 운동 이론
입자 통계 스핀-통계 정리 동일입자 맥스웰-볼츠만 보스아인슈타인 페르미-디락 패러스타틱스 애니오닉 통계량 브레이드 통계량
열역학적 앙상블 NVE 마이크로캐논학 NVT 규범적 µVT 그랜드 캐논어 NPH 이센탈피크-이소바르어 NPT 등온-이소바르식
모델 데비예 아인슈타인 이싱 팟츠
가능성 내부 에너지 엔탈피 헬름홀츠 자유 에너지 기브스 자유 에너지 잠재력 / 란다우 자유 에너지
과학자들 맥스웰 볼츠만 깁스 아인슈타인 에렌페스트 폰 노이만 톨먼 데비예 페르미 보스
v t

통계 역학에서 마이크로캐논 앙상블은 총 에너지가 정확하게 명시된 기계 시스템의 가능한 상태를 나타내는 통계적 앙상블이다.^[1] 이 시스템은 에너지나 입자를 환경과 교환할 수 없다는 의미에서 격리되어 (에너지의 보존에 의해) 시스템의 에너지가 시간에 따라 변하지 않는다고 가정한다.

마이크로캐논술 앙상블의 1차 거시적 변수는 시스템 내 총 입자 수(기호: N), 시스템 볼륨(기호: V), 시스템 내 총 에너지(기호: E)이다. 이들 각각은 앙상블에서 일정한 것으로 가정한다. 이 때문에 마이크로캐논 앙상블을 NVE 앙상블이라고 부르기도 한다.

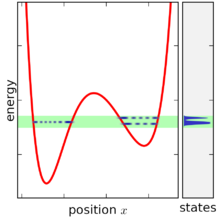
간단히 말해서, 마이크로캐논 앙상블은 에너지가 E를 중심으로 한 범위 안에 드는 모든 미시 상태에 동일한 확률을 할당함으로써 정의된다. 다른 모든 미세한 물질은 0의 확률이 주어진다. 확률은 최대 1까지 추가되어야 하기 때문에, 확률 P는 에너지 범위 내의 마이크로스테이트 W 수의 역행이다.

${\displaystyle P=1/W,}$

그런 다음 에너지의 범위는 무한히 좁을 때까지 폭에서 감소하고, 여전히 E를 중심으로 한다. 이 과정의 한계에 이르러서는 마이크로캐논 앙상블을 얻는다.^[1]

적용가능성

평형통계역학의 기본적인 가정(특히, preferious alqual probability의 가정)과 연관성이 있기 때문에, 마이크로캐논술 앙상블은 이론에서 중요한 개념적 구성 요소다.^[2] 평형통계역학의 근본적인 분포로 여겨지기도 한다. 그것은 또한 분자 역학 같은 몇몇 수치적 응용에서도 유용하다.^[3][4] 한편, 대부분의 비경쟁 시스템은 마이크로캐논 앙상블에서 수학적으로 설명하기가 번거롭고 엔트로피와 온도의 정의에 관한 모호함도 있다. 이러한 이유로 이론적 계산을 위해 다른 앙상블이 선호되는 경우가 많다.^[2][5][6]

실제 시스템에 마이크로캐논 앙상블의 적용가능성은 에너지 변동의 중요성에 따라 달라지는데, 이는 시스템을 준비할 때 제어되지 않은 요소뿐만 아니라 시스템과 그 환경 사이의 상호작용에서 비롯될 수 있다. 일반적으로 시스템이 거시적으로 크거나 정확히 알려진 에너지로 제조된 후 그 환경으로부터 거의 격리된 상태로 유지되는 경우 변동은 무시할 수 있다.^[7] 이런 경우 마이크로캐논 앙상블이 적용된다. 그렇지 않으면 표준 앙상블(불꽃나는 에너지)이나 웅장한 표준 앙상블(불꽃나는 에너지와 입자 번호)과 같이 서로 다른 앙상블이 더 적합하다.

특성.

열역학적 수량

마이크로캐논 앙상블의 근본적인 열역학적 잠재력은 엔트로피다. 에너지의 총 개수가 E 미만인 상태 수를 계산하는 위상 볼륨 함수 v(E)에 대해 각각 주어진 정의는 최소한 세 개 있다(v의 수학적 정의는 정밀식 섹션 참조).

마이크로캐논술 앙상블에서 온도는 외부 제어 파라미터가 아닌 파생 수량이다. 그것은 에너지와 관련하여 선택된 엔트로피의 파생물로 정의된다.^[8] 예를 들어 다음과 같이 "온도" T와_v T를_s 정의할 수 있다.

${\displaystyle 1/T_{v}=dS_{v}/dE,}$

${\displaystyle 1/T_{s}=dS_{s}/dE=dS_{\text{B}/dE.}$

엔트로피처럼 마이크로캐논 앙상블에서 온도를 이해하는 방법은 여러 가지가 있다. 보다 일반적으로, 이러한 앙상블 기반의 정의와 열역학적 정의 간의 대응은 특히 유한한 시스템에 대해서는 완벽하지 않다.

마이크로캐논 압력과 화학적 전위는 다음을 통해 주어진다.^[9]

${\displaystyle {\frac {p}{T}}={\frac {\partial S}{\partial V};\qquad {\frac {\mu }}}=-{\frac {\partial S}{\partial N}}}}}}$

위상 전환

그들의 엄격한 정의에 따르면, 위상 전환은 열역학적 전위 또는 그 파생상품에서 비분석적 행동에 해당한다.^[10] 이 정의를 사용하면 마이크로캐논술 앙상블의 위상 전환이 어떤 크기의 시스템에서도 일어날 수 있다. 이는 위상 전환이 열역학적 한계, 즉 무한히 많은 자유도를 가진 시스템에서만 발생할 수 있는 표준적이고 웅장한 표준 앙상블과 대비된다.^[10][11] 대략적으로, 표준 또는 웅장한 표준 앙상블을 정의하는 저장소는 유한 시스템의 자유 에너지에서 비분석적 행동을 "완만하게" 하는 변동을 도입한다. 이러한 스무딩 효과는 보통 거시 시스템에서 무시할 수 있으며, 이는 자유 에너지가 비분석적 행동에 매우 잘 근접할 수 있을 정도로 충분히 크다. 그러나 앙상블의 기술적 차이는 작은 시스템의 이론적 분석에 중요할 수 있다.^[11]

정보 엔트로피

주어진 기계 시스템(고정 N, V)과 주어진 에너지 범위의 경우 마이크로스테이트에 대한 확률 P의 균일한 분포(마이크로캐논 앙상블에서와 같이)는 앙상블 평균 - -log P를 최대화한다.^[1]

열역학적 유사점

Ludwig Boltzmann의 초기 통계역학 연구는 주어진 총 에너지 시스템 S = k log W에 대한 그의 eponymous 엔트로피 방정식을 이끌어냈다. 여기서 W는 그 에너지에서 시스템이 접근할 수 있는 고유 상태의 수입니다. 볼츠만은 이상적인 기체의 특별한 경우 외에 정확히 어떤 것이 계통의 뚜렷한 상태를 구성하는지에 대해 너무 깊이 설명하지 않았다. 이 주제는 임의의 기계 시스템에 대한 일반화된 통계 역학을 개발한 조시아 윌러드 깁스에 의해 완성될 수 있도록 조사되었고, 이 기사에서 설명한 마이크로캐논 앙상블을 정의했다.^[1] 깁스는 마이크로캐논학 앙상블과 열역학 사이의 유사점, 특히 자유도가 거의 없는 시스템의 경우 그것들이 어떻게 분해되는지를 신중하게 조사했다. 그는 Ω에 의존하지 않는 마이크로캐논 엔트로피의 두 가지 정의 - 위에서 설명한 부피와 표면 엔트로피를 추가로 소개했다. (표면 엔트로피는 Ω 의존적인 오프셋에 의해서만 볼츠만 엔트로피와 다르다는 점에 유의한다.)

볼륨 엔트로피 S와_v 관련 T는_v 열역학 엔트로피 및 온도와 밀접한 유사성을 형성한다. 는 것을 정확하게 보여줄 수 있다.

$(\displaystyle dE=)T_{\rm {v}dS_{\rm {v}-\langle P\angle dV,}$

(⟨P⟩은 열역학 제1법칙에 대한 예상대로 앙상블 평균 압력이다.) 표면(볼츠만) 엔트로피와 관련 T에_s 대해 유사한 방정식을 찾을 수 있지만, 이 방정식의 "압력"은 평균 압력과 무관한 복잡한 양이다.^[1]

마이크로캐논 T와_v T는_s 온도에 대한 유추에서 완전히 만족스러운 것은 아니다. 열역학적 한계를 벗어나면 여러 가지 아르테팩트가 발생한다.

• 두 시스템을 결합한 비교 결과: 각각 독립적인 마이크로캐논 앙상블에 의해 기술된 두 개의 시스템은 열 접촉될 수 있고 마이크로캐논 앙상블에 의해서도 기술된 결합 시스템으로 평형될 수 있다. 불행하게도 초기 T에 근거하여 두 시스템 사이의 에너지 흐름을 예측할 수 없다. 초기 T가 같을 때도 에너지가 전달될 수 있다. 더욱이 조합의 T는 초기 값과 다르다. 이는 온도가 집약적인 양이어야 하며, 두 개의 동일한 온도 시스템이 열 접촉에 의해 영향을 받지 않아야 한다는 직관과 배치된다.^[1]
• 소립자 시스템의 이상한 동작: 마이크로캐논론적 등전 정리 등 많은 결과가 T의 관점에서_s 작성되었을 때 1도 또는 2도의 자유 상쇄를 획득한다. 소형 시스템의 경우 이 오프셋은 유의하며, 따라서 S를_s 엔트로피의 아날로그로 만든다면, 자유도가 1~2도 밖에 없는 시스템에 대해 몇 가지 예외를 둘 필요가 있다.^[1]
• 거짓 음온: 음의 T는_s 에너지와 함께 상태 밀도가 감소할 때마다 발생한다. 어떤 시스템에서는 상태 밀도가 에너지에서 단조롭지 않기 때문에, 에너지가 증가함에 따라 T는_s 부호를 여러 번 변경할 수 있다.^[12][13]

이러한 문제들에 대한 선호되는 해결책은 마이크로캐논 앙상블의 사용을 피하는 것이다. 많은 현실적인 경우, 시스템은 에너지를 정확하게 알 수 없도록 열탕에 온도 조절된다. 그렇다면 보다 정확한 묘사는 규범적 앙상블이나 웅장한 규범적 앙상블인데, 둘 다 열역학과의 완전한 일치성을 가지고 있다.^[14]

앙상블에 대한 정확한 표현

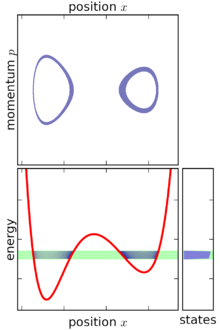
통계적 앙상블에 대한 정확한 수학적 표현은 "마이크로스테이트"의 개념이 이 두 경우에서 상당히 다르기 때문에 고려 중인 역학의 종류(양 또는 고전)에 따라 달라진다. 양자역학에서, 대각화는 특정한 에너지를 가진 이산형 미세현상 세트를 제공한다. 고전적인 기계적 케이스는 대신 표준 위상 공간보다 통합된 공간을 포함하며, 위상 공간에 있는 마이크로스테이트의 크기는 어느 정도 임의로 선택할 수 있다.

마이크로캐논학 앙상블을 구성하기 위해서는 두 종류의 역학에서 먼저 에너지의 범위를 명시하는 것이 필요하다. 함수 $f{\displaystyle (H\frac{}{}}$- ${\displaystyle \frac{E}{}}$ ${\displaystyle \frac{}{}}$)$$아래의 표현에서 {\$displaystyle$f({\$tfrac$ {$H-E}{\$omega$$}}})}($$H의 함수, 너비 Ω으로 E에서 정점)를 사용하여 상태를 포함하는 에너지 범위를 나타낼 것이다. 이 기능의 예는 다음과^[1] 같다.

${\displaystyle f(x)={\displaysty{case}1,&\mathrm {if}~x <{\tfrac {1}{1}2}},\0,&\mathrm {mathrm}.} \end{case}}}$

아니면, 더 부드럽게

${\displaystyle f(x)=e^{-\pi x^{2}.}$

양자역학

양자역학에서 통계적 앙상블은 $밀도{\displaystyle \stackrel{}{}}$ 행렬로 표현되며, ^ ${\displaystyle \stackrel{}{^}}$ ${\$로 표시된다$.$ 마이크로캐논술 앙상블은 시스템의 에너지 고유값과 에너지 고유값의 측면에서 브라켓 표기법을 사용하여 쓸 수 있다. i에 의해 색인화된 에너지 고유스테이트 ψ_i⟩의 완전한 기초를 부여받은 마이크로캐논 앙상블은^{[citation needed]}

${\displaystyle {\hat {\rho}}={\frac {1}{W}}\sum _{i}f\좌({\tfrac {H_{i}-E}{\omega }}\오른쪽) \psi _{i}\랑글 \langle \psi _{i},}$

여기서 H는_i $H{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ^ ${\displaystyle {\psi }_{}}$ i${\displaystyle {}_{}}$⟩${\displaystyle }$= ${\displaystyle H_{}}$ ${\displaystyle i{}_{}{}_{}}$ ⟩ ${\displaystyle i_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {\hat{H}\psi _{i}\rangele =H_{i} \psi _{i}$ \langele $}$에 의해 결정되는 에너지 고유값이다($$여기서 here는 시스템의 총 에너지 연산자). W 값은 $\rho {\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$을(를) 정규화된 밀도 행렬로$$ 요구하여 결정되며, 따라서

${\displaystyle W=\sum _{i}f\왼쪽({\tfrac {H_{i}-E}{\omega }}\오른쪽).}$

상태 볼륨 함수(엔트로피를 계산하는 데 사용)는 다음을 통해 제공된다.

${\displaystyle v(E)=\sum _{H_{i}<E}1.}$

마이크로캐논 앙상블은 에너지 폭이 0이 될 때 밀도 행렬의 한도를 취함으로써 정의되지만, 에너지 폭이 에너지 수준 사이의 간격보다 작아지면 문제가 있는 상황이 발생한다. 매우 작은 에너지 폭에 대해 앙상블은 E의 대부분의 값에 대해 전혀 존재하지 않는다. 왜냐하면 어떤 상태도 범위에 속하지 않기 때문이다. 복잡한 시스템에서는 에너지 수준이 우연히 같기 때문에 앙상블은 일반적으로 한 상태(또는 두 상태)만 포함한다(이 점에 대해 더 많은 논의를 위해 무작위 행렬 이론 참조). 더욱이 주량함수 역시 이산적인 증분만으로 증가하므로 그 파생상품은 무한하거나 영(0)에 불과하여 주의 밀도를 정의하기 어렵다. 이 문제는 에너지 범위를 0으로 완전히 가져가지 않고 상태 볼륨 기능을 부드럽게 함으로써 해결할 수 있지만, 이는 다른 변수(함께 NVEΩ 앙상블)에 추가하여 에너지 범위를 지정해야 하기 때문에 앙상블의 정의를 더욱 복잡하게 만든다.

고전 기계학

고전역학에서 앙상블은 시스템의 위상 공간에 걸쳐 정의된 관절 확률밀도함수 ((p₁, …p_n, …p, q₁, …q_n)로 표현된다.^[1] 위상 공간은 q₁, … q라고_n 하는 n개의 일반화된 좌표와 p₁, … p라고_n 하는 n개의 관련 표준적인 모멘텀을 가지고 있다.

마이크로캐논 앙상블의 확률밀도함수는 다음과 같다.

${\displaystyle \rho ={\frac {1}{h^{n}C}{\frac {1}{W}f({\tfrac {H-E}{\omega }),}$

어디에

• H는 시스템의 총 에너지(해밀턴어)이며, 위상의 함수(p₁, …q_n),
• h는 에너지×시간의 단위로 임의적이지만 미리 결정된 상수로, 하나의 마이크로 상태의 범위를 설정하고 정확한 치수를 ρ에 제공한다.^{[note 2]}
• C는 과대계수 보정계수로, 동일한 입자가 서로 자리를 바꿀 수 있는 입자계통에 자주 사용된다.^{[note 3]}

다시 W 값은 ρ이 정규화된 확률밀도함수라고 요구함으로써 결정된다.

${\displaystyle W=\int \ldots \int {\frac {1}{h^{n}C}f({\tfrac {H-E}{\omega }}})\,dp_{1}\ldots dq_{n}}}}$

이 적분은 전체 위상 공간을 차지한다. 상태 볼륨 함수(엔트로피를 계산하는 데 사용)는 다음에 의해 정의된다.

${\displaystyle v(E)=\int \ldots \int _{H<E}{{h^{n}C}\,dp_{1}\ldots dq_{n}.}$

에너지 폭 Ω을 0으로 취할 때 W 값은 W = Ω(dv/dE)으로 Ω에 비례하여 감소한다.

위의 정의를 바탕으로 마이크로캐논 앙상블은 일정한 에너지 표면을 중심으로 위상공간에서 무한히 얇은 껍데기로 시각화할 수 있다. 비록 마이크로캐논 앙상블이 이 표면에 국한되어 있지만, 반드시 그 표면에 균일하게 분포되어 있는 것은 아니다: 위상 공간의 에너지의 구배가 변화한다면, 마이크로캐논 앙상블은 다른 부분보다 표면의 어떤 부분에 "더 심한"(더 집중된) 것이다. 이 특징은 마이크로캐논 앙상블이 정상 상태 앙상블이 되어야 하는 피할 수 없는 결과다.

예

이상기체

마이크로캐논술 앙상블의 $기본{\displaystyle }$ 수량은 W${\displaystyle }$(${\displaystyle E}$, V${\displaystyle }$, $){\displaystyle W (E,V,N$이며, 이는 주어진 $({\displaystyle E}$, ${\displaystyle V}$, ${\displaystyle N}$) ${\displaystyle (E,V,N)}$과 호환되는 위상 공간 볼륨과 같다$.$ $W{\displaystyle }$ ${\displaystystyle$ W$}$로부터 모든 열역학적 수량을 계산할 수 있다. For an ideal gas, the energy is independent of the particle positions, which therefore contribute a factor of ${\displaystyle V^{N}}$ to ${\displaystyle W}$. The momenta, by contrast, are constrained to a ${\displaystyle 3N}$-dimensional (hyper-)spherical shell of radius ${\displaystyle {\sqrt {2mE}}}$$$; 그들의 기여는 이 껍질의 표면적 부피와 같다. $W$ ${\displaystyle W}$의 결과 식:^[15]

${\displaystyle W={\frac {V^{N}{N}{N!}}{{\frac{2\pi ^{3N/2}}:{\감마(3N/2}})}}}}\왼쪽(2mE\오른쪽)^{(3N-1)/2}}:$

여기서 $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle (.}$ ) ${\displaystyle \Gamma (.)}$은 감마함수이며, $N{\displaystyle !}$ ${\displaystyle$ N$!}$ 인자가 포함되어 입자의 분간성을 설명하였다(Gibbs 역설 참조). 큰 $N{\displaystyle }$ ${\displaystyle N}$ 한계에서$$ 볼츠만 엔트로피 $S{\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle {B\mathrm{}}_{}}$ ${\displaystyle \mathrm{로그}{}_{}W}$ ${\displaystyle S=k_{\mathrm {B}}\log W}$은(는)

${\displaystyle S=k_{\rm {B}}N\log \left[{\frac {V}{N}}\left({\frac {4\pi m}{3}}{\frac {E}{N}}\right)^{3/2}\right]+{\frac {5}{2}}k_{\rm {B}}N+O\left(\log N\right)}$

이것을 '사부르-'라고도 한다.테트로데 방정식.

온도는 에 의해 주어진다.

${\displaystyle {\frac {1}{T}}\equiv {\frac {\partial S}{\partial E}={\frac {3}{2}}:{\frac {Nk_{\mathrm{B}}{E}}}}}}}$

기체의 운동 이론에서 나온 유사한 결과와 일치한다. 압력을 계산하면 다음과 같은 이상적인 가스 법칙을 얻을 수 있다.

${\displaystyle {\frac {p}{T}}\equiv{\frac {\partial S}{\partial V}={\frac {Nk_{\mathrm{B}}}}{V}}}\quad \rightarrow quad pV=Nk_{\mathrmatrm {B}}}}}}}}$

마지막으로 화학전위 $\mu {\displaystyle }$ ${\displaystyle \mu }$은(는)

${\displaystyle \mu \equiv -T{\frac {\partial S}{\partial N}=k_{\rm {B}}T\log \left[{\frac {V}{N}\,\left({\frac {4\pi mE}{3]N}\오른쪽)^{3/2}\오른쪽]}$

균일한 중력장의 이상적 기체

마이크로캐논 위상 부피는 또한 균일한 중력장의 이상적인 기체에 대해 명시적으로 계산할 수 있다.^[16]

결과는 각각 $질량{\displaystyle }$ m ${\displaystyle m}$을(를) 가진 $N{\displaystyle }$ ${\displaystyle N}$ 입자의$$ 3차원 이상 기체에 대해 아래에 명시되어 있으며$,$ z 방향으로 무한히 길고 일정한 단면 면적 $A{\displaystyle }$ ${\\displaystyle A}$을(를) 갖는 열로 격리된 용기에 갇혀 있다$.$ 중력장은 강도 $g{\displaystyle }$ ${\displaystyle g}$과(와) 함께 마이너스 z 방향으로 작용하는 것으로 가정한다$.$ 위상 볼륨 $W{\displaystyle (E}$, ${\displaystyle N}$) ${\displaystyle W(E,N)}$은(는)

${\displaystyle W(E,N)={\frac {(2\pi )^{3N/2}A^{{N/2}}:{g^{{N/2}}:{g^{N}\감마(5N/2}})}E^{\frac{5N}{5N}-1}:{2-1}$

여기서 $E{\displaystyle }$ ${\displaystyle E}$은 총 에너지, 운동 플러스 중력이다.

높이 $z{\displaystyle }$ ${\displaystyle z}$의 함수로서의$$ 가스 밀도 $){\displaystyle \rho(z)}$은 위상 볼륨 좌표를 통해 통합하여 얻을 수 있다$$. 결과는 다음과 같다.

${\displaystyle \rho(z)=\왼쪽({\frac {5N}{2}}-1\오른쪽){\frac {mg}{E}}\왼쪽(1-{\frac {mgz}{E}\오른쪽)^{{\frac {5N}{2}}-2}}$

마찬가지로 속도 진도 ${\displaystyle v\stackrel{}{}}$→ $displaystyle {\vec{v}}}($모든 높이에 걸쳐 평균)의 분포는 다음과 같다.

${\displaystyle f( {\vec {v}} )={\frac {\Gamma (5N/2)}{\Gamma (3/2)\Gamma (5N/2-3/2)}}\times {\frac {m^{3/2} {\vec {v}} ^{2}}{2^{1/2}E^{3/2}}}\times \left(1-{\frac {m {\vec {v}} ^{2}}{2E}\오른쪽)^{\frac {5(N-1)}{2}}}$

표준 앙상블에서 이러한 방정식의 유사성은 각각 기압 공식과 맥스웰-볼츠만 분포다. 한계 $N{\displaystyle }$→ ${\displaystyle \mathrm{\infty }}$ ${\displaystyle N\rightarrow \infit$ $\}$에서 마이크로캐논과 표준 표현은 일치하지만, 유한 $N{\displaystyle }$ ${\displaystyle N$}에 대해서는 다르다$.$ 특히 마이크로캐논 앙상블에서 위치와 속도는 통계적으로 독립적이지 않다. 따라서 주어진 볼륨 $A{\displaystyle }$ d $z$의 평균 운동 $에너지$로 정의되는 운동 온도는 컨테이너 전체에 걸쳐 균일하지 않다$.$

${\displaystyle T_{\mathrm {kinetic}}}={\frac {3E}{5N-2}}\좌측(1-{\frac {mgz}){E}\오른쪽)$

대조적으로, 온도는 $표준{\displaystyle }$ 앙상블에서 모든 N {\$displaystyle N}$에 대해 균일하다$.$^[17]

참고 항목

• 절연계통
• 에르고딕 가설
• 로슈미트의 역설

메모들

참조