등온 과정

열역학
고전적인 카르노 히트 엔진
나뭇가지 고전적인 통계 화학의 양자 열역학 평형/비평형
법률 제로스 첫번째 둘째 셋째
시스템들 폐쇄형 시스템 오픈 시스템 격리 시스템 주 상태 방정식 이상 기체 실가스 상황 위상(매터) 평형 볼륨 제어 인스트루먼트 과정 이소바릭 아이소코리 등온 단열성 등엔트로픽 이센탈픽 준정전성 폴리트로픽 자유 확장 가역성 불가역성 내복원성 사이클 히트 엔진 히트 펌프 열효율
시스템 속성 주의: 이탤릭체로 표시된 켤레 변수 속성도 집약적이고 광범위한 속성 프로세스 기능 일하다. 열 국가 기능 온도/엔트로피(개요) 압력/볼륨 화학 퍼텐셜/입자수 증기 품질 속성 감소
재료 특성 속성 데이터베이스 비열 용량 ${\displaystyle c=}$ ${\displaystyle T}$ $\displaystyle \partial S\$ ${\displaystyle N}$ ${\displaystyle\partial T}$ 압축성 $\displaystyle \displays =-}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ $(\displaystyle\displayp)$ 열팽창 $\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ ${\displaystyle\partial T}$
방정식 카르노의 정리 클라우시우스 정리 기본 관계 이상기체의 법칙 맥스웰 관계 온사저 호혜 관계 브리지만 방정식 열역학 방정식 표
가능성 자유 에너지 자유 엔트로피 내부 에너지 ${\displaystyle U(S,V)}$ 엔탈피 ${\displaystyle H(S,p)=U+pV}$ 헬름홀츠 자유 에너지 ${\displaystyle A(T,V)=U-TS}$ 깁스 자유 에너지 ${\displaystyle G(T,p)=H-TS}$
역사 문화 역사 일반 엔트로피 가스 법칙 "영구 운동" 기계 철학 엔트로피와 시간 엔트로피와 생명 브라운 래칫 맥스웰의 악마 열사 역설 로슈미트의 역설 시너제틱스 이론들 열량론 Vis viva ('생체력') 열의 기계적 등가 동력 주요 출판물 실험적인 질문 ~에 대해서열 균형에 대하여 이종 물질 의 리플렉션 불의 원동력 타임라인 열역학 히트 엔진 예체능 교육 맥스웰의 열역학 표면 에너지 분산으로서의 엔트로피
과학자 베르누이 볼츠만 브리지만 카라테오도리 카르노 클라피론 클라우시우스 돈더 듀헴 깁스 폰 헬름홀츠 줄 루이스 마시외 맥스웰 폰 메이어 네른스트 온사게 플랑크 랭킨 스미톤 스틸 태트 톰슨 톰슨 판 데르 발스 워터스톤
다른. 핵생성 자가 조립 자기 조직화 질서와 무질서
카테고리
v t

열역학에서 등온 과정은 시스템의 온도 T가 일정하게 유지되는 열역학 과정의 한 종류이다: δT = 0.이는 일반적으로 시스템이 외부 열 저장소와 접촉하고 시스템이 열 교환을 통해 저장소의 온도에 지속적으로 조정될 수 있을 정도로 천천히 시스템이 변화할 때 발생합니다(준균형 참조).이와는 대조적으로 단열 프로세스는 시스템이 주변과 열을 교환하지 않는 것입니다(Q = 0).

간단히 말하면, 등온 과정에서는

• ${\displaystyle T=context{constant}}$
• $\displaystyle \Delta T=0}$
• ${\displaystyle dT=0}$
• 이상 기체의 경우에만 내부 에너지 ${\displaystyle \delta }$ U ${\displaystyle =}$ {$디스플레이$ 스타일 $\Delta$ U =$0}$

단열 프로세스 중:

• $(\displaystyle Q=0).}$

어원학

형용사 "등온"은 "같다"는 뜻의 그리스어 "등온"과 "열"을 뜻하는 "등온"에서 유래했다.

예

등온 과정은 고도로 구조화된 기계와 심지어 살아있는 세포를 포함하여 온도를 조절하는 수단을 가진 모든 종류의 시스템에서 발생할 수 있습니다.일부 열 엔진의 사이클 중 일부는 등온도로 수행됩니다(예: 카르노 ^[1]사이클).화학반응의 열역학적 분석에서는 먼저 등온조건에서 일어나는 일을 분석한 후 ^[2]온도의 영향을 고려하는 것이 일반적이다.용융이나 증발과 같은 상변화는 보통 일정한 ^[3]압력에서 발생할 때 등온 과정이기도 합니다.등온 프로세스는 종종 사용되며, 보다 복잡한 비등온 프로세스를 분석하는 출발점이 됩니다.

등온 과정은 이상 기체에 특히 중요합니다.이것은 이상적인 가스의 일정한 양의 내부 에너지는 ^[4]온도에 의해서만 결정된다는 줄의 제2법칙의 결과입니다.따라서 등온 과정에서 이상적인 가스의 내부 에너지는 일정합니다.이것은 이상적인 기체에는 분자간 ^[4]힘이 없다는 사실의 결과입니다.이는 이상적인 기체에 대해서만 해당됩니다. 내부 에너지는 압력뿐만 아니라 액체, 고체 및 실제 ^[5]기체의 온도에 따라 달라집니다.

기체의 등온 압축에서는 부피를 줄이고 ^[4]압력을 증가시키는 작업이 시스템에 수행됩니다.가스에 대한 작업을 하면 내부 에너지가 증가하고 온도가 상승하는 경향이 있습니다.일정한 온도를 유지하려면 시스템에 열이 발생하여 환경에 유입되어야 합니다.가스가 이상적이면 내부 에너지는 변하지 않기 때문에 환경에 유입되는 에너지의 양은 가스에 가해지는 작업과 동일합니다.등온 팽창의 경우 시스템에 공급되는 에너지가 주변 환경에서 작동합니다.어느 경우든 적절한 링크의 도움을 받아 가스량의 변화를 통해 유용한 기계적 작업을 수행할 수 있습니다.계산에 대한 자세한 내용은 작업 계산을 참조하십시오.

용기가 잘 단열되어 있어 가스가 열로 유입되지 않는 단열 공정의 경우 Q = 0. 작업이 수행되지 않은 경우(자유 팽창) 내부 에너지에는 변화가 없습니다.이상적인 가스의 경우 공정도 등온 ^[4]상태임을 의미합니다.따라서 공정이 등온임을 지정하는 것은 고유한 공정을 지정하는 데 충분하지 않습니다.

이상기체 상세

Boyle의 법칙이^[4] 적용되는 가스의 특수한 경우, 가스가 등온 상태로 유지되면 곱 pV(가스 압력의 경우 p, 가스의 부피의 경우 V)는 상수입니다.상수 값은 nRT입니다. 여기서 n은 현재 가스의 몰 수이고 R은 이상적인 가스 상수입니다.즉, 이상적인 가스 법칙 pV = nRT가 적용됩니다.^[4]그 때문에,

${\displaystyle p={nRT \over V} = text {constant} \over V}$

이 방정식에 의해 생성된 곡선군은 그림 1의 그래프에 나와 있습니다.각 곡선은 등온도라고 불리며, 이는 동일한 온도 T에서의 곡선을 의미합니다.이러한 그래프를 표시기 다이어그램이라고 하며, James Watt와 다른 사람들이 엔진의 효율성을 모니터링하기 위해 처음 사용했습니다.그림의 각 곡선에 해당하는 온도는 왼쪽 아래에서 오른쪽 상단으로 상승합니다.

작업의 계산

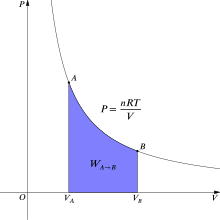
열역학에서, 기체가 상태 A에서 상태 B로^[6] 변할 때 수반되는 가역적 작업은 다음과 같습니다.

${\displaystyle W_{A\to B}=-\int_{V_{A}}^{V_{B}}p,dV}$

여기서 p는 가스 압력을 나타내고 V는 가스량을 나타냅니다.등온(상온 T) 가역 프로세스의 경우, 이 적분은 관련 PV(압력-용적) 등온 아래의 면적과 동일하며, 이상적인 기체의 경우 그림 2에서 보라색으로 표시된다.다시, p =nRT/V가 적용되며 T가 일정하면(이것은 등온 프로세스이므로), 작업에 대한 표현은 다음과 같습니다.

${\displaystyle W_{A\to B}=-\int_{V_{A}}^{V_{B}}p,dV=-\int_{V_{A}}^{V_{B}}{\frac {n}RT}{V}}dV=-nRT\int_{V_{A}}^{V_{B}}{\frac {1}{V}}}dV=-nRT\ln {frac {V_{B}}{V_{A}}}}}}:$

IUPAC 규약에서 작업은 주변 환경에 의해 시스템상의 작업으로 정의됩니다.예를 들어 시스템이 압축되어 있는 경우, 주변이 시스템에서 작업을 수행하므로 작업이 긍정적이고 시스템 내부 에너지가 증가합니다.반대로 시스템이 확장되면(즉, 확장을 둘러싼 시스템, 즉 자유로운 확장이 아닌 경우), 시스템이 주변 환경에서 작동하고 시스템의 내부 에너지가 감소하기 때문에 작업이 부정적입니다.

또한 이상적인 가스의 경우 온도가 일정하게 유지되면 시스템 U의 내부 에너지도 일정하므로 δU = 0이 된다. IUPAC 규약에 따르면 열역학 제1법칙에서는 δU = Q + W가 이상적 가스의 팽창 또는 열압축에 적합하다.

등온 공정의 예

이상적인 가스의 가역 팽창은 등온 공정에서 생성된 작업의 예로 사용될 수 있습니다.특히 관심을 끄는 것은 열이 사용 가능한 작업으로 전환되는 정도와 구속력과 팽창 범위 사이의 관계이다.

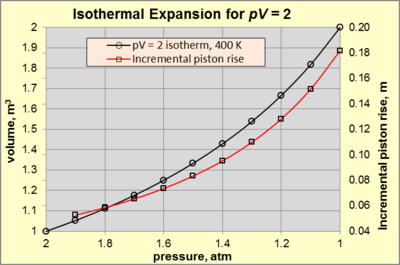
이상 기체의 등온 팽창 중에 p와 V는 모두 일정한 pV 생성물(즉, 일정한 T)과 함께 등온선을 따라 변화한다.400 K의 정적 평형 상태에서 높이 1 m, 면적 1² m(so³ 1 m volume)의 원통형 챔버 내의 작동 가스를 가정한다.주변은 300K의 공기와 1atm 압력(p로 지정_surr)으로 구성됩니다.작동 가스는 2atm(상태 A)의 작동 가스 압력을 생성하기에 충분한 힘을 발휘하는 기계 장치에 연결된 피스톤에 의해 제한됩니다.힘이 감소하는 상태 A의 변화가 있을 경우, 가스가 팽창하여 주변에 작업을 수행합니다.가해지는 힘이 감소하고 적절한 열이 가해져 pV = 2 [140·m³] (= 2 atm × 1 m³)를 유지하는 한 등온 팽창은 계속된다.팽창은 피스톤 운동이 충분히 느릴 경우 내부에서 가역성이 있으며 팽창 중 각 순간에 가스 온도와 압력이 균일하고 이상적인 가스 법칙에 부합한다고 합니다.그림 3은 2atm(상태 A)에서 1atm(상태 B)로의 등온 확장에 대한 pV = 2 [124·m³]에 대한 p-V 관계를 보여준다.

수행된 작업(${\displaystyle W_{}}$ A ${\displaystyle {\to }_{}}$(\$displaystyle W_{A\to$B$\})$에는 두 가지 구성요소가 있습니다.첫째, 주변기압에 대한 확장작업(W_pΔV)과 둘째, 사용가능한 기계작업(W_mech)이다.여기서_mech 출력 W는 크랭크 암을 돌리는 데 사용되는 피스톤의 움직임일 수 있습니다. 그러면 도르래가 침수된 염광에서 물을 끌어올릴 수 있습니다.

${\displaystyle W_{A\to B}=-p,V\left(\ln {frac {V_{B}}}{V_{A}}\right)=-W_{p\Delta V}-W_{\rm {mech}}$

시스템은 가해진 힘이 0에 도달하면 상태 B(pV = 2 [160·m³], p = 1atm 및 V = 2m³)에 도달합니다.이 시점에서 ${\displaystyle W_{}}$ A ${\displaystyle {\to }_{}}$ $({$B})는_pΔV –140.5kJ, W는 –101.3kJ입니다. W = –39.1kJ는 공정(-39.1kJ/-140.5KJ)에 공급되는 열의 27.9%에_mech 해당합니다.이는 명시된 조건에서 공정에서 얻을 수 있는 사용 가능한 기계적 작업의 최대 양입니다.W의_mech 퍼센티지는 pV와_surr p의 함수이며 p가 0에 가까워지면_surr 100%에 도달합니다.

등온 팽창의 특성을 더 추구하려면 그림 3의 빨간색 선을 참고하십시오.pV의 고정값은 피스톤 상승 대 압력 감소를 기하급수적으로 증가시킵니다.예를 들어, 압력이 2에서 0.6969atm으로 감소하면 피스톤이 0.0526m 상승합니다.이에 비해 압력이 0.39에서 1atm으로 감소하면 피스톤이 0.418m 상승합니다.

엔트로피 변화

등온 과정은 엔트로피의 변화를 계산하는데 특히 편리하다. 왜냐하면, 이 경우, 엔트로피 변화의 공식인 δS는 단순하기 때문이다.

${\displaystyle \Delta S=param frac {Q_{\text{rev}}}{T}}}$

여기서_rev Q는 시스템으로 전달되는 열(내부 가역)이고 T는 절대 ^[7]온도입니다.이 공식은 가정적인 가역 과정, 즉 평형이 항상 유지되는 과정에만 유효합니다.

단순한 예로는 일정한 온도와 압력에서 발생하는 평형상 전이(용융 또는 증발 등)가 있습니다.일정한 압력에서의 상전이의 경우, 시스템으로 전달되는 열은 변환의 엔탈피인 δH와_tr 같으며, 따라서 Q = ^[3]δH입니다_tr.주어진 압력에서 두 상이 평형 상태에 있는 전이 온도 T가_tr 있을 것이다(예를 들어, 한 기압에서 액체의 기화를 위한 정상 비등점).만약 이러한 평형 조건 하에서 전이가 일어난다면, 위의 공식을 사용하여 엔트로피^[7] 변화를 직접 계산할 수 있다.

$tr$$$$T_{\text{tr$

또 다른 예는 초기 부피_A V 및 압력_A P에서 최종 부피_B V 및 압력_B P로 이상 기체의 가역 등온 팽창(또는 압축)이다.작업 계산과 같이 가스로 전달되는 열은

$displaystyle$$$$B}}{V_{\text{$$A$

이 결과는 가역적인 과정을 위한 것이므로, 엔트로피 변화를 위한 공식으로^[7] 대체될 수 있다.

$A$$$$B}}{V_{\text{$$A$

이상적인 기체는 보일의 법칙에 따르기 때문에, 만약 원한다면, 이것은 다음과 같이 다시 쓰여질 수 있다.

$P$$$$A}}{P_{\text{$$B$

일단 얻어진 이 공식들은 이상적인 기체의 자유 팽창과 같은 비가역적인 과정에 적용될 수 있다.이러한 팽창은 또한 등온성이며 가역적 팽창과 동일한 초기 및 최종 상태를 가질 수 있습니다.엔트로피는 상태 함수이기 때문에(시스템이 평형 상태에 도달하기 위해 취하는 경로에 의존하지 않고) 시스템의 엔트로피 변화는 가역 프로세스와 동일하며 위의 공식에 의해 주어진다.자유팽창에 대한 결과 Q = 0은 프로세스가 되돌릴 수 없으므로 엔트로피 변화 공식에 사용할 수 없습니다.

가역팽창과 자유팽창의 차이는 주변의 엔트로피에서 찾을 수 있다.둘 다 주변은 일정한 온도 T이므로_sur δS = -Q/T이다. 주변으로 전달되는 열의 크기가 같고 시스템에 전달되는 열 Q와 반대이기 때문에 마이너스 부호가 사용된다.가역적인 경우, 주변의 엔트로피 변화는 시스템의 변화와 동일하고 반대이기 때문에 우주의 엔트로피 변화는 0입니다.자유팽창에서는 Q = 0이므로 주변의 엔트로피는 변하지 않고 우주의 엔트로피 변화는 계의 δS와 같다.

「 」를 참조해 주세요.

• 줄-톰슨 효과
• 줄 확장(자유 확장이라고도 함)
• 단열 과정
• 순환 과정
• 등압 과정
• 아이소코릭법
• 폴리트로픽 과정
• 자발적 과정

레퍼런스