힐베르트 공간
Hilbert space
수학에서 힐베르트 공간(David Hilbert의 이름을 따서 명명됨)은 선형 대수학과 미적분학의 방법을 (무한 차원) 유클리드 벡터 공간에서 무한 차원일 수 있는 공간으로 일반화할 수 있게 해줍니다. 힐베르트 공간은 수학과 물리학, 일반적으로 함수 공간으로 자연적으로 자주 발생합니다. 형식적으로 힐베르트 공간은 공간이 완전한 계량 공간인 거리 함수를 유도하는 내적을 갖춘 벡터 공간입니다.
초기 힐베르트 공간은 20세기 첫 10년 동안 다비드 힐베르트, 에르하르트 슈미트, 프리게스 리에즈에 의해 이러한 관점에서 연구되었습니다. 이들은 편미분 방정식, 양자역학, 푸리에 분석(신호 처리 및 열 전달에 대한 적용 포함) 및 에르고딕 이론(열역학의 수학적 기초를 형성하는) 이론에서 필수적인 도구입니다. 존 폰 노이만(John von Neumann)은 이러한 다양한 응용의 기초가 되는 추상적 개념을 위해 힐베르트 공간이라는 용어를 만들었습니다. 힐베르트 공간법의 성공은 함수 분석을 위한 매우 유익한 시대로 이어졌습니다. 고전적인 유클리드 벡터 공간을 제외하고 힐베르트 공간의 예로는 제곱 적분 가능 함수의 공간, 수열의 공간, 일반화 함수로 구성된 소볼레프 공간, 홀로모픽 함수의 하디 공간 등이 있습니다.
기하학적 직관은 힐베르트 공간 이론의 여러 측면에서 중요한 역할을 합니다. 피타고라스 정리와 평행사변형 법칙의 정확한 유사점은 힐베르트 공간에 있습니다. 더 깊은 수준에서 선형 부분 공간 또는 부분 공간(삼각형의 "고도를 떨어뜨리는" 아날로그)에 대한 수직 투영은 최적화 문제 및 이론의 다른 측면에서 중요한 역할을 합니다. 힐베르트 공간의 요소는 고전기하학의 데카르트 좌표와 유사하게 정규기하학에 대한 좌표에 의해 고유하게 지정될 수 있습니다. 이 기저가 셀 수 없이 무한할 때, 그것은 힐베르트 공간을 제곱합 가능한 무한열의 공간과 식별할 수 있게 해줍니다. 후자의 공간은 종종 힐베르트 공간이라고 불리는 오래된 문헌에 있습니다.
정의 및 일러스트레이션
동기 부여 사례: 유클리드 벡터 공간
힐베르트 공간의 가장 친숙한 예 중 하나는 R로 표시되고 점 곱이 장착된 3차원 벡터로 구성된3 유클리드 벡터 공간입니다. 점 곱은 두 벡터 x와 y를 취하고 실수 x ⋅ y를 만듭니다. x와 y를 직각좌표로 나타내면 점 곱은 다음과 같이 정의됩니다.
도트 제품은 특성을[1] 만족합니다.
- x와 y에서 대칭입니다. x ⋅ y = y ⋅ x.
- 첫 번째 인수인 (ax + bx) ⋅ y = a(x ⋅ y) + b(x ⋅ y)는 모든 스칼라 a, b 및 벡터 x, x, y에 대해 선형입니다.
- 모든 벡터 x, x ⋅ x ≥ 0에 대하여 x = 0인 경우에만 동일한 양의 정 확약입니다.
내적인 것은 내적인 것으로 내적인 것을 내적인 것이라고 하는데, 내적인 것은 내적인 것으로 내적인 것과 마찬가지로 내적인 것을 의미합니다. 이와 같은 내적이 구비된 벡터 공간을 (실제) 내적 공간이라고 합니다. 모든 유한 차원 내부 곱 공간도 힐베르트 공간입니다.[2] 그것을 유클리드 기하학과 연결하는 점 곱의 기본적인 특징은 그것이 ‖x ‖로 표시되는 벡터의 길이(또는 노름)와 그리고 공식을 통해 두 벡터 x와 y 사이의 각도 θ와 연관되어 있다는 것입니다.
유클리드 공간의 다변수 미적분학은 극한을 계산하는 능력과 극한이 존재한다는 결론을 내릴 수 있는 유용한 기준을 갖추는 능력에 의존합니다. 수학적 급수
일련의 스칼라들과 마찬가지로, 절대적으로 수렴하는 일련의 벡터들도 유클리드 공간의 어떤 극한 벡터 L로 수렴합니다.
이 성질은 유클리드 공간의 완전성을 표현합니다. 즉 절대적으로 수렴하는 급수는 일반적인 의미에서도 수렴한다는 것입니다.
힐베르트 공간은 종종 복소수를 대신합니다. C로 표시된 복소평면은 크기의 개념인 복소 모듈러스 z를 갖추고 있으며, 이는 복소 결합체를 갖는 z의 곱의 제곱근으로 정의됩니다.
z = x + iy가 z를 실수부와 허수부로 분해한 것이라면, 모듈러스는 일반적인 유클리드 2차원 길이입니다.
복소수 z와 w의 내적 곱은 w의 복소수 결합체를 갖는 z의 곱입니다.
이것은 복잡한 가치가 있습니다. ⟨z, w ⟩의 실수 부분은 일반적인 2차원 유클리드 점 제품을 제공합니다.
두 번째 예는 원소들이 복소수 z = (z, z)의 쌍인 공간 C입니다. 그런 다음 또 다른 벡터 w = (w, w)를 갖는 z의 내적은 다음과 같이 주어집니다.
⟨z, w ⟩의 실수 부분은 2차원 유클리드 점 곱입니다. 이 내부 곱은 에르미트 대칭이므로 z와 w를 교환한 결과가 복소 켤레임을 의미합니다.
정의.
힐베르트 공간(Hilbert space)은 실수 또는 복소 내적 공간으로, 내적에 의해 유도된 거리 함수와 관련하여 완전한 계량 공간이기도 합니다.[4]
복소 벡터 공간 H가 복소 내부 곱 공간이라고 하는 것은 다음 성질을 만족하는 의각 xdisplaystyle x,y} 쌍에 복소수를 연결하는 내부⟨ x,y ⟩ x,y\rangle}가 있다는 것을 의미합니다.
- 내적은 켤레 대칭이고, 즉 한 쌍의 원소의 내적은 스왑된 원소의 내적의 복소 켤레와 같습니다. 한 것은 ⟨ x x ⟩ {\ xx\rangle }가 실수라는 것입니다.
- 내부[nb 1] 제품은 첫 번째 인수에서 선형입니다. 모든 복소수에 a b b
- 원소 자체의 내적은 양의 확정적입니다.
성질 1과 성질 2로부터 복소 내적은 공액 선형이라고도 불리는 반선형이며, 이것은 다음을 의미합니다.
H는 실수 벡터 공간이고 내적은 실수 값을 취한다는 점을 제외하고는 실수 내적 공간은 동일한 방식으로 정의됩니다. 이러한 내부 제품은 쌍선형 맵이며( ⟨ ⋅,⋅ ⟩) {\style (H, H,\langle \cdot,\cdot \rangle )}이(가) 이중 시스템을 구성합니다.
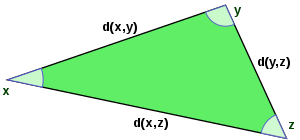
표준은 실수 값 함수입니다.
이 함수가 거리 함수라는 것은 첫 로 x{\ x와 y{\ y에서 대칭이고 두 로 x x와 자신 의 거리가 0이고, 그렇지 않으면 x 와 y y 사이의 거리가 양수여야 합니다. 마지막으로 삼각형 부등식은 삼각형 xyz의 한쪽 다리 길이가 다른 두 다리 길이의 합을 초과할 수 없음을 의미합니다.
이 마지막 성질은 궁극적으로 더 근본적인 코시-슈바르츠 불평등의 결과라고 주장합니다.
이렇게 정의된 거리 함수를 사용하면, 모든 내부 곱 공간은 계량 공간이며, 때로는 하우스도르프 사전 힐베르트 공간으로 알려져 있습니다.[6] 완전한 공간이기도 한 모든 힐베르트 이전의 공간은 힐베르트 공간입니다.[7]
H의 완전성은 H의 수열들에 대한 코시 기준의 형태를 사용하여 표현됩니다: 모든 코시 수열이 이 노름에 대해 공간의 원소로 수렴하면, 프리 힐베르트 공간 H는 완전합니다. 완전성은 다음과 같은 동등한 조건으로 특징지어질 수 있습니다: 만약 일련의 벡터들이
완전한 정규 공간으로서 힐베르트 공간은 정의상 바나흐 공간이기도 합니다. 이와 같이 부분 집합의 개방성과 폐쇄성과 같은 위상 개념이 잘 정의된 위상 벡터 공간입니다. 특히 중요한 것은 제한에 의해 유도된 내부 생성물도 완전한(완전한 미터 공간의 닫힌 집합) 힐베르트 공간의 닫힌 선형 부분 공간이라는 개념입니다.
두 번째 예: 시퀀스 공간
시퀀스 공간 l은 복소수의 모든 무한 시퀀스 z = (z, z, …)로 구성되어 다음과 같은 급수가 수렴합니다.
l의2 내부 제품은 다음과 같이 정의됩니다.
이 두 번째 급수는 이전 급수의 코시-슈바르츠 부등식과 수렴의 결과로 수렴합니다.
공간2 홀드의 완전성은 l의 일련의 원소가 절대적으로 수렴할 때마다 (정규적으로) l의2 원소로 수렴한다는 것을 전제로 합니다. 이 증명은 수학적 분석에서 기본이며, 공간의 원소들을 복소수의 수열(또는 유한 차원 유클리드 공간의 벡터)과 동일한 쉽게 조작할 수 있습니다.[10]
역사

힐베르트 공간이 개발되기 전에, 유클리드 공간의 다른 일반화들은 수학자들과 물리학자들에게 알려져 있었습니다. 특히, 추상적인 선형 공간(벡터 공간)에 대한 아이디어는 19세기 말에 약간의 견인력을 얻었습니다.[11] 이 공간은 반드시 기하학적 벡터로 이러한 요소를 식별하지 않고도 스칼라(예를 들어 실수 또는 복소수)와 함께 더하고 곱할 수 있는 공간입니다. 물리계에서의 위치 및 운동량 벡터와 같은 것들. 20세기에 접어들면서 수학자들이 연구한 다른 대상들,[12] 특히 수열의 공간(급수 포함)과 함수의 공간은 당연히 선형 공간으로 생각할 수 있습니다. 예를 들어 함수는 일정한 스칼라에 의해 더하거나 곱할 수 있으며, 이러한 연산은 공간 벡터의 덧셈과 스칼라 곱에 의해 충족되는 대수 법칙을 따릅니다.
20세기의 첫 10년 동안, 평행한 발전은 힐베르트 공간의 도입으로 이어졌습니다. 이들 중 첫 번째는 데이비드 힐베르트와 에르하르트 슈미트가 적분방정식을 연구하는 과정에서 [13]두 제곱 적분 가능한 실수 함수 f와 g가 [a, b] 구간에서 내적을 갖는다는 관측입니다.
유클리드 도트 제품의 많은 친숙한 특성을 가지고 있습니다. 특히 직교 함수족의 아이디어는 의미가 있습니다. 슈미트는 일반적인 점 제품과 이 내부 제품의 유사성을 이용하여 형태의 연산자에 대한 스펙트럼 분해의 유사성을 증명했습니다.
여기서 K는 x와 y에서 대칭인 연속 함수입니다. 그 결과 고유함수 전개는 함수 K를 다음과 같은 형태의 급수로 표현합니다.
여기서 함수 φ은 모든 n개의 ≠ m에 대하여 φ⟩ = 0이라는 의미로 직교합니다. 이 시리즈의 개별 용어를 기본 제품 솔루션이라고 부르기도 합니다. 그러나 적절한 의미에서 제곱 적분 가능 함수에 수렴하지 못하는 고유 함수 확장이 있습니다. 즉, 수렴을 보장하는 누락된 성분이 완전성입니다.[14]
두 번째 개발은 1904년 앙리 르베그가 도입한 리만 적분의 대안인 르베그 적분입니다.[15] 르베그 적분은 훨씬 더 광범위한 종류의 함수를 적분하는 것을 가능하게 했습니다. 1907년 프리게스 리에즈와 에른스트 지기스문트 피셔는 각각 독립적으로 사각형 르베그 적분 가능 함수의 공간 L이2 완전한 계량 공간임을 증명했습니다.[16] 기하학과 완전성 사이의 상호 작용의 결과로, 삼각형 급수에 대한 조셉 푸리에, 프리드리히 베셀, 마르크 앙투안 파르세발의 19세기 결과는 이러한 보다 일반적인 공간으로 쉽게 옮겨져 현재 일반적으로 리에즈-피셔 정리로 알려진 기하학적이고 분석적인 장치가 되었습니다.[17]
추가적인 기본 결과는 20세기 초에 증명되었습니다. 예를 들어, 리에즈 표현 정리는 1907년 모리스 프레셰와 프리게스 리에즈에 의해 독립적으로 확립되었습니다.[18] 존 폰 노이만(John von Neumann)은 무제한 에르미트 연산자에 대한 그의 연구에서 추상 힐베르트 공간이라는 용어를 만들었습니다.[19] 헤르만 바일과 노버트 위너와 같은 다른 수학자들은 이미 종종 물리적 동기가 있는 관점에서 특정 힐베르트 공간을 매우 자세히 연구했지만, 폰 노이만은 그것들을 완전하고 공리적으로 다룬 최초의 수학자였습니다.[20] 폰 노이만은 후에 양자역학의 [21]기초에 대한 그의 중요한 연구와 유진 위그너와의 계속된 연구에서 그것들을 사용했습니다. "힐베르트 공간"이라는 이름은 다른 사람들에게 곧 채택되었는데, 예를 들어 헤르만 바일이 양자역학과 군론에 관한 그의 책에서 채택한 것입니다.[22]
힐베르트 공간의 개념이 양자역학의 가장 좋은 수학적 공식 중 하나를 제공한다는 사실은 그 개념의 중요성을 강조했습니다.[23] 간단히 말해서, 양자 역학 시스템의 상태는 특정 힐베르트 공간의 벡터이고, 관측 가능한 것은 그 공간의 에르미트 연산자이며, 시스템의 대칭은 단일 연산자이며, 측정은 직교 투영입니다. 양자역학적 대칭과 단일 연산자 사이의 관계는 1928년 헤르만 바일의 연구에서 시작된 군의 단일 표현 이론의 발전에 원동력을 제공했습니다.[22] 반면, 1930년대 초에는 고전 역학이 힐베르트 공간(Koopman–von Neumann classical mechanics)의 관점에서 설명될 수 있고 고전 역학 시스템의 특정 특성이 에르고딕 이론의 틀에서 힐베르트 공간 기술을 사용하여 분석될 수 있다는 것이 분명해졌습니다.[24]
베르너 하이젠베르크의 양자 이론의 행렬역학 공식에 따르면 양자역학에서 관측 가능한 대수는 당연히 힐베르트 공간에 정의된 연산자의 대수입니다.[25] 폰 노이만은 1930년대에 힐베르트 공간에서 연산자의 고리로서 연산자 대수를 조사하기 시작했습니다. 폰 노이만과 그의 동시대 사람들이 연구한 대수의 종류는 현재 폰 노이만 대수로 알려져 있습니다.[26] 1940년대에 이스라엘 겔판드, 마크 나이마크, 어빙 시걸은 C*-대수라고 불리는 일종의 연산자 대수에 대한 정의를 내렸는데, 이것은 한편으로는 기저 힐베르트 공간에 대한 언급을 하지 않았고, 다른 한편으로는 이전에 연구된 연산자 대수의 많은 유용한 특징들을 외삽했습니다. 특히 기존 힐베르트 공간 이론의 많은 기초가 되는 자기 인접 연산자에 대한 스펙트럼 정리는 C*-대수로 일반화되었습니다.[27] 이러한 기법들은 이제 추상적인 고조파 분석과 표현 이론의 기초가 됩니다.
예
르베그 공간
레베그 공간은 측정 공간(X, M, μ)과 관련된 함수 공간이며, 여기서 X는 집합, M은 X의 부분 집합들의 σ-대수, μ는 M에 대한 가산 측도입니다. L2(X, μ)를 함수의 절대값 제곱의 르베그 적분이 유한한 X 위의 복소값 측정 가능한 함수의 공간이라 하자. 즉, L2(X, μ)의 함수 f에 대하여,
L2(X, μ)에서 함수 f와 g의 내적은 다음과 같이 정의됩니다.
이론물리학 문헌에서 두 번째 형태(첫 번째 원소의 conjug화)가 흔히 발견되는 경우. L의2 f와 g에 대하여, 적분은 코시-슈바르츠 부등식 때문에 존재하며, 공간 위에 내적을 정의합니다. 이 내부 제품을 장착한 L은2 실제로 완성되었습니다.[28] 르베그 적분은 완전성을 보장하기 위해 필수적입니다. 예를 들어, 실수 영역에서는 충분한 함수가 리만 적분 가능하지 않습니다.[29]
르베그 공간은 많은 자연 환경에서 나타납니다. 각각 실수선 및 단위 간격의 르베그 측도에 대한 제곱 적분 함수의 공간 L2(R) 및 L2([0,1])은 푸리에 변환 및 푸리에 급수를 정의하는 자연 도메인입니다. 다른 상황에서는, 이 조치가 실제 라인에서 일반적인 레베그 조치가 아닌 다른 것일 수도 있습니다. 예를 들어, w가 임의의 양의 측정 가능한 함수라면, [0, 1]을 만족하는 구간에 대한 모든 측정 가능한 함수의 공간
w L([0, 1])이라고 하고 w는 가중치 함수라고 합니다. 내부 제품은 다음과 같이 정의됩니다.
가중 공간 L2
w([0, 1])은 르베그 측정 가능 집합 A의 측도 μ가 다음과 같이 정의되는 힐베르트 공간2 L([0, 1], μ)과 동일합니다.
직교 다항식의 서로 다른 패밀리는 서로 다른 가중 함수에 대해 직교하기 때문에, 이와 같은 가중 L2 공간은 직교 다항식을 연구하는 데 자주 사용됩니다.[30]
소볼레프 공간
Hs 또는 W로s, 2 표시되는 소볼레프 공간은 힐베르트 공간입니다. 이것들은 미분이 수행될 수 있는 특수한 종류의 함수 공간이지만 (Hölder 공간과 같은 다른 바나흐 공간과는 달리) 내부 곱의 구조를 지원합니다. 미분이 허용되기 때문에 소볼레프 공간은 편미분방정식 이론의 편리한 설정입니다.[31] 그들은 또한 변분 연산에서 직접 방법 이론의 기초를 형성합니다.[32]
음이 아닌 정수와 ω ⊂ R의 경우, 소볼레프 공간 H(ω)는 s까지의 약한 도함수도 L인 L개의 함수를 포함합니다. H(H ω)의 내부 제품은
또한 스펙트럼 이론의 관점에서 볼레프 공간은 힐베르트 공간 구조에 보다 구체적으로 의존하여 연구됩니다. ω가 적합한 정의역이라면, 소볼레프 공간 H(H ω)를 베셀 퍼텐셜의 공간으로 정의할 수 있습니다. 대략적으로,
여기서 δ는 라플라시안이며 (1 - δ)는 스펙트럼 매핑 정리의 관점에서 이해됩니다. 비-정수에 대한 소볼레프 공간의 실행 가능한 정의를 제공하는 것 외에도, 이 정의는 의사 미분 연산자 연구에 이상적인 푸리에 변환 하에서 특히 바람직한 특성을 가지고 있습니다. 콤팩트 리만 다양체 위에서 이 방법들을 사용하면 호지 이론의 기초가 되는 호지 분해를 예를 들어 얻을 수 있습니다.[34]
복소함수의 공간
하디 스페이스
하디 공간은 복소 해석과 조화 해석에서 발생하는 함수 공간으로, 그 요소는 복소 영역에서 특정 홀로포밍 함수입니다.[35] 복소평면의 단위 디스크를 U로 표시합니다. 그렇다면 하디 공간 H2(U)는 U 위에 다음과 같은 복소함수들의 공간으로 정의됩니다.
r < 1에 대하여 경계를 유지합니다. 이 하디 공간에 대한 표준은 다음과 같이 정의됩니다.
디스크의 강건한 공간은 푸리에 급수와 관련이 있습니다. 함수 f가 H2(U)인 경우에만 해당합니다.
따라서2 H(U)는 원 위에 L이고2 음의 주파수 푸리에 계수가 사라지는 함수로 구성됩니다.
베르그만 공간
베르그만 공간은 복소함수를 갖는 힐베르트 공간의 또 다른 족입니다.[36] 복소 평면 (또는 고차원 복소 공간)에서 D를 유계 열린집합이라 하고, L2, h(D)를 L2(D)에 포함되는 복소함수 f의 공간이라 하자.
여기서 적분은 D의 르베그 측도와 관련하여 취합니다. 분명히 L2, h(D)는 L2(D)의 부분 공간이며, 사실 그것은 닫힌 부분 공간이며, 따라서 그 자신의 오른쪽에 있는 힐베르트 공간입니다. 이것은 D의 콤팩트 부분집합 K에 대해 유효한 추정의 결과입니다.
버그만 공간은 재생 커널 힐버트 공간의 한 예로서, 이 공간과 유사한 재생 특성을 검증하는 커널 K(ζ, z)와 함께 함수들의 힐버트 공간입니다. 하디 공간 H(D)는 Szeg ő 커널로 알려진 재생 커널도 인정합니다. 낟알을 재생하는 것은 수학의 다른 영역에서도 일반적입니다. 예를 들어, 고조파 분석에서 포아송 커널은 단위 볼에서 제곱 적분 가능한 고조파 함수의 힐베르트 공간에 대한 재생 커널입니다. 후자가 전혀 힐베르트 공간이라는 것은 조화 함수에 대한 평균값 정리의 결과입니다.
적용들
힐베르트 공간의 많은 응용은 힐베르트 공간이 일반적인 유한 차원 설정에서 투영 및 기저 변화와 같은 단순한 기하학적 개념의 일반화를 지원한다는 사실을 이용합니다. 특히 힐베르트 공간에 대한 연속 자기 인접 선형 연산자의 스펙트럼 이론은 행렬의 일반적인 스펙트럼 분해를 일반화하며, 이는 종종 수학 및 물리학의 다른 영역에 이론을 적용하는 데 중요한 역할을 합니다.
스텀-리우빌 이론

일반 미분방정식 이론에서는 적합한 힐베르트 공간에 대한 스펙트럼 방법을 사용하여 미분방정식의 고유값과 고유함수의 거동을 연구합니다. 예를 들어, 스투름-리우빌 문제는 바이올린 현 또는 드럼의 파동의 고조파 연구에서 발생하며, 일반 미분 방정식에서 중심적인 문제입니다.[38] 문제는 형태의 미분방정식입니다.
편미분방정식
힐베르트 공간은 편미분방정식 연구에서 기본적인 도구를 형성합니다.[31] 선형 타원 방정식과 같은 많은 종류의 편미분 방정식의 경우 함수의 클래스를 확장하여 일반화된 해(약해로 알려진)를 고려할 수 있습니다. 많은 약한 공식은 힐베르트 공간인 소볼레프 함수 클래스를 포함합니다. 적합한 약한 공식은 기하학적 문제, 해결책을 찾는 분석 문제, 또는 종종 더 중요한 문제로 축소되며, 주어진 경계 데이터에 대해 해결책이 존재하고 고유하다는 것을 보여줍니다. 선형 타원 방정식의 경우, 큰 종류의 문제에 대해 고유한 용해성을 보장하는 기하학적 결과 중 하나는 Lax-Milgram 정리입니다. 이 전략은 편미분방정식의 수치해에 대한 Galerkin 방법(유한요소법)의 기본을 형성합니다.[40]
대표적인 예가 R의 유계 도메인 ω δ에서 디리클레 경계 조건을 갖는 포아송 방정식 - δu = g입니다. 약한 공식은 연속적으로 미분 가능한 모든 함수 v가 경계에서 사라지는 함수 u를 찾는 것으로 구성됩니다.
이것은 약한 부분 도함수와 함께 u가 ω에서 제곱 적분될 수 있고 경계에서 사라지도록 함수 u로 구성된 힐베르트 공간 H(H ω)의 관점에서 재구성될 수 있습니다. 그런 다음 질문은 이 공간에서 모든 v에 대해 이 공간에서 당신을 찾는 것으로 줄어듭니다.
여기서 a는 연속적인 쌍선형 형태이고, b는 연속적인 선형 함수이며, 각각 다음과 같이 주어집니다.
포아송 방정식은 타원형이므로 이중선형 형태 a가 강압적이라는 것이 푸앵카레의 부등식으로부터 나옵니다. 그런 다음 Lax-Milgram 정리는 이 방정식의 해의 존재와 유일성을 보장합니다.[41]
힐베르트 공간은 많은 타원 편미분 방정식이 비슷한 방식으로 공식화될 수 있도록 해주며, 락스-밀그램 정리는 분석의 기본 도구입니다. 적절한 수정을 통해 포물선 편미분 방정식과 특정 쌍곡 편미분 방정식에 유사한 기법을 적용할 수 있습니다.[42]
에르고딕 이론

에르고딕 이론 분야는 혼돈 역학 시스템의 장기적인 행동에 대한 연구입니다. 에르고딕 이론이 적용되는 분야의 전형적인 경우는 열역학으로, 계의 미시적 상태는 매우 복잡하지만(물질 입자 간의 개별 충돌 앙상블을 이해하는 것은 불가능합니다), 충분히 긴 시간 간격 동안의 평균 행동은 다루기 쉽습니다. 열역학 법칙은 그러한 평균적인 행동에 대한 주장입니다. 특히 열역학 제0법칙의 한 공식은 충분히 긴 시간에 걸쳐 평형상태에 있는 열역학계에서 할 수 있는 유일한 기능적으로 독립적인 측정은 온도 형태의 총 에너지라고 주장합니다.[43]
에르고딕 역학 시스템은 해밀턴에 의해 측정된 에너지와는 별개로 위상 공간에 다른 기능적으로 독립적인 보존된 양이 없는 시스템입니다. 좀 더 구체적으로, 에너지 E가 고정되어 있다고 가정하고, ω를 에너지 E의 모든 상태로 구성된 위상 공간의 부분 집합(에너지 표면)이라고 하고, T를 위상 공간의 진화 연산자라고 합니다. 동적 시스템은 ω의 모든 불변 측정 가능한 함수가 거의 모든 곳에서 일정하다면 에르고딕입니다. 불변 함수 f는 다음에 대한 함수입니다.
폰 노이만 평균 에르고딕 정리는[24] 다음과 같습니다.
- U가 힐베르트 공간 H 위의 (strongly 연속적인) 단일 연산자들의 하나의 매개변수 부분군이고, P가 U의 공통 고정점들의 공간에 대한 직교 사영인 경우, {x ∈H Ux = x, ∀t > 0}
에르고딕 시스템의 경우, 시간 진화의 고정 집합은 상수 함수로만 구성되므로 에르고딕 정리는 다음과 같은 의미를 갖습니다: 함수 f ω L(∈, μ)에 대하여,
즉, 관측 가능한 f의 긴 시간 평균은 에너지 표면에 대한 기대 값과 같습니다.
푸리에 분석
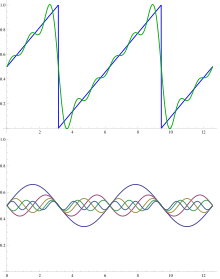

푸리에 분석의 기본 목표 중 하나는 함수를 주어진 기본 함수의 (가능하면 무한히) 선형 조합으로 분해하는 것입니다: 관련 푸리에 급수. 구간 [0, 1]에서 정의된 함수 f와 관련된 고전적인 푸리에 급수는 다음과 같은 형태의 급수입니다.
톱니 함수에 대한 푸리에 급수의 처음 몇 개 항을 더하는 예가 그림에 나와 있습니다. 기본 기능은 톱니 자체의 파장 λ보다 짧은 파장 λ/n(정수 n의 경우)을 가진 사인파(기본파인 n=1 제외)입니다. 모든 기본 함수는 톱니의 노드에 노드가 있지만 기본 함수를 제외한 모든 기본 함수에는 추가 노드가 있습니다. 톱니에 대한 합산된 용어의 진동을 깁스 현상이라고 합니다.
고전 푸리에 급수의 중요한 문제는 푸리에 급수가 함수 f로 수렴하는 경우 어떤 의미에서 수렴하는지를 묻습니다. 힐베르트 공간법은 이 질문에 대한 한 가지 가능한 답을 제공합니다.[46] 함수 e(θ) = e는 힐베르트 공간 L([0, 1])의 직교 기저를 형성합니다. 따라서, 임의의 제곱 적분 가능 함수는 급수로 표현될 수 있습니다.
또한, 이 급수는 힐베르트 공간 감각(즉, L2 평균)에서 수렴합니다.
추상적인 관점에서도 문제를 연구할 수 있습니다: 모든 힐베르트 공간은 정칙적 기저를 가지며, 힐베르트 공간의 모든 원소는 이러한 기저 원소의 배수의 합으로 독특한 방식으로 쓸 수 있습니다. 이러한 기저 요소에 나타나는 계수는 때때로 추상적으로 공간 요소의 푸리에 계수로 알려져 있습니다.[47] 추상화는 L2([0, 1])과 같은 공간에 대해 다른 기저 함수를 사용하는 것이 더 자연스러운 경우에 특히 유용합니다. 많은 상황에서 함수를 삼각 함수로 분해하는 것이 아니라 예를 들어 직교 다항식이나 웨이블릿으로 분해하고 [48]더 높은 차원에서 구면 조화 함수로 분해하는 것이 바람직합니다.[49]
예를 들어, 만약n e가 L2[0, 1]의 정규 기저 함수라면, L2[0, 1]의 주어진 함수는 유한 선형 조합으로[50] 근사될 수 있습니다.
계수 {a}은(는) 차이 ‖f - f ‖의 크기를 가능한 작게 만들기 위해 선택됩니다. 기하학적으로, 가장 좋은 근사는 {ej}의 모든 선형 조합으로 구성된 부분 공간에 대한 f의 직교 사영이며, 다음에[51] 의해 계산될 수 있습니다.
이 공식이 ‖f - f 차이를 최소화한다는 것은 Bessel의 부등식과 Parseval의 공식의 결과입니다.
물리적 문제에 대한 다양한 응용에서 함수는 미분 연산자(일반적으로 라플라스 연산자)의 물리적으로 의미 있는 고유 함수로 분해될 수 있습니다. 이는 미분 연산자의 스펙트럼을 참조하여 함수의 스펙트럼 연구의 기초를 형성합니다.[52] 구체적인 물리적 응용에는 드럼의 모양을 듣는 문제가 포함됩니다. 드럼 헤드가 낼 수 있는 기본적인 진동 모드를 고려할 때 드럼 자체의 모양을 추론할 수 있습니까?[53] 이 질문의 수학적 공식은 평면에서 라플라스 방정식의 디리클레 고유값을 포함하며, 이는 바이올린 현의 기본 진동 모드를 나타내는 정수와 직접 비유하여 기본 진동 모드를 나타냅니다.
스펙트럼 이론은 또한 함수의 푸리에 변환의 특정 측면의 기초가 됩니다. 푸리에 분석은 콤팩트 세트에 정의된 함수를 (바이올린 현 또는 드럼의 진동에 해당하는) 라플라시안의 이산 스펙트럼으로 분해하는 반면, 함수의 푸리에 변환은 유클리드 공간 전체에 정의된 함수를 라플라시안의 연속 스펙트럼에서 해당 성분으로 분해하는 것입니다. 푸리에 변환은 또한 기하학적이며, 한 힐베르트 공간(시간 영역)과 다른 공간(주파수 영역)의 등각이라고 주장하는 플랑드르 정리에 의해 정확하게 만들어졌습니다. 푸리에 변환의 이 등각 특성은 (연속 푸리에 변환에 대한 에너지 보존을 반영하기 때문에) 추상 고조파 분석에서 반복되는 주제입니다. 예를 들어 비상호적 고조파 분석에서 발생하는 구형 함수에 대한 플랑셰렐 정리에 의해 입증됩니다.
양자역학

존 폰 노이만(John von Neumann)이 개발한 양자역학의 수학적으로 엄격한 공식에서 [54]양자역학계의 가능한 상태(더 정확하게는 순수한 상태)는 상태 공간으로 알려진 복잡한 분리 가능한 힐베르트 공간에 상주하는 단위 벡터(상태 벡터라고 함)로 표현됩니다. norm 1(위상 인자)의 복소수까지 잘 정의됩니다. 즉, 가능한 상태는 일반적으로 복소 사영 공간이라고 불리는 힐베르트 공간의 사영화의 점입니다. 이 힐베르트 공간의 정확한 특성은 시스템에 따라 다릅니다. 예를 들어, 비 상대론적 스핀 0 입자의 위치와 운동량 상태는 모든 제곱 적분 가능 함수의 공간인 반면, 단일 양성자의 스핀 상태는 스피너의 2차원 복잡한 힐베르트 공간의 단위 요소입니다. 각 관측치는 상태 공간에 작용하는 자기 인접 선형 연산자로 표시됩니다. 관측치의 각 고유 상태는 연산자의 고유 벡터에 해당하고 관련 고유 값은 해당 고유 상태의 관측치 값에 해당합니다.[55]
두 상태 벡터 사이의 내적은 확률 진폭으로 알려진 복소수입니다. 양자역학적 시스템을 이상적으로 측정하는 동안 시스템이 주어진 초기 상태에서 특정 고유 상태로 붕괴될 확률은 초기 상태와 최종 상태 사이의 확률 진폭의 절대값의 제곱으로 제공됩니다.[56] 측정의 가능한 결과는 모든 고유값이 실제여야 하기 때문에 자기 인접 연산자의 선택을 설명하는 연산자의 고유값입니다. 주어진 상태에서 관측 가능한 확률 분포는 해당 연산자의 스펙트럼 분해를 계산하여 알 수 있습니다.[57]
일반적인 시스템에서 상태는 일반적으로 순수하지 않고, 대신 밀도 행렬로 제공되는 순수 상태 또는 혼합 상태의 통계적 혼합물로 표시됩니다. 즉 힐베르트 공간에서 추적 1의 자기 인접 연산자입니다.[58] 또한, 일반적인 양자 역학 시스템의 경우, 단일 측정의 효과는 대신 양의 연산자 가치 측정에 의해 설명되는 방식으로 시스템의 다른 부분에 영향을 미칠 수 있습니다. 따라서 일반 이론에서 상태와 관측 가능한 두 가지 구조는 순수 상태에 대한 이상화보다 상당히 복잡합니다.[59]
확률론
확률론에서 힐베르트 공간도 다양한 응용이 있습니다. 여기서 기본 힐베르트 공간은 L2 L무한한 첫 번째 및 두 번째 순간)를 갖는 주어진 확률 공간 상의 랜덤 변수의 공간입니다. 통계학에서 일반적인 연산은 랜덤 변수의 기대치를 차감하여 중심을 잡는 것입니다. X X가 랜덤 변수인 경우 - ( 가 중심입니다. 힐베르트 공간 보기에서, 이것은 기대 연산자의 커널에 {\ X의 직교 사영이며, 이것은 힐베르트 공간(사실상, 일정한 확률 변수가 1인 내적)에 대한 연속 선형 함수이며, 따라서 이 커널은 닫힌 부분 공간입니다.
조건부 기대는 힐베르트 공간에서 자연스럽게 해석됩니다.[60] Suppose that a probability space is given, where is a sigma algebra on the set , and is a probability measure on the measure space , F 가 의 시그마 아대수이면 그런 다음 조건부 E[ F] [ X은 F {F}} - 측정 가능 로 구성된 (ω, P) ^{2 P)}의 부분 공간에 X의 직교 투영입니다. If the random variable in is independent of the sigma algebra then conditional expectation , i.e., 에 투영됩니다. 측정 가능한 함수는 일정합니다. 마찬가지로 중심의 사영은 0입니다.
In particular, if two random variables and (in ) are independent, then the centered random variables and are orthogonal. (이는 두 변수가 공분산이 0임을 의미합니다. 즉, 상관이 없습니다.) 이 경우 기대 연산자의 커널에 있는 피타고라스 정리는 X 와 의 분산이 항등식을 만족함을 의미합니다.
마르팅게일 이론은 힐베르트 공간에서 공식화될 수 있습니다. 힐베르트 공간의 마팅게일은 각 n에 대하여 + 의 직교 사영이 공간의 요소들의 1, 2 …{\입니다.[62] If the are random variables, this reproduces the usual definition of a (discrete) martingale: the expectation of , conditioned on , 는 x 과 같습니다
힐베르트 공간은 또한 이토 미적분학의 기초 전체에서 사용됩니다.[63] 제곱 적분이 가능한 모든 마팅게일에 대해 (마팅게일의 2차 변화를 측도로 사용하여) 마팅게일에 대해 점진적으로 측정 가능한 프로세스의 등가 클래스 공간에 대한 힐버트 노름을 연관시킬 수 있습니다. Itô 적분은 먼저 단순한 과정에 대해 정의한 다음 힐베르트 공간에서 밀도를 이용하여 구성할 수 있습니다. 주목할 만한 결과는 이차 변동을 갖는 모든 마팅게일 M에 ⟨ M ⟩ t {\d_{t} 및 점진적으로 측정 가능한 프로세스 H를 을 증명하는 이토이소메트리입니다.
가우시안 과정 이론에서 특히 중요한 힐베르트 공간의 더 깊은 적용은 레오나르드 그로스 등이 양자장 이론에서 적분한 파인만 경로와 같은 무한 차원 공간에 대한 특정 형식적 적분을 이해하려는 시도입니다. 이와 같은 적분의 문제점은 무한차원 르베그 측도가 없다는 것입니다. 추상적인 위너 공간의 개념은 H에 대한 유한 가산 실린더 집합 측도에서 캐머런-마틴 공간이라고 불리는 힐베르트 공간 H를 조밀 부분집합으로 포함하는 바나흐 공간 B에 측도를 구성할 수 있게 합니다. B에 대한 결과 측정은 H의 요소에 의한 번역 하에 셀 수 없이 덧셈적이고 불변이며, 이는 비너 측정을 소볼레프 공간 ∞) ^{1}([0infty)}}의 가우시안 측정으로 수학적으로 엄격한 사고 방식을 제공합니다.
색지각
모든 실제 물리적 색상은 순수 스펙트럼 색상의 조합으로 나타낼 수 있습니다. 물리적 색상은 임의의 수의 스펙트럼 색상으로 구성될 수 있으므로 물리적 색상의 공간은 스펙트럼 색상보다 힐버트 공간으로 적절하게 표현될 수 있습니다. 인간은 색 지각을 위해 세 가지 종류의 원추세포를 가지고 있어, 지각 가능한 색은 3차원 유클리드 공간으로 나타낼 수 있습니다. 물리적 색상의 힐베르트 공간에서 인간이 인지할 수 있는 색상의 유클리드 공간까지의 다대일 선형 매핑은 많은 뚜렷한 물리적 색상이 인간에 의해 동일하게 인식될 수 있는 이유를 설명합니다(예: 순수한 노란색 빛 대 빨간색과 녹색 빛의 혼합, 메타머리즘 참조).[65][66]
특성.
피타고라스 정체성
힐베르트 공간 H에서 두 벡터 u와 v는 ⟨u, v ⟩ = 0일 때 직교합니다. 이에 대한 표기법은 u ⊥ v입니다. 더 일반적으로, S가 H의 부분 집합일 때, u ⊥ S라는 표기법은 u가 S의 모든 원소와 직교한다는 것을 의미합니다.
u와 v가 직교할 때는
n에 대한 유도에 의해, 이것은 직교 벡터들의 임의의 가군1 u, ..., u로n 확장됩니다.
언급한 피타고라스 정체성은 어떤 내부 제품 공간에서도 유효하지만, 피타고라스 정체성을 시리즈로 확장하기 위해서는 완전성이 필요합니다.[67] 직교벡터들의 급수 σu가 H에서 수렴하는 경우, 오직 일련의 정규분포의 제곱들이 수렴하는 경우에만, 그리고
평행사변형 항등식 및 편광

정의에 따라, 모든 힐베르트 공간도 바나흐 공간입니다. 또한 모든 힐베르트 공간에서 다음과 같은 평행사변형 항등식이 성립합니다.[68]
반대로, 평행사변형 항등식이 성립하는 모든 바나흐 공간은 힐베르트 공간이며, 내부 곱은 편광 항등식에 의해 표준에 의해 고유하게 결정됩니다.[69] 실제 힐베르트 공간의 경우, 편광 항등식은
복소 힐베르트 공간의 경우,
평행사변형 법칙은 임의의 힐베르트 공간이 균일하게 볼록한 바나흐 공간임을 의미합니다.[70]
최적 근사
이 하위 절에서는 힐베르트 사영 정리를 사용합니다. 만약 C가 힐베르트 공간 H의 비어 있지 않은 닫힌 볼록 부분집합이고 H의 x a 점이라면, C의 x와 점 사이의 거리를 최소화하는 고유한 점 y ∈ C가 존재하며,
이는 변환된 볼록 집합 D = C - x 에 최소 정규성을 갖는 점이 있다고 말하는 것과 같습니다. 증명은 모든 최소화 수열 (d) ⊂ D 가 코시 (평행선 항등식을 사용)이므로 최소 정규성을 갖는 D의 한 점으로 수렴 (완전성을 사용)된다는 것을 보여주는 것으로 구성됩니다. 보다 일반적으로, 이것은 모든 균일하게 볼록한 바나흐 공간에서 유지됩니다.[72]
이 결과를 H의 닫힌 부분공간 F에 적용하면 x에 가장 가까운 점 y ∈ F는 다음과 같이 특징지어짐을 알 수 있습니다.
이 점 y는 F에 대한 x의 직교 투영이며, 매핑 P: x → y는 선형입니다(정교 보법 및 투영 참조). 이 결과는 응용 수학, 특히 최소 제곱법의 기초를 이루는 수치 분석에서 특히 중요합니다.[74]
특히 F가 H와 같지 않을 때 F와 직교하는 0이 아닌 벡터 v를 찾을 수 있습니다(선택된 x ∉ F와 v = x - y). 매우 유용한 기준은 H의 부분집합 S에 의해 생성된 닫힌 부분공간 F에 이 관측치를 적용함으로써 얻어집니다.
- H의 부분 집합 S는 벡터 0이 S와 직교하는 유일한 벡터 v ∈인 경우(그리고 그것만 있는 경우) 조밀 벡터 부분 공간에 걸쳐 있습니다.
이중성
이중 공간 H*은 공간 H에서 기본 장으로 들어가는 모든 연속적인 선형 함수의 공간입니다. 그것은 다음과 같이 정의된 자연적인 규범을 가지고 있습니다.
Riesz 표현 정리는 이중 공간에 대한 편리한 설명을 제공합니다. H의 모든 원소 u에는 H*의 고유한 원소 φ가 존재하며, 이는 다음과 같이 정의됩니다.
Riesz 표현 정리는 u ↦ φ에 의해 정의된 H에서 H*까지의 지도가 객관적이며, 이는 이 지도를 등각 반선형 동형으로 만듭니다. 따라서 이중 H*의 모든 원소 φ에는 H에 오직 하나의 u가 존재하므로,
우변의 순서 역전은 u의 반직선성으로부터 φ의 선형성을 회복시킵니다. 실제의 경우, H에서 그 이중으로의 반선형 동형은 실제로 동형이고, 따라서 실제 힐베르트 공간은 그들 자신의 이중과 자연스럽게 동형입니다.
표현 벡터 u는φ 다음과 같은 방법으로 얻어집니다. φ ≠ 0일 때, 커널 F = Ker(φ)는 H와 같지 않은 H의 닫힌 벡터 부분 공간이므로 F와 직교하는 0이 아닌 벡터 v가 존재합니다. 벡터 u는 v의 적합한 스칼라 배수 λv입니다. φ(v) = ⟨v, u ⟩이 산출되어야 하는 요건
이 대응 φ ↔ u는 물리학에서 널리 사용되는 브라켓 표기법에 의해 이용됩니다. 물리학에서는 ⟨xy ⟩로 표시되는 내부 산물이 오른쪽에 선형이라고 가정하는 것이 일반적입니다.
Riesz 표현 정리는 기본적으로 내부 산물의 존재뿐만 아니라 공간의 완전성에도 의존합니다. 사실, 이 정리는 어떤 내부 곱 공간의 위상 이중성을 그 완성과 함께 식별할 수 있다는 것을 암시합니다.[77] 리에즈 표현 정리의 즉각적인 결과는 또한 힐베르트 공간 H가 반사적이라는 것이며, 이는 H에서 이중 이중 공간으로의 자연 지도가 동형임을 의미합니다.
약하게 수렴하는 수열
힐베르트 공간 H에서 {x} 수열은 다음과 같이 벡터 x ∈ H로 약하게 수렴합니다.
예를 들어, 임의의 정칙 수열 {fn}는 베셀의 부등식의 결과로 0으로 약하게 수렴합니다. 모든 약하게 수렴하는 수열 {xn}은 균일한 유계 원리에 의해 유계됩니다.
반대로, 힐베르트 공간의 모든 유계 수열은 약하게 수렴하는 수열(Alaoglu's theorem)을 인정합니다.[78] 이 사실은 볼자노와 같은 방법으로 연속 볼록 함수에 대한 최소화 결과를 증명하는 데 사용될 수 있습니다.위어스트라스d 정리는 R 위의 연속 함수에 사용됩니다. 여러 변형 중에서 하나의 간단한 문장은 다음과 같습니다.[79]
- 만약 f : H → R이 볼록 연속 함수라면, ‖ x ‖가 ∞하는 경향이 있을 때 f(x)가 + ∞하는 경향이 있는 반면, f는 어떤 점 x ∈ H에서 최소값을 허용합니다.
이 사실은 (그리고 그것의 다양한 일반화는) 변동의 미적분학에서 직접적인 방법의 기초입니다. 볼록 함수에 대한 최소화 결과는 H가 반사적이기 때문에 힐베르트 공간 H의 닫힌 경계 볼록 부분 집합이 약하게 콤팩트하다는 약간 더 추상적인 사실의 직접적인 결과이기도 합니다. 약하게 수렴하는 서브 시퀀스의 존재는 에베를라인-슈뮬리안 정리의 특별한 경우입니다.
바나흐 공백 속성
바나흐 공간의 모든 일반적인 속성은 힐베르트 공간에 대해 계속 유지됩니다. 열린 매핑 정리는 하나의 바나흐 공간에서 다른 공간으로 연속적인 주관적 선형 변환은 열린 집합을 열린 집합으로 보낸다는 것을 의미하는 열린 매핑이라고 말합니다. 상관 관계는 한 바나흐 공간에서 다른 바나흐 공간으로의 연속적이고 이분법적인 선형 함수가 동형(즉, 그 역도 연속적인 연속적인 선형 맵)이라는 유계 역 정리입니다. 이 정리는 힐베르트 공간의 경우 일반 바나흐 공간보다 증명이 상당히 간단합니다.[80] 열린 매핑 정리는 닫힌 그래프 정리와 동등하며, 한 바나흐 공간에서 다른 바나흐 공간으로의 선형 함수는 그래프가 닫힌 집합인 경우에만 연속적이라고 주장합니다.[81] 힐베르트 공간의 경우, 이는 무한 연산자에 대한 연구에서 기본적인 것입니다(닫힌 연산자 참조).
(기하학적) 한-바나흐 정리는 닫힌 볼록 집합이 힐베르트 공간의 초평면을 통해 그 바깥의 어떤 점과도 분리될 수 있다고 주장합니다. 이것은 가장 좋은 근사 특성의 즉각적인 결과입니다: 만약 y가 x에 가장 가까운 닫힌 볼록 집합 F의 원소라면, 분리 초평면은 그 중점을 지나는 세그먼트 xy에 수직인 평면입니다.[82]
힐베르트 공간의 연산자
유계 연산자
힐베르트 공간 H에서 두 번째 힐베르트 공간 H로 가는 연속 선형 연산자 A: H → H는 유계 집합을 유계 집합으로 매핑한다는 의미에서 유계입니다. 반대로 연산자가 유계이면 연속입니다. 이와 같은 유계 선형 연산자의 공간은 다음과 같은 연산자 규범을 갖습니다.
두 유계 선형 연산자의 합과 합성은 다시 유계와 선형입니다. H의 y에 대하여, x ∈ H를 ⟨Ax로 보내는 지도이며, y ⟩은 선형이고 연속적이므로, Riesz 표현 정리에 의하면 다음과 같은 형태로 표현될 수 있습니다.
H 위의 모든 유계 선형 연산자(연산자 H → H를 의미함)의 집합 B(H)는 연산자 대수의 한 종류인 C*-대수입니다.
A* = A이면 B(H)의 원소 A를 '자가접합' 또는 '허미시안'이라고 부릅니다. A가 에르미트와 ⟨Ax이고, x가 모든 x에 대해 0 ⟩ ≥이면 A를 '음이 아닌'이라고 하고, x = 0일 때만 평등이 유지되면 A를 '양'이라고 합니다. 자기 인접 연산자들의 집합은 A - B가 0의 ≥이면 A는 B의 ≥인 부분 순서를 인정합니다. A가 어떤 B에 대하여 B*B의 형태를 가지면 A는 음수가 아니고, B가 가역이면 A는 양수입니다. 음이 아닌 연산자 A에 대하여, 다음과 같은 고유한 음이 아닌 제곱근 B가 존재한다는 의미에서 역 또한 참입니다.
스펙트럼 정리에 의해 정확하게 만들어진 의미에서 자기 인접 연산자는 "실제" 연산자로 유용하게 생각될 수 있습니다. A*A = AA*이면 B(H)의 원소 A를 노멀이라고 합니다. 정상 연산자는 자기 인접 연산자와 자기 인접 연산자의 허수배의 합으로 분해됩니다.
B(H)의 원소 U는 U가 가역이고 그 역이 U*에 의해 주어지면 유니터리라고 불립니다. 이것은 또한 모든 x, y ∈ H에 대해 Ub on 및 ⟨ Ux, Uy ⟩ = ⟨x, y ⟩을 요구함으로써 표현될 수 있습니다. 단일 연산자는 H의 등각군인 합성 아래 군을 형성합니다.
B(H)의 원소는 유계 집합을 상대적으로 콤팩트한 집합으로 보내면 콤팩트합니다. 마찬가지로, 유계 연산자 T는 임의의 유계 수열 {xk}에 대하여, 수열 {Txk}이 수렴 서브수열을 갖는 경우 콤팩트합니다. 많은 적분 연산자는 콤팩트하며, 실제로 적분 방정식 연구에서 특히 중요한 힐베르트-슈미트 연산자로 알려진 특수한 종류의 연산자를 정의합니다. Fredholm 연산자는 동일성의 배수만큼 콤팩트 연산자와 다르며, 유한 차원의 커널과 커널을 갖는 연산자로서 동등하게 특징지어집니다. 프레드홀름 연산자 T의 지수는 다음과 같이 정의됩니다.
지수는 동형 불변이며 Atiyah-Singer 지수 정리를 통해 미분 기하학에서 깊은 역할을 합니다.
무한 연산자
무한 연산자는 힐베르트 공간에서도 다루기 쉽고 양자역학에 중요한 응용을 합니다.[84] 힐베르트 공간 H 위의 무한 연산자 T는 정의역 D(T)가 H의 선형 부분공간인 선형 연산자로 정의됩니다. 종종 정의역 D(T)는 H의 조밀한 부분공간이며, 이 경우 T는 조밀하게 정의된 연산자로 알려져 있습니다.
조밀하게 정의된 경계 없는 연산자의 인접은 경계 있는 연산자의 인접과 본질적으로 동일한 방식으로 정의됩니다. 자기 인접 무한 연산자는 양자역학의 수학적 공식에서 관측 가능한 것의 역할을 합니다. 힐베르트 공간 L2(R) 위의 자기 인접 무한 연산자들의 예는 다음과 같습니다.[85]
- 차동 연산기의 적절한 확장 여기서 i는 가상 단위이고 f는 소형 지지의 미분 가능한 함수입니다.
- 곱셈별 x 연산자:
이것들은 각각 운동량과 위치 관측 가능량에 해당합니다. A의 경우 도함수가 존재할 필요가 없고, B의 경우 곱함수가 제곱적분일 필요가 없기 때문에 A와 B는 모두 H에 정의되지 않습니다. 두 경우 모두 가능한 인수 집합은2 L(R)의 조밀한 부분 공간을 형성합니다.
시공
직접합
두 힐베르트 공간 H와1 H는2 (직교)직접합이라 불리는 다른 힐베르트 공간으로 결합할 수 있으며,[86]
모든 순서쌍(x, x)의 집합으로 구성되며, 여기서 x ∈ H, i = 1, 2 및 다음으로 정의되는 내적
보다 일반적으로, H가 i ∈ I로 색인된 힐베르트 공간의 가군이라면, H의 직접 합은 다음과 같습니다.
내부 제품은 다음과 같이 정의됩니다.
각각의i H는 모든 H의i 직접 합에서 닫힌 부분 공간으로 포함됩니다. 게다가, H는i 쌍대 직교합니다. 반대로, 힐베르트 공간 H에 닫힌 부분 공간 V, i ∈ I가 쌍대 직교하고 H에서 결합이 조밀한 경우 H는 V의 직접 합과 정준 동형입니다. 이 경우 H를 V의i 내부 직접 합이라고 합니다. 직접합(내부 또는 외부)은 i번째 직접합 H에i 대한 직교 사영 E의i 계열도 갖추고 있습니다. 이 사영들은 직교 조건을 만족시키는 유계, 자기 인접, 멱함수 연산자들입니다.
힐베르트 공간 H의 콤팩트한 자기 인접 연산자에 대한 스펙트럼 정리는 H가 연산자의 고유 공간의 직교 직접 합으로 분할되고 또한 고유 공간에 대한 투영의 합으로 연산자의 명시적 분해를 제공한다고 말합니다. 힐베르트 공간의 직접 합은 가변 수의 입자를 포함하는 시스템의 포크 공간으로도 양자역학에서 나타나며, 여기서 직접 합의 각 힐베르트 공간은 양자역학 시스템에 대한 추가 자유도에 해당합니다. 표현 이론에서, 피터-와일 정리는 힐베르트 공간 위의 콤팩트한 군의 단일 표현이 유한 차원 표현의 직접적인 합으로 분할되는 것을 보장합니다.
텐서곱
만약 x, y ∊ H와 x, y ∊ H라면, (보통) 텐서 곱 위의 내적을 다음과 같이 정의합니다. 단순한 텐서에, let.
그런 다음 이 공식은 H ⊗ H의 내부 곱으로 세스선형성에 의해 확장됩니다. H와 H의 힐베르트 텐서 곱은 때때로 H ⊗ ^ {\displaystyle {\widehat {\otimes}} H로 표시되며, 이 내부 곱과 관련된 메트릭에 대해 H ⊗ H를 완료하여 얻은 힐베르트 공간입니다.
예는 힐베르트2 공간 L([0, 1])에 의해 제공됩니다. L2([0, 1])의 두 사본의 힐베르트 텐서 곱은 제곱 [0, 1] 위의 제곱 적분 함수의 공간 L2([0, 1])2과 등각선적으로 선형 동형입니다.2 이 동형 사상은 단순 텐서 f ⊗ f를 함수로 보냅니다.
이 예는 다음과 같은 의미에서 전형적입니다.[88] 모든 단순 텐서 곱 x ⊗ x는 주어진 x* ∈ H를 매핑하는 H부터 H까지의 순위 1 연산자입니다.
단순 텐서에 정의된 이 매핑은 H ⊗ H와 H에서 H까지의 유한 순위 연산자 공간 사이의 선형 식별로 확장됩니다. 이는 H에서 H까지 힐베르트-슈미트 연산자의 힐베르트 공간 HS(H, H)를 갖는 힐베르트 텐서 곱 ⊗ ^ {\displaystyle {\widehat {\otimes}} H의 선형 등각으로 확장됩니다.
정규 기저
선형대수학으로부터 정규적인 기초에 대한 개념은 힐베르트 공간의 경우로 일반화됩니다.[89] 힐베르트 공간 H에서, 정규 기저는 다음 조건을 만족시키는 H의 원소들로 이루어진 군 {ek}k ∈ B입니다.
- 직교성: B의 다른 두 원소는 모두 직교합니다: 모든 k에 대하여 ⟨, e ⟩ = 0, k ≠ j를 갖는 j ∈ B.
- 정규화: 패밀리의 모든 요소는 모든 k개의 ∈ B에 대해 ‖ ‖ = 1이라는 norm 1을 갖습니다.
- 완성도: 가족 e, k ∈ B의 선형 스팬은 H에서 조밀합니다.
앞의 두 조건 기저를 만족하는 벡터들의 체계를 정칙 체계 또는 정칙 집합(또는 B가 셀 수 있는 경우 정칙 수열)이라고 합니다. 그러한 시스템은 항상 선형적으로 독립적입니다.
이름에도 불구하고, 정규 기저는 일반적으로 선형 대수의 의미에서 기초가 아닙니다(하멜 기저). 더 정확하게 말하면, 정규 기저는 힐베르트 공간이 유한 차원 벡터 공간인 경우에만 하멜 기저입니다.[90]
힐베르트 공간의 벡터들로 이루어진 정규적인 시스템의 완전성은 다음과 같이 동등하게 재작성될 수 있습니다.
- for every v ∈ H, if ⟨v, ek⟩ = 0 for all k ∈ B, then v = 0.
이것은 조밀한 선형 부분공간에 직교하는 유일한 벡터가 영벡터라는 사실과 관련이 있는데, 만약 S가 임의의 직교 집합이고 v가 S와 직교한다면, v는 전체 공간인 S의 선형 스팬의 폐쇄와 직교하기 때문입니다.
직교 기저의 예는 다음과 같습니다.
- 집합 {(1, 0, 0), (0, 1, 0), (0, 0, 1)}은 도트 곱과 R의3 직교 기저를 형성합니다.
- f(x) = exp(2 πinx)를 갖는 수열 {f n ∈ Z}은 복소 공간 L([0, 1])의 직교 기저를 형성합니다.
무한 차원의 경우, 선형 대수학의 의미에서 정규 기저는 기초가 되지 않을 것입니다. 양자를 구별하기 위해 후자의 기저는 하멜 기저라고도 불립니다. 기저 벡터의 스팬이 조밀하다는 것은 공간의 모든 벡터를 무한급수의 합으로 쓸 수 있다는 것을 의미하며, 직교성은 이 분해가 유일하다는 것을 의미합니다.
시퀀스 공간
복소수의 제곱합 가능한 수열의 공간ℓ 2 {2}}는 무한 수열의 집합입니다.
이 공간은 정규분포를 기준으로 합니다.
이 공간은 유한 차원 벡터의ℓ 2 n 2}^{n} 공간의 무한 차원 일반화입니다. 일반적으로 무한 차원 공간에서 닫힌 집합과 유계 집합이 반드시 (순차적으로) 콤팩트하지 않다는 것을 보여주기 위해 사용되는 첫 번째 예입니다. (모든 유한 차원 공간의 경우와 마찬가지로). 실제로 위의 직교 벡터 집합은 다음을 보여줍니다. 단위 볼(즉, norm이 1보다 작거나 같은 점들의 볼)에 있는 벡터들의 무한한 시퀀스입니다. 이 집합은 분명히 경계가 있고 닫혀 있습니다. 그러나 이러한 벡터의 하위 시퀀스가 어떤 것으로도 수렴되지 않으며 결과적으로ℓ 2 {2}}의 단위 볼은 콤팩트하지 않습니다. 직관적으로 이는 시퀀스의 다음 요소가 회피할 수 있는 "항상 다른 좌표 방향"이 있기 때문입니다.
공간ℓ 2 {2}}를 여러 가지 방법으로 일반화할 수 있습니다. 예를 들어, B가 임의의 집합이면, 다음과 같이[91] 정의되는 인덱스 집합 B를 갖는 힐베르트 수열 공간을 만들 수 있습니다.
여기서 B 위의 합은 다음과 같이 정의됩니다.
for all x, y ∈ l2(B). 여기서 합은 0이 아닌 항들을 셀 수 없을 정도로 많이 가지며, 코시-슈바르츠 부등식에 의해 무조건 수렴됩니다.
l2(B)의 정규 기저는 다음과 같은 집합 B에 의해 지수화됩니다.
베셀 부등식과 파르세발 공식
f, …, f를 H의 유한 정칙 시스템이라 하자. 임의의 벡터 x ∈ H에 대하여,
Then ⟨x, fk⟩ = ⟨y, fk⟩ for every k = 1, …, n. 따라서 x - y는 각 f와k 직교하므로 x - y는 y와 직교합니다. 피타고라스의 정체성을 두 번 사용하면 다음과 같습니다.
∈ I인 {f}를 H의 임의의 정칙계라고 하자. 앞의 부등식을 I의 모든 유한 부분집합 J에 적용하면 베셀의 부등식은 다음과 같습니다.
기하학적으로, 베셀의 부등식은 f에i 걸쳐 있는 선형 부분공간 위에 x의 정사영이 x의 정사영을 초과하지 않는다는 것을 의미합니다. 이것은 2차원에서 직각 삼각형의 다리 길이가 빗변의 길이를 초과하지 않을 수 있다는 주장입니다.
베셀의 부등식은 실제로 베셀의 부등식이 평등일 때를 지배하는 파르세발의 정체성이라는 더 강력한 결과로 가는 디딤돌입니다. 정의에 따라, 만약 {ek}k ∈ B가 H의 정규 기저라면, H의 모든 원소 x는 다음과 같이 쓸 수 있습니다.
B가 셀 수 없더라도 베셀의 부등식은 식을 잘 정의하고 셀 수 없이 많은 0이 아닌 항으로만 구성됨을 보장합니다. 이 합을 x의 푸리에 전개라고 하며, 개별 계수 ⟨x, e ⟩은 x의 푸리에 계수라고 합니다. 그러면 파르세발의 항등식은 다음과 같이 주장합니다.
반대로,[93] {ek}가 모든 x에 대해 Parseval의 아이덴티티가 유지되는 정규 직교 집합이면 {ek}는 정규 직교 기저입니다.
힐베르트 차원
존 보조정리의 결과로 모든 힐베르트 공간은 정칙 기저를 인정하며, 같은 공간의 정칙 기저 두 개는 같은 카디널리티를 가지며, 이를 공간의 힐베르트 차원이라고 합니다.[94] 예를 들어, l2(B)는 B로 지수화된 정규 기저를 가지므로, 그 힐베르트 차원은 B의 기수(유한 정수이거나 셀 수 있거나 셀 수 없는 기수일 수 있음)입니다.
힐베르트 차원은 하멜 차원(벡터 공간의 일반적인 차원)보다 크지 않습니다. 두 차원은 동일하고 둘 중 하나만 유한하면 됩니다.
파세발의 항등식의 결과로, 만약 {e}가 H의 정칙 기저라면, φ φ(x) = ⟨x로 정의되는 맵 ⟩: H → l(B), e is는 힐베르트 공간의 등각 동형 사상입니다. 이는 다음과 같은 쌍방향 선형 사상입니다.
분리 가능한 공간
힐베르트 공간은 계산 가능한 부분 집합이 조밀하게 포함된 경우에 분리 가능합니다. 조른의 보조정리와 함께 이것은 힐베르트 공간이 셀 수 있는 직교 기저를 인정하는 경우에만 분리 가능하다는 것을 의미합니다. 따라서 모든 무한 차원 분리 가능한 힐베르트 공간은 제곱합 가능한 수열 공간ℓ 2와 등각 동형입니다. ^{2}}
과거에는 힐베르트 공간을 정의의 일부로 분리할 수 있어야 했습니다.[96]
양자장이론에서
물리학에서 사용되는 대부분의 공간은 분리 가능하며, 이들은 모두 동형이기 때문에 어떤 무한 차원 분리 가능한 힐베르트 공간을 "힐베르트 공간" 또는 "힐베르트 공간"이라고 부르기도 합니다.[97] 양자장 이론에서도 대부분의 힐베르트 공간은 와이트만 공리에 의해 규정된 것처럼 사실상 분리 가능합니다. 그러나 분리할 수 없는 힐베르트 공간도 양자장 이론에서 중요하다는 주장이 종종 제기되는데, 이는 이론의 시스템이 무한한 자유도를 가지고 있고 (1차원보다 큰 공간의) 무한한 힐베르트 텐서 곱은 분리할 수 없기 때문입니다.[98] 예를 들어, 보손 장은 자연스럽게 텐서 곱의 요소로 간주될 수 있는데, 그 요소들은 각각의 공간 지점에서 조화 진동자를 나타냅니다. 이런 관점에서 보손의 자연 상태 공간은 분리할 수 없는 공간으로 보일 수 있습니다.[98] 그러나 물리적으로 의미 있는 필드를 포함할 수 있는 전체 텐서 제품의 분리 가능한 작은 부분 공간(관측 변수를 정의할 수 있음)에 불과합니다. 분리할 수 없는 또 다른 힐베르트 공간은 공간의 무한한 영역에 있는 입자들의 무한한 집합의 상태를 모델링합니다. 공간의 정규 기저는 연속 파라미터인 입자의 밀도에 의해 지수화되며, 가능한 밀도의 집합은 셀 수 없기 때문에 그 기저는 셀 수 없습니다.[98]
직교 보형 및 사영
S가 힐베르트 공간 H의 부분집합이라면, S에 직교하는 벡터들의 집합은 다음과 같이 정의됩니다.
집합 S는⊥ H의 닫힌 부분 공간이므로(내부 곱의 선형성과 연속성을 사용하여 쉽게 증명할 수 있음) 힐베르트 공간을 형성합니다. 만약 V가 H의 닫힌 부분공간이라면, V를⊥ V의 직교 여집합이라고 합니다. 실제로 모든 x ∈ H는 v ∈ V와 w ∈ V를 사용하여 x = v + w로 고유하게 쓸 수 있습니다. 따라서 H는 V와 V의⊥ 내부 힐베르트 직접 합입니다.
x를 v로 매핑하는 선형 연산자 P: H → H를 V에 대한 직교 사영이라고 합니다. H의 모든 닫힌 부분 공간 집합과 P = P인 모든 유계 자기 인접 연산자 P의 집합 사이에는 자연스러운 일대일 대응 관계가 있습니다. 구체적으로,
정리 — 직교 사영 P는 성질 P = P를 갖는 노름 ≤ 1의 H 위의 자기 인접 선형 연산자입니다. 또한, E = E가 형태 P인 임의의 자기 인접 선형 연산자 E, 여기서 V는 E의 범위입니다. H의 모든 x에 대하여, P(x)는 ‖x - v ‖ 거리를 최소화하는 V의 유일한 원소입니다.
이것은 PV(x)의 기하학적 해석을 제공합니다. 이것은 V의 요소에 의한 x에 대한 가장 좋은 근사입니다.[99]
사영 P와 P는 PP = 0인 경우 상호 직교라고 합니다. 이것은 U와 V가 H의 부분공간으로서 직교하는 것과 같습니다. 두 사영 P와 P의 합은 U와 V가 서로 직교하는 경우에만 사영이며, 그 경우 P + P = P입니다. 합성 PP는 일반적으로 사영이 아닙니다. 사실 합성은 두 사영이 통근하는 경우에만 사영이며, 이 경우 PP = P입니다.
코도메인을 힐베르트 공간 V로 제한함으로써, 직교 사영 P는 사영 매핑 π H → V를 생성하고, 이는 포함 매핑의 부가물입니다.
0이 아닌 닫힌 부분공간 V에 대한 직교 사영 P의V 연산자 노름은 다음과 같습니다.
따라서 힐베르트 공간의 모든 닫힌 부분공간 V는 P = P와 같은 노름의 연산자 P의 상이 됩니다. 적절한 사영 연산자를 갖는 성질은 힐베르트 공간을 특징짓습니다.[102]
- 2보다 높은 차원의 바나흐 공간은 (등각적으로) 모든 닫힌 부분 공간 V에 대하여 이미지가 P = P인 노름 1의 연산자 P가 존재하는 경우에만 힐베르트 공간입니다.
이 결과는 힐베르트 공간의 메트릭 구조를 특징짓는 반면, 위상 벡터 공간으로서의 힐베르트 공간의 구조 자체는 상보적 부분 공간의 존재 측면에서 특징지어질 수 있습니다.[103]
- 모든 닫힌 부분공간 V에 대하여 X가 내부의 직접합 V 공간 W와 같도록 닫힌 부분⊕ W가 존재하는 경우에만 바나흐 공간 X는 힐베르트 공간과 위상적으로 선형 동형입니다.
직교 보형은 몇 가지 기본적인 결과를 만족시킵니다. 이것은 U가 ⊂ V이면, V가 U의 종결에 포함되는 경우에만 동일한 값을 갖는 V ⊆ U라는 의미에서 단조 함수입니다. 이 결과는 한-바나흐 정리의 특별한 경우입니다. 부분공간의 폐쇄는 완전하게 직교 보형의 관점에서 특징지어질 수 있습니다: 만약 V가 H의 부분공간이라면, V의 폐쇄는 V와⊥⊥ 같습니다. 따라서 직교 여집합은 힐베르트 공간의 부분 공간 순서에 대한 갈루아 연결입니다. 일반적으로 부분 공간의 합에 대한 직교 여집합은 직교 여집합의 교집합입니다.[104]
V가i 닫혀 있으면,
스펙트럼 이론
힐베르트 공간의 자기 인접 연산자에 대한 잘 개발된 스펙트럼 이론이 있으며, 이는 실수 위의 대칭 행렬 또는 복소수 위의 자기 인접 행렬에 대한 연구와 거의 유사합니다.[105] 같은 의미에서 직교 사영 연산자의 적절한 합(사실상 적분)으로 자기 인접 연산자의 "각형화"를 얻을 수 있습니다.
연산자 T의 스펙트럼, σ(T)로 표시되는 것은 T λ에 연속적인 역수가 없는 복소수 λ의 집합입니다. T가 유계인 경우 스펙트럼은 항상 복소 평면에 콤팩트 집합이며 디스크 z ≤ ‖T ‖ 내부에 있습니다. T가 자기 인접이면 스펙트럼은 실수입니다. 실제로, 이것은 [m, M]구간에 포함됩니다.
또한 m과 M은 모두 실제로 스펙트럼 내에 포함되어 있습니다.
연산자 T의 고유 공간은 다음과 같습니다.
유한 행렬과 달리 T 스펙트럼의 모든 원소가 고유 값이어야 하는 것은 아닙니다. 선형 연산자 T - λ는 정사 행렬이 아니기 때문에 역수가 부족할 수 있습니다. 일반적인 의미에서 연산자의 스펙트럼의 요소를 스펙트럼 값이라고 합니다. 스펙트럼 값이 고유값일 필요는 없기 때문에 스펙트럼 분해가 유한 차원보다 더 미묘한 경우가 많습니다.
그러나 자기 인접 연산자 T의 스펙트럼 정리는 T가 콤팩트 연산자라고 가정할 경우 특히 간단한 형태를 취합니다. 콤팩트 자기접합 연산자에 대한 스펙트럼 정리는 다음과 같습니다.[106]
- 콤팩트한 자기 인접 연산자 T는 셀 수 있을 정도로(또는 유한하게) 많은 스펙트럼 값만을 갖습니다. T의 스펙트럼은 복소평면에서 가능한 0을 제외하고는 한계점이 없습니다. T의 고유 공간은 H를 직교 직접 합으로 분해합니다. 또한λ, E가 고유 공간λ H에 대한 직교 사영을 나타낸다면,여기서 총합은 B(H)의 표준에 대해 수렴합니다.
이 정리는 특히 힐베르트-슈미트 연산자에서 발생하는 많은 적분 연산자가 콤팩트하기 때문에 적분 방정식 이론에서 기본적인 역할을 합니다.
자기 인접 연산자에 대한 일반적인 스펙트럼 정리는 무한 합산이 아닌 일종의 연산자 값 리만-슈틸트제 적분을 포함합니다.[107] T와 연관된 스펙트럼 패밀리는 각 실수에 λ 연산자 E를 포함하며, 연산자의 널 공간(T - λ)에 대한 투영이며, 여기서 자기 인접 연산자의 양의 부분은 다음에 의해 정의됩니다.
연산자 E는λ 자기 인접 연산자에 정의된 부분 순서에 비해 단조 증가합니다. 고유값은 점프 불연속에 정확히 대응합니다. 하나는 다음과 같이 주장하는 스펙트럼 정리를 가지고 있습니다.
적분은 B(H)의 표준에 대해 수렴하는 리만-슈틸트제스 적분으로 이해됩니다. 특히 일반적인 스칼라 값 적분 표현을 사용합니다.
스펙트럼이 이제 실제가 아닌 복소수를 포함할 수 있기 때문에 측정된 연산자 값 Stieltjes가 대신λ 동일성의 해상도로 대체되어야 하지만, 다소 유사한 스펙트럼 분해는 정상 연산자에 대해 유지됩니다.
스펙트럼 방법의 주요 응용은 스펙트럼 매핑 정리로서, 적분을 형성하여 T의 스펙트럼에 정의된 임의의 연속 복소 함수 f를 자기 인접 연산자에 적용할 수 있습니다.
결과적으로 생성된 연속 함수 미적분학은 특히 의사 미분 연산자에 적용됩니다.[108]
무한 자기 결합 연산자의 스펙트럼 이론은 유한 연산자보다 약간 더 어렵습니다. 무한 연산자의 스펙트럼은 경계 연산자의 경우와 정확히 동일한 방식으로 정의됩니다. λ는 분해능 연산자일 경우 스펙트럼 값입니다.
잘 정의된 연속 연산자가 될 수 없습니다. T의 자기 결합성은 여전히 스펙트럼이 실제임을 보장합니다. 따라서 무제한 연산자와 함께 작업하는 본질적인 아이디어는 대신 λ가 비실체인 분해능 R을 보는 것입니다. 이것은 경계 정규 연산자이며, 이 연산자는 스펙트럼 표현을 인정하며, 이후 T 자체의 스펙트럼 표현으로 전달될 수 있습니다. 예를 들어 Laplace 연산자의 스펙트럼을 연구하는 데도 유사한 전략이 사용됩니다. 연산자를 직접 다루기보다는 Riesz 전위나 Bessel 전위와 같은 관련 분해능으로 보입니다.
이 경우 스펙트럼 정리의 정확한 버전은 다음과 같습니다.[109]
정리 — 힐베르트 공간 H 위에 조밀하게 정의된 자기 인접 연산자 T가 주어지면, R의 보렐 집합 위에 항등식 E의 고유한 해상도가 존재하므로, 다음과 같이
무한정 정규 연산자에 적용되는 스펙트럼 정리 버전도 있습니다.
대중문화에서는
토마스 핀촌(Thomas Pynchon)의 소설인 중력의 무지개(1973)에서 등장인물 중 하나는 "힐버트 스페이스"에 대한 말장난인 "새미 힐버트 스페이스(Sammy Hilbert-Spaess)"라고 불립니다. 이 소설은 또한 괴델의 불완전성 정리를 언급하고 있습니다.[110]
참고 항목
- 바나흐 공간 – 완전한 정규 벡터 공간
- 포크 공간 – 다중 입자 상태 공간
- 힐베르트 공간의 기본 정리
- 공간 – 지리학적으로 완전한 비양의 곡률 메트릭 공간 위키데이터 하는 페이지
- 하우스도르프 공간 – 위상 공간의 유형
- 힐베르트 대수
- 힐베르트 C*-모듈 – 힐베르트 공간의 개념을 일반화하는 수학적 대상
- 힐베르트 다양체 – 힐베르트 공간을 모델로 한 다양체
- L-semi-inner 제품 – 모든 표준 공간에 적용되는 내부 제품의 일반화
- 국부적으로 볼록한 위상 벡터 공간 – 볼록 열린집합으로 정의된 위상을 갖는 벡터 공간
- 연산자 이론 – 수학 분야
- 연산자 토폴로지 – 힐베르트 공간의 연산자 집합에 대한 토폴로지
- 양자 상태 공간 – 물리적 양자계를 나타내는 수학적 공간
- 부정 힐베르트 공간 – 함수해석학에서 "경계"와 연속 고유값의 연구를 연결하는 구성
- 위상 벡터 공간 – 근접 개념을 가진 벡터 공간
언급
메모들
- ^ Axler 2014, p. 164 §6.2
- ^ 그러나 일부 출처는 이러한 속성을 가진 유한 차원 공간을 무한 차원 공간에 대한 "힐버트 공간"이라는 용어를 보존하는 사전 힐버트 공간이라고 부릅니다. 예를 들어, 레비탄 2001을 참조하십시오.
- ^ 1974년 § 2.8 화성
- ^ 이 섹션의 수학 자료는 Dieudonné(1960), Hewitt & Stromberg(1965), Reed & Simon(1980) 또는 Rudin(1987)과 같은 기능 분석에 관한 모든 좋은 교과서에서 찾을 수 있습니다.
- ^ Schaefer & Wolff 1999, 페이지 122–202.
- ^ Dieudonné 1960, §6.2
- ^ 로마 2008, 327쪽
- ^ 로마 2008, p. 330 정리 13.8
- ^ a b Stein & Shakarchi 2005, 페이지 163}}
- ^ 1960년 디외도네
- ^ 주로 헤르만 그라스만의 작업에서, 아우구스트 페르디난트 뫼비우스(Boyer & Merzbach 1991, pp. 584–586)의 재촉으로 이루어졌습니다. 추상 벡터 공간에 대한 최초의 현대적 공리적 설명은 궁극적으로 Giuseppe Peano의 1888년 계정(Grattan-Guinness 2000, §5.2.2; O'Connor & Robertson 1996)에 등장했습니다.
- ^ 힐베르트 공간의 역사에 대한 자세한 설명은 부르바키 1987에서 찾을 수 있습니다.
- ^ 슈미트 1908
- ^ Titchmarsh 1946, §IX.1
- ^ 레베그 1904. 통합론의 역사에 대한 보다 자세한 내용은 Bourbaki(1987)와 Saks(2005)에서 확인할 수 있습니다.
- ^ 부르바키 1987.
- ^ Dunford & Schwartz 1958, § IV.16
- ^ Dunford & Schwartz(1958, §IV.16)에서 L[0,1]의 모든 선형 함수가 적분으로 표현되는 결과는 Fréchet(1907)과 Riesz(1907)에 의해 공동으로 기인합니다. 힐베르트 공간의 이중성이 힐베르트 공간 자체와 동일하다는 일반적인 결과는 Riesz(1934)에서 찾을 수 있습니다.
- ^ 폰 노이만 1929년
- ^ 클라인 1972, 1092쪽
- ^ 힐베르트, 노르트하임 & 폰 노이만 1927
- ^ a b 바일 1931.
- ^ 푸르고베치키 1981, 1-10쪽.
- ^ a b 폰 노이만 1932
- ^ Peres 1993, pp. 79–99.
- ^ 머피 1990, 페이지 112
- ^ 머피 1990, 페이지 72
- ^ 할모스 1957, 42조.
- ^ 휴이트 & 스트롬버그 1965년
- ^ Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- ^ a b Bers, John & Schechter 1981.
- ^ Giusti 2003.
- ^ 스타인 1970
- ^ 자세한 내용은 Warner(1983)에서 확인할 수 있습니다.
- ^ 하디 공간에 대한 일반적인 언급은 Duren(1970)이라는 책입니다.
- ^ Krantz 2002, §1.4
- ^ Krantz 2002, §1.5
- ^ 1988년 젊은 9장
- ^ Pedersen 1995, §4.4
- ^ 이러한 관점에서 유한요소법에 대한 보다 자세한 내용은 Brenner & Scott(2005)에서 확인할 수 있습니다.
- ^ 브레지스 2010, 9.5절
- ^ 에반스 1998
- ^ 파트리아 (1996), 2장과 3장
- ^ 아인시들러 & 워드(2011), 제안 2.14.
- ^ 리드 & 사이먼 1980
- ^ 예를 들어, 루딘(Rudin)(1987) 또는 폴랜드(Folland)(2009)는 이러한 관점에서 푸리에 급수를 처리할 수 있습니다.
- ^ 할모스 1957, §5
- ^ 바흐만, 나리치 & 베켄슈타인 2000
- ^ 스타인 앤 와이스 1971, § IV.2
- ^ Lanczos 1988, 212-213쪽
- ^ Lanczos 1988, 식 4-3.10
- ^ 스펙트럼 방법에 대한 고전적인 참조는 Courant & Hilbert 1953입니다. 더 최신의 계정은 Reed & Simon 1975입니다.
- ^ 카크 1966
- ^ 폰 노이만 1955
- ^ Holevo 2001, p. 17
- ^ Rieffel & Polak 2011, 페이지 55
- ^ Peres 1993, p. 101
- ^ Peres 1993, pp. 73
- ^ Nielsen & Chuang 2000, 페이지 90
- ^ Billingsley (1986), p. 477, ex. 34. 13}
- ^ 스테이플턴 1995
- ^ 휴이트 & 스트롬버그 (1965), 연습 16.45.
- ^ Karatzas & Shreve 2019, 3장
- ^ Stroock (2011), 8장.
- ^ Hermann Weyl (2009), "Mind and nature", Mind and nature: , selected writings on philosophy, mathematics, and physics, Princeton University Press.
- ^ Berthier, M. (2020), "Geometry of color perception. Part 2: perceived colors from real quantum states and Hering's rebit", The Journal of Mathematical Neuroscience, 10 (1): 14, doi:10.1186/s13408-020-00092-x, PMC 7481323, PMID 32902776.
- ^ 리드 & 사이먼 1980, 정리 12.6
- ^ 리드 & 사이먼 1980, 38페이지
- ^ 1988년 젊은, 23쪽
- ^ 1936년 클락슨.
- ^ 루딘 1987, 정리 4.10
- ^ Dunford & Schwartz 1958, II.4.29
- ^ 루드, 1987년 정리 4.11
- ^ Blanchet, Gérard; Charbit, Maurice (2014). Digital Signal and Image Processing Using MATLAB. Vol. 1 (Second ed.). New Jersey: Wiley. pp. 349–360. ISBN 978-1848216402.
- ^ Weidmann 1980, 정리 4.8
- ^ Peres 1993, pp. 77–78.
- ^ Weidmann(1980), 연습 4.11.
- ^ Weidmann 1980, §4.5
- ^ 부타초, Giaquinta & Hildebrandt 1998, 정리 5.17
- ^ Halmos 1982, 문제 52, 58
- ^ 1973년 루드
- ^ Trèves 1967, 18장
- ^ 이 섹션에 대한 일반적인 언급은 12장 루딘(Rudin, 1973)입니다.
- ^ 푸르고베치키(1981), 리드 & 사이먼(1980, 제8장) 및 폴랜드(1989) 참조.
- ^ Prugovečki 1981, III, §1.4
- ^ Dunford & Schwartz 1958, IV.4.17-18
- ^ Weidmann 1980, §3.4
- ^ Kadison & Ringrose 1983, 정리 2.6.4
- ^ 던포드 & 슈워츠 1958, § IV.4
- ^ 로마 2008, 218쪽
- ^ 루딘 1987, 정의 3.7
- ^ 유한 인덱스 집합의 경우 예를 들어 Halmos 1957, §5를 참조하십시오. 무한 지수 집합에 대해서는 Weidmann 1980, 정리 3.6을 참조하십시오.
- ^ a b 휴이트 & 스트롬버그(1965), 정리 16.26.
- ^ 레비탄 2001. Dunford & Schwartz (1958, §IV.4)와 같은 많은 저자들은 이것을 단지 차원이라고 말합니다. 힐베르트 공간이 유한 차원이 아닌 이상, 이것은 선형 공간으로서의 차원(하멜 기저의 카디널리티)과는 다릅니다.
- ^ 휴이트 & 스트롬버그(1965), 정리 16.29.
- ^ Prugovečki 1981, I, §4.2
- ^ 폰 노이만(1955)은 셀 수 있는 힐베르트 기저를 통해 힐베르트 공간을 정의하며, 이는 l과2 등각 동형에 해당합니다. 이 규칙은 양자역학의 대부분의 엄격한 처리에도 여전히 지속됩니다. 예를 들어 Sobrino 1996, 부록 B를 참조하십시오.
- ^ a b c Streater & Wightman 1964, 페이지 86–87
- ^ 영 1988, 정리 15.3
- ^ 폰 노이만 1955, 정리 16
- ^ 폰 노이만 1955, 정리 14
- ^ 가쿠타니 1939년
- ^ 린덴스트라우스와 차프리리 1971
- ^ 1957년 § 12
- ^ 힐베르트 공간의 스펙트럼 이론에 대한 일반적인 설명은 Riesz & Sz.-Nagy(1990)에서 찾을 수 있습니다. C*-대수어의 보다 정교한 설명은 Rudin(1973) 또는 Kadison & Ringrose(1997)에 있습니다.
- ^ 예를 들어, Riesz & Sz.-Nagy(1990, 6장) 또는 Weidmann 1980, 7장을 참조하십시오. 이 결과는 적분 커널에서 발생하는 연산자의 경우 Schmidt(1908)에게 이미 알려져 있었습니다.
- ^ Riesz & Sz.-Nagy 1990, §§107–108
- ^ 슈빈 1987
- ^ 1973년 루드, 정리 13.30.
- ^ Thomas, Pynchon (1973). Gravity's Rainbow. Viking Press. pp. 217, 275. ISBN 978-0143039945.
참고문헌
- Axler, Sheldon (18 December 2014), Linear Algebra Done Right, Undergraduate Texts in Mathematics (3rd ed.), Springer Publishing (published 2015), p. 296, ISBN 978-3-319-11079-0
- Bachman, George; Narici, Lawrence; Beckenstein, Edward (2000), Fourier and wavelet analysis, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98899-3, MR 1729490.
- Bers, Lipman; John, Fritz; Schechter, Martin (1981), Partial differential equations, American Mathematical Society, ISBN 978-0-8218-0049-2.
- Billingsley, Patrick (1986), Probability and measure, Wiley.
- Bourbaki, Nicolas (1986), Spectral theories, Elements of mathematics, Berlin: Springer-Verlag, ISBN 978-0-201-00767-1.
- Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin: Springer-Verlag, ISBN 978-3-540-13627-9.
- Boyer, Carl Benjamin; Merzbach, Uta C (1991), A History of Mathematics (2nd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
- Brenner, S.; Scott, R. L. (2005), The Mathematical Theory of Finite Element Methods (2nd ed.), Springer, ISBN 978-0-387-95451-6.
- Brezis, Haim (2010), Functional analysis, Sobolev spaces, and partial differential equations, Springer.
- Buttazzo, Giuseppe; Giaquinta, Mariano; Hildebrandt, Stefan (1998), One-dimensional variational problems, Oxford Lecture Series in Mathematics and its Applications, vol. 15, The Clarendon Press Oxford University Press, ISBN 978-0-19-850465-8, MR 1694383.
- Clarkson, J. A. (1936), "Uniformly convex spaces", Trans. Amer. Math. Soc., 40 (3): 396–414, doi:10.2307/1989630, JSTOR 1989630.
- Courant, Richard; Hilbert, David (1953), Methods of Mathematical Physics, Vol. I, Interscience.
- Dieudonné, Jean (1960), Foundations of Modern Analysis, Academic Press.
- Dirac, P.A.M. (1930), The Principles of Quantum Mechanics, Oxford: Clarendon Press.
- Dunford, N.; Schwartz, J.T. (1958), Linear operators, Parts I and II, Wiley-Interscience.
- Duren, P. (1970), Theory of Hp-Spaces, New York: Academic Press.
- Einsiedler, Manfred; Ward, Thomas (2011), Ergodic theory with a view towards number theory, Springer.
- Evans, L. C. (1998), Partial Differential Equations, Providence: American Mathematical Society, ISBN 0-8218-0772-2.
- Folland, Gerald B. (2009), Fourier analysis and its application (Reprint of Wadsworth and Brooks/Cole 1992 ed.), American Mathematical Society Bookstore, ISBN 978-0-8218-4790-9.
- Folland, Gerald B. (1989), Harmonic analysis in phase space, Annals of Mathematics Studies, vol. 122, Princeton University Press, ISBN 978-0-691-08527-2.
- Fréchet, Maurice (1907), "Sur les ensembles de fonctions et les opérations linéaires", C. R. Acad. Sci. Paris, 144: 1414–1416.
- Fréchet, Maurice (1904), "Sur les opérations linéaires", Transactions of the American Mathematical Society, 5 (4): 493–499, doi:10.2307/1986278, JSTOR 1986278.
- Giusti, Enrico (2003), Direct Methods in the Calculus of Variations, World Scientific, ISBN 978-981-238-043-2.
- Grattan-Guinness, Ivor (2000), The search for mathematical roots, 1870–1940, Princeton Paperbacks, Princeton University Press, ISBN 978-0-691-05858-0, MR 1807717.
- Halmos, Paul (1957), Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea Pub. Co
- Halmos, Paul (1982), A Hilbert Space Problem Book, Springer-Verlag, ISBN 978-0-387-90685-0.
- Hewitt, Edwin; Stromberg, Karl (1965), Real and Abstract Analysis, New York: Springer-Verlag.
- Hilbert, David; Nordheim, Lothar Wolfgang; von Neumann, John (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen, 98: 1–30, doi:10.1007/BF01451579, S2CID 120986758.
- Holevo, Alexander S. (2001), Statistical Structure of Quantum Theory, Lecture Notes in Physics, Springer, ISBN 3-540-42082-7, OCLC 318268606.
- Kac, Mark (1966), "Can one hear the shape of a drum?", American Mathematical Monthly, 73 (4, part 2): 1–23, doi:10.2307/2313748, JSTOR 2313748.
- Kadison, Richard V.; Ringrose, John R. (1997), Fundamentals of the theory of operator algebras. Vol. I, Graduate Studies in Mathematics, vol. 15, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0819-1, MR 1468229.
- Kadison, Richard V.; Ringrose, John R. (1983), Fundamentals of the Theory of Operator Algebras, Vol. I: Elementary Theory, New York: Academic Press, Inc.
- Karatzas, Ioannis; Shreve, Steven (2019), Brownian Motion and Stochastic Calculus (2nd ed.), Springer, ISBN 978-0-387-97655-6
- Kakutani, Shizuo (1939), "Some characterizations of Euclidean space", Japanese Journal of Mathematics, 16: 93–97, doi:10.4099/jjm1924.16.0_93, MR 0000895.
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Volume 3 (3rd ed.), Oxford University Press (published 1990), ISBN 978-0-19-506137-6.
- Kolmogorov, Andrey; Fomin, Sergei V. (1970), Introductory Real Analysis (Revised English edition, trans. by Richard A. Silverman (1975) ed.), Dover Press, ISBN 978-0-486-61226-3.
- Krantz, Steven G. (2002), Function Theory of Several Complex Variables, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2724-6.
- Lanczos, Cornelius (1988), Applied analysis (Reprint of 1956 Prentice-Hall ed.), Dover Publications, ISBN 978-0-486-65656-4.
- Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Gauthier-Villars.
- Levitan, B.M. (2001) [1994], "Hilbert space", Encyclopedia of Mathematics, EMS Press.
- Lindenstrauss, J.; Tzafriri, L. (1971), "On the complemented subspaces problem", Israel Journal of Mathematics, 9 (2): 263–269, doi:10.1007/BF02771592, ISSN 0021-2172, MR 0276734, S2CID 119575718.
- Marsden, Jerrold E. (1974), Elementary classical analysis, W. H. Freeman and Co., MR 0357693.
- Murphy, Gerald J. (1990), C*-algebras and Operator Theory, Academic Press, ISBN 0-12-511360-9.
- von Neumann, John (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen, 102: 49–131, doi:10.1007/BF01782338, S2CID 121249803.
- von Neumann, John (1932), "Physical Applications of the Ergodic Hypothesis", Proc Natl Acad Sci USA, 18 (3): 263–266, Bibcode:1932PNAS...18..263N, doi:10.1073/pnas.18.3.263, JSTOR 86260, PMC 1076204, PMID 16587674.
- von Neumann, John (1955), Mathematical Foundations of Quantum Mechanics, Princeton Landmarks in Mathematics, translated by Beyer, Robert T., Princeton University Press (published 1996), ISBN 978-0-691-02893-4, MR 1435976.
- Nielsen, Michael A.; Chuang, Isaac L. (2000), Quantum Computation and Quantum Information (1st ed.), Cambridge: Cambridge University Press, ISBN 978-0-521-63503-5, OCLC 634735192.
- O'Connor, John J.; Robertson, Edmund F. (1996), "Abstract linear spaces", MacTutor History of Mathematics Archive, University of St Andrews
- Pathria, RK (1996), Statistical mechanics (2 ed.), Academic Press.
- Pedersen, Gert (1995), Analysis Now, Graduate Texts in Mathematics, vol. 118, Berlin, New York: Springer-Verlag, ISBN 978-1-4612-6981-6, MR 0971256
- Peres, Asher (1993), Quantum Theory: Concepts and Methods, Kluwer, ISBN 0-7923-2549-4, OCLC 28854083
- Prugovečki, Eduard (1981), Quantum mechanics in Hilbert space (2nd ed.), Dover (published 2006), ISBN 978-0-486-45327-9.
- Reed, Michael; Simon, Barry (1980), Functional Analysis (vol I of 4 vols), Methods of Modern Mathematical Physics, Academic Press, ISBN 978-0-12-585050-6.
- Reed, Michael; Simon, Barry (1975), Fourier Analysis, Self-Adjointness (vol II of 4 vols), Methods of Modern Mathematical Physics, Academic Press, ISBN 9780125850025.
- Rieffel, Eleanor G.; Polak, Wolfgang H. (2011-03-04), Quantum Computing: A Gentle Introduction, MIT Press, ISBN 978-0-262-01506-6.
- Riesz, Frigyes (1907), "Sur une espèce de Géométrie analytique des systèmes de fonctions sommables", C. R. Acad. Sci. Paris, 144: 1409–1411.
- Riesz, Frigyes (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Math. Szeged, 7: 34–38.
- Riesz, Frigyes; Sz.-Nagy, Béla (1990), Functional analysis, Dover, ISBN 978-0-486-66289-3.
- Roman, Stephen (2008), Advanced Linear Algebra, Graduate Texts in Mathematics (Third ed.), Springer, ISBN 978-0-387-72828-5
- Rudin, Walter (1973). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 25 (First ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 9780070542259.
- Rudin, Walter (1987), Real and Complex Analysis, McGraw-Hill, ISBN 978-0-07-100276-9.
- Saks, Stanisław (2005), Theory of the integral (2nd Dover ed.), Dover, ISBN 978-0-486-44648-6Saks, Stanisław (2005), Theory of the integral (2nd Dover ed.), Dover, ISBN 978-0-486-44648-6원래 출판된 모노그라프제 마테마티츠네, vol. 7, 바르샤와, 1937.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Schmidt, Erhard (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Rend. Circ. Mat. Palermo, 25: 63–77, doi:10.1007/BF03029116, S2CID 120666844.
- Shubin, M. A. (1987), Pseudodifferential operators and spectral theory, Springer Series in Soviet Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13621-7, MR 0883081.
- Sobrino, Luis (1996), Elements of non-relativistic quantum mechanics, River Edge, New Jersey: World Scientific Publishing Co. Inc., Bibcode:1996lnrq.book.....S, doi:10.1142/2865, ISBN 978-981-02-2386-1, MR 1626401.
- Stapleton, James (1995), Linear statistical models, John Wiley and Sons.
- Stewart, James (2006), Calculus: Concepts and Contexts (3rd ed.), Thomson/Brooks/Cole.
- Stein, E (1970), Singular Integrals and Differentiability Properties of Functions, Princeton Univ. Press, ISBN 978-0-691-08079-6.
- Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9.
- Stein, E; Shakarchi, R (2005), Real analysis, measure theory, integration, and Hilbert spaces, Princeton University Press.
- Streater, Ray; Wightman, Arthur (1964), PCT, Spin and Statistics and All That, W. A. Benjamin, Inc.
- Stroock, Daniel (2011), Probability theory: an analytic view (2 ed.), Cambridge University Press.
- Teschl, Gerald (2009). Mathematical Methods in Quantum Mechanics; With Applications to Schrödinger Operators. Providence: American Mathematical Society. ISBN 978-0-8218-4660-5..
- Titchmarsh, Edward Charles (1946), Eigenfunction expansions, part 1, Oxford University: Clarendon Press.
- Trèves, François (1967), Topological Vector Spaces, Distributions and Kernels, Academic Press.
- Warner, Frank (1983), Foundations of Differentiable Manifolds and Lie Groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90894-6.
- Weidmann, Joachim (1980), Linear operators in Hilbert spaces, Graduate Texts in Mathematics, vol. 68, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90427-6, MR 0566954.
- Weyl, Hermann (1931), The Theory of Groups and Quantum Mechanics (English 1950 ed.), Dover Press, ISBN 978-0-486-60269-1.
- Young, Nicholas (1988), An introduction to Hilbert space, Cambridge University Press, ISBN 978-0-521-33071-8, Zbl 0645.46024.
외부 링크
- "Hilbert space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- 수학세계의 힐베르트 공간
- 245B, 주5: 테렌스 타오의 힐베르트 공간



















 y
y x
x 


























![{\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}}\right]+q(x)y=\lambda w(x)y}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4e93c4082311667644e8554f78774b963ffb0e)














 랜덤 변수인 경우
랜덤 변수인 경우  중심입니다. 힐베르트 공간 보기에서, 이것은 기대 연산자의
중심입니다. 힐베르트 공간 보기에서, 이것은 기대 연산자의 












 직교 사영이
직교 사영이 


![{\displaystyle E\left[\left(\int _{0}^{t}H_{s}dM_{s}\right)^{2}\right]=E\left[\int _{0}^{t}H_{s}^{2}d\langle M\rangle _{s}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ddc67bd90763bdda507f2bfd375f0106f921894)




































































