수직
Perpendicular
| 기하학. |
|---|
 |
| 지오메트리 |
기본 지오메트리에서 두 개의 기하학적 개체가 직각(90도 또는 1/2 라디안)으로 교차하는 경우 수직입니다.
두 선이 직각으로 [2]교차하면 직각이라고 합니다.구체적으로는 (1) 두 선이 만나면 첫 번째 선이 두 번째 선과 수직이고 (2) 교차점에서 첫 번째 선의 한쪽 직선 각도를 두 개의 합동 각도로 절단한다.수직도는 대칭임을 나타낼 수 있습니다. 즉, 첫 번째 선이 두 번째 선에 수직이면 두 번째 선도 첫 번째 선에 수직입니다.따라서 순서를 지정하지 않고 두 선을 (서로) 수직이라고 할 수 있습니다.
수직도는 세그먼트와 광선으로 쉽게 확장됩니다.예를 들어 B ( \ style \ { } )는 D ( \ displaystyle \ \ {} )에 대해 수직입니다.각각에서 무한선을 형성하기 위해 양방향으로 연장되었을 때 이들 2개의 결과 라인이 수직입니다.기호에서 A D { { AB } \ p { 、 선분 AB가 선분 [3]CD에 수직임을 나타냅니다.수직 기호에 대한 자세한 내용은 Up tack을 참조하십시오.
선은 교차하는 평면 내의 모든 선에 수직이면 평면에 수직이라고 합니다.이 정의는 선 사이의 수직성의 정의에 따라 달라집니다.
공간의 두 평면은 만나는 이면각이 직각이면 수직이라고 한다.
수직성은 더 일반적인 수학적인 직교 개념의 한 가지 특별한 예입니다; 수직성은 고전적인 기하학적 물체의 직교입니다.그러므로, 고급 수학에서, "수직"이라는 단어는 때때로 표면과 그것의 법선 사이의 것과 같이 훨씬 더 복잡한 기하학적 직교 조건을 설명하기 위해 사용됩니다.
수직의 다리
피트라는 단어는 수직과 관련하여 자주 사용됩니다.이 사용법은 위의 그림 및 설명에 예시되어 있습니다.다이어그램은 모든 방향으로 사용할 수 있습니다.발이 꼭 바닥에 있는 것은 아닙니다.
좀 더 정확히 말하면, A를 점으로 하고 m을 선으로 하자.만약 B가 m과 A를 통과하는 유일한 선과 m에 수직인 교점이라면, B는 A를 통과하는 이 수직의 발이라고 한다.
수직의 시공
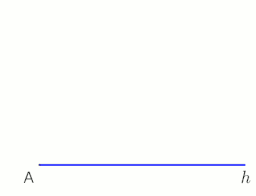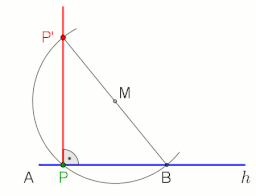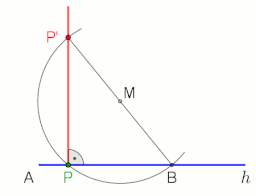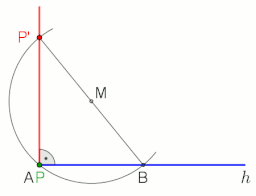
나침반과 직선 구조를 사용하여 점 P를 통과하는 선 AB에 수직이 되도록 하려면 다음과 같이 진행합니다(왼쪽 그림 참조).
- 1단계(빨간색) : P를 중심으로 한 원을 만들어 P에서 등거리에 있는 선 AB에 점 A'와 B'를 작성한다.
- 2단계(녹색): A'와 B'를 중심으로 반지름이 같은 원을 만듭니다.Q와 P가 이 두 원의 교차점이라고 하자.
- 3단계(파란색): Q와 P를 연결하여 원하는 수직 PQ를 작성합니다.
PQ가 AB에 수직임을 증명하려면 '와 QPB'에 대한 SSS 합치 정리를 사용하여 각도 OPA'와 OPB'가 동일하다는 결론을 내린다.그런 다음 삼각형 OPA'와 OPB'에 대한 SAS 일치 정리를 사용하여 각도 POA와 POB가 동일하다는 결론을 내립니다.
탈레스의 정리를 사용하여 점 P에서 또는 점 P를 통과하는 선 g에 대한 수직을 만들려면 오른쪽 애니메이션을 참조하십시오.
피타고라스 정리는 직각을 구성하는 방법의 기초로 사용될 수 있다.예를 들어 링크를 카운트함으로써 3:4:5의 길이로 3개의 체인을 만들 수 있다.이것들은 삼각형을 형성하기 위해 배치될 수 있으며, 삼각형의 가장 긴 변과 반대쪽의 직각을 가질 것이다.이 방법은 치수가 크고 높은 정확도가 필요하지 않은 정원과 밭을 배치하는 데 유용합니다.체인은 필요할 때마다 반복적으로 사용할 수 있습니다.
평행선과의 관계

2개의 선(a, b)이 모두 제3의 선(c)에 수직이면 제3의 선을 따라 형성되는 각도는 모두 직각이다.그러므로, 유클리드 기하학에서, 평행한 가정 때문에, 세 번째 선에 모두 수직인 두 선은 서로 평행합니다.반대로 한 선이 두 번째 선과 수직일 경우 두 번째 선과 평행한 모든 선과도 수직입니다.
오른쪽 그림에서는 수직각이 일치하고 횡단절단평행선에 의해 형성되는 교대내각이 일치하기 때문에 주황색 음영각은 모두 일치하고 녹색 음영각은 모두 일치한다.따라서 라인 a와 b가 평행하다면 다음 중 하나의 결론은 다른 모든 결론으로 이어진다.
- 다이어그램의 각도 중 하나는 직각입니다.
- 주황색 음영 각도 중 하나는 녹색 음영 각도 중 하나에 해당합니다.
- 선 c는 선 a에 수직이다.
- 선 c는 선 b에 수직이다.
계산 거리
점에서 선까지의 거리는 해당 선에서 가장 가까운 점까지의 거리입니다.여기서부터 지정된 점까지의 세그먼트가 선에 수직인 지점입니다.
마찬가지로 한 점에서 원곡선까지의 거리는 원곡선의 가장 가까운 점에 있는 원곡선에 대한 접선에 수직인 선분으로 측정됩니다.
수직 회귀 분석에서는 데이터 점에서 선까지의 수직 거리 제곱의 합을 최소화하여 데이터 점에 선을 적합시킵니다.
점에서 평면까지의 거리는 평면에 수직인 세그먼트를 따라 점으로부터의 길이로 측정되며, 이는 평면의 가장 가까운 점을 통과하는 평면의 모든 선에 수직임을 의미합니다.
함수 그래프
2차원 평면에서는 기울기의 곱이 -1이면 교차하는 2개의 선으로 직각을 형성할 수 있다.따라서 y = ax1 + b와12 y = ax2 + b의12 두 가지 선형 함수를 정의하면 함수의 그래프는 수직이 되며 aa = -1일 경우12 선이 교차하는 네 개의 직각을 만듭니다.그러나 기울기가 0이거나 정의되지 않은 경우(직선이 축과 평행)에는 이 방법을 사용할 수 없습니다.
다른 방법으로는 두 개의 선형 함수(ax1 + by1 + c1 = 02 및 ax + by2 + c2 = 0)가 있다고 가정합니다.선은 aa12 + bb = 0인 경우에만12 수직이 됩니다.이 방법은 벡터의 도트 곱(또는 더 일반적으로 내부 곱)에서 단순화됩니다.특히, 두 벡터는 내부곱이 0이면 직교하는 것으로 간주됩니다.
원형 및 기타 원추형으로
서클
원의 각 지름은 원과 교차하는 지점에서 해당 원에 대한 접선에 수직입니다.
화음을 이등분하는 원의 중심을 통과하는 선분은 화음에 수직이다.
두 개의 수직 화음의 교차가 한 화음을 a와 b로 나누고 다른 화음을 c와 d로 나눈다면 a2 + b2 + c2 + d는2 [4]직경의 제곱이 됩니다.
주어진 지점에서 교차하는 두 개의 수직 현의 길이 제곱합은 같은 지점에서 교차하는 다른 두 개의 수직 현의 길이 제곱합과 같으며 8r2 – 4p로2 주어진다(여기서 r은 원의 반지름이고 p는 중심점에서 [5]교차점까지의 거리).
탈레스의 정리는 원의 같은 점을 통과하지만 직경의 반대쪽 끝을 통과하는 두 선은 수직이라고 말한다.이것은 원의 지름이 지름의 두 끝점을 제외한 원의 모든 점에서 직각을 기울인다고 말하는 것과 같습니다.
줄임표
타원의 주축과 부축은 서로 수직이며 타원과 교차하는 지점에서 타원에 대한 접선에 대해 수직입니다.
포물선
포물선에서는 대칭축이 포물선과 교차하는 지점에서 직경, 다이렉트릭스 및 접선 각각에 수직이다.
접선상의 한 점에서 포물선의 꼭지점까지의 다른 접선은 포물선의 초점을 통과하는 선에 수직입니다.
포물선의 직교 특성은 포물선에 대한 두 접선이 서로 수직이면 직교 행렬에서 교차한다는 것입니다.반대로 다이렉트릭스에서 교차하는 2개의 접선은 수직이다.이는 직각의 어느 지점에서든 포물선이 직각으로 기울어진다는 것을 의미한다.
하이퍼볼라
쌍곡선의 점 P 또는 켤레 쌍곡선의 점 P에서 점근선까지의 수직 거리의 곱은 P의 위치와 무관한 상수이다.
직사각형 쌍곡선에는 서로 수직인 점근선이 있습니다.편심도는
폴리곤 단위
삼각형
직각삼각형의 다리는 서로 수직이다.
삼각형의 고도는 각각의 밑변과 수직이다.변의 수직 이등분선 또한 삼각형 기하학에서 중요한 역할을 한다.
이등변 삼각형의 오일러 선은 삼각형의 밑면에 수직이다.
드로즈-파니 선 정리는 삼각형의 직교 중심에서 교차하는 두 개의 수직선의 특성에 관한 것이다.
하코트의 정리는 정점을 통과하고 삼각형의 절기에 접하는 선에 수직인 선분들의 관계에 관한 것이다.
사변형
정사각형 또는 다른 사각형에서, 인접한 측면들의 모든 쌍으로 수직입니다.는 인접한 측면의 직각을 이루고 있는 두 쌍 가지고 있는 권리 trapezoid은 trapezoid.
각 네모꼴의 4maltitudes을 나타내는 쪽으로 맞은 편의 중간점을 통하여 수직이다.
한orthodiagonal 네 변은 대각선 수직이 사변형이다.이 정사각형, 그 마름모, 그리고는 연을 포함한다.브라마 굽타의 정리로써,orthodiagonal 네 변에, 한쪽의 중간부와 대각선의 교차점을 통해 줄을 서서 반대편에 수직이다 순환이다.
밴 Aubel의 정리까지, 만약 사각형 외부적으로, 선 세그먼트를 반대의 사각형의 센터 연결하고 같은 길이에 직각을 이루고 있는 사변형의 옆에 지어지게 된다.
3차원으로 선
로 3차원 데카르트 좌표계의 x, y, z축에 의해 잘 나타나 3차원 공간에서 최대 세줄 쌍별, 직각이 될 수 있다.
참고 항목
메모들
레퍼런스
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52-13504
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
외부 링크
- 정의: 인터랙티브 애니메이션과 수직.
- 나침반과 직선 가장자리를 가진 선의 수직 이등분선을 그리는 방법(애니메이션 데모).
- 나침반과 직선 가장자리로 광선의 끝 부분에 수직을 그리는 방법(애니메이션 데모).