민코스키 덧셈

기하학에서, 유클리드 공간에서 두 위치 벡터 A와 B의 세트의 민코프스키 합(일명 확장)은 A의 각 벡터, 즉 B의 각 벡터에 추가함으로써 형성된다.

${\displaystyle A+B=\\\\mathbf {a} +\mathbf {b} \, \mathbf {a} \in A, \mathbf {b} \in B\}.}$

이와 유사하게, Minkowski 차이(또는 기하학적 차이)^[1]는 다음과 같은 보완작용을 사용하여 정의된다.

${\displaystyle A-B=\왼쪽(A^{c}+(-B)\오른쪽)^{c}}}$

In general ${\displaystyle A-B\neq A+(-B)}$. For instance, in a one-dimensional case ${\displaystyle A=[-2,2]}$ and ${\displaystyle B=[-1,1]}$ the Minkowski difference ${\displaystyle A-B=[-1,1]}$, whereas ${\disp$$레이스타일 A+(-B)$$=A+B=[-3,3]$$}$

2차원 사례에서 민코프스키의 차이는 이미지 처리에서의 침식(모형학)과 밀접한 관계가 있다.

이 개념은 헤르만 민코프스키의 이름을 따서 지어졌다.

예

예를 들어, 우리가 두 세트 A와 B를 가지고 있다면, 각각 세 개의 위치 벡터(공식적으로, 점 3개)로 구성되며, R ${\displaystyle {\mathrm{}}^{}}$ ${\$ 좌표와 함께 두 삼각형의 정점을 나타낸다.

${\displaystyle A=\{(1,0), (0,1)\}$

그리고

${\displaystyle B=\{(0,0),(1,1),(1,-1)\}$

그럼 그들의 민코프스키 합계는

${\displaystyle A+B=\(1,0),(2,1),(2,1),(0,-1),(1,0),(1,0),(1,0),(1,2)\}}$

육각형의 정점들로 구성되어 있다.

Minkowski 추가의 경우 0 벡터만 포함하는 0$$ 세트 { 0${\displaystyle \},}$ ${\displaystyle \{0\}}$은(는) ID 요소: 벡터 공간의 모든 부분 집합 S에 대해,

$S+\{0\}=S.}$

빈 집합은 벡터 공간의 모든 부분 집합 S에 대해, 빈 집합과 빈 집합의 합은 비어 있는 집합이 다른 부분 집합마다 소멸하기 때문에 Minkowski 추가에서 중요하다.

$S+\emptyset =\emptyset.}$

For another example, consider the Minkowski sums of open or closed balls in the field ${\displaystyle \mathbb {K} ,}$ which is either the real numbers ${\displaystyle \mathbb {R} }$ or complex numbers ${\displaystyle \mathbb {C} .}$ If ${\displaystyle B_{r}:=\{s\in \mathb$$b {K} : s \leq r\}}$ is the closed ball of radius ${\displaystyle r\in [0,\infty ]}$ centered at ${\displaystyle 0}$ in ${\displaystyle \mathbb {K} }$ then for any ${\displaystyle r,s\in [0,\infty ],}$ ${\displaystyle B_{r}+B_{s}=B_{r+s}}$ and also ${\displaystyle cB_{r}=B_{ c r}}$ will hold for any scalar ${\displaystyle c\in \mathbb {K} }$ such that the product ${\displaystyle c r}$ is defined (which happens when ${\displaystyle c\neq 0}$ or ${\displaystyle r\neq \infty }$).$r{\displaystyle }$, ${\displaystyle s}$, ${\displaystyle r,s,}$ 및$$ $c{\displaystyle }$ ${\displaystyle c}$이(가) 모두 0이 아닌 경우, 0을 $중심$으로 닫힌 공 대신 열린 공으로 ${\displaystyle {Br}_{}}$ ${\$$displaystyle B_$${r}$이(가) 정의되었더라도 동일한 동일성이 유지될 것이다($$반경 $0$의 열린 공으로 가정 필요$).$${\displaystyle$ 0$}$이(가) 빈 집합임.닫힌 공과 열린 공의 민코스키 합은 열린 공이다.보다 일반적으로, 다른 세트와 함께 열린 서브셋의 Minkowski 합계는 오픈 서브셋이 될 것이다.

If ${\displaystyle G=\left\{\left(x,1/x\right):0\neq x\in \mathbb {R} \right\}}$ is the graph of ${\displaystyle f(x)={\frac {1}{x}}}$ and if and ${\displaystyle Y=\{0\}\times \mathbb {R} }$ is the ${\displaystyle y}$-axis in ${\displaystyle X={\mathbb{R}}^2}$${\displaystyle X=\mathbb {R} ^{2}}$ then the Minkowski sum of these two closed subsets of the plane is the open set ${\displaystyle G+Y=\{(x,y)\in \mathbb {R} ^{2}:x\neq 0\}=\mathbb {R} ^{2}\setminus Y}$ consisting of everything other than the ${\displaystyle y}$-axis.이것은 두 개의 닫힌 세트의 민코스키 합이 반드시 닫힌 세트가 아니라는 것을 보여준다.그러나 적어도 이들 세트 중 하나라도 콤팩트 서브셋이라면 두 개의 닫힌 서브셋의 민코스키 합계는 닫힌 서브셋이 된다.

민코프스키 합금 볼록스 선체

밍코우스키 덧셈은 다음 명제에서 알 수 있듯이 볼록한 선체를 채취하는 작동과 관련하여 잘 동작한다.

실제 벡터 공간의 ${\displaystyle {S\mathrm{}}_{}}$$$ 1 ${\$및 S$$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ S_${$2}}: 비어 $있지$ 않은 $모든$ 서브셋에 대해, 민코스키 합계의 볼록한 선체는 볼록한 선체의 Minkowski 합이다.

${\displaystyle \operatorname {Conv}(S_{1}+S_{2})=\operatorname {Conv}(S_{1})+\operatorname {Conv}(S_{2})}$

이 결과는 일반적으로 비어 있지 않은 세트의 유한 집합에 대해 더 많이 유지된다.

${\displaystyle \operatorname {Conv} \left(\sum {S_{n}\right)=\sum \operatorname {Conv}(S_{n}).}$

수학적 용어로는 민코프스키 합산과 볼록 선체의 형성이 통근 작업이다.^[2][3]

$S{\displaystyle }$ ${\displaystyle S}$이(가) 볼록 세트인 경우 ${\displaystyle \mu }$ S${\displaystyle }$+ ${\displaystyle \mu }$ ${\displaystyle S}$ ${\displaystyle \mu S+\lambda S}$도 볼록 세트일$$ 뿐 아니라

$\displaystyle \mu S+\lambda S=(\mu +\lambda )S}$

모든 $\mu$에 대해,${\displaystyle \mu }$ ${\displaystyle \ge }$ ${\displaystyle 0}$ ${\displaystyle \mu ,\lambda \geq$ 0$\}.$ 반대로, 이 "분산 속성"이 음이 아닌 모든 실제 숫자인 μ , μ ,${\displaystyle }\mu {\displaystyle }$ , ${\displaystyle \lambda }$ ${\displaystyle \mu ,\lambda }$에 대해 유지된다면 집합은 볼록이다$.$^[4]

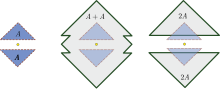
오른쪽 그림에는${\displaystyle }A{\displaystyle }$ + ${\displaystyle A2}$ 2 ${\displaystyle A}$. ${\displaystyle$A+$A\supsetneq 2A$에 대한 비콘벡스 세트의 예가 나와 있다$.$$}$

$1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$ 차원의$$ 예는 다음과 같다: $B{\displaystyle }$=${\displaystyle }$[ ${\displaystyle 1}$,${\displaystyle 2}$ ${\displaystyle ]}$ ${\displaystyle \cup }$[ ${\displaystyle 4}$,${\displaystyle 5}$ ${\displaystyle ]}$. ${\displaystyle$ B$=[1,2]\컵 [4,5].$$}$ It can be easily calculated that ${\displaystyle 2B=[2,4]\cup [8,10]}$ but ${\displaystyle B+B=[2,4]\cup [5,7]\cup [8,10],}$ hence again ${\displaystyle B+B\supsetneq 2B.$$}$

밍코우스키 합계는 2차원 볼록체의 둘레에 선형적으로 작용한다: 총의 둘레는 순환계의 합과 같다.또한 $K{\displaystyle }$ ${\displaystyle K}$이(가) 일정한 폭의 곡선이라면 $K{\displaystyle }$ ${\displaystyle K}$의 민코스키 합과 ${\displaystyle {180}^{}}$˚${\$회전이$$ 디스크인 것이다.이 두 가지 사실을 종합하면 일정한 폭의 곡선 둘레에 대한 바비어의 정리를 간단히 증명할 수 있다.^[5]

적용들

밍코우스키 덧셈은 수학 형태학에서 중심적인 역할을 한다.2D 컴퓨터 그래픽의 붓과 스트로크 패러다임(특히 Metafont의 Donald E. Knuth가 다양한 용도로 사용함)과 3D 컴퓨터 그래픽의 솔리드 스위프 작동에서 발생한다.또한 지구 이동자의 거리와 밀접하게 연결되어 있으며, 그 연장선상으로 최적의 교통수단을 갖추고 있는 것으로 나타났다.^[6]

모션 기획

밍코우스키 합계는 장애물들 사이에서 물체의 움직임을 계획하는 데 사용된다.그것들은 물체의 모든 허용 가능한 위치의 집합인 구성 공간의 계산에 사용된다.물체의 위치가 이 물체의 고정된 지점의 위치에 의해 고유하게 지정될 수 있는 평면 내 물체의 단순한 변환 운동 모델에서, 구성 공간은 장애물 집합과 원점에 배치되어 180도 회전하는 이동식 물체의 민코스키 합이다.

수치제어(NC) 가공

수치제어 가공에서 NC 공구의 프로그래밍은 그 궤적이 있는 커팅피스의 민코프스키 합이 자재의 커팅 모양을 제공한다는 점을 악용한다.

3D 솔리드 모델링

OpenSCAD Minkowski 합계는 두 가지 모양의 복합체를 생성하는 다른 모양의 형상을 나타내기 위해 사용된다.

집계가론

밍코우스키 합계는 집합체를 통해 수집할 개별 객체가 특징지어질 때 집합론에서도 자주 사용된다.^[7][8]

충돌 감지

민코프스키 합계, 특히 민코프스키 차이점은 물리학 엔진에서 볼록한 선체에 대한 충돌 감지 계산에 GJK 알고리즘과 함께 종종 사용된다.

Minkowski 합계를 계산하는 알고리즘

플라나 케이스

평면 내 볼록 폴리곤 2개

볼록 폴리곤 2개용 P그리고Q와의 비행기에m그리고n정점, 그들의 Minkowski 합은 기껏해야 볼록한 폴리곤이다.m+n정점 및 시간 O()로 계산할 수 있다.m+n)는 매우 간단한 절차에 의해, 다음과 같이 비공식적으로 설명할 수 있다.다각형의 가장자리와 폴리곤 경계를 따라 시계 반대 방향으로 주어진다고 가정한다.그러면 볼록 폴리곤의 이러한 가장자리가 극각으로 정렬되어 있음을 쉽게 알 수 있다.다음에서 지시된 가장자리의 순서 순서를 병합해 봅시다.P그리고Q일렬로S. 이 가장자리는 원래 방향과 평행하게 유지하면서 자유롭게 이동할 수 있는 고체 화살표라고 상상해 보십시오.시퀀스 순서대로 이 화살표를 조립하십시오.S이전 화살표의 머리에 다음 화살표의 꼬리를 붙임으로써.결과적인 폴리곤 체인은 사실상 볼록한 폴리곤이 될 것이라는 것이 밝혀졌는데, 이것은 민코프스키의 합이다.P그리고Q.

기타

한 폴리곤이 볼록하고 또 다른 폴리곤이 볼록하면, 이들의 밍코우스키 합계의 복잡성은 O(nm)이다.둘 다 비콘벡스일 경우 민코프스키 합계의 복잡성은 O(mn)²이다.

에센셜 민코스키 섬

유클리드 공간의 두 서브셋 중 필수적인 민코프스키 합+_e의 개념도 있다.통상적인 민코스키 합은 다음과 같이 쓸 수 있다.

$\displaystyle A+B=\left\{z\in \mathb {R}\{n}\, \, \,A\cap (z-B)\neq \emptyet \right\}.}$

따라서 본질적인 민코스키 합은 다음과 같이 정의된다.

${\displaystyle A+_{\mathrm {e} }B=\좌측\{z\in \mathb {R} \{n}\, \mu \좌측[]A\cap (z-B)\right]>0\right\}}$

여기서 μ는 n차원 Lebesgue 측정을 의미한다."필수"라는 용어의 이유는 다음과 같은 지표함수의 속성에 있다.

${\displaystyle 1_{A\,+\,B}(z)=\sup_{x\,\in,\mathb {R}^{n1}_{A}(x)1_{B}(z-x),}$

라고 볼 수 있다

${\displaystyle 1_{A\,+_{\mathrm {e}\}\,B}(z)=\mathop {\mathrm {ess\,sup}} _{x\,\in\,\mathb {R} ^{n1}_{A}1(x)1_{B}(z-x),},},},},},},},}}}}},},},}},},},},},},},}$

여기서 "sue supp"은 본질적인 우월감을 의미한다.

L^p 민코스키 섬

${\displaystyle {}^{}}$ ${\$의 K 및 L 콤팩트 볼록 부분 집합의 경우, Minkowski 합은 볼록 집합의 지지 함수로 설명할 수 있다$.$

${\displaystyle h_{K+L}=h_{K}+h_{L}.}$

p ≥ 1에 대해, Firey는^[9] 근원을 포함하는 $R$ n ${\$에 콤팩트 볼록 세트 K와 L의 L^p 민코프스키 합 K +_p L를 정의했다.

${\displaystyle h_{K+_{p}L}^{p}=h_{K}^{p}+h_{L}^{p}.}$

민코프스키 불평등에 의해, 함수_K+pL h는 다시 양성 동질적이고 볼록하며, 따라서 콤팩트 볼록 세트의 지지 기능이다.이^p 정의는 L Brunn-Minkowski 이론에서 기본이다.

참고 항목

• 블래쉬케 합
• 브룬-밍코프스키 정리, 밍코프시 합계의 부등식
• 콘볼루션
• 팽창
• 침식
• 구간 산술
• 혼합 볼륨(a.k.a.Quer massintegral 또는 내재 볼륨)
• 평행 곡선
• 샤플리-폴크만 보조정리
• 셈셋
• 위상 벡터 공간#속성
• 조노토프

메모들

참조

• Arrow, Kenneth J.; Hahn, Frank H. (1980). General competitive analysis. Advanced textbooks in economics. Vol. 12 (reprint of (1971) San Francisco, CA: Holden-Day, Inc. Mathematical economics texts. 6 ed.). Amsterdam: North-Holland. ISBN 978-0-444-85497-1. MR 0439057.
• Gardner, Richard J. (2002), "The Brunn-Minkowski inequality", Bull. Amer. Math. Soc. (N.S.), 39 (3): 355–405 (electronic), doi:10.1090/S0273-0979-02-00941-2
• Green, Jerry; Heller, Walter P. (1981). "1 Mathematical analysis and convexity with applications to economics". In Arrow, Kenneth Joseph; Intriligator, Michael D (eds.). Handbook of mathematical economics, Volume I. Handbooks in economics. Vol. 1. Amsterdam: North-Holland Publishing Co. pp. 15–52. doi:10.1016/S1573-4382(81)01005-9. ISBN 978-0-444-86126-9. MR 0634800.
• Henry Mann (1976), Addition Theorems: The Addition Theorems of Group Theory and Number Theory (Corrected reprint of 1965 Wiley ed.), Huntington, New York: Robert E. Krieger Publishing Company, ISBN 978-0-88275-418-5 – via http://www.krieger-publishing.com/subcats/MathematicsandStatistics/mathematicsandstatistics.html {{citation}}:외부 링크 위치 via=(도움말)
• Rockafellar, R. Tyrrell (1997). Convex analysis. Princeton landmarks in mathematics (Reprint of the 1979 Princeton mathematical series 28 ed.). Princeton, NJ: Princeton University Press. pp. xviii+451. ISBN 978-0-691-01586-6. MR 1451876.
• Nathanson, Melvyn B. (1996), Additive Number Theory: Inverse Problems and Geometry of Sumsets, GTM, vol. 165, Springer, Zbl 0859.11003.
• Oks, Eduard; Sharir, Micha (2006), "Minkowski Sums of Monotone and General Simple Polygons", Discrete and Computational Geometry, 35 (2): 223–240, doi:10.1007/s00454-005-1206-y.
• Schneider, Rolf (1993), Convex bodies: the Brunn-Minkowski theory, Cambridge: Cambridge University Press.
• Tao, Terence & Vu, Van (2006), Additive Combinatorics, Cambridge University Press.
• Mayer, A.; Zelenyuk, V. (2014). "Aggregation of Malmquist productivity indexes allowing for reallocation of resources". European Journal of Operational Research. 238 (3): 774–785. doi:10.1016/j.ejor.2014.04.003.
• Zelenyuk, V (2015). "Aggregation of scale efficiency". European Journal of Operational Research. 240 (1): 269–277. doi:10.1016/j.ejor.2014.06.038.

외부 링크

• "Minkowski addition", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Howe, Roger (1979), On the tendency toward convexity of the vector sum of sets, Cowles Foundation discussion papers, vol. 538, Cowles Foundation for Research in Economics, Yale University
• Minkowski Sums, Computing Geometric Algorithm 라이브러리에 있는
• 두 삼각형의 민코스키 섬과 조지 벡의 디스크와 폴리곤의 민코스키 섬, 울프램 시연 프로젝트.
• 민코프스키가 알렉산더 보고몰니의 볼록한 모양 추가: 애플릿
• Wikibooks:OpenSCAD 사용자 설명서/변환 #minkowski by Marius Kintel:적용
• Joan Gerard의 로봇공학과 민코스키의 응용