아티야-싱어 지수 정리
Atiyah–Singer index theorem| 밭 | 미분 기하학 |
|---|---|
| 에 의한 첫 번째 증명 | 마이클 아티야와 이사도레 싱어 |
| 첫 번째 증빙 인 | 1963 |
| 결과들 | 체르누스-보넷 정리 그로텐디크-리만-로흐 정리 히르제브루치 시그니처 정리 로클린의 정리 |
미카엘 아티야와 이사도레 싱어(1963)에 의해 증명된 미분 기하학에서 아티야-싱어 지수 정리에는 콤팩트 매니폴드의 타원형 미분 연산자에 대해 분석 지수(해결책 공간의 치수와 관련됨)가 위상학적 지수(일부 위상학적 데이터 측면에서 정의됨)와 동일하다고 명시되어 있다.[1] 체르누스-가우스-보넷 정리, 리만-로치 정리 등 그 밖의 많은 이론들을 특수한 사례로 포함하고 있으며 이론물리학에 응용하고 있다.[2][3]
역사
타원형 차동 연산자의 지수 문제는 이스라엘 겔판드에 의해 제기되었다.[4] 그는 지수의 호모토피 불변성을 알아차리고 위상학적 불변제를 이용하여 그것을 위한 공식을 요청했다. 동기부여 사례로는 리만-로치 정리 및 그 일반화, 히르제브루치-리만-로치 정리, 히르제브루치 시그니처 정리 등이 있다. 프리드리히 히르제브루흐와 아만드 보렐은 스핀다지관의 â 속성의 통합성을 증명해 보였으며, 아티야는 이 통합성이 디락 연산자의 지수(Atiyah와 Singer가 1961년에 재발견한 것)라면 설명할 수 있다고 제안했다.
아티야-싱어 정리는 1963년에 발표되었다.[1] 이 발표에서 스케치된 증거는 팔레스의 책에 나오기는 하지만 결코 그들이 출판한 것이 아니다.[5] 프린스턴대 리처드 팔레스가 주도한 세미나에서 파리에서 동시에 열린 '세미나르 카르탄-슈워츠 1963/64'[6]에도 등장한다. 파리에서의 마지막 회담은 아티야에 의해 경계가 있는 다지관에 있었다. 그들이 처음 발표한 증거는[7] 첫 번째 증거의 거미줄 이론을 K 이론으로 대체했고, 그들은 이것을 다른 일련의 논문에서 다양한 일반화의 증거를 제공하는 데 이용했다.[8]
- 1965년: 세르게이 P. 노비코프는 매끄러운 다지관에 있는 이성적인 폰트랴긴 계급의 위상학적 불변성에 관한 결과를 발표했다.[9]
- 로비온 커비와 로랑 C. 레네 톰의 논문과[11] 결합한 시벤만의 결과는 위상학적 다지관에 합리적인 폰트랴긴 계급의 존재를 증명했다.[10] 이성적인 폰트랴긴계급은 매끄럽고 위상적인 다지수에 대한 지수 정리의 필수적인 성분이다.
- 1969: Michael Atiyah는 임의의 미터 공간에 추상적인 타원 연산자를 정의한다. 추상 타원 연산자는 카스파로프의 이론과 코네스의 비확정적 미분 기하학에서 주인공이 되었다.[12]
- 1971: Isadore Singer는 인덱스 이론의 향후 확장을 위한 종합 프로그램을 제안한다.[13]
- 1972: Gennadi G. Kasparov는 추상적인 타원 연산자에 의한 K-homology의 실현에 관한 그의 작품을 발표한다.[14]
- 1973: 아티야, 라울 보트, 비제이 파토디는 멜로즈가 쓴 논문에서 설명한 열 방정식을 이용한 지수 정리의[15] 새로운 증거를 제시했다.[16]
- 1977: 데니스 설리번은 4와 다른 차원의 위상학적 다지관 위에 립스키츠와 퀘이콘 형식 구조의 존재와 고유성에 대한 정리를 확립한다.[17]
- 1983: 에드워드 비튼과[19] 루이스 알바레스 고메의 아이디어에 동기 부여된 에즈라 게틀러는[18] 지역 디락 운영자인 운영자들에게 지역 지수 정리의 짧은 증거를 제공했다; 이것은 많은 유용한 사례들을 포함한다.
- 1983: Nicolae Teleman은 벡터 번들에 값이 있는 서명 연산자의 분석 지표가 위상학적 불변제라는 것을 증명한다.[20]
- 1984: 텔레맨은 위상학적 다지수에 대한 지수 정리를 확립한다.[21]
- 1986년: 알랭 콘즈는 비확정 기하학에 대한 그의 기본 논문을 발표한다.[22]
- 1989년: 사이먼 K. Donaldson과 Sullivan은 차원 4의 Quasiconformal 다지관에 대한 Yang-Mills 이론을 연구한다. 그들은 2등급의 차등 형태에 대해 정의된 서명 연산자 S를 도입한다.[23]
- 1990: Connes와 Henri Moscovici는 지역 지수 공식을 비확정 기하학의 맥락에서 증명한다.[24]
- 1994: 코네스, 설리번, 텔레맨은 퀘이콘 형식 다지관의 서명 연산자에 대한 색인 정리를 증명한다.[25]
표기법
- X는 (경계가 없는) 소형 평활 다지관이다.
- E와 F는 X 위에 있는 부드러운 벡터 묶음이다.
- D는 E에서 F까지의 타원형 차동 연산자다. 따라서 국부 좌표에서는 F의 원활한 구간을 위해 E의 매끄러운 구간을 취하는 미분 연산자의 역할을 한다.
차동 연산자 기호
If D is a differential operator on a Euclidean space of order n in k variables , then its symbol is the function of 2k variables , given by dropping all terms of order less than n and/ i 를 로 대체 따라서 기호는 n의 변수 y에서 동질적이다. / 는 최고 주문 조건만 유지하고 차등 운영자는 "최저 주문 조건까지" 통근하기 때문에 와 통근하지 않아도 기호는 잘 정의되어 있다. 최소 1y가 0이 아닐 때마다 기호가 0이 아니면 연산자를 타원이라고 한다.
예: k 변수의 라플라스 연산자에는 y 2 + + k {\1}^{1}}이 있으며 y i s 중 하나가 0이 아닐 때마다 타원이 된다. 파동 연산자에는2 + + {\ 2가 의 일부 0이 아닌 값에 대해 사라지므로 이기호는 이 아니다.
매끄러운 다지관 X에서 순서 n의 차등 연산자의 기호는 국부 좌표도를 사용하여 거의 동일한 방식으로 정의되며, 각 등각 공간의 도 n 동종인 X의 등각 번들에 있는 함수다. (일반적으로 차동 연산자는 좌표 변환(제트 번들 참조)에서 다소 복잡한 방식으로 변환하지만, 최고 순서 용어는 텐서처럼 변환되므로 로컬 차트의 선택과 독립적인 등거리 공간에서 균일한 함수를 잘 정의한다.) 보다 일반적으로 두 벡터 번들 E와 F 사이의 차등 연산자 기호는 X의 등거리 공간에 대한 번들 Hom(E, F)의 풀백의 한 부분이다. X의 어떤 지점 x에서 0이 아닌 모든 비협착 벡터에 대해 Homx(Ex, F)의 요소가 반전 가능한 경우 미분 연산자를 타원이라고 한다.
타원 연산자의 주요 특성은 거의 변위할 수 없다는 것이다. 이것은 그들의 기호가 거의 변위할 수 없다는 사실과 밀접한 관련이 있다. 좀 더 정확히 말하면, 콤팩트 매니폴드의 타원 연산자 D에는 DDR과 DRD가−1 모두 콤팩트 연산자일 정도로 (비유니크) 파라메트릭스(또는 의사역전) D가 있다. 중요한 결과는 D의 커널이 유한한 것인데, 커널을 제외한 콤팩트 연산자의 모든 에이겐스페이스는 유한한 차원이기 때문이다. (타원 미분 연산자의 유사역학은 거의 미분 연산자가 아니다. 단, 타원형 유사분해 연산자다.)
분석지수
타원형 차동 연산자 D는 의사역할을 하므로 프레드홀름 연산자다. 모든 프레드홀름 연산자는 D의 낟알(Df = 0의 해법)과 D의 낟알의 낟알(Df = 0의 해법)의 낟알(Df = g와 같은 비균형 방정식의 우측에 있는 낟알의 제약조건)의 차이로 정의되는 지수를 가지고 있다. 바꾸어 말하면, 환언하면
- 지수(D) = 딤 커(D) - 딤 코커(D) = 딤 커(D) - 딤 커(D*)
이것을 D의 해석지수라고 부르기도 한다.
예: 다지관이 원(R/Z로 간주)이고, D가 어떤 복잡한 상수 λ에 대한 연산자 d/dx - λ이라고 가정하자.(이는 타원 연산자의 가장 간단한 예) 그렇다면 kernel이 2πi의 정수배수이고 그렇지 않으면 0이면 exp(expx)의 배수의 공간이며, adj의 낟알은 그 복잡한 결합으로 대체된 λ과 유사한 공간이다. 그래서 D는 지수 0을 가지고 있다. 이 예는 타원 연산자가 변함에 따라 타원 연산자의 커널과 코커넬이 불연속적으로 점프할 수 있으므로 연속적인 위상학적 데이터 측면에서 치수에 대한 좋은 공식은 없다는 것을 보여준다. 그러나 커널과 코커넬 치수의 점프는 같기 때문에, 그 치수의 차이로 주어진 지수는 실제로 연속적으로 변화하며, 지수 정리에 의한 위상학적 데이터의 관점에서 주어질 수 있다.
위상 지수
과(n {\ -차원 매니폴드 X 사이의 타원형 차동 연산자 의 위상학적 지수는 다음과 같다.
즉, 매니폴드 의 기본 호몰로지 클래스에 대한 혼합 코호몰로지 클래스 ch() ) 의 최상위 성분 값 여기,
- ( ) 은(는) 의 복잡한 접선 번들의 Todd 클래스다.
- is equal to , where
- is the Thom isomorphism for the sphere bundle
- : ( ) Q→ ; Q) 은 체르누어 문자다.
- is the "difference element" in associated to two vector bundles and on and an 하위 공간 S( ) 사이에 있는 이등형성 () {\.
- ( ) 은(는) 의 기호다.
또한 K-이론만을 사용하여 위상적 지수를 정의할 수도 있다(그리고 이러한 대체적 정의는 위의 체른 문자 구조와 어떤 의미에서 양립할 수 있다). X가 다지관 Y의 콤팩트 서브매니폴드인 경우 K(TX)에서 K(TY)까지 푸시포워드(또는 "shriek") 지도가 있다. K(TX) 요소의 위상학적 지수는 Y 일부 유클리드 공간과 함께 이 작업의 이미지로 정의되며, 이 공간에 대해 K(TY)는 정수 Z(Bott-periodicity의 결과)와 자연적으로 식별될 수 있다. 이 지도는 유클리드 공간에 X가 박혀 있는 것과 무관하다. 이제 위와 같은 차등 연산자는 자연스럽게 K(TX)의 요소를 정의하고 있으며, 이 지도 아래 Z의 이미지는 위상학적 지수(topological index)이다.
평소와 같이 D는 콤팩트 매니폴드 X를 통해 벡터 번들 E와 F 사이의 타원형 차동 연산자다.
지수 문제는 다음과 같다: (분석적) 지수 D는 다지관과 벡터 번들에서 도출된 기호 s와 위상학 데이터만을 사용하여 계산한다. 아티야-싱어 지수 정리는 이 문제를 해결하며 다음과 같이 명시한다.
- D의 분석지수는 위상학 지수와 같다.
위상학 지수는 그 가공할 정의에도 불구하고, 일반적으로 명시적으로 평가하기에 간단하다. 그래서 이것은 분석 지수를 평가할 수 있게 한다.(타원 연산자의 코커넬과 커널은 일반적으로 개별적으로 평가하기 매우 어렵다; 지수 정리는 우리가 적어도 그들의 차이를 평가할 수 있다는 것을 보여준다.) (서명과 같은) 다지관의 많은 중요한 불변량들은 적절한 미분 연산자의 지수로 주어질 수 있으므로, 지수 정리는 위상학적 자료의 관점에서 이러한 불변량을 평가할 수 있게 한다.
분석지수는 보통 직접 평가하기 어렵지만 적어도 분명히 정수다. 위상학적 지수는 정의상 합리적인 수치지만, 일반적으로 그것이 또한 필수적이라는 정의에서 전혀 명백하지 않다. 그래서 아티야-싱어 지수 정리는 위상학적 지수가 필수적이라는 것을 암시하듯이, 어떤 깊은 통합성 특성을 내포하고 있다.
타원형 차동 연산자의 지수는 연산자가 스스로 조정된 경우 분명히 사라진다. 또한 다지관 X의 치수가 홀수 치수로 사라지지 않는 유사 편차 타원 연산자가 있지만 홀수 치수가 있는 경우에도 사라진다.
그로텐디크-리만-로치와의 관계
그로텐디크-리만-로치 정리는 지수 정리가 실제 다지관의 설정에서 이 정리의 상대적이기 때문에 지수 정리의 배후에 있는 주요 동기 중 하나였다. 이제, 거의 복잡한 다지관의 f : → [\ fY}가 있다면, 역행도가[26] 있다.
= 이(가) 포인트라면 위의 문구를 복구한다. 여기서 ( ) 은 복합 벡터 번들의 그로텐디크 그룹이다. 이 정류 도표는 오른쪽에 있는 코호몰로지 집단은 부드러운 품종의 차우 링으로 대체되고, 왼쪽에 있는 그로텐디크 집단은 대수 벡터 번들의 그로텐디크 집단에 의해 주어지기 때문에 공식적으로 GRR 정리와 매우 유사하다.
아티야-싱어 지수 정리 확장
텔레맨 지수 정리
- 폐쇄적이고 지향적인 위상학적 다지관의 추상 타원 연산자(Atiyah 1970)에 대해 분석 지수는 위상학적 지수와 동일하다.
이 결과의 증거 특정한 고려 사항을 통해, 호지 이론의 combinatorial과 리프 시츠 manifolds(Teleman 1980년),(Teleman 1983년), Atiyah–Singer의 서명 사업자의 리프 시츠 manifolds(Teleman 1983년),는 카스파로프의 K-homology(카스파로프는 1972년)과 위상 cobordism로 늘리는(커비&Sieben에 확충 등 간다.mann 1977).
이 결과는 지수 정리가 단순히 차별성 문장이 아니라 위상적 문장이라는 것을 보여준다.
콘네스-도널드슨-술리반-텔레맨 지수 정리
(Donaldson & Sullivan 1989), (Connes, Sullivan & Teleman 1994):
- 모든 Quasiconformal 다지관의 경우 Hirzebruch–의 국부적 구조가 존재한다.Thom 특성 클래스.
이 이론은 짝수차원 퀘이콘폼 다지관(Compare (Donaldson & Sullivan 1989년)의 중간도 차등 형태에 대해 정의된 서명 연산자 S에 기초한다.
위상적 거미줄과 K-homology를 사용하면 퀘이콘 형식 다지관에 대한 지수 정리의 전체 문구를 제공할 수 있다(Connes, Sullivan & Teleman 1994 참조). 작품(Connes, Sullivan & Teleman 1994)은 "차원 2의 측정 가능한 리만 지도와 차원 4의 양-밀스 이론의 고차원적 친족에 기반한 특성 클래스에 대한 국지적 구성을 제공한다.
이러한 결과는 싱어의 프로그램 '수학의 전망'(Singer 1971)에 따라 상당한 진보를 구성한다. 동시에 위상학 다지관에 합리적인 폰트르자긴 계급을 효과적으로 구축한다. 논문(Teleman 1985년)은 톰의 합리적 폰트르자긴 계급(Thom 1956년)의 원구축과 지수 이론의 연결고리를 제공한다.
지수 공식은 위상론적 표현이라는 점을 언급하는 것이 중요하다. 밀너, 케르베어, 커비, 시벤만, 설리번, 도날드슨에 기인한 방해 이론은 위상학적 다지관의 소수만이 서로 다른 구조를 가지고 있으며 이것들은 반드시 독특한 것은 아니라는 것을 보여준다. Lipschitz와 Quasiconformal 구조물에 대한 Sullivan의 결과(Sullivan 1979)는 4와 다른 차원의 위상학적 다지관은 독특한 구조를 가지고 있다는 것을 보여준다(ID에 가까운 동위원소까지).
Quasiconformal 구조(Connes, Sullivan & Teleman 1994)와 보다 일반적으로 M에 의해 도입된 L-구조p p > n(n+1)/2. 힐섬(Hilsum 1999)은 지수 정리가 유지되는 것으로 알려진 차원 n의 위상학적 다지관에서 가장 약한 분석 구조물이다.
기타 확장자
- 아티야-싱어 정리는 타원 차동 연산자와 거의 동일한 방식으로 타원 유사 편차 연산자에 적용된다. 사실 기술적 이유로 초기 증명들은 대부분 미분비 연산자보다는 유사추적 연산자와 함께 작동했다: 그들의 추가적인 유연성은 증명들의 일부 단계를 더 쉽게 만들었다.
- 두 벡터 번들 사이에서 타원 연산자와 함께 작업하는 대신 타원형 콤플렉스로 작업하는 것이 때로는 더 편리하다.
- 벡터 묶음의 차이점은 기호가 이제 정확한 시퀀스를 형성한다는 것이다(영점 구간에서 벗어남). 콤플렉스에 0이 아닌 번들이 2개만 있는 경우 이는 기호가 0구간에서 벗어난 이형성임을 의미하기 때문에 2개의 항을 가진 타원형 콤플렉스는 두 벡터 번들 사이의 타원형 연산자와 본질적으로 동일하다. 반대로 타원형 복합체에 대한 지수 정리는 타원형 연산자의 경우 쉽게 축소할 수 있다: 2개의 벡터 번들은 복합체의 짝수 또는 홀수 용어의 합계에 의해 주어지며, 타원형 연산자는 타원형 복합체의 연산자와 그 조정자의 합으로, 짝수 번들의 합으로 제한된다.
- 다지관이 경계를 가질 수 있는 경우, 유한 지수를 보장하기 위해 타원 연산자의 영역에 일부 제한을 가해야 한다. 이러한 조건은 국부적 조건(영역의 섹션이 경계에서 사라지도록 요구하는 것과 같은 요구) 또는 보다 복잡한 전역 조건(영역의 섹션이 어떤 미분 방정식을 해결하도록 요구하는 것과 같은)일 수 있다. 지역 사건은 아티야와 보트가 해결했지만, 많은 흥미로운 운영자(예: 서명 운영자)가 지역 경계 조건을 인정하지 않는다는 것을 보여주었다. 이러한 연산자를 다루기 위해 아티야, 파토디, 싱어는 경계를 따라 다지관에 실린더를 부착한 다음 실린더를 따라 정사각형 통합이 가능한 섹션으로 도메인을 제한하는 것과 동등한 글로벌 경계 조건을 도입했다. 이 관점은 아티야-파토디-싱어 지수 정리의 멜로스(1993) 증명에서 채택된다.
- 하나의 타원 연산자 대신에, 사람들은 어떤 공간 Y에 의해 매개변수화된 타원 연산자 집단을 고려할 수 있다. 이 경우 지수는 정수가 아니라 Y의 K 이론의 한 요소다. 만약 가족 내 운영자들이 진짜라면, 지수는 Y의 진짜 K 이론에 있다. 이것은 Y의 진짜 K 이론에서 복잡한 K 이론에 이르는 지도가 항상 주입되는 것은 아니기 때문에 약간의 추가 정보를 준다.
- 타원 연산자와 통근하면서 콤팩트 매니폴드 X에 그룹 G의 집단 작용이 있는 경우, 일반 K이론을 등가원 K이론으로 대체한다. 더욱이, 사람들은 그룹 G의 고정점 서브매니폴드에서 나온 용어들로 렙체츠 고정점 정리의 일반화를 얻는다. 참고 항목: 등변 지수 정리를 참조하십시오.
- 아티야(1976)는 지수 정리를 콤팩트한 지수를 가진 이산 그룹이 작용하는 일부 비소형 다지관까지 확장하는 방법을 보여주었다. 이 경우 타원 연산자의 커널은 일반적으로 무한 치수지만, 폰 노이만 대수보다 모듈 치수를 사용하여 유한 지수를 얻을 수 있다. 이 지수는 정수 값보다는 일반적으로 실제 값이다. 이 버전은 L지수2 정리라고 불리며, Atiyah & Schmid(1977)에 의해 반이 구현된 Lie 그룹의 이산 직렬 표현들의 특성을 재도약하는 데 사용되었다.
- 칼리아스 지수 정리(Callias index organization)는 비콤팩트 홀수차원 공간에서 디락 연산자를 위한 지수 정리다. 아티야-싱어 지수는 컴팩트한 공간에서만 정의되며 치수가 홀수일 때 사라진다. 1978년 콘스탄티누스 칼리아스는 그의 박사 고문인 로마 자키우의 제안으로 힉스(Higgs) 분야라고 불리는 은둔자 행렬이 장착된 공간에 이 지수 정리를 도출하기 위해 축 변칙을 이용했다.[27] 디락 연산자의 지수는 힉스 필드의 구름을 무한대로 측정하는 위상학적 불변성 물질이다. U가 힉스 필드의 방향의 단위 행렬인 경우, 지수는 무한대의 (n-1)-sphere에 대한 U(dU)n−1의 적분에 비례한다. n이 짝수라면 언제나 0이다.
예
오일러 특성
M이 콤팩트 지향 다지관이라고 가정하자. 만약 우리가 E를 코탄젠트 번들의 짝수 외부 파워의 합으로, F를 홀수 파워의 합으로 본다면, D = d + d*를 정의하라, E에서 F까지의 지도로 간주한다. 그 다음 D의 위상학적 지수는 M의 호지 코호몰로지(Hodge cohomology)의 오일러 특성이고, 분석지수는 다지관의 오일러 등급이다. 이 운영자에 대한 지수 공식은 체르-가우스-보넷 정리를 산출한다.
히르제브루흐-리만-로흐 정리
X를 홀모픽 벡터 번들 V가 있는 복잡한 다지관으로 선택한다. 벡터 번들 E와 F를 짝수 또는 홀수를 가진 V 유형의 계수를 가진 미분형 묶음의 합계로 하고, 미분 연산자 D를 합계로 한다.
E로 한정된 그 다음 D의 해석 지수는 V:의 홀로모르픽 오일러 특성이다.
D의 위상학적 지수는 다음과 같다.
- ()= () )[ }(
X의 기본 등급에 대해 평가한 V의 체르누스 캐릭터와 X의 토드 등급의 제품. 위상학적 및 분석적 지수를 동일화함으로써 우리는 Hirzebruch-Remann-Roch 정리를 얻는다. 실제로 우리는 모든 복잡한 다지관에 대한 일반화를 얻는다. Hirzebruch의 증거는 투영적인 복잡한 다지관 X에만 효과가 있었다.
이러한 히르제브루치-리만-로치 정리의 파생은 타원 연산자보다는 타원 복합체에 대한 지수 정리를 사용한다면 더욱 자연스럽다. 우리는 콤플렉스를 그대로 받아들일 수 있다.
{\이 부여한 차등과 함께 그렇다면 I's cohomology 그룹은 그저 일관성 있는 코호몰로지 그룹i H(X, V)에 불과하므로, 이 단지의 분석 지수는 홀로모르픽 오일러 특성 σ(-1) i딤(Hi(X, V)이다. 이전과 같이 위상지수는 ch(V)Td(X)[X]이다.
히르제브루치 시그니처 정리
Hirzebruch 시그니처 정리에는 치수 4k의 콤팩트 지향 다지관 X의 서명이 다지관의 L속(L속)에 의해 주어진다고 명시되어 있다. 이는 다음과 같은 서명 연산자에 적용되는 아티야-싱어 지수 정리에서 비롯된다.
E와 F 번들은 X의 차동형 묶음에 대한 운영자의 +1과 -1 에겐스페이스에 의해 주어지며, 이는 k-폼에 작용한다.
Hodge * 연산자를 곱한다. 연산자 D는 호지 라플라시안이다.
E로 제한되며, 여기서 d는 Cartan 외부 파생 모델이고 d*는 그 부속품이다.
D의 분석 지수는 다지관 X의 시그니처로서 위상학적 지수는 X의 L속이기 때문에 이것들은 동일하다.
â속과 로클린의 정리
â 속은 모든 다지관에 대해 정의된 합리적인 숫자지만 일반적으로 정수는 아니다. 보렐과 히르제브루치는 그것이 스핀 다지관에 필수적이며, 게다가 치수가 4모드 8이라면 짝수 정수라는 것을 보여주었다. 이는 지수 정리에서 추론할 수 있으며, 이는 스핀 다지관의 â 속은 디락 연산자의 지수임을 의미한다. 치수 4모드 8에서 2의 추가 인자는 이 경우에 디락 연산자의 커널과 코커넬은 쿼터니온 구조를 가지고 있기 때문에 복잡한 벡터 공간은 치수가 짝수여서 지수가 짝수라는 사실에서 나온다.
차원 4에서 이 결과는 4차원 스핀 다지관의 서명이 16으로 분할된다는 로클린의 정리를 암시한다. 차원 4에서 â속은 서명의 8분의 1을 빼기 때문에 다음과 같다.
증명 기법
유사추적 연산자
유사계수 연산자는 유클리드 공간의 상수계수 연산자의 경우 쉽게 설명할 수 있다. 이 경우 상수계수 차등 연산자는 다항식별 곱셈의 푸리에 변환일 뿐이고, 상수계수 유사추상 연산자는 보다 일반적인 함수에 의한 곱셈의 푸리에 변환일 뿐이다.
지수 정리의 많은 증명들은 차등 연산자보다는 유사수분 연산자를 사용한다. 그 이유는 여러 가지 목적을 위해 미분양 연산자가 충분하지 않기 때문이다. 예를 들어, 양의 순서의 타원 미분 연산자의 의사역할은 미분 연산자가 아니라 유사분수 연산자다. 또한 K(B(X), S(X) (클러칭 함수)의 원소를 나타내는 데이터와 타원 유사 원소 연산자의 기호 사이에는 직접적인 일치성이 있다.
유사수분 연산자는 순서가 있는데, 이 순서는 임의의 실수나 짝수일 수 있고 기호(동탄 공간에 더 이상 다항식이 아님)가 있으며, 타원형 미분 연산자는 충분히 큰 동탄 벡터에 대해 기호를 변환할 수 없는 연산자를 말한다. 지수 정리의 대부분의 버전은 타원형 차동 연산자에서 타원형 유사 편차 연산자로 확장할 수 있다.
코보르디즘
초기 증명은 히르제브루흐-리만-로흐 정리(1954년)에 기초하였으며, 거미줄 이론과 유사추상 연산자를 포함하였다.
이 첫 번째 증거에 대한 생각은 대략 다음과 같다. V가 컴팩트한 매끄러운 방향 매니폴드 X의 부드러운 벡터 번들인 쌍(X, V)에 의해 생성된 링을 고려해 보십시오. 이 발전기에 부착된 링의 합과 곱은 (벡터 번들에 대한 명백한 조작과 함께) 다지관의 결합과 곱에 의해 주어지는 관계, 그리고 벡터 번들을 가진 다지기의 모든 경계를 고려하십시오. 0. 이것은 방향 다지기의 코보디즘 링과 유사하며, 다지관에도 벡터 번들이 있다는 것을 제외한다. 위상학적 및 분석적 지수는 모두 이 링에서 정수에 이르는 함수로 재해석된다. 그런 다음 이 두 기능이 사실 둘 다 동음이의어인지 확인한다. 그들이 동일하다는 것을 증명하기 위해서, 이 고리의 발전기 세트에서 그것들이 동일한지 확인하는 것만이 필요하다. 톰의 거미줄 이론은 발전기 세트를 제공한다. 예를 들어, 작은 묶음들이 짝수 치수 구 위에 있는 어떤 묶음들과 함께 있는 복잡한 벡터 공간을 제공한다. 따라서 지수 정리는 이러한 특히 단순한 사례에 대해 확인함으로써 증명될 수 있다.
케이이론
아티야와 싱어의 첫 번째 출판된 증거는 거미줄보다는 K-이론을 사용했다. i가 X에서 Y까지의 콤팩트 매니폴드를 포함하는 경우, 지수를 보존하는 Y의 X에서 타원 연산자로의 타원 연산자에 대한 'pushforward' 연산 i를! 정의했다. Y를 X가 내포하는 어떤 구체로 받아들임으로써, 이것은 구들의 경우로 지수 정리를 감소시킨다. Y가 구이고 X가 Y에 내장된 어떤 점이라면 Y의 모든 타원 연산자는 그 점의 어떤 타원 연산자의 i 아래에! 있는 영상이 된다. 이것은 지수 정리를 사소한 점의 경우로 축소시킨다.
열 방정식
아티야, 보트, 파토디(1973)는 열 방정식을 이용한 지수 정리에 대한 새로운 증거를 제시하였다(예: 참조). 베를라인, 게틀러 & 베르그네(1992년). 그 증명서는 (멜로즈 1993년)과 (길키 1994년)에도 게재되어 있다.
D가 부호 D*를 가진 차등 연산자인 경우, D*D와 DD*는 0이 아닌 고유값이 동일한 승수를 갖는 자체 부호 연산자다. 그러나 이들의 0 에겐스페이스는 D와 D*의 낟알의 치수가 되기 때문에 서로 다른 승수를 가질 수 있다. 따라서 D의 지수는 다음과 같다.
어떤 긍정적인 측면에서도 오른손은 두 열 연산자의 알맹이 차이의 흔적에 의해 주어진다. 이것들은 작은 양의 t에 대해 점증하지 않는 팽창을 가지고 있는데, 이는 t가 0의 경향이 있는 것으로 한도를 평가하는 데 사용될 수 있어 아티야-싱어 지수 정리의 증거를 제시한다. 작은 t에 대한 점증적 확장은 매우 복잡해 보이지만 불변 이론은 용어 사이에 큰 취소 사항이 있다는 것을 보여 주므로 선도적인 용어를 명시적으로 찾을 수 있다. 이러한 취소는 나중에 초대칭으로 설명되었다.
인용구
- ^ a b 아티야 & 싱어 1963.
- ^ 카야니 2020.
- ^ 해밀턴 2020, 페이지 11.
- ^ 겔판드 1960.
- ^ 팔레 1965년
- ^ 카르탄-슈와르츠 1965.
- ^ 아티야 & 싱어 1968a.
- ^ 아티야 & 싱어(1968a); 아티야 & 싱어(1968b); 아티야 & 싱어(1971a); 아티야&싱어(1971b).
- ^ 노비코프 1965년
- ^ 커비 & 시벤만 1969.
- ^ 톰 1956.
- ^ 아티야 1970년
- ^ 가수 1971.
- ^ 카스파로프 1972년
- ^ 아티야, 보트 & 파토디 1973.
- ^ 멜로스 1993.
- ^ 설리번 1979.
- ^ 게틀러 1983.
- ^ 비텐 1982.
- ^ 텔레맨 1983.
- ^ 텔레맨 1984.
- ^ 콘스 1986.
- ^ 도날드슨 & 설리번 1989.
- ^ 코네스 & 모스코비치 1990.
- ^ Connes, Sullivan & Teleman 1994.
- ^ "algebraic topology - How to understand the Todd class?". Mathematics Stack Exchange. Retrieved 2021-02-05.
- ^ 열린 공간에 대한 색인 정리
- ^ 콜리아스지에 관한 몇 가지 의견
참조
아티야의 논문은 그가 수집한 3권과 4권으로 재인쇄된다. (아티야 1988a, 1988b)
- Atiyah, M. F. (1970), "Global Theory of Elliptic Operators", Proc. Int. Conf. on Functional Analysis and Related Topics (Tokyo, 1969), University of Tokio, Zbl 0193.43601
- Atiyah, M. F. (1976), "Elliptic operators, discrete groups and von Neumann algebras", Colloque "Analyse et Topologie" en l'Honneur de Henri Cartan (Orsay, 1974), Asterisque, vol. 32–33, Soc. Math. France, Paris, pp. 43–72, MR 0420729
- Atiyah, M. F.; Segal, G. B. (1968), "The Index of Elliptic Operators: II", Annals of Mathematics, Second Series, 87 (3): 531–545, doi:10.2307/1970716, JSTOR 1970716 이 개혁은 그 결과를 등가 K-이론을 이용하여 일종의 렙체츠 고정점 정리로서 표현한다.
- Atiyah, Michael F.; Singer, Isadore M. (1963), "The Index of Elliptic Operators on Compact Manifolds", Bull. Amer. Math. Soc., 69 (3): 422–433, doi:10.1090/S0002-9904-1963-10957-X 지수 정리 발표.
- Atiyah, Michael F.; Singer, Isadore M. (1968a), "The Index of Elliptic Operators I", Annals of Mathematics, 87 (3): 484–530, doi:10.2307/1970715, JSTOR 1970715 이것은 코호몰로지 대신에 K-이론을 사용하여 증거를 제시한다.
- Atiyah, Michael F.; Singer, Isadore M. (1968b), "The Index of Elliptic Operators III", Annals of Mathematics, Second Series, 87 (3): 546–604, doi:10.2307/1970717, JSTOR 1970717 이 논문은 K-이론 버전에서 코호몰리학을 이용한 버전으로 전환하는 방법을 보여준다.
- Atiyah, Michael F.; Singer, Isadore M. (1971a), "The Index of Elliptic Operators IV", Annals of Mathematics, Second Series, 93 (1): 119–138, doi:10.2307/1970756, JSTOR 1970756 이 논문은 타원 연산자의 패밀리를 연구하는데, 여기서 지수는 이제 패밀리를 파라메트리하는 공간 이론의 한 요소가 되었다.
- 이것은 때때로 약간의 추가 정보를 짜낼 수 있을 때 진짜 타원 연산자의 가족을 연구한다Atiyah, Michael F.; Singer, Isadore M. (1971b), "The Index of Elliptic Operators V", Annals of Mathematics, Second Series, 93 (1): 139–149, doi:10.2307/1970757, JSTOR 1970757.
- 이것은 타원형 복합체의 내형성 렙체츠 수를 계산하는 정리를 말한다Atiyah, M. F.; Bott, R. (1966), "A Lefschetz Fixed Point Formula for Elliptic Differential Operators", Bull. Am. Math. Soc., 72 (2): 245–50, doi:10.1090/S0002-9904-1966-11483-0.
- 아티야, M.F.;Bott, R.(1967년),"A렙셰츠 고정 포인트 공식 타원 단지를", 수학 연보, 두번째 시리즈, 86(2):374–407, doi:10.2307/1970694, JSTOR 1970694와 아티야, M.F.;Bott, R(1968년),"렙셰츠 고정 포인트 공식 타원 단지형:.II. Applications", Annals 수학의, 두번째 시리즈, 88년(3):451–491, doi:10.2307/1970721, JSTOR 1970721 이러한 교정을, 그 결과의 일부 응용 프로그램은 이전의 종이에 발표를 준다.
- 아티야, M.;Bott, R.;Patodi하는 지키르 후세인, K.(1973년),"그 열 전도 방정식과 검지 정리에",을 발명하십시오.수학., 19(4):279–330, Bibcode:1973InMat..19..279A, doi:10.1007/BF01425417, MR0650828, S2CID 115700319.아티야, M.;Bott, R.;Patodi하는 지키르 후세인, K.(1975년),"Errata",을 발명하십시오.수학., 28(3):277–280, Bibcode:1975InMat..28..277A, doi:10.1007/BF01425562, MR0650829
- 아티야, 마이클 슈미드, 윌프레드(1977년),"이 불연속 시리즈의semisimple 이 씨 세력은 기하학적 구성",을 발명하십시오.수학. 42:1–62, Bibcode:1977InMat..42....1A, doi:10.1007/BF01389783, MR0463358, S2CID 189831012, 아티야, 마이클 슈미드, 윌프레드(1979년),"Erratum",을 발명하십시오.수학. 54(2):189–192, Bibcode:1979InMat..54..189A, doi:10.1007/BF01408936, MR0550183.
- Atiyah, Michael (1988a), Collected works. Vol. 3. Index theory: 1, Oxford Science Publications, New York: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853277-4, MR 0951894
- Atiyah, Michael (1988b), Collected works. Vol. 4. Index theory: 2, Oxford Science Publications, New York: The Clarendon Press, Oxford University Press, ISBN 978-0-19-853278-1, MR 0951895
- Baum, P.; Fulton, W.; Macpherson, R. (1979), "Riemann-Roch for singular varieties", Acta Mathematica, 143: 155–191, doi:10.1007/BF02684299, S2CID 83458307, Zbl 0332.14003
- Berline, Nicole; Getzler, Ezra; Vergne, Michèle (1992), Heat Kernels and Dirac Operators, Berlin: Springer, ISBN 978-3-540-53340-5 이는 열 방정식과 초대칭성을 사용하여 디락 연산자에 대한 지수 정리의 기본적인 증거를 제공한다.
- Bismut, Jean-Michel (1984), "The Atiyah–Singer Theorems: A Probabilistic Approach. I. The index theorem", J. Funct. Analysis, 57: 56–99, doi:10.1016/0022-1236(84)90101-0 비스무트는 열 방정식 방법보다는 확률론적 방법을 사용하여 타원형 복합체에 대한 정리를 증명한다.
- Cartan-Schwartz (1965), Séminaire Henri Cartan. Théoreme d'Atiyah-Singer sur l'indice d'un opérateur différentiel elliptique. 16 annee: 1963/64 dirigee par Henri Cartan et Laurent Schwartz. Fasc. 1; Fasc. 2. (French), École Normale Supérieure, Secrétariat mathématique, Paris, Zbl 0149.41102
- Connes, A. (1986), "Non-commutative differential geometry", Publications Mathématiques de l'Institut des Hautes Études Scientifiques, 62: 257–360, doi:10.1007/BF02698807, S2CID 122740195, Zbl 0592.46056
- Connes, A. (1994), Noncommutative Geometry, San Diego: Academic Press, ISBN 978-0-12-185860-5, Zbl 0818.46076
- Connes, A.; Moscovici, H. (1990), "Cyclic cohomology, the Novikov conjecture and hyperbolic groups" (PDF), Topology, 29 (3): 345–388, doi:10.1016/0040-9383(90)90003-3, Zbl 0759.58047
- Connes, A.; Sullivan, D.; Teleman, N. (1994), "Quasiconformal mappings, operators on Hilbert space and local formulae for characteristic classes", Topology, 33 (4): 663–681, doi:10.1016/0040-9383(94)90003-5, Zbl 0840.57013
- Donaldson, S.K.; Sullivan, D. (1989), "Quasiconformal 4-manifolds", Acta Mathematica, 163: 181–252, doi:10.1007/BF02392736, Zbl 0704.57008
- Gel'fand, I. M. (1960), "On elliptic equations", Russ. Math. Surv., 15 (3): 113–123, Bibcode:1960RuMaS..15..113G, doi:10.1070/rm1960v015n03ABEH004094 그의 수집된 작품들 중 1권, 페이지 65-75, ISBN 0-387-13619-3으로 다시 인쇄되었다. 120페이지에서 Gel'fand는 타원 연산자의 지수를 위상학적 데이터 측면에서 표현할 수 있어야 한다고 제안한다.
- Getzler, E. (1983), "Pseudodifferential operators on supermanifolds and the Atiyah–Singer index theorem", Commun. Math. Phys., 92 (2): 163–178, Bibcode:1983CMaPh..92..163G, doi:10.1007/BF01210843, S2CID 55438589
- Getzler, E. (1988), "A short proof of the local Atiyah–Singer index theorem", Topology, 25: 111–117, doi:10.1016/0040-9383(86)90008-X
- Gilkey, Peter B. (1994), Invariance Theory, the Heat Equation, and the Atiyah–Singer Theorem, ISBN 978-0-8493-7874-4 열 방정식 접근으로 아티야-싱어 정리를 증명하는 무료 온라인 교과서
- Hamilton, M. J. D. (2020). "The Higgs boson for mathematicians. Lecture notes on gauge theory and symmetry breaking". arXiv:1512.02632 [math.DG].
- Kayani, U. (2020). "Dynamical supersymmetry enhancement of black hole horizons". arXiv:1910.01080 [hep-th].
- Higson, Nigel; Roe, John (2000), Analytic K-homology, Oxford University Press, ISBN 9780191589201
- Hilsum, M. (1999), "Structures riemaniennes Lp et K-homologie", Annals of Mathematics, 149 (3): 1007–1022, arXiv:math/9905210, doi:10.2307/121079, JSTOR 121079, S2CID 119708566
- Kasparov, G.G. (1972), "Topological invariance of elliptic operators, I: K-homology", Math. USSR Izvestija (Engl. Transl.), 9 (4): 751–792, Bibcode:1975IzMat...9..751K, doi:10.1070/IM1975v009n04ABEH001497
- Kirby, R.; Siebenmann, L.C. (1969), "On the triangulation of manifolds and the Hauptvermutung", Bull. Amer. Math. Soc., 75 (4): 742–749, doi:10.1090/S0002-9904-1969-12271-8
- Kirby, R.; Siebenmann, L.C. (1977), Foundational Essays on Topological Manifolds, Smoothings and Triangulations, Annals of Mathematics Studies in Mathematics, vol. 88, Princeton: Princeton University Press and Tokio University Press
- Melrose, Richard B. (1993), The Atiyah–Patodi–Singer Index Theorem, Wellesley, Mass.: Peters, ISBN 978-1-56881-002-7 무료 온라인 교과서.
- Novikov, S.P. (1965), "Topological invariance of the rational Pontrjagin classes" (PDF), Doklady Akademii Nauk SSSR, 163: 298–300
- Palais, Richard S. (1965), Seminar on the Atiyah–Singer Index Theorem, Annals of Mathematics Studies, vol. 57, S.l.: Princeton Univ Press, ISBN 978-0-691-08031-4 이것은 정리의 원본 증거를 기술한다(아티야와 싱어는 원래 증명서를 스스로 출판한 적이 없고, 개선된 버전만).
- Shanahan, P. (1978), The Atiyah–Singer index theorem: an introduction, Lecture Notes in Mathematics, vol. 638, Springer, CiteSeerX 10.1.1.193.9222, doi:10.1007/BFb0068264, ISBN 978-0-387-08660-6
- Singer, I.M. (1971), "Future extensions of index theory and elliptic operators", Prospects in Mathematics, Annals of Mathematics Studies in Mathematics, vol. 70, pp. 171–185
- Sullivan, D. (1979), "Hyperbolic geometry and homeomorphisms", J.C. Candrell, "Geometric Topology", Proc. Georgia Topology Conf. Athens, Georgia, 1977, New York: Academic Press, pp. 543–595, ISBN 978-0-12-158860-1, Zbl 0478.57007
- Sullivan, D.; Teleman, N. (1983), "An analytic proof of Novikov's theorem on rational Pontrjagin classes", Publications Mathématiques de l'Institut des Hautes Études Scientifiques, Paris, 58: 291–293, doi:10.1007/BF02953773, S2CID 8348213, Zbl 0531.58045
- Teleman, N. (1980), "Combinatorial Hodge theory and signature operator", Inventiones Mathematicae, 61 (3): 227–249, Bibcode:1980InMat..61..227T, doi:10.1007/BF01390066, S2CID 122247909
- Teleman, N. (1983), "The index of signature operators on Lipschitz manifolds", Publications Mathématiques de l'Institut des Hautes Études Scientifiques, 58: 251–290, doi:10.1007/BF02953772, S2CID 121497293, Zbl 0531.58044
- Teleman, N. (1984), "The index theorem on topological manifolds", Acta Mathematica, 153: 117–152, doi:10.1007/BF02392376, Zbl 0547.58036
- Teleman, N. (1985), "Transversality and the index theorem", Integral Equations and Operator Theory, 8 (5): 693–719, doi:10.1007/BF01201710, S2CID 121137053
- Thom, R. (1956), "Les classes caractéristiques de Pontrjagin de variétés triangulées", Symp. Int. Top. Alg. Mexico, pp. 54–67
- Witten, Edward (1982), "Supersymmetry and Morse theory", J. Diff. Geom., 17 (4): 661–692, doi:10.4310/jdg/1214437492, MR 0683171
- Shing-Tung Yau, ed. (2009) [First published in 2005], The Founders of Index Theory (2nd ed.), Somerville, Mass.: International Press of Boston, ISBN 978-1571461377 - Atiyah, Bott, Hirzebruch 및 Singer에 대한 개인 계정
외부 링크
그 이론에 대한 링크
- Mazzeo, Rafe. "The Atiyah–Singer Index Theorem: What it is and why you should care" (PDF). Archived from the original (PDF) on October 10, 2002. PDF 프레젠테이션.
- Voitsekhovskii, M.I.; Shubin, M.A. (2001) [1994], "Index formulas", Encyclopedia of Mathematics, EMS Press
- Wassermann, Antony. "Lecture notes on the Atiyah–Singer Index Theorem". Archived from the original on March 29, 2017.
인터뷰 링크
- Raussen, Martin; Skau, Christian (2005), "Interview with Michael Atiyah and Isadore Singer" (PDF), Notices of AMS, pp. 223–231
- R. R. Seyley와 다른 (1999) 지수 이론과 의사 차등 운영자의 초기로부터의 회상 - 1998년 9월 덴마크의 Roskilde에서 열린 심포지엄 중 비공식적인 식후 대화를 부분적으로 기록한 것이다.


 대체
대체




 (
(



![{\displaystyle \operatorname {ch} (D)\operatorname {Td} (X)[X]=\int _{X}\operatorname {ch} (D)\operatorname {Td} (X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5047dfe347066ec21a7204bafb29b1da0b5e5029)

 .
.












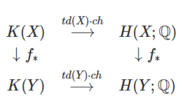

 . 이 정류 도표는 오른쪽에 있는 코호몰로지 집단은 부드러운 품종의
. 이 정류 도표는 오른쪽에 있는 코호몰로지 집단은 부드러운 품종의 


![{\displaystyle {\textrm {index}}(D)={\textrm {ch}}(V)\,{\textrm {Td}}(X)[X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88e47901dd14e82003ddb14f3be0c73530614911)







