닫힌 그래프 정리
Closed graph theorem수학에서, 닫힌 그래프 정리는 그래프 측면에서 연속함수의 특징을 나타내는 몇 가지 기본적인 결과 중 하나를 가리킬 수 있다.각각은 닫힌 그래프를 가진 함수가 반드시 연속적일 때 조건을 제시한다.
닫힌 그래프가 있는 그래프 및 맵
If is a map between topological spaces then the graph of is the set or equivalently,
하우스도르프 공간에 대한 모든 연속 함수는 닫힌 그래프를 가지고 있다.
변환 불변량 메트릭스(Cauchy)와 관련하여 위상이 완료된 (Cauchy) 두 위상 벡터 공간 사이에 선형 지도 : → , 이(가) 있고, 추가로 () L 이(가) 제품 위상의 의미에서 순차적으로 연속이라면 지도 L 은 con이다.주석과 그 그래프인 Gr L은 반드시 닫힌다.반대로 이(가) (1)a 대신 포함된 선형 지도인 경우, 의 그래프는 (1b)로 데카르트 제품 Y X에서 닫힌 것으로 알려져 있으며 은 연속성이므로 반드시 연속되어야 한다.[1]
닫힌 그래프가 없는 연속 지도 예제
If is any space then the identity map is continuous but its graph, which is the diagonal , is closed in 이(가) 하우스도르프일 경우에만.[2]특히 이(가) Hausdorff가 아닌 경우 : X→ 은(는) 연속적이지만 닫힌 그래프가 없다.
Let denote the real numbers with the usual Euclidean topology and let denote with the indiscrete topology (where note that is not Hausdorff and that every function valued in 디스플레이 은(는) 연속형).: → Y 을(를) 및 )= 0 로 정의한다 다음f : → Y은(는) 연속이지만 그래프는 Y에서 닫히지 않는다[3]
점 집합 위상에서의 폐쇄 그래프 정리
점 집합 위상에서 닫힌 그래프 정리는 다음과 같이 기술한다.
Closed graph theorem[4] — If is a map from a topological space into a compact Hausdorff space then the graph of is closed if and only if is continuous.
설정값 함수의 경우
설정값 함수에[5] 대한 닫힌 그래프 정리 - Hausdorff 콤팩트 범위 Y 의 경우 설정값 함수 : X→ Y 은(는) 위쪽 헤미콘과 F(x)가 모든 에 대해 닫힌 집합인 경우에만 닫힌 그래프를 가지고 있다
기능분석에서
If is a linear operator between topological vector spaces (TVSs) then we say that is a closed operator if the graph of is closed in when is endowed with the product topology.
닫힌 그래프 정리는 닫힌 선형 연산자가 특정 조건 하에서 연속적이라는 것을 보장하는 기능 분석에서 중요한 결과물이다.원래의 결과는 여러 번 일반화되었다.폐쇄형 그래프 이론의 잘 알려진 버전은 다음과 같다.
참고 항목
- 거의 열린 선형 지도
- 경계 공간 – 위상 벡터 공간
- 닫힌 그래프 – 제품 공간에서 닫힌 지도 그래프
- 닫힌 선형 연산자
- 불연속 선형 지도
- 카쿠타니 고정점 정리 – 콤팩트한 비빈 볼록 부분집합 S⊂ⁿ의 함수 f: S→Pow(S)가 고정점을 갖는 경우
- 개방형 매핑 정리(기능분석) – 선형 연산자가 개방될 수 있는 조건
- Ursescu 정리 – 닫힌 그래프의 일반화, 개방형 매핑, 균일한 경계 정리
- 웹베드 공간 – 열린 매핑과 닫힌 그래프 이론이 있는 공간
- 자리스키의 주정리 – 대수기하학과 정류대수의 정리
메모들
참조
- ^ 루딘 1991, 페이지 51-52.
- ^ 루딘 1991, 페이지 50.
- ^ 나리치 & 베켄슈타인 2011, 페이지 459–483.
- ^ Munkres 2000, 페이지 163–172.
- ^ Aliprantis, Charlambos; Kim C. Border (1999). "Chapter 17". Infinite Dimensional Analysis: A Hitchhiker's Guide (3rd ed.). Springer.
- ^ 쉐퍼 & 월프 1999, 페이지 78.
- ^ 트리에브 (2006), 페이지 173
참고 문헌 목록
- Bourbaki, Nicolas (1987) [1981]. Sur certains espaces vectoriels topologiques [Topological Vector Spaces: Chapters 1–5]. Annales de l'Institut Fourier. Éléments de mathématique. Vol. 2. Translated by Eggleston, H.G.; Madan, S. Berlin New York: Springer-Verlag. ISBN 978-3-540-42338-6. OCLC 17499190.
- Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
- Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.
- Köthe, Gottfried (1983) [1969]. Topological Vector Spaces I. Grundlehren der mathematischen Wissenschaften. Vol. 159. Translated by Garling, D.J.H. New York: Springer Science & Business Media. ISBN 978-3-642-64988-2. MR 0248498. OCLC 840293704.
- Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.
- Wilansky, Albert (2013). Modern Methods in Topological Vector Spaces. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC 849801114.
- Zălinescu, Constantin (30 July 2002). Convex Analysis in General Vector Spaces. River Edge, N.J. London: World Scientific Publishing. ISBN 978-981-4488-15-0. MR 1921556. OCLC 285163112 – via Internet Archive.
- "Proof of closed graph theorem". PlanetMath.
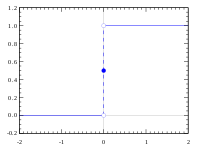

![{\displaystyle [-4,4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2933acc5278ef7016396bfd3230387904ed5f0f)
![{\displaystyle [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f94b820404eca2a458cb2c7d8c24be85fffccf90)















 정의한다
정의한다







