동적 시스템

수학에서, 동적 시스템은 함수가 주변 공간의 점의 시간 의존성을 설명하는 시스템입니다.예를 들어 시계추의 흔들림, 파이프 안의 물의 흐름, 공기 중의 입자의 무작위 움직임, 그리고 호수에서 봄마다 물고기의 수를 설명하는 수학적 모델이 포함됩니다.가장 일반적인 정의는 공간의 다른 선택과 시간의 측정 방법을 허용함으로써 일반적인 미분 방정식과 에르고드 이론과 같은 수학의 여러 개념을 통합합니다.시간은 정수, 실수 또는 복소수에 의해 측정될 수 있고, 물리적인 기원의 기억을 상실하는 보다 일반적인 대수적 객체가 될 수 있으며, 공간은 매끄러운 시공간 구조의 필요 없이 다양체 또는 단순 집합일 수 있다.

어느 시점에서도 동적 시스템은 적절한 상태 공간 내의 점을 나타내는 상태를 가진다.이 상태는 종종 실수의 튜플이나 기하학적 다양체의 벡터에 의해 주어진다.동적 시스템의 진화 규칙은 현재 상태에서 미래 상태가 어떻게 이어지는지를 기술하는 함수입니다.함수는 종종 결정론적이며, 즉 주어진 시간 간격 동안 현재 ^[1]^[2]상태에서 하나의 미래 상태만 뒤따릅니다.그러나 일부 시스템은 랜덤 이벤트가 상태 변수의 진화에도 영향을 미친다는 점에서 확률적이다.

물리학에서 동적 시스템은 "시간이 지남에 따라 상태가 변화하고 따라서 시간 미분 방정식을 따르는 입자 또는 입자의 앙상블"^[3]로 묘사된다.시스템의 미래 거동을 예측하기 위해 컴퓨터 시뮬레이션을 통해 이러한 방정식의 해석적 해법 또는 시간의 경과에 따른 적분을 실현한다.

동적 시스템 연구는 동적 시스템 이론의 초점으로 수학, 물리학,^[4]^[5] 생물학,^[6] 화학, 공학,^[7] 경제,^[8] 역사, 의학 등 다양한 분야에 응용된다.동적 시스템은 카오스 이론, 로지스틱 맵 다이내믹스, 분기 이론, 자기 조립 및 자기 조직화 과정, 그리고 카오스 개념의 가장 기본적인 부분입니다.

개요

역학계의 개념은 뉴턴 역학에 그 기원을 두고 있다.다른 자연과학 및 공학 분야와 마찬가지로 동적 시스템의 진화 규칙은 시스템의 상태를 미래의 짧은 시간 동안만 제공하는 암묵적인 관계입니다.(관계는 미분방정식, 차분방정식 또는 기타 시간척도 중 하나입니다.)미래의 모든 시간에 대한 상태를 판단하려면 관계를 여러 번 반복해야 합니다. 각 진행 시간은 작은 단계입니다.반복 절차는 시스템 해결 또는 시스템 통합이라고 합니다.시스템을 해결할 수 있는 경우, 초기 지점이 주어지면 궤적 또는 궤도로 알려진 지점의 집합인 미래의 모든 위치를 결정할 수 있습니다.

컴퓨터가 등장하기 전에 궤도를 찾는 것은 정교한 수학적 기술을 필요로 했고 소수의 동적 시스템에서만 달성할 수 있었다.전자계산기계에 구현된 수치방법은 동적 시스템의 궤도를 결정하는 작업을 단순화했다.

단순한 동적 시스템의 경우 궤적을 아는 것으로 충분하지만 대부분의 동적 시스템은 너무 복잡하여 개별 궤적 측면에서 이해할 수 없습니다.다음과 같은 이유로 문제가 발생합니다.

연구된 시스템은 대략적으로만 알 수 있습니다. 시스템의 매개변수를 정확하게 알 수 없거나 방정식에서 항이 누락될 수 있습니다.사용된 근사치는 수치 해법의 타당성 또는 관련성에 의문을 제기한다.이러한 문제를 해결하기 위해 랴푸노프 안정성 또는 구조적 안정성과 같은 여러 가지 안정성의 개념이 동적 시스템 연구에 도입되었다.동적 시스템의 안정성은 궤적이 동등한 모델 또는 초기 조건의 클래스가 있음을 암시한다.궤도를 비교하여 등가성을 확립하는 연산은 안정성에 대한 다른 개념과 함께 변화합니다.
궤적의 유형은 하나의 특정 궤적보다 더 중요할 수 있습니다.일부 궤적은 주기적인 반면, 다른 궤적은 시스템의 많은 다른 상태를 통과할 수 있습니다.응용 프로그램에서는 이러한 클래스를 열거하거나 시스템을 하나의 클래스 내에서 유지 관리해야 하는 경우가 있습니다.가능한 모든 궤적을 분류하면 동적 시스템, 즉 좌표 변경 시 변경되지 않는 특성이 정성적으로 연구된다.상태를 설명하는 두 개의 숫자를 가진 선형 동적 시스템과 시스템은 가능한 궤도 클래스가 이해되는 동적 시스템의 예입니다.
파라미터의 함수로서의 궤적의 동작이 애플리케이션에 필요한 것일 수 있습니다.파라미터가 변화함에 따라 동적 시스템은 동적 시스템의 질적 거동이 변화하는 분기점을 가질 수 있다.예를 들어, 유체의 난기류로의 이행과 같이 주기적인 움직임만 있는 상태에서 명백한 불규칙한 동작으로 바뀔 수 있습니다.
시스템의 궤적이 불규칙한 것처럼 보일 수 있습니다.이러한 경우, 하나의 매우 긴 궤적 또는 많은 다른 궤적을 사용하여 평균을 계산해야 할 수 있다.평균은 에르고딕 시스템에 대해 잘 정의되어 있으며 쌍곡 시스템에 대해 보다 상세한 이해가 이루어졌다.동적 시스템의 확률론적 측면을 이해하는 것은 통계 역학과 혼돈의 기초를 확립하는 데 도움이 되었다.

역사

많은 사람들은 프랑스 수학자 앙리 푸앵카레를 역학계의 ^[9]창시자로 여긴다.푸앵카레는 "천체역학의 새로운 방법" (1892–1899)과 "천체역학에 관한 강의" (1905–1910)라는 두 개의 고전적인 논문을 출판했습니다.그 속에서 그는 연구 결과를 3개 물체의 운동 문제에 성공적으로 적용하고 해법(빈도, 안정성, 점근성 등)의 거동을 상세하게 연구했다.이 논문들은 푸앵카레 반복정리를 포함했는데, 이것은 특정 시스템이 충분히 길지만 유한한 시간이 지나면 초기 상태에 매우 가까운 상태로 돌아간다는 것이다.

알렉산드르 랴푸노프는 많은 중요한 근사 방법을 개발했다.1899년에 그가 개발한 그의 방법은 상미분 방정식 집합의 안정성을 정의하는 것을 가능하게 한다.그는 역동적인 시스템의 안정성에 대한 현대 이론을 만들었다.

1913년, 조지 데이비드 버크호프는 3체 문제의 특별한 경우인 푸앵카레의 "마지막 기하학적 정리"를 증명하여 그를 세계적으로 유명하게 만들었다.1927년, 그는 그의 동적 시스템을 출판했다.버크호프의 가장 영속적인 결과는 1931년 에르고딕 정리라고 불리는 것을 발견한 것이다.에르고드 가설에 대한 물리학으로부터의 통찰력을 측정 이론과 결합함으로써, 이 정리는 적어도 원칙적으로는 통계 역학의 근본적인 문제를 해결했다.에르고딕 정리는 역학에도 영향을 끼쳤다.

Stephen Smale은 또한 상당한 발전을 이루었다.그의 첫 번째 공헌은 동적 시스템에 대한 중요한 연구를 시작한 스마일 편자였습니다.그는 또한 다른 많은 사람들에 의해 수행된 연구 프로그램의 개요를 설명했다.

올렉산드르 마이콜라오비흐 샤르코프스키는 1964년에 이산 역학계의 기간에 관한 샤르코프스키의 정리를 개발했다.이 정리의 함의 중 하나는 실선상의 이산 동적 시스템이 주기 3을 갖는다면, 그것은 다른 주기마다 주기점을 가져야 한다는 것이다.

20세기 후반부터 편미분 방정식에 대한 동적 시스템 관점이 인기를 끌기 시작했다.팔레스타인 기계 엔지니어 Ali H. Nayfeh는 기계 ^[10]및 엔지니어링 시스템에 비선형 역학 기술을 적용했다.그의 응용 비선형 역학에서의 선구적 업적은 선박, 크레인, 교량, 건물, 고층 빌딩, 제트 엔진, 로켓 엔진, 항공기,^[11] 우주선 등 일상생활에서 흔히 볼 수 있는 기계와 구조물의 건설과 유지에 영향을 미쳤다.

형식적 정의

가장 일반적인 ^[12]의미에서 동적계는 T가 모노이드이고, X는 비어 있지 않은 집합이며, δ는 함수인 튜플(T, X, δ)이다.

\displaystyle \Phi : U\subseteq (T\times X)\to X}

와 함께

\mathrm {proj} _{2}(U)=X

\mathrm {proj} _{2}(U)=X

\mathrm {proj} _{2}(U)=X

\mathrm {proj} _{2}(U)=X

2

\mathrm {proj} _{2}(U)=X

(

\mathrm {proj} _{2}(U)=X

)

=

{\

displaystyle \mathrm {proj} _{2}(U

)=

X}

(

\mathrm {proj} _{2}

서 p

\mathrm {proj} _{2}

\mathrm {proj} _{2}

\mathrm {proj} _{2}

2 {

displaystyle \mathrm {proj} _{2}

는

\mathrm {proj} _{2}

두 번째 투영 맵)

X의 임의의 x에 대해서:

{\displaystyle\Phi(0,x)=x}

\Displaystyle \Phi(t_{2},\Phi(t_{1},x)=\Phi(t_{2}+t_{1},x),}

$\,t_{1},\,t_{2}+t_{1}\in I(x)$ 의 $\,t_{1},\,t_{2}+t_{1}\in I(x)$ 2 + $\,t_{1},\,t_{2}+t_{1}\in I(x)$ $\,t_{1},\,t_{2}+t_{1}\in I(x)$ I ( $x$ ) { displaystyle \ , $t _ {$ 1} , $t$ _ {2 $}$ + $t$ _ { 1 $}\in I($ x $\,t_{1},\,t_{2}+t_{1}\in I(x)$ )} $\ t_{2}\in I(\Phi (t_{1},x))$ t 2 $\ t_{2}\in I(\Phi (t_{1},x))$ ∈ $\ t_{2}\in I(\Phi (t_{1},x))$ ( $φ$ t ( $\ t_{2}\in I(\Phi (t_{1},x))$ $\ t_{2}\in I(\Phi (t_{1},x))$ , $\ t_{2}\in I(\Phi (t_{1},x))$ x $){$ displaystyle \ $t_{2$ }\ $in$ I ( \ $Phi ($ $I(x):=\{t\in T:(t,x)\in U\}$ ${1$ } , $\ t_{2}\in I(\Phi (t_{1},x))$ x $\ t_{2}\in I(\Phi (t_{1},x))$ ) } 。 $I(x):=\{t\in T:(t,x)\in U\}$ 서 $I(x):=\{t\in T:(t,x)\in U\}$ I $I(x):=\{t\in T:(t,x)\in U\}$ ( x $I(x):=\{t\in T:(t,x)\in U\}$ ) : $I(x):=\{t\in T:(t,x)\in U\}$ { $I(x):=\{t\in T:(t,x)\in U\}$ 、 $I(x):=\{t\in T:(t,x)\in U\}$ x $I(x):=\{t\in T:(t,x)\in U\}$ ) ∈ $I(x):=\{t\in T:(t,x)\in U\}$ ） $display$ style I : ( $I(x):=\{t\in T:(t,x)\in U\}$ x ) 。X의 $임의의 x에 대해 =\{t\in$ T:(t $,$ x $I(x):=\{t\in T:(t,x)\in U\}$ )\ $in$ U\}.

특히 U $U=T\times X$ × $U=T\times X$ ( $I(x)=T$ $I(x)=T$ (x) = $I(x)=T$ ( $x$ $)$ = X $($ x) $=$ X (x (\ $display$ $style$ I (x) = $따라서$ δ는 X에서 T의 모노이드 작용을 정의한다.

함수 δ(t,x)는 동적 시스템의 진화 함수라고 불립니다.이것은 집합 X의 모든 점 x에 진화 파라미터라고 불리는 변수 t에 따라 고유한 이미지를 관련짓습니다.X는 위상 공간 또는 상태 공간이라고 불리며 변수 x는 시스템의 초기 상태를 나타냅니다.

우리는 종종 글을 쓴다.

{\displaystyle\Phi_{x}(t)\equiv\Phi(t,x)}

\Phi ^{t}(x)\equiv \Phi(t,x)

변수 중 하나를 상수로 받아들인다면요.

{\displaystyle\Phi_{x}:I(x)\to X}

x를 통과하는 흐름과 x를 통과하는 그래프 궤적이라고 합니다.세트

\displaystyle \gamma _{x}\equiv \{\Phi(t,x):t\in I(x)\}}

x를 통과하는 궤도는 x를 통과하는 흐름의 이미지입니다. 상태 공간 X의 부분 집합 S는 S의 모든 x와 T의 모든 t에 대해 δ 불변이라고 불립니다.

(\displaystyle\Phi(t,x)\in S).}

따라서 특히 S가 δ불변이라면 $I(x)=T$ ( $I(x)=T$ ) $I(x)=T$ \ $display style$ I ( x ) $=$ S의 모든 x에 대해 T $}$ 입니다 $I(x)=T$ .즉, x를 통과하는 흐름은 S의 모든 요소에 대해 항상 정의되어야 합니다.

보다 일반적으로 동적 시스템에 대한 두 가지 정의 클래스가 있습니다: 하나는 일반적인 미분 방정식에 의해 동기 부여되고 맛에서 기하학적이며, 다른 하나는 에르고드 이론에 의해 동기 부여되고 맛에서 측정 이론입니다.

기하학적 정의

기하학적 정의에서 동적 시스템은 튜플 $\langle {\mathcal {T}},{\mathcal {M}},f\rangle$ T $\langle {\mathcal {T}},{\mathcal {M}},f\rangle$ $\langle {\mathcal {T}},{\mathcal {M}},f\rangle$ $\langle {\mathcal {T}},{\mathcal {M}},f\rangle$ δ {\ $displaystyle \langle$ {\ $mathcal$ {T $}},$ {\ $mathcal$ { $M}},$ f\rangle $\langle {\mathcal {T}},{\mathcal {M}},f\rangle$ 입니다. ${\mathcal {T}}$ T {\ $displaystyle$ {\ $mathcal {T}}$ 은 ${\mathcal {T}}$ 시간 영역이며, 일반적으로 부정 또는 비제한 정수를 선택할 수 있는 영역이 많습니다. ${\mathcal {M}}$ {\ $displaystyle {M}}$ 은 ${\mathcal {M}}$ 다양체, 즉 Banach 공간이나 유클리드 공간, 또는 이산적인 경우에는 그래프입니다. f는 진화 규칙 t → f^t( $t\in {\mathcal {T}}$ T \ $displaystyle$ t $\in$ \ $mathcal$ ${$ $T$ 이므로^t f는 다양체 자체의 a형이다.즉, f는 시간 ${\mathcal {T}}$ T $($ 스타일)를 다지관의 미분 동형 공간에 매핑하는 "스무스한 $"$ 것입니다.즉, f(t)는 ${\mathcal {T}}$ T $(\$ 의 t마다 미분 동형입니다.

리얼 다이내믹 시스템

리얼 다이내믹 시스템, 리얼타임 다이내믹 시스템, 연속시간 다이내믹 시스템 또는 플로우는 T가 실수 R 내의 오픈 인터벌인 태플(T, M, δ)이며, M은 바나흐 공간에 국소적으로 미분형인 매니폴드이며, δ는 연속함수이다.δ가 연속적으로 미분 가능한 경우, 우리는 그 시스템이 미분 가능한 동적 시스템이라고 합니다.매니폴드 M이 R과ⁿ 국소 미분형일 경우 동적계는 유한차원이고, 그렇지 않을 경우 동적계는 무한차원이다.이것은 심플렉틱 구조를 상정하지 않습니다.T가 Real로 간주되면 다이내믹시스템은 글로벌 또는 플로우라고 불립니다.T가 음이 아닌 Real로 제한되면 다이내믹시스템은 세미플로우가 됩니다.

이산 동적 시스템

이산 동적계, 이산 시간 동적계는 태플(T, M, δ)이며, 여기서 M은 바나흐 공간과 국소 미분형 매니폴드이고, δ는 함수이다.T가 정수로 간주되면 캐스케이드 또는 맵입니다.T가 음이 아닌 정수로 제한되면 시스템을 세미 ^[14]캐스케이드라고 합니다.

셀 오토마톤

셀 오토마톤은 정수 또는 고차원 정수 그리드 등의 격자를 T로 하는 태플(T, M, δ)이며, M은 정수 격자(하나 이상의 차원을 갖는)에서 유한 집합까지의 함수 집합이며, δ a(국소 정의)의 진화 함수이다.이러한 셀룰러 오토마타는 동적 시스템입니다.M의 격자는 "공간" 격자를 나타내고 T의 격자는 "시간" 격자를 나타냅니다.

다차원 일반화

동적 시스템은 일반적으로 시간이라고 생각되는 단일 독립 변수에 걸쳐 정의됩니다.보다 일반적인 시스템 클래스는 여러 독립 변수에 걸쳐 정의되므로 다차원 시스템이라고 합니다.이러한 시스템은 예를 들어 이미지 처리와 같은 모델링에 유용합니다.

동적 시스템의 컴팩트화

국소 콤팩트 및 하우스도르프 토폴로지 공간 X 상에 글로벌 다이내믹 시스템(R, X, δ)이 주어지면 X의 원포인트 콤팩트화 X*에 대한 δ의 연속 확장 δ*를 연구하는 것이 종종 유용하다.원래 시스템의 미분 구조를 잃었지만 이제 콤팩트성 인수를 사용하여 새로운 시스템(R, X*, δ*)을 분석할 수 있습니다.

콤팩트 동적 시스템에서는 모든 궤도의 한계 집합이 비어 있지 않고 콤팩트하며 단순하게 연결됩니다.

이론적 정의 측정

동적 시스템은 공식적으로 측정 공간인 트리플렛(T, (X, δ, μ)의 측정 보존 변환으로 정의될 수 있다.여기서 T는 모노이드(통상 음이 아닌 정수), X는 세트, (X, δ, μ)는 확률 공간이며, 이는 δ가 X 위의 시그마 대수이며, μ는 (X, δ) 위의 유한 측도임을 의미한다.지도 δ: X → X는 δ 내의 δ마다 $\Phi ^{-1}\sigma \in \Sigma$ - $\Phi ^{-1}\sigma \in \Sigma$ $\Phi ^{-1}\sigma \in \Sigma$ ∈ $∈$ $\Phi ^{-1}\sigma \in \Sigma$ $display$ \ $display style$ \ Phi ^ { - $1$ ^ { - 1 \ in \ Sigma $\Phi ^{-1}\sigma \in \Sigma$ 이 있는 경우에만 δ 측정 가능하다고 합니다.map Φ is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving.그런 다음 이러한 δ에 대한 삼중항(T, (X, δ, μ), δ)을 동적 시스템으로 정의한다.

지도 δ는 동적 시스템의 시간 진화를 구현하고 있습니다.따라서 이산 다이내믹 시스템의 경우 $\scriptstyle \Phi ^{n}=\Phi \circ \Phi \circ \ldots \circ \Phi$ $=$ =∘ $\scriptstyle \Phi ^{n}=\Phi \circ \Phi \circ \ldots \circ \Phi$ $\scriptstyle \Phi ^{n}=\Phi \circ \Phi \circ \ldots \circ \Phi$ … $\scriptstyle \Phi ^{n}=\Phi \circ \Phi \circ \ldots \circ \Phi$ { $displaystyle$ \ $scriptstyle$ \ $Phi$ ^ { n } =\ 를 반복합니다.정수 n마다 Phi $\circ \circ \ldots \circ \Phi }$ 를 $\scriptstyle \Phi ^{n}=\Phi \circ \Phi \circ \ldots \circ \Phi$ 연구한다.연속적인 동적 시스템의 경우, 지도 δ는 유한한 시간 진화 맵으로 이해되며 구조가 더 복잡하다.

기하학적 정의와의 관계

측정값 이론적 정의는 측정값 보존 변환의 존재를 가정합니다.많은 다른 불변 척도가 하나의 진화 규칙과 연관될 수 있다.동적 시스템이 미분 방정식 시스템에 의해 주어지는 경우 적절한 조치를 결정해야 한다.이것은 미분방정식에서 시작하는 에르고드 이론을 전개하는 것을 어렵게 하기 때문에, 에르고드 이론 내에서 측정의 선택을 사이드 스텝으로 하여 선택되었다고 가정하는 동적 시스템 동기 정의를 가지는 것이 편리해진다.간단한 구성(때로는 크릴로프-보골류보 정리라고도 함)은 동적 시스템의 진화 규칙을 측정 보존 변환으로 만들기 위해 측정치를 구성하는 것이 항상 가능하다는 것을 보여준다.구조에서 주어진 상태 공간의 척도는 궤도의 모든 미래 지점에 대해 합산되어 불변성을 보장한다.

해밀턴 시스템의 리우빌 측정과 같은 자연 측정이 해밀턴 시스템의 주기적 궤도에서 지원되는 측정과 같은 다른 불변 측정보다 선택된다.무질서한 분산 시스템의 경우 불변 측정의 선택이 기술적으로 더 어렵다.측정치는 어트랙터에서 지원되어야 하지만, 어트랙터는 0의 르베그 측정치를 가지며, 불변 측정치는 르베그 측정치와 관련하여 특이해야 한다.위상 공간의 작은 영역은 시간 진화에 따라 축소됩니다.

쌍곡선 동적 시스템의 경우 시나이-룰레-보웬 측정이 자연스러운 선택으로 보인다.그것들은 동적 시스템의 안정적이고 불안정한 다양체의 기하학적 구조 위에 구성되어 있다; 그들은 작은 섭동 하에서 물리적으로 행동한다; 그리고 그들은 쌍곡계의 관측된 통계의 많은 부분을 설명한다.

동적 시스템 구축

시간의 진화 개념은 이전 섹션에서 보았던 동적 시스템 이론의 중심이다: 이 사실의 기본적인 이유는 이론의 시작 동기가 고전적인 기계 시스템의 시간 거동에 대한 연구였기 때문이다.그러나 상미분방정식은 동적 시스템이 되기 전에 풀어야 한다.예를 들어 다음과 같은 초기값 문제가 있습니다.

({displaystyle {dot {boldsymbol {x}}={\boldsymbol {x}})}, {\boldsymbol {x}})

{\boldsymbol {x}} _ {t=0} = boldsymbol {x} _ {0

어디에

$(\$ 는 $\scriptstyle {{\dot {{\boldsymbol {x}}}}}$ 재료점 x의 속도를 나타냅니다.
M은 유한 차원 다양체이다.
v: T × M → TM은 R 또는ⁿ C의ⁿ 벡터장으로 위상공간 M의 주어진 재료점에 작용하는 기존의 힘에 의해 유도되는 속도의 변화를 나타낸다.변경은 위상 공간 M의 벡터가 아니라 접선 공간 TM에 있습니다.

방정식에서 고차 미분이나 v(t,x)의 매개변수 t는 필요하지 않다. 왜냐하면 이것들은 고차원의 시스템을 고려함으로써 제거될 수 있기 때문이다.

이 벡터장의 특성에 따라 기계 시스템은

자율, v(t, x) = v(x)일 때
모든 t에 대해 v(t, 0) = 0일 때 균질

이 솔루션은 표준 ODE 기술을 사용하여 찾을 수 있으며 위에서 이미 소개한 진화 함수로 나타납니다.

{\boldsymbol {x}}(t)=\Phi(t, {\boldsymbol {x}}_{0})

다음으로 동적 시스템은 (T, M, δ)입니다.

위에 나타난 미분방정식 시스템의 일부 형식적인 조작은 동적 시스템이 만족해야 하는 방정식의 보다 일반적인 형태를 제공한다.

({displaystyle {dot {boldsymbol {x}}-{\boldsymbol {v}}=0\qquad\left(t,\boldsymbol {x}})\qquad\qquad\left(t,\Phi(t, {\boldsymbol {x}}_0})=0})

${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ 서 ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ G : ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ ( ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ × ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ ) ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ {\ $displaystyle$ {\ $mathfrak {G}:{(T\times$ M $)}^{M}}\to$ \ $mathbf {C}}}$ 는 ${\mathfrak {G}}:{{(T\times M)}^{M}}\to \mathbf {C}$ 진화 함수 집합에서 복소수 필드까지의 함수이다.

이 방정식은 복잡한 제약 조건을 가진 기계 시스템을 모델링할 때 유용합니다.

동적 시스템의 많은 개념은 무한 차원 다양체(국소 바나흐 공간)로 확장될 수 있으며, 이 경우 미분 방정식은 편미분 방정식입니다.

예

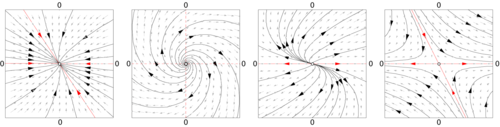
선형 동적 시스템

선형 동적 시스템은 분류된 모든 궤도의 동작과 단순한 기능 측면에서 해결할 수 있습니다.선형 시스템에서 위상 공간은 N차원 유클리드 공간이기 때문에 위상 공간의 모든 점은 N개의 숫자를 가진 벡터로 표현될 수 있다.선형 시스템의 분석은 그것들이 중첩 원리를 충족하기 때문에 가능하다: 만약 u(t)와 w(t)가 벡터장에 대한 미분 방정식을 충족한다면, u(t) + w(t)도 충족될 것이다.

플로우

흐름의 경우 벡터장 v(x)는 위상공간 내 위치의 아핀 함수이다.

{x}}=v(x)=Ax+b,

A행렬, b행렬은 숫자의 벡터, x행렬은 위치 벡터이다.이 시스템에 대한 해결책은 중첩 원리(선형성)를 사용하여 찾을 수 있습니다.A = 0인 경우 b ≠ 0은 b 방향의 직선일 뿐이다.

\displaystyle \Phi ^{t}(x_{1})=x_{1}+bt}

b가 0이고 A ≤ 0일 때 원점은 흐름의 평형(또는 단수) 지점이다. 즉, x = 0일 경우₀, 궤도는 거기에 남는다.다른 초기 조건의 경우, 움직임 방정식은 행렬의 지수로 주어진다: 초기 점 x의₀ 경우,

\displaystyle \Phi ^{t}(x_{0})=e^{tA}x_{0}.}

b = 0이면 A의 고유값에 따라 위상 공간의 구조가 결정됩니다.A의 고유값과 고유 벡터를 통해 초기 점이 원점에서 평형점으로 수렴할지 또는 분산될지를 결정할 수 있습니다.

A 0 0의 경우 두 개의 다른 초기 조건 사이의 거리는 대부분의 경우 기하급수적으로 빠르게 한 점을 향해 수렴하거나 기하급수적으로 빠르게 발산한다.선형 시스템은 분산의 경우 초기 조건에 민감한 의존성을 보입니다.비선형 시스템의 경우 이는 혼돈 동작을 위한 (필요하지만 충분하지 않은) 조건 중 하나입니다.

선형 벡터 필드 및 몇 가지 궤적이 있습니다.

지도

이산 시간 아핀 동적 시스템은 행렬 차분 방정식의 형태를 가집니다.

x_{n+1}=Ax_{n}+b,

A는 행렬이고 b는 벡터이다.연속형 경우와 마찬가지로 좌표 x → x + (1 - A)^–1b의 변화는 방정식에서 b항을 제거한다.새로운 좌표계에서 원점은 지도의 고정점이고 해는 선형계ⁿ₀ Ax이다.지도의 솔루션은 더 이상 곡선이 아니라 위상 공간에서 점프하는 지점입니다.궤도는 곡선 또는 섬유로 구성되어 있으며, 이는 지도의 작용에 따라 그 자체로 매핑되는 점들의 집합입니다.

연속형 경우와 마찬가지로 A의 고유값과 고유 벡터가 위상 공간의 구조를 결정합니다.예를 들어 u가 A의 고유벡터이고, 실제 고유값이 1보다 작을₁ 경우 α₁ u에 따라 α δ R을 갖는 점에 의해 주어진 직선은 지도의 불변곡선이 된다.이 직선의 점이 고정점에 연결됩니다.

다른 많은 이산 동적 시스템도 있습니다.

국소 역학

동적 시스템의 질적 특성은 부드러운 좌표 변화 하에서 변하지 않는다(이것은 때때로 질적 정의로 받아들여진다): 벡터장의 단수점 (v(x) = 0인 지점); 주기적 궤도는 위상 공간의 루프이고 t의 부드러운 변형이다.위상 공간은 루프가 되는 것을 바꿀 수 없습니다.동적 시스템의 위상 공간의 구조를 잘 이해할 수 있는 것은 특이점과 주기적인 궤도 부근이다.동적 시스템의 정성적 연구에서 접근방식은 동적 시스템을 최대한 단순하게 만드는 좌표의 변화(보통 지정되지 않았지만 계산 가능)가 있음을 보여주는 것이다.

수정

위상 공간의 대부분의 작은 패치에서의 흐름은 매우 단순화할 수 있습니다.y가 벡터장 v(y) 0 0인 점이라면 벡터장이 같은 크기의 일련의 병렬 벡터가 되는 y 주변 영역에 대한 좌표 변화가 있습니다.이것은 정류정리로 알려져 있다.

수정정리에 따르면 단수점으로부터 떨어져 있는 작은 부분에서의 점의 역학은 직선이다.패치는 여러 개의 패치를 함께 꿰매어 확장할 수 있으며, 이것이 위상공간 M 전체에 적용되면 동적 시스템을 통합할 수 있습니다.대부분의 경우 패치는 전체 단계 공간으로 확장할 수 없습니다.벡터 필드(v(x) = 0)에 특이점이 있을 수 있으며, 일부 점에 가까워짐에 따라 패치가 점점 더 작아질 수 있습니다.보다 미묘한 이유는 글로벌 제약입니다.패치에서는 궤적이 시작되어 일련의 다른 패치에 접속하면 원래 패치로 돌아갑니다.다음에 궤도가 위상 공간을 다른 방식으로 루프할 경우 일련의 패치에서 벡터 필드를 수정할 수 없습니다.

근주기 궤도

일반적으로 주기 궤도 부근에서는 정류 정리를 사용할 수 없습니다.푸앵카레는 주기 궤도 근처의 분석을 지도의 분석으로 바꾸는 접근법을 개발했다.궤도 θ에서 점₀ x를 선택하고 v(x₀)에 수직인 해당 근방의 위상 공간 내 점을 고려합니다.이 지점들은 궤도의 푸앵카레 구간 S( s, x)이다₀.이제 흐름은 S에서 시작하여 S로 돌아오는 점에 대한 맵인 Poincaré map F : S → S를 정의합니다.이 모든 점이 돌아오는 데 같은 시간이 걸리지는 않지만 시간은 x에₀ 가깝습니다.

주기 궤도와 푸앵카레의 교차점은 푸앵카레 지도 F의 고정점이다.환산으로 볼 때, 점은 x = 0이라고 가정할 수 있다.지도의 Taylor 급수는 F(x) = J · x² + O(x)이다. 따라서 좌표 h의 변화는 F를 선형 부분으로 단순화시키는 것만을 기대할 수 있다.

h^{-1}\circ h(x)=J\cdot x.

이것을 활용 방정식이라고 한다.이 방정식이 유지될 수 있는 조건을 찾는 것은 동적 시스템의 주요 연구 과제 중 하나였다.Poincaré는 모든 함수가 분석적이라고 가정하고 먼저 접근했으며 그 과정에서 비공진 조건을 발견했다.λ₁, ..., are가_ν J의 고유값일 경우, 하나의 고유값이 두 개 이상의 다른 고유값의 정수 선형 조합일 경우 공진합니다.함수 h에 대한 항의 분모에서 δ_i – δ(기타 고유값의 배수) 형식의 항이 발생하므로, 비공진 조건은 작은 제수 문제라고도 합니다.

활용 결과

켤레 방정식에 대한 해답의 존재에 대한 결과는 J의 고유값과 h에서 요구되는 평활도에 따라 달라집니다.J는 특별한 대칭을 가질 필요가 없으므로 고유값은 일반적으로 복소수입니다.J의 고유값이 단위 원에 없을 때 F의 고정점₀ x 근처의 역학을 쌍곡선이라고 하며, 고유값이 단위 원에 있고 복합체에 있을 때 역학을 타원이라고 합니다.

쌍곡선의 경우, 하트만-그로브만 정리는 지도의 고정점 근방을 선형 지도 J · x에 매핑하는 연속 함수의 존재 조건을 제공한다.쌍곡선 케이스는 구조적으로도 안정적입니다.벡터장의 작은 변화는 Poincaré 지도의 작은 변화만을 생성하며, 이러한 작은 변화는 복잡한 평면에서 J의 고유값 위치의 작은 변화에도 반영되어 지도가 여전히 쌍곡선임을 암시한다.

KAM(Kolmogorov-Arnold-Moser) 정리는 타원점 근처의 동작을 제공한다.

분기 이론

진화 맵 δ^t(또는 이 맵이 파생된 벡터 필드)가 파라미터 μ에 의존할 경우 위상 공간의 구조도 이 파라미터에 의존합니다.작은 변화가 특별한 값₀ μ에 도달할 때까지 위상 공간에 질적 변화를 일으키지 않을 수 있습니다.이 시점에서 위상공간은 질적으로 변화하며 동적계는 분기기를 거쳤다고 한다.

분기 이론은 위상 공간의 구조(일반적으로 고정점, 주기 궤도 또는 불변 토러스)를 고려하고 매개변수 μ의 함수로서 그 동작을 연구합니다.분기점에서 구조가 안정성을 변경하거나 새 구조로 분할되거나 다른 구조와 병합될 수 있습니다.지도의 테일러 계열 근사치와 좌표 변화에 의해 제거될 수 있는 차이에 대한 이해를 사용함으로써 동적 시스템의 분리를 카탈로그화할 수 있다.

시스템 패밀리_μ F의 쌍곡선 고정점₀ x의 분리는 분기점에서 계산된 시스템_μ DF(x₀)의 첫 번째 도함수의 고유값으로 특징지을 수 있다.지도의 경우 단위 원에 DF의 고유값이_μ 있을 때 분기가 발생합니다.흐름의 경우 가상 축에 고유값이 있을 때 발생합니다.자세한 내용은 분기 이론에 대한 주요 기사를 참조하십시오.

일부 분기는 위상 공간에서 매우 복잡한 구조를 초래할 수 있습니다.예를 들어 루엘은...타켄스 시나리오는 주기적인 궤도가 어떻게 토러스(torus)와 토러스(torus)로 갈라지는지를 묘사한다.또 다른 예에서, Feigenbaum period-doubleing은 안정된 주기적 궤도가 일련의 주기-double 분기 과정을 거치는 방법을 설명한다.

에르고딕 시스템

많은 동적 시스템에서는 위상 공간의 볼륨(실제로 θ차원 볼륨)이 변하지 않도록 시스템의 좌표를 선택할 수 있습니다.이 현상은 좌표가 위치와 운동량이고 부피가 (위치) × (운동량) 단위로 측정되는 한 뉴턴의 법칙에서 파생된 기계 시스템에서 발생합니다.흐름은 부분 집합 A의 점을 점 δ^t(A)로 가져가고 위상 공간의 불변성은 다음을 의미합니다.

\displaystyle \mathrm {vol}(A)=\mathrm {vol}(\Phi ^{t}(A)).}

해밀턴의 형식론에서는 좌표가 주어지면 적절한 (일반화된) 운동량을 도출하여 관련 부피가 흐름에 의해 보존되도록 할 수 있다.부피는 Liouville 측도로 계산된다고 한다.

해밀턴 시스템에서는 초기 조건에서 위치 및 운동량의 가능한 모든 구성에 도달할 수 없습니다.에너지 절약으로 인해 초기 상태와 동일한 에너지를 가진 상태만 액세스할 수 있습니다.동일한 에너지를 가진 상태는 위상 공간의 서브매니폴드인 에너지 셸 δ를 형성합니다.Liouville 측도를 사용하여 계산된 에너지 셸의 부피는 진화 하에 보존된다.

부피가 흐름에 의해 보존되는 시스템의 경우, Poincaré는 다음과 같은 반복 정리를 발견했다.위상 공간의 부피가 유한하다고 가정하고 F를 위상 공간 부피 보존 맵으로 하고 A를 위상 공간의 하위 집합으로 합니다.그러면 A의 거의 모든 점이 A로 무한히 자주 돌아갑니다.푸앵카레 반복정리는 충돌하는 원자의 동적 시스템에서 볼츠만의 엔트로피 증가 유도에 반대하기 위해 체르멜로에 의해 사용되었다.

볼츠만의 연구에서 제기된 문제들 중 하나는 그가 에르고드 가설이라고 부르는 시간 평균과 공간 평균 사이의 가능한 동일성이었다.가설은 전형적인 궤적이 영역 A에서 보내는 시간의 길이가 vol(A)/vol(Ω)이라고 말한다.

에르고드 가설은 통계 역학의 개발에 필요한 필수 속성이 아닌 것으로 판명되었고 물리적 시스템의 관련 측면을 포착하기 위해 일련의 다른 에르고드 유사 특성이 도입되었다.Koopman은 기능 분석을 이용하여 에르고드 시스템의 연구에 접근했다.관측 가능한 a는 위상 공간의 각 점에 숫자를 연관짓는 함수입니다(예: 순간 압력 또는 평균 높이).관측 가능한 값은 진화 함수 θ를^t 사용하여 다른 시간에 계산할 수 있다.이것에 의해, 전송 연산자인 연산자^t U가 도입됩니다.

\displaystyle(U^{t}a)(x)=a(\Phi^{-t}(x)).}

선형 연산자 U의 스펙트럼 특성을 연구함으로써 δ의^t 에르고드 특성을 분류할 수 있게 된다.관측 가능한 함수에 대한 흐름의 작용을 고려하는 Koopman 접근법을 사용할 때, δ를^t 포함하는 유한 차원 비선형 문제는 U를 포함하는 무한 차원 선형 문제에 매핑된다.

에너지 표면 δ로 제한된 리우빌 측정은 평형 통계 역학에서 계산된 평균의 기초가 된다.궤적을 따른 시간 평균은 볼츠만 계수 exp(-βH)로 계산한 공간 평균과 같다.이 아이디어는 시나이, 보웬 및 루엘(SRB)에 의해 분산 시스템을 포함하는 더 큰 클래스의 동적 시스템으로 일반화되었습니다.SRB 측정은 볼츠만 계수를 대체하며 카오스 시스템의 유인기에 정의된다.

비선형 동적 시스템 및 카오스

단순한 비선형 동적 시스템이나 심지어 부분 선형 시스템도 근본적으로 결정론적임에도 불구하고 전혀 예측할 수 없는 동작을 보일 수 있습니다.예측할 수 없어 보이는 이 행동을 혼돈이라고 부른다.쌍곡선 시스템은 혼돈 시스템에 기인하는 특성을 나타내는 정확하게 정의된 동적 시스템입니다.쌍곡선 시스템에서 궤도에 수직인 접선 공간은 두 부분으로 잘 분리될 수 있습니다. 하나는 궤도(안정 매니폴드)를 향해 수렴하는 점이고 다른 하나는 궤도(불안정 매니폴드)에서 분기하는 점입니다.

수학의 이 부문은 동적 시스템의 장기적인 질적 행동을 다룬다.여기서 초점은 동적 시스템을 정의하는 방정식에 대한 정확한 해법을 찾는 것이 아니라, "시스템이 장기적으로 안정된 상태로 안정될 것인가, 그렇다면 가능한 유인 요인은 무엇인가?" 또는 "시스템의 장기적 동작이 초기 조건에 따라 달라지는가?"와 같은 질문에 답하는 것이다."n?"

복잡한 시스템의 무질서한 동작은 문제가 아닙니다.기상학은 수년간 복잡하고 심지어 혼란스러운 행동을 수반하는 것으로 알려져 왔다.카오스 이론은 매우 놀라웠다. 왜냐하면 카오스는 거의 사소한 시스템 안에서 발견될 수 있기 때문이다.로지스틱 맵은 2차 다항식일 뿐이며 말굽 맵은 부분 선형입니다.

한정된 기간의 해결책

비선형 자율 ODE의 경우 유한한 ^[15]기간의 솔루션을 개발할 수 있습니다. 즉, 여기서 시스템은 자신의 역학에서 종료 시점에 값 0에 도달하고 그 후 영원히 0에 머무릅니다.이러한 유한 지속 해는 실선 전체로는 해석 함수일 수 없으며, 종료 시 립시츠 함수가 아닌 것이므로 립시츠 미분 방정식의 해답의 고유성을 지지하지 않는다.

예를 들어, 방정식은 다음과 같습니다.

\displaystyle y'=-{\text{sgn}}(y){\displayrt { y }},,,y(0)=1}

한정된 기간 솔루션을 허용합니다.

y(x)=paramfrac {1}{4}\left(1-{\frac {x}{2}}+\left 1-{\frac {x}{2}\right \2}

「」를 참조해 주세요.

레퍼런스

^ Strogatz, S. H. (2001). Nonlinear Dynamics and Chaos: with Applications to Physics, Biology and Chemistry. Perseus.
^ Katok, A.; Hasselblatt, B. (1995). Introduction to the Modern Theory of Dynamical Systems. Cambridge: Cambridge University Press. ISBN 978-0-521-34187-5.
^ "Nature". Springer Nature. Retrieved 17 February 2017.
^ Melby, P.; et al. (2005). "Dynamics of Self-Adjusting Systems With Noise". Chaos: An Interdisciplinary Journal of Nonlinear Science. 15 (3): 033902. Bibcode:2005Chaos..15c3902M. doi:10.1063/1.1953147. PMID 16252993.
^ Gintautas, V.; et al. (2008). "Resonant forcing of select degrees of freedom of multidimensional chaotic map dynamics". J. Stat. Phys. 130 (3): 617. arXiv:0705.0311. Bibcode:2008JSP...130..617G. doi:10.1007/s10955-007-9444-4. S2CID 8677631.
^ Jackson, T.; Radunskaya, A. (2015). Applications of Dynamical Systems in Biology and Medicine. Springer.
^ Kreyszig, Erwin (2011). Advanced Engineering Mathematics. Hoboken: Wiley. ISBN 978-0-470-64613-7.
^ Gandolfo, Giancarlo (2009) [1971]. Economic Dynamics: Methods and Models (Fourth ed.). Berlin: Springer. ISBN 978-3-642-13503-3.
^ 홈즈, 필립.Poincaré, 천체역학, 동적계 이론 및 혼돈.물리 보고서 193.3(1990): 137-163.
^ Rega, Giuseppe (2019). "Tribute to Ali H. Nayfeh (1933-2017)". IUTAM Symposium on Exploiting Nonlinear Dynamics for Engineering Systems. Springer. pp. 1–2. ISBN 9783030236922.
^ "Ali Hasan Nayfeh". Franklin Institute Awards. The Franklin Institute. 4 February 2014. Retrieved 25 August 2019.
^ 군티 M. 및 마졸라 C.(2012), "모노이드의 동적 시스템: 결정론적 체계와 운동에 대한 일반적인 이론을 향해"Minati G., Abram M., Pessa E.(편집), 일반적인 변화 이론을 향한 방법, 모델, 시뮬레이션 및 접근법, 173-185, 싱가포르:월드 사이언티픽스ISBN 978-981-4383-32-5
^ Mazzola C. and Gunti M. (2012), "역동학과 시간의 방향성"Minati G., Abram M., Pessa E. (ed.)에서 일반적인 변화 이론을 향한 방법, 모델, 시뮬레이션 및 접근법, 161-171, 싱가포르:월드 사이언티픽스ISBN 978-981-4383-32-5.
^ Galor, Oded (2010). Discrete Dynamical Systems. Springer.
^ Vardia T. Haimo (1985). "Finite Time Differential Equations". 1985 24th IEEE Conference on Decision and Control. pp. 1729–1733. doi:10.1109/CDC.1985.268832. S2CID 45426376.

Arnold, Vladimir I. (2006). "Fundamental concepts". Ordinary Differential Equations. Berlin: Springer Verlag. ISBN 3-540-34563-9.
Chueshov, I. D. Introduction to the Theory of Infinite-Dimensional Dissipative Systems. EMIS 사이트의 초판 온라인 버전 [1]을 참조하십시오.
Temam, Roger (1997) [1988]. Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer Verlag.

추가 정보

폭넓은 커버리지를 제공하는 작업:

Ralph Abraham and Jerrold E. Marsden (1978). Foundations of mechanics. Benjamin–Cummings. ISBN 978-0-8053-0102-1. (전재 : ISBN 0-201-40840-6)
수학과학 백과사전(ISSN 0938-0396)에는 현재 연구의 리뷰가 포함된 동적 시스템에 대한 하위 시리즈가 있습니다.
Christian Bonatti; Lorenzo J. Díaz; Marcelo Viana (2005). Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective. Springer. ISBN 978-3-540-22066-4.
Stephen Smale (1967). "Differentiable dynamical systems". Bulletin of the American Mathematical Society. 73 (6): 747–817. doi:10.1090/S0002-9904-1967-11798-1.

독특한 관점을 가진 소개 텍스트:

V. I. Arnold (1982). Mathematical methods of classical mechanics. Springer-Verlag. ISBN 978-0-387-96890-2.
Jacob Palis and Welington de Melo (1982). Geometric theory of dynamical systems: an introduction. Springer-Verlag. ISBN 978-0-387-90668-3.
David Ruelle (1989). Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. ISBN 978-0-12-601710-6.
Tim Bedford, Michael Keane and Caroline Series, eds. (1991). Ergodic theory, symbolic dynamics and hyperbolic spaces. Oxford University Press. ISBN 978-0-19-853390-0.{{cite book}}: CS1 maint: 여러 이름: 작성자 목록(링크)
Ralph H. Abraham and Christopher D. Shaw (1992). Dynamics—the geometry of behavior, 2nd edition. Addison-Wesley. ISBN 978-0-201-56716-8.

교재

Kathleen T. Alligood, Tim D. Sauer and James A. Yorke (2000). Chaos. An introduction to dynamical systems. Springer Verlag. ISBN 978-0-387-94677-1.
Oded Galor (2011). Discrete Dynamical Systems. Springer. ISBN 978-3-642-07185-0.
Morris W. Hirsch, Stephen Smale and Robert L. Devaney (2003). Differential Equations, dynamical systems, and an introduction to chaos. Academic Press. ISBN 978-0-12-349703-1.
Anatole Katok; Boris Hasselblatt (1996). Introduction to the modern theory of dynamical systems. Cambridge. ISBN 978-0-521-57557-7.
Stephen Lynch (2010). Dynamical Systems with Applications using Maple 2nd Ed. Springer. ISBN 978-0-8176-4389-8.
Stephen Lynch (2014). Dynamical Systems with Applications using MATLAB 2nd Edition. Springer International Publishing. ISBN 978-3319068190.
Stephen Lynch (2017). Dynamical Systems with Applications using Mathematica 2nd Ed. Springer. ISBN 978-3-319-61485-4.
Stephen Lynch (2018). Dynamical Systems with Applications using Python. Springer International Publishing. ISBN 978-3-319-78145-7.
James Meiss (2007). Differential Dynamical Systems. SIAM. ISBN 978-0-89871-635-1.
David D. Nolte (2015). Introduction to Modern Dynamics: Chaos, Networks, Space and Time. Oxford University Press. ISBN 978-0199657032.
Julien Clinton Sprott (2003). Chaos and time-series analysis. Oxford University Press. ISBN 978-0-19-850839-7.
Steven H. Strogatz (1994). Nonlinear dynamics and chaos: with applications to physics, biology chemistry and engineering. Addison Wesley. ISBN 978-0-201-54344-5.
Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.
Stephen Wiggins (2003). Introduction to Applied Dynamical Systems and Chaos. Springer. ISBN 978-0-387-00177-7.

대중화:

Florin Diacu and Philip Holmes (1996). Celestial Encounters. Princeton. ISBN 978-0-691-02743-2.
James Gleick (1988). Chaos: Making a New Science. Penguin. ISBN 978-0-14-009250-9.
Ivar Ekeland (1990). Mathematics and the Unexpected (Paperback). University Of Chicago Press. ISBN 978-0-226-19990-0.
Ian Stewart (1997). Does God Play Dice? The New Mathematics of Chaos. Penguin. ISBN 978-0-14-025602-4.

외부 링크

Arxiv 프리프린트 서버에는 동적 시스템에서 매일 (리퀘스트되지 않은) 원고가 제출됩니다.
동적인 시스템 백과사전 Scholarpedia의 일부 - 초빙된 전문가에 의해 동료가 리뷰 및 작성.
비선형 다이내믹스Elmer G의 분기 및 혼돈 모델.윈스
Sci. Nonlinear FAQ 2.0(2003년 9월)은 비선형 과학에 관한 정의, 설명 및 자원을 제공한다.

온라인 서적 또는 강의 노트

동적 시스템의 기하학적 이론.Nils Berglund의 강의는 고급 학부 수준의 ETH 강좌에 대해 기술하고 있습니다.
동적 시스템조지 D.Birkhoff의 1927년 저서는 이미 역동적인 시스템에 대한 현대적인 접근법을 취하고 있다.
혼돈: 고전과 양자.주기적 궤도 관점에서 동적 시스템에 대한 소개.
동적 시스템 학습동적 시스템 학습에 대한 튜토리얼입니다.
일반 미분 방정식과 동적 시스템.제럴드 테슐의 강의 노트

연구 그룹

다이내믹 시스템 그룹 그로닝엔, IWI, 그로닝엔 대학
혼돈 @ UMD. 동적 시스템 응용에 집중합니다.
[2], SUNY Stony Brook.회의, 연구자 및 미해결 문제 목록.
펜실베이니아 주 역학 기하학 센터입니다
캘리포니아 공대, 제어 및 동적 시스템입니다
Ecole Polytechnique Fédérale de Lausanne(EPFL) 비선형 시스템 연구소.
브레멘 대학교 동적 시스템 센터
옥스퍼드 대학교 시스템 분석, 모델링 및 예측 그룹
리스본 공과대학 슈페리어 테크니코 비선형 역학 그룹
동적 시스템, IMPA, 국립 마테마티카 연구소 Pura e Applicationada.
체코 과학 아카데미 컴퓨터 과학 연구소 비선형 다이내믹스 워크그룹
UPC 다이내믹 시스템 그룹 바르셀로나, 카탈로니아 폴리테크놀로지 대학
캘리포니아 대학, 산타 바바라 제어, 동적 시스템 및 계산 센터.

[1] Strogatz, S. H. (2001). Nonlinear Dynamics and Chaos: with Applications to Physics, Biology and Chemistry. Perseus.

[2] Katok, A.; Hasselblatt, B. (1995). Introduction to the Modern Theory of Dynamical Systems. Cambridge: Cambridge University Press. ISBN 978-0-521-34187-5.

[3] "Nature". Springer Nature. Retrieved 17 February 2017.

[4] Melby, P.; et al. (2005). "Dynamics of Self-Adjusting Systems With Noise". Chaos: An Interdisciplinary Journal of Nonlinear Science. 15 (3): 033902. Bibcode:2005Chaos..15c3902M. doi:10.1063/1.1953147. PMID 16252993.

[5] Gintautas, V.; et al. (2008). "Resonant forcing of select degrees of freedom of multidimensional chaotic map dynamics". J. Stat. Phys. 130 (3): 617. arXiv:0705.0311. Bibcode:2008JSP...130..617G. doi:10.1007/s10955-007-9444-4. S2CID 8677631.

[6] Jackson, T.; Radunskaya, A. (2015). Applications of Dynamical Systems in Biology and Medicine. Springer.

[7] Kreyszig, Erwin (2011). Advanced Engineering Mathematics. Hoboken: Wiley. ISBN 978-0-470-64613-7.

[8] Gandolfo, Giancarlo (2009) [1971]. Economic Dynamics: Methods and Models (Fourth ed.). Berlin: Springer. ISBN 978-3-642-13503-3.

[9] 홈즈, 필립.Poincaré, 천체역학, 동적계 이론 및 혼돈.물리 보고서 193.3(1990): 137-163.

[Rega-10] Rega, Giuseppe (2019). "Tribute to Ali H. Nayfeh (1933-2017)". IUTAM Symposium on Exploiting Nonlinear Dynamics for Engineering Systems. Springer. pp. 1–2. ISBN 9783030236922.

[fi-11] "Ali Hasan Nayfeh". Franklin Institute Awards. The Franklin Institute. 4 February 2014. Retrieved 25 August 2019.

[12] 군티 M. 및 마졸라 C.(2012), "모노이드의 동적 시스템: 결정론적 체계와 운동에 대한 일반적인 이론을 향해"Minati G., Abram M., Pessa E.(편집), 일반적인 변화 이론을 향한 방법, 모델, 시뮬레이션 및 접근법, 173-185, 싱가포르:월드 사이언티픽스ISBN 978-981-4383-32-5

[13] Mazzola C. and Gunti M. (2012), "역동학과 시간의 방향성"Minati G., Abram M., Pessa E. (ed.)에서 일반적인 변화 이론을 향한 방법, 모델, 시뮬레이션 및 접근법, 161-171, 싱가포르:월드 사이언티픽스ISBN 978-981-4383-32-5.

[14] Galor, Oded (2010). Discrete Dynamical Systems. Springer.

[15] Vardia T. Haimo (1985). "Finite Time Differential Equations". 1985 24th IEEE Conference on Decision and Control. pp. 1729–1733. doi:10.1109/CDC.1985.268832. S2CID 45426376.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[14]

[15]

Search

동적 시스템

네임스페이스

더

목차

개요

역사