분산분석
Analysis of variance분산 분석(analysis of variance, 분산 분석)은 평균 간의 차이를 분석하는 데 사용되는 통계 모형과 관련 추정 절차의 모음입니다.분산 분석은 통계학자 Ronald Fisher에 의해 개발되었습니다.분산 분석은 총 분산의 법칙을 기반으로 하며, 특정 변수에서 관측된 분산은 서로 다른 변동 요인에 기인하는 성분으로 분할됩니다.분산 분석은 가장 간단한 형태로 두 개 이상의 모집단 평균이 동일한지 여부에 대한 통계적 검정을 제공하므로 t-검정은 두 개의 평균을 넘어 일반화됩니다.즉, 분산 분석은 둘 이상의 평균 간의 차이를 검정하는 데 사용됩니다.
역사
20세기에 분산 분석이 결실을 맺었지만 스티글러에 따르면 선행 연구는 과거로 몇 세기에 걸쳐 진행됩니다.[1]여기에는 가설 검정, 제곱합 분할, 실험 기법 및 가법 모형이 포함됩니다.라플라스는 1770년대에 가설 테스트를 수행했습니다.[2]1800년경, 라플라스와 가우스는 천문학과 측지학에서 사용된 방법을 개선한 관측을 결합하기 위한 최소제곱법을 개발했습니다.또한 제곱합에 대한 기여도에 대한 많은 연구를 시작했습니다.Laplace는 잔차 제곱합에서 분산을 추정하는 방법을 알고 있었습니다.[3]1827년까지 Laplace는 대기 조석 측정에 관한 ANOVA 문제를 해결하기 위해 최소 제곱법을 사용했습니다.[4]1800년 이전에 천문학자들은 반응 시간("개인 방정식")으로 인한 관측 오차를 분리하고 오차를 줄이는 방법을 개발했습니다.[5]개인 방정식의 연구에서 사용된 실험 방법은 나중에 심리학의 신흥 분야에 받아들여졌고, 이 분야에서 강력한 (완전한 요인) 실험 방법이 개발되었고, 곧 무작위화와 눈가림이 추가되었습니다.[7]1885년에는 가법 효과 모형에 대한 설득력 있는 비수학적 설명이 가능했습니다.[8]
Ronald Fisher는 분산이라는 용어를 소개했고 이론적 집단 유전학에 관한 1918년 기사에서 그것의 공식적인 분석을 제안했습니다.멘델계 유산 추정에 관한 친족 [9]간의 상관관계데이터 분석에 분산 분석을 처음 적용한 것은 1921년에 발표된 "작물 변동 연구 I"[10]입니다. 이것은 시계열의 변동을 연간 원인과 느린 악화를 나타내는 성분으로 구분했습니다.Winifred Mackenzie와 함께 쓰고 1923년에 출판된 Fisher의 다음 작품인 Studies in Crop Variation II는 다양한 품종으로 파종되고 다양한 비료 처리를 받는 지역 간의 수확량 변화를 연구했습니다.[11]분산 분석은 Fisher의 1925년 저서 연구 종사자를 위한 통계적 방법에 포함된 후 널리 알려지게 되었습니다.
무작위화 모델은 여러 연구자들에 의해 개발되었습니다.첫번째는 1923년 저지 네이먼에 의해 폴란드어로 출판되었습니다.[12]
예



분산 분석은 변수 간의 복잡한 관계를 설명하는 데 사용할 수 있습니다.도그 쇼는 예를 제공합니다.도그 쇼는 이 품종의 무작위 표본이 아닙니다. 일반적으로 성인이고 순종이며 모범적인 개들로 제한됩니다.쇼의 개 무게 히스토그램은 그림에 표시된 노란색-주황색 분포처럼 다소 복잡할 수 있습니다.각 개의 특성 집합을 기반으로 개의 몸무게를 예측하려고 한다고 가정합니다.이를 위한 한 가지 방법은 이러한 특성을 바탕으로 개 개체군을 그룹으로 나누어 가중치 분포를 설명하는 것입니다.성공적인 그룹화는 (a) 각 그룹이 개의 무게의 낮은 분산(상대적으로 동질적임을 의미함)과 (b) 각 그룹의 평균이 구별되도록 개를 분할합니다(두 그룹의 평균이 동일한 경우, 그룹이 실제로 의미 있는 방식으로 분리되어 있다고 결론짓는 것은 타당하지 않습니다).
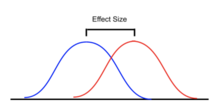
오른쪽 그림에서 그룹은 X1, X 등으로2 식별됩니다.첫 번째 그림에서, 개는 두 개의 이진 그룹(예: 그룹 1은 젊고, 단모이고, 그룹 2는 젊고, 장모인 개 등)의 곱(상호작용)에 따라 나뉩니다.각 그룹 내의 개 체중 분포(파란색으로 표시)는 비교적 큰 분산을 가지며, 평균은 그룹 간에 매우 유사하므로,이러한 특성에 따라 개를 그룹화하는 것은 개의 몸무게의 변화를 설명하는 효과적인 방법을 만들어내지 못합니다. 개가 어떤 그룹에 있는지를 아는 것은 단순히 개 쇼에 개가 있다는 것을 아는 것보다 우리가 그것의 몸무게를 훨씬 더 잘 예측할 수 있게 해주지 못합니다.따라서 이 그룹화는 전체 분포(노란색-주황색)의 변동을 설명하지 못합니다.
개를 애완동물 대 작업종, 덜 운동적인 것 대 더 운동적인 것으로 분류하여 체중 분포를 설명하려는 시도는 아마도 어느 정도 더 성공적일 것입니다.가장 무거운 쇼독들은 크고, 힘이 세고, 일하는 품종들일 가능성이 있는 반면, 애완동물로 기르는 품종들은 더 작고, 그래서 더 가벼운 경향이 있습니다.두 번째 그림에서 볼 수 있듯이, 분포의 분산은 첫 번째 경우보다 상당히 작고 평균은 더 구별할 수 있습니다.그러나 분포가 상당히 겹친다는 것은 예를1 들어 X와 X를2 확실하게 구별할 수 없다는 것을 의미합니다.동전 뒤집기에 따라 개를 그룹화하면 유사하게 보이는 분포가 생성될 수 있습니다.
품종별로 체중을 설명하려는 시도는 매우 적합한 결과를 가져올 가능성이 높습니다.모든 치와와는 가볍고 모든 세인트 버나드는 무겁습니다.세터와 포인터 간의 가중치 차이가 별개의 품종을 정당화하는 것은 아닙니다.분산 분석은 이러한 직관적 판단을 정당화하는 공식적인 도구를 제공합니다.이 방법의 일반적인 용도는 실험 데이터 분석 또는 모형 개발입니다.이 방법은 상관 관계에 비해 몇 가지 장점이 있습니다. 모든 데이터가 숫자여야 하는 것은 아니며 이 방법의 한 가지 결과는 설명 관계에 대한 신뢰도에 대한 판단입니다.
모델 클래스
분산 분석에 사용되는 모형에는 세 가지 부류가 있으며, 여기에 이들에 대한 개요가 설명되어 있습니다.
고정효과 모형
분산 분석의 고정 효과 모형(등급 I)은 실험자가 반응 변수 값의 변화 여부를 확인하기 위해 실험 대상에 하나 이상의 처리를 적용하는 상황에 적용됩니다.이를 통해 실험자는 모집단 전체에서 처리가 생성할 반응 변수 값의 범위를 추정할 수 있습니다.

랜덤 효과 모형
랜덤 효과 모형(class II)은 처리가 고정되지 않은 경우에 사용됩니다.이 문제는 다양한 요인 수준이 더 큰 모집단에서 표본 추출된 경우에 발생합니다.수준 자체가 랜덤 변수이기 때문에 일부 가정과 처리를 대조하는 방법(단순 차이의 다변량 일반화)은 고정 효과 모형과 다릅니다.[13]
혼합효과 모형
혼합 효과 모형(클래스 III)에는 고정 효과와 랜덤 효과 유형의 실험 요인이 모두 포함되어 있으며 두 유형에 대한 해석 및 분석이 적절하게 다릅니다.
예
각 텍스트는 치료법으로 간주되며, 좋은 입문 교재를 찾기 위해 대학 또는 대학 부서에서 교수 실험을 수행할 수 있습니다.고정 효과 모형에서는 후보 텍스트 목록을 비교합니다.랜덤 효과 모형은 랜덤하게 선택된 텍스트 목록 사이에 중요한 차이가 있는지 여부를 결정합니다.혼합 효과 모형에서는 (고정된) 현재 텍스트를 임의로 선택한 대안과 비교합니다.
고정 효과와 랜덤 효과를 정의하는 것은 여러 개의 경쟁 정의와 함께 이해하기 어려운 것으로 입증되었습니다.[14]
가정
분산 분석은 여러 접근법에서 연구되었으며, 가장 일반적인 접근법은 처리 및 블럭에 대한 반응을 연결하는 선형 모형을 사용합니다.모형은 모수에서 선형이지만 요인 수준에 걸쳐 비선형일 수 있습니다.여러 요소에 걸쳐 데이터가 균형을 이룰 때는 해석이 쉽지만, 불균형한 데이터에 대해서는 훨씬 더 깊은 이해가 필요합니다.
정규분포를 이용한 교과서 분석
분산 분석은 반응의 확률 분포에 대해 다음과 같은 가정을 하는 선형 모형의 관점에서 제시할 수 있습니다.[15][16][17][18]
- 관측치의 독립성 – 통계적 분석을 단순화하는 모형의 가정입니다.
- 정규성 – 잔차의 분포는 정규 분포입니다.
- 균질성(homoscedasticity)이라고 하는 분산의 동일성(또는 "균질성")—집단 내 데이터의 분산은 동일해야 합니다.
교과서 모델의 개별 가정은 오류가 고정 효과 모델에 대해 독립적이고 동일하며 정규적으로 분포되어 있음을 의미합니다. 즉, 오류displaystyle \varepsilon ε)가 독립적이고
랜덤화 기반 분석
무작위 대조군 실험에서 처리는 실험 프로토콜을 따라 무작위로 실험 단위에 할당됩니다.이 랜덤화는 객관적이며 실험을 수행하기 전에 선언됩니다.목적 랜덤 할당은 C. S. Peirce 및 Ronald Fisher의 아이디어를 따라 귀무 가설의 유의성을 검정하는 데 사용됩니다.이 디자인 기반 분석은 Francis J에 의해 논의되고 개발되었습니다. Rothamsted Experimental Station의 Anscombe와 Iowa State University의 Oscar Kempthorne의 작품.[19]켐프손과 그의 학생들은 단위 처리의 추가성을 가정하는데, 이것은 켐프손과 데이비드 R. 콕스의 책에서 논의됩니다.[20][21]
단위처리첨가도
가장 간단한 형태로, 단위 처리 가산성의[nb 1] 가정은 관측된 반응 ,j from experimental unit when receiving treatment can be written as the sum of the unit's response and the treatment-effect , that is [22][23][24]
Cox와 Kempthorne에 따르면 단위 처리 가산성의 가정은 일반적으로 직접적으로 위변조될 수 없습니다.그러나 치료 단위의 추가성의 많은 결과는 위조될 수 있습니다.랜덤화 실험의 경우 단위 처리 추가성의 가정은 모든 처리에 대해 분산이 일정하다는 것을 의미합니다.따라서 대비를 통해 단위 처리 가산성에 필요한 조건은 분산이 일정하다는 것입니다.
단위 처리 가산성 및 랜덤화의 사용은 유한 모집단 조사 표본 추출에서 표준으로 사용되는 설계 기반 추론과 유사합니다.
유도선형모형
Kempthorne은 앞에서 논의한 교과서 모델과 매우 유사한 도출된 선형 모델을 만들기 위해 무작위 분포와 단위 처리 가산성 가정을 사용합니다.[25]이 도출된 선형 모형의 검정 통계량은 근사 정리 및 시뮬레이션 연구에 따라 적절한 정규 선형 모형의 검정 통계량으로 근사화됩니다.[26]그러나 차이점이 있습니다.예를 들어, 랜덤화 기반 분석에서는 관측치 간에 작지만(엄격하게) 음의 상관 관계가 발생합니다.[27][28]랜덤화 기반 분석에서는 정규 분포에 대한 가정이 없으며 독립성에 대한 가정도 분명히 없습니다.반대로 관측치는 종속적입니다!
무작위화 기반 분석은 지루한 대수와 방대한 시간을 수반한다는 단점이 있습니다.무작위화 기반 분석은 복잡하고 정규 선형 모델을 이용한 접근법으로 근사화되기 때문에 대부분의 교사들은 정규 선형 모델 접근법을 강조합니다.모형 기반의 균형 무작위 실험 분석에 반대하는 통계학자는 거의 없습니다.
관측자료 통계모형
그러나 모형 기반 분석은 랜덤화되지 않은 실험이나 관측 연구의 데이터에 적용할 때 랜덤화의 보증이 부족합니다.[29]관측 데이터의 경우 Ronald Fisher와 그의 추종자들이 강조한 대로 신뢰 구간의 유도는 주관적인 모형을 사용해야 합니다.실제로 관측 연구의 치료 효과 추정치는 일반적으로 일관성이 없는 경우가 많습니다.실제로 "통계 모델"과 관측 데이터는 대중이 매우 신중하게 다루어야 할 가설을 제시하는 데 유용합니다.[30]
가정요약
정규 모형 기반 분산 분석에서는 잔차의 독립성, 정규성 및 분산의 동질성을 가정합니다.랜덤화 기반 분석에서는 잔차 분산의 동질성(단위 처리 가산성의 결과)만 가정하고 실험의 랜덤화 절차를 사용합니다.이 두 분석 모두 정규 모형 분석에 대한 가정과 무작위화 기반 분석에 대한 무작위화 및 추가성의 결과로 동질성이 필요합니다.
그러나 평균이 아닌 분산을 변경하는 공정(분산 효과라고 함)에 대한 연구가 분산 분석을 사용하여 성공적으로 수행되었습니다.[31]분산 분석의 전체 일반성에는 필요한 가정이 없지만 분산 분석 가설 검정에 사용되는 F-검정에는 지속적으로 관심을 가지는 가정과 실제적인 한계가 있습니다.
분산 분석의 가정을 만족시키지 못하는 문제는 종종 가정을 만족시키기 위해 변형될 수 있습니다.단위 처리 가산성의 특성은 "규모의 변화" 하에서 불변하지 않으므로 통계학자들은 단위 처리 가산성을 달성하기 위해 변환을 사용하는 경우가 많습니다.반응 변수가 확률 분포의 모수 계열을 따를 것으로 예상되는 경우, 통계학자는 분산을 안정화하기 위해 반응을 변환하도록 (실험 또는 관측 연구 프로토콜에) 지정할 수 있습니다.[32]또한 통계학자는 로그 변환이 곱셈 모형을 따르는 것으로 추정되는 반응에 적용되도록 지정할 수도 있습니다.[23][33]코시의 함수 방정식 정리에 따르면 로그는 실제 곱셈을 덧셈으로 변환하는 유일한 연속 변환입니다.[citation needed]
특성.
분산 분석은 결과의 차이만 관심을 가지는 비교 실험 분석에 사용됩니다.실험의 통계적 유의성은 두 분산의 비율로 결정됩니다.이 비율은 실험 관측치의 몇 가지 변경 가능성과는 무관합니다.모든 관측치에 상수를 추가해도 유의성이 변경되지 않습니다.모든 관측치에 상수를 곱해도 유의성이 변경되지 않습니다.따라서 분산 분석 통계적 유의성 결과는 관측치를 표현하는 데 사용되는 단위뿐만 아니라 상수 편의 및 스케일링 오류와는 무관합니다.기계적 계산 시대에는 데이터 입력을 단순화하기 위해 모든 관측치에서 상수를 빼는 것이 일반적이었습니다.[34][35]이것은 데이터 코딩의 예입니다.
알고리즘.
분산 분석의 계산은 여러 가지 평균과 분산을 계산하여 두 분산을 나누고 비율을 핸드북 값과 비교하여 통계적 유의성을 결정하는 것으로 특징지을 수 있습니다.처리 효과를 계산하는 것은 사소한 일입니다."모든 치료의 효과는 치료를 받는 관측치의 평균과 일반 평균의 차이를 취함으로써 추정됩니다."[36]

제곱합 분할

분산 분석에서는 기존의 표준화된 용어를 사용합니다.표본 분산의 정의 방정식은 s = n- ∑ i (yi - y ¯ ) 2 {\textstyle s^{2}={\frac {1}{n-1}}\sum _{i}(y_{i}-{\bar {y}})^{2}이고, 여기서 약수는 자유도(DF), 합은 제곱합(SS),그 결과를 평균 제곱(MS)이라고 하며 제곱 항은 표본 평균에서 벗어난 값입니다.분산 분석에서는 그랜드 평균에서 모든 관측치 편차를 기반으로 하는 총 분산, 적절한 처리 평균에서 모든 관측치 편차를 기반으로 하는 오차 분산, 그리고 처리 분산의 세 가지 표본 분산을 추정합니다.처리 분산은 대평균에서 처리 평균의 편차를 기반으로 하며, 결과에 각 처리의 관측치 수를 곱하여 관측치의 분산과 평균의 분산 사이의 차이를 설명합니다.
기본 기법은 전체 제곱합 SS를 모형에 사용된 효과와 관련된 성분으로 분할하는 것입니다.예를 들어, 여러 수준에서 한 가지 처리 유형을 사용하는 단순 분산 분석 모형입니다.
자유도 DF의 수는 비슷한 방식으로 분할할 수 있습니다. 이러한 성분 중 하나(오차의 경우)는 관련 제곱의 합을 설명하는 카이 제곱 분포를 지정하는 반면, 처리 효과가 없는 경우 "처리"의 경우에도 마찬가지입니다.
F-검정

F-검정은 총 편차의 요인을 비교하는 데 사용됩니다.예를 들어 일원 분산 분석 또는 단일 요인 분산 분석에서는 F 검정 통계량을 비교하여 통계적 유의성을 검정합니다.
여기서 MS는 mean square이고I {\은(는) 처리 총 건 수 입니다.
자유도가I - 1 {\displaystyle 이고 분모 자유도가 - 인 F 분포에 적용됩니다.검정 통계량은 각각 축척된 카이 제곱 분포를 따르는 두 개의 축척된 제곱합의 비율이므로 F-분포를 사용하는 것은 자연스러운 후보입니다.
F의 기대값은 1 + nσ 처리2 / σ 오류 2 1 + { _ _Error2}}({\displaystyle n}은 처리 샘플 크기)로 처리 효과가 없습니다.F 값이 1보다 커지면 증거가 귀무 가설과 점점 일치하지 않습니다.F를 증가시키는 두 가지 명백한 실험 방법은 엄격한 실험 제어를 통해 표본 크기를 증가시키고 오차 분산을 감소시키는 것입니다.
분산 분석 가설 검정의 결론에는 두 가지 방법이 있으며, 두 방법 모두 동일한 결과를 가져옵니다.
- 교과서적인 방법은 표로부터 결정된 F의 임계 값과 관찰된 F의 값을 비교하는 것입니다.F의 임계 값은 분자와 분모의 자유도와 유의 수준(α)의 함수입니다.F가 F를 ≥하면 귀무 가설이 기각됩니다.
- 컴퓨터 방법은 F 값이 관측값 이상일 확률(p-value)을 계산합니다.이 확률이 유의 수준(α)보다 작거나 같으면 귀무 가설이 기각됩니다.
분산 분석 F-검정은 고정된 비율의 거짓 양의 오차에 대한 거짓 음의 오차를 최소화한다는 의미에서 거의 최적인 것으로 알려져 있습니다(즉, 고정된 유의 수준에 대한 검정력 최대화).예를 들어, 다양한 치료법이 정확히 동일한 영향을 미친다는 가설을 검정하기 위해 F-검정의 p-값은 순열 검정의 p-값과 거의 유사합니다.설계가 균형을 이룰 때 근사치가 특히 가깝습니다.[26][37]이러한 순열 검정은 Rosenbaum에 의해 관찰된 것처럼 모든 대안 가설에 대해 최대 검정력을 갖는 검정의 특성을 나타냅니다.[nb 2]분산 분석 F-검정(모든 처리가 정확하게 동일한 효과를 갖는다는 귀무 가설의)은 여러 대안적 분포에 대한 강건성 때문에 실용적인 검정으로 권장됩니다.[38][nb 3]
확장 알고리즘
분산 분석은 분리 가능한 부분으로 구성되어 있으며 분산 분석과 가설 검정을 개별적으로 사용할 수 있습니다.분산 분석은 다른 통계적 도구를 지원하는 데 사용됩니다.회귀 분석은 먼저 데이터에 더 복잡한 모형을 적합시키는 데 사용된 다음 분산 분석을 사용하여 데이터를 적절하게 설명하는 단순(r) 모형을 선택하는 목적과 모형을 비교합니다."이러한 모형은 분산 분석과 관련 없이 적합될 수 있지만, 분산 분석 도구를 사용하여 적합 모형을 이해하고 계수 배치에 대한 가설을 검정할 수 있습니다."[39]"[[39]W]우리는 분산 분석을 다단계 모델을 이해하고 구조화하는 방법으로 생각합니다. 회귀 분석의 대안이 아니라 복잡한 고차원 추론을 요약하는 도구로..."[39]
단일 요인의 경우
분산 분석에 적합한 가장 간단한 실험은 단일 요인을 사용한 완전임의실험입니다.단일 요인을 사용하는 더 복잡한 실험은 무작위화에 대한 제약을 포함하며 완전 무작위화된 블록 및 라틴어 정사각형(및 변형: Greeco-Latin 정사각형 등)을 포함합니다.실험이 복잡할수록 여러 요인의 많은 복잡성이 공유됩니다.완전임의실험의 분석(모형, 데이터 요약, 분산 분석 표)에 대한 비교적 완전한 논의를 사용할 수 있습니다.
기존의 일원 분산 분석에 대한 몇 가지 대안이 있습니다. 예를 들어 다음과 같습니다.Welch의 이분산성 F 검정, 평균이 잘린 Welch의 이분산성 F 검정, 평균이 잘린 분산이 있는 Welch의 이분산성 F 검정, Brown-Forsy 검정, Alexander-Govern 검정, James 2차 검정 및 Kruskal-Wallis 검정, 일원 검정 R
각 데이터 점을 통계적 모델이라고 하는 다음과 같은 형태로 나타내는 것이 유용합니다.
- i = 1, 2, 3, ..., R
- j = 1, 2, 3, ..., C
- μ = 전체평균(mean)
- τ = X의 j 수준과 연관된 미분 효과(반응);이것은 전체적으로 τ의 값이 0에 더해진다고 가정합니다( ∑ j = 1 Cτ j = 0 =1}^{C}\tau _{j}=0}).
- ε = 특정 ij 데이터 값과 관련된 노이즈 또는 오류
즉, 모든 데이터 점은 세 가지 양을 합하여 나타낼 수 있다는 가산 모델을 구상합니다. 참 평균, 조사 중인 모든 요인 수준에서 평균, 그리고 특정 열(요인 수준)과 연관된 증분 성분,또한 특정 데이터 값에 영향을 미치는 다른 모든 것과 관련된 최종 구성 요소를 포함합니다.
다중 요인의 경우
분산 분석은 여러 요인의 효과를 연구하는 데 일반적으로 사용됩니다.실험에 각 요인 수준의 모든 조합에 관측치가 포함되어 있으면 요인이라고 합니다.요인 실험은 일련의 단일 요인 실험보다 더 효율적이며 요인의 수가 증가함에 따라 효율성이 증가합니다.[40]따라서 요인 설계가 많이 사용됩니다.
분산 분석을 사용하여 여러 요인의 효과를 연구하는 데는 복잡한 문제가 있습니다.요인 x, y 및 z가 있는 3-방향 분산 분석에서 분산 분석 모형에는 주효과도(x, y, z)에 대한 항과 교호작용에 대한 항(xy, xz, yz, xyz)이 포함됩니다.모든 항에는 가설 검정이 필요합니다.교호작용 항이 확산되면 일부 가설 검정에서 우연히 위양성이 발생할 위험이 증가합니다.다행히도, 경험에 의하면 높은 차수의 상호작용은 드물다고 합니다.[41][verification needed]교호작용 탐지 능력은 다중 요인 분산 분석의 주요 장점입니다.한 번에 하나의 요인을 검정하면 교호작용이 숨겨지지만 일관되지 않은 실험 결과가 나타납니다.[40]
상호작용이 있을 때는 주의를 요합니다.교호작용 항을 먼저 검정하고 교호작용이 발견된 경우 분석을 분산 분석 이상으로 확장합니다.교호작용이 발생한 후 분산 분석 절차를 계속 진행하는 것에 대한 권장 사항은 다양합니다.교호작용은 실험 데이터의 해석을 복잡하게 합니다.유의성 계산이나 추정된 처리 효과는 액면 그대로 사용할 수 없습니다."상당한 상호작용은 종종 주효과의 중요성을 가립니다."[42]이해력을 높이기 위해서는 그래픽 방법이 권장됩니다.회귀 분석은 종종 유용합니다.콕스(Cox, 1958)는 상호작용에 대한 장황한 논의를 제공합니다.[43]어떤 상호작용들은 (변환에 의해) 제거될 수 있지만, 다른 상호작용들은 제거되지 않습니다.
다중 요인 분산 분석에서는 비용을 줄이기 위해 다양한 기법이 사용됩니다.요인 설계에서 사용되는 한 가지 기법은 복제를 최소화하고(분석적 속임수를 지원하는 복제는 없을 가능성이 있음) 효과가 통계적으로(또는 실제적으로) 유의하지 않은 것으로 판명된 경우 그룹을 결합하는 것입니다.유의하지 않은 요인이 많은 실험은 많은 복제에서 지원하는 요인이 몇 개 있는 실험으로 바뀔 수 있습니다.[44]
연관분석
실험 설계를 지원하기 위해 몇 가지 분석이 필요한 반면, 요인의 변화가 공식적으로 반응에 통계적으로 유의한 변화를 가져온다는 것이 밝혀진 후에 다른 분석이 수행됩니다.실험은 반복적이기 때문에 한 실험의 결과는 다음 실험의 계획을 변경합니다.
준비분석
실험단위수
실험을 설계할 때 실험의 목표를 만족시키기 위해 실험 단위의 수를 계획합니다.실험은 종종 순차적입니다.
초기 실험은 치료 효과와 실험 오차에 대한 평균 편향되지 않은 추정치를 제공하도록 설계되는 경우가 많습니다.이후의 실험은 치료 효과가 중요한 크기를 갖는다는 가설을 검정하기 위해 설계되는 경우가 많습니다. 이 경우에는 다른 목표 중에서도 실험이 예산 범위 내에 있고 적절한 검정력을 가질 수 있도록 실험 단위의 수가 선택됩니다.
심리학에서는 일반적으로 표본 크기 분석 보고가 필요합니다."샘플 사이즈와 샘플 사이즈 결정에 이르게 된 과정에 대한 정보를 제공합니다."[45]실험이 수행되기 전에 실험 프로토콜에 작성된 분석은 보조금 신청서와 행정 검토 위원회에서 검토됩니다.
검정력 분석 외에 실험 단위의 수를 선택하는 공식적인 방법이 더 적습니다.여기에는 잘못된 음의 오류가 발생할 가능성을 제한하는 데 기반한 그래픽 방법, 예상 변동 증가(잔차 위)에 기반한 그래픽 방법 및 원하는 신뢰 구간을 달성하는 데 기반한 방법이 포함됩니다.[46]
전력분석
검정력 분석은 특정 분산 분석 설계, 모집단의 효과 크기, 표본 크기 및 유의 수준을 가정할 경우 귀무 가설이 성공적으로 기각될 확률을 평가하기 위해 분산 분석의 맥락에서 자주 사용됩니다.검정력 분석은 대립 가설이 참일 때 귀무 가설을 기각할 수 있는 합리적인 가능성을 갖기 위해 필요한 표본 크기를 결정함으로써 연구 설계에 도움이 될 수 있습니다.[47][48][49][50]
효과크기
분산 분석에서는 예측 변수와 종속 변수 간의 연관성의 강도 또는 완전 모형의 전체 표준화된 차이를 요약하기 위해 여러 표준화된 효과 측도가 제안되었습니다.표준화된 효과 크기 추정은 여러 연구 및 분야에 걸친 결과를 쉽게 비교할 수 있습니다.그러나 많은 전문 문헌에서 표준화된 효과 크기가 일반적으로 사용되지만 보고 목적으로 즉시 "의미 있는" 단위를 가지는 비표준화된 효과 크기 측정이 바람직할 수 있습니다.[51]
모델확인
분산 분석의 가정이 위배되는지 여부를 확인하기 위해 검정을 수행하는 경우도 있습니다.잔차를 검사하거나 분석하여 등분산성 및 총 정규성을 확인합니다.[52]잔차는 시간 및 모형화된 데이터 값을 포함하여 임의의 함수로 표시될 때 (평균 정규 분포가 0) 노이즈의 모양을 가져야 합니다.추세는 요인 간 또는 관측치 간의 교호작용을 암시합니다.
추적검사
분산 분석에서 통계적으로 유의한 효과가 나타나는 경우에는 종종 추가 검정이 뒤따릅니다.이렇게 하면 어떤 그룹이 다른 그룹과 다른지 또는 다른 여러 가지 초점 가설을 검정할 수 있습니다.사후 테스트는 종종 "계획된"(선험적) 또는 "사후 테스트"(post hoc)로 구분되는데, 계획된 테스트는 데이터를 보기 전에 결정되며, 사후 테스트는 데이터를 보고 난 후에만 구상됩니다("post hoc"이라는 용어는 일관되지 않게 사용됨).
후속 검정은 개별 그룹 평균의 "단순" 쌍별 비교일 수도 있고 "복합" 비교일 수도 있습니다(예: 그룹 A, B 및 C의 평균 풀링을 그룹 D의 평균과 비교).독립 변수에 순서 수준이 포함된 경우 비교를 통해 선형 및 이차 관계와 같은 추세 검정도 확인할 수 있습니다.후속 테스트에는 다중 비교 문제를 조정하는 방법이 포함되는 경우가 많습니다.
어떤 특정 집단, 변수 또는 요인이 통계적으로 다른 평균을 갖는지 확인하는 후속 검정에는 Tukey의 범위 검정과 Duncan의 새로운 다중 범위 검정이 포함됩니다.또한 이러한 테스트는 통계적이지 않은 사용자에게 언급된 테스트의 출력을 보다 투명하게 제공하기 위해 CLD(Compact Letter Display) 방법론을 따르는 경우가 많습니다.
스터디 디자인
분산 분석에는 여러 가지 유형이 있습니다.많은 통계학자들은 실험의 설계,[53] 특히 피실험자에 대한 치료법의 임의 할당을 지정하는 프로토콜에 기초하여 분산 분석을 수행합니다. 할당 메커니즘에 대한 프로토콜의 설명에는 치료법의 구조와 모든 차단에 대한 사양이 포함되어야 합니다.분산 분석을 관측 데이터에 적용하는 것도 일반적입니다.[54]
일부 인기 있는 설계에서는 다음과 같은 분산 분석 유형을 사용합니다.
- 일원 분산 분석은 두 개 이상의 독립적인 그룹(평균) 간의 차이(예: 작물의 요소 적용 수준이 다르거나 여러 세균 종에 대한 항생제 작용 수준이 다르거나 [55]환자 그룹에 대한 의약품의 효과 수준이 다르기 때문에)를 검정하는 데 사용됩니다.그러나 이러한 그룹이 독립적이지 않고 그룹(예: 경증, 중등도 및 중증 질환)에서 순서가 있거나 동일한 그룹의 환자에게 투여된 약물(예: 5mg/mL, 10mg/mL, 20mg/mL)의 용량에서 순서가 있는 경우 선형 추세 추정을 사용해야 합니다.그러나 일반적으로 일원 분산 분석은 t-검정을 통해 두 그룹 사례를 다룰 수 있기 때문에 최소 세 그룹 간의 차이를 검정하는 데 사용됩니다.[56]비교할 평균이 두 개뿐인 경우 t-검정과 분산 분석 F-검정은 동등하며 분산 분석과 t 사이의 관계는 F = t로 표시됩니다.
- 요인 분산 분석은 요인이 둘 이상 있을 때 사용됩니다.
- 반복측정 분산 분석은 각 요인에 대해 동일한 피실험자가 사용될 때 사용됩니다(예: 종단 연구에서).
- 다변량 분산 분석(MANOVA)은 반응 변수가 둘 이상 있을 때 사용됩니다.
주의사항
균형 실험(각 처리에 대해 표본 크기가 동일한 실험)은 비교적 쉽게 해석할 수 있으며, 불균형 실험은 더 많은 복잡성을 제공합니다.단일 요인(일원) 분산 분석의 경우 불균형 데이터에 대한 조정은 쉽지만 불균형 분석에는 강건성과 검정력이 모두 부족합니다.[57]보다 복잡한 설계의 경우 균형이 결여되면 더욱 복잡한 문제가 발생합니다."균형 데이터에 존재하는 주효과 상호작용의 직교성 특성이 불균형 사례로 전이되지는 않습니다.이는 분산 기법에 대한 일반적인 분석이 적용되지 않음을 의미합니다.따라서 불균형 요인의 분석은 균형 설계의 분석보다 훨씬 더 어렵습니다."[58]일반적인 경우에는 "분산 분석은 불균형 데이터에도 적용할 수 있지만 제곱합, 평균 제곱합 및 F-비율은 변동 요인이 고려되는 순서에 따라 달라집니다."[39]
분산 분석은 (일부) 통계적 유의성이 있는 검정입니다.미국 심리학회(및 다른 많은 단체)는 단순히 통계적 유의성을 보고하는 것은 불충분하고 신뢰 한계를 보고하는 것이 선호된다는 견해를 가지고 있습니다.[51]
일반화
분산 분석은 선형 회귀[59][60] 분석의 특별한 경우로 간주되며, 이는 일반 선형 모형의 특별한 경우입니다.[61]모든 관측치는 최소화할 모형(적합치)과 잔차(오차)의 합으로 간주됩니다.
Kruskal-Wallis 검정과 Friedman 검정은 정규성 가정에 의존하지 않는 비모수 검정입니다.[62][63]
선형 회귀로의 연결
아래에서는 다변량 분산 분석과 선형 회귀 분석 간의 연관성을 명확히 설명합니다.
- 관측치가 응답 와 인자 와 관련되도록 데이터의 선형 순서를 바꿉니다. 여기서 는{1 B \{1,2ldots,는 다른 인자를 나타내며 B 은(는) 총 인자 수를 나타냅니다.In one-way ANOVA and in two-way ANOVA . Furthermore, we assume the -th factor has levels, namely . Now,우리는 을 ∑ =1 BI b {\textstyle \sum _{b=1}^{B}로 원 핫 인코딩 할 수 있습니다.차원 벡터
원 핫 인코딩 함수 …, ↦{, } {\, 2I_{\{0,1\}^{은(는) i {\displaystyle - (, b {\ {의 항목이 다음과 같이 정의됩니다.
이 표기법을 사용하면 선형 회귀와 정확한 연관성을 가질 수 있습니다.단순히 yk 를 벡터 에 대해 회귀합니다 그러나 식별 가능성에 대한 우려가 있습니다.이러한 문제를 극복하기 위해 우리는 각 교호작용 집합 내의 매개변수의 합이 0과 같다고 가정합니다.여기서 F-통계 또는 기타 방법을 사용하여 개별 요인의 관련성을 확인할 수 있습니다.
예
첫 번째 요인이 2개의 수준을 가지고 두 번째 요인이 3개의 수준을 가지고 있다고 가정하는 이원 교호작용 예제를 고려할 수 있습니다.
일경우 i = =1}을를) 정의하고, 일 경우 b = 1 {\displaystyle b_{i}=1}, 2 = i {\displaystyle Z_{k,2}=i}을(를) 정의합니다.는 첫 번째 인자의 원 핫 인코딩이고 b 는 두 번째 인자의 원 핫 인코딩입니다.
그거로.
참고 항목
각주
- ^ 대부분의 텍스트에서 단위 치료 추가도는 단순히 추가성이라고 합니다.힝켈만과 켐프손은 형용사를 추가하고 엄격한 의미와 넓은 의미의 추가성을 구분합니다.이를 통해 161페이지의 여러 오류 소스(치료, 상태, 선택, 측정 및 샘플링)를 자세히 고려할 수 있습니다.
- ^ Rosenbaum(2002, 40페이지)은 섹션 5.7(순열 시험)을 인용합니다.Lehmann의 Testing Statistical Hypes(1959)의 Theorem 2.3(실제로 Theorem 3, 184페이지)
- ^ 분산 비교에 대한 F-검정의 평판은 엇갈립니다.서로 다른 두 표본의 분산이 동일한지 여부를 확인하는 것은 가설 검정으로 권장되지 않습니다.동일한 표본의 분산 추정치 두 개를 비교하는 분산 분석의 경우 권장됩니다.F-검정은 일반적으로 정규성 이탈에 대해 강건하지 않지만 분산 분석의 특수한 경우에는 강건한 것으로 확인되었습니다.Moore & McCave(2003)에서 인용한 내용:"분산 분석은 F 통계량을 사용하지만 두 모집단 표준 편차를 비교하는 F 통계량과는 다릅니다." (554페이지) "F 검정과 분산에 대한 추론을 위한 다른 절차는 강건성이 부족하여 실제로는 거의 사용할 수 없습니다." (556페이지) "[ANOVA F-test]는 중간 정도의 비정규성과 불균등한 분산에 상대적으로 둔감하며, 특히 표본 크기가 유사한 경우에 더욱 그렇습니다."(763페이지) ANOVA는 균질성을 가정하지만 강건합니다.균질성에 대한 통계 검정(F-검정)은 강건하지 않습니다.무어와 맥케이브는 경험칙을 추천합니다.
메모들
- ^ 스티글러 (1986)
- ^ 스티글러 (1986, p134)
- ^ 스티글러 (1986, p153)
- ^ 스티글러 (1986, pp 154–155)
- ^ 스티글러 (1986, pp 240–242)
- ^ 스티글러(Stigler, 1986, Chapter 7 – Psychophysics as a Counterpoint)
- ^ 스티글러 (1986, p 253)
- ^ 스티글러 (1986, pp 314–315)
- ^ 멘델계 유산 추정에 관한 친족 간의 상관관계로널드 A.피셔.에든버러 왕립학회의 철학적 거래. 1918.(제52권 399-433쪽)
- ^ Fisher, Ronald A. (1921). ") Studies in Crop Variation. I. An Examination of the Yield of Dressed Grain from Broadbalk". Journal of Agricultural Science. 11 (2): 107–135. doi:10.1017/S0021859600003750. hdl:2440/15170. S2CID 86029217.
- ^ Fisher, Ronald A. (1923). ") Studies in Crop Variation. II. The Manurial Response of Different Potato Varieties". Journal of Agricultural Science. 13 (3): 311–320. doi:10.1017/S0021859600003592. hdl:2440/15179. S2CID 85985907.
- ^ Scheffé(1959, p 291), "랜덤화 모델은 완전랜덤화 설계의 경우 Neyman(1923)에 의해, 랜덤화 블록의 경우 Neyman(1935)에 의해, 특정 귀무가설 하에 라틴어 정사각형의 경우 Welch(1937)와 Pitman(1937)에 의해, 그리고 많은 다른 설계의 경우 Kempthorne(1952, 1955)과 Wilk(1955)에 의해 처음 공식화되었습니다.")
- ^ Montgomery (2001, 12장: 무작위인자로 실험)
- ^ Gelman (2005, pp. 20–21)
- ^ Snedecor, George W.; Cochran, William G. (1967). Statistical Methods (6th ed.). p. 321.
- ^ 코크란 & 콕스 (1992, p48)
- ^ 하웰 (2002, p323)
- ^ Anderson, David R.; Sweeney, Dennis J.; Williams, Thomas A. (1996). Statistics for business and economics (6th ed.). Minneapolis/St. Paul: West Pub. Co. pp. 452–453. ISBN 978-0-314-06378-6.
- ^ 안스콤브 (1948)
- ^ Hinkelmann, Klaus; Kempthorne, Oscar (2005). Design and Analysis of Experiments, Volume 2: Advanced Experimental Design. John Wiley. p. 213. ISBN 978-0-471-70993-0.
- ^ Cox, D. R. (1992). Planning of Experiments. Wiley. ISBN 978-0-471-57429-3.
- ^ 켐프손 (1979, p30)
- ^ a b Cox (1958, 2장: 몇 가지 주요 가정)
- ^ 힝켈만과 켐프손 (2008, 1권, 전체에 걸쳐)2.3.3절에 소개됨: 실험 설계의 원칙;선형 모형; 모형의 개요)
- ^ Hinkelmann and Kempthorne (2008, 1권, 6.3절: 완전임의설계; 도출된 선형모델)
- ^ a b Hinkelmann and Kempthorne (2008, 1권, 6.6절: 완전 무작위 설계; 무작위화 검정 근사화)
- ^ Bailey (2008, 2.14장 "A More General Model" in Bailey, pp. 38–40)
- ^ 힌켈만과 켐프손 (2008, 1권, 7장: 치료법의 비교)
- ^ Kempthorne(1979, pp 125–126), "실험자는 자신의 결과에 변화를 일으킬 수 있다고 느끼는 다양한 원인 중 어떤 것이 실험적으로 통제되어야 하는지 결정해야 합니다.그것들은 그가 실험적으로 통제하지 않는 원인들입니다, 왜냐하면 그는 그것들을 인식하지 못하기 때문에, 그는 무작위화라는 장치로 통제해야 합니다." "[O]실험의 처리들이 완전 무작위화 절차를 사용하여 실험자에 의해 적용될 때만이 귀납적 추론음의 사슬입니다.실험자가 관찰한 효과를 치료와 치료에만 귀속시킬 수 있는 것은 이러한 상황에서만 가능합니다.이런 상황에서 그의 결론은 통계적인 의미에서 신뢰할 수 있습니다.")
- ^ 프리드먼[full citation needed]
- ^ 몽고메리 (2001, 3.8절: 분산효과 발견)
- ^ Hinkelmann and Kempthorne (2008, 1권, 6.10절: 완전임의설계; 변환)
- ^ 베일리 (2008)
- ^ Montgomery (2001, 섹션 3-3): 단일 요인에 대한 실험:분산 분석; 고정 효과 모형 분석)
- ^ Cochran & Cox (1992, p2 예제)
- ^ 코크란 & 콕스 (1992, p49)
- ^ Hinkelmann and Kempthorne (2008, 1권, 6.7절: 완전임의화된 설계; 동일하지 않은 반복 횟수를 갖는 CRD)
- ^ 무어와 맥케이브 (2003, 763페이지)
- ^ a b c 겔만 (2008)
- ^ a b 몽고메리 (2001, 5-2절: 요인 설계 소개;요인의 장점)
- ^ 벨 (2008, 섹션 8.4: 고차 상호작용은 거의 일어나지 않음)
- ^ Montgomery (2001, 섹션 5-1: 요인 설계 소개; 기본 정의 및 원칙)
- ^ Cox (1958, 6장: 요인실험에 대한 기본 개념)
- ^ 몽고메리 (2001, 섹션 5-3.7: 요인 설계 소개;2-요인 요인 설계; 셀당 하나의 관측치)
- ^ 윌킨슨 (1999, p596)
- ^ Montgomery (2001, 섹션 3-7: 샘플 크기 확인)
- ^ 하웰 (2002, Chapter 8: Power)
- ^ 하웰(2002, 11.12절: 검정력(분산 분석))
- ^ 하웰(2002, 13.7절: 요인 실험을 위한 검정력 분석)
- ^ 무어와 맥케이브 (2003, pp 778–780)
- ^ a b 윌킨슨 (1999, p599)
- ^ Montgomery (2001, 섹션 3-4: 모델 적정성 점검)
- ^ Cochran & Cox(1957, p 9), "실험을 수행하는 방식은 추론을 할 수 있는지 여부뿐만 아니라 추론을 하는 데 필요한 계산도 결정한다는 것이 일반적인 규칙입니다.")
- ^ "ANOVA Design". bluebox.creighton.edu. Retrieved 23 January 2023.
- ^ "One-way/single factor ANOVA". Archived from the original on 7 November 2014.
- ^ "The Probable Error of a Mean" (PDF). Biometrika. 6: 1–25. 1908. doi:10.1093/biomet/6.1.1. hdl:10338.dmlcz/143545.
- ^ Montgomery (2001, 섹션 3-3.4: 불균형 데이터)
- ^ Montgomery (2001, 섹션 14-2: 요인 설계의 불균형 데이터)
- ^ Gelman (2005, p.1) (후단 본문에 자격이 있음)
- ^ Montgomery (2001, 3.9절: 분산분석에 대한 회귀적 접근)
- ^ 하웰 (2002, p 604)
- ^ Howell (2002, 18장: 데이터에 대한 리샘플링 및 비모수적 접근법)
- ^ Montgomery (2001, 섹션 3-10: 분산 분석에서 비모수적 방법)
참고문헌
- Anscombe, F. J. (1948). "The Validity of Comparative Experiments". Journal of the Royal Statistical Society. Series A (General). 111 (3): 181–211. doi:10.2307/2984159. JSTOR 2984159. MR 0030181.
- Bailey, R. A. (2008). Design of Comparative Experiments. Cambridge University Press. ISBN 978-0-521-68357-9. 출판 전 장은 온라인으로 볼 수 있습니다.
- Belle, Gerald van (2008). Statistical rules of thumb (2nd ed.). Hoboken, N.J: Wiley. ISBN 978-0-470-14448-0.
- Cochran, William G.; Cox, Gertrude M. (1992). Experimental designs (2nd ed.). New York: Wiley. ISBN 978-0-471-54567-5.
- Cohen, Jacob (1988행동과학에 대한 통계적 검정력 분석(2차)루틀지 ISBN 978-0-8058-0283-2
- Cohen, Jacob (1992). "Statistics a power primer". Psychological Bulletin. 112 (1): 155–159. doi:10.1037/0033-2909.112.1.155. PMID 19565683. S2CID 14411587.
- 콕스, 데이비드 R. (1958)실험 계획.ISBN 978-0-471-57429-3으로 재인쇄됨
- Cox, David R. (2006). Principles of statistical inference. Cambridge New York: Cambridge University Press. ISBN 978-0-521-68567-2.
- 프리드먼, 데이비드 A. (2005)통계적 모델: 이론과 실천, 케임브리지 대학 출판부.ISBN 978-0-521-67105-7
- Gelman, Andrew (2005). "Analysis of variance? Why it is more important than ever". The Annals of Statistics. 33: 1–53. arXiv:math/0504499. doi:10.1214/009053604000001048. S2CID 13529149.
- Gelman, Andrew (2008). "Variance, analysis of". The new Palgrave dictionary of economics (2nd ed.). Basingstoke, Hampshire New York: Palgrave Macmillan. ISBN 978-0-333-78676-5.
- Hinkelmann, Klaus & Kempthorne, Oscar (2008). Design and Analysis of Experiments. Vol. I and II (Second ed.). Wiley. ISBN 978-0-470-38551-7.
- Howell, David C. (2002). Statistical methods for psychology (5th ed.). Pacific Grove, CA: Duxbury/Thomson Learning. ISBN 978-0-534-37770-0.
- Kempthorne, Oscar (1979). The Design and Analysis of Experiments (Corrected reprint of (1952) Wiley ed.). Robert E. Krieger. ISBN 978-0-88275-105-4.
- Lehmann, E.L. (1959) 검정 통계 가설존 와일리 앤 선즈.
- Montgomery, Douglas C. (2001). Design and Analysis of Experiments (5th ed.). New York: Wiley. ISBN 978-0-471-31649-7.
- 무어, 데이비드 S. & 매케이브, 조지 P. (2003).통계 실무에 대한 소개 (4e)WH 프리먼 & Co.ISBN 0-7167-9657-0
- Rosenbaum, Paul R. (2002).관찰 연구 (제2판).뉴욕: 스프링거-베를라그.ISBN 978-0-387-98967-9
- Scheffé, Henry (1959). The Analysis of Variance. New York: Wiley.
- Stigler, Stephen M. (1986). The history of statistics : the measurement of uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
- Wilkinson, Leland (1999). "Statistical Methods in Psychology Journals; Guidelines and Explanations". American Psychologist. 5 (8): 594–604. CiteSeerX 10.1.1.120.4818. doi:10.1037/0003-066X.54.8.594. S2CID 428023.
추가열람
- Box, G. e. p. (1953). "Non-Normality and Tests on Variances". Biometrika. 40 (3/4): 318–335. doi:10.1093/biomet/40.3-4.318. JSTOR 2333350.
- Box, G. E. P. (1954). "Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems, I. Effect of Inequality of Variance in the One-Way Classification". The Annals of Mathematical Statistics. 25 (2): 290. doi:10.1214/aoms/1177728786.
- Box, G. E. P. (1954). "Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems, II. Effects of Inequality of Variance and of Correlation Between Errors in the Two-Way Classification". The Annals of Mathematical Statistics. 25 (3): 484. doi:10.1214/aoms/1177728717.
- Caliński, Tadeusz; Kageyama, Sanpei (2000). Block designs: A Randomization approach, Volume I: Analysis. Lecture Notes in Statistics. Vol. 150. New York: Springer-Verlag. ISBN 978-0-387-98578-7.
- Christensen, Ronald (2002). Plane Answers to Complex Questions: The Theory of Linear Models (Third ed.). New York: Springer. ISBN 978-0-387-95361-8.
- 콕스, 데이비드 R. & 리드, 낸시 M. (2000)실험의 설계론 (Chapman & Hall/CRC).ISBN 978-1-58488-195-7
- Fisher, Ronald (1918). "Studies in Crop Variation. I. An examination of the yield of dressed grain from Broadbalk" (PDF). Journal of Agricultural Science. 11 (2): 107–135. doi:10.1017/S0021859600003750. hdl:2440/15170. S2CID 86029217. Archived from the original (PDF) on 12 June 2001.
- 프리드먼, 데이비드 A.; 피사니, 로버트; 퍼브스, 로저 (2007) 통계, 제4판.W.W. Norton & Company ISBN 978-0-393-92972-0
- Hettmansperger, T. P.; McKean, J. W. (1998). Edward Arnold (ed.). Robust nonparametric statistical methods. Kendall's Library of Statistics. Vol. 5 (First ed.). New York: John Wiley & Sons, Inc. pp. xiv+467 pp. ISBN 978-0-340-54937-7. MR 1604954.
- Lentner, Marvin; Thomas Bishop (1993). Experimental design and analysis (Second ed.). Blacksburg, VA: Valley Book Company. ISBN 978-0-9616255-2-8.
- 타바치닉, 바바라 G. & 피델, 린다 S. (2007)다변량 통계량(5판)을 사용합니다.보스턴: 피어슨 인터내셔널 에디션.ISBN 978-0-205-45938-4
- Wichura, Michael J. (2006). The coordinate-free approach to linear models. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge: Cambridge University Press. pp. xiv+199. ISBN 978-0-521-86842-6. MR 2283455.
- Phadke, Madhav S. (1989). Quality Engineering using Robust Design. New Jersey: Prentice Hall PTR. ISBN 978-0-13-745167-8.
외부 링크
- SOCR: 분산 분석 활동
- 랜덤화된 블럭, 분할 그림, 반복 측정 및 라틴 제곱 등 최대 3개의 처리 요인을 포함하는 모든 분산 분석 및 ANCOVA 모형의 예제 및 R(Southampton 대학)에서의 분석
- NIST/SEMATECH 전자수첩, 섹션 7.4.3: "평균이 동등합니까?"
- 분산 분석:서론











 (는) 처리
(는) 처리 
 분모 자유도가
분모 자유도가


 인자
인자 
 다른 인자를 나타내며 B
다른 인자를 나타내며 B  (는) 총 인자 수를 나타냅니다.In one-way ANOVA
(는) 총 인자 수를 나타냅니다.In one-way ANOVA 










 첫 번째 인자의 원 핫 인코딩이고 b
첫 번째 인자의 원 핫 인코딩이고 b ![{\displaystyle X_{k}=[a_{1},a_{2},b_{1},b_{2},b_{3},a_{1}\times b_{1},a_{1}\times b_{2},a_{1}\times b_{3},a_{2}\times b_{1},a_{2}\times b_{2},a_{2}\times b_{3},1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b0fb1da30e53e31a5462b3d096076dada5f8295)

![{\displaystyle X_{k}=[0,1,1,0,0,0,0,0,1,0,0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71b98d7ab058cee5179fa785b602b7b6a44ff624)


