최소 제곱
Least squares| 시리즈의 일부 |
| 회귀 분석 |
|---|
| 모델 |
| 견적 |
| 배경 |
최소 제곱법은 잔차 제곱의 합을 최소화함으로써 과도하게 결정된 시스템(미지의 방정식보다 더 많은 방정식 집합)의 해법을 근사하는 회귀 분석의 표준 접근법이다(잔차는 모형에 의해 제공된 관측치와 적합치 사이의 차이).각 개별 방정식의 결과에서 만들어집니다.
가장 중요한 응용 분야는 데이터 피팅입니다.문제의 독립 변수(x 변수)에 상당한 불확실성이 있는 경우 단순 회귀 분석 및 최소 제곱 방법에는 문제가 있습니다. 이러한 경우 변수 오차 모형을 적합시키는 데 필요한 방법론을 최소 제곱 대신 고려할 수 있습니다.
최소 제곱 문제는 알 수 없는 모든 항목에서 잔차가 선형인지 여부에 따라 선형 또는 일반 최소 제곱과 비선형 최소 제곱의 두 가지 범주로 나뉩니다.선형 최소 제곱 문제는 통계 회귀 분석에서 발생하며, 폐쇄형 솔루션을 사용합니다.비선형 문제는 대개 반복적인 정교화를 통해 해결된다. 각 반복에서 시스템은 선형으로 근사되므로 코어 계산은 두 경우 모두 유사하다.
다항식 최소 제곱은 종속 변수의 예측에서 독립 변수의 함수로서의 분산과 적합 곡선으로부터의 편차를 나타냅니다.
관측치가 자연히 충분한 통계량과 완만한 조건(예: 정규 분포, 지수 분포, 포아송 분포 및 이항 분포)을 만족하기 때문에 동일성을 갖는 지수 군에서 나온 경우 표준화된 최소 제곱 추정치와 최대우도 추정치는 동일합니다.[1]최소 제곱법은 모멘트 추정기로도 도출할 수 있다.
다음 설명은 대부분 선형 함수의 관점에서 제시되지만, 보다 일반적인 함수군에 대해 최소 제곱을 사용하는 것이 유효하고 실용적입니다.또한 국소 2차 근사를 우도에 반복적으로 적용함으로써(피셔 정보를 통해) 일반화 선형 모델을 적합시키기 위해 최소 제곱법을 사용할 수 있다.
최소 제곱법은 Adrien-Marie Legendre(1805)[2]에 의해 공식적으로 발견되어 발표되었지만, 일반적으로 이 방법에 상당한 이론적 진보에 기여하고 이전에 그의 [5][6]연구에 사용했을 수도 있는 칼 프리드리히 가우스(1795)[3][4]의 공인을 받았다.
역사
창립
과학자들 그리고 수학자들을 디스커버리의 나이는 동안 지구의 바다의 바다를 항해하도록 도전에 대한 해결책을 제공하고자 노력해 최소 2승법 천문학 및 측지의 필드 중에서 성장했다.배들 그곳에서 선원들은 더 이상 땅 목격에 항해에 의존할 수 있는 바다를, 안에서 항해하는 것을 촉진하기 위한 천체들의 행동의 정확한 설명이 단서였다.
는 18세기의 코스:[7]중에 일어난 여러 발전의 법은 절정을 이루었다.
- 진짜 가치의 다른 관찰은 조합은 측정, 오류 결합보다는 증가 감소시키면 아마도 먼저 로저 코츠로 1722년으로 표현된입니다.
- 다른 관찰의 결합은 동일한 조건에서 찍은 단순하고 녹음해 정확하게 단일 관측을 관찰하기 위해 최선을 노력하는 것에 어긋나다이 접근법 평균의 메서드로 알려져 있었다.이 접근법 특히 토비 어스 마이어는 동안 1750년에서 달의 librations을 연구하며, 피에르 시몽 라플라스 목성과 토성의 움직임에 1788년의 차이점을 설명하는 일에 그의 작품에서 사용되었다.
- 다른 관찰의 조합은 다른 조건 하에서 찍은 사진.메서드 적어도 절대 편차의 메서드로 알려지게 되었다.그것은 특히 로저 조셉 보스코까지 지구의 모양에 자신의 일에 1757년, 피에르 시몽 라플라스에 의해 1799년에 같은 문제에 대해 실시되었다.
- 는 최소 오차와 해결책은 달성되었는지를 평가하게 될 수 있는 기준의 개발.라플라스와 평가의 평가 오류 최소화되는 메서드를 오류의 확률 밀도의 수학적인 형태를 지정하려고 했다.이러한 목적을 위해, 라플라스, 추정 오차로 절대 편차의 합을 사용했다 우리가 지금 라플라스 분포는 오차 분포 모델을 만들라고 부르는 대칭 2면 지수 분포를 사용했다.그는 평균값이 최선의 추정치 계산을 얻기를 희망했었다 자신이 만들 수 있는 이러한 것 가장 단순한 가정을 느꼈다.대신, 그의 추정치는 후방 중앙값이었다.
방법
최소 제곱법에 대한 명확하고 간결한 설명은 [8]1805년에 Legendre에 의해 발표되었습니다.이 기법은 선형 방정식을 데이터에 적합시키는 대수적 절차로 설명되며, Langendre는 지구 형상에 대해 라플라스(Laplace)와 동일한 데이터를 분석하여 새로운 방법을 시연합니다.Legendre의 출판 후 10년 이내에, 최소 제곱법은 프랑스, 이탈리아, 그리고 프러시아에서 천문학과 측지학의 표준 도구로 채택되었고, 이것은 과학 [7]기술의 매우 빠른 수용을 구성한다.
1809년에 칼 프리드리히 가우스는 천체의 궤도를 계산하는 그의 방법을 발표했다.그 작업에서 그는 1795년부터 최소 제곱법을 가지고 있다고 주장했다.이것은 자연스럽게 Legendre와의 우선순위 논쟁으로 이어졌다.하지만 가우스의 공로를 인정하기 위해, 그는 레전드르를 넘어 최소 제곱법을 확률의 원리와 정규 분포와 연결하는 데 성공했다.그는 제한된 수의 미지의 매개변수에 의존하여 관측에 대한 확률 밀도의 수학적 형태를 지정하는 라플라스 프로그램을 완성하고 추정 오류를 최소화하는 추정 방법을 정의했다.가우스는 확률 밀도와 추정 방법을 모두 변경함으로써 산술 평균이 위치 모수의 최선의 추정치임을 보여주었다.그런 다음 밀도가 어떤 형태를 가져야 하는지, 위치 모수의 추정으로 산술 평균을 얻기 위해 어떤 추정 방법을 사용해야 하는지 물어봄으로써 문제를 해결했습니다.이 시도에서 그는 정규 분포를 발명했다.
가우스의 방법의 강도에 대한 초기 증명은 새롭게 발견된 소행성 세레스의 미래 위치를 예측하는 데 사용되었을 때 나왔다.1801년 1월 1일, 이탈리아 천문학자 주세페 피아치는 케레스를 발견했고 태양의 눈부신 빛 속에서 사라지기 전까지 40일 동안 그 경로를 추적할 수 있었다.이 자료를 바탕으로 천문학자들은 케플러의 복잡한 행성 운동 비선형 방정식을 풀지 않고 태양 뒤에서 나타난 케레스의 위치를 알아내려고 했다.헝가리 천문학자 프란츠 자버 폰 자흐가 케레스를 성공적으로 재배치할 수 있었던 유일한 예측은 24세의 가우스가 최소 제곱 분석을 사용하여 수행한 예측이었다.
1810년, 가우스의 연구를 읽은 후, 라플레이스는 중심 한계 정리를 증명한 후, 최소 제곱법과 정규 분포에 대한 큰 표본 정당성을 제공하기 위해 그것을 사용했다.1822년에 Gauss는 오차의 평균이 0이고 상관 관계가 없으며 분산이 동일한 선형 모형에서 계수의 최량 선형 불편 추정기가 최소 제곱 추정기라는 점에서 회귀 분석에 대한 최소 제곱 접근법이 최적이라고 진술할 수 있었다.이 결과는 가우스-마르코프 정리라고 알려져 있다.
최소 제곱 분석의 개념은 1808년 미국인 로버트 애드레인(Robert Adrain)에 의해 독립적으로 공식화되었습니다.다음 2세기 동안 오류 이론과 통계학에서 일하는 사람들은 최소 [9]제곱을 구현하는 많은 다른 방법들을 발견했다.
문제문
목적은 모형 함수의 모수를 데이터 세트에 가장 적합하도록 조정하는 것입니다.단순 데이터 세트는 n개의 포인트(데이터 쌍i , i 1, n으로 구성됩니다 여기서 x i { x_{ 변수이고 {는 관찰에 의해 발견된 종속 변수입니다.모델 함수는 f { f {\ 입니다.여기서 m의 조정 가능한 파라미터는 β(\{\로 유지됩니다.목표는 데이터에 "최적"으로 적합한 모형의 모수 값을 찾는 것입니다.데이터 점에 대한 모형의 적합성은 종속 변수의 관측 값과 모형이 예측한 값 사이의 차이로 정의된 잔차에 의해 측정됩니다.
최소 제곱 방법은 잔차 의 합을 최소화하여 최적의 매개변수 값을 찾습니다 S {\S[10]
2차원 모형의 예로는 직선 모형이 있습니다.y자리는 0 _이고 기울기는 1(\ \1로 나타내며 모델 함수는 f β + x(\ f {\{}})로 지정됩니다. 최소 제곱은 최소 작동한다.
데이터 점은 둘 이상의 독립 변수로 구성될 수 있습니다.예를 들어, 높이 측정 세트에 평면을 적합시킬 때 평면은 두 개의 독립 변수인 x와 z의 함수입니다.대부분의 경우 각 데이터 점에 하나 이상의 독립 변수와 하나 이상의 종속 변수가 있을 수 있습니다.
오른쪽은 r { r { i } = }에 대한 랜덤 변동을 나타내는 잔차 그림입니다. 선형 모델 α + x + i) \ ( Y { i= \ + \ x _ { } +이(가) 적절합니다.는 독립적이고 [10]랜덤한 입니다.
잔차 점이 모양과 비슷하고 랜덤하게 변동하지 않는 경우에는 선형 모형이 적절하지 않습니다.예를 들어, 잔차 플롯이 오른쪽과 같이 포물선 모양일 경우 포물선 모델 x + β x i + +U i )\{i}=\ x_ x_이(가) 데이터에 적합합니다.포물선 모델의 잔차는 r - α - ^ i -^ i - ^ i2 { }-{\ {\hathat {\}-{\wide hat {\ hat }}i}}}}-{{{{{\wide hat[10]을 통해 할 수 있다.
제한 사항
이 회귀 분석 공식에서는 종속 변수의 관측 오차만 고려하지만 대체 총 최소 제곱법은 두 변수 모두에서 오류를 설명할 수 있습니다.의미가 다른2개의 콘텍스트가 있습니다.
- 예측을 위한 회귀 분석입니다.여기서 모형은 적합에 사용된 데이터가 적용되는 유사한 상황에서 적용하기 위한 예측 규칙을 제공하기 위해 적합됩니다.여기서 이러한 미래 적용에 해당하는 종속 변수는 적합에 사용된 데이터의 변수와 동일한 유형의 관측 오차에 노출될 것이다.따라서 이러한 데이터에는 최소 제곱 예측 규칙을 사용하는 것이 논리적으로 일관됩니다.
- "진정한 관계"에 적합하기 위한 회귀.최소 제곱으로 적합을 유도하는 표준 회귀 분석에서는 독립 변수의 오차가 0이거나 무시할 수 있도록 엄격하게 제어된다는 암묵적인 가정이 있습니다.독립 변수의 오차가 무시할 수 없는 경우 측정 오류 모델을 사용할 수 있습니다. 이러한 방법은 독립 [11]변수의 관측 오류 존재를 고려하는 모수 추정치, 가설 검정 및 신뢰 구간으로 이어질 수 있습니다.대안적 접근법은 총 최소 제곱으로 모형을 적합시키는 것이다. 이것은 모형 적합에 사용하기 위한 목적 함수를 공식화할 때 다양한 오차 발생원의 효과의 균형을 맞추는 실용적인 접근법을 취하는 것으로 볼 수 있다.
최소 제곱 문제 해결
제곱합계의 최소값은 구배를 0으로 설정하여 구할 수 있습니다.모델에는 m개의 파라미터가 포함되어 있으므로 m개의 그라데이션 방정식이 있습니다.
기울기 방정식은 모든 최소 제곱 문제에 적용됩니다.각각의 특정 문제에는 모형과 그 [12]부분파생물에 대한 특정 표현이 필요하다.
최소
모형이 모수의 선형 조합으로 구성되어 있는 경우 회귀 모형은 선형 모형은 다음과 같습니다.
Letting and putting the independent and dependent variables in matrices and , respectively, we can compute the least squares in the following way.D D는 데이터의 집합입니다.[12][13]
최소값을 구하려면 손실의 구배를으로 설정하고 βboldsymbol})를 합니다.
마지막으로 손실의 구배를 0으로 설정하고β(\에 대해 해결하면 다음과 같은 결과를 얻을 수 있습니다.
비선형 최소 제곱
경우에 따라 비선형 최소 제곱 문제에 대한 폐쇄형 솔루션이 있지만 일반적으로는 없습니다.폐쇄형 솔루션이 없는 경우 수치 알고리즘을 사용하여 목표를 최소화하는 매개변수(\의 값을 구한다.대부분의 알고리즘에는 파라미터의 초기값 선택이 포함됩니다.그런 다음 매개변수를 반복적으로 세분화한다. 즉, 값은 연속적인 근사치에 의해 구해진다.
Jacobian J는 상수, 독립 변수 및 매개변수의 함수이므로 반복마다 변합니다.잔차는 다음과 같이 표시됩니다.
{\i의 제곱합을 최소화하기 위해 구배방정식은 0으로 설정되며 j \ \\ _ { 에 대해 해결됩니다.
정규 방정식은 행렬 표기로 다음과 같이 기술됩니다.
이것들은 가우스-뉴턴 알고리즘의 정의 방정식입니다.
선형 및 비선형 최소 제곱의 차이
- LLSQ(선형 최소 제곱)에서 모델 함수 f는 f 1 1 + 2 +δ { f}\}+i2}\의 모수의 선형 조합으로, 직선을 나타낼 수 있다.NLSQ(비선형 최소 제곱)에서 파라미터는 2, x \style \ x 의 함수로 나타납니다. f/ \ \ /\ _ 도함수가 일정하거나 독립 변수의 값에만 의존하는 경우 모델은 파라미터에서 선형입니다.그렇지 않으면 모형이 비선형입니다.
- NLSQ 문제에 대한 해결책을 찾기 위해 파라미터의 초기값이 필요합니다.LLSQ는 LLSQ를 사용합니다.
- NLSQ의 솔루션 알고리즘에서는 Jacobian을 LLSQ와 유사하게 계산할 필요가 있는 경우가 많습니다.부분 도함수에 대한 해석식은 복잡할 수 있다.해석식을 구하는 것이 불가능할 경우, 부분 도함수는 수치 근사치에 의해 계산되거나 야코비안을 추정해야 하며, 종종 유한한 차이에 의해 계산되어야 한다.
- 비컨버전스(알고리즘이 최소값을 찾지 못하는 것)는 NLSQ에서 일반적인 현상입니다.
- LLSQ는 글로벌하게 오목하기 때문에 비컨버전스는 문제가 되지 않습니다.
- NLSQ 해결은 보통 수렴 기준이 충족되면 종료해야 하는 반복 프로세스입니다.LLSQ 솔루션은 직접 방법을 사용하여 계산할 수 있지만, 다수의 매개변수가 있는 문제는 일반적으로 가우스-세이델 방법과 같은 반복 방법을 사용하여 해결할 수 있다.
- LLSQ에서는 솔루션이 고유하지만 NLSQ에서는 제곱합에 최소값이 여러 개 있을 수 있습니다.
- 오차가 예측 변수와 관련이 없는 조건에서는 LLSQ가 편향되지 않은 추정치를 산출하지만, 이 조건에서도 NLSQ 추정치는 일반적으로 편향됩니다.
이러한 차이는 비선형 최소 제곱 문제에 대한 해결책을 [12]찾을 때마다 고려해야 합니다.
예
물리학에서 도출한 간단한 예를 생각해 보세요.스프링은 스프링 y의 연장이 적용되는 힘 F에 비례한다는 후크의 법칙을 따라야 한다.
모델을 구성합니다. 여기서 F는 독립 변수입니다.힘 상수 k를 추정하기 위해 서로 다른 힘으로 일련의 n개의 측정을 수행하여 데이터 세트 i i), , \ (},displaystyle여기서i y는 측정된 스프링 [14]확장입니다.각 실험 관찰에는 오류 가 포함되어 있으므로 관찰에 경험적 모델을 지정할 수 있습니다.
알 수 없는 매개변수 k를 추정하기 위해 사용할 수 있는 방법은 많습니다.데이터의 m 변수에서 n개의 방정식이 하나의 미지의 방정식과 n개의 방정식을 가진 과잉 결정된 시스템을 구성하기 때문에, 우리는 최소 제곱을 사용하여 k를 추정한다.최소화할 제곱합은 다음과 같습니다.
힘 상수 k의 최소 제곱 추정치는 다음과 같습니다.
힘을 가하면 스프링이 팽창한다고 가정합니다.최소 제곱 피팅으로 힘 상수를 도출한 후 후크의 법칙에서 확장을 예측합니다.
불확도 정량화
단위 가중치를 사용한 최소 제곱 계산 또는 선형 회귀에서, var (β ^) {}}로 된 j번째 파라미터의 분산은 보통 다음과 같이 추정됩니다.
여기서 참 오차 분산 θ는2 잔차 제곱합(객관 함수)의 최소값을 기반으로 한 축소 카이 제곱 통계량인 추정치로 대체됩니다.분모인 n - m은 통계적 자유도이다.[12] 일반화는 유효 자유도를 참조한다.C는 공분산 행렬입니다.
통계 테스트
모수의 확률 분포를 알고 있거나 점근 근사치를 만들면 신뢰 한계를 찾을 수 있습니다.마찬가지로 잔차의 확률 분포를 알고 있거나 가정한 경우 잔차에 대한 통계적 검정을 수행할 수 있습니다.실험 오차의 확률 분포가 알려져 있거나 가정된 경우 종속 변수의 선형 조합의 확률 분포를 도출할 수 있다.오차가 정규 분포를 따른다고 가정하면 추론이 쉬우므로 모수 추정치와 잔차도 독립 [12]변수의 값에 따라 정규 분포를 따릅니다.
결과를 통계적으로 테스트하기 위해서는 실험 오류의 성격에 대한 가정을 할 필요가 있다.일반적인 가정은 오차가 정규 분포에 속한다는 것입니다.중심 한계 정리는 이것이 많은 경우에 좋은 근사치라는 생각을 뒷받침한다.
- 가우스-마르코프 정리오차가 독립 변수에 대해 조건부로 기대치가 0이고 상관 관계가 없으며 분산이 동일한 선형 모형에서 관측치의 선형 조합 중 가장 좋은 선형 불편 추정기는 최소 제곱 추정기입니다."최고"는 모수의 최소 제곱 추정치가 최소 분산을 갖는다는 것을 의미합니다.분산이 동일하다는 가정은 오차가 모두 동일한 분포에 속할 때 유효합니다.
- 오차가 정규 분포에 속하는 경우 최소 제곱 추정기는 선형 모형에서 최대우도 추정기이기도 합니다.
그러나 오차가 정규 분포를 따르지 않는다고 가정합니다.그럼에도 불구하고 중심 한계 정리는 표본이 상당히 큰 한 모수 추정치가 근사적으로 정규 분포를 따를 것임을 시사한다.따라서 오차 평균이 독립 변수와 독립적이라는 중요한 특성을 고려할 때 회귀 분석에서 오차항의 분포는 중요한 문제가 아닙니다.특히 오차항이 정규 분포를 따르는지 여부는 일반적으로 중요하지 않습니다.
가중 최소 제곱
가중 최소 제곱이라고 하는 일반화 최소 제곱의 특수한 경우는 δ(잔차의 상관 행렬)의 모든 대각선 외 항목이 null일 때 발생합니다. 공분산 행렬을 따라 관측치의 분산이 여전히 동일하지 않을 수 있습니다(헤테로세카스틱성).간단히 말하면, (표시 스타일 })의 분산이 스타일 })의 값에 따라 달라지는 경우, 오른쪽의 잔차 플롯에서 볼 수 있듯이 잔차 플롯이 더 ( 스타일i}) 값을 향해 "팬아웃" 효과를 발생시킵니다.한편, 균질성은 Y_})와 U_})의 분산이 동일하다고 가정하고 있다.[10]
주성분과의 관계
점의 집합을 의미하는지 그 초대 교장 요소를 가장 가깝게 데이터 포인트(로 최접근의 모눈 거리, 즉 수직인 힘에 의해 라인에 측정) 다가오면 그 선으로 표시될 수 있다.대조적으로, 선형 최소의 사각형 y{이\displaystyle}방향으로만 거리를 최소화하기 위해 노력한다.반면 PCA똑같이 모든 차원을 다루는 우선적으로, 데이터를 1차원의를 따라서, 두개의 비슷한 오류는 미터 법을 사용하면, 선형 최소 이승 것도 방법.
측정 이론과의 관계
주목할 만한 통계 학자 사라 반 드 기어는 최소 이승 추정자square-integrable 기능의 우주에 대한 척도로 해석될 수 있다는 것을 증명할 경험적 과정 이론과 Vapnik-Chervonenkis 차원을 사용했다.[15]
정규화
이 섹션에서는 대부분의 독자들을 이해할 기술적으로 될 수 있다.제발 도와 주세요 그것 non-experts 이해, 기술적인 세부 사항을 제거하지 않고 만들기를 개선하다(2월 2016년)( 어떻게 그리고 언제 이 템플릿 제거할 메시지를 배우다.). |
티호노프. NikolaiAleksandr. 정례화
어떤 맥락에서 보면은 최소 이승 해결책의 본격적으로 버전 더 좋을 수 있다.티호노프 조절(또는ridge 회귀), L2-norm 매개 변수 벡터의, 주어진 값보다 크지 않β ‖ 2{\displaystyle\와 같이 \beta)^{2}}‖ 제약 조건을 추가한다.[표창 필요한]Equivalently,[의심스러운 –을 논의하]그것 ‖ 2{\displaystyle \alpha)\beta)^{2}β α ‖}과α{\displaystyle \alpha}이 상수(제한 문제의 라그랑주 형식), 추가한 최소 이승 페널티의 구속 받지 않는 최소화 해결할 수 있다.를 베이즈의 맥락에서, 이것은 보통 전에 매개 변수 벡터에서 배포zero-mean을 배치하는 것 같다.
라소 메서드
최소제곱의 다른 정규화 버전은 Lasso(최소 절대수축 및 선택 연산자)이며, 파라미터 벡터의1 L-노름인 βδ { 가 주어진 [16][17][18]값 이하라는 제약을 사용한다.(상기와 같이 이는 αββ \\ 가 추가된 제곱 패널티를 제한 없이 최소화하는 것과 같다[dubious ].)베이지안 컨텍스트에서 이는 파라미터 [19]벡터에 제로 평균 라플라스 사전분포를 배치하는 것과 같다.최적화 문제는 최소 각도 회귀 알고리즘과 같은 특정 알고리즘뿐만 아니라 2차 프로그래밍 또는 보다 일반적인 볼록 최적화 방법을 사용하여 해결할 수 있습니다.
Lasso와 능선 회귀 분석의 주요 차이점 중 하나는 능선 회귀 분석에서는 패널티가 증가하면 모든 파라미터가 감소하지만 여전히 0이 아닌 상태로 유지된다는 것이다. 반면, Lasso에서는 패널티를 증가시키면 파라미터가 점점 더 0으로 몰리게 된다.매개변수를 0으로 설정하면 회귀 분석에서 피쳐가 선택 취소되므로 능선 회귀 분석보다 Lasso의 이점이 있습니다.따라서 Lasso는 더 관련된 피쳐를 자동으로 선택하고 다른 피쳐를 삭제하지만, Ridge 회귀 분석에서는 피쳐를 완전히 삭제하지 않습니다.샘플을 [20]부트스트랩하는 Bolasso와의 다른 값에 대응하는 회귀 계수를 분석하여 모든 [21]피쳐를 채점하는 FeaLect 등 일부 피쳐 선택 기법이 LASO를 기반으로 개발되었습니다.
L-정규화된1 공식은 파라미터가 0인 솔루션을 선호하는 경향이 있기 때문에 일부 상황에서 유용하며, 이는 더 적은 [16]변수에 의존하는 솔루션을 제공합니다.이러한 이유로, Lasso와 그 변형은 압축 감지 분야의 기본입니다.이 접근방식의 확장으로는 탄력적 네트워크 정규화가 있습니다.
「 」를 참조해 주세요.
- 관측치의 조정
- 베이지안 MMSE 추정기
- 최적 선형 불편 추정기(BLUE)
- 최적 선형 불편 예측(BLUP)
- 가우스-마르코프 정리
- L2 노름
- 최소 절대 편차
- 최소 제곱 스펙트럼 분석
- 측정 불확도
- 직교 투영
- 학습을 위한 근위 구배법
- 이차 손실 함수
- 평균 제곱근
- 편차의 제곱
레퍼런스
- ^ Charnes, A.; Frome, E. L.; Yu, P. L. (1976). "The Equivalence of Generalized Least Squares and Maximum Likelihood Estimates in the Exponential Family". Journal of the American Statistical Association. 71 (353): 169–171. doi:10.1080/01621459.1976.10481508.
- ^ 맨스필드 메리만, "최소 제곱법에 관한 저작 목록"
- ^ Bretscher, Otto (1995). Linear Algebra With Applications (3rd ed.). Upper Saddle River, NJ: Prentice Hall.
- ^ Stigler, Stephen M. (1981). "Gauss and the Invention of Least Squares". Ann. Stat. 9 (3): 465–474. doi:10.1214/aos/1176345451.
- ^ 브리태니커, "최소 제곱법"
- ^ 확률과 통계의 역사에서의 연구.29: 최소 제곱법의 발견 R. L. Plackett
- ^ a b Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Cambridge, MA: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
- ^ Legendre, Adrien-Marie (1805), Nouvelles méthodes pour la détermination des orbites des comètes [New Methods for the Determination of the Orbits of Comets] (in French), Paris: F. Didot, hdl:2027/nyp.33433069112559
- ^ Aldrich, J. (1998). "Doing Least Squares: Perspectives from Gauss and Yule". International Statistical Review. 66 (1): 61–81. doi:10.1111/j.1751-5823.1998.tb00406.x. S2CID 121471194.
- ^ a b c d A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 유지보수: 기타 (링크) - ^ Error-in-Variable에 대한 자세한 내용은, 을 참조해 주세요.
- ^ a b c d e f g h Williams, Jeffrey H. (Jeffrey Huw), 1956- (November 2016). Quantifying measurement : the tyranny of numbers. Morgan & Claypool Publishers,, Institute of Physics (Great Britain). San Rafael [California] (40 Oak Drive, San Rafael, CA, 94903, USA). ISBN 978-1-68174-433-9. OCLC 962422324.
{{cite book}}: CS1 maint: 위치(링크) CS1 maint: 여러 이름: 작성자 목록(링크) - ^ a b Rencher, Alvin C.; Christensen, William F. (2012-08-15). Methods of Multivariate Analysis. John Wiley & Sons. p. 155. ISBN 978-1-118-39167-9.
- ^ Gere, James M. (2013). Mechanics of materials. Goodno, Barry J. (8th ed.). Stamford, Conn.: Cengage Learning. ISBN 978-1-111-57773-5. OCLC 741541348.
- ^ van de Geer, Sara (June 1987). "A New Approach to Least-Squares Estimation, with Applications". Annals of Statistics. 15 (2): 587–602. doi:10.1214/aos/1176350362.
- ^ a b Tibshirani, R. (1996). "Regression shrinkage and selection via the lasso". Journal of the Royal Statistical Society, Series B. 58 (1): 267–288. JSTOR 2346178.
- ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome H. (2009). The Elements of Statistical Learning (second ed.). Springer-Verlag. ISBN 978-0-387-84858-7. Archived from the original on 2009-11-10.
- ^ Bühlmann, Peter; van de Geer, Sara (2011). Statistics for High-Dimensional Data: Methods, Theory and Applications. Springer. ISBN 9783642201929.
- ^ Park, Trevor; Casella, George (2008). "The Bayesian Lasso". Journal of the American Statistical Association. 103 (482): 681–686. doi:10.1198/016214508000000337. S2CID 11797924.
- ^ Bach, Francis R (2008). "Bolasso: model consistent lasso estimation through the bootstrap". Proceedings of the 25th International Conference on Machine Learning. Icml '08: 33–40. arXiv:0804.1302. Bibcode:2008arXiv0804.1302B. doi:10.1145/1390156.1390161. ISBN 9781605582054. S2CID 609778.
- ^ Zare, Habil (2013). "Scoring relevancy of features based on combinatorial analysis of Lasso with application to lymphoma diagnosis". BMC Genomics. 14: S14. doi:10.1186/1471-2164-14-S1-S14. PMC 3549810. PMID 23369194.
추가 정보
- Björck, Å. (1996). Numerical Methods for Least Squares Problems. SIAM. ISBN 978-0-89871-360-2.
- Kariya, T.; Kurata, H. (2004). Generalized Least Squares. Hoboken: Wiley. ISBN 978-0-470-86697-9.
- Luenberger, D. G. (1997) [1969]. "Least-Squares Estimation". Optimization by Vector Space Methods. New York: John Wiley & Sons. pp. 78–102. ISBN 978-0-471-18117-0.
- Rao, C. R.; Toutenburg, H.; et al. (2008). Linear Models: Least Squares and Alternatives. Springer Series in Statistics (3rd ed.). Berlin: Springer. ISBN 978-3-540-74226-5.
- Van de moortel, Koen (April 2021). "Multidirectional regression analysis".
- Wolberg, J. (2005). Data Analysis Using the Method of Least Squares: Extracting the Most Information from Experiments. Berlin: Springer. ISBN 978-3-540-25674-8.











 대한 무작위 변동은 선형 모델이 적절함을 나타냅니다.
대한 무작위 변동은 선형 모델이 적절함을 나타냅니다.

 기울기는
기울기는 

 (가) 적절합니다.
(가) 적절합니다. 독립적이고
독립적이고 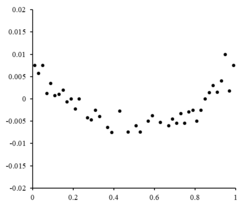















 값을 구한다.대부분의 알고리즘에는 파라미터의 초기값 선택이 포함됩니다.그런 다음 매개변수를 반복적으로 세분화한다. 즉, 값은 연속적인 근사치에 의해 구해진다.
값을 구한다.대부분의 알고리즘에는 파라미터의 초기값 선택이 포함됩니다.그런 다음 매개변수를 반복적으로 세분화한다. 즉, 값은 연속적인 근사치에 의해 구해진다.








 모수의 선형 조합으로, 직선을 나타낼 수 있다.NLSQ(비선형 최소 제곱)에서 파라미터는
모수의 선형 조합으로, 직선을 나타낼 수 있다.NLSQ(비선형 최소 제곱)에서 파라미터는  함수로 나타납니다.
함수로 나타납니다.







![{\displaystyle \operatorname {var} ({\hat {\beta }}_{j})=\sigma ^{2}\left(\left[X^{\mathsf {T}}X\right]^{-1}\right)_{jj}\approx {\hat {\sigma }}^{2}C_{jj},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d85cf89d392a9c191ff1fe3429654bd748a02b2b)



 분산이
분산이 





