단백질 설계

Protein design
이 기사는 합리적인 단백질 디자인에 관한 것입니다.단백질의 광범위한 공학을 보려면 단백질 공학을 참조하십시오.

단백질 디자인은 새로운 활동, 행동 또는 목적을 설계하고 단백질 [1]기능에 대한 기본적인 이해를 증진시키기 위해 새로운 단백질 분자를 합리적으로 설계하는 것입니다.단백질은 처음부터 설계할 수 있으며(새로운 설계), 또는 알려진 단백질 구조와 그 배열의 계산된 변형(단백질 재설계)을 통해 설계할 수 있다.합리적인 단백질 설계 접근방식은 특정 구조에 접히는 단백질 염기서열을 예측한다.이러한 예측 배열은 펩타이드 합성, 부위 지향 돌연변이 유발 또는 인공 유전자 합성과 같은 방법을 통해 실험적으로 검증될 수 있다.

합리적인 단백질 디자인은 1970년대 [2]중반으로 거슬러 올라간다.그러나 최근에는 단백질 구조의 안정성과 더 나은 계산 방법의 개발에 기여하는 다양한 인자에 대한 더 나은 이해로 인해 수용성 및 심지어 막 통과 펩타이드와 단백질의 성공적인 합리적 설계의 사례가 다수 있었다.

개요 및 이력

합리적인 단백질 설계의 목표는 특정 단백질 구조로 접히는 아미노산 서열을 예측하는 것입니다.단백질 사슬의 크기에 따라 기하급수적으로 증가하는 단백질 배열의 수는 많지만, 그들 중 일부만이 신뢰성 있고 빠르게 하나의 토종 상태로 접힐 것이다.단백질 설계는 이 부분집합 내에서 새로운 서열을 식별하는 것을 포함한다.단백질의 고유 상태는 사슬에 대한 최소 구조 자유 에너지입니다.따라서 단백질 설계는 자유 에너지 최소값으로 선택된 구조를 가진 서열을 찾는 것이다.어떤 의미에서는 단백질 구조 예측의 역행이다.설계에서는 제3의 구조를 특정하고, 거기에 접히는 시퀀스를 특정한다.따라서 역폴딩이라고도 합니다.단백질 설계는 최적화 문제입니다. 몇 가지 점수 기준을 사용하여 원하는 구조로 접히는 최적화된 시퀀스가 선택됩니다.

1970년대와 1980년대에 첫 번째 단백질이 합리적으로 설계되었을 때, 이러한 단백질의 배열은 다른 알려진 단백질의 분석, 배열 구성, 아미노산 전하 및 원하는 [2]구조의 기하학적 구조에 기초하여 수동으로 최적화되었다.첫 번째 설계된 단백질은 DDT 결합체를 포함한 베타 시트와 알파 헬리스로 구성된 3차 구조, 소 리보핵산가수분해효소, 알려진 촉매의 축소 버전을 설계한 Bernd Gutte에 기인한다.Urry와 동료들은 나중에 배열 구성에 대한 규칙을 기반으로 엘라스틴 유사 섬유 펩타이드를 설계했다.리처드슨과 동료들은 알려진 [2]단백질에 대한 배열 상동성이 없는 79개의 잔여 단백질을 설계했다.1990년대에 강력한 컴퓨터, 아미노산 배치 라이브러리 및 분자 역학 시뮬레이션을 위해 개발된 힘의 장이 등장하면서 구조 기반 컴퓨터 단백질 설계 도구의 개발이 가능해졌다.이러한 계산 도구의 개발에 따라 지난 30년 동안 단백질 설계에서 큰 성공을 거두었습니다.최초의 [3]단백질은 1997년 스티븐 메이요와 동료들에 의해 완성되었고, 얼마 지나지 않아 1999년 피터 S. 김과 동료들은 부자연스러운 오른손 코일 [4][5]코일의 이합체, 트리머, 테트라머를 설계했다.2003년, 데이비드 베이커의 실험실은 [6]자연에서 이전에 볼 수 없었던 완전한 단백질을 디자인했습니다.이후 2008년 베이커의 그룹은 두 가지 다른 [7]반응을 위해 효소를 계산적으로 설계했다.2010년, 가장 강력하고 광범위하게 중화시키는 항체 중 하나가 컴퓨터 설계 단백질 [8]프로브를 사용하여 환자 혈청에서 분리되었다.이러한 성공 및 기타 성공(예: 아래 예 참조)으로 인해 단백질 설계는 단백질 공학에서 사용할 수 있는 가장 중요한 도구 중 하나가 되었습니다.크고 작은 새로운 단백질의 디자인이 생물의학과 생명공학에 사용될 것이라는 큰 희망이 있다.


단백질 구조와 기능의 기본 모델

단백질 설계 프로그램은 생체 내 환경에서 단백질을 구동하는 분자 힘의 컴퓨터 모델을 사용합니다.문제를 다루기 쉽게 만들기 위해 이러한 힘은 단백질 설계 모델에 의해 단순화됩니다.단백질 설계 프로그램은 매우 다양하지만 다음과 같은 네 가지 주요 모델링 질문에 대처해야 합니다.설계의 대상 구조는 무엇이며, 대상 구조에서 허용되는 유연성, 검색에 포함되는 시퀀스 및 시퀀스 및 구조 스코어에 사용되는 힘 필드는 무엇입니까?

대상구조

Top7 단백질은 지금까지 자연에서[6] 볼 수 없었던 접힘을 위해 설계된 최초의 단백질 중 하나였습니다.

단백질 기능은 단백질 구조에 크게 의존하며, 합리적인 단백질 설계는 이 관계를 이용하여 표적 구조 또는 접힌 단백질을 설계함으로써 기능을 설계한다.따라서 합리적인 단백질 설계에서 정의상 대상 구조 또는 구조의 앙상블을 미리 알고 있어야 한다.이것은 특정 기능을 달성하는 단백질을 찾기 위해 다양한 방법이 사용되는 방향 진화와 같은 다른 형태의 단백질 공학과 배열이 알려져 있지만 구조는 알려지지 않은 단백질 구조 예측과 대조된다.

대부분의 경우 표적 구조는 다른 단백질의 알려진 구조에 기초한다.하지만 자연에서 볼 수 없는 새로운 접힘이 점점 가능해졌습니다.피터 S. 김과 동료들은 자연에서는 [4][5]볼 수 없었던 부자연스러운 코일 모양의 트리머와 테트라머를 디자인했다.David Baker의 연구실에서 개발된 단백질 Top7은 완전히 단백질 설계 알고리즘을 사용하여 완전히 새로운 [6]접힘으로 디자인되었습니다.최근 베이커와 동료들은 2차 구조 예측과 3차 구조 사이를 연결하는 단백질 접이식 깔때기를 기반으로 이상적인 구상 단백질 구조를 설계하기 위한 일련의 원리를 개발했습니다.단백질 구조 예측과 단백질 설계 둘 다에 기반을 둔 이 원칙들은 5가지 새로운 단백질 [9]토폴로지를 설계하는 데 사용되었다.

시퀀스 공간

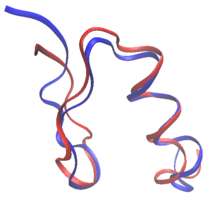
FSD-1(파란색으로 표시, PDB ID: 1FSV)은 완전한 단백질의 [3]첫 번째 새로운 컴퓨터 설계였다.표적 접힘은 단백질 Zif268(빨간색으로 표시, PDB id: 1ZAA) 구조의 잔류물 33-60에 있는 아연 손가락 접힘이었다.설계된 배열은 알려진 단백질 배열과 거의 동일성이 없었다.

합리적인 단백질 설계에서 단백질은 알려진 단백질의 배열과 구조에서 또는 de novo 단백질 설계에서 완전히 처음부터 다시 설계될 수 있다.단백질 재설계에서 배열의 대부분의 잔류물은 야생형 아미노산으로 유지되며, 소수는 돌연변이가 허용된다.de novo 설계에서는 시퀀스 전체가 사전 시퀀스를 기반으로 새롭게 설계됩니다.

de novo 설계와 단백질 재설계는 배열 공간에 대한 규칙을 확립할 수 있습니다. 즉, 각 변이 가능한 잔류물 위치에서 허용되는 특정 아미노산입니다.예를 들어, HIV를 광범위하게 중화시키는 항체를 선택하기 위한 RSC3 프로브의 표면 구성은 진화 데이터와 전하 균형에 기초하여 제한되었다.단백질 설계에 대한 초기의 많은 시도들은 배열 [2]공간에 대한 경험론적 규칙에 크게 기초했다.게다가, 섬유 단백질의 설계는 보통 배열 공간에 대한 엄격한 규칙을 따른다.예를 들어 콜라겐 기반 설계 단백질은 종종 Gly-Pro-X 반복 [2]패턴으로 구성됩니다.계산 기술의 등장은 배열 [3]선택에 인간의 개입 없이 단백질을 설계할 수 있게 한다.

구조 유연성

일반적인 단백질 설계 프로그램은 로타머 라이브러리를 사용하여 단백질 측쇄의 구조 공간을 단순화합니다.이 애니메이션은 Penultimate Rotamer [10]Library를 기반으로 이소류신 아미노산의 모든 로타머를 루프합니다.

단백질 설계에서는 단백질의 표적 구조가 알려져 있다.단, 합리적인 단백질 설계 접근방식은 대상 구조에 대해 설계할 수 있는 배열의 수를 증가시키고 배열이 다른 구조로 접힐 가능성을 최소화하기 위해 대상 구조에서 어느 정도 유연성을 모델링해야 한다.예를 들어, 단백질의 촘촘하게 포장된 핵심에 있는 하나의 작은 아미노산(예: 알라닌)의 단백질 재설계에서, 주변 측쇄를 다시 포장할 수 없는 경우, 표적 구조에 접히는 합리적인 설계 접근법에 의해 극소수의 돌연변이가 예측될 것이다.

따라서 설계 프로세스의 필수 파라미터는 사이드 체인과 백본 양쪽에 허용되는 유연성의 양입니다.가장 단순한 모델에서 단백질 골격은 단단하게 유지되는 반면 단백질 측쇄의 일부는 형태를 바꿀 수 있다.그러나 사이드 체인은 결합 길이, 결합 각도 및 이면각에서 많은 자유도를 가질 수 있습니다.이 공간을 단순화하기 위해 단백질 설계 방법은 결합 길이와 결합 각도에 대한 이상적인 값을 가정하는 로타머 라이브러리를 사용합니다.χ로타머라고 불리는 자주 관찰되는 몇 가지 저에너지 구성에 대한 이면각.

로타머 라이브러리는 많은 단백질 구조의 통계적 분석에서 파생됩니다.백본에 의존하지 않는 로타머 라이브러리는 모든 로타머를 [10]나타냅니다.이와는 대조적으로, 골격 의존형 로타머 라이브러리는 로타머가 [11]옆사슬 주위의 단백질 골격 배열에 따라 얼마나 나타날 수 있는지를 설명한다.대부분의 단백질 설계 프로그램은 로타머에 의해 기술된 영역의 단일 구성(예: 공간에서의 로타머 결정의 모드 값) 또는 여러 점을 사용합니다. 반면 OSPREE 단백질 설계 프로그램은 전체 연속 [12]영역을 모델링합니다.

합리적인 단백질 설계가 일반적인 등뼈 접힘 단백질을 보존해야 하지만, 약간의 등뼈 유연성을 허용하면 [13]단백질의 일반적인 접힘을 유지하면서 구조에 접히는 배열의 수를 크게 증가시킬 수 있다.염기서열 돌연변이가 종종 골격 구조에 작은 변화를 일으키기 때문에 골격 유연성은 단백질 재설계에서 특히 중요하다.더욱이, 골격 유연성은 결합 예측 및 효소 설계와 같은 단백질 설계의 보다 발전된 적용에 필수적일 수 있다.단백질 설계 백본 유연성의 일부 모델에는 작고 지속적인 글로벌 백본 이동, 타깃 폴드 주위의 이산 백본 샘플, 백러브 모션 및 단백질 루프 [13][14]유연성이 포함됩니다.

에너지 함수

다양한 잠재 에너지 기능의 비교.가장 정확한 에너지는 양자역학적 계산을 사용하는 것이지만 단백질 설계에는 너무 느리다.다른 극단적 발견적 에너지 함수는 통계적 용어에 기초하고 있으며 매우 빠릅니다.중간에는 물리적인 기반이지만 양자역학 [15]시뮬레이션만큼 계산 비용이 많이 들지 않는 분자역학 에너지 함수가 있습니다.

합리적인 단백질 설계 기법은 목표 접힘 하에서 안정적인 배열과 다른 저에너지 경쟁 상태를 선호하는 배열의 구별이 가능해야 한다.따라서 단백질 설계는 대상 구조에 얼마나 잘 접히느냐에 따라 시퀀스의 순위를 매기고 점수를 매길 수 있는 정확한 에너지 기능을 필요로 합니다.그러나 동시에, 이러한 에너지 기능은 단백질 설계 뒤에 있는 계산상의 문제를 고려해야 합니다.설계를 성공시키기 위한 가장 어려운 요건 중 하나는 계산의 정확성과 단순성을 모두 갖춘 에너지 함수입니다.

가장 정확한 에너지 함수는 양자역학적 시뮬레이션을 기반으로 하는 함수이다.그러나 그러한 시뮬레이션은 너무 느리고 일반적으로 단백질 설계에 실용적이지 않다.대신, 많은 단백질 설계 알고리즘은 분자역학 시뮬레이션 프로그램, 지식 기반 에너지 함수 또는 두 가지 혼합물을 사용합니다.물리 기반의 잠재 에너지 함수를 더 많이 사용하는 [15]경향이 있습니다.

AMBER 및 CHARMM과 같은 물리 기반 에너지 함수는 일반적으로 양자 역학적 시뮬레이션과 열역학, 결정학 및 스펙트럼 [16]분석의 실험 데이터에서 도출됩니다.이러한 에너지 함수는 전형적으로 물리적 에너지 기능을 단순화하고 쌍으로 분해할 수 있게 한다. 즉, 단백질 구성의 총 에너지는 각 원자 쌍 사이에 쌍으로 에너지를 더함으로써 계산될 수 있으며, 이는 최적화 알고리즘에 매력적이다.물리 기반 에너지 함수는 전형적으로 원자 사이의 매력적이고 반발적인 레너드-존스 항과 결합되지 않은 원자 간의 쌍방향 전기 정전기 쿨롱 항을[17] 모델링한다.

물 매개 수소 결합은 단백질-단백질 결합에 중요한 역할을 한다.이러한 상호작용 중 하나는 HIV-광대중화항체 VRC01(녹색)의 중쇄 잔류물 D457, S365와 HIV 외피단백질 GP120(보라색)[18]의 잔류물 N58, Y59 사이에 나타난다.

통계적 전위는 물리학 기반 전위와 달리 계산이 빠르고 복잡한 효과를 암묵적으로 설명하며 단백질 [19]구조의 작은 변화에 덜 민감하다는 장점이 있다.이러한 에너지 함수는 구조 데이터베이스의 출현 빈도로부터 에너지 값을 도출하는 것에 기초한다.

그러나 단백질 설계는 때때로 분자역학 힘장에서 제한될 수 있는 요구사항을 가지고 있다.분자역학 시뮬레이션에서 주로 사용되어 온 분자역학 힘장은 단일 시퀀스의 시뮬레이션에 최적화되어 있지만 단백질 디자인은 많은 시퀀스의 많은 구조를 탐색합니다.따라서 분자역학 힘장은 단백질 설계에 맞게 조정되어야 한다.실제로 단백질 설계 에너지 함수는 종종 통계 용어와 물리학 기반 용어를 모두 통합한다.예를 들어 가장 많이 사용되는 에너지 함수 중 하나인 로제타 에너지 함수는 CHARMM 에너지 함수에서 유래한 물리 기반 에너지 항과 로타머 확률 및 지식 기반 정전기와 같은 통계 에너지 항을 통합합니다.일반적으로 에너지 기능은 연구소 간에 고도로 맞춤화되며,[16] 모든 설계에 맞게 특별히 맞춤화됩니다.

효과적인 설계 에너지 기능에 대한 과제

물은 단백질을 둘러싸고 있는 분자의 대부분을 구성하고 단백질 구조의 주요 원동력이다.따라서 단백질 설계에서 물과 단백질 사이의 상호작용을 모형화하는 것은 매우 중요합니다.주어진 시간에 단백질과 상호작용하는 물 분자의 수는 엄청나며 각각의 물 분자는 많은 수의 자유도와 상호작용 파트너를 가지고 있습니다.대신 단백질 설계 프로그램은 그러한 물 분자의 대부분을 연속체로 모델링하여 소수성 효과와 용매화 [16]분극화 모두를 모델링합니다.

개별 물 분자는 때때로 단백질의 핵심과 단백질-단백질 또는 단백질-배위자 상호작용에서 중요한 구조적 역할을 할 수 있다.이러한 물을 모델링하지 못하면 단백질-단백질 계면의 최적 염기서열을 잘못 예측할 수 있다.대신 로타머에 물 분자를 첨가할 수 있다.

[16]


최적화 문제로서

이 애니메이션은 단백질 설계 검색의 복잡성을 나타내며, 일반적으로 모든 잔류물에서 가능한 모든 돌연변이의 모든 로타머 구성을 비교합니다.이 예에서 잔류물 Pe36 및 His106은 각각 아미노산 Tyr 및 Asn으로 변이될 수 있다.Pe와 Tyr는 로타머 라이브러리에 각각 4개의 로타머를 가지고 있고, Asn과 His는 로타머 라이브러리(리처드슨의 두 번째 로타머[10] 라이브러리)에 각각 7개와 8개의 로타머를 가지고 있습니다.애니메이션은 모든 (4 + 4) x (7 + 8) = 120개의 가능성을 통해 루프됩니다.표시된 구조는 미오글로빈의 구조이며 PDB ID는 1mbn입니다.

단백질 설계의 목적은 표적 구조에 접히는 단백질 배열을 찾는 것입니다.따라서 단백질 설계 알고리즘은 표적 접힘에 관한 각 배열의 모든 배열을 탐색하고 단백질 설계 에너지 함수에 의해 결정되는 각 배열의 최저 에너지 배합에 따라 배열 순위를 매겨야 한다.따라서 단백질 설계 알고리즘의 대표적인 입력은 목표 접힘, 배열 공간, 구조적 유연성 및 에너지 함수이며 출력은 목표 구조에 안정적으로 접힐 것으로 예상되는 하나 이상의 배열이다.

그러나 후보 단백질 배열의 수는 단백질 잔류물의 수와 함께 기하급수적으로 증가한다. 예를 들어 길이가 100인 단백질 배열은 20개이다100.또한 아미노산 측쇄 배치가 몇 개의 로타머(구조 유연성 참조)로 제한되더라도 각 배열에 대해 기하급수적으로 많은 배열을 얻을 수 있다.따라서 100개의 잔류 단백질에서 각 아미노산이 정확히 10개의 로타머를 가지고 있다고 가정하면 이 공간을 검색하는 검색 알고리즘은 200개 이상의 단백질 구조를 검색해야100 합니다.

가장 일반적인 에너지 함수는 로타머와 아미노산 유형 사이에서 쌍으로 분해될 수 있으며, 조합적인 것으로 문제를 제기하고, 이를 해결하기 위해 강력한 최적화 알고리즘을 사용할 수 있다.이 경우 각 배열에 속하는 각 배형의 총 에너지는 잔류 위치 간의 개별 및 쌍별 항의 합으로 공식화할 수 있다.설계자가 최상의 배열에만 관심이 있는 경우, 단백질 설계 알고리즘은 가장 낮은 에너지 배열의 가장 낮은 에너지 구성만 필요로 한다.이 경우 각 로타머의 아미노산 특이성을 무시할 수 있어 다른 아미노산에 속하는 모든 로타머를 동일하게 취급할 수 있다.허락하다ri 잔존 위치에서 회전하고 있다i단백질 사슬에서E(ri)로타머의 내부 원자 사이의 위치 에너지허락하다E(ri,r)는j, 2개의 네트워크 사이의 잠재적인 에너지입니다.ri 및 로타머rj 잔류 위치에서j그런 다음 최적화 문제를 최소 에너지의 적합성을 찾는 것으로 정의한다(conformation of the minimum energy(최소 에너지)ET):

(1)

최소화하는 문제ET는 NP-하드 문제입니다.[14][20][21]비록 문제의 클래스가 NP-hard이긴 하지만, 실제로 많은 단백질 설계 사례는 발견적 방법을 통해 정확하게 해결되거나 만족스럽게 최적화될 수 있다.


알고리즘

단백질 설계 문제를 위해 몇 가지 알고리즘이 특별히 개발되었습니다.이러한 알고리즘은 두 가지 광범위한 클래스로 나눌 수 있습니다. 즉, 런타임 보장은 없지만 솔루션의 품질을 보장하는 데드 엔드 제거와 같은 정확한 알고리즘과 정확한 알고리즘보다 빠르지만 결과의 최적성에 대한 보장이 없는 몬테 카를로 같은 경험적 알고리즘입니다.정확한 알고리즘은 단백질 설계 모델에 따라 최적화 과정이 최적으로 생산되었음을 보장합니다.따라서 정확한 알고리즘의 예측이 실험적으로 검증될 때 실패할 경우, 오차 발생원은 에너지 기능, 허용되는 유연성, 시퀀스 공간 또는 대상 구조(예: 설계할 수 없는 경우)[22]에 기인할 수 있다.

단백질 설계 알고리즘은 다음과 같습니다.이러한 알고리즘은 단백질 설계 문제의 가장 기본적인 공식만을 다루지만, 설계자가 허용되는 구조적 유연성(예: 단백질 골격 유연성)에 대한 개선사항과 같은 단백질 설계 모델에 대한 확장을 도입하기 때문에 최적화 목표가 변경될 때 등식 (1)을 다룬다.에너지 측면에서, 모델링을 개선하는 단백질 설계의 많은 확장은 이러한 알고리즘 위에 구축된다.예를 들어, Rosetta Design은 정교한 에너지 항과 몬테카를로를 기본 최적화 알고리즘으로 사용하는 백본 유연성을 통합한다.OSPREY의 알고리즘은 데드 엔드 제거 알고리즘과 A*를 기반으로 구축되어 연속적인 백본 및 사이드 체인 이동을 통합합니다.따라서, 이러한 알고리즘은 단백질 설계에 사용할 수 있는 다양한 종류의 알고리즘에 대한 좋은 관점을 제공합니다.

2020년 7월 과학자들은 새로운 단백질의 진화 기반 설계를 위해 게놈 데이터베이스를 사용하는 AI 기반 프로세스의 개발을 보고했다.그들은 디자인 [23][24]규칙을 식별하기 위해 딥 러닝을 이용했다.

수학적 보증 포함

막다른 골목의 배제

주요 기사:막다른 골목의 배제

Dead-end Elimation(DEE; 데드엔드 엘리미네이션) 알고리즘은 글로벌 최저 에너지 컨피규레이션(GMEC)의 일부가 아님을 증명할 수 있는 로타머를 제거함으로써 문제의 검색 공간을 반복적으로 줄입니다.각 반복에서 데드 엔드 제거 알고리즘은 각 잔류 위치에서 가능한 모든 로타머 쌍을 비교하고 각 로타머를 제거합니다.r′i항상 다른 로타머보다 높은 에너지를 가진다는 것을 보여줄 수 있다.ri따라서 GMEC의 일부가 아닙니다.

데드 엔드 제거 알고리즘의 다른 강력한 확장으로는 쌍 제거 기준 및 일반화된 데드 엔드 제거 기준이 있습니다.또한 이 알고리즘은 보증 가능한 연속 로타머를 처리하도록 확장되었습니다.

데드 엔드 제거 알고리즘은 각 반복에서 다항식 시간으로 실행되지만 컨버전스를 보장할 수는 없습니다.일정 횟수 반복 후 데드엔드 제거 알고리즘이 로타머를 더 이상 제거하지 않으면 로타머를 병합하거나 다른 검색 알고리즘을 사용하여 나머지 검색 공간을 검색해야 합니다.이러한 경우, 데드 엔드 제거는 검색 공간을 줄이기 위한 사전 필터링 알고리즘으로 작동하며, 나머지 검색 [14]공간을 검색하기 위해 A*, Monte Carlo, 선형 프로그래밍 또는 FASTER와 같은 다른 알고리즘이 사용됩니다.

분기 및 경계

주요 기사: 분기 및 경계

단백질 설계 컨피그레이션 공간은 단백질 잔류물이 임의의 방식으로 정렬되고 잔류물의 각 로타머에 나무가 분기하는 트리로 나타낼 수 있다.분기 알고리즘과 바운드알고리즘은 다음 표현을 사용하여 컨피규레이션트리를 효율적으로 탐색합니다.각 분기, 분기 및 결합 알고리즘에서 구성 공간을 제한하고 유망한 [14][25][26]분기만 탐색합니다.

단백질 설계의 일반적인 검색 알고리즘은 A* 검색 [14][26]알고리즘입니다.A*는 확장된 각 로타머의 에너지를 하한(보증)으로 하는 각 부분 트리 경로의 하한 점수를 계산합니다.각 부분 컨포메이션은 priority 큐에 추가되며, 각 반복에서 하한값이 가장 낮은 부분 패스가 큐에서 팝업되어 확장됩니다.알고리즘은 완전한 컨포메이션이 열거되면 정지하고 컨포메이션이 최적임을 보증합니다.

A* 점수f단백질 디자인에서 두 부분으로 이루어져 있다.f=g+h.g부분적 구성에 이미 할당되어 있는 로타머의 정확한 에너지입니다. h는 아직 할당되지 않은 로타머의 에너지 하한입니다.각각의 설계는 다음과 같습니다.d부분적 배치에서 마지막으로 할당된 잔류물의 지수입니다.

정수 선형 프로그래밍

상세 정보:선형 프로그래밍 integer 알 수 없는 정수 및 정수 프로그래밍

최적화의 문제ET(등식 (1)은 정수선형 프로그램(ILP)[27]으로 쉽게 공식화할 수 있다.가장 강력한 제제 중 하나는 이진 변수를 사용하여 최종 용액에 로타머와 가장자리의 존재를 나타내며, 각 잔류물에 대해 정확히 하나의 로타머와 각 잔류물 쌍에 대해 하나의 쌍방향 상호작용을 갖도록 솔루션을 제한한다.

S.T.

CPLEX와 같은 ILP 솔버는 단백질 설계상의 큰 문제에 대한 정확한 최적의 솔루션을 계산할 수 있습니다.이러한 해결사는 문제의 선형 프로그래밍 완화를 사용합니다.qi그리고.qij는 분기 및 컷 알고리즘과 조합하여 연속적인 값을 취할 수 있으며 최적의 솔루션을 위해 구성 공간의 일부만 검색할 수 있습니다.ILP 솔버는 사이드 체인 배치 [27]문제의 많은 인스턴스를 해결하는 것으로 나타났습니다.

선형 프로그래밍 듀얼에 대한 메시지 전달 기반 근사치

ILP 솔버는 심플렉스 등의 선형 프로그래밍(LP) 알고리즘이나 장벽 기반 메서드에 의존하여 각 브랜치에서 LP 완화를 수행합니다.이러한 LP 알고리즘은 범용 최적화 방법으로 개발되었으며 단백질 설계 문제(Equation (1))에 최적화되지 않았다.그 결과, 문제의 사이즈가 [28]클 때는, LP완화가 ILP솔러의 보틀 넥이 된다.최근에는 단백질 설계 문제의 LP 완화 최적화를 위해 메시지 전달 알고리즘에 기초한 여러 가지 대안이 특별히 설계되었다.이러한 알고리즘은 정수 프로그래밍의 이중 인스턴스 또는 원시 인스턴스 모두에 근사할 수 있지만, 최적성에 대한 보증을 유지하기 위해 단백질 설계 문제의 이중을 근사하는 데 사용될 때 가장 유용합니다. 왜냐하면 이중 보증을 근사하면 어떠한 해결책도 누락되지 않기 때문입니다.메시지 전달에 기초한 근사치에는 트리 재가중 최대 생성물 메시지 [29][30]전달 알고리즘 및 메시지 전달 선형 [31]프로그래밍 알고리즘이 포함됩니다.

보증 없는 최적화 알고리즘

몬테카를로와 모의 아닐링

몬테카를로는 단백질 설계에 가장 널리 사용되는 알고리즘 중 하나이다.가장 간단한 형태에서 몬테카를로 알고리즘은 잔기를 랜덤으로 선택하고, 그 잔기에서 랜덤으로 선택된 로타머(아미노산)를 평가한다.[21]단백질의 새로운 에너지,Enew 오래된 에너지와 비교된다.Eold 새로운 로타머는 다음과 같은 확률로 허용된다.

어디에β볼츠만 상수 및 온도T초기 라운드에서 높은 값을 선택하고 로컬 최소값을 [12]극복하기 위해 천천히 아닐되도록 선택할 수 있습니다.

빠른

FASTER 알고리즘은 아미노산 염기서열을 최적화하기 위해 결정론적 기준과 확률적 기준의 조합을 사용한다.FASTER는 먼저 DE를 사용하여 최적의 솔루션에 속하지 않는 로타머를 제거합니다.그런 다음 일련의 반복 단계가 로타머 할당을 [32][33]최적화합니다.

믿음의 전파

단백질 설계에 대한 믿음 전파에서 알고리즘은 각 잔기가 인접 잔기에 있는 각 로타머의 확률에 대해 갖는 믿음을 설명하는 메시지를 교환한다.이 알고리즘은 매번 메시지를 갱신하고 컨버전스 또는 일정 횟수 반복될 때까지 반복합니다.단백질 설계에서는 수렴이 보장되지 않습니다.메시지mi→ j(rj그 잔여물i모든 로타머에 전송(rj인접 잔류물로j는 다음과 같이 정의됩니다.

단백질 설계를 최적화하기 위해 최대 생성물 및 총 생성물 신뢰 전파가 모두 사용되었습니다.

설계된 단백질의 응용 및 예시

효소 설계

새로운 효소의 설계는 거대한 생명공학 및 생물의학 응용을 가진 단백질 설계를 사용하는 것입니다.일반적으로 단백질 구조를 설계하는 것은 효소를 설계하는 것과 다를 수 있다. 왜냐하면 효소의 설계는 촉매 메커니즘과 관련된 많은 상태를 고려해야 하기 때문이다.그러나 단백질 설계는 최소한 촉매 설계를 위해서는 촉매 메커니즘을 [34]삽입할 수 있는 발판이 필요하기 때문에 de novo 효소 설계의 필수 조건이다.

21세기 첫 10년 동안 데노보 효소 설계와 재설계에 큰 진전이 있었다.세 가지 주요 연구에서 데이비드 베이커와 동료들은 역알돌 반응,[35] 켐프 제거 반응,[36] 그리고 디엘스-알더 [37]반응을 위한 효소를 설계했다.게다가, Stephen Mayo와 동료들은 Kemp-엘리미네이션 [38]반응을 위해 가장 효율적인 것으로 알려진 효소를 설계하기 위해 반복적인 방법을 개발했다.또한 Bruce Donald의 실험실에서, 컴퓨터 단백질 설계는 Gramicidin S를 생산하는 비리보솜 펩타아제 단백질 도메인 중 하나의 특이성을 자연 기질인 페닐알라닌에서 하전 아미노산을 포함한 다른 인지되지 않은 기질로 전환하기 위해 사용되었다. 재설계된 효소는 근접한 활성을 가졌다.야생형 [39]동물에게요.

친화성을 위한 설계

단백질-단백질 상호작용은 대부분의 생물 작용에 관여한다.알츠하이머, 다양한 형태의 암(예: TP53) 및 인간 면역 결핍 바이러스(HIV) 감염과 같이 치료가 가장 어려운 많은 질병은 단백질-단백질 상호작용을 수반한다.따라서 이러한 질병을 치료하기 위해서는 상호작용의 파트너 중 하나를 결합시켜 질병을 유발하는 상호작용을 방해하는 단백질 또는 단백질 유사 치료제를 설계하는 것이 바람직하다.이것은 그것의 파트너에 대한 친화력을 위해 단백질 치료제를 설계하는 것을 필요로 한다.

단백질-단백질 상호작용은 단백질 안정성을 지배하는 원리가 단백질-단백질 결합을 지배하기 때문에 단백질 설계 알고리즘을 사용하여 설계될 수 있다.그러나 단백질-단백질 상호작용 설계는 단백질 설계에는 일반적으로 존재하지 않는 과제를 제시한다.가장 중요한 과제 중 하나는 일반적으로 단백질 사이의 계면이 단백질 코어보다 더 극성이며 결합은 용해와 수소 결합 [40]형성 사이의 균형을 수반한다는 것이다.이 과제를 극복하기 위해 Bruce Tidor와 동료들은 정전기의 기여에 초점을 맞추어 항체의 친화력을 향상시키는 방법을 개발했습니다.그들은 연구에서 설계된 항체의 경우, 계면에서 잔류물의 용해 비용을 줄이면 결합 [40][41][42]쌍의 친화력이 증가한다는 것을 발견했다.

스코어링 바인딩 예측

단백질 설계 에너지 기능은 결합 예측에 점수를 매기도록 조정되어야 한다. 결합은 자유 단백질의 가장 낮은 에너지 구성 사이의 균형을 수반하기 때문이다.EP그리고.EL결합 복합체의 최저 에너지 구성(EPL):

= L - - L { \ _ { G } =_ { } - E{ P } - _ {L} 。

K* 알고리즘은 자유 에너지 계산에 구조 엔트로피를 포함시킴으로써 알고리즘의 결합 상수를 근사합니다.K* 알고리즘은 자유 복합체와 결합 복합체 중 가장 낮은 에너지 구성만 고려합니다(세트로 표시됨).P,L,그리고.PL)는,[14] 각 복합체의 파티션 기능의 개산을 나타냅니다.

구체성을 고려한 설계

단백질-단백질 상호작용의 설계는 단백질이 많은 단백질과 상호작용할 수 있기 때문에 매우 구체적이어야 한다. 성공적인 설계는 선택적 결합제를 필요로 한다.따라서 단백질 설계 알고리즘은 온타깃(또는 포지티브 설계)과 오프타깃 결합(또는 네거티브 설계)[2][40]을 구별할 수 있어야 한다.특이성에 대한 설계의 가장 두드러진 예 중 하나는 Amy Keating과 동료가 20개의 bZIP 제품군 중 19개를 대상으로 한 특정 bZIP 결합 펩타이드의 설계이다. 이들 펩타이드의 8개는 [40][43][44]경쟁 펩타이드에 대한 의도된 파트너에게 특이적이었다.또한 앤더슨 및 동료는 신약 내성을 부여하는 약물 표적의 활성 부위의 돌연변이를 예측하기 위해 긍정 및 부정 설계를 사용했다. 긍정 설계는 야생형 활동을 유지하는 데 사용되었고 부정 설계는 약물의 [45]결합을 방해하기 위해 사용되었다.코스타스 마라나스와 동료들의 최근 컴퓨터 재설계는 칸디다 보이디니 자일로스 환원효소의 보조인자 특이성을 NADPH에서 [46]NADH로 실험적으로 전환할 수 있었다.

단백질 재포장

단백질 재표면은 단백질의 전체적인 주름, 코어 및 경계 영역을 그대로 유지하면서 단백질 표면을 설계하는 것으로 구성됩니다.단백질 재표면은 다른 단백질에 대한 단백질의 결합을 변화시키는데 특히 유용하다.단백질 재포장의 가장 중요한 적용 중 하나는 NIH 백신 연구 센터에서 광범위하게 중화되는 HIV 항체를 선택하기 위한 RSC3 프로브의 설계였다.먼저 gp120 HIV 엔벨로프 단백질과 이전에 발견된 b12-항체 사이의 결합 계면 바깥의 잔류물이 설계 대상으로 선택되었다.그런 다음 진화 정보, 용해성, 야생형과의 유사성 및 기타 고려사항에 기초하여 간격을 두고 배열이 선택되었다.그런 다음 RosettaDesign 소프트웨어를 사용하여 선택한 시퀀스 공간에서 최적의 시퀀스를 찾았습니다.RSC3는 나중에 장기 HIV 감염 비진행자의 [47]혈청에서 광범위하게 중화되는 항체 VRC01을 발견하기 위해 사용되었다.

구상단백질 설계

구상 단백질은 소수성 코어와 친수성 표면을 포함하는 단백질이다.구상 단백질은 여러 개의 구조를 가진 섬유 단백질과 달리 안정적인 구조를 가정합니다.구상 단백질의 3차원 구조는 일반적으로 섬유 단백질과 막 단백질보다 X선 결정학과 핵자기 공명을 통해 결정하기가 더 쉬우며, 이는 구상 단백질을 다른 유형의 단백질보다 단백질 설계에 더 매력적으로 만든다.대부분의 성공적인 단백질 설계에는 구상 단백질이 포함되어 있다.RSD-1과 Top7은 모두 구상 단백질의 새로운 설계였다.베이커 그룹에 의해 2012년에 5개의 단백질 구조가 추가로 설계, 합성 및 검증되었다.이러한 새로운 단백질은 생물학적 기능을 하지 않지만, 그 구조는 기능적인 활성 부위를 통합하기 위해 확장될 수 있는 빌딩 블록 역할을 하도록 의도되어 있다.구조는 2차 [48]구조를 지정하는 시퀀스 부분 간의 연결 루프를 분석하는 데 기초한 새로운 휴리스틱스를 사용하여 계산적으로 발견되었다.

막단백질 설계

다른 많은 막 관련 펩타이드 및 [50]단백질과 함께 몇몇 막 통과 단백질이 성공적으로 [49]설계되었다.최근 Costas Maranas와 그의 동료들은 E.coli에서 원하는 서브nm 크기로 Outer Membrane Porin Type-F(OmpF)의 모공 크기를 재설계하는 자동화된[51] 도구를 개발하여 이를 막에 조립하여 정확한 앙스트롬 스케일 분리를 수행했습니다.

기타 응용 프로그램

단백질 설계에서 가장 바람직한 용도 중 하나는 특정 화합물의 존재를 감지하는 단백질인 바이오센서이다.바이오센서 설계에는 TNT를 [52]포함한 부자연스러운 분자에 대한 센서가 포함되어 있습니다.최근에는 Kulman과 동료가 [53]PAK1의 바이오센서를 설계했습니다.

어떤 의미에서 단백질 설계는 배터리 [further explanation needed]설계의 하위 집합입니다.

「 」를 참조해 주세요.

레퍼런스

  1. ^ Korendovych, Ivan (March 19, 2018). "Minimalist design of peptide and protein catalysts". American Chemical Society. Retrieved March 22, 2018.
  2. ^ a b c d e f Richardson, JS; Richardson, DC (July 1989). "The de novo design of protein structures". Trends in Biochemical Sciences. 14 (7): 304–9. doi:10.1016/0968-0004(89)90070-4. PMID 2672455.
  3. ^ a b c Dahiyat, BI; Mayo, SL (October 3, 1997). "De novo protein design: fully automated sequence selection". Science. 278 (5335): 82–7. CiteSeerX 10.1.1.72.7304. doi:10.1126/science.278.5335.82. PMID 9311930.
  4. ^ a b Gordon, DB; Marshall, SA; Mayo, SL (August 1999). "Energy functions for protein design". Current Opinion in Structural Biology. 9 (4): 509–13. doi:10.1016/s0959-440x(99)80072-4. PMID 10449371.
  5. ^ a b Harbury, PB; Plecs, JJ; Tidor, B; Alber, T; Kim, PS (November 20, 1998). "High-resolution protein design with backbone freedom". Science. 282 (5393): 1462–7. doi:10.1126/science.282.5393.1462. PMID 9822371.
  6. ^ a b c Kuhlman, B; Dantas, G; Ireton, GC; Varani, G; Stoddard, BL; Baker, D (November 21, 2003). "Design of a novel globular protein fold with atomic-level accuracy". Science. 302 (5649): 1364–8. Bibcode:2003Sci...302.1364K. doi:10.1126/science.1089427. PMID 14631033. S2CID 1939390.
  7. ^ Sterner, R; Merkl, R; Raushel, FM (May 2008). "Computational design of enzymes". Chemistry & Biology. 15 (5): 421–3. doi:10.1016/j.chembiol.2008.04.007. PMID 18482694.
  8. ^ Wu, X; Yang, ZY; Li, Y; Hogerkorp, CM; Schief, WR; Seaman, MS; Zhou, T; Schmidt, SD; Wu, L; Xu, L; Longo, NS; McKee, K; O'Dell, S; Louder, MK; Wycuff, DL; Feng, Y; Nason, M; Doria-Rose, N; Connors, M; Kwong, PD; Roederer, M; Wyatt, RT; Nabel, GJ; Mascola, JR (August 13, 2010). "Rational design of envelope identifies broadly neutralizing human monoclonal antibodies to HIV-1". Science. 329 (5993): 856–61. Bibcode:2010Sci...329..856W. doi:10.1126/science.1187659. PMC 2965066. PMID 20616233.
  9. ^ Höcker, B (November 8, 2012). "Structural biology: A toolbox for protein design". Nature. 491 (7423): 204–5. Bibcode:2012Natur.491..204H. doi:10.1038/491204a. PMID 23135466. S2CID 4426247.
  10. ^ a b c Lovell, SC; Word, JM; Richardson, JS; Richardson, DC (August 15, 2000). "The penultimate rotamer library". Proteins. 40 (3): 389–408. CiteSeerX 10.1.1.555.4071. doi:10.1002/1097-0134(20000815)40:3<389::AID-PROT50>3.0.CO;2-2. PMID 10861930.
  11. ^ Shapovalov, MV; Dunbrack RL, Jr (June 8, 2011). "A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions". Structure. 19 (6): 844–58. doi:10.1016/j.str.2011.03.019. PMC 3118414. PMID 21645855.
  12. ^ a b Samish, I; MacDermaid, CM; Perez-Aguilar, JM; Saven, JG (2011). "Theoretical and computational protein design". Annual Review of Physical Chemistry. 62: 129–49. Bibcode:2011ARPC...62..129S. doi:10.1146/annurev-physchem-032210-103509. PMID 21128762.
  13. ^ a b Mandell, DJ; Kortemme, T (August 2009). "Backbone flexibility in computational protein design" (PDF). Current Opinion in Biotechnology. 20 (4): 420–8. doi:10.1016/j.copbio.2009.07.006. PMID 19709874.
  14. ^ a b c d e f Donald, Bruce R. (2011). Algorithms in Structural Molecular Biology. Cambridge, MA: MIT Press.
  15. ^ a b Boas, F. E. & Harbury, P. B. (2007). "Potential energy functions for protein design". Current Opinion in Structural Biology. 17 (2): 199–204. doi:10.1016/j.sbi.2007.03.006. PMID 17387014.
  16. ^ a b c d Boas, FE; Harbury, PB (April 2007). "Potential energy functions for protein design". Current Opinion in Structural Biology. 17 (2): 199–204. doi:10.1016/j.sbi.2007.03.006. PMID 17387014.
  17. ^ Vizcarra, CL; Mayo, SL (December 2005). "Electrostatics in computational protein design". Current Opinion in Chemical Biology. 9 (6): 622–6. doi:10.1016/j.cbpa.2005.10.014. PMID 16257567.
  18. ^ Zhou, T; Georgiev, I; Wu, X; Yang, ZY; Dai, K; Finzi, A; Kwon, YD; Scheid, JF; Shi, W; Xu, L; Yang, Y; Zhu, J; Nussenzweig, MC; Sodroski, J; Shapiro, L; Nabel, GJ; Mascola, JR; Kwong, PD (August 13, 2010). "Structural basis for broad and potent neutralization of HIV-1 by antibody VRC01". Science. 329 (5993): 811–7. Bibcode:2010Sci...329..811Z. doi:10.1126/science.1192819. PMC 2981354. PMID 20616231.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  19. ^ Mendes, J; Guerois, R; Serrano, L (August 2002). "Energy estimation in protein design". Current Opinion in Structural Biology. 12 (4): 441–6. doi:10.1016/s0959-440x(02)00345-7. PMID 12163065.
  20. ^ Pierce, NA; Winfree, E (October 2002). "Protein design is NP-hard". Protein Engineering. 15 (10): 779–82. doi:10.1093/protein/15.10.779. PMID 12468711.
  21. ^ a b Voigt, CA; Gordon, DB; Mayo, SL (June 9, 2000). "Trading accuracy for speed: A quantitative comparison of search algorithms in protein sequence design". Journal of Molecular Biology. 299 (3): 789–803. CiteSeerX 10.1.1.138.2023. doi:10.1006/jmbi.2000.3758. PMID 10835284.
  22. ^ Hong, EJ; Lippow, SM; Tidor, B; Lozano-Pérez, T (September 2009). "Rotamer optimization for protein design through MAP estimation and problem-size reduction". Journal of Computational Chemistry. 30 (12): 1923–45. doi:10.1002/jcc.21188. PMC 3495010. PMID 19123203.
  23. ^ "Machine learning reveals recipe for building artificial proteins". phys.org. Retrieved August 17, 2020.
  24. ^ Russ, William P.; Figliuzzi, Matteo; Stocker, Christian; Barrat-Charlaix, Pierre; Socolich, Michael; Kast, Peter; Hilvert, Donald; Monasson, Remi; Cocco, Simona; Weigt, Martin; Ranganathan, Rama (2020). "An evolution-based model for designing chorismatemutase enzymes". Science. 369 (6502): 440–445. Bibcode:2020Sci...369..440R. doi:10.1126/science.aba3304. PMID 32703877. S2CID 220714458.
  25. ^ Gordon, DB; Mayo, SL (September 15, 1999). "Branch-and-terminate: a combinatorial optimization algorithm for protein design". Structure. 7 (9): 1089–98. doi:10.1016/s0969-2126(99)80176-2. PMID 10508778.
  26. ^ a b Leach, AR; Lemon, AP (November 1, 1998). "Exploring the conformational space of protein side chains using dead-end elimination and the A* algorithm". Proteins. 33 (2): 227–39. CiteSeerX 10.1.1.133.7986. doi:10.1002/(sici)1097-0134(19981101)33:2<227::aid-prot7>3.0.co;2-f. PMID 9779790.
  27. ^ a b Kingsford, CL; Chazelle, B; Singh, M (April 1, 2005). "Solving and analyzing side-chain positioning problems using linear and integer programming". Bioinformatics. 21 (7): 1028–36. doi:10.1093/bioinformatics/bti144. PMID 15546935.
  28. ^ Yanover, Chen; Talya Meltzer; Yair Weiss (2006). "Linear Programming Relaxations and Belief Propagation – An Empirical Study". Journal of Machine Learning Research. 7: 1887–1907.
  29. ^ Wainwright, Martin J; Tommi S. Jaakkola; Alan S. Willsky (2005). "MAP estimation via agreement on trees: message-passing and linear programming". IEEE Transactions on Information Theory. 51 (11): 3697–3717. CiteSeerX 10.1.1.71.9565. doi:10.1109/tit.2005.856938. S2CID 10007532.
  30. ^ Kolmogorov, Vladimir (October 28, 2006). "Convergent tree-reweighted message passing for energy minimization". IEEE Transactions on Pattern Analysis and Machine Intelligence. 28 (10): 1568–1583. doi:10.1109/TPAMI.2006.200. PMID 16986540. S2CID 8616813.
  31. ^ Globerson, Amir; Tommi S. Jaakkola (2007). "Fixing max-product: Convergent message passing algorithms for MAP LP-relaxations". Advances in Neural Information Processing Systems.
  32. ^ Allen, BD; Mayo, SL (July 30, 2006). "Dramatic performance enhancements for the FASTER optimization algorithm". Journal of Computational Chemistry. 27 (10): 1071–5. CiteSeerX 10.1.1.425.5418. doi:10.1002/jcc.20420. PMID 16685715. S2CID 769053.
  33. ^ Desmet, J; Spriet, J; Lasters, I (July 1, 2002). "Fast and accurate side-chain topology and energy refinement (FASTER) as a new method for protein structure optimization". Proteins. 48 (1): 31–43. doi:10.1002/prot.10131. PMID 12012335. S2CID 21524437.
  34. ^ Baker, D (October 2010). "An exciting but challenging road ahead for computational enzyme design". Protein Science. 19 (10): 1817–9. doi:10.1002/pro.481. PMC 2998717. PMID 20717908.
  35. ^ Jiang, Lin; Althoff, Eric A.; Clemente, Fernando R.; Doyle, Lindsey; Rothlisberger, Daniela; Zanghellini, Alexandre; Gallaher, Jasmine L.; Betker, Jamie L.; Tanaka, Fujie (2008). "De Novo Computational Design of Retro-Aldol Enzymes". Science. 319 (5868): 1387–91. Bibcode:2008Sci...319.1387J. doi:10.1126/science.1152692. PMC 3431203. PMID 18323453.
  36. ^ Röthlisberger, Daniela; Khersonsky, Olga; Wollacott, Andrew M.; Jiang, Lin; Dechancie, Jason; Betker, Jamie; Gallaher, Jasmine L.; Althoff, Eric A.; Zanghellini, Alexandre (2008). "Kemp elimination catalysts by computational enzyme design". Nature. 453 (7192): 190–5. Bibcode:2008Natur.453..190R. doi:10.1038/nature06879. PMID 18354394.
  37. ^ Siegel, JB; Zanghellini, A; Lovick, HM; Kiss, G; Lambert, AR; St Clair, JL; Gallaher, JL; Hilvert, D; Gelb, MH; Stoddard, BL; Houk, KN; Michael, FE; Baker, D (July 16, 2010). "Computational design of an enzyme catalyst for a stereoselective bimolecular Diels-Alder reaction". Science. 329 (5989): 309–13. Bibcode:2010Sci...329..309S. doi:10.1126/science.1190239. PMC 3241958. PMID 20647463.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
  38. ^ Privett, HK; Kiss, G; Lee, TM; Blomberg, R; Chica, RA; Thomas, LM; Hilvert, D; Houk, KN; Mayo, SL (March 6, 2012). "Iterative approach to computational enzyme design". Proceedings of the National Academy of Sciences of the United States of America. 109 (10): 3790–5. Bibcode:2012PNAS..109.3790P. doi:10.1073/pnas.1118082108. PMC 3309769. PMID 22357762.
  39. ^ Chen, CY; Georgiev, I; Anderson, AC; Donald, BR (March 10, 2009). "Computational structure-based redesign of enzyme activity". Proceedings of the National Academy of Sciences of the United States of America. 106 (10): 3764–9. Bibcode:2009PNAS..106.3764C. doi:10.1073/pnas.0900266106. PMC 2645347. PMID 19228942.
  40. ^ a b c d Karanicolas, J; Kuhlman, B (August 2009). "Computational design of affinity and specificity at protein–protein interfaces". Current Opinion in Structural Biology. 19 (4): 458–63. doi:10.1016/j.sbi.2009.07.005. PMC 2882636. PMID 19646858.
  41. ^ Shoichet, BK (October 2007). "No free energy lunch". Nature Biotechnology. 25 (10): 1109–10. doi:10.1038/nbt1007-1109. PMID 17921992. S2CID 5527226.
  42. ^ Lippow, SM; Wittrup, KD; Tidor, B (October 2007). "Computational design of antibody-affinity improvement beyond in vivo maturation". Nature Biotechnology. 25 (10): 1171–6. doi:10.1038/nbt1336. PMC 2803018. PMID 17891135.
  43. ^ Schreiber, G; Keating, AE (February 2011). "Protein binding specificity versus promiscuity". Current Opinion in Structural Biology. 21 (1): 50–61. doi:10.1016/j.sbi.2010.10.002. PMC 3053118. PMID 21071205.
  44. ^ Grigoryan, G; Reinke, AW; Keating, AE (April 16, 2009). "Design of protein-interaction specificity gives selective bZIP-binding peptides". Nature. 458 (7240): 859–64. Bibcode:2009Natur.458..859G. doi:10.1038/nature07885. PMC 2748673. PMID 19370028.
  45. ^ Frey, KM; Georgiev, I; Donald, BR; Anderson, AC (August 3, 2010). "Predicting resistance mutations using protein design algorithms". Proceedings of the National Academy of Sciences of the United States of America. 107 (31): 13707–12. Bibcode:2010PNAS..10713707F. doi:10.1073/pnas.1002162107. PMC 2922245. PMID 20643959.
  46. ^ Khoury, GA; Fazelinia, H; Chin, JW; Pantazes, RJ; Cirino, PC; Maranas, CD (October 2009). "Computational design of Candida boidinii xylose reductase for altered cofactor specificity". Protein Science. 18 (10): 2125–38. doi:10.1002/pro.227. PMC 2786976. PMID 19693930.
  47. ^ Burton, DR; Weiss, RA (August 13, 2010). "AIDS/HIV. A boost for HIV vaccine design". Science. 329 (5993): 770–3. Bibcode:2010Sci...329..770B. doi:10.1126/science.1194693. PMID 20705840. S2CID 206528638.
  48. ^ Jessica Marshall (November 7, 2012). "Proteins made to order". Nature News. Retrieved November 17, 2012.
  49. ^ OPM 데이터베이스에서 막 통과 알파 헤어핀 단백질 설계
  50. ^ OPM 데이터베이스의 막 관련 펩타이드 및 단백질 설계
  51. ^ Chowdhury, Ratul; Kumar, Manish; Maranas, Costas D.; Golbeck, John H.; Baker, Carol; Prabhakar, Jeevan; Grisewood, Matthew; Decker, Karl; Shankla, Manish (September 10, 2018). "PoreDesigner for tuning solute selectivity in a robust and highly permeable outer membrane pore". Nature Communications. 9 (1): 3661. Bibcode:2018NatCo...9.3661C. doi:10.1038/s41467-018-06097-1. ISSN 2041-1723. PMC 6131167. PMID 30202038.
  52. ^ Looger, Loren L.; Dwyer, Mary A.; Smith, James J. & Hellinga, Homme W. (2003). "Computational design of receptor and sensor proteins with novel functions". Nature. 423 (6936): 185–190. Bibcode:2003Natur.423..185L. doi:10.1038/nature01556. PMID 12736688. S2CID 4387641.
  53. ^ Jha, RK; Wu, YI; Zawistowski, JS; MacNevin, C; Hahn, KM; Kuhlman, B (October 21, 2011). "Redesign of the PAK1 autoinhibitory domain for enhanced stability and affinity in biosensor applications". Journal of Molecular Biology. 413 (2): 513–22. doi:10.1016/j.jmb.2011.08.022. PMC 3202338. PMID 21888918.

추가 정보