튜링머신
Turing machine| 튜링머신 |
|---|
| 기계. |
| 변형 |
| 과학 |


튜링 기계는 [2]규칙의 표에 따라 테이프에 있는 기호를 조작하는[1] 추상적인 기계를 설명하는 수학적인 계산 모델입니다.모델의 단순성에도 불구하고 어떤 컴퓨터 [3]알고리즘도 구현할 수 있습니다.
이 기계는 기계의 알파벳이라고 불리는 유한한 집합의 기호들로부터 그려진 하나의 기호를 담을 수 있는 이산형 [5]셀들로 나누어진 무한한[4] 메모리 테이프에서 작동합니다.기계 작동의 어느 지점에서나 이 셀들 중 하나 위에 위치하는 "헤드"와 유한한 상태 집합에서 선택된 "상태"를 가지고 있습니다.작동의 각 단계에서 머리는 세포 안에 있는 기호를 읽습니다.그런 다음, 기호와 기계 자신의 현재 상태를 바탕으로 기계는 같은 셀에 기호를 쓰고, 왼쪽이나 [6]오른쪽으로 한 걸음 머리를 움직이거나 계산을 중단합니다.어떤 대체 기호를 쓸 것인지, 어떤 방향으로 머리를 움직일 것인지, 그리고 멈출 것인지의 선택은 현재 상태와 읽혀지는 기호의 각 조합에 대해 무엇을 할 것인지를 지정하는 유한한 표에 기초합니다.실제 컴퓨터 프로그램처럼 튜링 머신이 절대 멈추지 않는 무한 루프로 들어가는 것은 가능합니다.
튜링 기계는 1936년 앨런 튜링([7][8]Alan Turing)에 의해 발명되었는데, 그는 이것을 "a-machine" (자동 기계)[9]라고 불렀습니다.튜링의 박사학위 지도교수인 알론조 처치가 후에 [10]리뷰에서 "튜링 머신"이라는 용어를 만들어냈습니다.이 모델로 튜링은 부정적인 두 가지 질문에 답할 수 있었습니다.
- 테이프에 있는 임의의 기계가 "원형"인지(예: 정지 또는 계산 작업을 계속하지 못하는지)를 결정할 수 있는 기계가 존재합니까?
- 테이프에 임의의 기계가 주어진 [11][12]기호를 인쇄하는지 여부를 결정할 수 있는 기계가 존재합니까?
따라서 임의의 계산이 가능한 매우 간단한 장치에 대한 수학적 설명을 제공함으로써, 그는 일반적으로 계산의 특성을 증명할 수 있었고, 특히 Entscheidungs 문제('결정 문제')[13]의 계산 불가능성을 증명할 수 있었습니다.
튜링 기계는 기계적 [14]계산의 힘에 대한 근본적인 한계의 존재를 증명했습니다.그들은 임의의 계산을 표현할 수 있지만, 그들의 미니멀리즘 디자인은 실제로 계산하기에 너무 느립니다: 실제 컴퓨터는 튜링 기계와 달리 랜덤 액세스 메모리를 사용하는 다양한 디자인을 기반으로 합니다.
튜링 완성도는 계산 모델 또는 명령 시스템이 튜링 기계를 시뮬레이션하는 능력입니다.튜링이 완료된 프로그래밍 언어는 이론적으로 컴퓨터가 수행할 수 있는 모든 작업을 표현할 수 있습니다. 유한 메모리의 한계가 무시된다면 거의 모든 프로그래밍 언어는 튜링이 완료됩니다.
개요
튜링 머신은 컴퓨터가 수행하는 모든 데이터 조작을 제어하는 중앙 처리 장치(CPU)의 이상적인 모델로, 데이터를 저장하기 위해 순차 메모리를 사용하는 표준 머신입니다.일반적으로 순차 메모리는 기계가 읽기 및 쓰기 작업을 수행할 수 있는 무한 길이의 테이프로 표현됩니다.
형식 언어 이론의 맥락에서 튜링 기계(오토마톤)는 알파벳의 유효한 문자열의 임의의 부분 집합을 열거할 수 있습니다.이러한 방식으로 열거할 수 있는 문자열 집합을 재귀적으로 열거 가능한 언어라고 합니다.튜링 머신은 출력 문자열을 열거하는 것이 아니라 유효한 입력 문자열을 인식하는 모델로 동등하게 정의될 수 있습니다.
튜링 기계 M과 임의의 문자열이 주어지면, 일반적으로 M이 결국 생성할지 여부를 결정하는 것은 불가능합니다.이는 정지 문제가 해결할 수 없기 때문이며, 이는 컴퓨팅의 이론적 한계에 큰 영향을 미칩니다.
튜링 머신은 무제한 문법을 처리할 수 있으며, 이는 무한한 방법으로 1차 논리를 강력하게 평가할 수 있음을 의미합니다.이것은 람다 미적분학을 통해 유명하게 증명됩니다.
다른 튜링 기계를 시뮬레이션할 수 있는 튜링 기계는 범용 튜링 기계(UTM, 또는 간단히 범용 기계)라고 불립니다.또 다른 수학적 형식주의인 람다 미적분학은 알론조 교회에 의해 도입되었습니다.교회-튜링 논문의 기초를 형성하기 위해 튜링과 얽혀있는 교회의 작업.이 논문은 튜링 기계, 람다 미적분학,계산의 다른 유사한 형식주의는 논리학과 수학에서 효과적인 방법의 비공식적인 개념을 포착하고, 따라서 어떤 특정한 형식주의에 얽매이지 않고 수학적으로 정확한 방법으로 알고리즘이나 "기계적 절차"에 대해 추론할 수 있는 모델을 제공합니다.튜링 기계의 추상적인 특성을 연구하는 것은 컴퓨터 과학, 계산 가능성 이론, 그리고 복잡성 이론에 대한 많은 통찰력을 제공했습니다.
물리적 설명
튜링은 1948년에 발표한 "지능형 기계"에서 자신의 기계는 다음과 같이 기술했습니다.
...무한한 메모리 용량은 사각형으로 표시된 무한 테이프 형태로 얻어졌습니다. 각 테이프에는 기호를 인쇄할 수 있습니다.기계에는 언제든지 하나의 기호가 있습니다. 이 기호를 스캔 기호라고 합니다.기계는 스캔한 기호를 변경할 수 있으며, 기계의 동작은 부분적으로 해당 기호에 의해 결정되지만 다른 곳의 테이프에 있는 기호는 기계의 동작에 영향을 미치지 않습니다.그러나 테이프는 기계를 통해 앞뒤로 이동할 수 있으며, 이것은 기계의 기본적인 작동 중 하나입니다.따라서 테이프에 있는 기호는 결국 [15]이닝을 가질 수 있습니다.
— Turing 1948, p. 3[16]
묘사
튜링 기계는 테이프에 기계적으로 작동하는 기계를 수학적으로 모델링합니다.이 테이프에는 기계가 테이프 헤드를 사용하여 한 번에 하나씩 읽고 쓸 수 있는 기호가 있습니다.동작은 "상태 42에서 볼 수 있는 기호가 0이면 a를 쓰고, 볼 수 있는 기호가 1이면 상태 17로 변경하고, 상태 17에서 볼 수 있는 기호가 0이면 a를 쓰고 상태 6으로 변경합니다." 등의 유한한 기본 명령 집합에 의해 완전히 결정됩니다.원래 기사에서 튜링은 "계산 가능한 수에 대하여, 엔츠샤이둥스 문제에 대한 응용, 아래 참고문헌 참조"에서 메커니즘이 아니라 자신이 "컴퓨터"라고 부르는 사람을 상상하고, 이 사람은 이러한 결정론적인 기계적 규칙을 슬라브적으로 실행합니다.


튜링 머신은 다음과 같이 구성됩니다.
- 세포들로 나누어진 테이프, 하나는 옆에 있습니다.각각의 셀은 어떤 유한한 알파벳의 기호를 포함합니다.알파벳에는 특별한 공백 기호(여기서는 '0'으로 표기)와 하나 이상의 다른 기호가 포함되어 있습니다.테이프는 임의로 왼쪽과 오른쪽으로 확장할 수 있다고 가정하여 튜링 기계는 항상 계산에 필요한 만큼의 테이프를 공급받습니다.이전에 작성되지 않은 셀은 빈 기호로 채워지는 것으로 가정합니다.일부 모델에서는 테이프의 왼쪽 끝에 특별한 기호가 표시되어 있습니다. 테이프는 오른쪽으로 연장되거나 무한 확장 가능합니다.
- 테이프에 기호를 읽고 쓸 수 있는 헤드로, 한 번에 하나(및 하나만)의 셀을 좌우로 이동할 수 있습니다.일부 모델에서는 머리가 움직이고 테이프는 정지해 있습니다.
- 튜링 기계의 상태를 저장하는 상태 레지스터로, 이는 매우 많은 것 중 하나입니다.이 중에서 상태 레지스터가 초기화되는 특별 시작 상태가 있습니다.튜링은 이러한 상태들이 계산을 수행하는 사람이 보통 있을 "마음의 상태"를 대체한다고 썼습니다.
- 기계가 현재 있는 상태(qi)와 테이프에서 읽고 있는 기호(aj)가 주어졌을 때(현재 머리 아래에 있는 기호), 기계가 순서대로 다음을 수행하도록 지시하는 유한한[17] 명령어[18] 표입니다(5-튜플 모델의 경우).
- 기호를 지우거나 씁니다(a를 a로j1 바꿉니다j).
- 헤드를 이동합니다(d로k 설명되며 한 걸음 왼쪽의 경우 'L' 또는 한 걸음 오른쪽의 경우 'R' 또는 한 걸음 오른쪽의 경우 'N' 값을 가질 수 있습니다.
- 규정된 대로 동일한 상태 또는 새로운 상태를 가정합니다(상태i1 q로 이동).
4-튜플 모델에서는 기호(aj1)를 지우거나 쓰는 것과 머리를 왼쪽 또는 오른쪽(dk)으로 움직이는 것이 별도의 지침으로 지정됩니다.표는 (ia) 기호를 지우거나 쓰거나 (ib) 머리를 왼쪽 또는 오른쪽으로 움직이도록 기계에 지시한 다음, (ii) 규정된 대로 동일한 또는 새로운 상태를 가정하지만, 동일한 명령에서 동작 (ia)와 (ib) 둘 다는 하지 않습니다.일부 모델에서는 표에 기호와 상태의 현재 조합에 대한 항목이 없으면 기계가 중지되고, 다른 모델에서는 모든 항목을 채워야 합니다.
기계의 모든 부분(즉, 기계의 상태, 기호 모음, 주어진 시간에 사용된 테이프)과 작업(인쇄, 지우기 및 테이프 모션 등)은 유한하고 개별적이며 구별 가능합니다. 무제한의 테이프와 런타임을 통해 무한한 양의 스토리지 공간을 확보할 수 있습니다.
형식적 정의
Hopcroft & Ullman (1979, 페이지 148)에 이어 a (한 테이프)튜링 기계는 공식적으로 M = ⟨ γ ,δ , 0 , F ⟩ M =\ Qdisplay 로 정의될 수 있습니다.
- \Gamma은(는) 유한하고 비어 있지 않은 테이프 알파벳 기호 집합입니다.
- {\ \Gamma는 공백 기호(계산 중 어느 단계에서든 테이프에서 무한히 자주 발생할 수 있는 유일한 기호)입니다.
- { { b} {\\{b\}}는 입력 기호의 집합, 즉 초기 테이프 내용에 나타나는 것이 허용되는 기호의 집합입니다;
- Q Q은(는) 유한하고 비어 있지 않은 상태 집합입니다.
- q Q이(가) 초기 상태입니다.
- Q F Q은(는) 최종 상태 또는 수락 상태의 집합입니다.초기 테이프 내용은 F {\ F 에서 최종적으로 중지되는 경우 M M에서 허용된다고 합니다.
- :(∖ { l \ r {,R} \delta Q \R\}}는 전이 함수라고 불리는 부분 함수이며, 여기서 L은 왼쪽 시프트, R은 오른쪽 시프트입니다.현재 상태 및 현재 테이프 기호에 δ 이(가) 정의되어 있지 않으면 시스템이 중단됩니다. 직관적으로 전환 기능은 현재 상태에서 전환된 다음 상태를 지정합니다. 이 상태는 헤드가 가리키는 현재 기호를 덮어쓰는 기호이며 다음 헤드 이동입니다.

상대적으로 흔하지 않은 변형은 방향 {L {\,R의 세 번째 요소로서 "이동 없음"을 허용합니다.
3-상태 비지 비버를 위한 7-튜플은 다음과 같습니다(튜링 기계 예제에서 비지 비버에 대해 더 자세히 참조).
- 상태);
- = 1 {\ \1\}(알파벳 기호 포함);
- {\ b =}(공백 기호);
- = {\ \Sima \}}(입력 기호);
- 초기 상태);
- 최종 상태);
- ◦={\ \transiton =} 아래의 상태표(transition function)를 하십시오.
처음에는 모든 테이프 셀이 0{\ 0)로 표시됩니다.
| 테이프 기호 | 현재상태A | 현재상태B | 현재상태C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 기호 쓰기 | 테이프이동 | 다음상태 | 기호 쓰기 | 테이프이동 | 다음상태 | 기호 쓰기 | 테이프이동 | 다음상태 | |
| 0 | 1 | R | B | 1 | L | A | 1 | L | B |
| 1 | 1 | L | C | 1 | R | B | 1 | R | 멈춤 |
튜링 머신을 시각화하거나 구현하는 데 필요한 추가 세부 정보
van Emde Boas (1990)의 말에 따르면, p. 6: "[위와 유사한 그의 공식적인 7-튜플 설명]은 기계가 어떻게 행동하고 계산이 어떻게 보일지에 대한 부분적인 정보만을 제공합니다."
예를 들어.
- 기호가 실제로 어떻게 생겼는지에 대한 많은 결정과 기호를 무한정 읽고 쓰는 실패 방지 방식이 필요할 것입니다.
- 왼쪽 시프트 및 오른쪽 시프트 작업은 테이프 헤드를 가로질러 이동시킬 수 있지만 실제로 튜링 기계를 만들 때는 테이프 헤드를 머리 아래로 앞뒤로 미끄러지도록 하는 것이 더 실용적입니다.
- 테이프는 유한하고 필요에 따라 빈칸으로 자동 확장될 수 있지만(수학적 정의에 가장 가까운), 한쪽 또는 양쪽 끝에서 무한히 뻗어나가고 테이프 헤드가 명시적으로 주어진 유한 조각을 제외하고 빈칸으로 미리 채워진 것으로 생각하는 것이 더 일반적입니다. (물론 이는(실제로는 구현할 수 없습니다.)테이프의 길이는 고정할 수 없습니다. 테이프가 입력 크기에 비례하는 경우 선형 경계 오토마톤, 엄격하게 고정된 길이인 경우 유한 상태 머신으로 기계가 수행할 수 있는 계산 범위가 심각하게 제한되기 때문입니다.
대체 정의
문헌의 정의는 때때로 주장이나 증명을 더 쉽게 또는 더 명확하게 하기 위해 약간씩 다르지만, 이것은 항상 결과 기계가 동일한 계산 능력을 갖도록 하는 방식으로 이루어집니다.예를 들어 집합을 { {\\{에서 {\,N로 변경할 수 있습니다. 여기서 N("없음" 또는 "No-operation")은 컴퓨터를 왼쪽 또는 오른쪽으로 이동하지 않고 동일한 테이프 셀에 유지할 수 있습니다.이것은 기계의 계산 능력을 증가시키지 않을 것입니다.
가장 일반적인 규약은 튜링/데이비스(1936)의 규약에 따라 "튜링 테이블"의 각 "튜링 지시"를 9개의 5개의 튜링 중 하나로 나타냅니다(The Undecable, p. 126–127 and Davis(2000) p. 152).
- (정의 1): (qi, Sj, Sk/E/N, L/R/Nm, q)
- (현재 상태i q, 스캔한j 기호 S, 인쇄 기호k S/소거 E/non N, move_tape_one_square left L/오른쪽 R/non N, 새 상태m q )
다른 저자들(Minsky (1967) p. 119, Hopcroft and Ullman (1979) p. 158, Stone (1972) p. 9)은 스캔된 기호j S 바로 뒤에 새로운 상태m q가 나열되는 다른 관습을 채택합니다:
- (정의 2): (qi, Sjm, q, Sk/E/N, L/R/N)
- (현재 상태i q, 스캔한j 기호 S, 새 상태m q, 인쇄 기호k S/소거 E/non N, move_tape_one_square left L/오른쪽 R/non N )
이 문서의 나머지 부분에는 "정의 1"(튜링/데이비스 협약)이 사용됩니다.
| 현재상태 | 스캔기호 | 인쇄기호 | 테이프이동 | 최종(즉, 다음) 상태 | 5분의 1 | |
|---|---|---|---|---|---|---|
| A | 0 | 1 | R | B | (A, 0, 1, R, B) | |
| A | 1 | 1 | L | C | (A, 1, 1, L, C) | |
| B | 0 | 1 | L | A | (B, 0, 1, L, A) | |
| B | 1 | 1 | R | B | (B, 1, 1, R, B) | |
| C | 0 | 1 | L | B | (C, 0, 1, L, B) | |
| C | 1 | 1 | N | H | (C, 1, 1, N, H) |
다음 표에서 튜링의 원래 모델은 그가 N1, N2, N3 (cf)라고 불렀던 처음 세 줄만 허용했습니다.미결판의 튜링, 페이지 126).그는 0번째 기호 S = "margo" 또는 "blank" 등의 이름을 붙여 "margo square"를 지우도록 허용했습니다.그러나 그는 비인쇄를 허용하지 않았으므로 모든 명령행은 "인쇄 기호k S" 또는 "지우기"를 포함합니다(post(1947)의 각주 12 참조, The Undecable, p. 300).약어는 튜링(Turing)의 것입니다(The Undecision, p. 119).1936-1937년 튜링의 최초 논문 이후 기계 모델은 9가지 유형의 다섯 개의 튜플을 모두 허용했습니다.
| 현재 m-구성 (튜링 상태) | 테이프 기호 | 인쇄작업 | 테이프 모션 | 최종 m-구성 (튜링 상태) | 5분의 1의 | 5분의 1의 코멘트 | 사분의 일 | |
|---|---|---|---|---|---|---|---|---|
| N1 | qi | ㅅj | 인쇄k( S) | 왼쪽L | qm | (qi, Sj, Sk, L, qm) | "공백" = S, 1=S 등 | |
| N2 | qi | ㅅj | 인쇄k( S) | 오른쪽 R | qm | (qi, Sj, Sk, R, qm) | "공백" = S, 1=S 등 | |
| N3 | qi | ㅅj | 인쇄k( S) | 없음N | qm | (qi, Sj, Sk, N, qm) | "공백" = S, 1=S 등 | (qi, Sj, Sk, qm) |
| 4 | qi | ㅅj | 없음N | 왼쪽L | qm | (qi, Sj, N, L, qm) | (qi, Sj, L, qm) | |
| 5 | qi | ㅅj | 없음N | 오른쪽 R | qm | (qi, Sj, N, R, qm) | (qi, Sj, R, qm) | |
| 6 | qi | ㅅj | 없음N | 없음N | qm | (qi, Sj, N, N, qm) | 직접 "점프" | (qi, Sj, N, qm) |
| 7 | qi | ㅅj | 지우다 | 왼쪽L | qm | (qi, Sj, E, L, qm) | ||
| 8 | qi | ㅅj | 지우다 | 오른쪽 R | qm | (qi, Sj, E, R, qm) | ||
| 9 | qi | ㅅj | 지우다 | 없음N | qm | (qi, Sj, E, N, qm) | (qi, Sj, E, qm) |
모든 튜링 테이블(명령어 목록)은 위의 9개의 5-튜플로 구성할 수 있습니다.기술적인 이유로 세 가지 비인쇄 또는 "N" 지침(4, 5, 6)을 일반적으로 사용할 수 있습니다.예를 들어 튜링 머신의 예를 참조합니다.
4-튜플의 사용은 덜 빈번하게 발생합니다: 이것들은 튜링 명령의 추가적인 무화를 나타냅니다(cf).Post(1947), Boolos & Jeffrey(1974, 1999), Davis-Sigal-Weyuker(1994); 또한 Post-Turing 기계에서 자세히 보기.
"상태"
튜링 기계의 맥락에서 사용되는 "상태"라는 단어는 두 가지를 의미할 수 있기 때문에 혼란의 원인이 될 수 있습니다.튜링 이후의 대부분의 주석가들은 수행할 현재 명령의 이름/지정자, 즉 상태 레지스터의 내용을 의미하는 "상태"를 사용했습니다.그러나 Turing (1936)은 그가 기계의 "m-configuration"이라고 부르는 것의 기록과 계산을 통해 기계의 (또는 사람의) "진행 상태", 즉 전체 시스템의 현재 상태를 강하게 구별했습니다.튜링이 "상태 공식"이라고 부른 것은 현재의 명령어와 테이프의 모든 기호를 모두 포함합니다.
따라서 어느 단계에서든 계산의 진행 상태는 테이프의 지시사항과 기호에 따라 완전히 결정됩니다.즉, 시스템의 상태는 테이프의 기호로 구성된 단일 표현(기호 시퀀스)과 δ(다른 곳에서는 나타나지 않아야 함), 그리고 지시 사항의 메모에 의해 설명될 수 있습니다.이 식을 "상태 공식"이라고 합니다.
— The Undecidable, pp. 139–140, emphasis added
그의 논문 초기에 튜링은 이것을 더욱 발전시켰습니다. 그는 테이프의 모든 기호와 함께 스캔된 사각형 아래에 현재 "m-구성"(명령어의 라벨) 기호를 배치한 예를 제시했습니다(The Undecision, p. 121). 이것을 "완전한 구성"(The Undecision, p. 118).한 줄에 "완전한 구성"을 인쇄하려면 스캔한 기호의 왼쪽에 상태 레이블/m-구성을 배치합니다.
이 변형은 Kleene(1952)에서 볼 수 있는데, 여기서 Kleene은 기계의 "상황"의 괴델 수를 쓰는 방법을 보여줍니다. 그는 "m-configuration" 기호4 q를 테이프의 대략 6개의 빈 칸의 중앙에 스캔된 칸 위에 놓고(이 글의 튜링 테이프 그림 참조) 스캔된 칸의 오른쪽에 놓습니다.그러나 Kleene은 "q4" 그 자체를 "기계 상태"라고 말합니다(Kleene, p. 374–375).Hopcroft와 Ullman은 이 합성을 "즉시 기술"이라고 부르며 스캔된 기호의 왼쪽에 "현재 상태"(명령어-라벨, m-구성)를 두는 튜링 규칙을 따릅니다(149쪽). 즉, 순간 기술은 공백이 아닌 기호의 왼쪽, 기계의 상태, 현재 기호의 합성입니다.머리로 스캔하고 오른쪽에 빈 기호가 없습니다.
예: 3 "이동" 후 3-상태 2-심볼 비지 비버의 총 상태(아래 그림의 "실행" 예에서 따옴):
- 1A1
이것은 세 번의 움직임 후에 테이프가...000110000 ...그 위에서, 머리는 가장 오른쪽에 있는 1을 스캔하고 있고, 상태는 A입니다.공백(이 경우 "0"s로 표시됨)은 여기에 표시된 것과 같이 전체 상태의 일부가 될 수 있습니다. B01; 테이프에는 1개의 테이프가 있지만 머리는 0("공백")을 왼쪽으로 스캔하고 있으며 상태는 B입니다.
튜링 기계의 맥락에서 "상태"는 설명되는 것으로 명확히 해야 합니다: 현재 명령어, 또는 현재 명령어와 함께 테이프의 기호 목록, 또는 스캔된 기호의 왼쪽 또는 오른쪽에 배치된 현재 명령어와 함께 테이프의 기호 목록.
튜링의 전기 작가 앤드류 호지스(1983: 107)는 이러한 혼란을 지적하고 논의했습니다.
"상태" 다이어그램
| 테이프 기호 | 현재상태A | 현재상태B | 현재상태C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 기호 쓰기 | 테이프이동 | 다음상태 | 기호 쓰기 | 테이프이동 | 다음상태 | 기호 쓰기 | 테이프이동 | 다음상태 | |
| 0 | P | R | B | P | L | A | P | L | B |
| 1 | P | L | C | P | R | B | P | R | 멈춤 |

오른쪽: 위의 표는 "상태 전이" 다이어그램으로 표현됩니다.
일반적으로 큰 테이블이 테이블 왼쪽에 있는 것이 좋습니다(Booth, 페이지 74).이들은 표 형태의 컴퓨터로 보다 쉽게 시뮬레이션됩니다(Booth, 페이지 74).그러나 특정 개념, 예를 들어 "재설정" 상태를 가진 기계와 반복 패턴을 가진 기계(cf).Hill and Peterson p. 244ff)—그림으로 볼 때 더 쉽게 볼 수 있습니다.
그림이 표의 개선사항을 나타내는지 여부는 독자가 특정 맥락에 대해 결정해야 합니다.
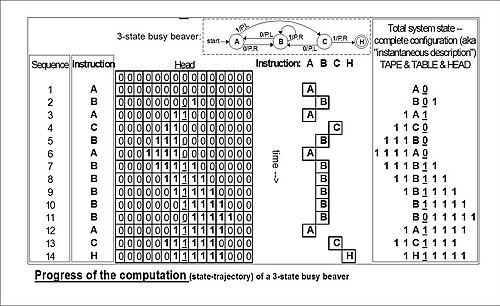
이러한 도표는 시간과 공간을 통한 계산 과정("궤적")이 아니라 시간에 동결된 표의 스냅샷을 나타낸다는 점에 독자는 다시 한 번 주의해야 합니다.바쁜 비버 머신이 "실행"될 때마다 항상 같은 상태 궤도를 따르지만, 이는 가변 입력 "파라미터"를 제공받을 수 있는 "복사" 머신의 경우에는 해당되지 않습니다.
"계산의 진행"이라는 다이어그램은 세 상태의 바쁜 비버의 "상태"(명령) 진행을 처음부터 끝까지 보여줍니다.맨 오른쪽에는 각 단계의 튜링 "완전한 구성"(클라인 "상황", 홉크로프트-울만 "즉각 묘사")이 있습니다.기계를 정지시키고 클리어하여 "상태 레지스터"와 테이프 전체를 블랭크할 경우, 이러한 "구성"을 사용하여 진행 중인 모든 곳에서 계산을 다시 시작할 수 있습니다(cf).튜링(Turing, 1936) 결정할 수 없는 것, 페이지 139-140).
등가 모델
단순한 보편적 튜링 기계보다 더 많은 계산 능력을 가지고 있다고 생각될 수 있는 많은 기계들은 더 이상의 힘을 가지고 있지 않다고 보여질 수 있습니다(Hopcroft and Ullman p. 159, cf).민스키(1967).연산 속도가 빨라지거나, 메모리 사용량이 적거나, 명령어 집합이 작아질 수도 있지만, 더 강력한 연산(즉, 더 많은 수학적 함수)을 수행할 수는 없습니다.(교회-튜링 논문은 어떤 종류의 기계에서도 이것이 사실이라고 가정합니다: "계산"될 수 있는 모든 것은 어떤 튜링 기계에 의해 계산될 수 있다는 것입니다.
튜링 머신은 스택의 선입선출(LIFO) 요구 사항을 완화하여 보다 유연하고 간결하게 만든 단일 스택 푸시다운 오토마톤(PDA)과 동등합니다.또한 튜링 기계는 머리 부분의 왼쪽 테이프를 모델링하고 오른쪽 테이프를 모델링하는 하나의 스택을 사용함으로써 표준 LIFO 의미론을 가진 2 스택 PDA와 동등합니다.
다른 극단적인 경우, 일부 매우 단순한 모델은 튜링과 동등한 것으로 판명됩니다. 즉, 튜링 기계 모델과 동일한 계산 능력을 갖는 것입니다.
일반적인 등가 모델은 다중 테이프 튜링 기계, 다중 트랙 튜링 기계, 입력 및 출력이 있는 기계 및 비결정론 튜링 기계(NDTM)이며, 이는 액션 테이블이 심볼 및 상태의 각 조합에 대해 최대 하나의 엔트리를 갖는 결정론적 튜링 기계(DTM)와 반대입니다.
읽기 전용, 오른쪽으로 움직이는 튜링 기계는 DFA와 동등합니다(NDFA에서 DFA로 변환 알고리즘을 사용하여 변환하는 NFA뿐만 아니라).
실용적이고 실용적인 목적을 위해 동등한 레지스터 머신을 일반적인 어셈블리 프로그래밍 언어로 사용할 수 있습니다.
관련 질문은 구체적인 프로그래밍 언어로 표현되는 계산 모델이 튜링 등가인지 여부입니다.실제 컴퓨터의 계산은 유한한 상태를 기반으로 하기 때문에 튜링 기계를 시뮬레이션 할 수는 없지만 프로그래밍 언어 자체가 반드시 이러한 한계를 가지고 있는 것은 아닙니다.Kirner et al., 2009는 범용 프로그래밍 언어 중 일부는 튜링이 완전한 반면 다른 언어는 그렇지 않다는 것을 보여주었습니다.예를 들어, ANSIC의 모든 인스턴스(표준이 레거시 이유로 특정 동작을 의도적으로 정의하지 않은 상태로 두므로 다른 인스턴스가 가능함)는 유한 공간 메모리를 의미하므로 ANSIC는 튜링과 동등하지 않습니다.이는 포인터라고 불리는 메모리 참조 데이터 유형의 크기가 언어 내부에서 액세스 가능하기 때문입니다.그러나 파스칼과 같은 다른 프로그래밍 언어에는 이러한 기능이 없으므로 원칙적으로 튜링이 완벽하게 수행될 수 있습니다.프로그래밍 언어의 메모리 할당이 실패하도록 허용되는 것처럼 원칙적으로 튜링이 완료된 것일 뿐입니다. 즉, 실패한 메모리 할당을 무시할 때 프로그래밍 언어는 튜링이 완료될 수 있지만 실제 컴퓨터에서 실행 가능한 컴파일된 프로그램은 완료될 수 없습니다.
c-machine, oracle o-machine 선택
그의 논문 초기(1936)에 튜링은 "자동 기계"(구성에 의해 완전히 결정되는 움직임)와 "선택 기계"(선택 기계)를 구별했습니다.
...오디오 모션은 구성에 의해 부분적으로만 결정됩니다...이러한 기계가 이러한 모호한 구성 중 하나에 도달하면 외부 운영자가 임의로 선택할 때까지 계속 진행할 수 없습니다.만약 우리가 공리계를 다루기 위해 기계를 사용한다면 이는 사실일 것입니다.
— The Undecidable, p. 118
튜링(1936)은 선택 기계를 사용하는 대신 a-기계를 사용하여 "[힐베르트] 미적분학의 모든 증명 가능한 공식을 찾는" 방법을 설명하는 각주 외에는 더 자세히 설명하지 않습니다.그는 "선택은 항상 두 가지 가능성 0과 1 사이에 있다고 가정합니다.각 증명은 i, i, ..., i(i = 0 또는 1, i = 0 또는 1, ..., i = 0 또는 1)의 순서로 결정되며, 따라서 숫자 2 + i2 + i2 + i2 + ...+내가n 증명을 완전히 결정합니다.자동 기계는 연속적으로 증명 1, 증명 2, 증명 3, ..."을 수행합니다(각주 ‡, The Undecision, 페이지 138).
이것은 실제로 결정론적(즉, a-) 튜링 기계가 비결정론적 튜링 기계의 작용을 모방하기 위해 사용될 수 있는 기술입니다.튜링은 이 문제를 각주로 풀었고 더 이상의 고려에서 제외한 것으로 보입니다.
오라클 머신(Oracle machine) 또는 o-머신(o-machine)은 계산을 완료하기 위해 "기계가 될 수 없다고 말하는 것 외에" 특정되지 않은 개체인 "오라클"의 결정을 "기다리는" 튜링 a-머신입니다(Turing(1939), The Undecable, p. 166–168).
유니버설 튜링 머신

튜링은 결정할 수 없는 것에서 다음과 같이 썼습니다. 128쪽 (이탤릭체 추가):
계산 가능한 시퀀스를 계산하는 데 사용할 수 있는 단일 기계를 발명하는 것은 가능합니다.만약 이 기계 U가 어떤 계산기 M의 세미콜론으로 구분된 5중의 문자열로 시작하는 테이프와 함께 공급된다면, U는 M과 같은 수열을 계산할 것입니다.
이 발견은 이제 당연하게 여겨지지만, 그 당시 (1936년)에는 놀라운 [citation needed]것으로 여겨졌습니다.튜링이 "보편적 기계"라고 부른 계산 모델.U'는 줄여서 어떤 사람들은 (cf)라고 생각합니다.Davis(2000)는 저장 프로그램 컴퓨터의 개념을 이끈 근본적인 이론적 돌파구였습니다.
튜링의 논문은... 본질적으로 현대 컴퓨터의 발명과 그에 수반된 프로그래밍 기술의 일부를 포함하고 있습니다.
— Minsky (1967), p. 104
계산 복잡도 측면에서 멀티 테이프 범용 튜링 기계는 시뮬레이션하는 기계에 비해 로그 인자별로 느릴 뿐입니다.이 결과는 1966년 F. C. Hennie와 R. E. Stearns에 의해 얻어졌습니다. (Arora and Barak, 2009, 정리 1.9)
실제 기계와의 비교

튜링 기계는 더 단순한 오토마타와 달리 실제 기계만큼 강력하고 실제 프로그램이 할 수 있는 어떤 동작도 실행할 수 있다고 종종[according to whom?] 여겨집니다.이 진술에서 무시되는 것은 실제 기계는 유한한 수의 구성만 가질 수 있기 때문에 유한 상태의 기계에 불과하지만 튜링 기계는 계산에 사용할 수 있는 무제한의 저장 공간을 가지고 있다는 것입니다.
튜링 기계가 실제 컴퓨터의 유용한 모델인 이유를 설명하는 여러 가지 방법이 있습니다.
- 실제 컴퓨터가 계산할 수 있는 모든 것, 튜링 기계도 계산할 수 있습니다.예를 들어, "튜링 머신은 재귀적 절차 및 알려진 매개 변수 전달 메커니즘을 포함하여 프로그래밍 언어에서 발견되는 모든 유형의 서브루틴을 시뮬레이션할 수 있습니다"(Hopcroft and Ullman p. 157).또한 충분히 큰 FSA는 IO와 상관없이 실제 컴퓨터를 모델링할 수 있습니다.따라서 튜링 기계의 한계에 대한 진술은 실제 컴퓨터에도 적용될 것입니다.
- 차이점은 튜링 기계가 무한한 양의 데이터를 조작할 수 있는 능력에만 있습니다.그러나 튜링 기계(실제 기계와 같은)는 유한한 양의 데이터만 조작할 수 있습니다.
- 튜링 기계처럼 실제 기계는 더 많은 디스크나 다른 저장 매체를 획득함으로써 필요에 따라 저장 공간을 넓힐 수 있습니다.
- 단순한 추상 모델을 사용하는 실제 기계 프로그램에 대한 설명은 튜링 기계를 사용하는 설명보다 훨씬 더 복잡한 경우가 많습니다.예를 들어, 알고리즘을 설명하는 튜링 기계는 수백 개의 상태를 가질 수 있는 반면, 주어진 실제 기계의 등가 결정론적 유한 오토마톤(DFA)은 쿼드릴리온을 가질 수 있습니다.이로 인해 DFA 표현을 분석할 수 없게 됩니다.
- 튜링 기계는 메모리 사용량과 무관하게 알고리즘을 설명합니다.현재 기계가 가지고 있는 메모리에는 한계가 있지만, 이 한계는 시간에 따라 임의로 증가할 수 있습니다.튜링 머신은 기존 컴퓨팅 머신 아키텍처의 발전에 관계없이 (이론적으로) 영원히 유지될 알고리즘에 대한 진술을 할 수 있게 해줍니다.
- 튜링 기계는 [dubious ]알고리즘의 설명을 단순화합니다.튜링과 동등한 추상적 기계에서 실행되는 알고리즘은 임의의 정밀도 데이터 유형을 사용할 수 있고 메모리 부족을 포함하지는 않지만 예기치 않은 조건을 처리할 필요가 없기 때문에 실제 기계에서 실행되는 알고리즘보다 일반적입니다.

한계
계산 복잡도 이론
튜링 기계의 한계는 특정 배열의 강점을 잘 모델링하지 못한다는 것입니다.예를 들어, 현대의 저장 프로그램 컴퓨터는 실제로 랜덤 액세스 저장 프로그램 기계 또는 RASP 기계 모델로 알려진 보다 구체적인 형태의 추상 기계의 예입니다.범용 튜링 기계와 마찬가지로, RASP는 유한 상태 기계의 명령어 외부에 있는 "메모리"에 프로그램을 저장합니다.보편적 튜링 기계와 달리, RASP는 임의의 정수(cf)를 포함할 수 있는 메모리 "셀"인 구별 가능하고 번호가 매겨진 무한한 수의 "레지스터"를 가지고 있습니다.엘곳과 로빈슨(1964), 하트마니스(1971), 특히 쿡-리쇼(1973); 랜덤 액세스 머신에서의 참조).RASP의 유한 상태 기계에는 간접 주소 지정 기능이 탑재되어 있습니다(예: 한 레지스터의 내용을 다른 레지스터를 지정하는 주소로 사용할 수 있습니다). 따라서 RASP의 "프로그램"은 레지스터 시퀀스의 모든 레지스터를 주소 지정할 수 있습니다.이 구별의 결과는 일반적인 튜링 기계에서는 불가능한 기억 지수에 기초하여 수행될 수 있는 계산 최적화가 있다는 것입니다. 따라서 튜링 기계가 러닝 타임을 제한하는 기초로 사용될 때,"허위 하한"은 특정 알고리즘의 실행 시간에서 증명될 수 있습니다(튜링 기계의 잘못된 단순화 가정으로 인해).튜링 머신 모델이 아닌 계산의 RASP 모델을 사용할 때 더 빠르게 수행되는 것을 보여줄 수 있는 알고리즘인 이진 탐색이 그 예입니다.
상호작용
컴퓨팅 초기에 컴퓨터 사용은 일반적으로 주어진 입력 데이터로부터 출력 데이터를 각각 생성하는 배치 처리(즉, 대화형 작업이 아닌 작업)로 제한되었습니다.튜링 기계가 발명된 입력에서 출력까지의 함수의 계산 가능성을 연구하는 계산 가능성 이론은 이러한 관행을 반영합니다.
1970년대부터 컴퓨터의 상호작용적인 사용이 훨씬 더 일반적이 되었습니다.원칙적으로 외부 에이전트를 테이프에서 읽고 튜링 기계와 동시에 쓰기를 통해 모델링할 수 있지만 실제로 상호 작용이 일어나는 방식과 일치하는 경우는 거의 없습니다. 따라서 상호 작용을 설명할 때 I/O 오토마타와 같은 대안이 선호됩니다.
역사
역사적 배경 : 계산기계
앨런 튜링 (1912–1954)의 제자이자 평생 친구였던 로빈 간디 (1919–1995)는 "계산 기계"라는 개념의 계통을 찰스 배비지 (1834년경)로 거슬러 올라가 실제로 "배비지의 논문"을 제안합니다.
분석의 모든 개발과 운영은 이제 기계에 의해 실행될 수 있습니다.
— (italics in Babbage as cited by Gandy, p. 54)
배비지의 분석 엔진에 대한 간디의 분석은 다음과 같은 다섯 가지 작업을 설명합니다(cf. 52-53).
- 산술 함수 +, -, ×, 여기서 -는 y ≥ x이면 "적절한" 뺄셈 x - y = 0을 나타냅니다.
- 모든 연산 순서는 연산입니다.
- 작업의 반복(작업 P의 n번 반복).
- 조건부 반복(시험 T의 "성공"에 대한 조건부 작업 P의 n번 반복).
- 조건부 이동(즉, 조건부 "Go to").
간디는 "(1), (2), (4)에 의해 계산될 수 있는 함수는 정확히 튜링이 계산할 수 있는 함수이다"라고 말합니다(53쪽).그는 Percy Ludgate (1909), Leonardo Torres Quevedo (1914),[20][21] Maurice d'Ocagne (1922), Louis Couffignal (1933), Vannevar Bush (1936), Howard Aiken (1937)의 제안을 포함한 "보편적 계산기"에 대한 다른 제안들을 인용합니다.단,
… 산술 연산의 고정된 반복 가능한 시퀀스를 프로그래밍하는 데 중점을 둡니다.일반적인 계산 기계 이론에 대한 조건부 반복과 조건부 전달의 근본적인 중요성은 인식되지 않고 있습니다.
— Gandy p. 55
Entscheidungs 문제("결정 문제"):1900년 힐베르트의 열 번째 문제.
1900년에 유명한 수학자 데이비드 힐버트가 제기한 힐버트의 문제와 관련하여, 문제 #10의 한 측면은 정확한 틀이 만들어지기 전까지 거의 30년 동안 떠돌았습니다.10번에 대한 힐베르트의 원래 표현은 다음과 같습니다.
10. 디오판토스 방정식의 용해도 결정.알 수 없는 양의 임의의 숫자와 합리적인 적분 계수를 갖는 디오판토스 방정식이 주어졌을 때:방정식이 유리 정수로 풀 수 있는지 여부를 유한 개의 연산에서 결정할 수 있는 프로세스를 고안합니다.Entscheidungs 문제 [1차 논리에 대한 결정 문제]는 주어진 논리식이 유한한 많은 연산에 의해 그 타당성 또는 만족도를 결정할 수 있는 절차를 알 때 해결됩니다.Entscheidungs 문제는 수학적 논리의 주된 문제로 여겨져야 합니다.
— quoted, with this translation and the original German, in Dershowitz and Gurevich, 2008
1922년에 이르러서는 "Entscheidungs problem"이라는 개념이 약간 발전하였고, H. Behmann은 다음과 같이 말했습니다.
... Entscheidungs 문제의 가장 일반적인 형태는 다음과 같습니다.
일반적으로 적용할 수 있는 꽤 확실한 처방이 필요한데, 이것은 주어진 순수한 논리적 주장의 진의 또는 거짓을 유한한 단계로 결정할 수 있게 해 줄 것입니다.
— Gandy p. 57, quoting Behmann
베만은...일반적인 문제는 어떤 수학적 명제가 참인지를 결정하는 문제와 동등합니다.
— ibid.
만약 어떤 사람이 엔체이둥 문제를 풀 수 있다면, 그 사람은 "많은 (혹은 심지어 모든) 수학적 문제를 푸는 절차"를 갖게 될 것입니다.
— ibid., p. 92
1928년 국제 수학자 대회에서 힐베르트는 "그의 질문을 꽤 정확하게 했습니다.첫째, 수학은 완성되었습니까?둘째, 수학은 일관성이 있었나요?그리고 세 번째로 수학은 결정적이었는가?"(호지스 페이지 91, 호킹 페이지 1121).1930년 쿠르트 괴델은 힐베르트가 은퇴 연설을 한 바로 그 회의에서 처음 두 가지 질문에 대답했습니다. 세 번째 질문인 엔체이둥 문제는 1930년대 중반까지 기다려야 했습니다.
문제는 처음에는 프린스턴 대학교의 알론조 처치 교수가 "효과적인 계산 가능성"이라고 부른 "확실한 일반 적용 가능한 처방"에 대한 정확한 정의가 필요하다는 것이었습니다. 그리고 1928년에는 그러한 정의가 존재하지 않았다는 것입니다.그러나 그 후 6-7년 동안 에밀 포스트는 Church와 그의 두 학생 Stephen Kleene과 J. B.와 마찬가지로 방에서 방으로 옮겨 다니며 지시 목록에 따라 표시를 지우는 노동자에 대한 정의를 발전시켰습니다. 로서는 교회의 람다-칼큘러스와 괴델의 재귀 이론을 이용하여(1934).Church의 논문(1936년 4월 15일 발행)은 Entscheidungs 문제가 정말로 "결정할 수 없는" 것이며 거의 1년 차이로 튜링을 이겼다는 것을 보여주었습니다(튜링의 논문은 1936년 5월 28일 제출, 1937년 1월 발행).한편 에밀 포스트는 1936년 가을에 간략한 논문을 제출하여 튜링은 포스트보다 우선권을 갖게 되었습니다.Church가 Turing의 논문을 참조하는 동안, Turing은 Church의 논문을 연구하고 부록을 추가하는 시간을 가졌는데, 거기서 그는 Church의 lambda-calculus와 그의 기계가 동일한 함수를 계산할 것이라는 증거를 스케치했습니다.
하지만 교회가 한 일은 좀 다른 것이었고, 어떤 의미에서는 더 약한 것이었습니다. 튜링의 구성은 더 직접적이었고, 첫 번째 원칙들로부터 논쟁을 일으켜 교회의 시연에서 차이를 좁혔습니다.
— Hodges p. 112
그리고 포스트는 계산 가능성에 대한 정의를 제안했을 뿐이며 교회의 "정의"를 비판했을 뿐 아무것도 증명하지 못했습니다.
알란 튜링의 기계
1935년 봄, 케임브리지의 킹스 칼리지에서 젊은 석사생이었던 튜링은 도전에 나섰고, 논리학자 M. H. A. 뉴먼의 강의에 자극을 받아 괴델의 업적과 엔체이둥 문제에 대해 배웠습니다.뉴먼은 '기계'라는 단어를 사용했습니다...1955년 튜링의 사망 기사에서 뉴먼은 다음과 같이 썼습니다.
'기계적 프로세스란 무엇입니까?'라는 질문에 답합니다.튜링은 '기계가 할 수 있는 일'이라는 독특한 답을 답했고, 컴퓨팅 기계의 일반적인 개념을 분석하는 매우 동의하기 쉬운 작업에 착수했습니다.
— Gandy, p. 74
간디는 다음과 같이 말합니다.
저는 튜링이 일을 시작할 때부터 엔체이둥 문제의 결정 불가능성에 대한 증거를 목표로 삼았다고 생각하지만 모르겠습니다.그는 1935년 여름 그랜트체스터 목초지에 누워있을 때 그 논문의 '본심'이 떠올랐다고 제게 말했습니다.'주요 아이디어'는 그의 계산 분석이거나 보편적인 기계가 존재한다는 사실, 그래서 해결 불가능성을 증명하기 위한 대각선 주장일 수 있습니다.
— ibid., p. 76
간디는 위의 뉴먼의 진술이 "오해의 소지가 있다"고 믿었지만, 이 의견은 모두가 공유하지 않습니다.튜링은 기계에 평생 관심이 있었습니다: "앨런은 어렸을 때 타자기를 발명하는 것을 꿈꿨습니다; [그의 어머니] 부인.튜링은 타자기를 가지고 있었고, 타자기를 '기계적'이라고 부르는 것이 무엇을 의미하는지 자문하는 것으로 시작할 수 있었습니다(호지스 페이지 96).Princeton에서 박사 과정을 밟는 동안, Turing은 부울 논리 곱셈기를 만들었습니다(아래 참조)."Ordinals에 기초한 논리 체계"라는 제목의 그의 박사 논문은 "계산 가능한 함수"에 대한 다음과 같은 정의를 포함합니다.
위에서 '함수의 값이 순수하게 기계적인 프로세스에 의해 발견될 수 있다면 효과적으로 계산할 수 있다'고 기술했습니다.우리는 기계에 의해 수행될 수 있는 순수한 기계적인 프로세스로 이해하는 이 진술을 문자 그대로 받아들일 수 있습니다.이 기계들의 구조에 대한 수학적인 설명을 특정한 정상적인 형태로 제공하는 것이 가능합니다.이러한 아이디어의 발전은 저자가 계산 가능한 함수를 정의하고, 계산 가능성을 효과적으로 식별하도록 합니다.이 세 가지 정의[세 번째는 π-calculus]가 동치임을 증명하는 것은 다소 힘들지만 어렵지 않습니다.
— Turing (1939) in The Undecidable, p. 160
앨런 튜링(Alan [7]Turing)은 1936년에 "a-기계" (자동 기계를 발명했습니다.튜링은 1936년 5월 31일 런던 수학 협회에 논문을 제출했습니다.Hodges 1983:112), 그러나 1937년 초에 출판되었고 인쇄물은 1937년 2월에 입수할 수 있었습니다(cf.호지스 1983:129) 튜링의 박사 지도교수인 알론조 처치가 후에 [22]리뷰에서 "튜링 머신"이라는 용어를 만들어 냈습니다.이 모델로 튜링은 부정적인 두 가지 질문에 답할 수 있었습니다.
- 테이프에 있는 임의의 기계가 "원형"인지(예: 정지 또는 계산 작업을 계속하지 못하는지)를 결정할 수 있는 기계가 존재합니까?
- 테이프에 임의의 기계가 주어진 [23][24]기호를 인쇄하는지 여부를 결정할 수 있는 기계가 존재합니까?
따라서 임의의 계산이 가능한 매우 간단한 장치에 대한 수학적 설명을 제공함으로써, 그는 일반적으로 계산의 특성을 증명할 수 있었고, 특히 Entscheidungs 문제('결정 문제')[25]의 계산 불가능성을 증명할 수 있었습니다.
튜링이 영국으로 돌아왔을 때 그는 결국 "에니그마"라고 불리는 암호화 기계에 의해 만들어진 독일의 비밀 코드를 깨는 공동 책임을 지게 되었습니다. 그는 또한 ACE(자동 컴퓨팅 엔진)의 설계에 참여하게 되었습니다. [튜링의] ACE 제안은 효과적으로 자체적으로 포함되어 있었고, 그 근원은 EDVAC에 있지 않았습니다 [미국의 제안]ive], 그러나 그 자신의 보편적 기계에서"(Hodges p. 318).Kleene (1952) Turing의 논문에 의해 명명된 것의 기원과 성격에 대해서는 여전히 논쟁이 계속되고 있습니다.그러나 튜링이 자신의 계산-기계 모델로 증명한 것은 그의 논문 "계산 가능한 수에 대하여, Entscheidungs 문제에 대한 응용"(1937)에 나와 있습니다.
[힐버트 엔체이둥 문제는 해결책을 가질 수 없다는 것을...따라서 함수 미적분학 K의 주어진 공식 U가 증명 가능한지 여부를 결정하는 일반적인 과정, 즉 이 공식들 중 어느 하나의 U가 제공되어 결국 U가 증명 가능한지 여부를 말할 기계는 존재할 수 없다는 것을 보여주기 위해 제안합니다.
— from Turing's paper as reprinted in The Undecidable, p. 145
튜링의 예(그의 두 번째 증거):"이 기계가 0을 인쇄할 수 있습니까?"라는 일반적인 절차를 묻는다면, 질문은 "결정할 수 없습니다.
1937-1970: "디지털 컴퓨터", "컴퓨터 과학"의 탄생
1937년 Princeton에서 박사 논문 작업을 하던 중, Turing은 디지털 (Boolean-logic) 곱셈기를 처음부터 만들어 자신만의 전기기계 릴레이를 만들었습니다(Hodges p. 138)."앨런의 과제는 릴레이 작동 스위치 네트워크에서 튜링 기계의 논리적 설계를 구현하는 것이었습니다."(Hodges p. 138).튜링이 처음에는 단지 호기심이 많고 실험을 하고 있었을지 모르지만, 같은 방향으로 꽤 진지한 작업이 독일(Konrad Zuse 1938년)과 미국(Howard Aiken)과 George Stibitz 1937년)에서 진행되고 있었습니다. 그들의 작업의 결실은 추축국과 연합군이 제2차 세계 대전에서 사용했습니다.Hodges p. 298–299).1950년대 초중반 하오 왕과 마빈 민스키는 튜링 기계를 더 단순한 형태(마틴 데이비스의 포스트 튜링 기계의 전신)로 축소했습니다. 동시에 유럽 연구자들은 새로운 전자 컴퓨터를 현재 "튜링 기계"라고 불리는 것과 같은 컴퓨터와 같은 이론적 물체로 축소했습니다.1950년대 말과 1960년대 초, 우연하게도 Melzak과 Lambek (1961), Minsky (1961), 그리고 Shepherdson과 Sturgis (1961)의 병행적인 발전은 유럽의 연구를 더 발전시켰고 튜링 기계를 카운터 기계라고 불리는 더 친절하고 컴퓨터 같은 추상적인 모델로 줄였습니다; Elgot과 Robinson (1964), Hartmanis (1971),Cook과 Reckhow(1973)는 레지스터 머신과 랜덤 액세스 머신 모델로 이 작업을 더욱 진행했지만, 기본적으로 모두 산술과 같은 명령어 집합을 가진 다중 테이프 튜링 머신에 불과합니다.
1970-현재: 계산 모델로서
오늘날 카운터, 레지스터 및 랜덤 액세스 기계와 그들의 사이어인 튜링 기계는 계산 이론의 질문을 조사하는 이론가들의 선택 모델이 되고 있습니다.특히 계산 복잡도 이론은 튜링 기계를 사용합니다.
계산에서 조작하기 좋아하는 개체(음이 아닌 정수 또는 영숫자 문자열과 같은 숫자)에 따라 두 가지 모델이 기계 기반 복잡도 이론에서 지배적인 위치를 차지했습니다.
문자열 지향 계산을 위한 표준 모델을 나타내는 오프라인 멀티테이프 튜링 머신...과 이상화된 폰 노이만 스타일의 컴퓨터를 모델로 하는 쿡과 레코가 소개한 랜덤 액세스 머신 (RAM).
— van Emde Boas 1990:4
관련된 알고리즘 분석 영역에서만 RAM 모델이 이 역할을 대신합니다.
— van Emde Boas 1990:16
참고 항목
- 산술 계층
- 유한한 크기와 유계 에너지의 무한 테이프 튜링 기계의 불가능성을 보여주는 베켄슈타인 유계
- Bloop 및 Floop
- 중단 문제와 관련된 정보에 대한 차이틴 상수 또는 오메가(컴퓨터 과학)
- 중식실
- 튜링으로 완성된 세포 자동화 장치인 콘웨이의 생명의 게임
- 디지털 무한대
- 황제의 새로운 마음
- 열거자 (이론 컴퓨터 과학 분야)
- 제닉스
- Gödel, Escher, Bach: 영원한 황금 땋음, 다른 주제들 중에서 Church-Turing 논제를 논하는 유명한 책
- 더 많은 참조를 위해 문제 중지
- 하버드 대학의 건축학
- 명령형 프로그래밍
- 튜링 기계의 단순한 2차원 유사체인 랭턴 개미와 터미테스
- 앨런 튜링의 이름을 딴 사물 목록
- 하버드 대학 건축물을 개조함
- 양자 튜링 기계
- 정보이론의 또 하나의 선도적 사상가인 클로드 섀넌.
- 튜링 기계 예제
- 튜링 스위치
- 튜링 타르핏, 튜링이 완전함에도 불구하고, 실용적인 컴퓨팅에 일반적으로 쓸모없는 것으로 여겨지는 모든 컴퓨팅 시스템 또는 언어
- 뉴럴 네트워크에 대한 튜링의 초기 아이디어를 위해 조직화되지 않은 기계.
- 폰 노이만 건축
메모들
- ^ 민스키 1967:107 "그의 1936년 논문에서, A. M. 튜링은 현재 그의 이름을 가지고 있는 추상적인 기계의 종류를 정의했습니다.튜링 기계는 기호의 시퀀스를 저장(그리고 나중에 복구)할 수 있는 특수한 종류의 환경, 즉 테이프와 관련된 유한한 상태의 기계입니다." 또한 Stone 1972:8에서 "기계"라는 단어가 따옴표로 표시되어 있습니다.
- ^ 스톤 1972:8은 "이 "기계"는 추상적인 수학적 모델이다"라고 진술하고 있으며, CF도 마찬가지입니다."튜링 머신 모델"을 설명하는 Sipser 2006:137ff.Rogers 1987(1967):13은 "튜링의 특징화"를, Booolos Burgess와 Jeffrey 2002:25는 "특정한 종류의 이상화된 기계"를 언급합니다.
- ^ Sipser 2006:137 "튜링 머신은 실제 컴퓨터가 할 수 있는 모든 것을 할 수 있습니다."
- ^ Cf. Sipser 2002:137.또한 Rogers 1987(1967):13은 "양방향으로 무한한 길이의 종이 테이프"를 설명하고 있습니다.민스키 1967:118: "테이프는 양방향으로 무한한 것으로 간주됩니다."Boolos Burgess와 Jeffrey 2002:25는 "필요에 따라 빈 칸을 추가하기 위해 각 끝에 누군가가 배치되어 있다"는 가능성을 포함합니다.
- ^ Cf. Rogers 1987 (1967):13.다른 저자들은 "square"라는 단어를 사용합니다.불로스 버지스 제프리 2002:35, 민스키 1967:117, 펜로즈 1989:37
- ^ Boolos Burgess Jeffry 2002:25는 테이프를 따라 움직이는 기계를 설명합니다.펜로즈 1989:36-37은 무한 테이프로 "이동하기 어려울 수도 있다!"고 말하며 자신을 "불편하다"고 설명합니다."; 그는 "테이프가 우리의 유한한 장치가 움직일 수 있는 어떤 외부 환경을 나타내는 것으로 생각하기를 원한다"고 생각하고, "테이프"가 사물을 묘사하는 편리한 방법이라는 것을 관찰한 후, "장치는 이 환경으로부터 모든 입력을 받는다"고 제안합니다.튜링 기계 모델의 일부 변형은 또한 머리를 움직이거나 멈추는 대신에 같은 위치에 있도록 합니다.
- ^ a b Hodges, Andrew (2012). Alan Turing: The Enigma (The Centenary ed.). Princeton University Press. ISBN 978-0-691-15564-7.
- ^ 1935년 중반, M. H. A. 뉴먼이 그의 강의에서 제기한 질문(아마도 역사 부분에서 더 자세히 볼 수 있을 것입니다) 후에 그에게 이 아이디어가 떠올랐습니다: "확실한 방법이 있었거나, 뉴먼이 말했듯이, 수학적 진술에 적용될 수 있는 "기계적 과정"이 있었고, 그것이 증명 가능한지에 대한 답을 제시할 수 있었습니다." (호지스 1983:93).튜링은 1936년 5월 31일 런던 수학 협회에 논문을 제출했습니다.Hodges 1983:112), 그러나 1937년 초에 출판되었고 인쇄물은 1937년 2월에 입수할 수 있었습니다(cf.호지스 1983:129).
- ^ Davis 2000:151의 각주 참조.
- ^ 알론조 Burge, Tyler; Enderton, Herbert, eds. (2019-04-23). The Collected Works of Alonzo Church. Cambridge, MA, US: MIT Press. ISBN 978-0-262-02564-5.교회의 수집품( )에 대한 참고 사항 참조.
- ^ 튜링 1936년 미결정 1965:132-134; 튜링의 "원형"에 대한 정의는 119페이지에서 찾을 수 있습니다.
- ^ — Turing, Alan Mathison (1937). "On Computable Numbers, with an Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. Series 2. 42 (1): 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. 재인쇄 위치:
- ^ 튜링 1936 미결정 1965:145
- ^ Sipser 2006:137은 "튜링 머신은 실제 컴퓨터가 할 수 있는 모든 것을 할 수 있습니다.그럼에도 불구하고 튜링 기계조차도 특정한 문제를 해결할 수 없습니다.매우 실제적인 의미에서, 이러한 문제들은 계산의 이론적 한계를 벗어난 것입니다."
- ^ 위키사전에서 "이닝"의 정의 보기
- ^ A.M. Turing (Jul 1948). Intelligent Machinery (Report). National Physical Laboratory. 여기: p.3-4
- ^ 때때로 작업 테이블 또는 전환 함수라고 합니다.
- ^ 보통 5배수[5배수]: qa→qad이지만, 때로는 4배수[4배수]도 있습니다.
- ^ p.149; 특히 Hopcroft와 Ullman은 F{\ F의 모든 상태에서 δ{\이(가) 정의되지 않았다고 가정합니다.
- ^ L. 토레스 퀘베도.엔사요소브레 오토마티카 – Su definition. Extension teórica de susapaciones, Revista de la Academia de Ciencias Exacta, Revista 12, pp. 391-418, 1914
- ^ 토레스 퀘베도.L. (1915)."Automatique" "Saé sur'Automatique - Sadefinition" Etendue theorique des applications", "Vue Génerale des Sciences Pureset Applicationquées, vol. 2, pp. 601-611"
- ^ 알론조 Burge, Tyler; Enderton, Herbert, eds. (2019-04-23). The Collected Works of Alonzo Church. Cambridge, MA, US: MIT Press. ISBN 978-0-262-02564-5.교회의 수집품( )에 대한 참고 사항 참조.
- ^ 튜링 1936년 미결정 1965:132-134; 튜링의 "원형"에 대한 정의는 119페이지에서 찾을 수 있습니다.
- ^ — Turing, Alan Mathison (1937). "On Computable Numbers, with an Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. Series 2. 42 (1): 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. 재인쇄 위치:
- ^ 튜링 1936 미결정 1965:145
참고문헌
이 글은 인용문이 불명확합니다.(2019년 11월 (이메시지를 및 ) |
1차 문헌, 전재 및 편집물
- B. Jack Copelanded.(2004),본질적인 튜링: 컴퓨팅, 논리, 철학, 인공 지능, 인공 생명 분야의 신묘한 글과 에니그마의 비밀, 클라렌던 출판사(옥스퍼드 대학 출판부), 영국 옥스퍼드, ISBN 0-19-825079-7튜링 논문과 에밀 포스테레에게 보낸 "튜링의 관습"에 대한 그의 비판과 도날드 W. 데이비스의 튜링의 유니버설 컴퓨팅 머신에 대한 수정 사항이 포함되어 있습니다.
- 마틴 데이비스 (ed.) (1965), 결정하지 못한 것, 레이븐 프레스, 휴렛, 뉴욕.
- 에밀 포스트(Emil Post, 1936), 무한결합과정—공식 1", Journal of Symbol Logic, 1, 103–105, 1936결정하지 못한 것에서 재인쇄, pp. 289ff.
- 에밀 포스트(Emil Post, 1947), "화의 문제의 재발적 해결 불가능성", 상징 논리학 저널, vol. 12, pp. 1-11결정할 수 없는 사건에서 재인쇄, pp. 293ff.이 논문의 부록에서 1936-1937년 튜링의 논문에 대한 논평과 수정 사항을 게시합니다.특히 범용 컴퓨팅 머신 코딩에 대한 수정 사항이 포함된 각주 11과 튜링의 첫 번째 및 두 번째 증명에 대한 주석이 포함된 각주 14를 참조합니다.
- Turing, A.M. (1936). "On Computable Numbers, with an Application to the Entscheidungsproblem". Proceedings of the London Mathematical Society. 2 (published 1937). 42: 230–265. doi:10.1112/plms/s2-42.1.230. S2CID 73712. (및 ).많은 컬렉션에서 재인쇄되었습니다. 예를 들어 <미결정>, pp. 115–154. 많은 장소에서 웹에서 이용할 수 있습니다.
- 앨런 튜링, 1948, "지능형 기계""사이버네틱스:'핵심 서류' 에드 C.R. 에반스와 A.D.J. 로버트슨.볼티모어:University Park Press, 1968. p. 31.에서 재인쇄됨
- F.C. 헤니와 R.E. 스턴스.멀티테이프 튜링 기계의 두 테이프 시뮬레이션JACM, 13(4):533–546, 1966.
계산가능성이론
- Boolos, George; Richard Jeffrey (1999) [1989]. Computability and Logic (3rd ed.). Cambridge UK: Cambridge University Press. ISBN 0-521-20402-X.
- Boolos, George; John Burgess; Richard Jeffrey (2002). Computability and Logic (4th ed.). Cambridge UK: Cambridge University Press. ISBN 0-521-00758-5. 몇몇 부분은 버지스에 의해 상당히 개작되었습니다.람벡 "주판 기계"의 맥락에서 튜링 기계의 제시 (cf.기계)와 재귀 함수를 등록하여 동등성을 나타냄.
- 테일러 L. 부스(1967), 순차 기계와 오토마타 이론, 존 와일리 앤 선즈, 뉴욕.대학원 수준의 공학 텍스트; 다양한 주제에 걸쳐 있으며, 제9장 튜링 머신에는 일부 재귀 이론이 포함되어 있습니다.
- Martin Davis (1958). Computability and Unsolvability. McGraw-Hill Book Company, Inc, New York.12-20페이지에서 그는 덧셈, 계승 함수, 뺄셈(x ≥ y), 적절한 뺄셈(x < y인 경우 0), 아이덴티티 함수와 다양한 아이덴티티 함수, 곱셈에 대한 5개의 튜플 테이블의 예를 제시합니다.
- Davis, Martin; Ron Sigal; Elaine J. Weyuker (1994). Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science (2nd ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1.
- Hennie, Fredrick (1977). Introduction to Computability. Addison–Wesley, Reading, Mass. QA248.5H4 1977.90-103페이지에서 헤니는 UTM에 대해 예제와 흐름도를 사용하지만 실제 '코드'는 사용하지 Hennie, Fredrick (1977). Introduction to Computability. Addison–Wesley, Reading, Mass. QA248.5H4 1977.않습니다.
- Hopcroft, John; Ullman, Jeffrey (1979). Introduction to Automata Theory, Languages, and Computation (1st ed.). Addison–Wesley, Reading Mass. ISBN 0-201-02988-X. "언어"의 기계적 해석, NP-완전성 등의 문제를 중심으로.
- Hopcroft, John E.; Rajeev Motwani; Jeffrey D. Ullman (2001). Introduction to Automata Theory, Languages, and Computation (2nd ed.). Reading Mass: Addison–Wesley. ISBN 0-201-44124-1.
- Stephen Kleene (1952), 메타수학 입문, 북홀랜드 출판사, 네덜란드 암스테르담, 10번째 인상 (1971년 6번째 재인쇄 수정 포함)대학원 수준의 텍스트; XIII장 계산 가능 함수의 대부분은 재귀 함수의 계산 가능성에 대한 튜링 기계 증명 등에 있습니다.
- Knuth, Donald E. (1973). Volume 1/Fundamental Algorithms: The Art of computer Programming (2nd ed.). Reading, Mass.: Addison–Wesley Publishing Company.계산(하드웨어와 소프트웨어 모두) 개발에서 튜링 기계의 역할과 관련하여, 1.4.5 History and Bibliography pp. 225ff 및 2.6 Knuth, Donald E. (1973). Volume 1/Fundamental Algorithms: The Art of computer Programming (2nd ed.). Reading, Mass.: Addison–Wesley Publishing Company.History and 2.6 히스토리 및 서지 페이지 456ff.
- Zohar Manna, 1974, 계산의 수학적 이론.재인쇄, 도버, 2003.ISBN 978-0-486-43238-0
- 마빈 민스키, 계산: 유한하고 무한한 기계, 프렌티스-홀, 주식회사, N.J., 1967.8장 8.2절 "정지 문제의 해결 불능"을 참조합니다.
- Christos Papadimitriou (1993). Computational Complexity (1st ed.). Addison Wesley. ISBN 0-201-53082-1. 2장: 튜링 기계, 페이지 19-56.
- 하틀리 로저스(Hartley Rogers, Jr.), 재귀 함수 및 효과적 계산가능성 이론, MIT Press, Cambridge MA, 페이퍼백 에디션 1987, 오리지널 McGraw-Hill 에디션 1967, ISBN 0-262-68052-1 (pbk)
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. 3장: 교회-튜링 논문, 125-149쪽
- Stone, Harold S. (1972). Introduction to Computer Organization and Data Structures (1st ed.). New York: McGraw–Hill Book Company. ISBN 0-07-061726-0.
- Peter van Emde Boas 1990, Machine Models and Simulations, pp. 3-66, Jan van Leuwen, ed., 이론 컴퓨터 과학 핸드북, A권: 알고리즘과 복잡성, MIT Press/Elsevier, [place?], ISBN 0-444-88071-2(A권).QA76.H279 1990.
교회론
- Nachum Dershowitz; Yuri Gurevich (September 2008). "A natural axiomatization of computability and proof of Church's Thesis" (PDF). Bulletin of Symbolic Logic. 14 (3). Retrieved 2008-10-15.
- Roger Penrose (1990) [1989]. The Emperor's New Mind (2nd ed.). Oxford University Press, New York. ISBN 0-19-851973-7.
작은 튜링 기계
- Rogozhin, Yurii, 1998, "22개의 상태와 2개의 기호가 있는 범용 튜링 기계", 루마니아 정보 과학 기술 저널, 1(3), 259-265, 1998. (소형 범용 튜링 기계에 대한 알려진 결과 조사)
- Stephen Wolfram, 2002, 새로운 종류의 과학, Wolfram Media, ISBN 1-57955-008-8
- 브런피엘, 제프, 학생 수학상 수상, 네이처, 2007년 10월 24일
- 짐 자일스(Jim Giles, 2007), 가장 단순한 '보편적 컴퓨터'가 2007년 10월 24일 학생 $25,000를 수상했습니다.
- 알렉스 스미스 볼프람 유니버셜 오브 울프람 2, 3 튜링 머신, 볼프람 2, 3 튜링 머신 연구상
- 본 프랫(Vaughan Pratt), 2007, "단순 튜링 기계, 범용성, 인코딩 등", FOM 이메일 목록2007년10월29일
- Martin Davis, 2007, "가장 작은 보편적 기계", 그리고 보편적 튜링 기계의 정의 FOM 이메일 목록.2007년 10월 26일~27일
- Alasdair Urquhart, 2007 "가장 작은 보편적 기계", FOM 이메일 목록2007년10월26일
- 헥터 제닐(Wolfram Research), 2007 "가장 작은 보편적 기계", FOM 이메일 목록2007년10월29일
- Todd Rowland, 2007, "FOM에 대한 혼란", Wolfram Science 메시지 보드, 2007년 10월 30일.
- Olivier and Marc RAYNAUD, 2014, 튜링 머신을 달성하기 위한 프로그래밍 가능한 프로토타입 Blaise Pascal University(프랑스 클레르몽페랑)의 Wayback Machine" LIMOS 연구소에서 2016-01-14 보관.
다른.
- Martin Davis (2000). Engines of Logic: Mathematicians and the origin of the Computer (1st ed.). W. W. Norton & Company, New York. ISBN 978-0-393-32229-3.
- Robin Gandy, "The Confluence of Ideas in 1936", Rolf Herken 페이지 51-102, 아래 참조.
- 스티븐 호킹 (편집자), 2005, 신은 정수를 창조했습니다: 역사를 바꾼 수학적 돌파구, 러닝 프레스, 필라델피아, ISBN 978-0-7624-1922-7호킹이 쓴 튜링에 대한 간략한 해설과 전기와 함께 튜링의 1936-1937년 논문을 포함합니다.
- Rolf Herken (1995). The Universal Turing Machine—A Half-Century Survey. Springer Verlag. ISBN 978-3-211-82637-9.
- 앤드류 호지스, 앨런 튜링: 에니그마, 사이먼 앤 슈스터, 뉴욕.Cf. 그의 증명에 이르는 역사와 토론을 위한 "진실의 정신" 장.
- Ivars Peterson (1988). The Mathematical Tourist: Snapshots of Modern Mathematics (1st ed.). W. H. Freeman and Company, New York. ISBN 978-0-7167-2064-5.
- Roger Penrose, The New Mind: 컴퓨터, 정신, 그리고 물리학의 법칙에 관하여, 옥스포드 대학 출판부, 옥스포드와 뉴욕, 1989 (1990 수정), ISBN 0-19-851973-7
- Paul Strathern (1997). Turing and the Computer—The Big Idea. Anchor Books/Doubleday. ISBN 978-0-385-49243-0.
- Hao Wang, "튜링의 컴퓨팅 기계 이론의 변형", Journal of the Association for Computing Machines (JACM) 4, 63–92 (1957).
- Charles Petzold, The Annoted Turing, John Wiley & Sons, Inc., ISBN 0-470-22905-5
- Arora, Sanjeev; Barak, Boaz, "복잡성 이론: 현대적 접근법", Cambridge University Press, 2009, ISBN 978-0-521-42426-4, 섹션 1.4, "끈과 보편적 튜링 기계로서의 기계" 및 1.7, "정리 1.9의 증명"
- Kantorovitz, Isaiah Pinchas (December 1, 2005). "A note on turing machine computability of rule driven systems". SIGACT News. 36 (4): 109–110. doi:10.1145/1107523.1107525. S2CID 31117713.
- Kirner, Raimund; Zimmermann, Wolf; Richter, Dirk: "실제 프로그래밍 언어의 결정 불가능성 결과에 대하여", 15에서. Kolroquium Programmiersprachen und Grundlagen der Programmierung (KPS'09), Maria Taferl, 오스트리아, 2009년 10월.
 (는) 유한하고 비어 있지 않은 상태 집합입니다.
(는) 유한하고 비어 있지 않은 상태 집합입니다.
 허용된다고 합니다.
허용된다고 합니다.







