폼의 법칙

형식의 법칙(이하 LoF)은 1969년에 출판된 G. 스펜서 브라운이 쓴 책으로 수학과 철학의 경계를 서고 있다. LoF는 다음과 같은 세 가지 뚜렷한 논리 시스템을 설명한다.

• 모델에서 부울 산수를 포함하는 "기본 산술" (LoF 4장에 설명됨)
• 모델에는 2개 요소 부울 대수(이하 약칭 2), 부울 논리 및 고전 명제 미적분학을 포함하는 "1차 대수"(LoF 6장)
• 유한한 오토마타와 알론조교회의 제한된 재귀산술(RRA)을 해석한 "2도 등가"(제11장)이다.

"경계 대수"는 1차 대수학과 1차 산술의 결합을 뜻하는 메과르의 (2011년)^[1] 용어다. 형태 법칙은 때때로 LoF뿐만 아니라 "1차 대수학"을 느슨하게 언급한다.

책

이 섹션은 검증을 위해 추가 인용구가 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. (2018년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

서문은 이 작품이 1959년에 처음 발굴되었다고 말하고 있으며, 스펜서 브라운은 베르트랑 러셀이 그의 노력을 지지한다고 언급하고 있다. 그는 또한 런던대학의 J. C. P. Miller가 교정 읽기를 돕고 다른 지도를 해준 것에 대해 감사한다. 1963년 스펜서 브라운은 런던대학교 체육학과 교수인 해리 프로스트의 초빙을 받아 논리의 수학에 관한 강의를 했다.

LoF는 1960년경 저자가 한 전자공학에서의 작업에서, 그리고 이후 런던대학의 확장프로그램의 후원으로 그가 행한 수학논리에 대한 강의에서 나왔다. LoF는 여러 판에 등장했다. 두 번째 판본 시리즈는 1972년에 "최초 미국판 서약"과 함께 등장했는데, 이 판본은 자기주석의 역설의 사용을 강조하였다.^[2] 가장 최근의 것은 1997년 독일어 번역으로, 절판된 적이 없다.

수학은 겨우 55ppm을 채울 뿐이고 다소 초보적이다.^{[original research?]} 그러나 LoF의 신비롭고 선언적인 산문, 그리고 역설에 대한 사랑은 모두를 위한 도전적인 읽기로 만든다. 스펜서 브라운은 비트겐슈타인과 R. D. 라잉의 영향을 받았다. LoF는 또한 찰스 샌더스 피어스, 베르트랑 러셀, 알프레드 노스 화이트헤드의 글에서 나온 많은 주제들을 반향한다.

책 전체는 '이것'이 무엇인지 알려주는 대신 독자에게 지시를 내리는 작전적인 방식으로 쓰여진다. G. 스펜서 브라운의 역설에 대한 관심에 따라, 무엇인가라는 말을 하는 유일한 문장은, 이 책에서 그러한 진술은 사용되지 않는다고 하는 진술이다.^[3] 이 한 문장을 제외하고 이 책은 E-Prime의 예로 볼 수 있다.

리셉션

표면적으로는 형식적인 수학과 철학으로 이루어진 작품인 LoF는 컬트 고전적인 무언가가 되었다: 그것은 Heinz von Foerster가 전 지구 카탈로그를 위해 그것을 검토할 때 찬사를 받았다.^[4] LoF에 동의하는 사람들은 LoF가 수수께끼 같은 "의식의 수학"을 구현하는 것으로, LoF의 대수적 상징성은 인식의 암묵적 뿌리인 "언어"를 포착하는 것으로 지적한다. LoF는 1차 대수학에서는 논리학, 부울대수학, 산술학 사이의 현저한 연관성과 언어와 정신의 철학이 드러난다고 주장한다.

바나쉐프스키(1977년)^[5]는 1차 대수학이 부울대수의 새로운 표기법일 뿐이라고 주장한다. 실제로 2element Boolean 대수 2는 1차 대수학의 의도된 해석으로 볼 수 있다. 그러나 1차 대수학의 표기법은 다음과 같다.

• 부울 알헤브라스뿐만 아니라 모든 격자까지 특성화하는 이중성을 완벽하게 활용한다.
• 논리 및 2에서 구문적으로 구별되는 문장이 동일한 의미론을 가질 수 있는 방법을 강조한다.
• 부울 대수 계산, 그리고 전위적 논리와 삼단논리의 증명들을 극적으로 단순화한다.

더욱이 1차 대수학의 구문은 2 이외의 공식 시스템과 보초 논리학으로 확장될 수 있어 경계 수학이 가능하다(아래 § 관련 작업 참조).

LoF는 그 중에서도 하인츠 폰 포어스터, 루이 카우프만, 니클라스 루만, 훔베르토 마투라나, 프란시스코 바렐라, 윌리엄 브릭렌에 영향을 주었다. 이 작가들 중 몇몇은 다양한 흥미로운 방법으로 1차 대수학을 수정했다.

LoF는 4색 정리, 페르마의 마지막 정리, 골드바흐의 추측과 같이 아주 오래 서 있는 어떤 잘 알려진 수학적인 추측들은 1차 대수학의 확장을 이용하여 증명할 수 있다고 주장했다. 스펜서-브라운은 결국 4가지 색 정리의 소박한 증거를 유포했지만, 회의론에 부딪쳤다.^[6]

양식(1장)

기호:

「표식」이나 「크로스」라고도 불리는데, 「형식법」의 본질적인 특징이다. 스펜서-브라운의 모방할 수 없고 수수께끼 같은 패션에서 마크는 인식의 근원을 상징한다. 즉, 이원론적 마크는 "이것만 빼고 이것"과 "이것"을 구별할 수 있는 능력을 나타낸다.

LoF에서 십자가는 "생존"의 도면을 나타내며, 다음을 한꺼번에 나타내는 것으로 생각할 수 있다.

• 어떤 것 주위에 경계를 긋고, 따라서 그 경계를 다른 모든 것들과 구분하는 행위
• 경계선을 그어서 모든 것과 구별되는 것,
• 경계의 한 쪽에서 다른 쪽으로 건너가는 것.

세 가지 방법 모두 구별을 하는 인지적 실체(예: 사람)의 부분에 작용하는 것을 의미한다. LoF의 설명에 따르면:

"첫 번째 명령:

• 구별하다.

다음과 같은 방법으로 잘 표현할 수 있다.

• 구별을 두도록 하자
• 구별을 찾아라.
• 구별을 보아라.
• 구별을 설명하라.
• 구별을 정의하십시오.

또는:

• 구별할 수 있도록 하라.(LoF, 2장 참고)

표시 상태의 대척점은 표시되지 않은 상태인데, 이것은 그야말로 아무것도 아닌 공허함, 또는 빈 공간으로 대표되는 표현할 수 없는 무한함이다. 그것은 단순히 십자가의 부재일 뿐이다. 어떤 구별도 이루어지지 않았고 어떤 것도 교차되지 않았다. 표시된 상태와 공허는 형태 법칙의 두 원시적 가치다.

십자가는 하나의 "기호로 간주되는" 상태와 그렇게 고려되지 않은 다른 상태 사이의 구별을 나타내는 것으로 볼 수 있다. 이 사실로부터 몇몇 의식과 언어의 이론과 함께 묘한 공명이 일어난다. 역설적으로, 그 형태는 한 번에 관찰자와 관찰자가 되며, 관찰을 하는 창조적인 행동이기도 하다. LoF(배경 물질 제외)는 다음과 같은 단어로 마감한다.

...첫 번째 구분인 마크와 관찰자는 서로 교환할 수 있을 뿐만 아니라, 형태상으로도 동일하다.

C. S. Peirce는 1890년대에 관련 통찰력에 도달했다; § 관련 작업을 참조한다.

1차 산술(4장)

일차 산술의 구문은 다음과 같다. 단지 두 개의 원자 표현이 있다.

• 빈 십자가;
• 빈 페이지의 전부 또는 일부("void")

두 가지 귀납적 규칙이 있다.

• 어떤 표현에도 십자 기호를 쓸 수 있다.
• 어떤 두 가지 표현도 연결될 수 있다.

1차 산술의 의미론들은 아마도 LoF의 유일한 명시적 정의인 "생존은 완벽한 연속이다"에 지나지 않을 것이다.

"표시되지 않은 상태"를 공허의 동의어가 되게 하라. 빈 십자가가 "표시된 상태"를 나타내도록 하라. 교차하는 것은 한 값, 즉 표시되지 않았거나 표시된 상태에서 다른 값으로 이동하는 것이다. 이제 "산술적" 공리 A1과 A2를 기술할 수 있으며, 이 공리는 1차 산술(따라서 모든 형태의 법칙):

"A1. 소명의 법칙" 한 주에서 두 번 전화하는 것은 한 번 전화하는 것과 구별할 수 없다. 두 번 구별하는 것은 한 번 구별하는 것과 같은 효과가 있다. 예를 들어 "빛이 있게 하라"고 했다가 다시 "빛이 있게 하라"고 말하는 것은 한 번 말하는 것과 같다. 공식:

${\displaystyle \ =}$

"A2. 건널목의 법칙" 표시되지 않은 상태에서 표시된 상태로 건너간 후 표시된 상태에서 다시 교차("재역전")하면 표시되지 않은 상태로 되돌아간다. 그래서 안굴 건널목을 되짚어보고 있다. 공식:

${\displaystyle \ =}$

A1과 A2에서 모두 '='의 오른쪽에 있는 표현은 '='의 왼쪽에 있는 표현보다 기호가 적다. 이는 모든 일차 산술 식을 A1과 A2를 반복적으로 적용함으로써 표시 상태 또는 표시되지 않은 상태의 두 상태 중 하나로 단순화할 수 있음을 시사한다. 이것이 바로 사실이고, 그 결과 표현은 '간단하다'는 것이다. 일차 산술 주제의 두 가지 기본 계량법은 다음과 같다.

• 모든 유한한 표현은 독특한 단순화를 가지고 있다. (LoF의 T3);
• 초기 표시 또는 표시되지 않은 상태에서 시작하여, A1과 A2의 제한된 반복 적용 횟수로 표현식을 "만족"할 수 없으며, 단순화가 초기 상태와 다른 표현식을 생성할 수 없다. (LoF의 T4).

따라서 논리적 등가성의 관계는 모든 주요 산술적 표현을 두 개의 등가 등급, 즉 십자가로 단순화하는 것과 공허로 단순화하는 것으로 나눈다.

A1과 A2는 직렬 및 병렬 전기 회로의 특성 및 플로우차트를 포함한 다른 방식의 다이어그램 프로세스에서 느슨한 아날로그를 가지고 있다. A1은 병렬 연결에 해당하고 A2는 직렬 연결에 해당하며, 구별은 단순히 배선을 추가하는 것이 아니라 회로의 두 지점이 연결되는 방식을 변경하는 것에 해당한다는 이해에 해당한다.

일차 산술은 수학 및 컴퓨터 과학의 다음과 같은 공식 언어와 유사하다.

• 순서가 1인 Dyck 언어(null 알파벳 포함)
• 촘스키 계층 구조에서 가장 간단한 문맥 없는 언어
• 강하게 정상화되고 융합되는 리프레시 시스템.

LoF의 "지표의 미적분"이라는 문구는 "주산수"와 동의어다.

캐논의 개념

LoF 특유의 개념은 "캐논"의 개념이다. LoF는 canon을 정의하지 않지만, 다음의 2개의 주석에서 발췌한 2개가 적절하다.

지휘의 더 중요한 구조는 때때로 캐논이라고 불린다. 그들은 지도적 결함을 별자리 안에서 집단화하는 방식으로 나타나며, 따라서 결코 서로 독립적이지 않다. 캐논은 건설 중인 시스템 외부에 있는 것(즉, 시스템 외부에 있는 것)의 구별을 가지고 있지만(예: '구분을 그린다(draw a difference)'는 중심적인 중요성이 있다고 해도 캐논은 아니다. 캐논(canon)은 허가나 허용은 하되 건설이나 창조는 하지 않는 명령 또는 명령의 집합이다.

...수학적 의사소통의 주된 형태는 서술이 아니라 명령이다... 음악은 비슷한 예술 형식이다. 작곡가는 자신이 마음속에 품고 있는 일련의 소리들을 묘사하려고 시도조차 하지 않고, 그것을 통해 생겨난 감정들의 집합은 말할 것도 없이, 만약 그것들이 연주자에 의해 복종된다면, 그 명령들을 듣는 사람에게, 듣는 사람에게, 그리고 작곡가의 원래 경험의 재현을 가져올 수 있는 일련의 명령들을 기록한다.

이러한 발췌문은 논의 중인 논리적 시스템의 공식 언어인 목적어 언어와 목적어 언어와 구별되는 언어인 금속언어(종종 자연어) 사이의 금속언어의 구별과 관련이 있다. 첫 번째 인용구는 그 운하가 금속구조의 일부라고 주장하는 것 같다. 두 번째 인용구는 목적어 문장이 본질적으로 저자에 의해 독자에게 전달되는 명령이라고 주장하는 것 같다. 두 주장 모두 표준 금속공학에 관한 것이 아니다.

1차 대수 (6장)

구문

유효한 1차 산술 식이 있을 경우, 선택적 숫자 첨자가 있는 여러 개의 라틴 문자를 하나 이상의 위치에 삽입하십시오. 그 결과는 1차 대수 공식이다. 수학과 논리에 그렇게 채택된 글자를 변수라고 한다. 1차 대수변수는 원시 값이나 그 보완 값을 쓸 수 있는 위치를 나타낸다. 동일한 변수의 여러 인스턴스(instance)는 동일한 원시 값의 여러 위치를 나타낸다.

논리적 등가성을 지배하는 규칙

'='라는 기호는 두 개의 논리적으로 동등한 식을 연결할 수 있다. 그 결과는 방정식이다. "논리적으로 동등하다"는 것은 두 표현이 동일한 단순성을 갖는다는 것을 의미한다. 논리적 동등성은 규칙 R1과 R2에 의해 지배되는 일차 대수 공식의 집합에 대한 동등성 관계다. "C"와 "D"를 각각 적어도 하나의 보조양식 A를 포함하는 공식으로 한다.

• R1, 동등의 대체. C에서 A의 하나 이상의 인스턴스를 B로 대체하여 E가 된다. A=B이면 C=E.
• R2, 균일 교체. C와 D에서 A의 모든 인스턴스를 B로 교체한다. C는 E가 되고 D는 F가 된다. C=D이면 E=F. A=B는 필요하지 않다.

R2는 일차 대수 시연(아래 참조)에 매우 자주 사용되며 거의 항상 조용히 사용된다. 이러한 규칙들은 거의 무의식적으로 논리학이나 대부분의 수학에서 일상적으로 발동된다.

1차 대수학은 방정식, 즉 infix '='로 연결된 공식 쌍으로 구성된다. R1과 R2는 하나의 방정식을 다른 방정식으로 변환할 수 있게 한다. 따라서 1차 대수학은 부울대수를 포함한 많은 대수적 구조와 마찬가지로 품종인 등식 형식 체계다. 등가 논리는 프린키마티카(예: Peirce,^1,2,3 Johnson 1892) 이전에는 일반적이었으며, 현재 옹호자(Gries and Schneider 1993)가 있다.

전통적인 수학 논리는 접두사 개찰구로 표시된 tautological 공식으로 구성된다. 1차 대수 공식 A가 tutology라는 것을 나타내려면 "A = "를 간단히 쓰시오. R1과 R2의 '='를 쌍변환으로 대체하면, 결과 규칙은 전통적인 논리로 유지된다. 그러나 전통적인 논리는 주로 규칙모드 폰에 의존한다. 따라서 전통적인 논리는 타당하다. 등거리-수직적 이분법은 수학논리와 수학의 나머지 부분을 구분하는 것의 많은 부분을 확장시킨다.

이니셜

초기란 의사결정 절차에 의해 증명 가능한 일차 대수 방정식이며, 따라서 공리가 아니다. LoF는 다음과 같은 이니셜을 제시한다.

J1:

A A

= .

위의 "="의 오른쪽에 없는 것은 의도적인 것이다.

J2:

A B

C

=

A C B C

.

J2는 전위논리와 부울대수의 친숙한 분배 법칙이다.

계산에 더 적합한 또 다른 이니셜 집합은 다음과 같다.

J0:

A

=

a

J1a:

A A

=

.

C2:

A

AB

=

A

B

.

일차 대수학이 격자( lat子)인 것은 C2 덕분이다. J1a의 덕택에 상한이 있는 보완 격자로, J0에 의해 그에 상응하는 하한과 정체성 요소가 된다. J0도 A2의 대수적 버전이며, 빈 페이지를 가진 가명이 어떤 것인지 명확하게 한다.

LoF의 T13은 C2를 다음과 같이 일반화한다. 일차 대수(또는 전위 논리학) 공식 B는 가지가 있는 순서 트리로 볼 수 있다. 다음:

T13: A와 A의 복사본이 B의 같은 분기에 있는 한, 보조양식 A는 임의로 A의 그것보다 더 큰 B의 어떤 깊이로도 복사할 수 있다. 또한, B의 같은 분기에 A의 여러 가지 사례가 주어지면, 가장 얕은 경우를 제외한 모든 인스턴스는 중복된다.

T13에 대한 증거는 유도를 필요로 하지만, 그 기초가 되는 직관은 명확해야 한다.

C2 또는 이에 상응하는 이름을 다음과 같이 지정한다.

• LoF의 "세대";
• 존슨(1892)의 "제외"
• 윌리엄 브릭튼의 작품에 나오는 "Pervasion".

아마도 C2의 힘을 가진 공리 또는 규칙의 첫 번째 예는 C. S. Peirce의 실존적 그래프의 T13과 AA=A를 결합한 "Iteration의 법칙"이었을 것이다.

LoF는 결합은 통근과 결부된 것으로 읽을 수 있으며 따라서 명시적으로 가정하거나 증명할 필요가 없다고 주장한다. (피에르는 그의 실존적 그래프에 대해 비슷한 주장을 했다.) 한 마침표를 임시로 표기하여 그룹을 설정한다. 연결 통근자와 관련자는 다음에서 증명할 수 있다.

• 초기 AC.D=CD.A와 그 결과 AA=A(Byrne 1946). AA=A는 모든 격자를 수용하는 흡수법의 쉬운 결과이기 때문에 이 결과는 모든 격자를 수용한다.
• 이니셜 AC.D=AD.C와 J0. J0는 하한을 가진 격자만을 보유하므로, 이 방법은 경계 격자(일차 대수 및 2 포함)에 대해서만 보유한다. 동시성은 사소한 것이므로 A=로 설정하기만 하면 된다. 연관성: 교류.D = CA.D = CD.A = A.CD.

연관성을 입증하면 그 기간은 폐기될 수 있다.

메과이어(2011년)의 이니셜은 AC이다.D=CD.A, B1, B2, J0, B3, J1a, B4, C2로 불린다. 설계상 이들 이니셜은 아벨 그룹인 아래 G1-G3의 공리와 매우 유사하다.

증명 이론

1차 대수학에는 세 가지 종류의 입증된 주장이 포함되어 있다.

• 결과는 시연에 의해 검증된 일차 대수 방정식이다. 시연은 각 단계가 초기 결과 또는 이전에 입증된 결과에 의해 정당화된 일련의 단계로 구성된다.
• 정리란 어떤 증거, 즉 금속어로 공식화된 논증에서 입증된 진술로, 훈련된 수학자와 논리학자가 이를 수용한다.
• 위에서 정의한 초기. 시위와 증거는 마치 공리인 것처럼 초기를 유발한다.

결과와 정리 사이의 구분은 수학, 논리를 포함한 모든 형식 시스템에 적용되지만, 대개 명시적이지는 않다. 시연 또는 의사결정 절차는 컴퓨터로 수행 및 검증할 수 있다. 정리의 증거는 있을 수 없다.

A와 B를 일차 대수 공식으로 하자. A=B의 시연은 다음 두 가지 방법 중 하나로 진행될 수 있다.

• B를 얻을 때까지 단계별로 A를 수정하거나, 그 반대로 A를 수정한다.
• 및 를 모두 단순화하십시오. 이것은 "계산"이라고 알려져 있다.

일단 A=B가 입증되면, A=B를 호출하여 후속 시연에서 단계를 정당화할 수 있다. 일차 대수 시연과 계산은 종종 J1a, J2, C2 이하가 필요하며, 결과(LoF의 C3), (C1), AA=A(C5) 이하가 필요하다.

LoF의 결과 C7'은 임의의 1차 대수 공식을 2를 초과하지 않는 등가 공식으로 변환하는 알고리즘을 가능하게 한다. 결과는 정상 형태, 즉 결막 정상 형태의 1차 대수 아날로그다. LoF(T14–15)는 모든 공식에 정상적인 형태가 있다는 잘 알려진 부울 대수 정리의 1차 대수 아날로그를 증명한다.

A를 어떤 공식 B의 보조 공식이 되게 하라. C3과 쌍을 이룰 때 J1a는 계산을 위한 폐쇄조건으로 볼 수 있다: B는 A와 (A)가 모두 B의 깊이 0에 나타나는 경우에만 tautology이다. 관련 조건은 자연 공제의 일부 버전에서 나타난다. 계산에 의한 데모는 대개 다음과 같다.

• 중복 보조공식을 제거하기 위해 T13을 반복적으로 호출하는 행위
• 양식이 있는 보조양식을 지우는 중.

계산의 마지막 단계는 항상 J1a를 호출한다.

LoF는 다음과 같은 표준 메타테오리의 우아한 새로운 증거를 포함한다.

• 완전성: 모든 일차 대수 결과는 이니셜(T17)에서 입증할 수 있다.
• 독립성: J1은 J2로부터 증명될 수 없으며, 그 반대의 경우도 마찬가지다(T18).

그 지각논리가 완전하다는 것은 수학논리에서 모든 첫 번째 대학과정에서 가르쳐진다. 그러나 부울대수의 대학 과정에서는 2의 완성도를 거의 언급하지 않는다.

해석

Marked 및 Unmarked 상태를 Boolean 값 1과 0(또는 True 및 False)으로 읽는 경우, 1차 대수학에서는 2(또는 Sential logic)를 해석한다. LoF는 일차대수가 삼단논법을 어떻게 해석할 수 있는지를 보여준다. 이러한 해석 각각은 아래 하위섹션에서 논의된다. 1차 대수학 연장이 표준 1차 논리를 해석할 수 있도록 하는 것은 아직 행해지지 않았지만, 페어스의 베타 실존 그래프는 이 연장이 실현 가능하다는 것을 시사한다.

2소 부울 대수 2

1차 대수학은 2소 부울 대수 2에 대한 우아한 미니멀리스트 표기법이다. 허용:

• 부울 조인(+) 또는 만남(×) 중 하나 연결 해석
• A의 해석의 보충역
• 0 (1) 조인(미트)이 결합을 해석할 경우 빈 마크를 해석한다(제로 피연산자에 적용되는 이항 연산은 해당 연산의 ID 요소와 동일하다고 간주될 수 있거나 다른 방식으로 말하면 누락된 피연산자는 기본적으로 ID 요소와 같은 작용을 하는 것으로 간주될 수 있기 때문이다).

조인($만나$)이 AC를 해석하면, 미팅(조인)은 $A$의${\$overline${C}}}}}\\\\\\overline$ {C$\}\}\}\}\}\}\}\}\}$따라서 1차 대수학과 2는 이소형이지만, 1차 대수 보완은 무효가 될 수 있다. 이 세부사항으로, 2는 1차 대수학의 모델이다. 1차 산술은 2의 산술 공리화를 제안한다: 1+1=1+0=1=1=0, 0+0=0=0=~1.

${\displaystyle 세트}$ B${\displaystyle }$= ${\displaystyle \B$${\displaystyle }$ ${\displaystyle$ ${\displaystyle ,\}}$$$${\displaystyle }$ ${\displaystyle \}}$은(는) 부울 도메인 또는 캐리어다. In the language of universal algebra, the primary algebra is the algebraic structure ${\displaystyle \langle B,-\ -,{\overline {-\ }},{\overline {\ \ }}\rangle }$ of type ${\displaystyle \langle 2,1,0\rangle }$. The expressive adequacy of the Sheffer stroke points to the primary algebra also being a ${\displaystyle \langle B,{\overline {-\ -\ }},{\overline {\ \ }}\rangle }$ algebra of type ${\displaystyle \langle 2,0\rangle }$. In both cases, the identities are J1a, J0, C2, and ACD=CDA. Since the primary algebra and 2 are isomorphic, 2 can be seen as a ${\displaystyle \langle B,+,\lnot ,1\rangle }$ algebra of type ${\displaystyle \langle 2,1,0\rangle }$. This description of 2 is simpler than the conventional one, namely an ${\displaystyle \langle B,+,\time$$s ,\lnot ,$1$,0\angle }$ 타입${\displaystyle \mathrm{type}}$ 2,${\displaystyle 2}$,${\displaystyle }$1, ${\displaystyle 1}$,${\displaystyle 0,}$ ${\displaystyle 0}$ ${\displaystyle ⟩}$ ${\displaystyle \langle$2$,2,1,0,0\rangele$ $\}$의 대수$$.

부울적 의미에서는 가능한 두 해석은 서로 이중적이다. (부울 대수에서, 방정식 전체에서 AND £ OR과 1 £ 0을 교환하면 동일한 유효 방정식이 산출된다.) 어떤 해석을 선택하든 정체성은 불변하므로, 변환이나 계산 방식은 그대로 유지된다. 각 형식의 해석만 다를 것이다. 예: J1a는 입니다. ${\displaystyle \mathrm{병렬}}$ 처리를 OR로 해석하고 1로 해석하면 interpreting${\displaystyle \mathrm{}}$A${\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \neg A\lor$ A$=1}이($가$$) 참이다. 대칭접합을 AND와 0으로 해석하면 $\neg {\displaystyle \mathrm{}}$ ${\displaystyle A}$= ${\displaystyle 0}$ ${\displaystyle \neg A\land A=0}$이(가) 참인$$ 것으로 해석된다$({\displaystyle \mathrm{}\mathrm{및}}${$$A = 1 {\displaystyle $\ng$A\$$$lor A=1$}의 이중).

전위 논리학

빈 페이지는 거짓을 나타내도록 하고, 십자가는 그렇지 않은 것으로 읽도록 한다. 그러면 1차 산술에는 다음과 같은 보초적 판독값이 있다.

= 거짓

= 참 = 거짓이 아님

= 사실이 아님 = 거짓

1차 대수학에서는 지각 논리를 다음과 같이 해석한다. 글자는 어떤 주어진 보초적 표현을 나타낸다. 따라서 다음과 같다.

A이 아닌 해석

A 또는 B를 해석하다

A, B가 아니라 If A가 B를 해석한다.

해석 안 함(A 아님 B 아님)

또는 그렇지 않다(A이면 B가 아님)

또는 A와 B.

a b a b

,

a b AB

둘 다 B 또는 A가 B와 동일한 경우에만 A를 해석한다.

그러므로 지각논리의 어떤 표현도 일차 대수번역을 가지고 있다. 동등하게, 1차 대수학에서는 보초적 논리를 해석한다. 표시 또는 표시되지 않은 상태에 모든 변수를 할당하면, 이 1차 대수 변환은 1차 산술 식까지 감소하므로 단순화할 수 있다. 각 변수에 대한 두 원시적 가치의 가능한 모든 할당에 대해 이 연습을 반복하면 원래의 표현이 상호론적인지 만족스러운지 여부를 알 수 있다. 이것은 전통적인 진리표의 정신에 있어서 결정 절차의 한 예다. N 변수를 포함하는 일부 일차 대수 공식을 고려할 때, 이 결정 절차는 2개의^N 일차 산술 공식을 단순화해야 한다. Quine의 "진실 가치 분석"의 정신에서 보다 덜 지루한 의사결정 절차는 Meguire(2003)를 참조한다.

슈워츠(1981)는 1차 대수학이 고전적인 명제 미적분학(proposal accountry)과 구문론적으로, 의미론적으로, 그리고 증거론적으로 등가임을 증명했다. 마찬가지로 1차 대수학도 고전적 진리 값인 참과 거짓, 논리 결합형 NOT, OR, AND, 괄호에서 통상적인 방법으로 쌓아올린 표현으로 구문론적으로 동등하다는 것을 알 수 있다.

표시되지 않은 상태를 거짓으로 해석하는 것은 전적으로 자의적이다; 그 상태는 똑같이 참으로 잘 읽힐 수 있다. 필요한 것은 연결에 대한 해석이 OR에서 AND로 바뀌는 것이다. 만약 A THEN B가 이제 와 같이 번역된다면. 보다 일반적으로, 1차 대수학은 "self-dual"이며, 이는 어떤 1차 대수 공식도 각각 다른 것의 이중인 2개의 sential 또는 Boolean 판독치를 가지고 있다는 것을 의미한다. 자기 이중성의 또 다른 결과는 De Morgan의 법칙이 부적절하다는 것이다; 그러한 법칙들은 처음부터 1차 대수학의 구문에 내장되어 있다.

일차 대수학, 일차 대수학, 일차 대수학, 일차적 논리학의 구별의 실체가 지금 나타나고 있다. 후자의 형식에서는 "아무것도"로 운영되는 보완/부정화가 잘 형성되지 않는다. 그러나 빈 십자가는 잘 형성된 일차 대수적 표현으로 원시적인 값인 마크 상태를 나타낸다. 따라서 비어 있지 않은 십자가는 연산자가 되는 반면 비어 있는 십자가는 원시 값을 나타내기 때문에 연산자가 된다. 따라서 1차 대수학에서는 연산자와 연산자의 지금까지 구별된 수학적 개념은 사실 단일 근본 작용의 다른 면에 불과하며, 구별을 만든다.

삼단논법

LoF의 부록 2는 전통적인 삼단논법과 소르미를 1차 대수학으로 번역하는 방법을 보여준다. 유효한 삼단논법은 단순히 일차 대수학 번역을 빈 십자가로 단순화하는 것이다. 렛 A*는 문자 그대로, 즉 A나 $A$의${\$를 의미하며 무관심하다$.$ Then every syllogism that does not require that one or more terms be assumed nonempty is one of 24 possible permutations of a generalization of Barbara whose primary algebra equivalent is ${\displaystyle {\overline {A^{*}\ B }}\ \ {\overline {{\overline {B }$$}\ C^{*}{\Big }}\A^{*}}\ C$이 24개의 가능한 순열은 아리스토텔레스와 중세 논리에서 타당하다고 간주되는 19개의 삼단논법 형식을 포함한다. 삼단논리의 이 일차 대수적 해석은 일차 대수학이 일차적 논리와 용어 논리를 해석할 수 있고, 일차 대수학이 콰인의 부울적 용어 도식(1982년: Part II)에 친화성을 가지고 있다는 것을 시사하기도 한다.

계산의 예

라이프니츠의 비경쟁적 프래클라룸 이론의 다음과 같은 계산은 일차 대수학의 실증적 힘을 예시한다. Let C1 be ${\displaystyle {\overline {{\overline {A }}{\Big }}}}$ =A, C2 be ${\displaystyle A\ {\overline {A\ B }}=A\ {\overline {B }}}$, C3 be ${\displaystyle {\overline {\ \ }}\ A={\overline {\ \ }}}$, J1a be ${\displaystyle \stackrel{}{A}}$$={\$이$($가) OI로 하자면 변수와 보조양식이 일치성 및 연관성이 허용하는 방식으로 다시 정렬된 것이다.

[(P→R)∧(Q→S)]→[(P∧Q)→(R∧S)]	프래클라룸 이론.
P R Q S P Q R S .	1차 대수역
P R Q S P Q R S .	C1
P R Q S P Q R S .	C1
P P R Q S Q R S .	OI.
P R Q S Q R S .	C2
P R Q Q S R S .	OI.
P R Q S R S .	C2
P Q S R R S .	OI.
P Q S R S .	C2
P Q S R S .	C1
P Q S S R .	OI.
P Q B R .	J1a.
B P Q R .	OI.
B	C3. $◻{\displaystyle }$ ${\displaystyle \square }$

마그마와의 관계

1차 대수학은 1933년 헌팅턴이 지적한 점을 구체화한다: 부울 대수학은 하나의 단항 연산 외에 2가 아닌 1이항 연산도 요구한다. 그래서 부울 알헤브라는 거의 알려지지 않은 사실들이 마그마이다. (마그마는 후기가 범주 이론에 의해 전용될 때까지 그룹오이드라고 불렸다.) 이를 보려면 1차 대수학(primary 대수학)이 정류자임을 유의하십시오.

• 일차 대수 대칭성이 통근하고 관련되기 때문에 세미그룹;
• J0의 덕택에, 정체성 요소가 있는 모노이드.

그룹은 또한 부울 보충의 그룹 상대인 역(reverse)이라고 불리는 단항 연산을 요구한다. a의 반을 나타냅시다. 그룹 ID 요소를 표시하십시오. 그러면 그룹과 1차 대수학 모두 같은 서명이 붙는데, 이는 모두 〈2,1,0〉 타입의${\displaystyle }$type$$ -${\displaystyle ,,\stackrel{}{\backslash }}$의$\displaystyle \langle -\,{\overline{-\},{\overline{\\\}}}{\overline{\\\}}}}}}.$ 따라서 1차 대수학은 경계 대수다. 경계 표기법에서 아벨리아 그룹에 대한 공리는 다음과 같다.

• G1. abc = acb(왼쪽부터 연관성 추정)
• G2.
• G3.

G1과 G2에서 연결의 공통성과 연관성을 위와 같이 도출할 수 있다. G3와 J1a는 동일하다는 점에 유의한다. = A2를 대체하는 경우 G2와 J0은 동일할 것이다. 이것은 경계 표기법으로 그룹 이론의 산술적 정체성을 정의하는 것이다.

1차 대수학과는 두 가지 면에서 아벨 그룹과 다르다.

• A2부터 ≠. 1차 대수학이 집단이라면 =은 지탱할 것이고, a 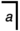= 또는 a = 중 하나는 1차 대수 결과가 되어야 할 것이다. $그룹$ 이론에서 요구하는 바와 같이, $상호 기본$ 대수학 보완책이며$,$ 이는 그룹 $이론$과 기본 대수학에서$$모두 해당된다는$$ 점에 유의하십시오$.$
• C2는 다른 마그마로부터 1차 대수학을 명확하게 구분하는데, C2는 격자를 정의하는 흡수 법칙과 부울 대수 중심의 분배 법칙을 증명할 수 있기 때문이다.

A2와 C2는 모두 B에서 주문 집합으로 이어진다.

제2도 방정식 (11장)

LoF 11장에서는 "무한" 깊이를 가지고 있다고 볼 수 있는 재귀적 공식으로 구성된 2도 방정식을 소개한다. 어떤 재귀적 공식은 표시되거나 표시되지 않은 상태로 단순화된다. 다른 사람들은 주어진 깊이가 짝수인지 홀수인지에 따라 두 주 사이에 무한히 "오큐빌"한다. 구체적으로 특정 재귀적 공식은 연속적인 시간 간격에 걸쳐 참과 거짓 사이에서 진동하는 것으로 해석될 수 있으며, 이 경우 공식은 "상상적인" 진리 값을 갖는 것으로 간주된다. 따라서 시간의 흐름은 1차 대수학으로 도입될 수 있다.

터니(1986)는 이러한 재귀적 공식을 알론조교회의 제한된 재귀적 산술(RRA)을 통해 어떻게 해석할 수 있는지를 보여준다. Church는 1955년에 유한한 오토마타의 자명적인 공식화로서 RRA를 도입했다. 터니(1986)는 2도 방정식을 Church의 RRA로 번역하는 일반적인 방법을 제시하며, LoF 11장의 공식 E1, E2, E4를 사용하여 자신의 방법을 설명한다. 이 RRA로의 번역은 스펜서 브라운이 E1과 E4에게 준 이름, 즉 "기억"과 "카운터"를 조명한다. 따라서 RRA는 LoF의 상상적 진실 가치 개념을 공식화하고 명확히 한다.

관련업무

고트프리드 라이프니즈는 19세기 말과 20세기 초 이전에 출판되지 않은 암기에 부울 논리를 발명했다. 그의 표기법은 접속사로 읽혀지는 LoF와 이형화되었고, X의 보완으로 읽혀지는 "비(X)"가 있었다. 대수 논리학에서 라이프니츠의 선구적 역할에 대한 인정은 루이스(1918)와 레셔(1954년)에 의해 예견되었다. 그러나 라이프니츠의 업적에 대한 충분한 감상은 1980년대에 출판되어 렌젠(2004)에서 검토된 볼프강 렌젠의 작품을 기다려야 했다.

찰스 샌더스 피어스(1839–1914)는 세 가지 작업맥에서 1차 대수학을 예상했다.

1. 그가 1886년에 쓴 두 논문은 논리 대수학을 채용할 것을 제안했지만, 하나의 상징인 스트림어는 LoF의 십자가와 거의 동일하다. 그 스트리머의 의미론들은 페어스가 그 밑에 아무것도 없는 스트림러를 쓴 적이 없다는 것을 제외하고는 십자가의 의미론들과 동일하다. 이 논문들 중 한 편에서 발췌한 것이 1976년에 발표되었지만,^[7] 1993년이 되어서야 완전히 발표되었다.^[8]
2. 1902년 백과사전 기사에서 Peirce는 이 항목의 방식으로 부울 대수학 및 보초적 논리를 설명했는데, 각 공식 깊이가 증가하면서 '(), '''와 '[]'' 사이에서 전환되는 두 가지 형태의 괄호를 사용했다는 것을 제외한다.^[9]
3. 그의 알파 실존적 그래프의 구문은 단지 결합일 뿐이고, 접속사로 읽히고, 난자에 의한 외함이며, 부정으로 읽힌다.^[10] 일차 대수 연동을 접속사로 읽는 경우, 이 그래프는 일차 대수(Kauffman 2001)와 이형이다.

아이러니하게도, LoF는 위의 (2)와 (3)의 형식적인 출처인 Peirce's Collected Papers의 제4권을 인용한다. (1)-(3)는 (1960년대) 당시와 (영국) LoF가 쓰여진 장소에서 사실상 알려지지 않았다. LoF가 침묵하고 있는 Peirce의 기호학은 LoF의 철학적 측면을 아직 밝혀내지 못했을 것이다.

카우프만(2001)은 1917년 베르트랑드 러셀의 제자였던 장 니코드가 쓴 글의 LoF와 비슷한 또 다른 표기법을 논하고 있다.

위의 형식주의는 일차 대수학처럼 경계 수학의 모든 예, 즉 구문이 문자와 괄호(첨가 장치)로 한정된 수학이다. 이런 성격의 미니멀리스트 구문은 "경계 표기법"이다. 경계 표기법에는 infix, 접두사 또는 사후 수정 연산자 기호가 없다. 매우 잘 알려진 세트 이론의 곱슬곱슬한 교정기('{, '}')는 경계 표기법으로 볼 수 있다.

라이프니츠, 페이르체, 니코드의 작품은 에밀 포스트의 랜드마크 1920년 논문(LoF가 인용한 것) 앞에 썼듯이 메타테리히가 무죄로 되어 있어, 보초적 논리가 완성되어 있음을 증명하고, 힐베르트와 우카시오비츠가 모델을 이용하여 공리 독립성을 증명하는 방법을 보여주기 전에 증명하고 있다.

크레이그(1979)는 세계, 그리고 인간이 어떻게 인지하고 그 세계와 상호작용하는가는 풍부한 부울 구조를 가지고 있다고 주장했다. 크레이그는 정통 논리학자였고 대수 논리학의 권위자였다.

LoF가 쓰여진 후인 1970년대에 2세대 인지과학이 등장했다. 인지과학과 부울 대수학, 논리학, 세트 이론과의 관련성에 대해서는 라코프(1987년)와 라코프(2001년)를 참조한다. 어느 책도 LoF를 인용하지 않는다.

생물학자들과 인지과학자 훔베르토 마투라나와 그의 제자 프란시스코 바렐라는 모두 그들의 글에서 LoF를 논하는데, 이 논문은 "멸종"을 근본적인 인지행위로 식별한다. 버클리 심리학자 겸 인지과학자인 엘리너 로쉬는 분류라는 밀접하게 관련된 개념에 대해 광범위하게 글을 썼다.

1차 대수학과의 친화성이 가능한 기타 공식 시스템에는 다음이 포함된다.

• 일반적으로 부울대수의 격자 구조와 매우 유사한 단순학. 몇몇 작가들에게 있어서, 단순학은 단순히 부울대수의 모델일 뿐이며, 따라서 일차대수의 모델이기도 하다.
• 본질적으로 부울 대수보다 풍부한 편협학
• 화이트헤드(1934년)의 체계로, 그 근본 원초적 원초적 원초적 원초적 원초적 원초적 원초적 원초적

일차 산술과 대수학은 보초적 논리와 부울 대수에 대한 최소론적 형식주의다. 세트 이론의 힘을 가진 다른 미니멀리스트 공식론에는 다음과 같은 것들이 있다.

• 람다 미적분학;
• 두 개(S 및 K) 또는 한 개(X)의 원시 결합자를 사용한 결합 논리
• 단지 세 가지 원시 개념으로 이루어진 수학 논리: 하나의 결합형, NAND(일차 대수번역은 A ${\$ 또는$$, 한 달에 한 $번씩{\displaystyle \stackrel{}{}A}$의${\displaystyle \stackrel{}{}}$B의$${\$displaystystyle {A}}}\\\\\\\coverline$ {B$}}}),$ 일반 수량화 및 이진 원자 형태la, 세트 멤버십을 나타낸다. 이것이 퀴네(1951년)의 제도다.
• 베타 실존 그래프(단일 이진 술어가 설정된 멤버 자격을 나타냄) 이것은 아직 탐구되지 않았다. 위에서 언급한 알파 그래프는 베타 그래프의 특별한 경우다.

참고 항목

• 부울 대수(간단한 영어 위키백과)
• 부울 대수(소개)
• 부울 대수(로직)
• 부울 대수(구조)
• 부울 알헤브라가 표준으로 정의됨
• 부울 논리학
• 귀속 그래프
• 실존 그래프
• 부울 대수 주제 목록
• 마크 앤 스페이스
• 프로그래밍 및 메타프로그래밍
• 명제 미적분학
• 2소 부울 대수

메모들

참조

• 양식 법판:
  • 1969. 런던: 앨런 & 언윈, 하드커버.
  • 1972. 크라운 출판사, 하드커버: ISBN 0-517-52776-6
  • 1973년. 밴텀 북스, 페이퍼백 ISBN 0-553-07782-1
  • 1979년 E.P. 더튼, 페이퍼백 ISBN 0-525-47544-3
  • 1994. 포틀랜드 OR: 코냑 컴퍼니, 페이퍼백 ISBN 0-9639899-0-1
  • 1997년 독일어 번역, '제세체 데르 폼'이라는 제목. 뤼벡: 보흐마이어 베를라크. ISBN 3-89094-321-7
  • 2008년 보흐메이에 베를라크, 라이프치히, 제5회 국제판. ISBN 978-3-89094-580-4
• 보스토크, 데이빗 1997년 중간 논리학. 옥스퍼드 유니브 누르다
• 번, 리, 1946년 "부울대수의 두 공식", 미국수학협회 회보: 268–71.
• Craig, William (1979). "Boolean Logic and the Everyday Physical World". Proceedings and Addresses of the American Philosophical Association. 52 (6): 751–78. doi:10.2307/3131383. JSTOR 3131383.
• David Gries, Schneider, F B, 1993. 이산수학에 대한 논리적 접근법. 스프링거-베를라크.
• 1892년 윌리엄 어니스트 존슨, "논리 미적분학", 마인드 1 (ns): 3–30.
• Louis H. Kauffman, 2001 "The Mathical of C.S. Peirce", 사이버네틱스 및 휴먼 노하우 8: 79–110.
• -----, 2006년, "지도 색 정리 개편"
• --------, 2006a. "형식의 법칙 – 수학과 기초의 탐구" 북어음(Hence hence big)
• 2004년, Lenzen, Wolfgang, D, Gabbay의 "Leibniz's Logic"과 Woods, J, Eds, 현대 논리의 대두: 라이프니츠에서 프레지(논리의 역사 핸드북 – Vol. 3)까지. 암스테르담: 엘스비에, 1-83.
• 라코프, 조지 1987년 여자, 불, 그리고 위험한 것들. 시카고 대학 출판부.
• -------- 그리고 라파엘 E. 누녜스, 2001년 수학의 출처: 구체화된 마음이 어떻게 수학을 존재로 불러오는지. 기본 도서.
• Meguire, P. G. (2003). "Discovering Boundary Algebra: A Simplified Notation for Boolean Algebra and the Truth Functors". International Journal of General Systems. 32: 25–87. CiteSeerX 10.1.1.106.634. doi:10.1080/0308107031000075690. S2CID 9460101.
• --------, 2011. 경계 대수 : 기본논리와 부울대수에 대한 더 간단한 접근법. VDM 출판사 ISBN 978-3639367492. LoF가 십자형 아래에 배치하는 것을 괄호 안에 감싸는 표기법을 포함하여 이 항목의 많은 부분을 위한 출처. Steers는 LoF의 좀 더 투기적인 측면을 벗어났다.
• 1951년 윌러드 퀴네 수학 논리학, 2부. 하버드 대학 출판부.
• --------, 1982. 논리학의 방법들, 4번째 에드. 하버드 대학 출판부.
• Rescher, Nicholas (1954). "Leibniz's Interpretation of His Logical Calculi". Journal of Symbolic Logic. 18 (1): 1–13. doi:10.2307/2267644. JSTOR 2267644. S2CID 689315.
• Schwartz, Daniel G. (1981). "Isomorphisms of G. Spencer-Brown's Laws of Form and F. Varela's Calculus for Self-Reference". International Journal of General Systems. 6 (4): 239–55. doi:10.1080/03081078108934802.
• Turney, P. D. (1986). "Laws of Form and Finite Automata". International Journal of General Systems. 12 (4): 307–18. doi:10.1080/03081078608934939.
• A. N. 화이트헤드, 1934, "표시, 등급, 번호, 검증", 마인드 43(n.s): 281–97, 543. 543페이지의 코리겐다는 많고 중요하며, 나중에 이 글의 재인쇄는 그것들을 포함하지 않는다.
• 더크 배커 (edd.) (1993), 칼킬 데르 폼. Suhrkamp; Dirk Baeker (ed.), Publice der Form. 수하르캄프.
• 더크 배커 (edd.) (1999), 폼의 문제, 스탠포드 대학 출판부.
• 더크 배커 (edd.) (2013), A Mathical of Form, A Society of Observes, A Society of Observers, Cybernetics & Human Knowing, vol. 20, no. 3-4.

외부 링크

• 형태 법칙들, 리처드 슈프의 웹사이트 보관소
• 1973년 에살렌에서 열린 스펜서-브라운 회담. 자기반복형식은 "방정식의 정도와 유형론"이라는 절에 도입된다.
• 루이 H. 카우프만 "박스 대수학, 경계 수학, 논리학, 형식의 법칙"
• 키셀, 마티아스 "비체계적이지만 이해하기 쉬운 형태의 법칙 소개"
• 2002년부터 1차 대수학 및 관련 형식주의가 논의되어 온 형태 포럼의 법칙.
• Moshe Klein의 G.S.B와의 만남
• 형태 법칙의 개념에 대한 쉬운 단계별 소개인 마크 마크
• Louis Kauffman과 Arthur Collings의 BF 미적분학과 부정의 제곱근; 가상의 논리적 가치를 추가함으로써 형태의 법칙을 확장한다. (상상적 논리적 가치는 <형식의 법칙> 제11장에 소개되어 있다.)
• 폼의 법칙 과정 - 스펜서 브라운의 마지막 학생인 레온 콘라드가 작가와 함께 작품을 연구한 형태 법칙 본문을 통해 사람들을 안내하는 무료 온라인 과정.