삼단논법

삼단논법은 연역적 추론을 적용하여 주장되거나 진실이라고 가정되는 두 가지 명제를 바탕으로 결론을 도출하는 논리적인 논쟁의 일종이다.

삼단논법은 (아리스토텔레스가 기원전 350년 그의 저서 "Previor Analytics"에서 정의한) 가장 초기의 형태에서, 두 개의 진정한 전제(제안 또는 진술)가 효과적으로 결론 또는 주장이 ^[1]전달하고자 하는 주요 포인트를 암시할 때 발생합니다.예를 들어, 모든 인간은 죽음(대전제)이고 소크라테스는 인간(소전제)이라는 것을 알면, 우리는 소크라테스가 죽음이라고 정당하게 결론지을 수 있다.삼단논법의 인수는 보통 3행 형식으로 나타납니다.

모든 사람은 죽는다.
소크라테스는 남자다.
그러므로, 소크라테스는 ^[2]죽는다.

고대에는 두 개의 경쟁적인 삼단논법 이론이 존재했다.아리스토텔레스의 삼단논법과 스토아식 삼단논법.^[3]중세 이후로, 범주형 삼단 논법과 삼단 논법은 보통 서로 바꿔서 사용되었습니다.이 기사는 오직 이 역사적 용도와 관련이 있다.삼단논법은 반복된 관찰에 의해 사실이 결정되는 귀납적 추론과 대조적으로, 기존의 진술을 결합함으로써 사실이 결정되는 역사적 연역적 추론의 핵심이었다.

학문적 맥락에서, 삼단논법은 고틀롭 프레게, 특히 그의 Begriffsschrift에 이은 1차 술어 논리로 대체되었다.그러나 삼단논법은 상황에 따라서는 ^[4][5]논리에 대한 일반 청자의 입문에도 여전히 유용하다.

초기 역사

고대에는 두 개의 경쟁적인 삼단논법 이론이 존재했다.아리스토텔레스의 삼단논법과 스토아식 삼단논법.^[3]

아리스토텔레스

아리스토텔레스는 삼단논법을 "어떤 (특정적인) 것들이 가정되어 왔고,^[6] 이러한 것들이 그렇게 되기 때문에 필연적으로 가정된 결과와는 다른 어떤 것"이라고 정의한다.이러한 매우 일반적인 정의에도 불구하고, 이전 분석에서 아리스토텔레스는 자신을 범주형 모달 삼단 ^[7]논법을 포함한 세 개의 범주형 명제로 구성된 범주형 삼단 논법으로 제한합니다.

삼단논법을 이해의 도구로 사용한 것은 아리스토텔레스의 논리적 추론 논의로 거슬러 올라갈 수 있다.12세기 중반 이전에 중세 논리학자들은 지배적인 구 논리학, 즉 로지카 베투스에 크게 기여한 작품인 범주 및 해석과 같은 제목을 포함한 아리스토텔레스의 작품 중 일부에만 익숙했다.새로운 논리학, 즉 로지카 노바의 시작은 아리스토텔레스가 삼단논법에 대한 그의 이론을 개발한 사전 분석의 재등장과 함께 일어났다.

재발견과 동시에 Prior Analytics는 논리학자들에 의해 "폐쇄적이고 완전한 교리의 집합체"로 간주되어 당대 사상가들이 토론하고 재구성할 여지가 거의 없었습니다.아리스토텔레스의 주장 문장의 삼단 논법에 대한 이론은 시간이 지남에 따라 개념에 작은 체계적 변화만 일어나면서 특히 주목할 만하다고 여겨졌다.이 삼단논법의 이론은 존 부리던과 같은 사람들에 의해 일반적으로 논리가 재작업되기 전까지는 보다 포괄적인 결과 논리의 맥락에 들어가지 않을 것이다.

그러나 아리스토텔레스의 사전 분석론에는 모달 삼단 논법에 대한 그러한 포괄적인 이론, 즉 '필요', '가능', 또는 '일관적으로'라는 모달 단어를 포함하는 적어도 하나의 모달화된 전제가 있는 삼단 논법은 통합되지 않았다.아리스토텔레스의 용어는, 그의 이론의 이러한 측면에서, 모호하고 많은 경우 불분명한 것으로 여겨졌으며, 심지어 그의 해석에 대한 진술과 모순된다.이론의 이 특정 구성요소에 대한 그의 원래 주장은 상당한 양의 대화에 맡겨졌고, 그 결과 당시의 논평가들에 의해 제시된 광범위한 해결책을 도출했다.아리스토텔레스에 의해 제시된 모달 삼단 논법에 대한 시스템은 궁극적으로 실용에 적합하지 않다고 여겨질 것이고 새로운 구별과 새로운 이론으로 대체될 것이다.

중세 삼단논법

보이티우스

보이티우스 (475–526년)는 고대 아리스토텔레스의 논리를 더 쉽게 접근할 수 있도록 하는 데 기여했다.그의 라틴어 번역인 Prior Analytics는 12세기 이전에는 주로 사용되지 않았지만, 범주형 삼단 논법에 대한 그의 교과서는 삼단 논법의 논의를 확장하는 데 중심적이었다.보에티우스의 논리적 유산은 아리스토텔레스의 기여에 대한 명확하고 일차적으로 정확한 발표뿐만 아니라 그가 개인적으로 그 분야에 추가한 어떤 추가 사항보다, 이전의 이론을 후대의 논리학자들에게 효과적으로 전달하는 데 있다.

피터 아벨라드

라틴 서부의 중세 논리학의 첫 번째 공헌자 중 하나인 피터 아벨라르는 보에티우스의 논평과 논문에 기초한 논리학 토론인 변증법에서 삼단논법의 개념과 그에 부수되는 이론에 대한 철저한 평가를 했다.삼단논법에 대한 그의 관점은 로지카 성분버스 같은 다른 작품에서도 찾아볼 수 있다.데 딕토 모달 문장과 데 레 모달 문장의 아벨라르의 도움으로, 중세 논리학자들은 아리스토텔레스의 모달 삼단 논법 모형의 보다 일관된 개념을 형성하기 시작했다.

장 부리단

중세 후기의 가장 중요한 논리학자로 여겨지는 프랑스 철학자 장 부리단 (1300년경–1361년)은 두 가지 중요한 업적을 남겼다.결론과 변증법의 개요에 관한 논문에서는 삼단논법의 개념, 그 구성요소와 구별, 그리고 논리적 능력을 확장하기 위해 도구를 사용하는 방법에 대해 논의했다.부리단의 논의 이후 200년 동안 삼단논리에 대해서는 거의 언급되지 않았다.논리의 역사학자들은 중세 이후 시대의 주요한 변화는 본래의 근원에 대한 대중의 인식에 대한 변화, 논리의 정교함과 복잡성에 대한 인식의 감소, 그리고 논리적 무지의 증가라고 평가해 왔다. 그래서 20세기 초반의 논리학자들은 전체 시스템을 제거했다고 생각하게 되었다.무수한^[8]

근대사

아리스토텔레스의 삼단논법은 수 세기 동안 서양 철학적 사상을 지배했다.삼단논법 자체는 가정을 검증하는 것이 아니라 가정으로부터 타당한 결론을 도출하는 것이다.그러나 시간이 지나면서 사람들은 가정을 검증하는 것의 중요성을 잊은 채 논리적인 측면에 집중했다.

17세기에, 프랜시스 베이컨은 공리에 대한 실험적인 검증은 엄격히 이루어져야 하며,^[9] 자연에서 결론을 도출하는 최선의 방법으로 삼단논법 자체를 받아들일 수 없다고 강조했다.베이컨은 자연 관찰에 대한 보다 귀납적인 접근을 제안했는데, 이것은 실험을 포함하고 보다 일반적인 결론을 ^[9]만들기 위해 공리를 발견하고 구축하는 것으로 이어졌다.그러나, 자연에서 결론을 도출하는 완전한 방법은 논리나 삼단논법의 범위가 아니며, 귀납법은 아리스토텔레스의 후속 논문인 사후 분석에서 다루어졌다.

19세기에 삼단논법의 수정은 분리적 ("A 또는 B")과 조건적 ("A의 경우 B") 진술을 다루기 위해 통합되었다.임마누엘 칸트는 논리학 (1800)에서 논리는 완성된 과학이며 아리스토텔레스 논리학에는 알아야 할 논리의 모든 것이 포함된다고 주장한 것으로 유명하다.(이 작업은 종종 논리 자체에 대한 혁신으로 간주되는 칸트의 성숙한 철학을 반드시 대표하는 것은 아니다.)비록 아비센 논리나 인도 논리학과 같은 다른 논리체계가 있었지만, 칸트의 의견은 고틀롭 프레게가 그의 Begriffsschrift (개념 스크립트)를 출판한 1879년까지 서양에서 이의 없이 존재했다.이것은 수량화 및 변수를 사용하여 범주형 서술문을 표현하는 방법인 미적분을 도입했다.

주목할 만한 예외는 베르나르 볼자노의 저서 위센샤프트슬레(과학 이론, 1837년)에서 발전한 논리로, 사후에 출판된 책 뉴 안티칸트(1850년)에서 칸트에 대한 직접적인 비판으로 적용되었다.볼자노의 작업은 20세기 후반까지만 해도 오스트리아 제국의 일부였던 보헤미아의 지적 환경 때문에 대부분 간과되어 왔다.지난 20년 동안 볼자노의 작품은 다시 등장하여 번역과 현대 연구의 주제가 되었다.

이것은 삼단논리학적 추론을 가정하면서 센텐셜 논리학과 1차 술어 논리의 급속한 발전을 이끌었고, 따라서 2000년 이후 많은 ^{[original research?]}사람들에 의해 갑자기 쓸모없다고 여겨졌다.아리스토텔레스 체계는 주로 입문 자료와 역사 연구에서 현대 학계에서 설명된다.

이 현대적 강등의 한 가지 주목할 만한 예외는 믿음의 교리와 로마 로타의 사도 재판소의 관리들에 의해 아리스토텔레스식 논리를 계속 적용하는 것입니다.이들은 여전히 옹호자들에 의해 만들어진 어떠한 주장도 삼단논법의 형식으로 제시되어야 한다고 요구합니다.

불의 아리스토텔레스 수용

아리스토텔레스의 논리에 대한 조지 불의 변함없는 수용은 논리학 역사학자 존 코코란에 의해 사상의 법칙에 대한 ^[10][11]접근 가능한 서론에서 강조되었다.Corcoran은 Prior Analytics와 사고의 법칙에 ^[12]대한 포인트 바이 포인트 비교도 작성했습니다.Corcoran에 따르면, 불은 아리스토텔레스의 논리를 완전히 받아들이고 지지했다.불의 목표는 다음과 같이 아리스토텔레스의 논리를 "아래로,^[12] 넘어서는" 것이었다.

1. 방정식을 포함한 수학적 기초 제공
2. 타당성 평가에 방정식이 추가됨에 따라 처리할 수 있는 문제의 클래스를 확장한다.
3. 처리할 수 있는 어플리케이션의 범위를 넓히고 있습니다.예를 들어, 2개의 용어의 명제를 임의의 수의 용어로 확장합니다.

좀 더 구체적으로, 불은 아리스토텔레스가 말한 것에 동의했다; 불의 '불화'는 그렇게 불릴 수 있다면, 아리스토텔레스가 말하지 않은 것과 관련이 있다.첫째, 기초의 영역에서, 불은 아리스토텔레스의 네 가지 명제 형태를 하나의 형태, 즉 방정식의 형태로 줄였는데, 그것 자체가 혁명적인 아이디어였다.둘째, 논리 문제의 영역에서, 아리스토텔레스의 추론 규칙("완벽한 삼단 논법")은 방정식을 푸는 규칙으로 보완되어야 한다는 불의 교리를 포함시킨 또 다른 혁명적 아이디어인 방정식 해법을 추가했다.셋째, 응용 분야에서, 아리스토텔레스는 단지 두 개의 주제의 명제와 주장만을 다룰 수 있는 반면, 불의 시스템은 다항 명제와 주장을 다룰 수 있었다.예를 들어, 아리스토텔레스의 시스템은 "사각형인 사각형은 마름모꼴이다" 또는 "사각형인 사각형인 사각형은 마름모꼴이다"에서 "사각형인 사각형은 마름모꼴이다"라고 추론할 수 없었다.

기본구조

범주형 삼단논법은 세 부분으로 구성됩니다.

1. 주요 전제
2. 소전제
3. 결론

각 부품은 범주형 명제이며 각 범주형 명제에는 두 개의 범주형 ^[13]항이 포함됩니다.아리스토텔레스에서 각 전제는 "모든 A는 B", "어떤 A는 B", "아니오 A는 B" 또는 "어떤 A는 B가 아니다"의 형태로 되어 있다. 여기서 "A"는 하나의 용어이고, 다른 "B"는 다른 용어이다.

• "All A are B" 및 "No A are B"는 보편적 명제이다.
• "Some A are B"와 "Some A are B"는 특정 명제이다.

더 현대적인 논리학자들은 약간의 변화를 허용한다.각 전제에는 결론과 공통되는 한 가지 용어가 있다.대전제에서는 이것이 주요 용어(결론의 술어), 소전제에서는 이것이 마이너 용어(결론의 주제)이다.예를 들어 다음과 같습니다.

주요 전제:모든 인간은 죽는다.

부전제:모든 그리스인은 인간이다.

결론:모든 그리스인은 죽는다.

세 개의 서로 다른 항은 각각 범주를 나타냅니다.위의 예에서 인간, 인간, 인간, 그리스인은 주요 용어이고 그리스인은 마이너 용어입니다.그 전제들은 또한 서로 하나의 공통점을 가지고 있는데, 그것은 중간항으로 알려져 있다. 이 예에서는 인간이다.결론적으로 두 전제는 모두 보편적이다.

주요 전제:모든 인간은 죽는다.

부전제:모든 사람은 인간이다.

결론:모든 사람은 죽는다.

여기서, 주요 용어는 죽음이고, 마이너 용어는 남자이고, 중간 용어는 인간입니다.다시 말씀드리지만, 두 가지 전제는 보편적이기 때문에 결론도 마찬가지입니다.

다신교

다원론 또는 소라이트는 일련의 불완전한 삼단논법이 배열되어 있어 첫 번째의 주어가 결론에서 마지막의 주어와 결합될 때까지 각 전제의 술어가 다음 주어를 형성한다.예를 들어, 어떤 사람은 모든 사자는 큰 고양이이고, 모든 큰 고양이는 포식자이고, 모든 포식자는 육식동물이라고 주장할 수 있다.그러므로 모든 사자가 육식동물이라고 결론짓는 것은 소라이트 논쟁을 구성하는 것이다.

종류들

이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2020년 7월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기)

가능한 삼단논법은 무한히 많지만 논리적으로 구별되는 타입은 256개, 유효한 타입은 24개뿐입니다(아래에 열거되어 있습니다.삼단논법은 형식(주: M – Middle, S – Subject, P – 술어)을 취한다.:

주요 전제:모든 M은 P입니다.

부전제:모든 S는 M이다.

결론:모든 S는 P입니다.

삼단논법의 전제 및 결론은 다음과 같이 문자로 표기된 네 가지 유형 중 하나입니다^[14].문자의 의미는 다음 표에 나와 있습니다.

코드	수량자	주제	코퓨라	술어	유형	예
A	모든.	S	이다	P	보편적 긍정	모든 인간은 죽는다.
E	아니요.	S	이다	P	보편적 부정	인간은 완벽하지 않다.
I	몇개	S	이다	P	특정 긍정	어떤 사람들은 건강합니다.
O	몇개	S	없다	P	특정 부정	어떤 사람들은 영리하지 않다.

이전 분석에서 아리스토텔레스는 구체적인 예를 제시하기보다는 주로 A, B, C(그리스 문자 알파, 베타 및 감마)를 용어 자리 표시자로 사용합니다.코풀라로 사용하는 것이 아니라 그대로 사용하는 것이 전통이기 때문에 All As are B가 아니라 All As are B입니다.범주형 문장을 간결하게 쓸 수 있도록 a, e, i, o를 infix 연산자로 사용하는 것이 전통적이고 편리한 관행이다.다음 표는 술어 로직에서의 보다 긴 형식, 간결한 줄임말 및 동등한 표현을 나타내고 있습니다.

형태	속기	술어 논리
A는 모두 B다.	AaB	$\displaystyle \forall x(A(x)\오른쪽 화살표 B(x)}$ 또는 $\displaystyle \neg \exists x(A(x)\land \neg B(x)}$
A는 B가 아니다.	AeB	$\displaystyle \neg \exists x(A(x)\land B(x)}$ 또는 $\displaystyle \forall x(A(x)\오른쪽 화살표\neg B(x)}$
어떤 A는 B다.	아이비	$\displaystyle \exists x(A(x)\land B(x)}$
B가 아닌 A도 있다.	AoB	$\displaystyle \exists x(A(x)\land \neg B(x)}$

여기서의 규칙은 문자 S가 결론의 주제이고, P가 결론의 술어이고, M이 중간 용어라는 것입니다.메이저 전제는 M과 P를 링크하고 마이너 전제는 M과 S를 링크한다.그러나 중간 용어는 그것이 나타나는 각 전제의 주어 또는 술어가 될 수 있습니다.장조, 단조, 중간 용어의 서로 다른 위치는 그림으로 알려진 삼단 논법의 또 다른 분류를 야기한다.각 경우에 S-P라는 결론이 나온다면, 네 가지 수치는 다음과 같다.

	그림 1	그림 2	그림 3	그림 4
주요 전제	M-P	P-M	M-P	P-M
소전제	S~M	S~M	M~S	M~S

(그러나 아리스토텔레스의 인물에 대한 취급에 따라 피터 아벨라르나 장 부리단 같은 논리학자들은 제4의 인물에 대해 제1의 인물과 구별되는 인물로서 거부한다.

모든 것을 종합하면, 256개의 가능한 삼단논법이 있다(논리적으로는 차이가 없지만, 장전제와 부전제의 순서가 바뀌면 512개).각 전제 및 결론은 A, E, I 또는 O 타입이 될 수 있으며 삼단논법은 4개의 숫자 중 하나가 될 수 있습니다.삼단논법은 전제와 결론에 대한 글자와 숫자에 대한 숫자를 제시함으로써 간략하게 설명할 수 있다.예를 들어, 아래의 삼단논법 BARBARA는 AAA-1 또는 "첫 번째 그림의 A-A-A"입니다.

가능한 256개의 삼단논법 형태 중 대부분은 유효하지 않다(전제에서 논리적으로 결론은 따르지 않는다).다음 표에 유효한 양식을 나타냅니다.이들 중 일부는 때때로 실존적 오류를 범하는 것으로 간주되는데, 이는 빈 범주를 언급하면 무효라는 것을 의미한다.이 논쟁적인 패턴들은 이탤릭체로 표시되어 있다.이탤릭체로 된 4가지 패턴(펠라프톤, 다랍티, 페사포 및 바말립)을 제외한 모든 패턴은 약해진 분위기이다. 즉, 전제로부터 더 강력한 결론을 도출할 수 있다.

그림 1	그림 2	그림 3	그림 4
바바라	체사레	다티시	칼레메스
셀러런트	카메스트레스	디스미스	디마티스
다리아이	페스티노	페리슨	프레시슨
페리오	바로코	보카르도	칼레모스
바르바리	세자로	펠라프톤	페사포
셀라론트	카메스트로스	다랍티	바마립

그림 1: 음이 세 배입니다."삼단논법의 글자는 음악에서 가장 잘 표현될 수 있다. 예를 들어 E를 보자." - 마릴린 다모드^{[필요한 건]}

A, E, I, O라는 문자는 중세 학교 때부터 다음과 같은 형태의 니모닉 이름을 형성하기 위해 사용되어 왔다: '바바라'는 AAA, 'Celarent'는 EAE 등을 의미한다.

각 전제 및 결론 옆에는 문장의 간략한 설명이 있습니다.따라서 AAI-3에서는 "모든 제곱은 직사각형"이라는 전제가 "MaP"가 됩니다. 기호는 첫 번째 항("제곱")이 중간 항이고 두 번째 항("직각")이 결론의 술어이며 두 항 사이의 관계는 "a"로 표시됩니다(모든 M은 P).

다음 표는 근본적으로 다른 모든 삼단논법을 보여줍니다.비슷한 삼단논법은 같은 전제를 공유하며 단지 다른 방식으로 쓰여질 뿐이다.예를 들어, "어떤 애완동물은 고양이" (Darii에서는 SiM)는 "어떤 고양이는 애완동물" (Datisi에서는 MiS)로 표기될 수도 있다.

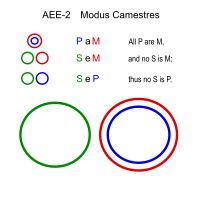
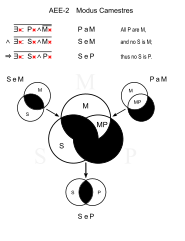
벤 다이어그램에서 검은색 영역은 요소가 없음을 나타내고 빨간색 영역은 하나 이상의 요소를 나타냅니다.술어 논리식에서 표현식 위의 수평 막대는 해당 표현식의 결과를 부정("논리적이지 않음")하는 것을 의미합니다.

(정점과 모서리로 구성된) 그래프를 사용하여 삼단 ^[15]논법을 평가할 수도 있습니다.

예

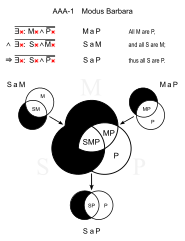남자 S: 그리스어 P: 필살기

바바라(AAA-1)

모든 사람은 죽는다.(MaP)

모든 그리스인은 남자다. (SaM)

①그리스인은 모두 죽는다.(SaP)

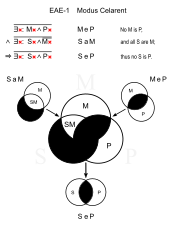파충류 S: 뱀 P: 퍼

셀러런트(EAE-1)

유사:Cesare(EAE-2)

어떤 파충류도 털을 가지고 있지 않다. (MeP)

모든 뱀은 파충류이다.

①털이 있는 뱀은 없다.(SeP)

캠스트레스(AEE-2)
파충류 S: 퍼 P: 뱀 Camestres는 본질적으로 S와 P가 교환된 Celarent와 같습니다. 유사: 캘리메스(AEE-4) 모든 뱀은 파충류이다. 털이 있는 동물은 파충류이다.(SEM) ①털이 달린 동물은 뱀이 아니다.(Sep)

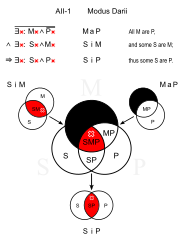토끼 S: 애완동물 P: 퍼

Darii (AII-1)

유사: Datisi(AII-3)

모든 토끼는 털을 가지고 있다.

어떤 애완동물은 토끼이다.(SiM)

①털이 있는 애완동물도 있다.(SiP)

Disamis (IAI-3)
토끼 S: 퍼 P: 애완동물 Disamis는 본질적으로 S와 P가 교환된 Darii와 같다. 유사: Dimatis (IAI-4) 어떤 토끼들은 애완동물이다. (MiP) 모든 토끼는 털을 가지고 있다. (MaaS) ① 동물을 키우는 모피 중에는 애완동물이 있는 것도 있습니다.(SiP)

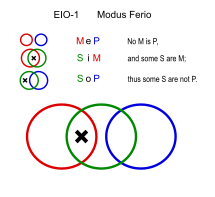숙제 S: 읽기 P: 재밌다

페리오(EIO-1)

유사:Festino(EIO-2), Ferison(EIO-3), Fresison(EIO-4)

숙제는 재미없다. (Mep)

어떤 독서는 숙제다. (SiM)

①독서는 재미없다.(SoP)

포유류 S: 애완동물 P: 고양이

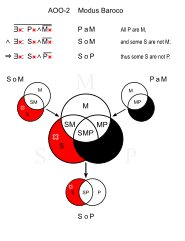
바로코(AOO-2)

모든 고양이는 포유동물이다. (PaM)

어떤 애완동물은 포유류가 아니다. (SoM)

①고양이가 아닌 애완동물이 있다.(SoP)

고양이 S: 포유류 P: 애완동물

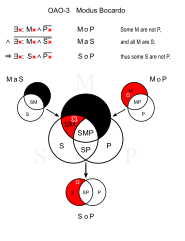
보카르도 (OAO-3)

어떤 고양이들은 애완동물이 아니다. (MoP)

모든 고양이는 포유동물이다. (MaaS)

① 애완동물이 아닌 포유류도 있다.(SoP)

---

남자 S: 그리스어 P: 필살기

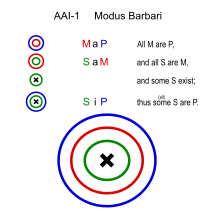
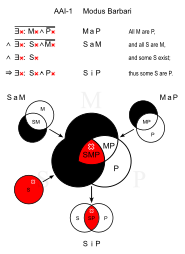
바르바리(AAI-1)

모든 사람은 죽는다.(MaP)

모든 그리스인은 남자다. (SaM)

①그리스인 중에는 필멸자가 있다.(SiP)

Bamalip (AAI-4)
남자 S: 필탈 P: 그리스어 Bamalip은 S와 P가 교환되는 Barbari와 똑같습니다. 모든 그리스인은 남자다. (PaM) 모든 사람은 인간이다. § 그리스인 인간도 있다.(SiP)

파충류 S: 뱀 P: 퍼

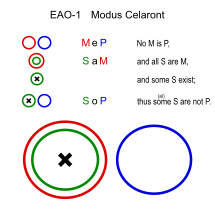
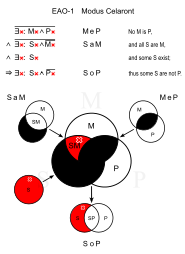
Celaront (EAO-1)

유사:세자로(EAO-2)

어떤 파충류도 털을 가지고 있지 않다. (MeP)

모든 뱀은 파충류이다.

①털이 없는 뱀도 있다.(SoP)

발굽 S: 인간 P: 말

카메스트로(AEO-2)-2)

유사: Calemos (AEO-4)

모든 말에는 발굽이 있다. (PaM)

인간은 발굽이 없다.(SEM)

①말이 아닌 인간도 있다.(SoP)

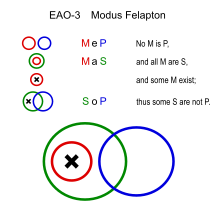꽃 S: 플랜트 P: 동물

Felapton (EAO-3)

유사:Fesapo (EAO-4)

꽃은 동물이다. (MeP)

모든 꽃은 식물이다. (MaaS)

①동물이 아닌 식물도 있다.(SoP)

정사각형 S: 마름모꼴 P: 직사각형

Darapti (AAI-3)

모든 사각형은 직사각형입니다.(MaP)

모든 사각형은 마름모꼴이다. (MaaS)

② 직사각형 모양의 마름모꼴도 있다.(SiP)

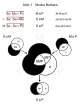
모든 삼단논법의 표

이 표는 벤 다이어그램으로 표현되는 24개의 유효한 삼단 논법을 보여줍니다.열은 유사성을 나타내며 전제의 조합별로 그룹화됩니다.경계는 결론에 대응합니다.실존적 가정을 가진 사람들은 좌절되었다.

수치	A a A		A e E				A i I		A o O		E i I
1	바바라	바르바리			셀러런트	셀라론트	다리아이				페리오
2			카메스트레스	카메스트로스	체사레	세자로			바로코		페스티노
3		다랍티				펠라프톤	다티시	디스미스		보카르도	페리슨
4		바마립	칼레메스	칼레모스		페사포		디마티스			프레시슨

삼단논법의 용어

이 섹션에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2020년 7월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기) 이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2020년 7월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

아리스토텔레스와 함께 우리는 소크라테스와 같은 단수 용어와 그리스인과 같은 일반 용어를 구별할 수 있다.아리스토텔레스는 (a)와 (b)를 더욱 구별했다.

그리스에서와 같이 비분배형과는 대조적으로 그러한 서술은 분포형이라고 알려져 있다.아리스토텔레스의 삼단논법은 분배적 포식에만 효과가 있는 것이 분명하다. 왜냐하면 우리는 모든 그리스인이 동물이고, 동물도 많고, 따라서 모든 그리스인은 수적이다.아리스토텔레스의 관점에 따르면 단수항은 유형(a)이고 일반항은 유형(b)이다.그러므로 인간은 소크라테스를 단정할 수 있지만 소크라테스는 어떤 것도 단정할 수 없다.따라서, 삼단논법에서 명제의 주어 또는 술어 위치에 있는 용어가 서로 호환되려면, 그 용어가 일반 용어이거나, 또는 호명된 범주형 용어여야 한다.결과적으로, 삼단논법의 명제는 범주형 명제여야 하며, 범주형 용어만을 사용하는 삼단논법은 범주형 삼단논법이라고 불리게 되었다.

삼단논법에서 단일한 용어가 발생하는 것을 막을 수 있는 것은 분명하지만, 그러한 삼단논법은 타당하더라도 단정적인 삼단논법은 아니다.예를 들어 소크라테스는 인간이고, 모든 사람은 죽음이며, 따라서 소크라테스는 죽음이다.직감적으로 이것은 모든 그리스인이 남자인 만큼 유효하고, 모든 사람은 죽음이며, 따라서 모든 그리스인은 인간이다.그것의 타당성이 삼단논법 이론으로 설명될 수 있다고 주장하는 것은 우리가 소크라테스가 인간이라는 것을 보여줄 것을 요구할 것이다.소크라테스가 인간이라는 것은 소크라테스와 동일한 모든 것과 동등하다고 주장할 수 있기 때문에, 우리의 비범주적 삼단논법은 위의 동등성을 사용하고 그 다음에 바바라를 인용함으로써 정당화될 수 있다.

실존적 Import

이 섹션에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 클레임을 확인하고 인라인 인용을 추가하여 개선해 주십시오. 독창적인 연구로만 구성된 진술은 삭제되어야 한다.(2020년 7월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기) 이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2020년 7월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

스테이트먼트에 false라는 용어가 포함되어 있는 경우, 그 용어에 인스턴스가 없는 경우, 스테이트먼트는 그 용어에 관한 존재적 Import를 가지고 있다고 한다.All A is B 형식의 범용 스테이트먼트가 True, False 또는 A가 없는 경우 무의미하다고 간주되는지는 애매합니다.이러한 경우 거짓으로 간주될 경우 All A is B라는 문장은 A에 관한 존재적 Import를 가지고 있습니다.

아리스토텔레스의 논리체계는 사례가 없는 경우를 다루지 않는다고 주장되고 있다.아리스토텔레스의 목표는 "과학의 동반 논리"를 개발하는 것이었다.그는 인어공주나 유니콘과 같은 소설을 시와 문학의 영역으로 격하시킨다.그의 마음속에서는 그것들은 과학의 테두리 밖에 존재하기 때문에 그는 논리에 그러한 존재하지 않는 실체를 위한 여지를 남기지 않는다.이것은 사려 깊은 선택이지 부주의로 빠뜨린 것이 아니다.엄밀히 말하면, 아리스토텔레스 과학은 정의를 찾는 것이고, 여기서 정의는 '사물의 본질을 나타내는 문구'이다.존재하지 않는 실체는 아무것도 될 수 없기 때문에 아리스토텔레스의 생각으로는 본질은 가지고 있지 않다...이것이 그가 염소발톱(또는 유니콘)과 같은 가상의 실체를 위한 장소를 남기지 않는 이유이다." ^[16]

그러나 이후 개발된 많은 논리 시스템은 인스턴스가 없는 경우를 고려합니다.중세 논리학자들은 실존적 수입의 문제를 알고 있었고 부정적인 명제는 실존적 수입을 수반하지 않으며, 대체되지 않는 주제를 가진 긍정적인 명제는 거짓이라고 주장했다.

다음의 문제가 발생합니다.

예를 들어 A가 없고 AaB가 AiB를 수반하는 경우 AiB는 A에 대해 실존적 수입이며 AaB도 마찬가지이다.또, AiB가 BiA를 수반한다고 인정되면, AiB나 AaB도 B에 대해서 실존적인 수입을 가진다.마찬가지로 A가 없는 경우 AoB가 false이고 AeB가 AoB를 수반하고 AeB가 BeA를 수반하는 경우 AeB와 AoB는 모두 A와 B에 대해 존재적 중요성을 가집니다.따라서 모든 보편적 범주형 문장은 두 용어와 관련하여 실존적 의미를 갖는다.AaB와 AeB가 각각 A가 B이고 A가 B인 일반 자연어로 된 문장의 사용을 공정하게 나타낸다면 다음과 같은 결과가 발생한다.

"날아다니는 말은 모두 신화다"는 것은 날아다니는 말이 없다면 잘못된 것이다.

"아무도 불 먹는 토끼가 없다"가 사실이라면 "불 먹는 토끼가 있다"는 말이 사실이고, 그 외 다른 것도 마찬가지입니다.

만약 보편적 문장이 존재하지 않는다고 판단되면, 반대편의 제곱은 여러 측면에서 실패하며(예를 들어 AaB는 AiB를 수반하지 않음), 다수의 삼단논법은 더 이상 유효하지 않다(예를 들어 BaC, AaB-> AiC).

이러한 문제와 역설은 자연어 문장과 삼단논법 형식의 문장에서 모두 발생하는데, 이는 모호성, 특히 모든 것에 대한 모호성 때문이다."프레드가 자신의 모든 책이 퓰리처상 수상작이라고 주장한다면, 프레드는 자신이 책을 썼다고 주장하는 건가요?그렇지 않다면, 그가 주장하는 것이 사실인가요?만약 제인이 그녀의 친구들 중 아무도 가난하지 않다고 말한다면, 만약 그녀가 친구가 없다면 그것이 사실일까?

1차 술어 미적분은 보편적 진술에 관해 실존적 의미를 가지지 않는 공식을 사용함으로써 그러한 모호성을 회피한다.실존적 주장은 명시적으로 진술되어야 한다.따라서 자연어 문장(All A는 B, No A는 B, Some A는 B, Some A는 B, Some A는 B가 아닌 형식)은 용어 A 및/또는 B에 대한 존재적 Import가 명시적이거나 전혀 이루어지지 않는 1차 술어 미적분으로 나타낼 수 있다.따라서 AaB, AeB, AiB 및 AoB의 4가지 형식을 존재 수입의 모든 조합에서 1차 술어로 나타낼 수 있으므로, 어떤 해석이 반대편의 제곱과 전통적으로 유효한 삼단논법의 타당성을 보존하는지 확인할 수 있다.Strawson은 이러한 해석이 가능하다고 주장하지만, 그의 견해로는 위의 질문 e에 대한 답변은 "아니오"이다.

그러나 현대 수리논리학에서는 집합론의 관점에서 "all", "some" 및 "no"라는 단어를 포함하는 서술이 가능하다.모든 A의 세트가${\displaystyle }$s ($)$ {$displaystyle$ s$(A)},$ 모든$$ B의 세트가${\displaystyle }$s ($)$ {$displaystyle$ s$(B$로 라벨이 붙어 있는 경우:

• "All A is B"(AaB)는 $)$와 같습니다.{ $displaystyle$ s$(A$$)$는 s${\displaystyle (}$${\displaystyle B}$${\displaystyle )<img\; alt="\{\backslash displaystyle\; s(B)\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/f65aa264ff97536512e9859988aca5de64bc03f5"\; style="vertical-align:\; -0.838ex;\; width:4.664ex;\; height:2.843ex;">}$ $또는{\displaystyle }$ $s{\displaystyle }$(A$)$의 서브셋입니다.{ $displaystyle$ s$(A)\subseteq$s$B$
• "No A is B"(AeB)는 "s${\displaystyle }$($A)$ {$displaystyle$s($A)}$와${\displaystyle }$s ($)$ {$displaystyle$ s$(B$$)}$의 교집합" 또는${\displaystyle }s{\displaystyle }$ ($)$s (${\displaystyle B)}$ $=$ s$$(A)\$cap ($B)\$empt$와 같습니다.
• "Some A is B"(AiB)는 "s $)$ {$displaystyle$s($A)}$와${\displaystyle }$s ($)$ {$displaystyle$ s$(B)}$의 교집합" $또는{\displaystyle }$s (${\displaystyle A}$)${\displaystyle )}$ ${\displaystyle s}$(${\displaystyle B)}$\$displaystyle$s($A)\cap$ s$(B$) \$emptysset$)에 해당합니다.
• "Some A is not B"(AoB)는 $)$와 동등합니다.{ $displaystyle$$$s($A)}$$$는$B$${\displaystyle )}$의 서브셋이 아닙니다.{ $displaystyle s($B)\$nsubseteq(B$는${\displaystyle }$s$B)$의 서브셋이 아닙니다.

정의상 빈 세트 $「\displaystyle \emptyset」$는 모든 세트의 서브셋입니다.이 사실로부터, 이 수학 규칙에 따르면, A가 없는 경우, "All A is B"와 "No A is B"는 항상 참인 반면, "Some A is B"와 "Some A is B"는 항상 거짓인 것을 알 수 있다.이는 또한 AaB가 AiB를 수반하지 않으며, 위의 삼단 논법 중 일부는 A가 없는 경우 유효하지 않음을 의미합니다( ${\displaystyle }$(${\displaystyle A}$ ) ${\displaystyle =}$ \ $displaystyle$s ( A ) = \ $emptyset$}$$ 。

삼단논법의 오류

사람들은 삼단논법으로 ^[17]추론할 때 종종 실수를 한다.

예를 들어, 어떤 A는 B, 어떤 B는 C, 사람들은 어떤 A는 ^[18][19]C라는 최종적인 결론에 도달하는 경향이 있다.하지만, 이것은 고전 논리의 법칙에 따르지 않는다.예를 들어 고양이(A)가 검은 것(B), 검은 것(B)이 텔레비전(C)인 경우도 있지만, 고양이(A)가 텔레비전(C)인 파라미터와는 일치하지 않는다.이는 삼단논법의 구조(III-1)에서 중간항은 대전제 또는 소전제에서 분배되지 않기 때문에 "미분포 중간항"이라고 불리는 패턴이다.그렇기 때문에, 형식적인 논리를 따르기 어려울 수 있고, 실제로 논쟁이 ^[20]유효한지 확인하기 위해서는 더 면밀한 안목이 필요하다.

삼단논법의 타당성을 결정하는 것은 각 문장의 각 용어의 분포를 결정하는 것을 포함하며, 이는 그 용어의 모든 구성원을 설명하는지를 의미한다.

단순한 삼단논리학적 패턴에서 잘못된 패턴의 오류는 다음과 같습니다.

• 미분포 중간:어느 전제 조건도 중간 기간의 모든 구성원을 차지하지 않기 때문에 결과적으로 주요 용어와 마이너 용어를 연결하는 데 실패한다.
• 주요 용어의 불법 취급:결론은 주요 용어의 모든 구성원(P – 제안이 부정적이라는 의미)을 포함하지만, 주요 전제는 이들을 모두 설명하지 않는다(즉, P는 긍정 술어이거나 특정 주제이다).
• 소용어 불법 취급: 위와 동일하지만 소용어(S – 명제는 보편적이라는 의미) 및 소전제(S는 특정 주어 또는 긍정 술어 중 하나)에 대하여.
• 전용 구내:두 전제는 모두 음수입니다. 즉, 메이저 용어와 마이너 용어가 연결되어 있지 않습니다.
• 부정적인 전제에서 긍정적인 결론:어느 하나의 전제가 부정적이면 결론도 부정적이 되어야 한다.
• 긍정적인 전제에서 나온 부정적인 결론:양쪽 전제가 모두 긍정적이면 결론도 긍정적이여야 한다.

기타 삼단논법

• 분리 삼단 논법
• 가설 삼단 논법
• 법률 삼단논법
• 다신교
• 운율 삼단 논법
• 준동음설
• 통계 삼단 논법

「 」를 참조해 주세요.

• 삼단논법의 오류
• 논거론
• 불교 논리
• 엔티엠
• 형식 오류
• 논리적 오류
• 삼단논법의 오묘함
• 반복(논리)
• 벤도

레퍼런스

원천

• 아리스토텔레스, [기원전 350년경] 1989년이전 분석, R 번역스미스, 해켓.ISBN 0-87220-064-7
• 블랙번, 사이먼[1994] 1996."동음주의"옥스포드 철학 사전.옥스퍼드 대학 출판부ISBN 0-19-283134-8.
• 브로드디, 알렉산더1993년 중세 논리 입문옥스퍼드 대학 출판부ISBN 0-19-824026-0.
• 코피, 어빙1969. 논리 입문 (제3판).맥밀런 컴퍼니
• 1972년, 존 코코란입니다"고대 논리의 완전성." 기호논리 저널 37:696~702.
• - 1994. "논리의 기초:아리스토텔레스의 논리에 대한 현대적 해석"고대 철학 14장 9절~24절.
• 코코란, 존, 하산 마수드.2015. "현재의 Import:새로운 메타오렘; 역사, 철학, 교육학적 오해"논리의 역사와 철학 36 (1):39~61.
• 엥글브레센, 조지1987년 신 삼단논법피터 랭
• 햄블린, 찰스 레오나드.1970년 오류.런던:메튜엔.ISBN0-416-70070-5.
  • 삼단논법의 타당성에 대하여:「분포의 개념에 근거해, 중세 후기에 심플한 일련의 타당성 룰이 마침내 작성되었다」
• 1987년 1월 [1957년]우카시에비치현대 형식 논리학의 관점에서 본 아리스토텔레스의 삼단 논법뉴욕: 갈랜드 출판사.ISBN 0-8240-6924-2.OCLC 15015545
• 말링크, 마르코 2013년아리스토텔레스의 삼단논법케임브리지, 매사추세츠: 하버드 대학 출판부.
• 귄터 팻치그 1968년아리스토텔레스의 삼단논법 이론: 선행분석서 A권의 논리철학 연구.도르트레흐트: 레이델.
• 니콜라스, 1966년.갤런과 삼단논법.피츠버그 대학 출판부ISBN 978-0822983958.
• 스마일리, 티모시 1973년"삼단논법이란 무엇인가?철학논리 저널 2:136-54.
• 스미스, 로빈, 1986년"즉시 명제와 아리스토텔레스의 증명 이론"고대 철학 6장 47~68절.
• 톰, 폴 1981년"삼단논법"철학.뮌헨.ISBN 3-88405-002-8.

외부 링크

• Smith, Robin. "Aristotle's Logic". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
• 쿠츠우쿠-아기라키, 안젤리키아리스토텔레스의 주장적 삼단논법(이사벨/HOL의 공식 증명 발전, 공식 증명 자료 보관)
• Lagerlund, Henrik. "Medieval Theories of the Syllogism". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
• 아리스토텔레스의 사전 분석: 아리스토텔레스의 삼단 논법에 대한 주석 문헌인 범주 삼단 논법 이론
• 퍼지 삼단논법 체계
• 퍼지 삼단논리 알고리즘 및 응용분산추론 접근법 개발
• 아리스토텔레스 삼단논법과 인도/티베타 삼단논법의 비교
• 만유불교의 철학 (XX장)III – 삼단논법의 구성원(아바야바)
• 온라인 삼단논법 기계 삼단논법의 모든 오류, 숫자, 용어, 그리고 형태를 탐구하기 위한 대화형 삼단논법 기계입니다.