부울 함수

수학에서 부울 함수는 인수와 결과가 2요소 집합(일반적으로 {true, false}, {0,1} 또는 {-1,^[1]^[2]1})의 값을 가정하는 함수입니다.다른 이름으로는 특히 오래된 컴퓨터 과학 ^[3]^[4]문헌에서 사용되는 스위칭 함수나 논리학에서 사용되는 진실 함수(또는 논리 함수)가 있습니다.부울 함수는 부울 대수와 스위칭 ^[5]이론의 주제이다.

부울 함수의 형식은 $f:\{0,1\}^{k}\to \{0,1\}$ : $f:\{0,1\}^{k}\to \{0,1\}$ { 0 , $f:\{0,1\}^{k}\to \{0,1\}$ } $f:\{0,1\}^{k}\to \{0,1\}$ { $f:\{0,1\}^{k}\to \{0,1\}$ , 1 $f:\{0,1\}^{k}\to \{0,1\}$ } { { $displaystyle$ f : \ { 0 , $1 \$ } { 0 , 1 \ } \ $to$ \ { 0 , 1 \ $}$ { $displaystyle$ $\{0,1\}$ \ { 0 , 1 \ $\{0,1\}$ } 입니다.여기서 $\{0,1\}$ $\{0,1\}$ , $\{0,1\}$ $}$ 은 $\{0,1\}$ 부울 도메인이고 $k는$ 부울함수의 정수라고 불립니다.경우 k=0{\displaystyle k=0},{0,1}{\displaystyle\와 같이{0,1\}의 함수는 정수 요소}. 다중 출력, f:{0,1}k→{0,1}mm을과(\{0,1\}^{m}};1{\displaystyle m> 1}이나 vector-valued 지향 Boolea을 가진 부울 함수이다.n재미ction(^[6]암호화의 S박스).

$2^{2^{k}}$ $(\displaystyle$ k $)$ 인수를 $가진$ 2k $(\$ 2 $^{$ $k})$ 의 $2^{{2^{k}}}$ $2^{k}$ 부울 함수가 $2^{2^{k}}$ .이는 $2k$ (\ $displaystyle 2^{$ }) 엔트리의 $2^{k}$ 다른 진실 테이블 수와 동일합니다.

모든k(\ $displaystyle$ k) - ary $k$ 부울 $k$ 는k(\ $displaystyle$ k) $x_{1},...,x_{k}$ x $x_{1},...,x_{k}$ , $x_{1},...,x_{k}$ . , x $x_{1},...,x_{k}$ (\ $displaystyle$ x_ ${1$ }, $x_{$ k $x_{1},...,x_{k}$ 에서 명제 공식으로 표현할 수 있으며, 두 개의 명제 공식은 동일한 부울 함수를 표현하는 경우에만 논리적으로 동일합니다.

예

16개의 바이너리 부울 함수

기본적인 대칭 부울 함수(논리 연결 또는 로직 게이트)는 다음과 같습니다.

NOT, negration 또는 complete - 입력이 false("not")일 때 true를 반환합니다.

AND 또는 접속사 - 모든 입력이 참("both")일 때 참입니다.

OR 또는 분리 - 입력이 참("둘 중 하나")이면 참입니다.

XOR 또는 배타적 분리 - 입력 중 하나가 참이고 다른 입력이 거짓("같지 않음")인 경우 참입니다.

NAND 또는 셰퍼 스트로크 - 모든 입력이 참("둘 다 아님")이 아닐 때 참입니다.
NOR 또는 논리 no - 입력이 모두 참("둘 다")인 경우 참입니다.
XNOR 또는 논리적 동등성 - 두 입력이 동일한 경우("동일") True

더 복잡한 함수의 예로는 (홀수 입력의) 과반수 함수가 있습니다.

표현

부울 회로로 표시되는 부울 함수

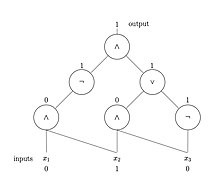
부울 함수는 다양한 방법으로 지정할 수 있습니다.

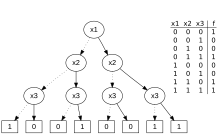
진실 테이블: 인수의 가능한 모든 값에 대한 값을 명시적으로 나열합니다.
- 마르칸드 다이어그램: 2차원 그리드에 배열된 진실 테이블 값(카노 맵에서 사용)
- 이진수 결정 다이어그램: 이진수 트리 하단에 진실 테이블 값을 나열합니다.
- Venn 다이어그램, 평면 영역의 색상으로 진실 표 값을 나타냅니다.

대수적으로, 기본적인 부울 함수를 사용하는 명제 공식으로서:

부정 정규 형식, 인수와 그 보완의 AND와 OR의 임의 혼합
인수와 그 보어의 AND의 OR로서 분리 정규 형식
인수와 그 보어의 OR의 AND로서의 접속 정규형
함수를 고유하게 식별하는 표준화된 공식인 표준 정규 형식:
- 인수 AND의 XOR로서의 대수 정규형 또는 제갈킨 다항식(보수가 허용되지 않음)
- 모든 인수 또는 보어(소수)를 포함하는 AND의 OR인 완전(규범적) 분리 정규 형식
- 모든 인수 또는 보어(최대 용어)를 포함하는 OR의 AND인 완전(규범) 접속 정규형
- 블레이크 표준형, 함수의 모든 주요 함수의 OR

부울 공식도 그래프로 표시할 수 있습니다.

명제 지향 비순환 그래프
- 부울 회로인 로직 게이트의 디지털 회로 다이어그램
- And-Inverter 그래프, AND만 사용하고 NOT만 사용

전자회로를 최적화하기 위해 Quine-McCluskey 알고리즘 또는 Karnaugh 맵을 사용하여 부울식을 최소화할 수 있습니다.

분석.

특성.

부울 함수는 다음과 같은 다양한 ^[7]속성을 가질 수 있습니다.

상수:인수에 관계없이 항상 참이거나 항상 거짓입니다.
모노톤: 인수 값의 모든 조합에 대해 인수를 false에서 true로 변경하면 출력이 false에서 true로 전환될 뿐 true에서 false로 전환되지 않습니다.함수는 특정 변수의 변화와 관련하여 단조로운 경우 해당 변수에서 단일 상태라고 합니다.
선형: 각 변수에 대해 변수 값을 뒤집으면 항상 참 값이 달라지거나 차이가 생기지 않습니다(패리티 함수).
대칭: 값은 인수 순서에 의존하지 않습니다.
Read-Once: 각 변수의 단일 인스턴스로 결합, 분리 및 부정으로 표현할 수 있습니다.
균형: 진실 테이블이 0과 1의 동일한 양을 포함하는 경우.함수의 해밍 가중치는 참값 표에 있는 1의 수입니다.
구부러짐: 그 도함수는 모두 평형입니다(자기상관 스펙트럼은 0입니다).
m번째 순서에 영향을 받지 않는 상관 관계: 출력이 최대 m개의 인수의 모든 (선형) 조합과 상관되지 않은 경우
회피: 함수의 평가에서 항상 모든 인수의 값이 필요한 경우
부울 함수는 임의의 부울 함수를 (구성에 의해) 만드는 데 사용할 수 있는 경우 셰퍼 함수입니다(기능 완전성 참조).
함수의 대수적 차수는 대수적 정규 형식에서 가장 높은 차수의 단항 순서이다.

회로 복잡도는 부울 함수를 계산할 수 있는 회로의 크기 또는 깊이에 따라 분류하려고 합니다.

파생 함수

부울함수는 양의 섀넌 보조인자(섀넌 확장)에서 불의 확장정리를 사용하여 분해할 수 있으며, 이는 인수 중 하나를 고정함으로써 발생하는 (k-1)-아리 함수이다.입력 세트(선형 부분 공간)에 선형 제약 조건을 부과하여 얻은 일반(k-ary) 함수를 하위 ^[8]함수라고 합니다.

인수 중 하나에 대한 함수의 부울 도함수는 함수의 출력이 선택한 입력 변수에 민감할 때 참인 (k-1)-ary 함수입니다. 이것은 대응하는 2개의 보조 인자의 XOR입니다.리드-뮬러 확장에는 미분 및 보조 인수가 사용됩니다.이 개념은 x 및 x + ^[8]dx에서 함수의 차이(XOR)로 구해지는 dx 방향의 k-ary 도함수로 일반화할 수 있다.

부울 함수의 뫼비우스 변환(또는 불-뫼비우스 변환)은 단항 지수 벡터의 함수로서 다항식(대칭 정규 형식)의 계수 집합이다.그것은 자기 역행의 변환이다.고속 푸리에 ^[9]변환과 유사한 나비 알고리즘("고속 뫼비우스 변환")을 사용하여 효율적으로 계산할 수 있습니다.동시 부울 함수는 뫼비우스 변환과 동일하다. 즉, 진실 표(최소) 값은 대수(단항) ^[10]계수와 동일하다.k개의 ^[11]인수에는 2^2^(k-1)개의 일치 함수가 있다.

암호 분석

부울 함수의 월시 변환은 선형 함수(Walsh 함수)로의 분해 계수를 제공하는 k-ary 정수값 함수이며, 푸리에 변환에 의한 실수값 함수의 고조파 분해와 유사합니다.그 사각형은 전력 스펙트럼 또는 월시 스펙트럼이다.단일 비트 벡터의 Walsh 계수는 해당 비트와 Boolean 함수의 출력과의 상관관계에 대한 척도입니다.최대(절대값) Walsh 계수는 ^[8]함수의 선형성이라고 합니다.모든 월시 계수가 0(즉, 하위 함수가 균형을 이루는)의 가장 높은 비트 수(순서)를 복원력이라고 하며, 이 함수는 그 순서에 ^[8]영향을 받지 않는 상관 관계라고 한다.월시 계수는 선형 암호 해석에서 중요한 역할을 합니다.

부울 함수의 자기상관은 k-ary 정수값 함수로 입력의 특정 변화 세트와 함수 출력 간의 상관관계를 제공합니다.주어진 비트 벡터에 대해 이는 해당 방향의 도함수의 해밍 무게와 관련이 있습니다.최대 자기 상관 계수(절대값)를 절대 ^[7]^[8]지시계수라고 합니다.모든 자기상관계수가 특정 비트수에서 0(즉, 도함수가 평형)이면 함수는 해당 순서로 전파기준을 만족하는 것으로 간주되며, 모두 0이면 함수는 구부러진 ^[12]함수입니다.자기 상관 계수는 미분 암호 해석에서 중요한 역할을 합니다.

부울 함수의 월시 계수와 그 자기 상관 계수는 자기 상관과 파워 스펙트럼이 월시 변환 ^[8]쌍임을 나타내는 위너-킨친 정리와 동등하게 관련된다.

이러한 개념은 출력 비트(좌표)를 개별적으로 고려함으로써 자연스럽게 벡터 부울 함수로 확장될 수 있습니다.또,^[6] 그 컴포넌트라고 불리는 출력 비트의 모든 선형 함수 세트를 철저히 조사함으로써 확장될 수 있습니다.성분의 월시 변환 세트는 선형 ^[13]^[14]근사 테이블(LAT) 또는 상관 ^[15]^[16]행렬로 알려져 있으며 입력 및 출력 비트의 서로 다른 선형 조합 간의 상관 관계를 설명합니다.성분의 자기상관계수 세트는 자기상관표이며,^[14] 입력 비트와 출력 비트 간의 상관관계를 나열하는 보다 널리 사용되는 차분분포표(DDT)^[13]^[14]에^[17] 대한 성분의 월시 변환에 의해 관련됩니다(S 상자 참조).

실수 다항식 형식

유닛 하이퍼큐브에서

임의의 부울 $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ f ( $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ ) : $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ { $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ , $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ { $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ , $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ $}$ {{ $displaystyle$ f $(x):$ $\{0,1\}^{n}\rightarrow$ \{ $0,1\}}$ 은 $f(x):\{0,1\}^{n}\rightarrow \{0,1\}$ (는) R $\mathbb {R} ^{n}$ {\ $displaystyle \mathbb {R}^{n$ 의 다선형 다항식에 의해 실도메인으로 고유하게 확장(간접)할 수 있습니다.

({displaystyle f^{*}(x)={a\in {0,1\}^{n}f(a)\sum _{i}_{i}=1}x_{i}\sum _{i}(1-x_{i})}})

예를 들어 이진 XOR

x\oplus y

x

x

의

확장자

는

x\oplus y

다음

과 같습니다

.

0(1-x)(1-y)+1x(1-x)y+0xy

어느 쪽인가 하면

x+y-2xy

1-x

예로는 부정(

1-x

-

1-x

x \

displaystyle 1-x

),

1-x

AND(

x

y \

displaystyle

xy

xy

) 및 OR(

x+y-xy

+

x+y-xy

-

x+y-xy

y

x+y-xy

\

displaystyle

x + y -

xy

x+y-xy

)가 있습니다.모든 피연산자가 독립적일 때(변수를 공유하지 않음) 함수의 다항식은 부울 공식에서 연산자의 다항식을 반복적으로 적용하여 찾을 수 있습니다.계수를 모듈로 2로 계산하면 대수 정규형(제갈킨 다항식)을 구한다.

다항식의 계수에 대한 직접식은 적절한 도함수를 취함으로써 도출할 수 있다.

{\displaystyle {displaystyle} {lcl} f^{*}(00)&=&(f^{*})(00)&(\f^{1}f^{*}(00)&=-f(00)+f(01)\f^{*}(10)&(\f^2)&(\)

이는 부분적으로 순서가 매겨진 비트 벡터 세트의 뫼비우스 반전으로 일반화되어 있습니다.

{{displaystyle f^{*}(m)=\sum _{a\sumeq m}(-1)^{a + m}f(a)}

|a|

서

|a|

displaystyle

a는

|a|

비트

a

의

a

가중치를 나타냅니다. modulo 2를 취했을 경우, 이것은 부울 뫼비우스 변환으로, 대수 정규 형식 계수를 제공합니다.

{f}(m)=\bigoplus_{a\capeq m}f(a)

두 경우 모두 합계는 m으로 덮인 모든 비트 벡터 a에 걸쳐 취해진다. 즉, a의 "1" 비트는 m의 1 비트의 서브셋을 형성한다.

도메인이 n차원 하이퍼큐브 $[0,1]^{n}$ $[0,1]^{n}$ {\ $displaystyle$ [ $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ $1$ ]^{ $n$ n $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ [ $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ 0 , $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ ] $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ [ $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ , $]$ \ $displaystyle$ f $^{*}$ : $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ [ $0$ , $1$ ]^{ $n}$ \ $rightarrow [ 0$ , $1$ ] n }으로 $f^{*}(x):[0,1]^{n}\rightarrow [0,1]$ 제한되는 경우 부울 함수는 양의 f가 됩니다.변수(개별 확률 x). 이 경우 패리티 함수에 대한 누적 보조항이 있습니다.부울 함수의 다항 형식은 퍼지 로직으로의 자연스러운 확장으로도 사용될 수 있습니다.

대칭 하이퍼큐브에서

대부분의 경우 부울 도메인은 $\{-1,1\}$ { - $\{-1,1\}$ 1 , $\{-1,1\}$ $}$ { displaystyle \ { - 1 $,$ 1 \ $\{-1,1\}$ { $displaystyle$ \ { - $1$ \ } $\{-1,1\}$ and 、 false("0")를 1로 매핑하고 true("1")를 -1로 매핑합니다(부울 함수의 분석 참조). $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ ) : $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ { - $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ , $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ { - $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ , $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ $}$ { $displaystyle$ g $(x):$ $\{-1,1\}^{n}\rightarrow \{-1,1\}$ 은 $g(x):\{-1,1\}^{n}\rightarrow \{-1,1\}$ (는) 다음과 같이 지정됩니다.

{{displaystyle g^{*}(x)={a\in {{-1,1\}^{n}}g(a)}\sum _{i:a_{i}=-1}{\frac {1-x_{i}}}}\sum _{i:{i}}}{{\sum {\frac {i:a:{i}}}}}}}{{{{1}}}}}}}}{{{\sum}}}}}}}}}}{{{\sum}}}}}}}}}}}

대칭 부울 도메인을 사용하면 부정이 -1의 곱셈에 해당하고 선형 함수는 단수(XOR은 곱셈)이기 때문에 분석의 특정 측면이 단순해집니다.따라서 이 다항식은 함수(위 참조)의 월시 변환(이 문맥에서는 푸리에 변환이라고도 함)에 대응합니다.다항식은 또한 이제 예상

E(X)=P(X=1)-P(X=-1)\in [-1,1]

E (

E(X)=P(X=1)-P(X=-1)\in [-1,1]

)

E(X)=P(X=1)-P(X=-1)\in [-1,1]

(

E(X)=P(X=1)-P(X=-1)\in [-1,1]

E(X)=P(X=1)-P(X=-1)\in [-1,1]

) -

E(X)=P(X=1)-P(X=-1)\in [-1,1]

(

E(X)=P(X=1)-P(X=-1)\in [-1,1]

1)

E(X)=P(X=1)-P(X=-1)\in [-1,1]

[ -

E(X)=P(X=1)-P(X=-1)\in [-1,1]

]

{

display

E

(X

)

E(X)=P(X=1)-P(X=-1)\in [-1,1]

=

P(X=1)-P(X-in)

[ - 1 ] {display E(

X=

1)-P(X-in1] [1]이라는 점을 제외하고는 표준 부울 영역의 것과 동일한 통계 해석을 가집니다.

적용들

부울 함수는 복잡성 이론의 문제뿐만 아니라 논리 게이트를 사용하는 전자 회로에 구현되는 디지털 컴퓨터의 프로세서 설계에서도 기본적인 역할을 합니다.

부울 함수의 속성은 암호학, 특히 대칭 키 알고리즘 설계에서 중요합니다(대체 상자 참조).

협동 게임 이론에서 모노톤 부울 함수는 단순한 게임(투표 게임)이라고 불리며, 이 개념은 사회적 선택 이론의 문제를 해결하기 위해 적용된다.

「」를 참조해 주세요.

레퍼런스

^ "Boolean function - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-05-03.
^ Weisstein, Eric W. "Boolean Function". mathworld.wolfram.com. Retrieved 2021-05-03.
^ "switching function". TheFreeDictionary.com. Retrieved 2021-05-03.
^ Davies, D. W. (December 1957). "Switching Functions of Three Variables". IRE Transactions on Electronic Computers. EC-6 (4): 265–275. doi:10.1109/TEC.1957.5222038. ISSN 0367-9950.
^ McCluskey, Edward J. (2003-01-01), "Switching theory", Encyclopedia of Computer Science, GBR: John Wiley and Sons Ltd., pp. 1727–1731, ISBN 978-0-470-86412-8, retrieved 2021-05-03
^ ^a ^b Carlet, Claude. "Vectorial Boolean Functions for Cryptography" (PDF). University of Paris. Archived (PDF) from the original on 2016-01-17.
^ ^a ^b "Boolean functions — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-01.
^ ^a ^b ^c ^d ^e ^f Tarannikov, Yuriy; Korolev, Peter; Botev, Anton (2001). Boyd, Colin (ed.). "Autocorrelation Coefficients and Correlation Immunity of Boolean Functions". Advances in Cryptology — ASIACRYPT 2001. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. 2248: 460–479. doi:10.1007/3-540-45682-1_27. ISBN 978-3-540-45682-7.
^ Carlet, Claude (2010), "Boolean Functions for Cryptography and Error-Correcting Codes" (PDF), Boolean Models and Methods in Mathematics, Computer Science, and Engineering, Encyclopedia of Mathematics and its Applications, Cambridge: Cambridge University Press, pp. 257–397, ISBN 978-0-521-84752-0, retrieved 2021-05-17
^ Pieprzyk, Josef; Wang, Huaxiong; Zhang, Xian-Mo (2011-05-01). "Mobius transforms, coincident Boolean functions and non-coincidence property of Boolean functions". International Journal of Computer Mathematics. 88 (7): 1398–1416. doi:10.1080/00207160.2010.509428. ISSN 0020-7160.
^ Nitaj, Abderrahmane; Susilo, Willy; Tonien, Joseph (2017-10-01). "Dirichlet product for boolean functions". Journal of Applied Mathematics and Computing. 55 (1): 293–312. doi:10.1007/s12190-016-1037-4. ISSN 1865-2085.
^ Canteaut, Anne; Carlet, Claude; Charpin, Pascale; Fontaine, Caroline (2000-05-14). "Propagation characteristics and correlation-immunity of highly nonlinear boolean functions". Proceedings of the 19th International Conference on Theory and Application of Cryptographic Techniques. EUROCRYPT'00. Bruges, Belgium: Springer-Verlag: 507–522. ISBN 978-3-540-67517-4.
^ ^a ^b Heys, Howard M. "A Tutorial on Linear and Differential Cryptanalysis" (PDF). Archived (PDF) from the original on 2017-05-17.
^ ^a ^b ^c "S-Boxes and Their Algebraic Representations — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-04.
^ Daemen, Joan; Govaerts, René; Vandewalle, Joos (1995). Preneel, Bart (ed.). "Correlation matrices". Fast Software Encryption. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. 1008: 275–285. doi:10.1007/3-540-60590-8_21. ISBN 978-3-540-47809-6.
^ Daemen, Joan (10 June 1998). "Chapter 5: Propagation and Correlation - Annex to AES Proposal Rijndael" (PDF). NIST. Archived (PDF) from the original on 2018-07-23.
^ Nyberg, Kaisa (December 1, 2019). "The Extended Autocorrelation and Boomerang Tables and Links Between Nonlinearity Properties of Vectorial Boolean Functions" (PDF). Archived (PDF) from the original on 2020-11-02.

추가 정보

Crama, Yves; Hammer, Peter L. (2011), Boolean Functions: Theory, Algorithms, and Applications, Cambridge University Press, doi:10.1017/CBO9780511852008, ISBN 9780511852008
"Boolean function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Janković, Dragan; Stanković, Radomir S.; Moraga, Claudio (November 2003). "Arithmetic expressions optimisation using dual polarity property". Serbian Journal of Electrical Engineering. 1 (71–80, number 1): 71–80. doi:10.2298/SJEE0301071J.
Arnold, Bradford Henry (1 January 2011). Logic and Boolean Algebra. Courier Corporation. ISBN 978-0-486-48385-6.
Mano, M. M.; Ciletti, M. D. (2013), Digital Design, Pearson

[1] "Boolean function - Encyclopedia of Mathematics". encyclopediaofmath.org. Retrieved 2021-05-03.

[2] Weisstein, Eric W. "Boolean Function". mathworld.wolfram.com. Retrieved 2021-05-03.

[3] "switching function". TheFreeDictionary.com. Retrieved 2021-05-03.

[4] Davies, D. W. (December 1957). "Switching Functions of Three Variables". IRE Transactions on Electronic Computers. EC-6 (4): 265–275. doi:10.1109/TEC.1957.5222038. ISSN 0367-9950.

[5] McCluskey, Edward J. (2003-01-01), "Switching theory", Encyclopedia of Computer Science, GBR: John Wiley and Sons Ltd., pp. 1727–1731, ISBN 978-0-470-86412-8, retrieved 2021-05-03

[:2-6] Carlet, Claude. "Vectorial Boolean Functions for Cryptography" (PDF). University of Paris. Archived (PDF) from the original on 2016-01-17.

[:0-7] "Boolean functions — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-01.

[:1-8] ^ ^a ^b ^c ^d ^e ^f Tarannikov, Yuriy; Korolev, Peter; Botev, Anton (2001). Boyd, Colin (ed.). "Autocorrelation Coefficients and Correlation Immunity of Boolean Functions". Advances in Cryptology — ASIACRYPT 2001. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. 2248: 460–479. doi:10.1007/3-540-45682-1_27. ISBN 978-3-540-45682-7.

[9] Carlet, Claude (2010), "Boolean Functions for Cryptography and Error-Correcting Codes" (PDF), Boolean Models and Methods in Mathematics, Computer Science, and Engineering, Encyclopedia of Mathematics and its Applications, Cambridge: Cambridge University Press, pp. 257–397, ISBN 978-0-521-84752-0, retrieved 2021-05-17

[10] Pieprzyk, Josef; Wang, Huaxiong; Zhang, Xian-Mo (2011-05-01). "Mobius transforms, coincident Boolean functions and non-coincidence property of Boolean functions". International Journal of Computer Mathematics. 88 (7): 1398–1416. doi:10.1080/00207160.2010.509428. ISSN 0020-7160.

[11] Nitaj, Abderrahmane; Susilo, Willy; Tonien, Joseph (2017-10-01). "Dirichlet product for boolean functions". Journal of Applied Mathematics and Computing. 55 (1): 293–312. doi:10.1007/s12190-016-1037-4. ISSN 1865-2085.

[12] Canteaut, Anne; Carlet, Claude; Charpin, Pascale; Fontaine, Caroline (2000-05-14). "Propagation characteristics and correlation-immunity of highly nonlinear boolean functions". Proceedings of the 19th International Conference on Theory and Application of Cryptographic Techniques. EUROCRYPT'00. Bruges, Belgium: Springer-Verlag: 507–522. ISBN 978-3-540-67517-4.

[:3-13] Heys, Howard M. "A Tutorial on Linear and Differential Cryptanalysis" (PDF). Archived (PDF) from the original on 2017-05-17.

[:4-14] "S-Boxes and Their Algebraic Representations — Sage 9.2 Reference Manual: Cryptography". doc.sagemath.org. Retrieved 2021-05-04.

[15] Daemen, Joan; Govaerts, René; Vandewalle, Joos (1995). Preneel, Bart (ed.). "Correlation matrices". Fast Software Encryption. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer. 1008: 275–285. doi:10.1007/3-540-60590-8_21. ISBN 978-3-540-47809-6.

[16] Daemen, Joan (10 June 1998). "Chapter 5: Propagation and Correlation - Annex to AES Proposal Rijndael" (PDF). NIST. Archived (PDF) from the original on 2018-07-23.

[17] Nyberg, Kaisa (December 1, 2019). "The Extended Autocorrelation and Boomerang Tables and Links Between Nonlinearity Properties of Vectorial Boolean Functions" (PDF). Archived (PDF) from the original on 2020-11-02.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

Search

부울 함수

네임스페이스

더

목차

예

표현

분석.