XNOR 게이트

입력		출력
A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

XNOR 게이트(때로는 ENOR, EXNOR 또는 NXOR로 발음되며 배타적 NOR로 발음되기도 한다.XAND 대신 Exclusive AND로 발음되는 디지털 로직 게이트로, 이 게이트는 독점 OR(XOR)^[1] 게이트의 논리적 보완물이다.그것은 물질적 양수라고도 알려진 수학 논리의 논리 결합체 $\leftrightarrow$ 파운드가 ${\displaystyle \좌우타로우$ $\leftrightarrow$ 와 동등하다.2입력판은 논리적인 평등을 구현하여, 오른쪽의 진리표에 따라 작용하며, 따라서 관문을 "평등문"이라고 부르기도 한다.게이트에 대한 두 입력이 동일한 경우 높은 출력(1)이 발생한다.두 입력이 모두 아닌 한 개만 하이(1)일 경우 낮은 출력(0)이 발생한다.

XNOR 연산을 나타내기 위해 사용되는 대수 표기법은 $S=A\odot B$ = $S=A\odot B$ ⊙ $S=A\odot B$ ${\displaystyle$ S $=A\odot$ B $}$ 이다 $S=A\odot B$ The algebraic expressions $(A+{\overline {B}})\cdot ({\overline {A}}+B)$ and $A\cdot B+{\overline {A}}\cdot {\overline {B}}$ both represent the XNOR gate with inputs A and B.

기호

XNOR 관문에는 두 가지 기호가 있다. 하나는 독특한 모양을 하고 있고 다른 하나는 직사각형 모양과 라벨을 가지고 있다.XNOR 게이트의 두 기호 모두 반전 버블이 추가된 XOR 게이트의 기호다.

고유 기호

직사각형 기호

하드웨어 설명

XNOR 게이트는 대부분의 TTL 및 CMOS IC 제품군에 표시된다.표준 4000 시리즈 CMOS IC는 4077, TTL IC는 74266(개방형 수집기 구현)이다.두 개 모두 4개의 독립형 투인치 XNOR 게이트를 포함한다.(지금의 구식) 74S135는 2입력 XOR/XNOR 게이트 4개 또는 3입력 XNOR 게이트 2개를 구현했다.

TTL 74LS 구현, 74LS266은 물론 CMOS 게이트(CD4077, 74HC4077, 74HC266 등)도 텍사스인스트루먼트나 NXP 등 대부분의 반도체 제조업체에서 공급할 수 있다.^[2]그것들은 대개 관통 홀 DIP와 SOIC 형식(SOIC-14, SOC-14 또는 TSSOP-14)으로 제공된다.

데이터시트는 대부분의 데이터시트 데이터베이스와 공급업체에서 쉽게 구할 수 있다.

핀아웃

4077 및 74x266 장치(SN74LS266, 74HC266, 74266 등)의 핀아웃 다이어그램은 다음과 같다.

74HC266N, 74LS266 및 CD4077 쿼드 XNOR 플라스틱 이중 인라인 패키지 14핀 패키지(PDIP-14) IC의 핀아웃 다이어그램.

입력 A1
입력 B1
출력 Q1(A1과 B1의 로직 레벨이 동일한 경우에만 높음)
출력 Q2
입력 B2
입력 A2
V_ss(GND) 공통 전원 및 신호 접지 핀
입력 A3
입력 B3
출력 Q3
출력 Q4
입력 B4
입력 A4
CMOS용 V_dd(TTL용 V_cc) 양극 전원 공급 장치(허용 전압 범위는 데이터시트 참조)

대안

혼합 게이트 3개를 사용하는 XNOR 게이트 회로

특정 유형의 게이트를 사용할 수 없는 경우, 동일한 기능을 구현하는 회로를 다른 가용 게이트에서 구성할 수 있다.XNOR 기능을 구현하는 회로는 XOR 게이트에 이어 NOT 게이트에서 사소한 방식으로 구성할 수 있다. $(A+{\overline {B}})\cdot ({\overline {A}}+B)$ ) $){\displaystyle(A+{\overline{B}})\$ cdot $({\overline{A}+B)}$ 라는 표현을 고려한다면 AND, OR 및 NOT 게이트를 사용하여 XNOR 게이트 회로를 직접 구성할 수 있다 $(A+{\overline {B}})\cdot ({\overline {A}}+B)$ 그러나 이 접근법은 세 가지 다른 종류의 5개의 관문을 필요로 한다.

As alternative, if different gates are available we can apply Boolean algebra to transform $(A+{\overline {B}})\cdot ({\overline {A}}+B)\equiv (A\cdot B)+({\overline {A}}\cdot {\overline {B}})$ as stated above, and apply de Morgan's Law to the last term to get $(A\cdot B)+{\overline {(A+B)}}$ ( $(A\cdot B)+{\overline {(A+B)}}$ $(A\cdot B)+{\overline {(A+B)}}$ $(A\cdot B)+{\overline {(A+B)}}$ ) $(A\cdot B)+{\overline {(A+B)}}$ + $(A\cdot B)+{\overline {(A+B)}}$ + B $(A\cdot B)+{\overline {(A+B)}}$ )의 ${\$ ( $A\$ cdot B $)+{\overline{(A+B)}}}}.$ 오른쪽과 $(A\cdot B)+{\overline {(A+B)}}$ 같이 3개의 관문만 사용하여 구현할 수 있다.

XNOR 게이트 회로는 4개의 NOR 게이트로 만들 수 있다.실제로 NAND와 NOR 게이트는 모두 이른바 '범용 게이트'로 어떤 논리 기능도 NAND 논리나 NOR 논리만으로 구성할 수 있다.NOR 게이트 4개를 NAND 게이트로 교체하면 XOR 게이트가 발생하는데, 출력 또는 입력 중 하나(예: 5번째 NAND 게이트)를 뒤집어 XNOR 게이트로 변환할 수 있다.

원하는 게이트	낸드 건설	NOR 시공

An alternative arrangement is of five NAND gates in a topology that emphasizes the construction of the function from $(A\cdot B)+({\overline {A}}\cdot {\overline {B}})$ , noting from de Morgan's Law that a NAND gate is an inverted-input OR gate.또 다른 대안으로는 $(A+{\overline {B}})\cdot ({\overline {A}}+B)$ ( $(A+{\overline {B}})\cdot ({\overline {A}}+B)$ ) $(A+{\overline {B}})\cdot ({\overline {A}}+B)$ ( $){\displaystyle (A+{\overline{B})\cdot ({\overline{A}}}}}})$ 의 함수 구성을 강조하는 위상의 NOR 게이트 5개를 드 모건의 법칙에 따라 NOR 게이트가 역입력 및 게이트라는 점을 언급하는 것이다 $(A+{\overline {B}})\cdot ({\overline {A}}+B)$

원하는 게이트	낸드 건설	NOR 시공

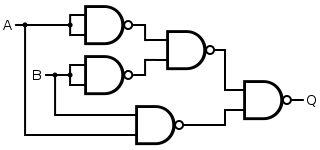NAND 구조의 경우, 낮은 배열은 짧은 전파 지연(입력 변경과 출력 변경 사이의 시간 지연)의 이점을 제공한다.NOR 시공의 경우 상부 배치에는 더 적은 수의 관문이 필요하다.

XNOR가 완전한 범용 논리 게이트가 아님에도 불구하고 반대 관점에서 XNOR 게이트만을 사용하여 다른 게이트를 구축할 수 있다.NOT와 XOR 게이트는 이런 방식으로 건설될 수 있다.

세 개 이상의 입력

게이트당 입력이 3개 이상인 제조업체에서 다른 게이트(OR, NOR, AND, NAND)를 사용할 수 있지만 XOR 게이트와 XNOR 게이트의 경우는 엄격히 사실이 아니다.그러나 이진 논리 연산 개념을 두 개의 공유 "C"와 네 개의 출력에 대한 독립 "A"와 "B" 입력을 가진 SN74S135의 세 개의 입력으로 확장하는 것은 진실 표에 따르는 장치였다.

입력			출력
A	B	C	Y
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

이것은 사실상 Y = NOT ((A XOR B) XOR C)이다.이를 해석하는 또 다른 방법은 짝수의 입력이 참일 경우 출력이 참이라는 것이다.2입력 XNOR 게이트와 달리 논리적인 "등가" 함수를 구현하지 않는다.

또한 XOR 함수는 모든 입력의 합계에 대해 패리티 함수 또는 Mod2로 작용하는 것처럼 보인다.모든 입력의 합이 짝수일 경우 *y*가 1과 어떻게 같으며, 이는 모든 입력의 합이 홀수일 경우 y = 0임을 의미한다.여기서 x XOR y XOR z = 짝수(x+y+z)라고 결론을 내릴 수 있다.

참고 항목

참조

^ "Exclusive-NOR Gate Tutorial". Retrieved 6 May 2018.
^ "XNOR Logic Gates". Retrieved 6 May 2018.

외부 링크

[:0-1] "Exclusive-NOR Gate Tutorial". Retrieved 6 May 2018.

[2] "XNOR Logic Gates". Retrieved 6 May 2018.

[1]

[2]

v t 논리 연결 장치
Tautology/True $\top$ $\top$
대체 거부(NAND 게이트) $\uparrow$ $\uparrow$ 컨버스 시사 $\displaystyle \왼쪽 화살표 }$ 시사(IMMLY 게이트) $\rightarrow$ → ${\디스플레이$ 스타일 \오른쪽 $화살표 }$ 분리(OR 게이트) $\lor$ $\lor$
부정(NOT 게이트) $\neg$ $\neg$ 단독 또는 (XOR 게이트) $\not \leftrightarrow$ ${\displaystyle \not \좌우$ 이동 $}$ Bicondient (XNOR 게이트) $\leftrightarrow$ ${\디스플레이$ 스타일 $\좌우$ 이동 $}$ 문(디지털 버퍼)
공동 거부(NOR 게이트) $\downarrow$ ↓ $\downarrow$ NIMPLY 게이트(Nonimplication $)({\displaystyle \nrightarrow })$ $\nrightarrow$ 컨버스 비임플렉스 $\displaystyle \nleftarrow }$ 접속사(AND 게이트) $\land$ $\land$
모순/거짓 $\bot$ $\bot$
철학포털

Search

XNOR 게이트

네임스페이스

더

목차

기호

하드웨어 설명

핀아웃

대안

세 개 이상의 입력

참고 항목

참조

외부 링크