정규 분포

정규 분포

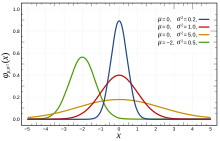확률밀도함수 빨간색 곡선은 표준 정규 분포입니다.
누적분포함수
표기법	$({displaystyle {N}}({mu,\sigma ^{2}))$
파라미터	${\displaystyle \mu \mu \mathbb{}}$ R$$\ $displaystyle$\$mu \ in$ \ $mathbb${$R$} $=$ 평균(위치) 2 $>$ 0 \ $style$ \ display ^ {$2}$\ $in$ \$mathbb$ {$R$} _ { $>$ 0} = 분산 (표준 척도)
지지하다	$\displaystyle x\in \mathbb {R}$
PDF	${\displaystyle {\frac {1}{\frac {2\pi }}e^{-{\frac {1}{2}}\leftfrac {x-\mu}{\frac }{\frac }}{\frac }}{2}}$
CDF	${\displaystyle {frac {1}{2}}\left[1+\operatorname {erf}\leftfrac {x-\mu}{\displaystyle {x-}}}\right}}$
양분위수	${\displaystyle\mu +\display\operatorname{erf}^{-1}(2p-1)}$
의미하다	${\displaystyle\mu}$
중앙값	${\displaystyle\mu}$
모드	${\displaystyle\mu}$
분산	$\displaystyle \display ^{2}}$
미친	$\displaystyle \displaystyle {2/\pi }$
왜도	${\displaystyle 0}$
예: 첨도	${\displaystyle 0}$
엔트로피	${\displaystyle {1}{2}}\log(2\pi \pi ^{2})+{\frac {1}{2}}$
MGF	$\displaystyle \exp(\mu t+\display ^{2}t^{2}/2)}$
CF	$(\displaystyle \exp(i\mu t-\display ^{2}t^{2}/2)}$
피셔 정보	${\displaystyle {I}({mu,\display})={pmatrix}1/\display ^{2}&0&2/\display ^{2}\end{pmatrix}}$ ${\displaystyle {I}({mu,\display ^{2})={pmatrix}1/\display ^{2}&0&1/(2\display ^{4})\end{pmatrix}}}$
쿨백-라이블러 발산	${\displaystyle {1 \over2} \{\frac {\frac _{1}\right} {\frac {\frac {\mu _{0}} + {\frac {\frac _{1}-\mu _{0}} {{2}-1+\ln {{{{1} {\over} {\frac {\frac {\fright} {{{{{{0}}}}}} {\frac {\frac {\fright}$

통계에 관한 시리즈의 일부
확률론
확률 악리 결정론 시스템. 부정론 랜덤성
확률 공간 샘플 공간 이벤트 종합적인 이벤트 초급 이벤트 상호 배타성 결과 싱글턴 실험. 베르누이 재판 확률 분포 베르누이 분포 이항 분포 정규 분포 확률 측도 랜덤 변수 베르누이 과정 연속 또는 이산 기대치 마르코프 연쇄 관측치 랜덤 워크 확률 과정
보충 이벤트 결합 확률 한계 확률 조건부 확률
인디펜던스 조건부 독립성 확률의 법칙 대수의 법칙 베이즈 정리 불의 부등식
벤도 트리 다이어그램
v t

통계학에서 정규 분포(가우스, 가우스 또는 라플라스-가우스 분포라고도 함)는 실수치 랜덤 변수의 연속 확률 분포의 한 종류입니다.확률 밀도 함수의 일반적인 형태는 다음과 같습니다.

${\displaystyle f(x)=frac {1}{\displayrt {2\pi }}}}e^{-{\frac {1}{2}\display\frac {x-\mu}}}{\right}}$

$파라미터{\displaystyle }$μ {\$displaystyle \mu}$는 분포의 평균 또는 기대치(및 중앙값과 모드)이며 파라미터 $\mu {\displaystyle }${\$displaystyle$ \$sigma}$는 분포의 표준 편차입니다.분포의 분산은 $(\$^{$2$^[1] $이하$이며, 가우스 분포를 갖는 랜덤 변수는 정규 분포라고 하며 정규 편차라고 합니다.

정규 분포는 통계에서 중요하며 자연 및 사회 과학에서 분포를 ^[2][3]알 수 없는 실제 값 랜덤 변수를 나타내기 위해 자주 사용됩니다.이들의 중요성은 부분적으로 중심 한계 정리 때문이다.일부 조건에서, 유한 평균과 분산을 갖는 랜덤 변수의 많은 표본(관측치)의 평균은 그 자체로 랜덤 변수이며, 표본의 수가 증가함에 따라 분포가 정규 분포로 수렴된다는 것을 명시하고 있다.따라서 측정 오류와 같이 많은 독립 공정의 합이 될 것으로 예상되는 물리적 수량은 정규 ^[4]분포에 가까운 분포를 갖는 경우가 많습니다.

더욱이, 가우스 분포는 분석 연구에서 중요한 몇 가지 고유한 특성을 가지고 있다.예를 들어, 정규 편차 고정 집합의 선형 조합은 정규 편차입니다.불확실성의 전파 및 최소 제곱 매개변수 적합과 같은 많은 결과와 방법은 관련 변수가 정규 분포를 따를 때 명시적인 형태로 분석적으로 도출될 수 있다.

정규 분포를 비공식적으로 종곡선이라고 ^[5]부르기도 합니다.그러나 다른 많은 분포는 종 모양입니다(예: Cauchy, Student's t 및 로지스틱 분포).

일변량 확률 분포는 다변량 정규 분포의 벡터와 행렬 정규 분포의 행렬에 대해 일반화됩니다.

정의들

표준 정규 분포

가장 간단한 정규 분포의 경우를 표준 정규 분포 또는 단위 정규 분포라고 합니다.이는 μ ${\displaystyle =}$ $(\displaystyle \mu$=$0)$$$및$$ $\mu {\displaystyle }$ ${\displaystyle =}$ $(\displaystyle$ \$displaystyle = 1$)인 특수한 경우로, 다음과 같은 확률 밀도 함수(또는 밀도)로 설명됩니다.

$({displaystyle \varphi (z) = parfrac {e^{-z^{2}/2}}} {\pi rt {2\pi }}})$

$변수{\displaystyle }$z(\$displaystyle$ z$)$의 평균은 0이고 분산 및 표준 편차는 1입니다.밀도${\displaystyle }\theta {\displaystyle }$ ( ${\displaystyle z}$)$${$displaystyle \varphi (z)}$는 z $0$에서 $피크{\displaystyle \mathrm{}}$1/$2$ {$style$ 1$/{\displayrt {2\pi$}}이고 z$=$ + ${\displaystyle 1}$(\$displaystyle$ $z$$=+$$1$$\}$ $및{\displaystyle }$ z$=$ - ${\displaystyle 1}$(\$displaystyle$ z= 1)입니다.

위의 밀도는 표준 정규 분포로 가장 일반적으로 알려져 있지만, 일부 저자들은 정규 분포의 다른 버전을 설명하기 위해 이 용어를 사용했습니다.예를 들어, Carl Friedrich Gauss는 표준 노멀을 다음과 같이 정의했다.

${\displaystyle \varphi (z)=varfrac {e^{-z^{2}}}{\displayrt {\pi }}}$

Stephen Stigler는^[6] 표준 노멀을 다음과 같이 정의했습니다.

$\displaystyle \varphi(z)=e^{-\pi z^{2}}$

${\displaystyle {has\mathrm{}}^{}}$ 2 ${\displaystyle {}^{}1}$/ ( 2${\displaystyle \pi }$ )$$\ $displaystyle$ \ $displaystyle ^$ {2} =$1$/ ($2$ \ $pi$)$$。

일반 정규 분포

모든 정규 분포는 표준 정규 분포의 버전입니다. 이 정규 분포의 도메인은 $계수{\displaystyle }$ ${\$ {\displaystyle $\sigma$}($$$표준$ 편차)만큼 연장되고 다음으로$$μ {\$displaystyle \mu$}($$평균값)로 변환됩니다.

$({displaystyle f(x\mid \mu,\display ^{2})=varphi \leftfac\frac {x-\mu}{\display }}\right)$

확률 밀도는 적분이 1이 되도록 1/$${\(\$displaystyle$ 1$/\sigma)$ 스케일링해야 합니다.

Z$(\displaystyle$ Z$)$가 표준 정규 편차인 $경우{\displaystyle }$ $X{\displaystyle }$ $=$ ${\displaystyle \delta }$Z +$$μ(\$displaystyle$X=\$sigma$ Z$+\mu)$는 기대값$$$$$μ$(\displaystyle $\mu$) $및{\displaystyle }$ 표준 편차$δ$(\displaystyle \displaystyle$)$로 정규 $분포{\displaystyle }$Z(\$displaystyl$$)$를 나타냅니다.$e$ Z는$\mu {\displaystyle }$ {\$displaystyle \sigma$$}$의 배수로 스케일링/신장할 수 있으며$$$μ$ {\$displaystyle$$X$$\}$라고 $하는{\displaystyle }$ 다른 정규 분포를 얻을 수 있습니다. 반대로$$X {\$displaystyle$ X$}$가$$μ {\$displaystyle \mu$$}$ 및$$$$ 2 \$s$의 정규 $편차$인 $경우{\displaystyle }$$igma$^{$2$ 이$X{\displaystyle }$(\$displaystyle$ X$)$ 분포는$$ Z ${\displaystyle =}$ (${\displaystyle X}$ -${\displaystyle \mu }$) / $（$ \$display$ Z$$ = ( $X$- \$mu$) /\display$$} $공식$에 따라 다시 변환하여 "표준" 정규 분포로 변환할 수 있습니다.이 변형을 $X$의 $표준화$된 형태라고도 $합니다$

표기법

표준 가우스 분포(평균 및 단위 분산이 0인 표준 정규 분포)의 확률 밀도는 그리스 문자 ${\$ {\$displaystyle \phi$}($$phi)^[7]로 종종 표시됩니다.그리스 문자 phi의 대체 형태인 phi$(\displaystyle \varphi$도 꽤 자주 사용된다.

정규 분포는 N${\displaystyle (\mu }$, ${\displaystyle {2\mathrm{}}^{}}$ 2)${\displaystyle {}^{}}${$displaystyle$ N$(\mu ,\sigma$^{$2})$ $또는$ N${\displaystyle (\mu }$, ${\displaystyle {2\mathrm{}}^{}}$2) ${\displaystyle {N}(\$mu $,\sigma$^{$2$^[8]이라고 $불립니다{\displaystyle }$.따라서 랜덤 $변수{\displaystyle }$X(\$displaystyle$ X$)$가 $평균{\displaystyle }$μ(\$displaystyle \mu)$ 및$$ 표준 편차$\theta {\displaystyle }$(\$displaystyle \sigma$로 정규 분포되어 있으면 다음과 같이 쓸 수 있습니다.

$(\displaystyle X\sim {N}}(\mu,\sigma ^{2}).}$

대체 파라미터화

일부 저자는 편차 또는 $분산{\displaystyle }$ 값$$$(\$$$$^{2$ 대신$$ $정밀도{\displaystyle }$ "\$displaystyle \tau"$를 분포의 폭을 정의하는 파라미터로 사용할 것을 권장합니다$.$정밀도는 보통 분산의 $역수$인${\displaystyle }$1/$(\$ 1$/\sigma$^{$2$^[9]로 정의됩니다.분포의 공식은 다음과 같습니다.

${\displaystyle f(x)=frac {2\pi }}e^{-\display (x-\mu)^{2}/2}}$

이 선택은 $\displaystyle\sigma}$가 0에 매우 가까울 때 수치 계산에서 유리하며 다변량 정규 분포를 갖는 변수의 베이지안 추론 등 일부 컨텍스트에서 공식을 단순화할 수 있다고 주장됩니다.

또는 표준편차 $cal{\displaystyle {}^{\mathrm{}}}$′ ${\displaystyle {}^{}1}$ / ${\$ { $displaystyle$ \$display$^ { \ $prime$ } =$1$/ \ $display }$의 역수를 정밀도로 정의할 수 있으며, 이 경우 정규분포의 표현은

${\displaystyle f(x)=paramfrac {\pi }}{\paramrt {2\pi }}e^{-(param ^{\prime })^{2}(x-\mu)^{2}/2.}$

스티글러에 따르면, 이 공식은 훨씬 간단하고 기억하기 쉬운 공식과 분포의 분위수에 대한 간단한 근사 공식 때문에 유리합니다.

정규 분포는 자연 모수 ${\displaystyle 1\frac{}{}}$ 1 $=$ μ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$2 \ $displaystyle$\$textstyle \theta$_ { { } ${\displaystyle {}_{}}$ $flac$$${ $mu$$$} { \ $displaystyle \textstyle \theta$ _ ${ }$}} ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle {2\mathrm{}}_{}}$ 2 2$$、 2 2 ${\displaystyle 、\frac{}{}}$ 、 、 、 - ${\displaystyle \frac{2}{}}$ 、 、 、 、 、 、 、 、 stat normal normal normalstylestylestyle normal normal 、 、 、 、 、 、 、 、 、 normal normal 2 2 ${\displaystyle \frac{{normal\mathrm{}}^{}}{}}$ normal normal정규 분포에 대한 이중 기대 모수는 θ₁ = μ 및 θ₂² = μ + µ입니다².

누적분포함수

표준 정규 분포의 누적 분포 함수(CDF)는 보통 대문자 그리스 문자$\delta {\displaystyle \mathrm{}}$(\$displaystyle \Phi)$로 표시되며 적분이다.

${\displaystyle \Phi(x)=black {1}{\displayrt {2\pi }}\int _{-\infty }^{x}e^{-t^{2}/2},dt}$

관련 오류 함수 ${\displaystyle \mathrm{erf}}$ ${\displaystyle (}$ (${\displaystyle x}$) { $displaystyle \operatorname {erf$} ($x)}$ 은 정규$$ 분포가 [${\displaystyle }$-${\displaystyle x}$ , $]$\ $display$ style [ -$x$ , x $]$의 범위에 들어가는 랜덤 변수의 확률을 나타냅니다.다음은 예를 제시하겠습니다.

${\displaystyle \operatorname {erf}(x)=black {2}{\displayrt {{pi}}\int _{0}^{x}e^{-t^{2}},dt}$

이러한 적분은 기본 함수로 표현될 수 없으며, 종종 특수 함수라고 한다.그러나 많은 수치 근사치가 알려져 있습니다.자세한 내용은 아래를 참조하십시오.

두 기능은 밀접하게 관련되어 있습니다.즉,

${\displaystyle \Phi(x)=param frac {1}{2}}\left [1+\operatorname {erf}\left\frac {x}{\paramrt {2}}\right}}\left]}$

$밀도$f {\$displaystyle$f$\},$ $평균{\displaystyle }$μ {\$displaystyle \mu}$ 및$$ 편차 ${\$ {\$displaystyle \sigma$의 일반 정규 분포의 경우 누적 분포 함수는 다음과 같습니다.

${\displaystyle F(x)=\Phi \frac {x-\mu }{\flac }}\left [1+\operatorname {erf} \leftfrac {x-\mu} {\flac {\fright} {\flight}$

표준 일반 CDF의 $보완물$인${\displaystyle }$Q (${\displaystyle x}$ ) ${\displaystyle =1}$ -${\displaystyle \mathrm{\delta }}$ (${\displaystyle x}$) {$display style$Q (x) =$1$- \$Phi (x$는 특히 엔지니어링 ^[10][11]텍스트에서 Q-함수라고 불립니다.그것은 확률은 표준 정상적인 무작위 변수 X의{X\displaystyle}){\displaystyle)}:P(X>)){P(X>^)\displaystyle}. Q{Q\displaystyle}-function의 Φ{\displaystyle \Phi}의 이러한 간단한 변화 다른 정의는,,를 초과한 값 또한 사용은 O를 준다ccasi온리온으로^[12]

표준 정규 CDF$δ$의 그래프(\$displaystyle$ \Phi$$})는 점(0,1/2)을 중심으로 2배의 회전 대칭을 갖습니다. 즉,${\displaystyle }\delta {\displaystyle \mathrm{}}$( -${\displaystyle x}$ )$$ - ${\displaystyle \mathrm{\delta }}$(${\displaystyle x}$ ) {$displaystyle \Phi$($$x )$$$= 1$- \$Phi$( x ) 。 반감시적분할 수 있습니다.

$\displaystyle \int \Phi(x),dx=x\Phi(x)+\varphi(x)+C.}$

표준 정규 분포의 CDF는 부품별로 시리즈로 통합함으로써 확장할 수 있습니다.

${\displaystyle \Phi(x)=blac {1}{\flac {2\pi}}+{\flac {2\pi}}\cdot e^{-x^{2}/2}\left[x+{x^{3}}+{\flac {x{5}}{3\cdot {cdots}}+{cdots}{cdots}}{cdflac {1}{cdots}}{cdfrac}{1}{{1}{1}{1}{cd}}}}}+\cdots\right]}$

어디$!$ {\$displaystyle!!$}은$($는) 이중 계수를 나타냅니다.

큰 x에 대한 CDF의 점근팽창도 부품별 적분을 사용하여 도출할 수 있다.자세한 내용은 오류 함수 #점근 ^[13]확장을 참조하십시오.

Taylor 계열 근사치를 사용하면 표준 정규 분포의 누적분포함수에 대한 빠른 근사치를 구할 수 있습니다.

${\displaystyle \Phi (x)\약 {frac {1}{\sumrt {2\pi }}\sum _{k=0}^{\frac {\frac 1\right}^{k}x^{\left(2k+1\오른쪽)}}{2^{k}k!\left(2k+1\오른쪽)}}}$

표준편차와 적용범위

정규 분포에서 추출한 값의 약 68%는 평균으로부터 1개의 표준 편차 θ 내에 있고, 값의 약 95%는 2개의 표준 편차 내에 있으며, 약 99.7%는 3개의 표준 ^[5]편차 내에 있습니다.이 사실은 68-95-99.7(emirical) 규칙 또는 3-시그마 규칙이라고 불립니다.

보다 정확히 말하면, 정규 편차가${\displaystyle \mu }$ - n$$ { $displaystyle$\ $mu$ - n \ $sigma$} ~$\mu {\displaystyle }$ ${\displaystyle +}$ ${\displaystyle n}$ { $displaystyle \ mu$ +$n$ \ $sigma$} 범위에$$ 있을 확률은 다음과 같습니다.

$\displaystyle F(\mu +n\flash)-F(\mu -n\flash )=\Phi(-n)=\operatorname {erf}\lefts\flac {n}{\flacrt {2}\오른쪽.}$

유효 숫자 ${\displaystyle \mathrm{12개}}$에서 n ${\displaystyle =}$1,${\displaystyle 2}$,${\displaystyle \dots ,}$ 6$({displaystyle$ n$=1,$ 2,\ldots$,6})$의 $값$은 다음과 같습니다.^[14]

${\displaystyle n}$	$(\displaystyle p=F(\mu +n\display)-F(\mu -n\display)}$	$(\displaystyle\text{예}}1-p)$	${\displaystyle\text{또는 }}}1(텍스트는 }}p}$	OEIS
1	0.682689492137	0.317310507863	3개 .15148718753	OEIS: A178647
2	0.95499736104	0.045500263896	스물한 살 .9778945080	OEIS: A110894
3	0.997300203937	0.002699796063	370 .398347345	OEIS: A270712
4	0.99936657516	0.000063342484	15787 .192673
5	0.9999426697	0.000000573303	1744277 .89362
6	0.999998027	0.0000001973	506797345 .897

$큰{\displaystyle }$n(\$displaystyle$ n$)$의 경우 약 $1{\displaystyle \mathrm{}}$- ${\displaystyle pe\frac{{}^{}}{}}$e - ${\displaystyle \frac{{{n\mathrm{}}^{}}^{}}{}}$2 / ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{n\sqrt{}}{}}$ ${\displaystyle \frac{\sqrt{/}}{}}$ /$$ { \ $displaystyle 1-p \ about$ \ $frac${ $e$^ { - n ^ { - n ^ { $2$} / 2 } { $n{$ \$sqrt$ {$pi$ / 2 $}}}$} 。

분위수 함수

분포의 분위수 함수는 누적 분포 함수의 역함수입니다.표준 정규 분포의 분위수 함수를 프로빗 함수라고 하며, 역오차 함수로 나타낼 수 있습니다.

$\displaystyle \Phi ^{-1}(p)=sqrt {2}}\operatorname {erf}^{-1}(2p-1),\display p\in(0,1).}$

$(\displaystyle\mu)$ 및$$ ${\displaystyle {분산}^{}}$이 2$(\$인 일반 랜덤 변수의 경우, 분위수 함수는 다음과 같습니다.

${\displaystyle F^{-1}(p)=\mu +\pi ^{-1}(p)=\mu +\p}\operatorname {erf}^{-1}(2p-1),\p\in(0,1)입니다.}$

표준 정규 분포의 $\delta {\displaystyle {\mathrm{}}^{}}$-${\displaystyle {}^{}{1}^{}}$ (${\displaystyle p}$ $)\displaystyle \Phi$^{-$1}(p)$은 일반적으로$$ ${\displaystyle z_{}}$p\$displaystyle z_{p$로 표시됩니다.이 값은 가설 검정, 신뢰 구간 구성 및 Q–Q 그림에 사용됩니다.일반 랜덤 $변수{\displaystyle }$ X$(\displaystyle$ X$)$는 확률 $1{\displaystyle \mathrm{}}$- $(\displaystyle 1-p$의 μ ${\displaystyle +}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}${\(\displaystyle \$mu +z_$${p}\sigma$$$$})$를 $초과$하며,${\displaystyle }확률{\displaystyle \mathrm{}}$ 2${\displaystyle (\backslash }$$displaystyle \$${\displaystyle p})$의 $간격{\displaystyle }$μ ± ${\displaystyle z_{}}$ ${\displaystyle {}_{}}${\(\displaystyle 2$(\$p)를$$ 벗어납니다.$ntile{\displaystyle {}_{}}$ z $({$는 1.96입니다.따라서 일반 랜덤 변수는 5%의 경우에 한해 $간격{\displaystyle \mathrm{\mu }}$± 1.${\displaystyle 96}$({$displaystyle \mu \pm 1.96\$display$})$을 벗어납니다.

다음 표는 X$(\displaystyle$ X$)$가 지정된 $확률{\displaystyle }$p(\$displaystyle$ p$)$의 $범위{\displaystyle }$μ ± ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$†(\$displaystyle \mu$\pm $z_{p}\sigma$})에$$ $위치$하도록 계량 $z{\displaystyle {}_{}}$(\$displaystyle$ $z_{p$})를$$ 나타냅니다.이러한 값은 정규 분포(또는 점근 정규 분포)^[15][16]가 있는 표본 평균 및 기타 통계 추정기에 대한 공차 구간을 결정하는 데 유용합니다.$다음{\displaystyle \sqrt{\mathrm{}}}$ 표는 ${\displaystyle {\mathrm{2erf}}^{}}$- ${\displaystyle 1^{}\mu }$ (${\displaystyle }$p ) ${\displaystyle ={\mathrm{\delta }}^{}}$ -${\displaystyle {}^{}}$1 (${\displaystyle \frac{}{\mathrm{}}}$ + ${\displaystyle \frac{1}{}}$ 2$){$ $displaystyle${ $erf }\operatorname {erf }^$ { -$1$ ( p ) $=$\$Phi$^{-$1}\left({\frac {p+1}{2}}\right$ 위와 같이${\displaystyle {}^{}}\delta {\displaystyle {\mathrm{}}^{}}$ - $)\displaystyle \Phi$^{-$1}(p)$이 아닙니다$.$

${\displaystyle p}$	${\displaystyle z_{p}}$		${\displaystyle p}$	${\displaystyle z_{p}}$
0.80	1.281551565545		0.999	3.290526731492
0.90	1.644853626951		0.9999	3.890591886413
0.95	1.959963984540		0.99999	4.417173413469
0.98	2.326347874041		0.999999	4.891638475699
0.99	2.575829303549		0.9999999	5.326723886384
0.995	2.807033768344		0.99999999	5.730728868236
0.998	3.090232306168		0.999999999	6.109410204869

$작은$$$p {$displaystyle$ p$\}$의 경우, 분위함수는 유용한 점근팽창 $\delta {\displaystyle {\mathrm{}}^{}}$-${\displaystyle {}^{}{1}^{}}$ (${\displaystyle p}$ ) ${\displaystyle =}$ - ${\displaystyle \sqrt{\mathrm{in}1\frac{\mathrm{}}{}}}$ ${\displaystyle \sqrt{\frac{{p\mathrm{}}^{}}{}}}$ ${\displaystyle \sqrt{\frac{{}^{}}{}\frac{{}^{}}{}}}$- ${\displaystyle \sqrt{\ln }}$( ${\displaystyle 1\mathcal{}}$ ${\displaystyle \sqrt{p\frac{\mathrm{}}{}}}$ ${\displaystyle \sqrt{\frac{{}^{}}{}}}$ - ${\displaystyle \sqrt{\ln }（}$ $2$ ${\displaystyle ）}$ +$$( $1$. \ $displaystyle$ \ Phi$^$ { - 1$$= - { - { \ $frac }$ { p } { p } { p } { p } { p } { p } } { $displaystyln$ } { p } { p } { p } { p } } } 。$}$^[17]

정규 분포는 처음 두 개를 초과하는 누적량(평균 및 분산 제외)이 0인 유일한 분포입니다.또한 지정된 평균 및 ^[18][19]분산에 대해 최대 엔트로피를 갖는 연속 분포입니다.Geary는 평균과 분산이 유한하다고 가정할 때 일련의 독립적 도면으로부터 계산된 평균과 분산이 ^[20][21]서로 독립적인 유일한 분포임을 보여 주었습니다.

정규 분포는 타원 분포의 하위 클래스입니다.정규 분포는 평균에 대해 대칭이며 실제 선 전체에서 0이 아닙니다.따라서 개인의 체중이나 주식가격과 같이 본질적으로 긍정적이거나 강하게 치우친 변수에는 적합하지 않을 수 있다.이러한 변수는 로그 정규 분포 또는 파레토 분포와 같은 다른 분포로 더 잘 설명할 수 있습니다.

$값{\displaystyle }$x(\$displaystyle$x$$)가 평균에서 몇 가지 표준 편차 이상 떨어져 있을 경우 정규 분포의 값은 사실상 0입니다(예: 3개의 표준 편차가 분포의 0.27%를 제외한 모든 범위에 해당).따라서 특이치의 유의한 부분, 즉 평균으로부터 많은 표준 편차가 떨어져 있는 값, 정규 분포 변수에 최적인 최소 제곱 및 기타 통계적 추론 방법이 이러한 데이터에 적용될 때 종종 매우 신뢰할 수 없을 것으로 예상하는 경우에는 적절한 모형이 아닐 수 있습니다.그러한 경우, 보다 엄격한 분포를 가정하고 적절한 강력한 통계 추론 방법을 적용해야 한다.

가우스 분포는 평균 또는 분산이 유한한지 여부에 관계없이 동일한 분포의 합계를 끌어당기는 안정적인 분포군에 속합니다.제한 사례인 가우스를 제외하고, 모든 안정적인 분포는 무거운 꼬리와 무한 분산을 가집니다.안정적이고 분석적으로 표현될 수 있는 확률 밀도 함수를 가진 몇 안 되는 분포 중 하나이며, 다른 분포는 코시 분포와 레비 분포입니다.

과

$밀도{\displaystyle }$ f$x$$평균{\displaystyle }$μ\$displaystyle\mu}$ $$및$$ 가$(\displaystyle\sigma>0$의 정규분포에는 다음 속성이 있습니다.

• 분포의 모드,^[22] 중위수 및 평균인 점 x $=$, {\$displaystyle$ x=\$mu}$의 둘레는 대칭입니다.
• 단언할 수 없습니다. 첫 번째 도함수는 <,$x$> ,\$displaystyle$ x$>$ \$mu$, 0 은 ${\displaystyle x}$ ${\displaystyle =}$ $\mu {\displaystyle }$ 입니다$.\displaystyle$ x = \$mu .$ }
• 곡선과 $(\displaystyle$ x$)$ 축으로$$ 둘러싸인 영역은 통일성(즉, 1과 동일)입니다.
• 첫 번째 도함수는 $f{\displaystyle {}^{\mathrm{}}}$ (${\displaystyle x}$ ) ${\displaystyle =}$ -${\displaystyle \frac{x}{}}$ - μ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$f (${\displaystyle x}$) .$${ $displaystyle f^$ { \ $prime$} ( x ) = - { \ $frac${ $x$- \ $mu$} { \ f ( x )$}$ f ($$$x$ ) （ x ) 。$}$
• 밀도는$$두 개의 ${\displaystyle \mathrm{변곡점}(f}$의 2차 도함수가 $0$이고 부호가 변경됨)이 있으며, x ${\displaystyle =}$ μ -$$μ - （ \ $displaystyle$$$x = \$mu$- \ $display ）$와 x ${\displaystyle =\mu }$ +${\displaystyle \mu }$ .$${ $displaystyle$ x = \ $mu$+ \ $sign$}에서 평균으로부터 한 표준 편차가 있습니다.
• 그 밀도는 통나무 오목하다.^[22]
• 그 밀도는 무한히 미분 가능하며, 정말로 ^[23]2차 초평활화이다.

또한 표준 정규 분포의 밀도$μ$ ${\displaystyle =}$ $({displaystyle$$\mu$ ${\displaystyle =}$$$0} $및$ $θ$ = 1({$displaystyle \mu$ $=$$$1)도$$ 다음과 같은 $특성$을 가진다.

• 첫 번째 도함수는 $\phi {\displaystyle {}^{}}$′ ${\displaystyle （}$ ${\displaystyle x}$ )$=$ - ${\displaystyle xx}$（ x${\displaystyle }$）$$。{ $displaystyle$ \$varphi$^{\prime }($x)=-x$\varphi$(x)$이다.$}$
• 두 번째 도함수는 ($x{\displaystyle {}^{\mathrm{}}}$)$=$ ( ${\displaystyle {x\mathrm{}}^{}}$2 -${\displaystyle 1}$)${\displaystyle \phi }$ (${\displaystyle x}$ $){$ $displaystyle \varphi$^{\$prime$ \$prime$}(x)=($x^{2}-1)\varphi(x)}$입니다.
• 일반적으로 n번째 도함수는${\displaystyle {}^{}}$$display$ (${\displaystyle {}^{}x}$)${\displaystyle {}^{}=}$( -${\displaystyle {}^1}$) ${\displaystyle n_{}}$ ${\displaystyle {He}_{}}$ n${\displaystyle }$（${\displaystyle x}$)$$、 \ $displaystyle$ \$varphi ^$ { ( n )$= displaydisplaydisplay$（ x )^{ $n$} = { n } \$operatorname${ $He$} ${\displaystyle {\mathrm{\_<img\; alt="\{\backslash displaystyle\; \backslash varphi\; ^\{(n)\}(x)=(-1)^\{n\}\backslash operatorname\; \{He\}\; \_\{n\}(x)\backslash varphi\; (x),\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/f2ba13000c0fb8936cf5dae7d671cc01633da524"\; style="vertical-align:\; -0.838ex;\; width:29.08ex;\; height:3.343ex;">}}_{}}$$${ $n （ x$ ) （ $）$
• μ$({displaystyle \mu})$ 및$$$$${\displaystyle \mu }$({$displaystyle$\mu$})$를 갖는 정규 분포 $변수{\displaystyle }$X({$displaystyle$ \displaystyle$$\displaystyle \$mu$})가$$ 특정 집합에 있을 확률은 $분율{\displaystyle }$ Z$=$ -${\displaystyle }$μ${\displaystyle )}$ / ${\$ {$displaystyle$ Z=($X-\mu}/\display})$가 정규 분포를 갖는다는 사실을 사용하여 계산할 수 있습니다.

★★★

$변수{\displaystyle }$ X$({displaystyle$X})의$$ 플레인 모멘트와 절대 모멘트는 각각 ${\displaystyle X^{}}$p({$displaystyle$ X$^{p$}) ${\displaystyle 및}$ ${\displaystyle {}^{}}$p({$displaystyle X$^{p$\})$의 기대치입니다.$X의$$$$기대치{\displaystyle }$μ(\$displaystyle\$$mu)$가 0인 경우 이러한 파라미터를 중심 모멘트라고 하며, 그렇지 않은 경우 이러한 파라미터를 비중심 모멘트라고 합니다.일반적으로 관심 있는 것은 정수 ${\displaystyle 차수}$가 p$\displaystyle$$p$인 순간뿐입니다.

X$(디스플레이 스타일$ X$)$가 정규 분포를 갖는 $경우{\displaystyle }$, 중심 모멘트가 아닌 모멘트가 존재하며 실제 부분이 -1보다 큰 p$($디스플레이$$ $스타일$ p$)$에 대해 유한합니다.음이 아닌 $정수{\displaystyle }$p {\$style$ p$\}$의 경우 $일반$ 중심 모멘트는 다음과 같습니다.^[25]

$\displaystyle \operatorname {E} \left [ ( X - \ mu )^{ p } \ right ]= scape { cases } 0 & { \ text { if } p { text { } , 、 \ \ scapter ^ { p } ( p - 1 ) { \ { }}}} text }는입니다.&{\text{if}}}p'text{nowledge}입니다. {caseend {case}}\end {case}$

$여기{\displaystyle }$ n$!$ {\$displaystyle$ n$!!$}은$($는) n$.\$displaystyle$$n.$과$와) $같은{\displaystyle }$ 패리티를 가진 $n.\$$displaystyle$ n$$.부터1까지의 모든 $숫자$의 곱을 나타냅니다.

중심 절대 모멘트는 모든 짝수 순서의 일반 모멘트와 일치하지만 홀수 순서의 경우 0이 아닙니다.음수가 아닌 $정수{\displaystyle }$p의 경우$,$ {\$display$ p$}$

$\displaystyle\operatorname{E}\left [X-\mu^{p}\right]&=\표시^{p}(p-1)!!\cdot {cases} {cdot {\pi } {\text {if}\cdot {frac}\cdot {p/2}\gam}\cdot {frac}\text {frcdap}\frcd}\frcd\frcd$

마지막 공식 또한 어떤non-integer p>;− 1.{\displaystyle p>, -1 유효합니다.는 언제μ ≠ 0말},{\displaystyle \mu \neq 0,}은 평야 그리고 절대적인 순간 1F1{\displaystyle{}_{1}F_{1}합류하는 초 기하 기능 면에서}와 U.{미국\displaystyle}[표창 필요한]표현될 수 있다.

${displaystyle {rightsigma cdot ( {p}\cdot (xisplaystyle {E}\left[X^{p}\right]=\cdigma ^{p})}U\left(-{\frac {p}{2}), {\frac {1}{2}\left\frac\frac {2}\frac {2}\right}, \operatorname {E}\left[X ^p}\ 2\cdpot}\}} 정렬된 {\end}}$

이러한 표현은$$p\$style$p가$$ 정수가 아닌 $경우$에도 유효합니다.일반화 Hermite 다항식을 참조하십시오.

★★★		모멘트 심심 central central central central central
1	$\mu}{\displaystyle\}$	${\displaystyle 0}$
2	$}+\display style \mu ^{2display ^{2}$	$displaystyle \display ^{2}}$
3	$^{ \ style displaystyle \mu ^{3}+3\mu \display ^{2}}$	${\displaystyle 0}$
4	$^{displaystyle\mu ^{4}+6\mu ^{2}\mu ^{2}+3\mu ^{4}.$	$3 style displaystyle 3\display ^{4}}$
5	$^{^{315displaystyle \ ^{5}+10\mu ^{3}\mu ^{2}+15\mu ^{4}$	${\displaystyle 0}$
6	$^{^{2}\mu ^{2mu ^{2}\mu ^{6}\displaystyle$	$15displaystyle 15\display ^{6}}$
7	$^{^{5105}\displaystyle \\mu ^{5}\mu ^{2}+105\mu ^{3}\mu ^{6$	${\displaystyle 0}$
8	$^{}+mu}\displaystyle \^{4}+mu^{6mu^{4}\displaystyle}\mu^{4}+mu^{2}}\mu^{6}+105\mu^{8}$	$105displaystyle 105\display ^{8}}$

X$({displaystyle$X})가$$ ${\displaystyle \mathrm{간격}}$[${\displaystyle a,}$b$](\{{\displaystyle }$displaystyle $[a,$ b])에 있는 $경우$를 조건으로$$ 하는 X$({displaystyle$$X$})의 예상은 다음과 같습니다.

$\ a -displaystyle \operatorname {E} \left[X\mid a\fl]$

$여기$서$$f {\$displaystyle$$$$}$와 F {\$displaystyle$ F$\}$는 각각 X의 밀도 및 누적 분포 함수입니다. b $= {\$ {\$displaystyle$ b=\$infty}$의 경우 이를 역밀스 비율이라고 합니다.위에서는$X$의$$밀도 f({$displaystyle$$$X$})$가 인버스 밀스 비율과 같이 표준 표준 밀도 대신 사용되므로, 여기서는 $we({displaystyle$ \$sigma })$이 아닌 ${\$$$({displaystyle \sigma$$^{2})로 표시됩니다.

및

$(\displaystyle \mu)$및$$ 표준편차θ$(\displaystyle \sigma)$를^[26] 갖는 $정규밀도{\displaystyle }$f(\$displaystyle$ f$)$의 푸리에 변환은 다음과 같습니다.

$_ style {f}(t)={-infty}^{-in}$

$여기$서 i$\displaystyle$i는$$ 가상 단위입니다.$평균{\displaystyle }$ ${\displaystyle \mathrm{\mu }}$ ${\displaystyle =}$0$(\displaystyle$ \$mu =$ 0$)$인 경우 첫 번째 계수는 1이고, 푸리에 변환은 상수 계수를 제외하고 주파수 영역의 정규 밀도이며, 평균 0 및 ${\displaystyle 표준}$ $편차{\displaystyle \mathrm{}}$ 1/θ$(\displaystyle$ 1$/\display$ $\})$입니다. 특히 표준 정규 분포$\delta {\displaystyle }$(\$displaystyle \vari$})는$$ 고유푸입니다.푸리에 변환의 음질

확률론에서, 실수치 $랜덤$ $X$의 확률 분포의 푸리에 변환은 $X$의 $기대치$로 정의되는 변수 특성 함수 ${\displaystyle {\delta }_{}}$X (${\displaystyle t}$) \ $displaystyle$\ $varphi _$ { $X }$($t$ )에$$ 밀접하게 관련되어 있다.s $실변수{\displaystyle }$ t$\displaystyle$ t$($푸리에 변환의 주파수 파라미터)의 함수입니다.이 정의는 복합값 $변수{\displaystyle }$ t$\displaystyle$^[27]t로 해석적으로 확장할 수 있습니다.둘 사이의 관계는 다음과 같습니다.

$displaystyle \varphi _{X}(t)=hat {f}(-t)}$

및 함수

실수 랜덤 $변수{\displaystyle }$X의 모멘트 생성 함수({$displaystyle$X})는 실수$$ $파라미터{\displaystyle }$ t${displaystyle$ t$\}$의 함수로서 ${\displaystyle e^{}}$ t$X$의 $기대치{\displaystyle {}^{}}$({$displaystyle$ e$^{tX$입니다.$밀도{\displaystyle }$f{$displaystyle$ f$\}$의 정규 분포에서는$$μ의 $평균값$({$displaystyle\$muyle f$}$ 및$$ 편차)입니다$.$$aystyle \module$ $\},$ 모멘트 생성 함수가 존재하며 다음과 같습니다.

$M [ tdisplaystyle M(t)=\operatorname {E}[E]$

적분 생성 함수는 모멘트 생성 함수의 로그, 즉

$g M)=\ t g)=\ln M(t)=\mu t+{1}{2display ^{2}}$

$이것$은 t$${\$displaystyle$ t$\}$의 2차 다항식이므로 첫 번째 2개의 누적수(${\displaystyle$ \$mu}}$와 분산 ${\displaystyle {2\mathrm{}}^{}}$2 {\$displaystyle \sigma$^{$2$만이 0이 아닙니다.

Stein의 방법에서 무작위 변수${\displaystyle }$X ~$μ,$2)의 Stein 연산자와 클래스는 $A{\displaystyle \mathcal{}f}$ (${\displaystyle x}$ )$$${\displaystyle =}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}{}^{}}$ f ${\displaystyle (}$ (${\displaystyle x}$) -${\displaystyle }$(${\displaystyle x}$ -${\displaystyle \mu }$ )$f$ ($x$)$=$ \ $style$ {$mathcal$ {$A }$ （ x ） 。절대 연속 f: ( [ () < $∞$ \ $displaystyle$ f : \ $mathbb { R }$ \ $to$ \ $mathbb${$R$} ( ） } \ $mathbb${ $E$} [ $f$' ($X$ ) ] < \ $infty$$}$ 。

바리안스

$\delta {\displaystyle }${$displaystyle \displaystyle$f$(x)}$의 한계에서는 확률밀도 $)$는 최종적으로 x μ(\$displaystyle$ x\neq$$$\mu$에서 0이 되는 경향이 있지만, ${\displaystyle x}$${\displaystyle }$$=$${\displaystyle \mu }$(\$displaystyle x$=\mu$)$의 적분이 1이면 제한 없이 증가합니다.따라서 정규 분포는 $\sigma {\displaystyle }$ ${\displaystyle =}$ { $displaystyle$ \ $displaystyle = 0$}일 때 정규 분포로 정의할 수 없습니다.

단, 분산이 0인 정규분포를 일반화함수로 정의할 수 있습니다.구체적으로는 Dirac의 "$함수{\displaystyle }$" ${\$ { $displaystyle$$\mu$ 즉 $평균\mu {\displaystyle (x}$ - ${\displaystyle \mu }$)로 변환된$$ f$x$) $=$ (${\displaystyle x}$ -$$μ $).\displaystyle$ f$(x$ - mu $)$는 CDF입니다.$평균{\displaystyle }$μ(\$displaystyle\mu$ 즉

$Fdisplaystyle F(x)=case}0&{\textif}x}x <\mu\text{cases}\mu\{cases}}\mu\case}$

대대 maximum maximum

지정된 $평균{\displaystyle }$μ ${\displaystyle$ \mu$$$\}$ 및 분산 ${\displaystyle {2\mathrm{}}^{}}$2 {\$displaystyle$ \sigma$^{2$}의 모든 확률 분포 $중{\displaystyle }$정규 ${\displaystyle \mathrm{분포}}$ N${\displaystyle ({}^{}}$ , ${\displaystyle {2\mathrm{}}^{}}$2$$)(\^[28]$displaystyle$ N$(\mu ,\sigma$^{$2}))$은 엔트로피가 최대인 분포입니다.X$(\displaystyle$ X$)$가 확률 $밀도{\displaystyle }$ f$)$ {$displaystyle$ f$(x$의 연속 랜덤 변수인 $경우{\displaystyle }$ X$(\displaystyle$ X$)$의 엔트로피는 다음과 같이 정의됩니다^[29][30][31].

$H _displaystyle H(int _{-\infty }^{\infty }f(x)\log f(x), variary}$

$여기$서${\displaystyle }$f (${\displaystyle x}$ ) log${\displaystyle f}$f ( $){$ $displaystyle$ f$(x)\log$ f$(x)}$는${\displaystyle }$f (${\displaystyle x)}$ $=$ { $displaystyle$ f$(x$)=$0$일 때 항상 0으로 간주됩니다.분포가 적절하게 정규화되어 있고 지정된 분산을 갖는다는 제약조건에 따라 이 함수를 최대화할 수 있습니다.두 개의 Lagrange 승수를 가진 함수가 정의됩니다.

$L= _ }^{\inftyleft_{-\}{\(xinfty \}^{\interf(\interf }) }) }$

$여기$서 f$)$ {$displaystyle$ f$(x)}$는 현재 $(\displaystyle\mu)$ 및 $(\displaystyle\$displaystyle\$display$를 갖는 밀도함수로 간주됩니다.

엔트로피가 최대일 때 f$)$에 대한 작은 변동 $x)\$$displaystyle$ f(x)\delta f$$$(x)$는$$L(\$displaystyle$ L$)$에 대한 변동 L$(\displaystyle\delta$ L$)$을 생성합니다.

$0= L=\ _ (murighty}{display 0=\int_{-infty} f(xtfty}\fty}\fty }$

이 값은 임의의 ${\displaystyle \mathrm{작은}}$f$($x)\$displaystyle$ f$($x)\delta f(x$)\backslash$$displaystyle$ f$(x)}$에 $대해{\displaystyle }$ 해결하면 다음과 같이 됩니다.

$=e^{-\ _displayda displaystyle f(x)=e^{-\displayda _{0}-1-\displayda (x-\mu)^2}}$

$(\$ _${0})$ 및$$ $(\displaystyle \lambda$})에$$ 대해 푸는 제약 방정식을 사용하면 정규 분포의 밀도를 얻을 수 있습니다.

${{(}}}{\displaystyle f(x,\mu,\display =snapfrac {\display {\pi}}}}{{{{{\display {\display2}}}}}}}}$

정규 분포의 엔트로피는 다음과 같습니다.

$Hdisplaystyle H(X)=tfrac {1}{2}})(1+\log(2\display ^{2}\pi))}}}}}}}}},$

★★★★

한계

중심 한계 정리는 특정(공통) 조건에서 많은 랜덤 변수의 합이 거의 정규 분포를 갖는다는 것을 나타냅니다.$구체적$으로는 X${\displaystyle {}_{}{1\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle {}_{}}$(\$displaystyle X_{1},\ldots,X_{n})$은 독립적이고 동일한 분포의 랜덤 변수이며, 평균은 0, 분산 ${\displaystyle {2\mathrm{}}^{}}$2$(\displaystyle$ \$sigma ^{2$})이며,$Z$(\$displaystyle$ Z$$$)$는 n$(\$displaystyle {qrt})로 $스케일링됩니다.$$n}}}$

$Zdisplaystyle Z=sqrt {n}\sum _{i=1}^{n}X_{i}\right}$

그 후 n${displaystyle$ n$}$이 $증가$하면 Z$(\displaystyle$ Z$)$의 확률분포는 평균과 분산이 0인 정규분포 ${\displaystyle {2\mathrm{}}^{}}$2(\$displaystyle \sigma$^{$2$가 됩니다.

이 정리는 의존도 및 분포의 모멘트에 특정 제약이 가해지는 경우 독립적이지 않거나 동일한 분포가 아닌 변수$i )$로 확장할$$ 수 있습니다.

실제로 접한 많은 검정 통계, 점수 및 추정기에는 특정 랜덤 변수의 합계가 포함되어 있으며, 영향 함수를 사용하여 더 많은 추정치를 랜덤 변수의 합계로 나타낼 수 있다.중심 한계 정리는 이러한 통계 모수가 점근 정규 분포를 가질 것임을 암시합니다.

는 특정 수 를 들어 다음과 같습니다. 예를 들어 다음과 같습니다.

• $이항분포{\displaystyle }$B$($ p$)$는 $(\displaystyle$np$$$$$)$$$및 $큰n$(\displaystyle np($)$에 대해$$ ${\displaystyle \mathrm{평균n}}$(\$displaystyle$ np$)$ 및 ${\displaystyle \mathrm{분산n}(\backslash }$$displaystyle$np($1-p$))로$$ 거의 정규 분포를 따릅니다.
• $파라미터{\displaystyle }$ $"\displaystyle \lambda"$의 포아송 분포는 $"\displaystyle \lambda$^[38]의 큰 값에 대한 $평균값 "\displaystyle$ \lambda$"$ 및$분산값{\displaystyle }$ "\displaystyle \lambda$"$에서 거의 정규 분포를 따릅니다.
• 카이 제곱 분포 ${\displaystyle {2\mathrm{}}^{}2}$ ( k )$$\ $displaystyle$ \ $chi$^ { 2$（ k$） 。$큰$ k \ $displaystyle$k$$variance$$ 2 $22$k$$, 。
• Student'$s{\displaystyle }$ ${\displaystyle \mathrm{t-분포}}$ t${\displaystyle (}$ ${\displaystyle )}$ $){displaystyle$ t$(\nu)}$은$($는) 평균이 0이고 분산이 1인 경우, the { $displaystyle \nu$}이$$(가) 클 경우)

이러한 근사치가 충분히 정확한지 여부는 그러한 근사치가 필요한 목적과 정규 분포에 대한 수렴 속도에 따라 달라집니다.일반적으로 이러한 근사치가 분포의 꼬리 부분에서 정확도가 떨어지는 경우가 있습니다.

중심 한계 정리의 근사 오차에 대한 일반적인 상한이 Berry-Esseen 정리에 의해 주어지고 근사치의 개선은 Edgeworth 확장에 의해 주어집니다.

이 정리는 많은 균일한 노이즈 소스의 합을 가우스 노이즈로 모델링하는 데에도 사용할 수 있습니다.'AWGN' 참조.

하나 이상의 독립적이거나 상관된 정규 변수의 함수에 대한 확률 밀도, 누적 분포 및 역 누적 분포는 광선^[39] 추적의 수치 방법(Matlab 코드)을 사용하여 계산할 수 있습니다.다음 섹션에서는 몇 가지 특별한 경우를 살펴보겠습니다.

X$(\displaystyle$ X$)$가 $(\displaystyle \mu)$ 및$$ 분산이 $(\$^{$2$인 $경우{\displaystyle }$,

• ${\displaystyle a}$ X${\displaystyle }$+$$ (\$displaystyle$ $a$$)$ $및$ b (\$displaystyle$ $b$$)$의 $실수$에 대해서도, $평균{\displaystyle \mu }$+ b (\$displaystyle a\mu$+ b$)$ 및 ${\displaystyle 표준}$ 편차 a$$(\$displaystyle$ a$\sigma$의 정규 분포가 됩니다. 즉, 선형 변환에서는 정규 분포 패밀리가 닫힙니다.ons(온스.
• $X의$({$displaystyle$X})는$$ 로그 정규 분포를 따릅니다. e^X ~ ln(N(μ, δ²)).
• X$(\displaystyle$ X$)$의 절대값이 정규 분포 X~N_f(μ, θ²)을 접었습니다.μ ${\displaystyle =}$ $(\displaystyle$ \$mu =$ 0$$)인 경우 이를 반정규 분포라고 합니다.
• 정규화 잔차의 절대값인 X - μ / μ는 X${\displaystyle }$-${\displaystyle \mu }$ /${\displaystyle \mu }$ ~ ${\displaystyle {\delta \mathrm{}}_{}}$1 {\$displaystyle X-\mu /\sigma \chi$ _${1$의 자유도를 갖는 카이 분포를 가진다.
• X/mu의 제곱은 ${자유}^{}$도 X 2 / - 2${}^{}$~ ${1\mathrm{}}_{}^{}$ ${}_{}^{}{}^{}$ ( ${\mu \mathrm{}}^{}$2${}^{}$/ ${2\mathrm{}}^{}$2 $){$ $textstyle$ X$^{2}/\sigma ^{2}\sim \chi$ _${1}^{2$}({mu $^2}/\mu^{2$의 비중심 카이-mu 분포입니다. ($표시 = 0$\$mu)$
• 정규 $변수{\displaystyle }$ x$(\displaystyle$ x$)$의 로그 우도는 확률 밀도 함수의 로그일 뿐입니다.
  $$\displaystyle \ln p(x)=-{\frac {1}{2}}\frac {x-\frac}{\frac}\ln \left(\frac {2\pi}}}\right)=-{\frac {1}-\frac {{pi }}}\ln \frac {\frac}}}$$

  
  이 값은 표준 정규 변수의 스케일링 및 시프트된 제곱이므로 스케일링 및 시프트된 카이 제곱 변수로 분포됩니다.
• [a, b] 구간으로 제한된 변수 X의 분포를 잘린 정규 분포라고 합니다.
• (X - ⁻²μ)는 위치 0 및 척도 θ의⁻² Levy 분포를 가진다.

의 된 정규

• ${\displaystyle {X\mathrm{}}_{}}$ 1$({$과 ${\displaystyle {X\mathrm{}}_{}}$2$({$$displaystyle X_{2})$가 2개의 독립된 정규 랜덤 변수이며, $평균$은 ${\displaystyle {\mu \mathrm{}}_{}}$$$1({$displaystyle$\$mu_{1$$\}),$ ${\displaystyle {표준편차}_{}}$는 1$({$${2$ $(\${2})입니다$.$${\displaystyle {X1\mathrm{}}_{}}$+ $({$}+$X_{2})$도 정규 ^[proof]분포를 따릅니다.$평균$은${\displaystyle {}_{}{}_{}}$ +$$({$displaystyle \mu _{$$1$}+\$mu$$$_${$$2$}}, 분산은 ${\displaystyle {}_{}^{}}$+ $({$ _${1}+{2$입니다.
• 특히 X$(표시 스타일$ X$)$와 Y$(표시 스타일$ Y$)$가 평균과 ${\displaystyle {분산}^{}}$이 0인 독립 정규 편차 with 2$($스타일 \$sigma$^{$2$인 $경우{\displaystyle }$X +$$($표시 스타일$ X$+Y)$와${\displaystyle }$X -$$($표시$ 스타일 $X-Y)$도 평균과 2(${\displaystyle {표시\mathrm{}}^{}}$ 스타일 X-Y)의 독립 정규 분포입니다.$${\$displaystyle$ 2$\sigma$^{$2$ 이것은 편광 ^[40]정체성의 특별한 경우입니다$.$
• ${\displaystyle {X\mathrm{}}_{}}$ 1$(\$ ${\displaystyle {X\mathrm{}}_{}}$ 2$(\$가 $(\displaystyle$$\sigma$$)$와 편차$display$(\displaystyle \sigma$)$를 갖는 2개의 독립된 정규 편차이며$,$ $a{\displaystyle }$(\$displaystyle$ a$)$와$$b(\$displaystyle$ b$)$가 임의의 실수인 $경우{\displaystyle {}_{}}$ 변수,
  $$displaystyle X_{3}=syslogfrac {AX_{1}+BX_{b}-{b}_{b}{b})}}+\mu }$$

  
  또한 $평균{\displaystyle }$μ(\$displaystyle\mu)$ 및$$ 편차 $(\displaystyle\displaystyle$displaystyle)를 사용하여 정규 분포도 안정적입니다(지수 ${\displaystyle \mathrm{\alpha }}$ ${\displaystyle =}$2 \$displaystyle$ \$alpha = 2$ $$） 。

의 정규

${\displaystyle {X\mathrm{}}_{}}$ 1$({$과 X$$({$displaystyle X_{2})$가 평균 0과 분산 1을 갖는 두 개의 독립된 표준 정규 랜덤 변수인 $경우{\displaystyle {}_{}}$,

• 이들의 합과 차이는 평균 0과 분산 2: X ${\displaystyle {1\mathrm{}}_{}}$± ${\displaystyle {X\mathrm{}}_{}2}$ ~${\displaystyle }$N ( ${\displaystyle 0}$,${\displaystyle 2}$ $){$ $displaystyle X_{1}\pm$ X_${2}\sim$N($0,2$으로 정규 분포를 따릅니다.
• $제품{\displaystyle }$ Z ${\displaystyle =}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$ X$$ ({$displaystyle$ Z =$X$_ {$1} X$_ {$2}$ )는$$ 밀도 $함수{\displaystyle {}_{}}$ f ${\displaystyle Z_{}}$(${\displaystyle z}$ ) ${\displaystyle =}$ ${\displaystyle {-}^{}}$ - 1 ${\displaystyle {}^{}{}_{}{0\mathrm{}}_{}}$ (${\displaystyle z}$) = \$pi$^ { - 1$K$_ 0 ( $z$ )K _ { 0 ($$z$$} ( k _$$$displaystyle$ $0$$$)의 ${\displaystyle {제품\mathrm{}}_{}}$ 분포를^[41] 따릅니다.이 분포는 z ${\displaystyle =}$0(\$displaystyle$ z$=0$에서 $대칭$이며, 특성 함수 ${\displaystyle {\delta }_{}}$Z (${\displaystyle t}$ )$=$ ($+$ ${\displaystyle {t\mathrm{}}^{}{}^{}}$2) -${\displaystyle 1^{}}$ / $(\$ _${Z}(t$)= ($1+t^{$2})^{-$1/$2$\})$를 가지고 있습니다.
• 이 비율은 표준 Cauchy 분포를 $따릅니다{\displaystyle {}_{}}$.${\displaystyle {X\mathrm{}}_{}}$1/${\displaystyle {X\mathrm{}}_{}}$2 ~ ${\displaystyle \mathrm{Cauchy}}$⁡ (${\displaystyle 0}$ ,${\displaystyle 1}$) { $displaystyle X_{1$} / $X_{2}\sim \operatorname {Cauchy}$ (0$$, 1)$\}$
• 유클리드 $노름{\displaystyle \sqrt{{}_{}^{}}}$ ${\displaystyle \sqrt{{X\mathrm{}}_{}^{}}}$ 1${\displaystyle \sqrt{{\mathrm{}}_{}^{}}}$ + ${\displaystyle \sqrt{{X\mathrm{}}_{}^{}}}$ ${\displaystyle \sqrt{{\mathrm{}}_{}^{}}}$({$displaystyle {X_{1}^{2}+X_{2}^2}})$는 레일리 분포를 가진다.

의 독립된 에 대한

• 독립적인 정규 편차의 선형 조합은 정규 편차입니다.
• ${\displaystyle {X\mathrm{}}_{}}$1, ${\displaystyle {X\mathrm{}}_{}}$2,${\displaystyle \dots ,}$ ${\displaystyle X_{}}$n({$displaystyle X_{1},X_{2},\ldots,X_{n})$이 독립 표준 정규 랜덤 변수인 $경우{\displaystyle {}_{}}$, 제곱합은 n$({displaystyle$ n$}$ 자유도의$$ $카이{\displaystyle }$ 제곱 분포를 가집니다.
  $${\displaystyle X_{1}^{2}+\cdots +X_{n}^2}\sim \chi _{n}^2}.}$$

  
• 수단과 만약 X1, X2,…, Xn{\displaystyle X_{1},X_{2},\ldots ,X_{n}}독립심 일반적으로 분산된 확률 변수μ{\displaystyle \mu}와 변동이}서, 자신들의 샘플 평균 사용함을 입증할 수 있는 건 그 견본 표준 deviation,[42]에 상관이 없다 2{\displaystyle \sigma ^{2}σ. 바수의 정리 또는 코크란의 [43]정리입니다.이 두 수량의 비율은 자유도가$(\displaystyle n-1)$인 학생의 t-분포를 갖는다.
  $${{displaystyle t={\overline {X}-\mu }{S/{\sqrt {n}}}=sqrt {{\frac {1}{n}}(X_{1}+\cdots +X_{n}-\mu}{\displayrt {\frac{\frac {n-1}}}}}}{{\}}}}}}{\frac {\frac}}}}}}}{\frac {\frcd}}}}}}}}}}}}}}}$$

  
• ${\displaystyle {X1\mathrm{}}_{}}$ ${\displaystyle {X2\mathrm{}}_{}\dots ,}$ $(\$ X_${1}, X_{2},\ldots$$,$ $X\_{\displaystyle {}_{}}$${n$${\displaystyle {}_{}{}_{}}$, ${\displaystyle {Y2\mathrm{}}_{},}$ $…,$ ${\displaystyle {Ym}_{}}$(\$displaystyle Y_{1$},$Y_{2$},\$ldots, Y_{$m$$})이 독립된 정규 랜덤 변수일 $경우{\displaystyle {}_{}}$ 정규화합계의 비율은 다음과 같습니다.
  $${\displaystyle F=frac {\left(X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^2}/n}{\left(Y_{1}^2}+Y_{2}^{2}+\cdots +Y_{m}^{2}\right)/m}}\sim F_{n,m}.}$$

  

상관된 여러 정규 변수에 대한 연산

• 정규 벡터의 2차 형식, 즉 복수의 독립적 또는 상관된 정규 변수의 $2차$ 함수 $=$ ${}_{}^{}$x ${}_{}$ +${\theta }_{}$x $j$ +$c$ { $textstyle$q = \$sum x_{i$}^2} + \$sum x_{j$$}$ + c}는 일반화 카이-제곱 변수이다.

밀도 함수에 대한 연산

분할 정규 분포는 서로 다른 정규 분포의 밀도 함수의 축척 단면을 결합하고 밀도를 재스케일링하여 하나로 통합하는 측면에서 가장 직접적으로 정의됩니다.잘린 정규 분포는 단일 밀도 함수의 단면을 재스케일링한 결과입니다.

무한 나눗셈과 크라메르의 정리

임의의 양의 $정수{\displaystyle }$n(\$displaystyle\$$text$${$$n$$})$에 대해 $평균{\displaystyle }$μ 및$$이 $2$$(\$displaystyle$\sigma$$^{$$2$})인 정규분포는 각각 $평균{\displaystyle \frac{}{}}$ ${\displaystyle \frac{\mu }{}}$n(\$displaystyle\frac\mu})$의 독립 정규편차의$$합이 됩니다.} 및$$ $분산{\displaystyle \frac{{}^{}}{}}$ $2n(style$ {$frac$^{$2}}$ {n$\})$입니다$.$이 성질을 무한 ^[45]나눗셈이라고 합니다.

Conversely, if ${\displaystyle X_{1}}$ and ${\displaystyle X_{2}}$ are independent random variables and their sum ${\displaystyle X_{1}+X_{2}}$ has a normal distribution, then both ${\displaystyle X_{1}}$ and ${\displaystyle X_{2}}$ must be normal deviates.^[46]

This result is known as Cramér's decomposition theorem, and is equivalent to saying that the convolution of two distributions is normal if and only if both are normal. Cramér's theorem implies that a linear combination of independent non-Gaussian variables will never have an exactly normal distribution, although it may approach it arbitrarily closely.^[32]

Bernstein's theorem

Bernstein's theorem states that if ${\displaystyle X}$ and ${\displaystyle Y}$ are independent and ${\displaystyle X+Y}$ and ${\displaystyle X-Y}$ are also independent, then both X and Y must necessarily have normal distributions.^[47][48]

More generally, if ${\displaystyle X_{1},\ldots ,X_{n}}$ are independent random variables, then two distinct linear combinations ${\textstyle \sum {a_{k}X_{k}}}$ and ${\textstyle \sum {b_{k}X_{k}}}$will be independent if and only if all ${\displaystyle X_{k}}$ are normal and ${\textstyle \sum {a_{k}b_{k}\sigma _{k}^{2}=0}}$, where ${\displaystyle \sigma _{k}^{2}}$ denotes the variance of ${\displaystyle X_{k}}$.^[47]

Extensions

The notion of normal distribution, being one of the most important distributions in probability theory, has been extended far beyond the standard framework of the univariate (that is one-dimensional) case (Case 1). All these extensions are also called normal or Gaussian laws, so a certain ambiguity in names exists.

• The multivariate normal distribution describes the Gaussian law in the k-dimensional Euclidean space. A vector X ∈ R^k is multivariate-normally distributed if any linear combination of its components Σ^k
  _j=1a_j X_j has a (univariate) normal distribution. The variance of X is a k×k symmetric positive-definite matrix V. The multivariate normal distribution is a special case of the elliptical distributions. As such, its iso-density loci in the k = 2 case are ellipses and in the case of arbitrary k are ellipsoids.
• Rectified Gaussian distribution a rectified version of normal distribution with all the negative elements reset to 0
• Complex normal distribution deals with the complex normal vectors. A complex vector X ∈ C^k is said to be normal if both its real and imaginary components jointly possess a 2k-dimensional multivariate normal distribution. The variance-covariance structure of X is described by two matrices: the variance matrix Γ, and the relation matrix C.
• Matrix normal distribution describes the case of normally distributed matrices.
• Gaussian processes are the normally distributed stochastic processes. These can be viewed as elements of some infinite-dimensional Hilbert spaceH, and thus are the analogues of multivariate normal vectors for the case k = ∞. A random element h ∈ H is said to be normal if for any constant a ∈ H the scalar product(a, h) has a (univariate) normal distribution. The variance structure of such Gaussian random element can be described in terms of the linear covariance operator K: H → H. Several Gaussian processes became popular enough to have their own names:
  • Brownian motion,
  • Brownian bridge,
  • Ornstein–Uhlenbeck process.
• Gaussian q-distribution is an abstract mathematical construction that represents a "q-analogue" of the normal distribution.
• the q-Gaussian is an analogue of the Gaussian distribution, in the sense that it maximises the Tsallis entropy, and is one type of Tsallis distribution. Note that this distribution is different from the Gaussian q-distribution above.
• The Kaniadakis κ-Gaussian distribution is a generalization of the Gaussian distribution which arises from the Kaniadakis statistics, being one of the Kaniadakis distributions.

A random variable X has a two-piece normal distribution if it has a distribution

${\displaystyle f_{X}(x)=N(\mu ,\sigma _{1}^{2}){\text{ if }}x\leq \mu }$

${\displaystyle f_{X}(x)=N(\mu ,\sigma _{2}^{2}){\text{ if }}x\geq \mu }$

where μ is the mean and σ₁ and σ₂ are the standard deviations of the distribution to the left and right of the mean respectively.

The mean, variance and third central moment of this distribution have been determined^[49]

${\displaystyle \operatorname {E} (X)=\mu +{\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})}$

${\displaystyle \operatorname {V} (X)=\left(1-{\frac {2}{\pi }}\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}}$

${\displaystyle \operatorname {T} (X)={\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})\left[\left({\frac {4}{\pi }}-1\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}\right]}$

where E(X), V(X) and T(X) are the mean, variance, and third central moment respectively.

One of the main practical uses of the Gaussian law is to model the empirical distributions of many different random variables encountered in practice. In such case a possible extension would be a richer family of distributions, having more than two parameters and therefore being able to fit the empirical distribution more accurately. The examples of such extensions are:

• Pearson distribution — a four-parameter family of probability distributions that extend the normal law to include different skewness and kurtosis values.
• The generalized normal distribution, also known as the exponential power distribution, allows for distribution tails with thicker or thinner asymptotic behaviors.

Statistical inference

Estimation of parameters

It is often the case that we do not know the parameters of the normal distribution, but instead want to estimate them. That is, having a sample ${\displaystyle (x_{1},\ldots ,x_{n})}$ from a normal ${\displaystyle N(\mu ,\sigma ^{2})}$ population we would like to learn the approximate values of parameters ${\displaystyle \mu }$ and ${\displaystyle \sigma ^{2}}$. The standard approach to this problem is the maximum likelihood method, which requires maximization of the log-likelihood function:

${\displaystyle \ln {\mathcal {L}}(\mu ,\sigma ^{2})=\sum _{i=1}^{n}\ln f(x_{i}\mid \mu ,\sigma ^{2})=-{\frac {n}{2}}\ln(2\pi )-{\frac {n}{2}}\ln \sigma ^{2}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}.}$

Taking derivatives with respect to ${\displaystyle \mu }$ and ${\displaystyle \sigma ^{2}}$ and solving the resulting system of first order conditions yields the maximum likelihood estimates:

${\displaystyle {\hat {\mu }}={\overline {x}}\equiv {\frac {1}{n}}\sum _{i=1}^{n}x_{i},\qquad {\hat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.}$

Sample mean

Estimator ${\displaystyle \textstyle {\hat {\mu }}}$ is called the sample mean, since it is the arithmetic mean of all observations. The statistic ${\displaystyle \textstyle {\overline {x}}}$ is complete and sufficient for ${\displaystyle \mu }$, and therefore by the Lehmann–Scheffé theorem, ${\displaystyle \textstyle {\hat {\mu }}}$ is the uniformly minimum variance unbiased (UMVU) estimator.^[50] In finite samples it is distributed normally:

${\displaystyle {\hat {\mu }}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n).}$

The variance of this estimator is equal to the μμ-element of the inverse Fisher information matrix ${\displaystyle \textstyle {\mathcal {I}}^{-1}}$. This implies that the estimator is finite-sample efficient. Of practical importance is the fact that the standard error of ${\displaystyle \textstyle {\hat {\mu }}}$ is proportional to ${\displaystyle \textstyle 1/{\sqrt {n}}}$, that is, if one wishes to decrease the standard error by a factor of 10, one must increase the number of points in the sample by a factor of 100. This fact is widely used in determining sample sizes for opinion polls and the number of trials in Monte Carlo simulations.

From the standpoint of the asymptotic theory, ${\displaystyle \textstyle {\hat {\mu }}}$ is consistent, that is, it converges in probability to ${\displaystyle \mu }$ as ${\displaystyle n\rightarrow \infty }$. The estimator is also asymptotically normal, which is a simple corollary of the fact that it is normal in finite samples:

${\displaystyle {\sqrt {n}}({\hat {\mu }}-\mu )\,{\xrightarrow {d}}\,{\mathcal {N}}(0,\sigma ^{2}).}$

Sample variance

The estimator ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ is called the sample variance, since it is the variance of the sample (${\displaystyle (x_{1},\ldots ,x_{n})}$). In practice, another estimator is often used instead of the ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$. This other estimator is denoted ${\displaystyle s^{2}}$, and is also called the sample variance, which represents a certain ambiguity in terminology; its square root ${\displaystyle s}$ is called the sample standard deviation. The estimator ${\displaystyle s^{2}}$ differs from ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ by having (n − 1) instead of n in the denominator (the so-called Bessel's correction):

${\displaystyle s^{2}={\frac {n}{n-1}}{\hat {\sigma }}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.}$

The difference between ${\displaystyle s^{2}}$ and ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ becomes negligibly small for large n's. In finite samples however, the motivation behind the use of ${\displaystyle s^{2}}$ is that it is an unbiased estimator of the underlying parameter ${\displaystyle \sigma ^{2}}$, whereas ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ is biased. Also, by the Lehmann–Scheffé theorem the estimator ${\displaystyle s^{2}}$ is uniformly minimum variance unbiased (UMVU),^[50] which makes it the "best" estimator among all unbiased ones. However it can be shown that the biased estimator ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ is "better" than the ${\displaystyle s^{2}}$ in terms of the mean squared error (MSE) criterion. In finite samples both ${\displaystyle s^{2}}$ and ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ have scaled chi-squared distribution with (n − 1) degrees of freedom:

${\displaystyle s^{2}\sim {\frac {\sigma ^{2}}{n-1}}\cdot \chi _{n-1}^{2},\qquad {\hat {\sigma }}^{2}\sim {\frac {\sigma ^{2}}{n}}\cdot \chi _{n-1}^{2}.}$

The first of these expressions shows that the variance of ${\displaystyle s^{2}}$ is equal to ${\displaystyle 2\sigma ^{4}/(n-1)}$, which is slightly greater than the σσ-element of the inverse Fisher information matrix ${\displaystyle \textstyle {\mathcal {I}}^{-1}}$. Thus, ${\displaystyle s^{2}}$ is not an efficient estimator for ${\displaystyle \sigma ^{2}}$, and moreover, since ${\displaystyle s^{2}}$ is UMVU, we can conclude that the finite-sample efficient estimator for ${\displaystyle \sigma ^{2}}$ does not exist.

Applying the asymptotic theory, both estimators ${\displaystyle s^{2}}$ and ${\displaystyle \textstyle {\hat {\sigma }}^{2}}$ are consistent, that is they converge in probability to ${\displaystyle \sigma ^{2}}$ as the sample size ${\displaystyle n\rightarrow \infty }$. The two estimators are also both asymptotically normal:

${\displaystyle {\sqrt {n}}({\hat {\sigma }}^{2}-\sigma ^{2})\simeq {\sqrt {n}}(s^{2}-\sigma ^{2})\,{\xrightarrow {d}}\,{\mathcal {N}}(0,2\sigma ^{4}).}$

In particular, both estimators are asymptotically efficient for ${\displaystyle \sigma ^{2}}$.

Confidence intervals

By Cochran's theorem, for normal distributions the sample mean ${\displaystyle \textstyle {\hat {\mu }}}$ and the sample variance s² are independent, which means there can be no gain in considering their joint distribution. There is also a converse theorem: if in a sample the sample mean and sample variance are independent, then the sample must have come from the normal distribution. The independence between ${\displaystyle \textstyle {\hat {\mu }}}$ and s can be employed to construct the so-called t-statistic:

${\displaystyle t={\frac {{\hat {\mu }}-\mu }{s/{\sqrt {n}}}}={\frac {{\overline {x}}-\mu }{\sqrt {{\frac {1}{n(n-1)}}\sum (x_{i}-{\overline {x}})^{2}}}}\sim t_{n-1}}$

This quantity t has the Student's t-distribution with (n − 1) degrees of freedom, and it is an ancillary statistic (independent of the value of the parameters). Inverting the distribution of this t-statistics will allow us to construct the confidence interval for μ;^[51] similarly, inverting the χ² distribution of the statistic s² will give us the confidence interval for σ²:^[52]

${\displaystyle \mu \in \left[{\hat {\mu }}-t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+t_{n-1,1-\alpha /2}{\frac {1}{\sqrt {n}}}s\right],}$

${\displaystyle \sigma ^{2}\in \left[{\frac {(n-1)s^{2}}{\chi _{n-1,1-\alpha /2}^{2}}},{\frac {(n-1)s^{2}}{\chi _{n-1,\alpha /2}^{2}}}\right],}$

where t_k,p and χ 2
k,p are the pth quantiles of the t- and χ²-distributions respectively. These confidence intervals are of the confidence level 1 − α, meaning that the true values μ and σ² fall outside of these intervals with probability (or significance level) α. In practice people usually take α = 5%, resulting in the 95% confidence intervals.

Approximate formulas can be derived from the asymptotic distributions of ${\displaystyle \textstyle {\hat {\mu }}}$ and s²:

${\displaystyle \mu \in \left[{\hat {\mu }}- z_{\alpha /2} {\frac {1}{\sqrt {n}}}s,{\hat {\mu }}+ z_{\alpha /2} {\frac {1}{\sqrt {n}}}s\right],}$

${\displaystyle \sigma ^{2}\in \left[s^{2}- z_{\alpha /2} {\frac {\sqrt {2}}{\sqrt {n}}}s^{2},s^{2}+ z_{\alpha /2} {\frac {\sqrt {2}}{\sqrt {n}}}s^{2}\right],}$

The approximate formulas become valid for large values of n, and are more convenient for the manual calculation since the standard normal quantiles z_α/2 do not depend on n. In particular, the most popular value of α = 5%, results in z_0.025 = 1.96.

Normality tests

Normality tests assess the likelihood that the given data set {x₁, ..., x_n} comes from a normal distribution. Typically the null hypothesis H₀ is that the observations are distributed normally with unspecified mean μ and variance σ², versus the alternative H_a that the distribution is arbitrary. Many tests (over 40) have been devised for this problem. The more prominent of them are outlined below:

Diagnostic plots are more intuitively appealing but subjective at the same time, as they rely on informal human judgement to accept or reject the null hypothesis.

• Q–Q plot, also known as normal probability plot or rankit plot—is a plot of the sorted values from the data set against the expected values of the corresponding quantiles from the standard normal distribution. That is, it's a plot of point of the form (Φ⁻¹(p_k), x_(k)), where plotting points p_k are equal to p_k = (k − α)/(n + 1 − 2α) and α is an adjustment constant, which can be anything between 0 and 1. If the null hypothesis is true, the plotted points should approximately lie on a straight line.
• P–P plot – similar to the Q–Q plot, but used much less frequently. This method consists of plotting the points (Φ(z_(k)), p_k), where ${\displaystyle \textstyle z_{(k)}=(x_{(k)}-{\hat {\mu }})/{\hat {\sigma }}}$. For normally distributed data this plot should lie on a 45° line between (0, 0) and (1, 1).

Goodness-of-fit tests:

Moment-based tests:

• D'Agostino's K-squared test
• Jarque–Bera test
• Shapiro–Wilk test: This is based on the fact that the line in the Q–Q plot has the slope of σ. The test compares the least squares estimate of that slope with the value of the sample variance, and rejects the null hypothesis if these two quantities differ significantly.

Tests based on the empirical distribution function:

• Anderson–Darling test
• Lilliefors test (an adaptation of the Kolmogorov–Smirnov test)

Bayesian analysis of the normal distribution

Bayesian analysis of normally distributed data is complicated by the many different possibilities that may be considered:

• Either the mean, or the variance, or neither, may be considered a fixed quantity.
• When the variance is unknown, analysis may be done directly in terms of the variance, or in terms of the precision, the reciprocal of the variance. The reason for expressing the formulas in terms of precision is that the analysis of most cases is simplified.
• Both univariate and multivariate cases need to be considered.
• Either conjugate or improper prior distributions may be placed on the unknown variables.
• An additional set of cases occurs in Bayesian linear regression, where in the basic model the data is assumed to be normally distributed, and normal priors are placed on the regression coefficients. The resulting analysis is similar to the basic cases of independent identically distributed data.

The formulas for the non-linear-regression cases are summarized in the conjugate prior article.

Sum of two quadratics

Scalar form

The following auxiliary formula is useful for simplifying the posterior update equations, which otherwise become fairly tedious.

${\displaystyle a(x-y)^{2}+b(x-z)^{2}=(a+b)\left(x-{\frac {ay+bz}{a+b}}\right)^{2}+{\frac {ab}{a+b}}(y-z)^{2}}$

This equation rewrites the sum of two quadratics in x by expanding the squares, grouping the terms in x, and completing the square. Note the following about the complex constant factors attached to some of the terms:

1. The factor ${\displaystyle {\frac {ay+bz}{a+b}}}$ has the form of a weighted average of y and z.
2. ${\displaystyle {\frac {ab}{a+b}}={\frac {1}{{\frac {1}{a}}+{\frac {1}{b}}}}=(a^{-1}+b^{-1})^{-1}.}$ This shows that this factor can be thought of as resulting from a situation where the reciprocals of quantities a and b add directly, so to combine a and b themselves, it's necessary to reciprocate, add, and reciprocate the result again to get back into the original units. This is exactly the sort of operation performed by the harmonic mean, so it is not surprising that ${\displaystyle {\frac {ab}{a+b}}}$ is one-half the harmonic mean of a and b.

Vector form

A similar formula can be written for the sum of two vector quadratics: If x, y, z are vectors of length k, and A and B are symmetric, invertible matrices of size ${\displaystyle k\times k}$, then

${\displaystyle {\begin{aligned}&(\mathbf {y} -\mathbf {x} )'\mathbf {A} (\mathbf {y} -\mathbf {x} )+(\mathbf {x} -\mathbf {z} )'\mathbf {B} (\mathbf {x} -\mathbf {z} )\\={}&(\mathbf {x} -\mathbf {c} )'(\mathbf {A} +\mathbf {B} )(\mathbf {x} -\mathbf {c} )+(\mathbf {y} -\mathbf {z} )'(\mathbf {A} ^{-1}+\mathbf {B} ^{-1})^{-1}(\mathbf {y} -\mathbf {z} )\end{aligned}}}$

where

${\displaystyle \mathbf {c} =(\mathbf {A} +\mathbf {B} )^{-1}(\mathbf {A} \mathbf {y} +\mathbf {B} \mathbf {z} )}$

Note that the form x′ A x is called a quadratic form and is a scalar:

${\displaystyle \mathbf {x} '\mathbf {A} \mathbf {x} =\sum _{i,j}a_{ij}x_{i}x_{j}}$

In other words, it sums up all possible combinations of products of pairs of elements from x, with a separate coefficient for each. In addition, since ${\displaystyle x_{i}x_{j}=x_{j}x_{i}}$, only the sum ${\displaystyle a_{ij}+a_{ji}}$ matters for any off-diagonal elements of A, and there is no loss of generality in assuming that A is symmetric. Furthermore, if A is symmetric, then the form ${\displaystyle \mathbf {x} '\mathbf {A} \mathbf {y} =\mathbf {y} '\mathbf {A} \mathbf {x} .}$

Sum of differences from the mean

Another useful formula is as follows:

where ${\textstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.}$

With known variance

For a set of i.i.d. normally distributed data points X of size n where each individual point x follows ${\displaystyle x\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$ with known variance σ², the conjugate prior distribution is also normally distributed.

This can be shown more easily by rewriting the variance as the precision, i.e. using τ = 1/σ². Then if ${\displaystyle x\sim {\mathcal {N}}(\mu ,1/\tau )}$ and ${\displaystyle \mu \sim {\mathcal {N}}(\mu _{0},1/\tau _{0}),}$ we proceed as follows.

First, the likelihood function is (using the formula above for the sum of differences from the mean):

${\displaystyle {\begin{aligned}p(\mathbf {X} \mid \mu ,\tau )&=\prod _{i=1}^{n}{\sqrt {\frac {\tau }{2\pi }}}\exp \left(-{\frac {1}{2}}\tau (x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left(-{\frac {1}{2}}\tau \sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right].\end{aligned}}}$

Then, we proceed as follows:

${\displaystyle {\begin{aligned}p(\mu \mid \mathbf {X} )&\propto p(\mathbf {X} \mid \mu )p(\mu )\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]{\sqrt {\frac {\tau _{0}}{2\pi }}}\exp \left(-{\frac {1}{2}}\tau _{0}(\mu -\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(n\tau ({\bar {x}}-\mu )^{2}+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&=\exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}+{\frac {n\tau \tau _{0}}{n\tau +\tau _{0}}}({\bar {x}}-\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}\right)\end{aligned}}}$

In the above derivation, we used the formula above for the sum of two quadratics and eliminated all constant factors not involving μ. The result is the kernel of a normal distribution, with mean ${\displaystyle {\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}}$ and precision ${\displaystyle n\tau +\tau _{0}}$, i.e.

${\displaystyle p(\mu \mid \mathbf {X} )\sim {\mathcal {N}}\left({\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}},{\frac {1}{n\tau +\tau _{0}}}\right)}$

This can be written as a set of Bayesian update equations for the posterior parameters in terms of the prior parameters:

${\displaystyle {\begin{aligned}\tau _{0}'&=\tau _{0}+n\tau \\[5pt]\mu _{0}'&={\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\\[5pt]{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}}$

That is, to combine n data points with total precision of nτ (or equivalently, total variance of n/σ²) and mean of values ${\displaystyle {\bar {x}}}$, derive a new total precision simply by adding the total precision of the data to the prior total precision, and form a new mean through a precision-weighted average, i.e. a weighted average of the data mean and the prior mean, each weighted by the associated total precision. This makes logical sense if the precision is thought of as indicating the certainty of the observations: In the distribution of the posterior mean, each of the input components is weighted by its certainty, and the certainty of this distribution is the sum of the individual certainties. (For the intuition of this, compare the expression "the whole is (or is not) greater than the sum of its parts". In addition, consider that the knowledge of the posterior comes from a combination of the knowledge of the prior and likelihood, so it makes sense that we are more certain of it than of either of its components.)

The above formula reveals why it is more convenient to do Bayesian analysis of conjugate priors for the normal distribution in terms of the precision. The posterior precision is simply the sum of the prior and likelihood precisions, and the posterior mean is computed through a precision-weighted average, as described above. The same formulas can be written in terms of variance by reciprocating all the precisions, yielding the more ugly formulas

${\displaystyle {\begin{aligned}{\sigma _{0}^{2}}'&={\frac {1}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\[5pt]\mu _{0}'&={\frac {{\frac {n{\bar {x}}}{\sigma ^{2}}}+{\frac {\mu _{0}}{\sigma _{0}^{2}}}}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\[5pt]{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}}$

With known mean

For a set of i.i.d. normally distributed data points X of size n where each individual point x follows ${\displaystyle x\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$ with known mean μ, the conjugate prior of the variance has an inverse gamma distribution or a scaled inverse chi-squared distribution. The two are equivalent except for having different parameterizations. Although the inverse gamma is more commonly used, we use the scaled inverse chi-squared for the sake of convenience. The prior for σ² is as follows:

${\displaystyle p(\sigma ^{2}\mid \nu _{0},\sigma _{0}^{2})={\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\nu _{0}/2}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\propto {\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}}$

The likelihood function from above, written in terms of the variance, is:

${\displaystyle {\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right]\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]\end{aligned}}}$

where

${\displaystyle S=\sum _{i=1}^{n}(x_{i}-\mu )^{2}.}$

Then:

${\displaystyle {\begin{aligned}p(\sigma ^{2}\mid \mathbf {X} )&\propto p(\mathbf {X} \mid \sigma ^{2})p(\sigma ^{2})\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]{\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\frac {\nu _{0}}{2}}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\\&\propto \left({\frac {1}{\sigma ^{2}}}\right)^{n/2}{\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\exp \left[-{\frac {S}{2\sigma ^{2}}}+{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]\\&={\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}+n}{2}}}}}\exp \left[-{\frac {\nu _{0}\sigma _{0}^{2}+S}{2\sigma ^{2}}}\right]\end{aligned}}}$

The above is also a scaled inverse chi-squared distribution where

${\displaystyle {\begin{aligned}\nu _{0}'&=\nu _{0}+n\\\nu _{0}'{\sigma _{0}^{2}}'&=\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-\mu )^{2}\end{aligned}}}$

or equivalently

${\displaystyle {\begin{aligned}\nu _{0}'&=\nu _{0}+n\\{\sigma _{0}^{2}}'&={\frac {\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{\nu _{0}+n}}\end{aligned}}}$

Reparameterizing in terms of an inverse gamma distribution, the result is:

${\displaystyle {\begin{aligned}\alpha '&=\alpha +{\frac {n}{2}}\\\beta '&=\beta +{\frac {\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{2}}\end{aligned}}}$

With unknown mean and unknown variance

For a set of i.i.d. normally distributed data points X of size n where each individual point x follows ${\displaystyle x\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$ with unknown mean μ and unknown variance σ², a combined (multivariate) conjugate prior is placed over the mean and variance, consisting of a normal-inverse-gamma distribution. Logically, this originates as follows:

1. From the analysis of the case with unknown mean but known variance, we see that the update equations involve sufficient statistics computed from the data consisting of the mean of the data points and the total variance of the data points, computed in turn from the known variance divided by the number of data points.
2. From the analysis of the case with unknown variance but known mean, we see that the update equations involve sufficient statistics over the data consisting of the number of data points and sum of squared deviations.
3. Keep in mind that the posterior update values serve as the prior distribution when further data is handled. Thus, we should logically think of our priors in terms of the sufficient statistics just described, with the same semantics kept in mind as much as possible.
4. To handle the case where both mean and variance are unknown, we could place independent priors over the mean and variance, with fixed estimates of the average mean, total variance, number of data points used to compute the variance prior, and sum of squared deviations. Note however that in reality, the total variance of the mean depends on the unknown variance, and the sum of squared deviations that goes into the variance prior (appears to) depend on the unknown mean. In practice, the latter dependence is relatively unimportant: Shifting the actual mean shifts the generated points by an equal amount, and on average the squared deviations will remain the same. This is not the case, however, with the total variance of the mean: As the unknown variance increases, the total variance of the mean will increase proportionately, and we would like to capture this dependence.
5. This suggests that we create a conditional prior of the mean on the unknown variance, with a hyperparameter specifying the mean of the pseudo-observations associated with the prior, and another parameter specifying the number of pseudo-observations. This number serves as a scaling parameter on the variance, making it possible to control the overall variance of the mean relative to the actual variance parameter. The prior for the variance also has two hyperparameters, one specifying the sum of squared deviations of the pseudo-observations associated with the prior, and another specifying once again the number of pseudo-observations. Note that each of the priors has a hyperparameter specifying the number of pseudo-observations, and in each case this controls the relative variance of that prior. These are given as two separate hyperparameters so that the variance (aka the confidence) of the two priors can be controlled separately.
6. This leads immediately to the normal-inverse-gamma distribution, which is the product of the two distributions just defined, with conjugate priors used (an inverse gamma distribution over the variance, and a normal distribution over the mean, conditional on the variance) and with the same four parameters just defined.

The priors are normally defined as follows:

${\displaystyle {\begin{aligned}p(\mu \mid \sigma ^{2};\mu _{0},n_{0})&\sim {\mathcal {N}}(\mu _{0},\sigma ^{2}/n_{0})\\p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})&\sim I\chi ^{2}(\nu _{0},\sigma _{0}^{2})=IG(\nu _{0}/2,\nu _{0}\sigma _{0}^{2}/2)\end{aligned}}}$

The update equations can be derived, and look as follows:

${\displaystyle {\begin{aligned}{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\\\mu _{0}'&={\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\\n_{0}'&=n_{0}+n\\\nu _{0}'&=\nu _{0}+n\\\nu _{0}'{\sigma _{0}^{2}}'&=\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\end{aligned}}}$

The respective numbers of pseudo-observations add the number of actual observations to them. The new mean hyperparameter is once again a weighted average, this time weighted by the relative numbers of observations. Finally, the update for ${\displaystyle \nu _{0}'{\sigma _{0}^{2}}'}$ is similar to the case with known mean, but in this case the sum of squared deviations is taken with respect to the observed data mean rather than the true mean, and as a result a new "interaction term" needs to be added to take care of the additional error source stemming from the deviation between prior and data mean.

Occurrence and applications

The occurrence of normal distribution in practical problems can be loosely classified into four categories:

1. Exactly normal distributions;
2. Approximately normal laws, for example when such approximation is justified by the central limit theorem; and
3. Distributions modeled as normal – the normal distribution being the distribution with maximum entropy for a given mean and variance.
4. Regression problems – the normal distribution being found after systematic effects have been modeled sufficiently well.

Exact normality

Certain quantities in physics are distributed normally, as was first demonstrated by James Clerk Maxwell. Examples of such quantities are:

• Probability density function of a ground state in a quantum harmonic oscillator.
• The position of a particle that experiences diffusion. If initially the particle is located at a specific point (that is its probability distribution is the Dirac delta function), then after time t its location is described by a normal distribution with variance t, which satisfies the diffusion equation ${\displaystyle {\frac {\partial }{\partial t}}f(x,t)={\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}f(x,t)}$. If the initial location is given by a certain density function ${\displaystyle g(x)}$, then the density at time t is the convolution of g and the normal PDF.

Approximate normality

Approximately normal distributions occur in many situations, as explained by the central limit theorem. When the outcome is produced by many small effects acting additively and independently, its distribution will be close to normal. The normal approximation will not be valid if the effects act multiplicatively (instead of additively), or if there is a single external influence that has a considerably larger magnitude than the rest of the effects.

• In counting problems, where the central limit theorem includes a discrete-to-continuum approximation and where infinitely divisible and decomposable distributions are involved, such as
  • Binomial random variables, associated with binary response variables;
  • Poisson random variables, associated with rare events;
• Thermal radiation has a Bose–Einstein distribution on very short time scales, and a normal distribution on longer timescales due to the central limit theorem.

Assumed normality

I can only recognize the occurrence of the normal curve – the Laplacian curve of errors – as a very abnormal phenomenon. It is roughly approximated to in certain distributions; for this reason, and on account for its beautiful simplicity, we may, perhaps, use it as a first approximation, particularly in theoretical investigations.

— Pearson (1901)

There are statistical methods to empirically test that assumption; see the above Normality tests section.

• In biology, the logarithm of various variables tend to have a normal distribution, that is, they tend to have a log-normal distribution (after separation on male/female subpopulations), with examples including:
  • Measures of size of living tissue (length, height, skin area, weight);^[53]
  • The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth; presumably the thickness of tree bark also falls under this category;
  • Certain physiological measurements, such as blood pressure of adult humans.
• In finance, in particular the Black–Scholes model, changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal (these variables behave like compound interest, not like simple interest, and so are multiplicative). Some mathematicians such as Benoit Mandelbrot have argued that log-Levy distributions, which possesses heavy tails would be a more appropriate model, in particular for the analysis for stock market crashes. The use of the assumption of normal distribution occurring in financial models has also been criticized by Nassim Nicholas Taleb in his works.
• Measurement errors in physical experiments are often modeled by a normal distribution. This use of a normal distribution does not imply that one is assuming the measurement errors are normally distributed, rather using the normal distribution produces the most conservative predictions possible given only knowledge about the mean and variance of the errors.^[54]
• In standardized testing, results can be made to have a normal distribution by either selecting the number and difficulty of questions (as in the IQ test) or transforming the raw test scores into "output" scores by fitting them to the normal distribution. For example, the SAT's traditional range of 200–800 is based on a normal distribution with a mean of 500 and a standard deviation of 100.

• Many scores are derived from the normal distribution, including percentile ranks ("percentiles" or "quantiles"), normal curve equivalents, stanines, z-scores, and T-scores. Additionally, some behavioral statistical procedures assume that scores are normally distributed; for example, t-tests and ANOVAs. Bell curve grading assigns relative grades based on a normal distribution of scores.
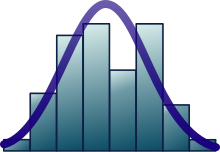
• In hydrology the distribution of long duration river discharge or rainfall, e.g. monthly and yearly totals, is often thought to be practically normal according to the central limit theorem.^[55] The blue picture, made with CumFreq, illustrates an example of fitting the normal distribution to ranked October rainfalls showing the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.

Methodological problems and peer review

John Ioannidis argues that using normally distributed standard deviations as standards for validating research findings leave falsifiable predictions about phenomena that are not normally distributed untested. This includes, for example, phenomena that only appear when all necessary conditions are present and one cannot be a substitute for another in an addition-like way and phenomena that are not randomly distributed. Ioannidis argues that standard deviation-centered validation gives a false appearance of validity to hypotheses and theories where some but not all falsifiable predictions are normally distributed since the portion of falsifiable predictions that there is evidence against may and in some cases are in the non-normally distributed parts of the range of faslsifiable predictions, as well as baselessly dismissing hypotheses for which none of the falsifiable predictions are normally distributed as if were they unfalsifiable when in fact they do make falsifiable predictions. It is argued by Ioannidis that many cases of mutually exclusive theories being accepted as "validated" by research journals are caused by failure of the journals to take in empirical falsifications of non-normally distributed predictions, and not because mutually exclusive theories are true, which they cannot be, although two mutually exclusive theories can both be wrong and a third one correct.^[56]

Computational methods

Generating values from normal distribution

In computer simulations, especially in applications of the Monte-Carlo method, it is often desirable to generate values that are normally distributed. The algorithms listed below all generate the standard normal deviates, since a N(μ, σ²) can be generated as X = μ + σZ, where Z is standard normal. All these algorithms rely on the availability of a random number generator U capable of producing uniform random variates.

• The most straightforward method is based on the probability integral transform property: if U is distributed uniformly on (0,1), then Φ⁻¹(U) will have the standard normal distribution. The drawback of this method is that it relies on calculation of the probit function Φ⁻¹, which cannot be done analytically. Some approximate methods are described in Hart (1968) and in the erf article. Wichura gives a fast algorithm for computing this function to 16 decimal places,^[57] which is used by R to compute random variates of the normal distribution.
• An easy-to-program approximate approach that relies on the central limit theorem is as follows: generate 12 uniform U(0,1) deviates, add them all up, and subtract 6 – the resulting random variable will have approximately standard normal distribution. In truth, the distribution will be Irwin–Hall, which is a 12-section eleventh-order polynomial approximation to the normal distribution. This random deviate will have a limited range of (−6, 6).^[58] Note that in a true normal distribution, only 0.00034% of all samples will fall outside ±6σ.
• The Box–Muller method uses two independent random numbers U and V distributed uniformly on (0,1). Then the two random variables X and Y
  $${\displaystyle X={\sqrt {-2\ln U}}\,\cos(2\pi V),\qquad Y={\sqrt {-2\ln U}}\,\sin(2\pi V).}$$

  
  will both have the standard normal distribution, and will be independent. This formulation arises because for a bivariate normal random vector (X, Y) the squared norm X² + Y² will have the chi-squared distribution with two degrees of freedom, which is an easily generated exponential random variable corresponding to the quantity −2ln(U) in these equations; and the angle is distributed uniformly around the circle, chosen by the random variable V.
• The Marsaglia polar method is a modification of the Box–Muller method which does not require computation of the sine and cosine functions. In this method, U and V are drawn from the uniform (−1,1) distribution, and then S = U² + V² is computed. If S is greater or equal to 1, then the method starts over, otherwise the two quantities
  $${\displaystyle X=U{\sqrt {\frac {-2\ln S}{S}}},\qquad Y=V{\sqrt {\frac {-2\ln S}{S}}}}$$

  
  are returned. Again, X and Y are independent, standard normal random variables.
• The Ratio method^[59] is a rejection method. The algorithm proceeds as follows:
  • Generate two independent uniform deviates U and V;
  • Compute X = √8/e (V − 0.5)/U;
  • Optional: if X² ≤ 5 − 4e^1/4U then accept X and terminate algorithm;
  • Optional: if X² ≥ 4e^−1.35/U + 1.4 then reject X and start over from step 1;
  • If X² ≤ −4 lnU then accept X, otherwise start over the algorithm.

  The two optional steps allow the evaluation of the logarithm in the last step to be avoided in most cases. These steps can be greatly improved^[60] so that the logarithm is rarely evaluated.

• The ziggurat algorithm^[61] is faster than the Box–Muller transform and still exact. In about 97% of all cases it uses only two random numbers, one random integer and one random uniform, one multiplication and an if-test. Only in 3% of the cases, where the combination of those two falls outside the "core of the ziggurat" (a kind of rejection sampling using logarithms), do exponentials and more uniform random numbers have to be employed.
• Integer arithmetic can be used to sample from the standard normal distribution.^[62] This method is exact in the sense that it satisfies the conditions of ideal approximation;^[63] i.e., it is equivalent to sampling a real number from the standard normal distribution and rounding this to the nearest representable floating point number.
• There is also some investigation^[64] into the connection between the fast Hadamard transform and the normal distribution, since the transform employs just addition and subtraction and by the central limit theorem random numbers from almost any distribution will be transformed into the normal distribution. In this regard a series of Hadamard transforms can be combined with random permutations to turn arbitrary data sets into a normally distributed data.

Numerical approximations for the normal CDF and normal quantile function

The standard normal CDF is widely used in scientific and statistical computing.

The values Φ(x) may be approximated very accurately by a variety of methods, such as numerical integration, Taylor series, asymptotic series and continued fractions. Different approximations are used depending on the desired level of accuracy.

• Zelen & Severo (1964) give the approximation for Φ(x) for x > 0 with the absolute error ε(x) < 7.5·10⁻⁸ (algorithm 26.2.17):
  $${\displaystyle \Phi (x)=1-\varphi (x)\left(b_{1}t+b_{2}t^{2}+b_{3}t^{3}+b_{4}t^{4}+b_{5}t^{5}\right)+\varepsilon (x),\qquad t={\frac {1}{1+b_{0}x}},}$$

  
  where ϕ(x) is the standard normal PDF, and b₀ = 0.2316419, b₁ = 0.319381530, b₂ = −0.356563782, b₃ = 1.781477937, b₄ = −1.821255978, b₅ = 1.330274429.
• Hart (1968) lists some dozens of approximations – by means of rational functions, with or without exponentials – for the erfc() function. His algorithms vary in the degree of complexity and the resulting precision, with maximum absolute precision of 24 digits. An algorithm by West (2009) combines Hart's algorithm 5666 with a continued fraction approximation in the tail to provide a fast computation algorithm with a 16-digit precision.
• Cody (1969) after recalling Hart68 solution is not suited for erf, gives a solution for both erf and erfc, with maximal relative error bound, via Rational Chebyshev Approximation.
• Marsaglia (2004) suggested a simple algorithm^{[note 1]} based on the Taylor series expansion
  $${\displaystyle \Phi (x)={\frac {1}{2}}+\varphi (x)\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+{\frac {x^{7}}{3\cdot 5\cdot 7}}+{\frac {x^{9}}{3\cdot 5\cdot 7\cdot 9}}+\cdots \right)}$$

  
  for calculating Φ(x) with arbitrary precision. The drawback of this algorithm is comparatively slow calculation time (for example it takes over 300 iterations to calculate the function with 16 digits of precision when x = 10).
• The GNU Scientific Library calculates values of the standard normal CDF using Hart's algorithms and approximations with Chebyshev polynomials.

Shore (1982) introduced simple approximations that may be incorporated in stochastic optimization models of engineering and operations research, like reliability engineering and inventory analysis. Denoting p = Φ(z), the simplest approximation for the quantile function is:

This approximation delivers for z a maximum absolute error of 0.026 (for 0.5 ≤ p ≤ 0.9999, corresponding to 0 ≤ z ≤ 3.719). For p < 1/2 replace p by 1 − p and change sign. Another approximation, somewhat less accurate, is the single-parameter approximation:

The latter had served to derive a simple approximation for the loss integral of the normal distribution, defined by

This approximation is particularly accurate for the right far-tail (maximum error of 10⁻³ for z≥1.4). Highly accurate approximations for the CDF, based on Response Modeling Methodology (RMM, Shore, 2011, 2012), are shown in Shore (2005).

Some more approximations can be found at: Error function#Approximation with elementary functions. In particular, small relative error on the whole domain for the CDF ${\displaystyle \Phi }$ and the quantile function ${\displaystyle \Phi ^{-1}}$ as well, is achieved via an explicitly invertible formula by Sergei Winitzki in 2008.

History

Development

Some authors^[65][66] attribute the credit for the discovery of the normal distribution to de Moivre, who in 1738^{[note 2]} published in the second edition of his "The Doctrine of Chances" the study of the coefficients in the binomial expansion of (a + b)ⁿ. De Moivre proved that the middle term in this expansion has the approximate magnitude of ${\textstyle 2^{n}/{\sqrt {2\pi n}}}$, and that "If m or 1/2n be a Quantity infinitely great, then the Logarithm of the Ratio, which a Term distant from the middle by the Interval ℓ, has to the middle Term, is ${\textstyle -{\frac {2\ell \ell }{n}}}$."^[67] Although this theorem can be interpreted as the first obscure expression for the normal probability law, Stigler points out that de Moivre himself did not interpret his results as anything more than the approximate rule for the binomial coefficients, and in particular de Moivre lacked the concept of the probability density function.^[68]

In 1823 Gauss published his monograph "Theoria combinationis observationum erroribus minimis obnoxiae" where among other things he introduces several important statistical concepts, such as the method of least squares, the method of maximum likelihood, and the normal distribution. Gauss used M, M′, M′′, ... to denote the measurements of some unknown quantity V, and sought the "most probable" estimator of that quantity: the one that maximizes the probability φ(M − V) · φ(M′ − V) · φ(M′′ − V) · ... of obtaining the observed experimental results. In his notation φΔ is the probability density function of the measurement errors of magnitude Δ. Not knowing what the function φ is, Gauss requires that his method should reduce to the well-known answer: the arithmetic mean of the measured values.^{[note 3]} Starting from these principles, Gauss demonstrates that the only law that rationalizes the choice of arithmetic mean as an estimator of the location parameter, is the normal law of errors:^[69]

where h is "the measure of the precision of the observations". Using this normal law as a generic model for errors in the experiments, Gauss formulates what is now known as the non-linearweighted least squares method.^[70]

Although Gauss was the first to suggest the normal distribution law, Laplace made significant contributions.^{[note 4]} It was Laplace who first posed the problem of aggregating several observations in 1774,^[71] although his own solution led to the Laplacian distribution. It was Laplace who first calculated the value of the integral ∫ e^−t2 dt = √π in 1782, providing the normalization constant for the normal distribution.^[72] Finally, it was Laplace who in 1810 proved and presented to the Academy the fundamental central limit theorem, which emphasized the theoretical importance of the normal distribution.^[73]

It is of interest to note that in 1809 an Irish-American mathematician Robert Adrain published two insightful but flawed derivations of the normal probability law, simultaneously and independently from Gauss.^[74] His works remained largely unnoticed by the scientific community, until in 1871 they were exhumed by Abbe.^[75]

In the middle of the 19th century Maxwell demonstrated that the normal distribution is not just a convenient mathematical tool, but may also occur in natural phenomena:^[76] "The number of particles whose velocity, resolved in a certain direction, lies between x and x + dx is

Naming

Since its introduction, the normal distribution has been known by many different names: the law of error, the law of facility of errors, Laplace's second law, Gaussian law, etc. Gauss himself apparently coined the term with reference to the "normal equations" involved in its applications, with normal having its technical meaning of orthogonal rather than "usual".^[77] However, by the end of the 19th century some authors^{[note 5]} had started using the name normal distribution, where the word "normal" was used as an adjective – the term now being seen as a reflection of the fact that this distribution was seen as typical, common – and thus "normal". Peirce (one of those authors) once defined "normal" thus: "...the 'normal' is not the average (or any other kind of mean) of what actually occurs, but of what would, in the long run, occur under certain circumstances."^[78] Around the turn of the 20th century Pearson popularized the term normal as a designation for this distribution.^[79]

Many years ago I called the Laplace–Gaussian curve the normal curve, which name, while it avoids an international question of priority, has the disadvantage of leading people to believe that all other distributions of frequency are in one sense or another 'abnormal'.

— Pearson (1920)

Also, it was Pearson who first wrote the distribution in terms of the standard deviation σ as in modern notation. Soon after this, in year 1915, Fisher added the location parameter to the formula for normal distribution, expressing it in the way it is written nowadays:

The term "standard normal", which denotes the normal distribution with zero mean and unit variance came into general use around the 1950s, appearing in the popular textbooks by P. G. Hoel (1947) "Introduction to mathematical statistics" and A. M. Mood (1950) "Introduction to the theory of statistics".^[80]

See also

• Bates distribution – similar to the Irwin–Hall distribution, but rescaled back into the 0 to 1 range
• Behrens–Fisher problem – the long-standing problem of testing whether two normal samples with different variances have same means;
• Bhattacharyya distance – method used to separate mixtures of normal distributions
• Erdős–Kac theorem – on the occurrence of the normal distribution in number theory
• Full width at half maximum
• Gaussian blur – convolution, which uses the normal distribution as a kernel
• Modified half-normal distribution
• Normally distributed and uncorrelated does not imply independent
• Ratio normal distribution
• Reciprocal normal distribution
• Standard normal table
• Stein's lemma
• Sub-Gaussian distribution
• Sum of normally distributed random variables
• Tweedie distribution – The normal distribution is a member of the family of Tweedie exponential dispersion models.
• Wrapped normal distribution – the Normal distribution applied to a circular domain
• Z-test – using the normal distribution

Notes

References

Citations

Sources

External links

• "Normal distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Normal distribution calculator, More powerful calculator